Ориентация прямой, плоскости в пространстве
СОДЕРЖАНИЕ
Введение
. Понятие ориентации
. Правые и левые ориентации
. Произведения ориентаций
. Стороны прямой на плоскости и
плоскости в пространстве
. Деформации базисов и ориентации
. Заключение
Список литературы
ВВЕДЕНИЕ
Ориентация - это выбор одного класса систем
координат, связанных между собой «положительно» в некотором определенном
смысле. Каждая система задает ориентацию, определяет класс, к которому она
принадлежит. Все координатные системы делятся на два класса- правые (также
используется термины положительные или стандартные) и левые.
Цель работы:
) Ввести понятие «ориентации» вполне
строгим образом.
) Дать понятие «одноименным» и
«разноименным» ориентациям.
) Научится определять ориентацию прямой,
плоскости и пространства.
) Научится определять левую и правую
ориентацию.
.
Определение ориентации прямой, плоскости
и пространства
На прямой α мы
можем перемещаться в одном из двух противоположных направлений. Ориентировать
прямую - значит выбрать на ней одно из этих двух направлений (Рис.1). Выбор
одного из этих направлений называется ориентацией прямой, а прямую с заданной
на ней ориентацией мы будем называть ориентированной прямой или осью.
(Бескин Н. М.. Деление отрезка в данном
отношении. М.: Наука, 1973, с.5)
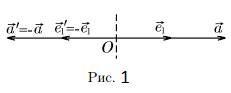
Чтобы ввести понятие ориентации вполне строгим
образом, нам понадобится понятие "упорядоченного множества".
Пусть Х - произвольное множество (с элементами
А, В, С …). Заданное на Х отношение (обозначаемое символ <) называется
отношением порядка, когда оно обладает следующими свойствами:
) Если А <B,
то A≠B
(свойство антирефлексивности).
) Если A<B
и B<C,
то A<C
(свойство транзитивности).
) ЕслиA
≠
B, то либо A<B,
либо B<A(свойство
полноты).
Отношение порядка называется отношением
предшествования, когда выполнено следующее дополнительное свойство:
) Если А<B,
то существует такие элементы C1
,C2и
D, что
1 <A<D<B<C2
По любому отношению порядка « < » мы можем
построить новое отношение порядка « <' » (называемое отношением, противоположных
данному), считая, по определению, что
А<'В тогда и только тогда, когда
В<А.
Мы принимаем в качестве аксиомы следующее
утверждение.
У. На любой прямой существует два взаимно
противоположных отношения предшествования.
Наглядно, каждое из этих отношений определяется
заданием на прямой некоторого направления движения. Именно, А< B
в одном из этих отношений, если точка В получается из точки A
движением в данном направлении.
Определение 1.1.Каждое из предусмотренных
аксиомой У отношений предшествования называется ориентацией прямой. Прямая с
заданной на ней ориентацией называется ориентированной прямой или осью.
Определение 1.2. Невырожденные направленные
отрезки АВ и А1В1прямой α
называются одноименными, если А<В в некоторой ориентации тогда и только
тогда, когда А1<В1в той же ориентации.
Отношение одноименности рефлексивно и
симметрично. И из свойства 2) отношений порядка вытекает, что оно транзитивно.
Таким образом отношение одноименности направленных отрезков прямой является
отношением эквивалентности.
Ориентации на прямой можно отождествить с
классами одноименных направленных отрезков.
Определение 1.3. Отличные от нуля векторы АВ и А1В1
прямой α называется
одноименными, если одноименны направленные отрезки
АВ и А1В1,
т.е. если А1< В1в
ориентации, в которой А<В.
Отношение одноименности отличных от нуля
векторов прямой является отношением эквивалентности.
Определение 1.4. Каждый отличный от нуля вектор
прямой α
называется
базисом на этой прямой (или, точнее базисом соответствующего множества Vecta(1)).
Ориентациями прямой являются классы одноименных
базисов на этой прямой.
Базис АВ называется положительно ориентированным
(по отношению к данной ориентации прямой α), если
он представляет эту ориентацию, т.е. если А< B в данной ориентации. В
противном случае базис AB
называется отрицательно ориентированным. (Постников М.М. Аналитическая
геометрия, М.1986 г., с.63)
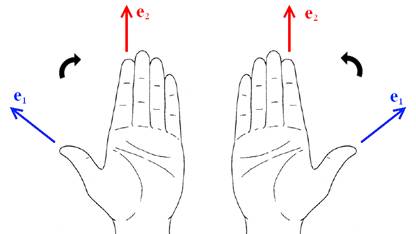
Базис на плоскости называется
право ориентированным, если кратчайший поворот от первого вектора базиса ко
второму происходит против часовой стрелки, или лево ориентированным, если в
обратную сторону.
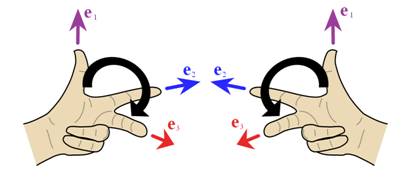
Базис в пространстве называется
право ориентированным, если концы базисных векторов от первого до третьего
видны против часовой стрелки, или лево ориентированным, если в обратную
сторону. Эти названия связаны со строением рук.
Ориентацией базиса называется
его свойство быть правым или левым. Ориентация плоскости или пространства -
выбор какие базисы (правые или левые) считать положительными, а какие
отрицательными. (Ссылка https://ru.wikiversity.org/wiki/Ориентация)
Первое определение ориентации (выбор отношения
предшествия) на плоскость и пространство непосредственно не переносится. Иначе
обстоит дело с двумя другими определениями.
Определение 2.1. Два базиса а1, ..., аn
и b1, ..., bn
на плоскости (n = 2) или в
пространстве (n = 3) называются
одноименными, если определитель |С| матрицы перехода Сот первого базиса ко
второму положителен:
|С| >0.
Если |С|<0, то базисы называются
разноименными.
Отношение одноименности базисов является
отношением эквивалентности.
Определение 2.2. Классы одноименных базисов
называются ориентациями (соответственно - прямой, плоскости и пространства).
На прямой, на плоскости и в пространстве существует
точно две различные ориентации: базисы, принадлежащие одной и той же
ориентации, одноименны, а базисы, принадлежащие различным ориентациям,
разноименны.
Определение 2.3.Прямая, плоскость или
пространство, для которой (ого) выбрана некоторая ориентация, называется
ориентированной (ым). Для каждой ориентации O
другая возможная ориентация обозначается символом -O
и называется противоположной ориентацией. О базисе, принадлежащем некоторой
ориентации, говорят, что он определяет эту ориентацию.
Базис ориентированной (ого) прямой, плоскости
или пространства, определяющий данную ориентацию, называется положительно
ориентированным (по отношению к данной ориентации), а базис, определяющий
противоположную ориентацию, называется отрицательно ориентированным.
Базисы а1,...,
аn и b1, ..., bn тогда и только тогда одноименны, когда построенные для
них определители а
и
а
и  b
имеют один и тот же знак.
b
имеют один и тот же знак.
Определение 2.4. Упорядоченная тройка (А, В, С)
точек плоскости (или пространства) называется неколлинеарной тройкой, если
точки
А, В, Сне принадлежат одной прямой. Аналогично,
упорядоченная четверка (А, В, С, D)
точек пространства называется некомпланарной четверкой, если точки А, В, С, Dне
принадлежат одной плоскости. Такие тройки и четверки называются также тройками
и четверками точек общего положения.
Замечание 1. Введя, по аналогии, понятие пары
(А, В) точек общего положения как упорядоченной пары, состоящей из различных
точек Аи В, мы немедленно получим, что это понятие в точности совпадает с
понятием невырожденного направленного отрезка. Таким образом, понятия
неколлинеарной тройки и некомпланарной четверки можно рассматривать как
непосредственные обобщения на случай плоскости и пространства понятия
невырожденного направленного отрезка.
Для любой неколлинеарной тройки (А, В, С) точек
плоскости векторы АВ и АС неколлинеарные (т. е. линейно независимы) и потому
образуют базис плоскости. Аналогично, для любой некомпланарной, четверки (А, В,
С, D) точек
пространства векторы АВ, AC,
AD образуют базис
пространства.
Определение 2.5. Две неколлинеарные тройки (А,
В, С) и (А', В', С') точек плоскости (две некомпланарные четверки (А, В, С, D)
и (А', В', С', D') точек
пространства) называются одноименными, если соответствующие базисы АВ, АС и
А'В', А'С' (базисы АВ, AC,
AD и А'В', А'С', A'D')
одноименны.
Ориентации плоскости (пространства) можно
отождествить с классами одноименных неколлинеарных троек (некомпланарных
четверок) точек этой плоскости (пространства).
Определение 2.6.Упорядоченные тройки (А, В, С) и
(А’, В', С') точек окружности 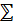 (состоящие каждая из попарно
различных точек) называются одноименными, если базисы АВ, АС и А'В', А'С' плоскости, в которой расположена
окружность 2, одноименны.
(состоящие каждая из попарно
различных точек) называются одноименными, если базисы АВ, АС и А'В', А'С' плоскости, в которой расположена
окружность 2, одноименны.
Класс одноименных троек точек окружности
называется ее ориентацией, а окружность, для которой выбрана некоторая
ориентация, называется ориентированной. Сравнив это определение с определением
2.5 одноименности неколлинеарных точек плоскости, мы немедленно заметим, что
они, по существу, совпадают.
Это означает, что между ориентациями плоскости и
ориентациями расположенной в этой плоскости окружности существует естественное
биективное соответствие. Иначе говоря, на ориентированной плоскости каждая
окружность автоматически ориентирована, и, обратно, задание на плоскости
ориентированной окружности однозначно определяет некоторую ориентацию
плоскости.
Для определения ориентации на плоскости
соответствует представлению «по часовой стрелке - против часовой стрелки», а в
пространстве мы пользуемся правилом Буравчика (правило винта), или правило правой
руки- варианты мнемонического правила для определения направления векторного
произведения и тесно связанного с этим выбора правого базиса в трехмерном
пространстве, соглашения о положительной ориентации базиса в нём, и
соответственно - знака любого аксиального вектора, определяемого через
ориентацию базиса.
Если посмотреть на правую руку со стороны ладони,
то большой и указательный пальцы будут образовывать базис, ориентированный
«против часовой стрелки». На этом основании ориентация плоскости «против
часовой стрелки» обычно называется правой ориентацией, а противоположная ее
ориентация - левой.
Аналогично, в пространстве правой ориентацией
называется ориентация, определенная «базисом», состоящим из большого,
указательного и среднего пальцев правой руки, а противоположная ориентация
называется левой. Здесь, к сожалению, нет общепринятого соглашения, какую ориентацию
считать «положительной». Большинство авторов (и я в том числе) считаю
«положительной» правую ориентацию. Однако во многих (особенно старых) учебниках
за положительную ориентацию принимается левая ориентация.
Заметим, что термин «правая» и «левая» по
отношению к ориентациям пространства имеют уже инвариантный смысл, поскольку
«посмотреть на пространство с другой стороны» мы не можем. Тем не менее,
определить их внутренним математическим способом нельзя.
3. Произведения
ориентаций
Пусть b1 и b2- две
ориентированные прямые на плоскости. Предполагая, что эти прямые не
параллельны, выберем на каждой из них положительно ориентированный базис. Пусть
это будет вектор b1 на прямой b1 и
вектор b2 на прямой b2. Так
как векторы b1 и b2 по условию не коллинеарны, они
составляют некоторый базис на плоскости. Оказывается, что ориентация плоскости,
определенная базисом b,
b 2,
не зависит от выбора векторов bl,
b2 и
определяется исключительно ориентациями прямых b1
и b2(взятых
в данном порядке).
Действительно, пусть b'1 и b'2 - другие положительно ориентированные
базисы прямых а1 и а2.
Тогда b'1 = kl
bl
и b'2
= k2
b2,
где k1>
0 и k2>
0. Поэтому матрица перехода от базиса b1
b2к базису b'1 и b'2 имеет вид

и ее определитель k1k2
положителен.
Следовательно, базис b'1,b'2 определяет ту же ориентацию плоскости, что
и базис b1
b2.
Таким образом, для задания ориентации плоскости
достаточно задать ориентации двух не параллельных прямых этой плоскости.
(В. Н. Задорожный, Высшая математика для
технических университетов. Аналитическая геометрия с.45)
Определение 1. Построенная ориентация плоскости
называется произведением данных ориентаций прямых b1 и b2
и обозначается символом o1o2, где o1- ориентация
прямой b1, а o2 -
ориентация прямой b2
Очевидно, что
2o1≠-o1o2
и
(-o1)o2=o1(-o2)=-o1o2
При перестановке прямых b1
и b2
или при смене ориентации одной из них результирующая ориентация плоскости
переходит в противоположную.
Отсюда, в частности, вытекает, что для любой
ориентации о плоскости и любой ориентации о2 прямой b2существует
такая ориентация o1
прямой b1,
что o=o1o2.
Действительно, выберем произвольно некоторую
ориентацию o'1
прямой а1 и построим
ориентацию о'1о2.Если
окажется, что o = o'1o2,
то все в порядке: ol=o'1. Если
же о1о2≠о,
то обязательно о'1 о2≠-о и потому о 1=-о'1.
Пусть теперь b и П - ориентированные
прямая и плоскость в пространстве (с ориентациями оb
и oп соответственно).
Предполагая прямую a
и плоскость П не параллельными, рассмотрим ориентацию пространства,
определенную базисом b1, b2, bз, где b1- некоторый положительно
ориентированный базис прямой b, а b2, b3 - некоторый
положительно ориентированный базис плоскости
П.
Если b'1=klb1- другой положительно ориентированный
базис прямой b (так
что k1>0), а b'2 = k2b2+ k'2b3, b'3 =k'3a2+ k3a3- другой
положительно ориентированный базис плоскости П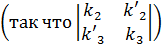 , то базис b1, b2, b3 пространства
связан с базисом b1 b2, b3 матрицей перехода
, то базис b1, b2, b3 пространства
связан с базисом b1 b2, b3 матрицей перехода
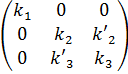
определитель, которой равен k1 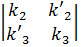 и
потому положителен.
и
потому положителен.
Следовательно, ориентация пространства,
определенная базисом b1, b2, b3, не
зависит от выбора базисов b1и
b2, b3и
определяется исключительно данными ориентациями оb
и оп прямой b
и плоскости П.
Таким образом, для задания ориентации
пространства достаточно задать ориентации произвольной прямой и произвольной не
параллельной ей плоскости.
Определение 2. Построенная ориентация пространства
называется произведением ориентаций оb
и oп и обозначается
символом oboп.
Аналогично определяется ориентация опоb (задаваемая базисом b2, b3, b1). Впрочем, ясно, что она совпадает с
ориентацией оbоп:
Оп Оb
= Оb
Оп.
Далее, очевидно, что
(-Ob)Oп
=Ob(-Oп)=-
Оb
Оп
откуда, как и выше, вытекает, что для любой
ориентации o пространства и
любой ориентации оb прямой b (любой
ориентации оп плоскости П)
существует такая ориентация oп
плоскости П (ориентация оb
прямой
а), что o
= oboп
Аналогичным образом определяется произведение o1o2o3
ориентаций трех прямых, b1
,b2
,b3
обладающих тем свойством, что параллельные им прямые, проходящие через одну
точку, не лежат в одной плоскости (такие прямые называются прямыми общего положения).Впрочем, это
произведение сводится к уже определенным произведениям:
1o2o3=
o1 (o2o3).
Таким образом, для задания ориентации
пространства достаточно задать ориентации трех прямых общего положения (взятых
в данном порядке).
Заметим, что при четной перестановке прямых b1
,b2
,b3 ориентация o1o2o3
не меняется, а при нечетной - переходит в противоположную.
4. Стороны прямой на
плоскости и плоскости в пространстве
Как известно, любая прямая а на плоскости разбивает эту плоскость на
две полуплоскости: точки А и В плоскости, не принадлежащие прямой  , тогда и только тогда принадлежат
одной полуплоскости, когда отрезок
, тогда и только тогда принадлежат
одной полуплоскости, когда отрезок 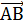 не пересекает прямую
не пересекает прямую  .
.
Аналогично, любая плоскость П в пространстве
разбивает пространство на два полупространства,
причем две точки А, В, не
принадлежащие плоскости, тогда и только и тогда принадлежат одному
полупространству, когда отрезок 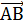 не
пересекает плоскость.
не
пересекает плоскость.
Определение 1.
Говорят, что у прямой  в плоскости (или у
плоскости П в пространстве) выбрана сторона, если
выбрана одна из полуплоскостей, на которые прямая
в плоскости (или у
плоскости П в пространстве) выбрана сторона, если
выбрана одна из полуплоскостей, на которые прямая  разбивает
плоскость (соответственно, если выбрано одно из полупространств, на которые
плоскость П разбивает пространство). Выбранная полуплоскость (полупространство)
или соответствующая сторона называется при этом положительной, а другая полуплоскость (полупространство)
- отрицательной.
разбивает
плоскость (соответственно, если выбрано одно из полупространств, на которые
плоскость П разбивает пространство). Выбранная полуплоскость (полупространство)
или соответствующая сторона называется при этом положительной, а другая полуплоскость (полупространство)
- отрицательной.
Пусть е
- произвольный вектор, не параллельный прямой а
(плоскости П). Выбрав на прямой α
(плоскости П) произвольную точку О,
отложим от нее вектор  ,
т. е. построим направленный отрезок
,
т. е. построим направленный отрезок 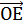 =
е. Если точка Е окажется при этом в положительной полуплоскости (положительном
полупространстве), то мы будем говорить, что вектор
=
е. Если точка Е окажется при этом в положительной полуплоскости (положительном
полупространстве), то мы будем говорить, что вектор 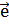 направлен в положительную сторону прямой
α(плоскости П). Это определение
нуждается, конечно, в проверке, корректности, т. е. в доказательстве
независимости полуплоскости (полупространства), содержащей точку Е, от выбора точки О. Другими словами, мы должны доказать, что если для точек О и О' прямой а (плоскости П) и точек Е
и Е', не принадлежащих этой прямой (этой плоскости), имеет место
равенство
направлен в положительную сторону прямой
α(плоскости П). Это определение
нуждается, конечно, в проверке, корректности, т. е. в доказательстве
независимости полуплоскости (полупространства), содержащей точку Е, от выбора точки О. Другими словами, мы должны доказать, что если для точек О и О' прямой а (плоскости П) и точек Е
и Е', не принадлежащих этой прямой (этой плоскости), имеет место
равенство 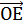 =
= 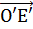 ,
то
точки Е и Е' принадлежат одной
полуплоскости(одному полупространству).
,
то
точки Е и Е' принадлежат одной
полуплоскости(одному полупространству).
Пусть это не так, т. е. пусть отрезок 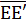 пересекается
с прямой α
(плоскостью П). Ясно, что это возможно тогда и только тогда, когда прямые OO' и
ЕЕ' пересекаются. С другой стороны,
поскольку векторы
пересекается
с прямой α
(плоскостью П). Ясно, что это возможно тогда и только тогда, когда прямые OO' и
ЕЕ' пересекаются. С другой стороны,
поскольку векторы 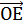 и
и
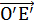 равны, эти прямые должны быть
параллельны (причем совпадать они не могут). Полученное противоречие
доказывает, что точки Еи Е' принадлежат одной и той же полуплоскости
(полупространству).
равны, эти прямые должны быть
параллельны (причем совпадать они не могут). Полученное противоречие
доказывает, что точки Еи Е' принадлежат одной и той же полуплоскости
(полупространству).
Предложение 1. Пусть е и е'- два коллинеарных
вектора, не параллельных прямой α (плоскости
П), и пусть вектор 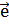 направлен в положительную сторону
прямой α(плоскости П).
Вектор
направлен в положительную сторону
прямой α(плоскости П).
Вектор  тогда и только тогда обладает тем же
свойством, когда отношение е': е
положительно.
тогда и только тогда обладает тем же
свойством, когда отношение е': е
положительно.
Доказательство. Пусть е = 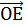 и е'=
и е'= 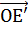 , где О- некоторая точка прямой
, где О- некоторая точка прямой  (плоскости
П). Точки Еи Е' тогда и только тогда лежат в разных полуплоскостях
(полупространствах), когда отрезок ЕЕ' пересекается
с прямой
(плоскости
П). Точки Еи Е' тогда и только тогда лежат в разных полуплоскостях
(полупространствах), когда отрезок ЕЕ' пересекается
с прямой  (плоскостью
П). Но прямая ЕЕ' имеет с прямой α (плоскостью
П) одну-единственную точку пересечения О. Следовательно,
точки Еи Е' тогда и только тогда лежат в разных полуплоскостях
(полупространствах), когда отрезок
(плоскостью
П). Но прямая ЕЕ' имеет с прямой α (плоскостью
П) одну-единственную точку пересечения О. Следовательно,
точки Еи Е' тогда и только тогда лежат в разных полуплоскостях
(полупространствах), когда отрезок 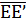 содержит точку О, т. е. когда
содержит точку О, т. е. когда 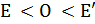 (в ориентации прямой ЕЕ', в которой Е<Е'). Для завершения
доказательства осталось заметить, что Е<О<
Е' тогда и только тогда, когда
отношение е': е отрицательно.
(в ориентации прямой ЕЕ', в которой Е<Е'). Для завершения
доказательства осталось заметить, что Е<О<
Е' тогда и только тогда, когда
отношение е': е отрицательно.
Определение 2.
Мы будем говорить, что ориентированная прямая 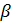 направлена в положительную сторону прямой
направлена в положительную сторону прямой  (плоскости
П), если ее положительно ориентированный вектор
(плоскости
П), если ее положительно ориентированный вектор  направлен
в положительную сторону прямой
направлен
в положительную сторону прямой  (плоскости П).
(плоскости П).
Согласно предложению 1 это определение
корректно.
Если в одной ориентации прямая 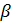 направлена
в положительную сторону прямой
направлена
в положительную сторону прямой  (плоскости П), то
в другой ориентации она будет направлена, очевидно, в отрицательную сторону.
Это означает, что выбор на прямой α (плоскости П)
положительной стороны определяет на каждой прямой
(плоскости П), то
в другой ориентации она будет направлена, очевидно, в отрицательную сторону.
Это означает, что выбор на прямой α (плоскости П)
положительной стороны определяет на каждой прямой 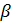 , не параллельной прямой α (плоскости П), некоторую
ориентацию, а именно, ориентацию, в которой эта прямая направлена в положительную
сторону прямой
, не параллельной прямой α (плоскости П), некоторую
ориентацию, а именно, ориентацию, в которой эта прямая направлена в положительную
сторону прямой  (плоскости
П).
(плоскости
П).
Другими словами, ориентацию прямой на плоскости
или в пространстве можно определить как выбор стороны на некоторой прямой
(плоскости), не параллельной данной прямой.
Поскольку ориентации
непараллельных прямых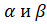 , лежащих в одной плоскости,
определяют некоторую ориентацию плоскости и поскольку, согласно только что
сказанному, ориентация прямой
, лежащих в одной плоскости,
определяют некоторую ориентацию плоскости и поскольку, согласно только что
сказанному, ориентация прямой 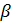 определяется заданием стороны прямой
определяется заданием стороны прямой  , мы получаем, что для задания
ориентации плоскости достаточно задать в этой плоскости ориентированную прямую
и некоторую ее сторону.
, мы получаем, что для задания
ориентации плоскости достаточно задать в этой плоскости ориентированную прямую
и некоторую ее сторону.
Обратно, для задания ориентации прямой
достаточно задать некоторую ориентацию плоскости, содержащей эту прямую, и одну
из сторон этой прямой в плоскости.
Аналогично, для задания ориентации пространства
достаточно задать ориентированную плоскость и некоторую ее сторону, а для
задания ориентации плоскости достаточно задать ориентацию пространства и
некоторую сторону этой плоскости.
Так же можно сказать что, задание ориентации на
одной прямой автоматически определяет ориентацию на любой другой параллельной
прямой.
Другими словами, это означает, что ориентации
параллельных прямых можно сравнивать, т. е. можно говорить о том, совпадают они
или нет.
. Деформации
базисов и ориентации
Рассмотрим произвольную вектор-функцию a(t)числовой
переменной t(пробегающей,
замкнутый интервал [0,1] числовой оси R), т. е. отображение, сопоставляющее
каждому t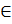 [0, 1] некоторый
вектор a(t)(на прямой, в плоскости или в
пространстве). При заданном базисе e1,...,еп
(где,
как всегда, n - 1, 2 или 3) вектор-функция a(t) однозначно определяется координатами
[0, 1] некоторый
вектор a(t)(на прямой, в плоскости или в
пространстве). При заданном базисе e1,...,еп
(где,
как всегда, n - 1, 2 или 3) вектор-функция a(t) однозначно определяется координатами
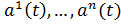 (1)
(1)
вектора a(t)в базисе e1,..., еп, являющимися
обыкновенными числовыми функциями переменной t.Таким
образом, задание вектор-функции a(t) равносильно
(при фиксированном базисе) заданию n
обыкновенных (числовых) функций (1).
Определение 1. Вектор-функция a(t)называется непрерывной, если все
функции (1) непрерывны.
Из формул преобразования координат при замене
базиса (Постников М.М. п. 7 § 3) немедленно вытекает, что это определение
корректно (не зависит от выбора базиса), т. е. что если координаты (1)
вектор-функции a(t)непрерывны в одном базисе, то они
непрерывны и в любом другом базисе.
Определение 2. Два базиса 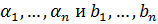 (прямой,
плоскости или пространства) называются деформируемыми друг в друга, если
существуют такие векторные функции a1(t),...,an(t)числового
параметра t
(прямой,
плоскости или пространства) называются деформируемыми друг в друга, если
существуют такие векторные функции a1(t),...,an(t)числового
параметра t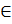 [0,1], что:
[0,1], что:
. Для любого i= 1,…, п вектор  i(0) совпадает с вектором
i(0) совпадает с вектором  i,а вектор
i,а вектор  i(1) - с вектором bi
i(1) - с вектором bi
2. Для любого i=1, ...,п вектор  i(t)непрерывно зависит от t.
i(t)непрерывно зависит от t.
3. Для
любого t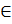 [0,1] векторы
[0,1] векторы  1(t),...,
1(t),..., n(t) линейно независимы,
т. е. составляют базис.
n(t) линейно независимы,
т. е. составляют базис.
В этом случае о векторах  1(t),...,
1(t),..., n(t) говорят, что они
составляют деформацию, связывающую
базис
n(t) говорят, что они
составляют деформацию, связывающую
базис  1,...,
1,..., n с базисом
n с базисом 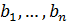 .
.
Предложение 1. Отношение деформируемости базисов
является на множестве всех базисов отношением эквивалентности.
Доказательство. Отношение деформируемости
базисов рефлексивно, симметрично, Таким образом, нам нужно доказать только
транзитивность, т. е. что если существует деформация 1(t),...,
1(t),..., n(t)),связывающая
базис
n(t)),связывающая
базис  1,...,
1,..., n с базисом
n с базисом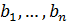 , и деформация
, и деформация 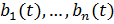 связывающая базис
связывающая базис 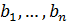 с базисом
с базисом  , то существует и деформация
, то существует и деформация 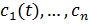 (t), связывающая базис
(t), связывающая базис  1,...,
1,..., n с базисом
n с базисом  .
Но такую деформацию ничего не стоит •построить. Например, ее можно определить
формулами
.
Но такую деформацию ничего не стоит •построить. Например, ее можно определить
формулами

Предложение 2. Два базиса  1,...,
1,..., n и
n и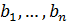 тогда и только тогда одноименны,
когда они деформируемы. друг в друга.
тогда и только тогда одноименны,
когда они деформируемы. друг в друга.
Лемма. Пусть
α1, α 2- произвольный
базис на плоскости. Тогда любой другой базис b1,b2деформируем либо в базис
α1 ,α2, либо в базис  .
.
Аналогично, пусть а1, а2, а3- произвольный базис в пространстве. Тогда
любой другой базис 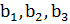 деформируем либо в
базис
деформируем либо в
базис  , либо в базис
, либо в базис 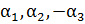 .
.
Замечание 1. Доказательство леммы может вызвать
возражения по крайней мере по двум пунктам. Во-первых, оно использует
«механические» понятия. Во- вторых, хотя вся излагаемая здесь теория по
существу не связана с понятием измерения (носит, как говорят, аффинный
характер), в этом доказательстве используются преобразования (вращения),
определение которых существенно опирается на понятие длины. Оба эти возражения
можно снять, перестроив доказательство на алгебраический лад, для чего
достаточно описать все требуемые преобразования формулами, вообще не упоминая
об их геометрическом смысле.
6. Заключение
плоскость ориентация базис вектор
Наглядный смысл ориентации прямой состоит в
выборе некоторого (из двух возможных) направления движения по этой прямой, а
ориентации плоскости - в выборе направления вращения в этой плоскости (т. е. задания
направления движения по любой окружности в плоскости).
Аналогично, в пространстве ориентации можно
представлять себе как выбор одного из двух возможных типов винтового движения
(«правовинтового» и «левовинтового»).
Формально ориентацию прямой, плоскости или
пространства можно определить тремя равносильными способами:
) либо как класс одноименных базисов-,
2)либо как класс одноименных упорядоченных
систем точек общего положения, состоящих в случае прямой из двух точек, в
случае плоскости - из трех точек и в случае пространства - из четырех точек;
)либо как класс деформируемых друг в друга
базисов.
При этом
) ориентация прямой в плоскости (в
пространстве) однозначно определяется заданием в этой плоскости (в
пространстве) некоторой стороны произвольной прямой (плоскости), не
параллельной данной прямой;
) ориентация плоскости (пространства)
однозначно определяется заданием в плоскости (в пространстве) произвольной
ориентированной прямой (плоскости) вместе с некоторой ее стороной;
) обратно, ориентация прямой в плоскости
(плоскости в пространстве) однозначно определяется заданием стороны этой прямой
(плоскости) и некоторой ориентации плоскости (пространства) ;
) наконец, сторона прямой в плоскости
(плоскости в пространстве) однозначно определяется заданием ориентаций прямой и
плоскости (плоскости и пространства).
Свойства 2), 3) и 4) можно объединить в
следующей формулировке:
Из трех объектов:
а) ориентация прямой в плоскости.(плоскости
в пространстве),
б) ориентация плоскости (пространства),
в) сторона прямой в плоскости(плоскости в
пространстве)
любые два однозначно определяют третий.
Список литературы
1.
Постников М.М. Аналитическая геометрия, М.1986 г., с.63.
.
Бескин Н. М.. Деление отрезка в данном отношении. М.: Наука, 1973, с.5.
3.
Ссылка <https://ru.wikiversity.org/wiki/Ориентация>.
.
Богданова К. Ю.. Учебник физики для 11 класса
<http://kaf-fiz-1586.narod.ru/11bf/content_11.htm>, §2 с.15.
. Ссылка <http://dic.academic.ru/dic.nsf/bse/167513/Ориентация>.
.
В. Н. Задорожный, Высшая математика для технических университетов.
Аналитическая геометрия с.45.
.
Ссылка <https://ru.wikipedia.org/wiki/Ориентация>.