Методы оптимальных решений транспортной задачи
«Методы
оптимальных решений»
1. Транспортная задача
Стройматериалы с 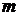 складов
поставляются на
складов
поставляются на 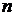 строительных
объектов. Потребности строительных объектов в материалах равны
строительных
объектов. Потребности строительных объектов в материалах равны 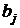 тыс.ед.,
тыс.ед., 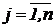 . Запасы
стройматериалов на складах составляют
. Запасы
стройматериалов на складах составляют 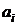 тыс.ед. Затраты на перевозку
1тыс.ед. стройматериалов в ден.ед представлены матрицей затрат
тыс.ед. Затраты на перевозку
1тыс.ед. стройматериалов в ден.ед представлены матрицей затрат 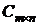 .
Запланировать перевозку с минимальными затратами при заданном дополнительном
условии.
.
Запланировать перевозку с минимальными затратами при заданном дополнительном
условии.
Необходимо:
1) свести исходные данные в таблицу 1.1.
Таблица 1.1
Потребности строительных объектов,
тыс.ед. 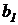
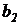
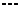
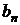
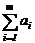
2) составить математическую модель задачи;
3) привести её к стандартной транспортной
задаче с балансом запасов и потребностей;
) построить начальный опорный план задачи
методом минимального элемента;
) решить задачу методом потенциалов;
) проанализировать полученные результаты.
Таблица 2
|
Строительный
объект Склад
|
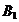 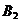 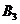 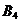 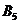 Запасы стройматериалов на складах,
тыс.ед. Запасы стройматериалов на складах,
тыс.ед.
|
|
|
|
|
|
|
 4836730 4836730
|
|
|
|
|
|
|
|
 8465925 8465925
|
|
|
|
|
|
|
|
 3585420 3585420
|
|
|
|
|
|
|
|
 58106815 58106815
|
|
|
|
|
|
|
|
Потребности
строительных объектов, тыс.ед.
|
10
|
20
|
18
|
12
|
25
|
90 85
|
2) составляем
математическую модель задачи:
Ограничения по запасам:
математический задача транспортный
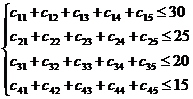
Ограничения по потребностям:
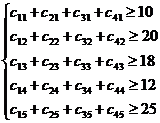
Целевая функция:
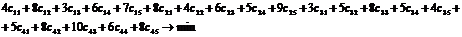
3) Проверим необходимое и
достаточное условие разрешимости задачи:
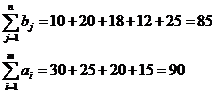
Как видно, суммарная потребность
груза в пунктах назначения меньше запасов груза на складах. Следовательно,
модель исходной задачи является открытой. Чтобы получить закрытую модель,
введем дополнительную, фиктивную, потребность, равной 5 (90-85=5). Тарифы
перевозки груза из склада во все объекты полагаем равной нулю. Занесем данные в
таблицу:
Таблица 3
|
|
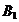 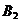 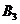 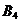 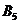 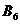 Запасы стройматериалов на складах,
тыс.ед. Запасы стройматериалов на складах,
тыс.ед.
|
|
|
|
|
|
|
|
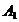 48367030 48367030
|
|
|
|
|
|
|
|
|
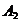 84659025 84659025
|
|
|
|
|
|
|
|
|
 35854020 35854020
|
|
|
|
|
|
|
|
|
 581068015 581068015
|
|
|
|
|
|
|
|
|
Потребности
строительных объектов, тыс.ед.
|
10
|
20
|
18
|
12
|
25
|
5
|
90 90
|
) Используя метод наименьшей стоимости, построим
первый опорный план задачи.
Наименьшая стоимость = 3. Для этого элемента
запасы равны 30, а потребности 18. Поскольку минимальным является 18, то
вычитаем его:
Таблица 4
Строительный объект Склад 
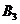
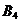
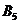
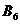 Запасы стройматериалов на складах,
Запасы стройматериалов на складах,
|
тыс.ед.
|
|
|
|
|
|
|
|
|
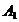 48367030-18=12 48367030-18=12
|
|
|
|
|
|
|
|
|
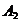 84 84659025
|
|
|
|
|
|
|
|
|
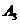 35 35854020
|
|
|
|
|
|
|
|
|
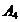 58 581068015
|
|
|
|
|
|
|
|
|
Потребности
строительных объектов, тыс.ед.
|
10
|
18-18=0
|
12
|
25
|
5
|
90 90
|
Наименьшая стоимость = 3. Для этого элемента
запасы равны 20, а потребности 10. Поскольку минимальным является 10, то
вычитаем его:
Таблица 5
|
Строительный
объект Склад
|
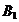 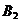 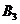 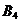 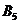 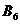 Запасы стройматериалов на складах,
тыс.ед. Запасы стройматериалов на складах,
тыс.ед.
|
|
|
|
|
|
|
|
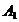 48367012
|
|
|
|
|
|
|
|
|
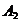 84659025
|
|
|
|
|
|
|
|
|
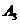 35 35854020-10=10
|
|
|
|
|
|
|
|
|
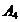 581068015
|
|
|
|
|
|
|
|
|
Потребности
строительных объектов, тыс.ед.
|
10-10=0
|
20
|
0
|
12
|
25
|
5
|
90 90
|
Наименьшая стоимость = 4. Для этого элемента
запасы равны 25, а потребности 20. Поскольку минимальным является 20, то
вычитаем его:
Таблица 6
|
Строительный
объект Склад
|
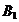 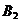 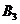 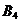 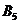 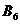 Запасы стройматериалов на складах,
тыс.ед. Запасы стройматериалов на складах,
тыс.ед.
|
|
|
|
|
|
|
|
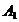 48367012
|
|
|
|
|
|
|
|
|
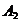 84659025-20=5
|
|
|
|
|
|
|
|
|
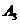 3 35854010
|
|
|
|
|
|
|
|
|
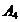 581068015
|
|
|
|
|
|
|
|
|
Потребности
строительных объектов, тыс.ед.
|
0
|
20-20=0
|
0
|
12
|
25
|
5
|
90 90
|
Таблица 7
|
Строительный
объект Склад
|
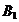 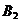 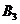 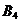 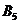 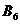 Запасы стройматериалов на складах,
тыс.ед. Запасы стройматериалов на складах,
тыс.ед.
|
|
|
|
|
|
|
|
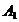 48367012-7=5 48367012-7=5
|
|
|
|
|
|
|
|
|
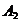 8465900 8465900
|
|
|
|
|
|
|
|
|
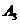 3585400 3585400
|
|
|
|
|
|
|
|
|
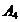 581068015 581068015
|
|
|
|
|
|
|
|
|
Потребности
строительных объектов, тыс.ед.
|
0
|
0
|
0
|
7-7=0
|
15
|
5
|
90
90
|
Опорный план не является оптимальным, так как
существуют оценки свободных клеток, для которых ui + vj
> cij
Выбираем максимальную оценку свободной клетки с15=7
В эту клетку ставим знак +, а в остальных
вершинах многоугольника чередующие знаки.
Таблица 9
|
Строительный
объект Склад
|
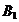 4 4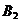 5 5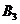 3 3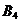 6 6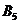 8 8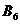 0Запасы
стройматериалов на складах, тыс.ед. 0Запасы
стройматериалов на складах, тыс.ед.
|
|
|
|
|
|
|
|
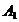 04(10)83(18)6(2)-7+030 04(10)83(18)6(2)-7+030
|
|
|
|
|
|
|
|
|
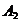 -184(20)65(5)9025 -184(20)65(5)9025
|
|
|
|
|
|
|
|
|
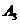 -435854(20)020 -435854(20)020
|
|
|
|
|
|
|
|
|
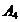 058106(5)+8(5)-0(5)15 058106(5)+8(5)-0(5)15
|
|
|
|
|
|
|
|
|
Потребности
строительных объектов, тыс.ед.
|
10
|
20
|
18
|
12
|
25
|
5
|
90 90
Таблица 10
|
Строительный
объект Склад
|
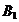 4 4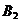 5 5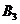 3 3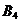 6 6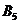 8 8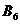 0Запасы
стройматериалов на складах, тыс.ед. 0Запасы
стройматериалов на складах, тыс.ед.
|
|
|
|
|
|
|
|
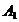 04(10)83(18)67(2)030 04(10)83(18)67(2)030
|
|
|
|
|
|
|
|
|
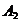 -184(20)65(5)9025 -184(20)65(5)9025
|
|
|
|
|
|
|
|
|
 -435854(20)020 -435854(20)020
|
|
|
|
|
|
|
|
|
 058106(7)8(3)0(5)15 058106(7)8(3)0(5)15
|
|
|
|
|
|
|
|
|
Потребности
строительных объектов, тыс.ед.
|
10
|
20
|
18
|
12
|
25
|
5
|
90 90
|
Проверим оптимальность опорного плана. Найдем
предварительные потенциалы ui, vj. по занятым клеткам
таблицы, в которых ui + vj = cij, полагая, что
u1 = 0.
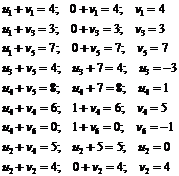
Потенциалы занесем в таблицу.
Проведем оценки свободных клеток:
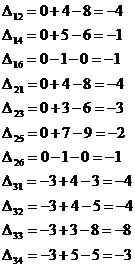
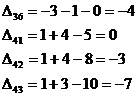
Опорный план является оптимальным,
так все оценки свободных клеток удовлетворяют условию ui + vj
≤ cij.
Минимальные затраты составят:
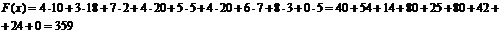 6) 6)
Из 1-го склада необходимо груз
направить в 1-й объект (10), в 3-й объект (18), в 5-й объект (2)
Из 2-го склада необходимо груз
направить в 2-й объект (20), в 4-й объект (5)
Из 3-го склада необходимо весь груз
направить в 5-й объект
Из 4-го склада необходимо груз
направить в 4-й объект (7), в 5-й объект (3)
На 4-ом складе остался
невостребованным груз в количестве 5 ед.
Похожие работы на - Методы оптимальных решений транспортной задачи
|