Класичні задачі давнини: подвоєння куба, трисекція кута, квадратура круга
Класичні
задачі давнини: подвоєння куба трисекція кута квадратура круга
ВСТУП
геометричний куб кут
Багато років світ вивчає і досліджує
різні проблеми. Деякі з них зіграли важливу роль в становленні геометрії.
Наприклад, древні геометричні задачі, найбільш відомі з них це задачі на
побудову: задача про квадратуру круга, подвоєння куба і трисекція кута. Вчені
всіх часів приділили цим проблемам багато час, пропонували свої розв’язання.
Врешті було доведено, що ці задачі неможливо розв’язати лише за допомогою
циркуля та лінійки. З часом змінилася постановка задачі: «довести
нерозв’язність» - що було великим кроком вперед. Разом з тим, пропонувалась
велика кількість розв’язків за допомогою нетрадиційних інструментів. Все це
призвело до виникнення абсолютно нових ідей в геометрії.
Задачі формулюються так:
· Задача про
квадратуру круга. Побудувати сторону квадрата, площа якого рівна площі даного
круга.
· Задача про
подвоєння куба: побудувати ребро куба, об’єм якого вдвічі більший, за об’єм
даного.
· Задача про
трисекцію кута: розділити довільний кут на три рівні частини.
В даній курсовій роботі ми
розглянемо ці задачі, причини їх виникнення і методи їх розв’язання.
РОЗДІЛ І. МЕТОДИ ПОБУДОВ ЗАДАЧ
ДАВНИНИ
. ПОДВОЄННЯ КУБА
Побудувати ребро куба, об’єм
якого вдвічі більший, за об’єм даного. Якщо 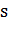
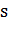 - сторона даного куба,
- сторона даного куба, 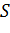
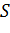 - шукана сторона куба, об’єм якого
вдвічі більше, ніж об’єм заданого, то
- шукана сторона куба, об’єм якого
вдвічі більше, ніж об’єм заданого, то
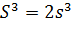
Отже,
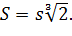
Отже, для того, щоб
розв'язати задачу досить побудувати вираз 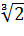
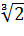 .
.
Ця задача є частковим
випадком іншої задачі:
Задача. Дано два відрізка 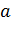
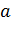 і
і 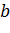
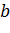 . Побудувати два середніх
пропорційних, тобто два відрізка
. Побудувати два середніх
пропорційних, тобто два відрізка 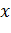
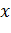 і
і 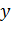
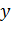 , котрі задовольняють рівняння:
, котрі задовольняють рівняння:
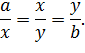
З цієї рівності випливає, що
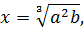
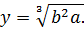
І якщо 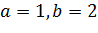
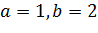 , то
, то
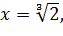
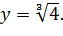
Подвоєння куба потребує
побудови виразу 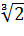
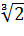 або графічного вираження коренів
рівняння
або графічного вираження коренів
рівняння
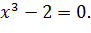
Це рівняння третьої степені
не має раціональних коренів и тому не є розв’язним в квадратних радикалах. А,
отже, вираз 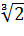
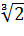 не може бути побудований циркулем
та лінійкою.
не може бути побудований циркулем
та лінійкою.
Для вирішення цієї задачі
потрібні конічні перерізи або вищі криві, які можуть бути побудовані по точкам
або за допомогою нестандартних інструментів.
1.1 Побудова за допомогою
конічних перерізів
Графічне розв’язання за допомогою
конічних перерізів.
) Розглянемо параболи:
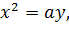
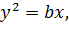
координатами точки їх перетину, яка
не збігається з початком, будуть числа
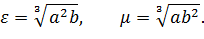
2)
Побудуємо два конічні перерізи
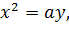
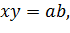
тоді точка їх перетину, яка не
співпадає з початком, має координати:
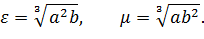
3) Розглянемо коло
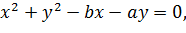
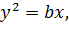
Тоді точка їх перетину, відмінна від
початку, має координати
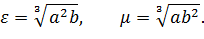
В усіх випадках знаходження середніх
пропорційних зводиться до знаходження точок перетину двох конічних перерізів.
Якщо 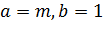
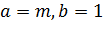 , то
, то
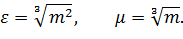
Для того, щоб знайти 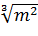
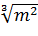 можна використати будь-який зі
способів.
можна використати будь-який зі
способів.
Для 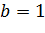
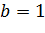 останній метод є найбільш зручним.
В такому випадку рівняння параболи має вигляд
останній метод є найбільш зручним.
В такому випадку рівняння параболи має вигляд
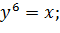
вона не залежить від 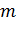
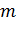 і її можна побудувати.
і її можна побудувати.
Координатами центра в такому
випадку будуть числа:
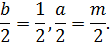
Оскільки коло проходитиме
через початок координат, то немає необхідності знаходити її радіус.
1.2 Побудова за допомогою
конхоїди Нікомеда
Вирішення за допомогою конхоїди
Нікомеда.
) Нікомед знайшов криву
вищого степеня, яку надзвичайно просто побудувати, а використовуватись може не
лише для графічного подвоєння куба, але і для трисекції кута і графічного
розв’язання рівнянь третього степеня. Саму криву можна отримати наступним
шляхом:
Нехай дано точку 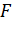
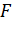 , довільну пряму
, довільну пряму 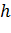
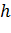 і відкладемо на ній від точки
і відкладемо на ній від точки 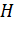
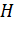 її перетину з
її перетину з 
 відрізок
відрізок 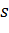
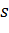 . Отриманиі таким чином точки при
зміні прямої
. Отриманиі таким чином точки при
зміні прямої 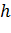
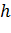 утворюють деяку криву
утворюють деяку криву 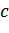
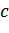 - конахоїду Нікомеда.
- конахоїду Нікомеда.
Точку 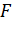
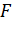 називають полюсом кривої, пряму
називають полюсом кривої, пряму 
 - її основою, а
- її основою, а 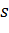
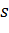 - інтервалом.
- інтервалом.
Неважко побудувати механізм,
за допомогою якого можна було б креслити цю криву.
Нікомед побудував такий
механізм, який вважається найдревнішим інструментом для креслення кривих, після
циркуля.
2) Виведемо рівняння цієї
кривої.
Із подібних трикутників 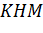
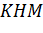 і
і 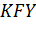
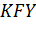 випливає, що:
випливає, що:
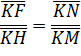
або
різносторонні полюси від
основи 
 .
.
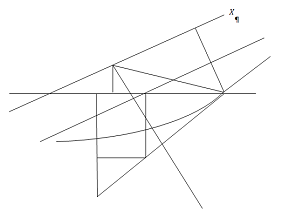
Положення системи координат
при цьому ясно з рисунку. 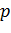
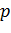 -
-
Із рівняння видно, що це
крива четвертого порядку, має свою точку 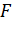
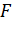 своєю подвійною точкою і
скалдається з двох частин, які мають основу
своєю подвійною точкою і
скалдається з двох частин, які мають основу 
 спільною асимптотою. Крива більше
того проходить через дві уявні циклічні точки.
спільною асимптотою. Крива більше
того проходить через дві уявні циклічні точки.
) Тепер покажемо як за
допомогою цієї кривої визначити обидва середніх пропорційних між двома
відрізками 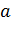
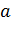 і
і 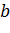
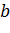 .
.
Два взаємно перпендикулярні
відрізки 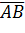
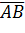 і
і 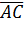
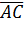 (з малюнку 1) нехай будуть
відповідно рівні
(з малюнку 1) нехай будуть
відповідно рівні 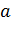
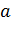 і
і 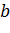
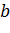 . І нехай
. І нехай
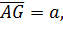
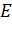
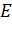 буде серединою відрізка
буде серединою відрізка 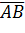
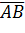 і пряма
і пряма 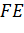
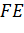 буде перпендикулярна до
буде перпендикулярна до 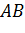
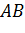 так, що
так, що
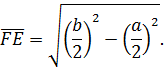
Потім проведемо пряму 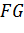
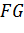 і паралельно їй через точку
і паралельно їй через точку 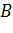
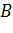 пряму
пряму 
 і інтервал
і інтервал 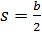
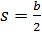 , вона перетне пряму
, вона перетне пряму 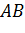
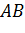 в точці
в точці 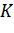
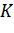 і отримаємо точку
і отримаємо точку 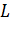
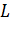 за допомогою четвертої вершини
прямокутника
за допомогою четвертої вершини
прямокутника 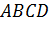
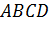 .
.
Тепер за допомогою обчислень
неважко довести, що 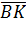
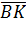 і
і 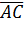
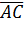 .
.
Якщо
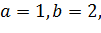
то
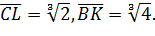
4) Якщо потрібно визначити два
середніх пропорційних, то нема необхідності в побудові всієї кривої, а досить
накреслити ту частину, яка за припущення містить точки перетину.
Саму точку перетину на
практиці зручно знаходити за допомогою паперової смужки, на котру
нанести відрізок 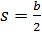
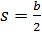 , переміщаючи її певним чином.
, переміщаючи її певним чином.
Таке знаходження 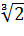
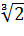 за допомогою паперової смужки ні в
яком разі не буде лише приблизним вирішенням задачі.
за допомогою паперової смужки ні в
яком разі не буде лише приблизним вирішенням задачі.
1.3 Побудова за допомогою цисоїди
Діоклеса
Розв’язання за за допомогою цисоїди
Діоклеса.
) Діоклес знайшов для
вирішення задачі криву, яка хоч і не може бути побудована за допомогою такого
простого механізму, як конхоїда, але тісно пов’язана з розглядуваною задачею.
Нехай 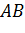
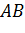 буде ламаним відрізком, що має
довжину 1. Проведемо через його кінці перпендикуляри
буде ламаним відрізком, що має
довжину 1. Проведемо через його кінці перпендикуляри 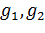
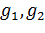 і візьмемо на
і візьмемо на 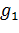
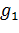 довільну точку. Цій точці
довільну точку. Цій точці 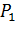
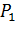 ми на
ми на 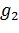
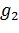 відкладемо таку точку
відкладемо таку точку 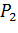
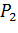 , для якої
, для якої
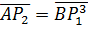
(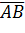
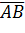 приймається за одиницю)
приймається за одиницю)
Таким чином, якщо припустити 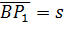
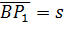 , то
, то 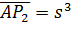
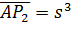 .
.
Тепер проведемо прямі 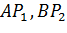
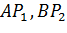 , які перетнуться в точці
, які перетнуться в точці 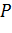
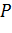 , яка при зміні
, яка при зміні 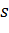
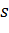 опише деяку криву, цисоїду
Діоклеса.
опише деяку криву, цисоїду
Діоклеса.
2) Виведемо рівняння цієї
кривої (малюнок 2).
Рівняння прямої 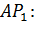
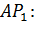
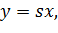
а прямої 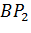
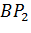
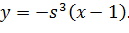
Виключивши 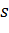
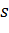 з обох рівнянь отримаємо
з обох рівнянь отримаємо
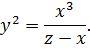
Це і є рівняння цисоїди.
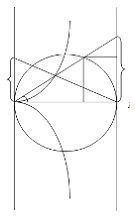
3) Властивість, яка може бути
використана для побудови.
Побудуємо на 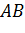
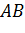 півколо і припустимо, що кут
півколо і припустимо, що кут 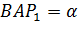
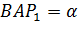 . Нехай пряма
. Нехай пряма 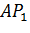
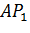 перетинає півколо не тільки в точці
перетинає півколо не тільки в точці
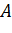
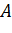 , а ще в деякій точці
, а ще в деякій точці 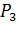
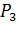 , тоді
, тоді 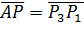
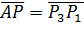 .
.
Для того, щоб довести це,
досить тільки показати, що обидва відрізки мають різні за довжиною проекції на
прямій 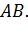
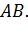
Проекція відрізка 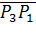
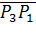 на
на 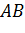
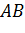 є
є
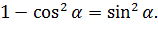
Проекція відрізка 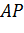
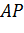 (абсциса точки
(абсциса точки 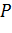
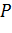 ) може бути знайдена, якщо в
рівнянні припустити
) може бути знайдена, якщо в
рівнянні припустити 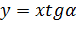
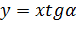 і потім визначити
і потім визначити 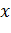
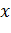 .
.
Ми знайдемо, що
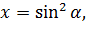
що і є доведенням теореми.
1.4 Побудова за допомогою двох
прямих кутів
Розв’язання за допомогою двох прямих
кутів.
Нехай дано дві взаємно
перпендикулярні прямі 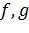
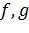 , нехай
, нехай 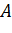
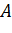 - довільна точка на
- довільна точка на 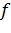
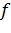 і
і 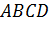
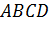 - прямокутна ламана лінія, вибрана
так, що
- прямокутна ламана лінія, вибрана
так, що 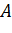
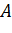 і
і 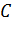
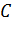 лежать на
лежать на 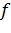
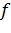 , а
, а 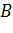
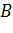 і
і 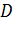
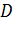 - на
- на 
 . Тоді:
. Тоді:
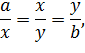
тобто 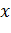
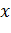 і
і 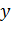
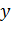 будуть двома середніми
пропорційними між
будуть двома середніми
пропорційними між 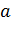
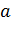 і
і 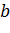
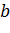 .
.
) Якщо 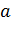
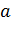 і
і 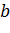
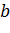 дані, то згідно з вищесказаним,
дані, то згідно з вищесказаним, 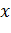
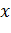 і
і 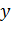
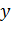 можна визначити, побудувавши
прямокутну ламану лінію
можна визначити, побудувавши
прямокутну ламану лінію 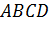
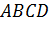 . Дві вершини її
. Дві вершини її 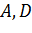
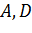 дані, а інші дві
дані, а інші дві 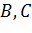
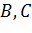 мають бути побудовані.
мають бути побудовані.
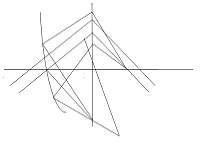
Цього можна домогтись лише
наближеними методами, побудувавши криву помилок для точки 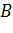
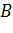 або
або 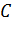
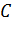 .
.
Для цього через 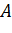
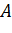 проводять довільну пряму 1, в точці
її перетину з
проводять довільну пряму 1, в точці
її перетину з 
 проводять перпендикуляр 2 і
опускають з
проводять перпендикуляр 2 і
опускають з 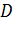
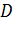 перпендикуляр на 2. Його очка
перетину
перпендикуляр на 2. Його очка
перетину 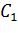
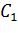 з прямою 2 це точка кривої помилок.
з прямою 2 це точка кривої помилок.
Аналогічно визначаємо і другу
точку 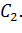
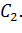
Завжди можна точки 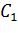
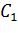 і
і 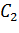
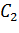 визначити так, щоб вони лежали
близько до прямої
визначити так, щоб вони лежали
близько до прямої 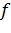
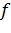 . Тоді криву помилок на цій короткій
відстані можна розглядати як майже пряму.
. Тоді криву помилок на цій короткій
відстані можна розглядати як майже пряму.
2) Якщо є два рухомі прямі
кути, то задача може бути строго розв’язана.
Треба лише обидва прямих кути
розташувати на площині рисунка так, щоб вони дотикались вздовж одного катета, і
щоб другий катет одного кута проходив через 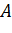
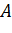 , а другий катет другого кута -
через
, а другий катет другого кута -
через 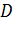
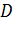 . Вершина першого кута повинна
лежати на
. Вершина першого кута повинна
лежати на 
 , а другого на
, а другого на 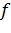
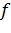 .
.
Правильного розміщення кути
досягають після короткого переміщення, в результаті чого виходить строге
розв’язання запропонованої задачі.
Якщо
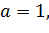
то
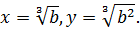
Таким чином, якщо
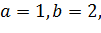
то
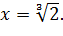
2.
ТРИСЕКЦІЯ КУТА
геометричний куб кут
Задача про трисекцію кута - ще одна
з задач давнини. Поділом кута на три рівні частини також займалось багато
математиків. Але і ця задача також не була вирішена за допомогою циркуля та
лінійки. Однак, якщо не обмежуватись лише цими інструментами, то задачу можна
побудувати. Звичайно, цей розв’язок не буде задовольняти поставлені умови
повністю, але це, очевидно, буде певним математичним здобутком.
В ході розв’язання цієї задачі було
відкрито цілий ряд дуже важливих та цікавих кривих. Наприклад, спіраль
Архімеда..
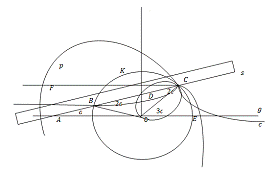
Нехай
Нехай
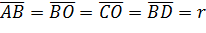
та
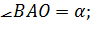
тоді
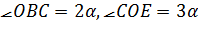
при цьому
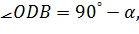
тобто

З цього випливає простий
метод трисекції кута 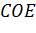
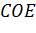 , метод яким найпростіше можна
виконати за допомогою паперової площини.
, метод яким найпростіше можна
виконати за допомогою паперової площини.
Нехай дано 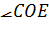
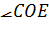 . Опишемо навколо
. Опишемо навколо 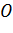
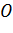 двільним радіусом
двільним радіусом 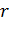
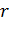 коло
коло 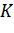
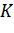 , яка перетне сторони кута в точках
, яка перетне сторони кута в точках 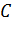
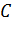 і
і 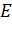
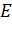 .
.
Нанесемо тепер на край
паперової площини відрізок 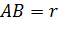
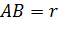 , помістимо паперову площину в
площину рисунка так, щоб край її проходив через
, помістимо паперову площину в
площину рисунка так, щоб край її проходив через 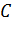
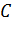 , точка
, точка 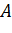
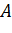 лежала на
лежала на 
 і точка
і точка 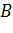
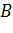 на
на 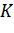
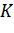 .
.
Тоді вже
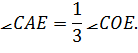
Правильне положення паперової
площини вдається знайти з повною строгістю після деякого її переміщення.
Трисекція кута вказаним
шляхом виконується строго.
Метод є не тільки корисним,
але й теоретично цікавий, так як з нього можна вивести цілий ряд методів
трисекції кута.
2.1
Побудова за допомогою конхоїди Нікомеда
Трисекція кута за допомогою конхоїди
Нікомеда.
Щоб надати паперовій площині 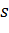
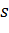 правильне положення можна: край її
прикладати до
правильне положення можна: край її
прикладати до 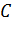
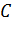 , точку
, точку 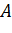
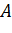 поміщають на пряму
поміщають на пряму 
 і переміщати паперову площину до
тих пір, поки
і переміщати паперову площину до
тих пір, поки 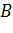
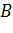 не потрапить на коло
не потрапить на коло 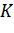
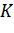 . При цьому переміщення точки
. При цьому переміщення точки 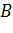
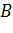 опише конхоїду
опише конхоїду 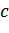
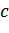 , для якої
, для якої 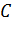
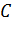 буде полюсом,
буде полюсом, 
 - основою,
- основою, 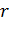
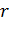 - інтервалом.
- інтервалом.
Точка перетину 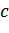
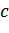 з
з 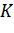
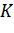 і буде шуканою точкою
і буде шуканою точкою 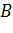
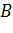 . Звідси випливає застосування
конхоїди для трисекції кута.
. Звідси випливає застосування
конхоїди для трисекції кута.
На рисунку креслять також
пряму 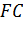
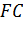 , паралельну до
, паралельну до 
 .
.
Нехай тепер даний буде
довільний кут 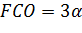
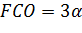 .
.
Відкладають на стороні 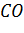
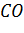 довільний відрізок
довільний відрізок 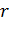
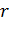 і отримують таким чином точку
і отримують таким чином точку 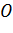
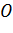 , як центра, радіусом
, як центра, радіусом 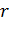
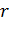 і будують конхоїду, яка має точку
і будують конхоїду, яка має точку 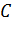
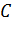 своїм полюсом, пряму
своїм полюсом, пряму 
 - основа, відрізок
- основа, відрізок 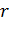
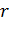 - інтервалом. Точка
- інтервалом. Точка 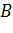
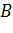 перетину цієї конхоїди з колом
перетину цієї конхоїди з колом 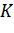
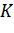 і визначає третю частину кута
і визначає третю частину кута 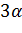
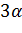 .
.
Легко бачити, що для кожного
даного кута треба креслити конхоїду, в силу чого цей метод має лише історичний
інтерес.
2.2 Побудова за допомогою равлика
Паскаля
Уявімо тепер паперову
поверхня, яка розташована в площині рисунка так, що край її проходить через 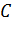
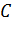 і точка
і точка 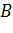
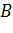 лежить на колі
лежить на колі 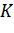
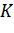 , це можна виконати нескінченною
множиною способів. Точка
, це можна виконати нескінченною
множиною способів. Точка 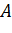
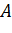 описує при цьому деяку криву
описує при цьому деяку криву 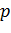
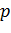 , так званого равлика Паскаля.
, так званого равлика Паскаля.
З рисунка ясно, що навпаки,
за допомогою равлика Паскаля можна розділити довільний кут на три частини.
Нехай даний нарисований
равлик Паскаля. 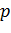
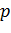 і точка
і точка 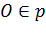
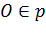 .
.
Якщо потрібно розділити кут
на три частини, то проводять пряму 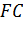
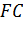 так, щоб тук
так, щоб тук 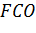
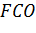 дорівнював даному куту. Якщо тепер
проведемо через
дорівнював даному куту. Якщо тепер
проведемо через 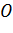
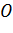 пряму
пряму 
 , паралельну до
, паралельну до 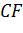
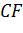 , то
, то 
 перетне равлик Паскаля у деякій
точці
перетне равлик Паскаля у деякій
точці 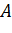
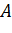 , причому, як видно з рисунка,
, причому, як видно з рисунка,
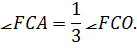
Отже, за допомогою накресленого
равлика Паскаля можна ділити на три рівні частини довільний кут.
Квадратура круга
Різні способи побудови
Задача про квадратуру круга відома
вже тисячі років і завжди привертала до себе увагу математиків. Вона
формулюється так: побудувати квадрат, площа якого була б рівна площі даного
круга.
Довгий час існували сумніви щодо
вирішуваності задачі. Ці сумніви підтвердилися ще тим, що грецький геометр
Гіппократ зміг перетворити квадрат на деякі «кругові луночки» - частина
площини, обмежена дугами двох кіл.
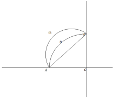
На малюнку
зображена «луночка» 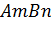
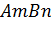 , рівновелика трикутнику
, рівновелика трикутнику 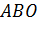
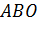 (який неважко перетворити в
рівновеликий йому квадрат).
(який неважко перетворити в
рівновеликий йому квадрат).
Були виказані припущення про
невирішуваність задачі за допомогою циркуля та лінійки. Робили спроби довести
невирішуваність задачі про квадратуру круга взагалі.
Площа круга радіуса 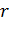
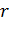 рівна
рівна
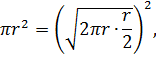
тобто рівна площі квадрата зі
стороною 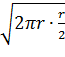
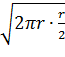 , котра будується як середнє
пропорційне між відрізками
, котра будується як середнє
пропорційне між відрізками 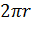
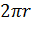 і
і 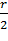
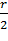 .
.
Якби було можливо, знаючи
радіус круга 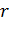
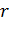 , побудувати відрізок довжиною
, побудувати відрізок довжиною 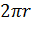
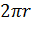 , то такий квадрат легко можна було
б побудувати.
, то такий квадрат легко можна було
б побудувати.
И навпаки: якби при даному 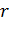
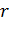 можна було б побудувати квадрат,
рівновеликий кругу, то можна було б побудувати відрізок, рівний довжині кола.
Насправді, якщо
можна було б побудувати квадрат,
рівновеликий кругу, то можна було б побудувати відрізок, рівний довжині кола.
Насправді, якщо 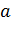
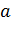 - сторона квадрата, то
- сторона квадрата, то 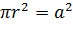
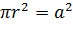 , отже,
, отже, 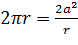
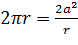 і шуканий відрізок будується як
четвертий пропорційний відрізок до відрізків
і шуканий відрізок будується як
четвертий пропорційний відрізок до відрізків 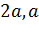
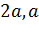 і
і 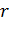
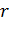 .
.
Отже, задача про квадратуру
круга рівносильна до задачі про спрямлення кола, тобто побудови відрізка
довжиною 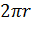
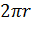 . При
. При 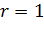
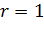 довжина кола дорівнює
довжина кола дорівнює 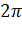
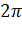 . Таким чином задача про спрямлення
кола призвела до вивчення властивостей числа
. Таким чином задача про спрямлення
кола призвела до вивчення властивостей числа 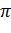
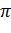 .
.
Як наслідок, було доведено
ірраціональність числа 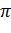
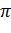 , але це ще не було вирішенням
питання про квадратуру круга.
, але це ще не було вирішенням
питання про квадратуру круга.
В ході подальших роздумів,
було доведено, що, для побудови шуканого відрізка, потрібно аби 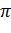
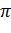 було числом алгебраїчним, а не
трансцендентним. Що не так.
було числом алгебраїчним, а не
трансцендентним. Що не так.
Таким чином нарешті була
вирішена проблема квадратури крута: квадратура круга неможлива за допомогою
циркуля та лінійки.
Незважаючи на те, що задача
про спрямлення кола і задача про квадратуру круга за допомогою циркуля та
лінійки теоретично точно нерозв’язна, існують методи наближеного розв’язання
цих задач з достатньою для практичних цілей наближеною точністю.
Якщо розділити коло точками
на достатньо велику кількість достатньо малих дуг, то периметр многокутника,
для якого ці точки служать послідовно вершинами, може бути прийнятий за довжину
кола.
Відомо, що ще Архімед
визначив, що 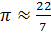
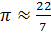 . При такому припущенні відрізок
. При такому припущенні відрізок 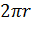
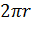 будується як три цілих і одна сьома
діаметра даного кола. Ця побудова дає наближене розв’язання задачі з надлишком,
причому відносна похибка не перевищує
будується як три цілих і одна сьома
діаметра даного кола. Ця побудова дає наближене розв’язання задачі з надлишком,
причому відносна похибка не перевищує 
 .
.
Цікавий прийом спрямлення
кола за допомогою лище циркуля запропонував італійський геометр Маскероні.
Нехай 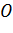
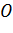 - центр даного кола,
- центр даного кола, 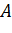
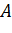 - деяка точка, яка належить даному
колу.
- деяка точка, яка належить даному
колу.
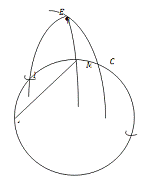
Будуємо
чотири послідовні вершини правильного вписаного шестикутника 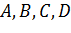
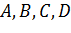 . Нехай
. Нехай 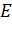
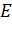 - точка перетину кола
- точка перетину кола 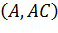
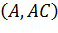 і кола
і кола 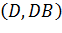
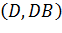 . Нехай в перетині дуги
. Нехай в перетині дуги 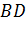
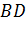 даного кола з колом
даного кола з колом 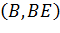
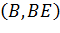 утворюється точка
утворюється точка 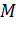
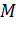 . Тоді довжина відрізка
. Тоді довжина відрізка 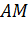
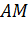 рівна одній четвертій частині
довжини кола з точністю до
рівна одній четвертій частині
довжини кола з точністю до 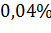
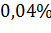 .
.
Виявляється, що при 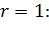
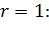
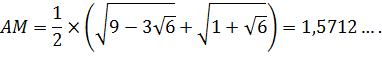
Тоді як 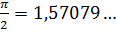
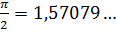 .
.
Оригінальний прийом
спрямлення кола був запропонований польським математиком Коханським. Суть
методу ясна з малюнку:
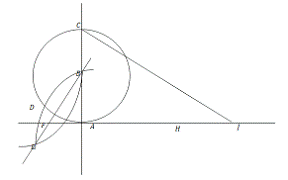
На рисунку 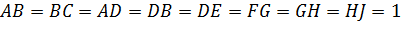
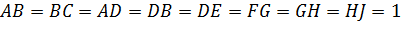 .
.
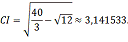
Тобто відрізок 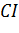
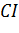 дає наближену величину довжини
півкола, радіус якого
дає наближену величину довжини
півкола, радіус якого 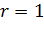
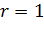 .
.
Спосіб Коханського цікавий
тим, що він відтворюється лінійкою і циркулем постійного розхилу.
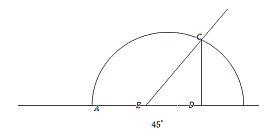
Простий спосіб спрямлення
кола за допомогою циркуля і лінійки запропонував Мюллер. Хід побудови легко
простежити по рисунку:
ВИСНОВОК
Отже, ми розглянули три знамениті
задачі давнини. Багато років світ вивчав і досліджув їх. Вони зіграли важливу
роль в становленні геометрії. Ми показали, що ці задачі неможливо розв’язати
лише за допомогою циркуля та лінійки.
В даній курсовій роботі ми
розглянули ці задачі, причини їх виникнення і методи їх розв’язання.
В роботі було розглянуто різні
методи наближених побудов задач квадратури круга, трисекції кута та подвоєння
куба. Наведено детальні способи побудов нерозв’язних задач. До деяких із них
наведено наслідки, задачі, які випливають з побудови даних, нерозв’язних за
допомогою циркуля і лінійки, задач.
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
1. Адлер А. теория
геометрических построений/Пер.с кем.3-у изд.Л.,1940, 232с.
. Аксенова М.В., Храмов
Г.И. Єнциклопедия по математике. М.: Аванта+, 1995, 162с.
3. Аргунов Б.И., Балк М.Б.
Геометрические построения на плоскости. 2-е изд. М, 1957, 226с.
. Глейзер Г. И. История
математики в школе. - М.: Просвещение, 1964. - С. 324-325.
5. Колесников М. Лобачевский./.
Серия «Жизнь замечательных людей». - М.: Молодая гвардия, 1965. - 320 стр. с
илл.
. Прасолов В. В.. Три
классические задачи на построение. Удвоение куба, трисекция угла, квадратура
круга. М.: Наука, 1992. 80 с. Серия «Популярные лекции по математике», выпуск
62.
7. Широков П.А. Краткий очерк
основ геометрии Лобачевского./. - М.: Наука, 1983. - 76 стр.
. Щетников А. И. Как
были найдены некоторые решения трёх классических задач древности?
Математическое образование, № 4 (48), 2008, с. 3-15.Смилга
В.П. В погоне за красотой./. Н-п издание. - М.: Молодая гвардия, 1968. - 200
стр. с илл.