Математическая модель возмущенного движения

Математическая модель возмущенного движения

Введение

Объекты, с которыми имеет дело техника, органами управления. Математически поведение такого объекта описывается некоторыми уравнениями, куда входят и управляющие параметры, характеризующие положение «рулей». Естественно, возникает вопрос об отыскании наилучшего (оптимального) в том или ином смысле управления движением. Например, речь может идти о достижении цели движения за минимальное время. Этот вопрос является задачей вариационного исчисления. В отличие от классических вариационных задач, где управляющие параметры меняются в некоторой открытой области (без границы), теория оптимальное управление охватывает и тот случай, когда управляющие параметры могут принимать и граничные значения. Последнее обстоятельство особенно существенно с прикладной точки зрения, поскольку при управлении техническим объектом именно положение «руля» «на упоре» часто обеспечивает оптимальное управление.

Центральным результатом теории оптимальное управление, является принцип максимума Понтрягина, дающий общее необходимое условие оптимальности управления. Этот результат и связанные с ним исследования, проведённые Л. С. Понтрягиным и его сотрудниками, послужили исходным пунктом разработки теоретических, вычислительных и прикладных аспектов теории оптимального управления. Практически , применение теории оптимального управления является единственным способом получения преимущества при конструировании сложного многокритериального объекта при условии что все прочие возможности для обеспечении заданных параметров его функционирования уже исчерпаны . С такой ситуацией обычно приходится сталкиваться при разработке передовых образцов вооружения, когда потенциал органов управления уже достигнут за счет использования передовых промышленных технологий. Практически процесс оптимизации является итерационным. После решения задачи оптимизации по первоначальному критерию следует корректировка этого критерия с учетом возможностей практической реализации системы, отписываемой математической моделью.

математическая модель беспилотный движение

1. Постановка задачи

Требуется синтез оптимального управления при осуществлении разворота. За управляемый параметр принять угол крена. Для заданного канал управления ЛА разработать математическую модель возмущенного движения. Определить переходные характеристики переходного процесса БПЛА с оптимальным регулятором. Сравнить результаты с полученными другими методами. Отследить влияние ограничений на управляемый параметр в результатах моделирования маневра.

Известные параметры ЛА:

,

,

,

,

,

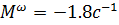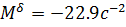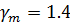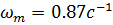V=288 м/с,

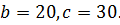
2. Разработка математической модели БПЛА

Уравнения могут быть получены из основных теорем динамики твердого тела:

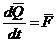,(1)

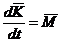.(2)

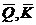- главный вектор и главный момент относительно центра масс количества движения твердого тела ;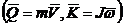

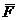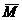и - главный вектор и главный момент относительно центра масс внешних сил, действующих на твердое тело.

Если рассматривать самолет как твердое тело в произвольный момент времени, то к нему будут приложены:

внешние силы, действующие на самолет ;

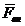сила тяги двигателя ;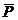

внутренние кориолисовые силы инерции из-за движения масс внутри твердой оболочки .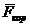

Тогда уравнения примут вид:

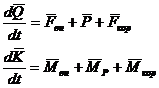 (3)

Причем, первое уравнение описывает движение центра масс относительно БПЛА, а второе - движение БПЛА относительно центра масс БПЛА.

Наиболее удобно исследовать движение БПЛА, пользуясь подвижными системами координат в начале с центром масс БПЛА. При проектировании производной по времени от какого-либо вектора 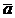на оси любой подвижной системы координат Οxyz, вращающейся с угловой скоростью 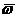 относительно выбранной системы отсчета (неподвижной), должны быть применены известные из векторного анализа формулы:

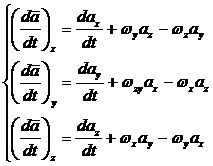(4)

Движение центра масс БПЛА

Пренебрегая скоростью и ускорением перемещения центра масс БПЛА относительно его корпуса, производная от количества движения по времени будет равна:

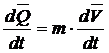(5)

Учитывая (4), разделяем полученные уравнения на проекции по осям XYZ, получим систему динамических уравнений движения в проекциях на оси системы координат, помещенных в центр масс БПЛА:

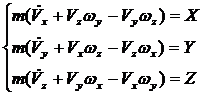 (6)

где X,Y и Z - проекции сил на соответствующие оси

Векторное уравнение движения центра масс с учетом того, что:

-      

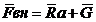
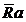-       - главный вектор аэродинамических сил, приложенный в центре масс БПЛА

-       - сила тяжести

примет вид:

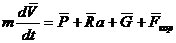(7)

Наиболее простую и удобную форму система динамических уравнений движения центра масс БПЛА примет, если векторное уравнение спроектировать на оси траекторной системы координат ox_кy_кz_к.

Применяя формулу (6) для проектирования левой части уравнения (7) и учитывая, что 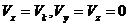, получим:

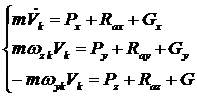(8)

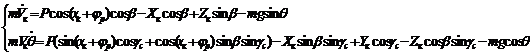(9)

Допущения:

-       рассматриваем продольное движение БПЛА (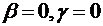) тогда:

-       считаем самолет жестким телом, не учитываем кориолисовые силы инерции ;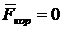

-       не учитываем слагаемые, связанные с вращением Земли;

-       не учитываем изменение массу БПЛА из-за выгорания топлива.

Тогда уравнения движения центра масс в траекторной системе примут вид:

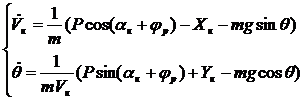(10)

Движение относительно центра масс БПЛА.

Динамические уравнения движения БПЛА относительно его центра масс в проекциях на какие-либо оси могут быть выведены из уравнения момента количества движения системы переменного состава. Наиболее простую форму уравнения примут, если использовать для записи уравнений в проекциях главные центральные оси инерции БПЛА. Направление этих осей относительно твердой оболочки БПЛА совпадают со связанными осями координат. Учитывая (4), вычисляем проекции производной по времени от вектора кинетического момента (2) БПЛА, получим систему скалярных уравнений:

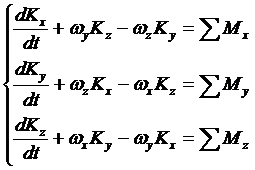(11)

где

K_x, K_y, K_z - проекции вектора кинетического момента БПЛА на связанные оси координат;

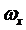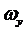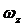,,- проекции вектора абсолютной угловой скорости БПЛА на те же оси;

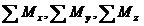-проекции главного момента аэродинамических сил и сил тяги относительно центра масс на те же оси.

Проекции вектора кинетического момента

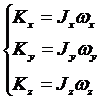 (12)

Тогда система уравнений (11) примет вид (без учета угловой скорости суточного вращения Земли, угловой скорости БПЛА относительно нормальной системы координат и угловой скорости, возникающей из-за кривизны поверхности):

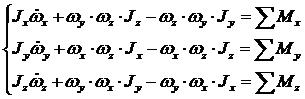(13)

Преобразовав систему (11) получим:

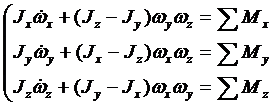(14)

Допущения:

-       рассматриваем продольное движение БПЛА, пренебрегаем связью между продольным и боковым движением: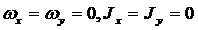

-       моменты инерции БПЛА не являются функциями времени.

В силу введенных допущений получаем:

Кинематические уравнения движения центра масс БПЛА.

Кинематические уравнения связывают между собой кинематические и геометрические характеристики поступательного движения центра масс самолёта и вращения его относительно центра масс, а также угловые скорости подвижных систем координат с параметрами движения самолёта.

Кинематическое уравнение движения центра масс БПЛА в векторной форме , где 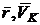- радиус-вектор вектор скорости центра масс БПЛА относительно рассматриваемой системы отсчета. Для получения скалярных кинематических уравнений движения центра масс найдем проекции вектора скорости центра масс БПЛА на оси координат, относительно которых рассматривается движение БПЛА. Проектируя вектор скорости 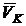 на нормальные оси координат и используя таблицу направляющих косинусов, получим кинематические уравнения движения центра масс БПЛА:

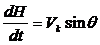(16)

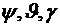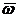Кинематические уравнения, описывающие вращение БПЛА относительно нормальной системы координат, устанавливают связь между производными углов - по времени и проекциями на связанные оси вектора угловой скорости  БПЛА относительно системы отсчета, связанной с Землей. Поскольку вращение БПЛА может быть представлено как изменение углов 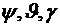, определяющих положение БПЛА относительно Земли, вектор угловой скорости БПЛА 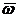 равен геометрической сумме угловых скоростей элементарных поворотов:

, 

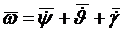Это уравнение является кинематическим уравнением вращательного движения БПЛА в векторной форме. Проектируя векторы 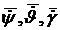 на направление связанных осей OX, OY и OZ получим:

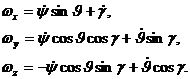
Так как в данной работе преследуется цель демонстрации алгоритма оптимально управления , то рассматриваемая система может быть упрощена до системы в которой рассматривается только боковое движение в котором изменение траектории осуществляется только за счет угла крена , а угол крена в свою очередь регулируется рулями. Также следует учесть что полет идет на постоянной высоте.

С учетом того, что рассматривается боковое движение БПЛА, система дифференциальных уравнений с учетом допущений примет вид:

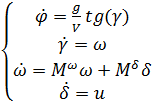 (17)

3. Разработка алгоритма оптимального управления

Обратимся к описанию системы управления в пространстве состояний. Модель объекта управления задается системой обыкновенных дифференциальных уравнений, возможно, нестационарной и нелинейной:

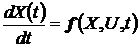, (18)

где X(t)=(x₁(t),x₂(t),…,x_n(t)) - вектор состояния объекта управления, U(t)=(u₁(t),u₂(t),…,x_r(t)) - вектор управления.

С точки зрения классической теории автоматического управления, задача управляющего устройства - выработка такого управления U(t), чтобы качество функционирования системы удовлетворяло заданным требованиям (показатели точности, запаса устойчивости, быстродействия системы находились в заданных пределах). Однако эта задача может быть сформулирована и в другой форме: задача управляющего устройства - выработка такого управления, чтобы качество функционирования системы было наилучшим в определённом смысле (например, быстродействие должно быть максимальным). Такая постановка задачи имеет ряд особенностей.

. Если не ограничиваться рассмотрением линейных стационарных систем, то в условиях задачи в общем случае необходимо оговаривать начальное X⁰=Х(t₀) и конечное состояния объекта X¹=Х(t₁). Тем самым задаётся временной интервал [t₀; t₁], для которого и требуется найти оптимальное управление. Границы этого интервала и соответствующее значение вектора X далеко не всегда оказываются фиксированными. В конкретных задачах часть из этих граничных условий может быть неизвестна или может принадлежать некоторой области. Следствием этого является разнообразие задач оптимизации управления.

. Для реальных объектов управления, как правило, приходится учитывать ограничения на составляющие вектора управления или на переменные состояния. Таким образом, оптимальное управление ищется среди допустимых управлений, принадлежащих некоторой замкнутой области С в r-мерном пространстве управлений. Допустимым управлением является всякая кусочно-непрерывная функция 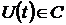 при .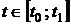

. При достаточном разнообразии критериев качества управления их принято задавать единым способом в форме функционала

,

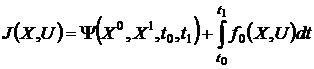где виды f₀ определяют конкретный критерий для рассматриваемой задачи.

В итоге основную задачу определения оптимального управления можно сформулировать следующим образом: пусть заданы уравнения объекта управления (18), начальное и конечное состояния объекта. Среди всех допустимых уравнений, для которых траектории системы (18) проходят через начальное и конечное состояние, выбрать такое, для которого .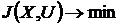

Это задача синтеза оптимального управления.

Второй вариант постановки задачи оптимизации - задача синтеза оптимального регулятора. Её отличие состоит в том, что управление ищется не как функция времени U(t), а как функция вектора состояния системы U(X). Тем самым непосредственно определяется уравнение регулятора, обеспечивающего оптимальное качество системы, т.е. уравнение оптимального регулятора.

Выбором подынтегральной функции f₀ и функции минимизируемого функционала задаются конкретные критерии оптимальности управления. Здесь может быть достигнуто широкое разнообразие. Рассмотрим наиболее распространенные на практике критерии.

. Критерий максимального быстродействия сводится к минимизации времени перехода объекта из состояния X⁰ в X¹, другими словами, времени переходного процесса:

.

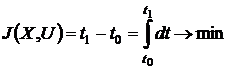2. Критерий минимального расхода топлива

,

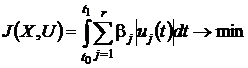где x_j(t) - составляющие вектора управления, _j - весовые коэффициенты, выбором значений которых можно учесть расход горючего или другого рабочего тела на формирование сигналов управления по разным каналам.

. Комбинированный критерий

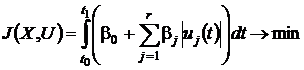
позволяет учесть при соответствующем выборе весовых коэффициентов и время переходного процесса, и расход топлива.

4. Критерий минимума интеграла от квадрата ошибки системы:

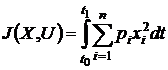 или .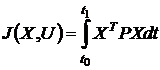

Здесь ^Т - символ транспонирования вектора, P - матрица весовых коэффициентов размерностью 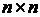. Если рассматривается стационарная система, то t₁ в этом критерии чаще всего задаётся бесконечным, а x_i(t₁)=0, i=1,2,...n.

. Тот же критерий для конечного интервала времени иногда вводится с учётом конечной ошибки системы:

,

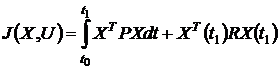где R - матрица размерностью 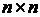; момент t₁ задаётся фиксированным 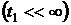; значения x_i(t₁) в условиях задачи не фиксируются.

. Критерий минимума расхода энергии:

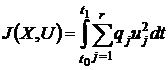 или ,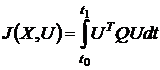

где Q - симметричная матрица размерностью .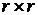

7. Квадратичный критерий качества в наиболее общем виде:

 ,

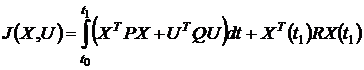где . Это комплексный критерий, обеспечивающий минимизацию интеграла от ошибки и расхода энергии. Если рассматривается 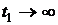, то последнее слагаемое отсутствует.

Оптимизация управления или структуры и параметров управляющего устройства в соответствии с таким критерием в литературе получила название «аналитическое конструирование оптимальных регуляторов» (АКОР).

. В задачах оптимизации управления конечным состоянием системы используется критерий вида:

 .

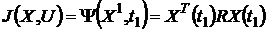Конечное состояние в условиях задачи, очевидно, не задаётся.

Например, для системы самонаведения ракеты в качестве критерия оптимальности может рассматриваться конечный промах (квадрат конечного промаха):

,

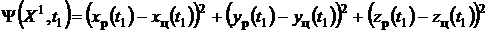то есть сумма квадратов разностей координат ракеты и цели в момент t₁ окончания процесса наведения.

Для задач синтеза оптимального управления при отсутствии ограничений на управление используют классические методы вариационного исчисления.

При наличии ограничений на управление наиболее удобен принцип максимума Л.С. Понтрягина. Для этих же задач применяется метод динамического программирования, разработанный Дж. Беллманом.

Эти методы позволяют получить аналитическое решение для наиболее простых задач или свести решение задачи к решению некоторой системы нелинейных алгебраических уравнений, которое может быть далее получено стандартным численным методом.

Однако при достаточной сложности модели объекта управления это оказывается слишком трудоёмким, и приходится применять численные методы оптимизации.

Остановимся подробнее на важнейшем в теории оптимального управления понятии функционала.

Функционал - это числовая функция, определенная на некотором множестве функций. Другими словами, функционал формализует закон, по которому каждой функции X из некоторого множества, или класса, функций ставится в соответствие число J (рисунок 112):

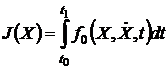. (19)

Здесь X - возможно векторная функция, называемая также кривой или точкой функционального пространства, f₀ - интегрант.

Решение задачи оптимизации функционала состоит в нахождении его экстремума, а также функции  из заданного множества (допустимой области C функционального пространства), доставляющей этот экстремум: 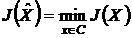 или .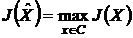

Понятие экстремума функционала, а также необходимые и достаточные условия достижения экстремума во многом совпадают с аналогичными понятиями и условиями для функции.

Функционал достигает локального экстремума на кривой x₀(t), если разность J(x₀)-J(x) сохраняет знак в некоторой окрестности x₀, т.е. при 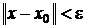, где 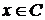 - области определения функционала.

Если 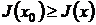 для всех 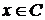, то x₀ доставляет функционалу абсолютный максимум, если 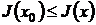 - абсолютный минимум.

Первое необходимое условие достижения локального экстремума: J=0, где J - первая вариация, или первый дифференциал функционала.

Второе необходимое условие: 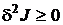 для минимума или  для максимума. Выполнение этого условия проверяется на кривых, удовлетворяющих первому необходимому условию. Здесь ²J - вторая вариация, или второй дифференциал функционала.

Достаточное условие локального экстремума состоит в одновременном выполнении первого и второго необходимых условий при строгом неравенстве во втором.

Оптимизация по критерию Красовского:

Для процесса описываемого уравнением:

,

,

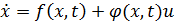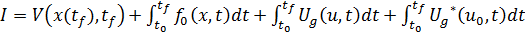является управление(при )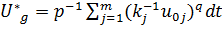

,

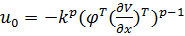где V- решение линейного уравнения в частных производных:

,

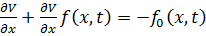Здесь V - непрерывная функция, имеющая непрерывные производные по x,t. В выражении для I слагаемое 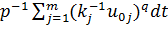 соответствует "работе" управлений в оптимальной системе.

Как классический функционал, так и функционал обобщенной работы А.А. Красовского дает возможность учесть гладкие ограничения на управление. Вообще говоря, процесс задания параметров функционала является многоэкстремальной многомерной задачей, решаемой в сочетании с теорией экспертных систем. Следует также отметить, что минимизация функционала обобщенной работы эквивалентна минимизации функционала Больца, при дополнительном изопараметрическом ограничении

.

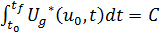Это интегральное равенство характеризует задание обобщенной работы управлений в оптимальной системе . Отсюда происходит название ФОР.

Теперь , используя данный критерий применительно к системе (17) , запишем минимизируемый функционал

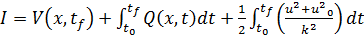, (20)

из которого :

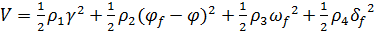, (21)

с учетом ограничений Q1 и Q2 , запишем гамильтониан:

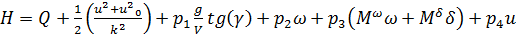. (22)

Определим из условия 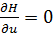 управление как .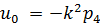

Далее определяются функции невязки и граничные условия :

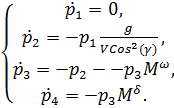 (23

)

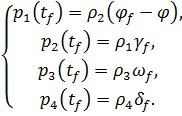 (24)

В случае учета ограничений на управление, система 23 примет вид:

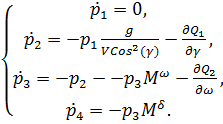
4. Алгоритм с прогнозирующей моделью

В данной задаче для решения поставленной задачи используется алгоритм с прогнозирующей моделью.

) Находится гамильтониан:

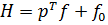. (25)

2) находится управление из условия :

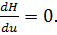 (26)

3) Полагается :

,

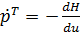4) Интервал оптимизации разбивается на шаги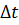

5) Полагается t=t0

6) Система уравнений 17 интегрируется в прямом времени при u=0 от t до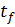

7) Вычисляются граничные условия для p:

.

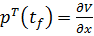8) Интегрируются совместно системы 17 и 24 в обратном времени вдоль решения полученного в п.6

) Вычисляется u0

10) С управлением, найденным в п.9 интегрируются система 17 на 1 шаг вперед.

) Если 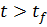 то алгоритм завершает работу. Если нет, то 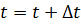, возврат к п.6

Программный код, реализующий данный алгоритм представлен в приложении А.

5. Результаты моделирования

При моделировании были получены следующие параметры:

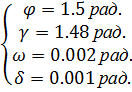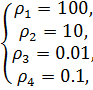 ,при t =10 сек.  и k=0.001

Результаты моделирования представлены в приложении Б.

В данном случае ЛА выходит на заданные углы по окончанию маневра, а варьированием параметров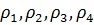  

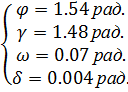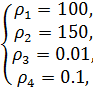 ,при t =10 сек.  и k=0.001

можно добиться получения семейства оптимальных траекторий

В случае, если ограничения на управление не используются , то ЛА теряет устойчивость при определенной комбинации параметров  

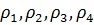
Результаты представлены в приложении В

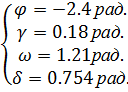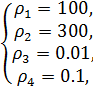 ,при t =10 сек.  и k=0.001

Однако , есть ограничения на управления учесть , то при тех же параметрах получим:

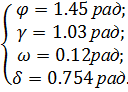
Результаты моделирования данного случая представлены в приложении В.

6. Сравнение результатов с известными решениями

Для задач оптимизации динамических систем, в частности, систем управления, применяют особую форму записи уравнений для определения допустимых экстремалей - с использованием функции Гамильтона. Эта форма получила наиболее широкое распространение для задач с дифференциальными связями и принята за основу в методах оптимизации систем при наличии ограничений в форме неравенств.

Рассмотрим задачу синтеза оптимального управления для объекта, модель которого задана в виде (23.1). Такая задача может рассматриваться как задача Лагранжа, причем модель объекта дает n дифференциальных связей (аргумент t в явном виде далее не учитывается для сокращения записи):

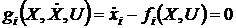, i=1,2,...,n, (27)

а критерий качества приводится к функционалу:

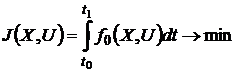. (28)

При решении такой задачи составляют функцию Лагранжа

,

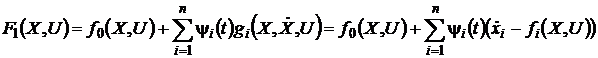для которой далее записывают систему уравнений Эйлера-Лагранжа и применяют другие условия достижения экстремума.

Если дифференциальные связи приводятся к форме (21) или (27), может быть введена функция Гамильтона

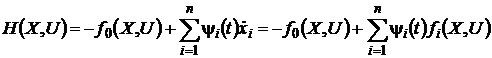. (29)

Сравнивая выражения, нетрудно установить взаимно однозначное соответствие между функциями Лагранжа и Гамильтона:

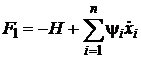 или 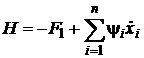. (30)

Функции _i(t) называются сопряженными переменными. Они могут быть определены по функции Гамильтона (29

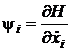, i=1,2,...,n. (31)

Запишем уравнения Эйлера-Лагранжа, учитывая (30):

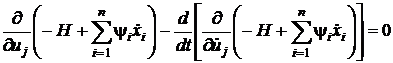, j=1,2,...,r.

Раскрыв скобки и продифференцировав, получим:

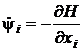, i=1,2,...,n; (32)

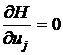, j=1,2,...,r. (33)

Полученная система уравнений (25.5)-(25.7) называется системой уравнений Эйлера-Лагранжа в канонической форме.

Рассмотрим условия трансверсальности.

Для подвижных концов на основе (24.5) с учетом (25.3) получим:

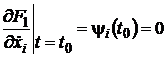 или 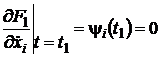. (34)

Для свободных концов на основе (24.6) с учетом (25.3), (25.8):

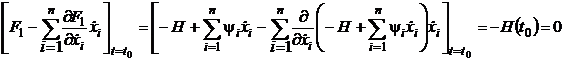
или 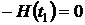. (35)

При работе с функцией Гамильтона вместо (34), (35) обычно применяется следующее общее выражение для условий трансверсальности:

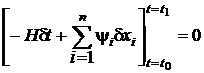. (36)

Запись в форме (25.10) трактуется следующим образом:

заключенное в скобки условие применяется как для левой t=t₀, так и для правой t=t₀ границ (концов временного интервала);

если рассматриваемая граница задана, для нее вариация t=0, если задано граничное условие x_i0 или x_i1, для данной границы и соответствующего i вариация x_i=0, следовательно все слагаемые в (36), содержащие такие вариации, тождественно равны нулю;

-    для всех отсутствующих в задаче граничных условий соответствующие вариации t и x_i являются ненулевыми и взаимно независимыми, следовательно, условие (36) будет выполняться только при равенстве нулю соответствующих сомножителей при вариациях, то есть при выполнении системы условий (34)-(35).

Рассмотренная система необходимых и достаточных условий достижения экстремума функционала в рамках вариационного исчисления обеспечивает получение локальных экстремумов. Этого вполне достаточно в задачах без ограничений на переменные состояния объекта управления или на управляющие сигналы. Если область допустимых управлений не ограничена, абсолютный экстремум совпадает с локальным. Если в задаче рассматривается некоторая ограниченная область допустимых состояний или управлений, задачу оптимизации нельзя свести к определению локального экстремума. Абсолютный экстремум в ряде случаев может совпадать с границей допустимой области.

Для задач с ограничениями используются специальные методы оптимизации, наиболее известными из которых являются принцип максимума Понтрягина и динамическое программирование Беллмана. Наиболее удобен для решения практических задач в силу своей простоты принцип максимума. Рассмотрим этот метод для задач с ограничением на управление.

Основная формулировка принципа максимума соответствует задаче обеспечения минимума функционала путем выбора оптимального управления в пределах некоторой области допустимых управлений: .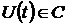

Для достижения минимума функционала (28) при заданных уравнениях объекта управления (25.1) необходимо достижение максимума функции Гамильтона по управлению

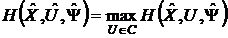 (37)

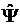при фиксированных  и , соответствующих экстремуму, и соблюдении условий трансверсальности.

Следует подчеркнуть, что речь здесь идет о достижении абсолютного экстремума.

Отметим также важную особенность, определяющую удобство применения принципа максимума: уравнение (25.11) позволяет свести задачу обеспечения минимума функционала к задаче обеспечения максимума функции Гамильтона как функции одной или нескольких переменных - составляющих вектора управления U. Предусматривается решение такой задачи для всех моментов времени в пределах рассматриваемого интервала.

Обычно область С определяется неравенствами 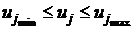, j=1,2,...,r.

Оптимальное управление на основе (25.11) может быть получено в следующих вариантах:

как локальный экстремум внутри области C в соответствии с условиями (25.7);

как абсолютный экстремум на границе области С (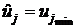 или );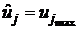

как кусочно-непрерывная функция, на отдельных временных интервалах совпадающая с границами, а на других - принимающая значения внутри области C.

В последнем случае для точек разрыва управления (при t=t^*) следует учитывать недопустимость скачкообразного изменения переменных состояния объекта управления (условия припасовывания):

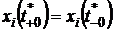, i=1,2,...,n;

и условия Вейерштрассе-Эрдмана:

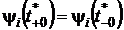, i=1,2,...,n; .

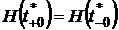Для того что бы выяснить насколько оптимально решение по критерию Красовского , решим эту задачу с помощью принципа максимума методом Ньютона.

Решение задачи методом Ньютона включает в себя следующие шаги:

.        Выбирается некоторое начальное приближение .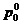

2.      Решается 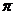- система с начальными условиями 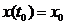, на интервале .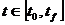

3.      Вычисляется вектор .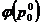

4.      В соответствии с формулой Тейлора, 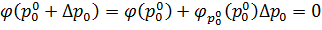, откуда

5.      Определяется следующее приближение для вектора p₀: 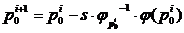, где скалярный множитель 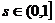. Выбор величины s происходит из требования 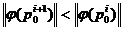. В качестве нормы 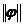 принимают либо 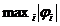, либо .

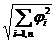.        Проверяется условие 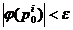, i = 1, 2, …, невыполнение которого возвращает алгоритм к п.1. Здесь 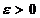- любая малая положительная величина.

Матрица 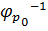 - обратная матрице частных производных .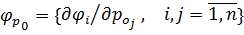

В качестве 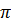-системы следует принять совместное решение систем (17) и (24).

Управление находится из принципа максимума :

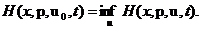 (26)

В соответствии с условиями трансверсальности следует принять функцию невязок в виде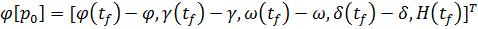(27):

(27)

Далее, решим исходную систему данным методом, используя те же начальные параметры что и для алгоритма с прогнозирующей моделью. :

Полученные результаты :

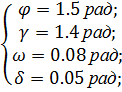
при t =3.5 сек.

В данном случае следует пояснить : как видно из алгоритма решения методом Ньютона - решается задача с правым свободным концом при предельных режимах отклонения угла крена. Данное решение может быть принято как оптимальное по быстродействию , однако следует учесть что после совершения маневра ЛА не восстанавливает свое исходное состояние в пространстве, и продолжает движение с креном 1.4 рад.

В случае , если возникнет необходимость обеспечить исходное состояние ЛА в пространстве связанной системы координат, то можно решить эту задачу добавив в вектор конечных состояний условие 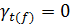 при этом решение будет выглядеть следующим образом :

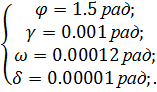
при t =11.8 сек.

В данном случае длительность процесса обеспечивается общей инерционностью системы , и необходимостью фактически двойного изменения угла крена, что приводит систему в состояние , при котором на предельном управлении она движется очень ограниченное время , остальное же можно рассматривать как переходный процесс до и после такого движения.

Заключение

Решение задачи оптимального управления методом Красовского подходит для нахождения решения компромиссного характера для всей системы , для всей системы , и далеко не всегда обеспечивает выход на заданные режимы полета. Однако требуемого решения можно достигнуть произведя нужною балансировку свободных коэффициентов , что и было сделано в данном случае. Компромиссное решение может оказаться полезным в условиях неопределенности дальнейших действий ЛА, так как вывод ЛА из разворота на предельных режимах может создать неблагоприятные условия для дальнейшего маневрирования.

Список использованных источников

1) Кабанов С.А. Оптимизация динамики систем при действии возмущений . М: ФИЗМАТЛИТ, 2008

) Кабанов С.А. Управление системами на прогнозирующих моделях. СПб: Издательство С-Петербургского университета, 1997

)Е.М. Воронов Методы оптимизации управления многообъектными многокритериальными системами на основе стабильно-эффективных угровых решений. М: Издательство МГТУ им. Баумана, 2001

)Кабанов С.А. прикладные задачи оптимального управления . СПб: БГТУ , 2007

5)Бородавкин В.А. Зверев А.И. Кабанов С.А. Санников В.А. Шалыгин А.С Траектории. Аэродинамика. Характеристики летательных аппаратов. СПб: БГТУ , 1989

) Лебедев А.А. Чернобровкин Л.С. Динамика полета М: Машиностроение , 1973

ПриложениеА

Исходный код программы реализующей алгоритм с прогнозирующей моделью

t0=0=10=0.1=9.8;=288;=-1.8=-22.4=0.00001;

%%=1.56;(1)=0;(1)=0;(1)=0;(1)=0;(1)=0;=[t0:dt:tf];

%%(1)=0;(1)=0;(1)=0;(1)=0;(1)=0;(1)=0;(1)=0;(1)=0;(1)=1;=1;t_now=1:length(t)(t_now)=qfi(t_now);(t_now)=qgamma(t_now);(t_now)=qomega(t_now);(t_now)=qdelta(t_now);i=t_now:length(t)(i+1)=fi(i)+dt*g/v*tan(gamma(i));(i+1)=gamma(i)+dt*omega(i);(i+1)=omega(i)+dt*(Mw*omega(i)+Md*delta(i));

delta(i+1)=delta(i)+dt*u(i);(i+1)=u(i);;(t_now)=ro2*(fi(length(t))-fzad);(t_now)=ro1*gamma(length(t));(t_now)=ro3*omega(length(t));(t_now)=ro4*delta(length(t));=p1;=p2;=p3;=p4;i=t_now:length(t)

fi(i+1)=fi(length(t)-i+1)-dt*g/v*tan(gamma(i));

gamma(i+1)=gamma(length(t)-i+1)-dt*omega(i);

omega(i+1)=omega(length(t)-i+1)-dt*(Mw*omega(i)+Md*delta(i));

delta(i+1)=delta(length(t)-i+1)-dt*u(i);

p1(i+1)=p1(i);

p2(i+1)=p2(i)-dt*(-p1(i)*g/(v*cos(gamma(i))*cos(gamma(i))));

p3(i+1)=p3(i)-dt*(-p2(i)-p3(i)*Mw);

p4(i+1)=p4(i)-dt*(-p3(i)*Md);;=-k*p4(length(t));(t_now)=UU;(t_now+1)=qfi(t_now)+dt*g/v*tan(qgamma(t_now));(t_now+1)=qgamma(t_now)+dt*qomega(t_now);qgamma(t_now+1)>1.5

qgamma(t_now+1)=1.5;;(t_now+1)=qomega(t_now)+dt*(Mw*qomega(t_now)+Md*qdelta(t_now));qomega(t_now+1)>1.45

qomega(t_now+1)=1.45;;

qdelta(t_now+1)=qdelta(t_now)+dt*qu(t_now);(t_now+1)=qu(t_now);(t_now+1)=qx(t_now)+dt*v*cos(qfi(t_now+1));(t_now+1)=qz(t_now)+dt*v*sin(qfi(t_now+1));=-0.000001*p1(t_now)*g/v*tan(qgamma(t_now))+p2(t_now)*qomega(t_now)+p3(t_now)*(Mw*omega(t_now)+Md*delta(t_now));(t_now+1)=tt(t_now)+W;;=fix(100*tt(length(t)));

progn_fi=qfi_gamma=qgamma_delta=qdelta_u=qu_omega=qomega=[t0:dt:tf+dt];(t, progn_fi);(t,progn_gamma);(t,progn_omega);(t, progn_delta);(t,progn_u);

%%

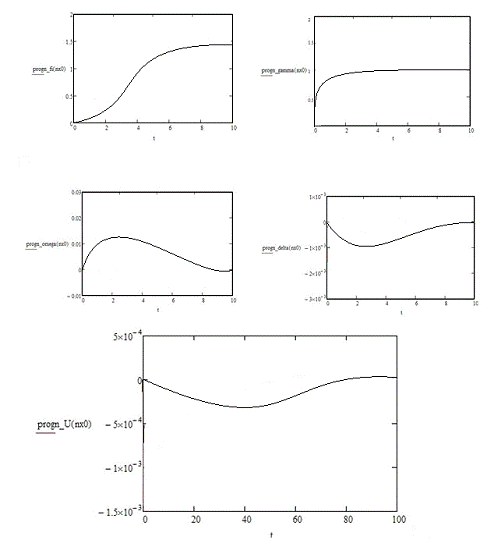
Приложение Б

Графики изменения исследуемых величин

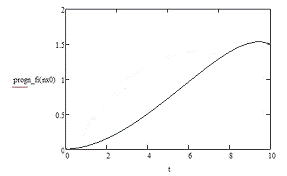
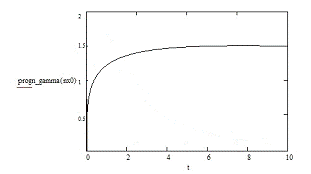
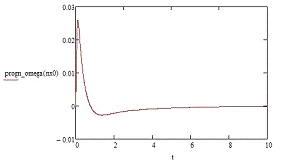
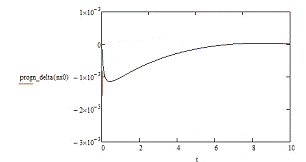
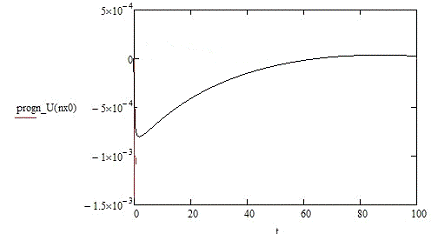
Приложение В

Графики изменения исследуемых величин