Исследование операций и системный анализ
Исследование
операций и системный анализ
Контрольная работа № 1
А. Исходя из содержания задачи, установить
возможные состояния системы и построить размеченный граф состояний.
Б. Составить по размеченному графу состояний
систему дифференциальных уравнений Колмогорова и затем - систему алгебраических
уравнений для финальных вероятностей состояний.
В. Путем решения системы алгебраических
уравнений определить финальные вероятности состояний исследуемой системы.
Задача 1.1.
Состояние технического устройства
(ТУ) непрерывно контролируется в процессе эксплуатации. В любой момент времени
ТУ может выйти из строя. В случае возникновения отказа немедленно
осуществляется восстановление его готовности. И поток отказов и поток
восстановления - простейшие. Параметр потока отказа - λ, среднее
время восстановления - tср,
интенсивность восстановления - 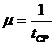 .
.
Рассчитать и построить графики
зависимостей вероятности состояния готовности к работе (исправного состояния) -
Рr от времени восстановления (времени
восстановления отказов) - tср при
различных значениях параметра потока отказов - λ.
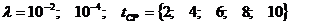
Решение:
1.) Заданное техническое
устройство может находиться всего в двух состояниях: 1 - исправное; 2 -
неисправное. При этом параметр потока отказов λ; а
интенсивность немедленного восстановления - 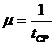
μ
λ
2.) По размеченному графику состояний
составим систему дифференциальных уравнений Колмогорова:
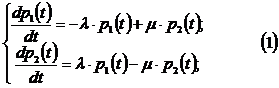
Кроме того, исправим очевидное соотношение:
Выразим через из соотношения (2) и
подставим в систему (1) Получим:
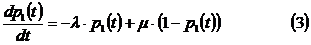
Будем искать решение уравнения (3) в
виде:
Тогда 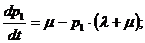
 ,
,
Откуда 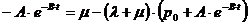 ;
;
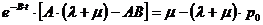
Следовательно: 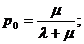
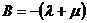
Параметр А определим из начальных
условий:
При 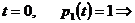
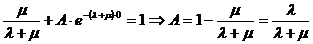
Тогда окончательный результат имеет
вид:
вероятность нахождения ТУ в
исправном состоянии
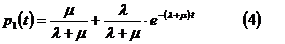
.) Рассчитаем и построим
графики зависимостей 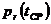 при различных
значениях λ
и
заданных . При этом будем считать, что
при различных
значениях λ
и
заданных . При этом будем считать, что 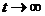 (финальное состояние ТУ), и из
формулы (4) получим:
(финальное состояние ТУ), и из
формулы (4) получим:
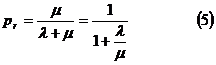
Результаты расчета сведены в таблицу
и представлены на графике:
Задача 1.2
На борту самолёта находится агрегат,
который может отказать. Поток отказов - ω. Отказ обнаруживается только в
процессе регламентного технического обслуживания. Среднее время между
техническими обслуживаниями равно ТСР, среднее время технического обслуживания
равно ТТО, среднее время обнаружения неисправности равно:
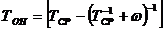
Определить финальные вероятности
состояний агрегата.
Дано:
|
№№
Вариантов
|
ω1 1/ч
|
Тто,
ч
|
Тср,
лет
|
|
1
|
10-4
|
2,0
|
0,8
|
Решение:
1. Г, S1
- готовность;
2. ТО, S2
- техническое обслуживание;
. СО/ТО, S3
- скрытый отказ;
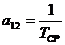 ;
; 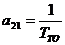 ;
; 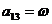 ;
; 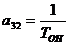 .
.
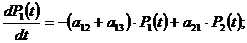
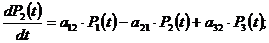
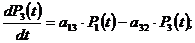
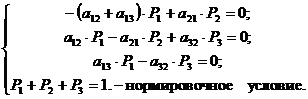
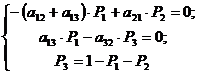
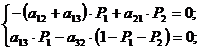
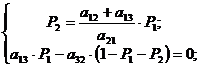
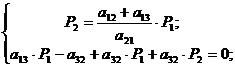
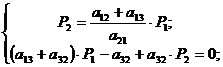
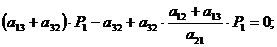
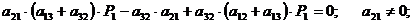
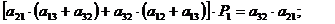
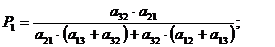
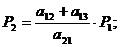
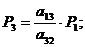
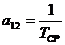 ;
; 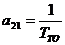 ;
; 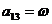 ;
; 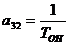 .
.
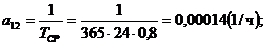
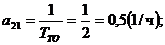
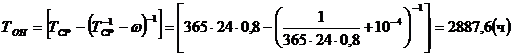 .
.
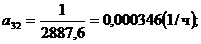
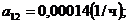 ;
; 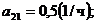 ;
; 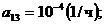 ;
; 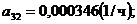 .
.
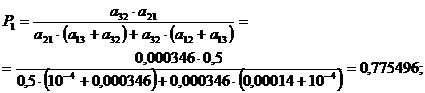
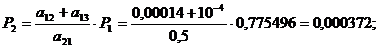
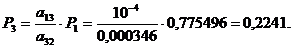
Получили:
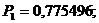
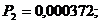
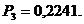
Задача 1.3
Техническое устройство (ТУ) подвергается
простейшему потоку отказов с интенсивностью λ. Отказ
обнаруживается не сразу, а через случайное время, распределенное по
показательному закону с параметром ν. Как
только отказ обнаружен, производится осмотр ТУ, в результате которого он либо
отправляется в ремонт (вероятность этого ρ), либо
списывается и заменяется новым. Время осмотра случайно и описывается
показательным законом и параметром γ, время
ремонта - показательное с параметром μ.
Время замены списанного ТУ новым - показательное
с параметром κ.
Найти финальное состояние ТУ и определить какую
долю в среднем ТУ будет работать нормально и какую долю времени в среднем ТУ
будет находиться с необнаруженным отказом.
|
№№
вар
|
1
|
|
λ,
1/ч
|
0,01
|
|
ν,
1/ч
|
1,0
|
|
ρ
|
0,8
|
|
γ,
1/ч
|
10,0
|
|
μ,
1/ч
|
0,5
|
|
κ,
1/ч
|
2,0
|
Решение:
.) Заданное техническое устройство может
находиться в следующих состояниях:
1 - исправное состояние
- неисправное состояние с необнаруженным отказом
- неисправное состояние с обнаруженным отказом
без осмотра
- неисправное состояние с обнаруженным отказом
после осмотра
- неисправное состояние в процессе ремонта и
перевода в (1)
- неисправное состояние в процессе списания и
замены в (1)
Размеченный график состояния системы таков:
2.) По размеченному графику состояний
составим систему дифференциальных уравнений Колмогорова:
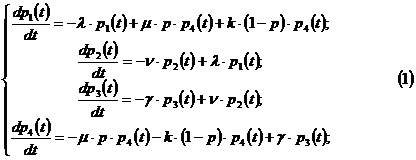
Так как нас интересуют лишь
финальные состояния системы, то левые части равенств системы приравняем к нулю,
а знак зависимости от времени опустим, и четвертое уравнение системы заменим
очевидным равенством (2):
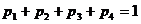
Получим: 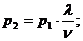
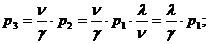

Обозначим 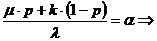
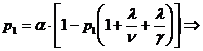
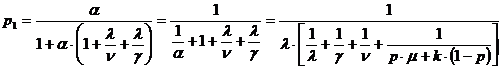
Тогда 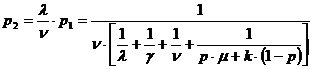
Произведем теперь численный расчет
требуемых величин:
а.) Финальные вероятности состояний
ТУ таковы:
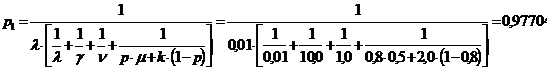
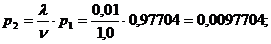
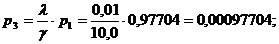
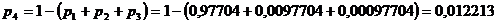
б) ТУ в среднем будет работать
нормально в течении 97,7% времени работы; ТУ будет находиться в среднем с
необнаруженным отказом в течении 0,9% времени.
Контрольная работа № 2
алгебраический
колмогоров вероятность
А. Исходя из содержания задачи,
установить тип системы массового обслуживания по характеру входящего потока,
распределению времени обслуживания, числу обслуживающих приборов, длины
очереди.
Б. Установить, какие характеристики
рассматриваемой СМО должны быть определены и, пользуясь приведенными в
Приложении справочными формулами, определить их характеристики.
В. Сделать выводы по результатам
расчетов.
Задача № 2.1.
Авиационная касса имеет два окошка,
в каждом из которых продаются авиабилеты в два пункта: в Саратов и в Волгоград.
Потоки пассажиров, приобретающих билеты в Саратов и в Волгоград, одинаковы по
интенсивности, которая равна λ0. Среднее
время обслуживания пассажира (продажи ему билета) равна 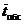 . Поступило
рационализаторское предложение: для уменьшения дли очередей и времени
пребывания в них (в интересах пассажиров) сделать обе кассы
специализированными: в первой продавать билеты только в Саратов, а во второй -
только в Волгоград. Считая потоки простейшими, проверить разумность такого
предложения для значений параметров, приведенных в таблице 2.1.
. Поступило
рационализаторское предложение: для уменьшения дли очередей и времени
пребывания в них (в интересах пассажиров) сделать обе кассы
специализированными: в первой продавать билеты только в Саратов, а во второй -
только в Волгоград. Считая потоки простейшими, проверить разумность такого
предложения для значений параметров, приведенных в таблице 2.1.
|
№№
вар
|
1
|
|
λ0
1/мин
|
0,1
|
|
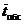 , мин0,45 , мин0,45
|
|
Решение:
Для решения задачи необходимо сравнить два
варианта:
а) одна очередь с интенсивностью 2λ0
и экспоненциальным временем обслуживания с параметром μ;
б) две независимые очереди с интенсивностью
потока в каждой из них λ0
и экспоненциальным временем обслуживания с параметром μ;
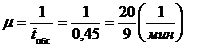
б) Во втором варианте воспользуемся
формулами таблицы п. 3.1 МУ (колонка 5), так как в этом случае при Nпр = 1; Eнак = ∞.
Тогда среднее время пребывания пассажира в системе
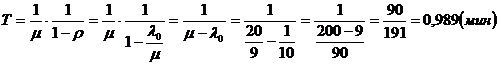
а) В первом варианте воспользуемся
формулами таблицы п. 3.1 МУ (колонка 7), где принимаем n = 2 =Nпр , а ёмкость
очереди m такова,
чтобы вместимость всех приходящих пассажиров: m = 1.
В этом случае 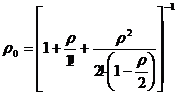 , где
, где  ,
,
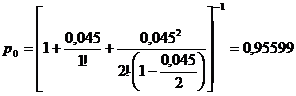 .
.
Следовательно, 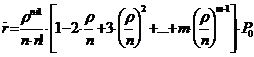 , получаем
, получаем 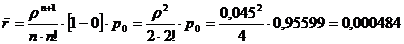 ,
,
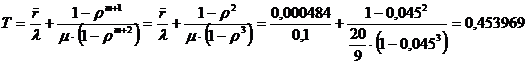
Так как время получения
пассажирского билета в первом варианте почти в два раза меньше, чем во втором,
то время пребывания в очередях увеличивается, и превращение касс в
специализированные не является разумным.
Задача № 2.2.
Авиационная техническая база (АТБ)
имеет одно место для обслуживания самолетов, которые прибывают на обслуживание
случайным образом и, если их не могут сразу обслужить, они становятся в
очередь. На длину очереди ограничений нет.
Промежуток времени t между двумя
последовательными прибытиями самолетов удовлетворяет экспоненциальному закону с
параметром λ. Время
обслуживания на АТБ также имеет экспоненциальное распределение с параметром μ. Значения λ и μ приведены в
таблице 2.2.
Определить:
· вероятность простоя АТБ - Р0,
· среднюю длину очереди -  ,
,
· среднее время ожидания в очереди - 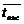 ,
,
· общее время обслуживания АТБ - 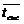 .
.
|
№№
вар
|
1
|
|
λ,
1/сутки
|
1
|
|
μ,
1/час
|
1,0
|
Решение:
Техническое обслуживание самолётов на АТБ
является системой массового обслуживания с пуассоновским входящим потоком и
экспоненциальным временем обслуживания. СМО - одноканальная (одно место
обслуживания, Nпр
= 1), с ожиданием и без ограничения длины очереди (Енак = ∞ ).
Воспользуемся формулами таблицы п.3.1 МУ
(колонка 5).
Это допустимо, так как отношение 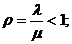
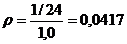 .
.
Тогда получим:
вероятность простоя Р0 = 1 - ρ =
1 - 0,0417 = 0,9583.
средняя длина очереди 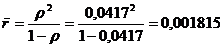 .
.
среднее время нахождения в очереди 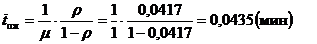
общее время обслуживания АТБ 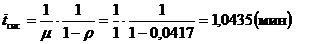
Задача № 2.3.
В АТБ в ангаре имеется n мест для
технического обслуживания самолетов и перед ангаром m стоянок для
ожидания обслуживания. Поток прибывающих на обслуживание самолетов -
пуассоновский с параметром λ, время технического обслуживания -
случайная величина, распределенная по экспоненциальному закону с параметром μ. Варианты
значений n, m, λ и μ приведены в
таблице 2.3.
Определить:
o вероятность простоя АТБ - Р0,
o вероятность того, что прибывающему
самолету будет отказано в обслуживании - Ротк,
o среднее число занятых мест
обслуживания - 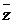 ,
,
o среднее число самолетов, стоящих в
очереди на обслуживание - 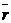 ,
,
o среднее время оживания в очереди - 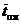 ,
,
o общее время, затраченное на
обслуживание - 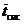 .
.
|
№№
вар
|
1
|
|
n
|
3
|
|
m
|
3
|
|
λ,
1/сутки
|
3,5
|
|
μ,
1/час
|
0,15
|
Решение:
Техническое обслуживание самолётов на АТБ
является системой массового обслуживания с пуассоновским входящим потоком и
экспоненциальным временем обслуживания. СМО - многоканальная (Nпр
= n), с ожиданием и
ограничениtv длины
очереди (Енак = m
).
Воспользуемся формулами таблицы п.3.1 МУ
(колонка 7).
Параметр 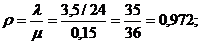
Тогда получим:
вероятность простоя
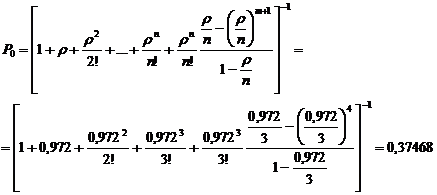
вероятность того, что прибывающему
самолёту будет отказано в обслуживании 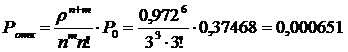
среднее число занятых мест обслуживания
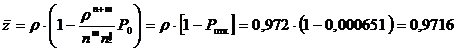
среднее число самолётов, стоящих в
очереди обслуживания
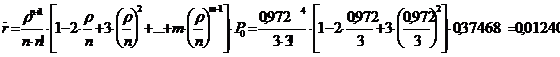
среднее время ожидания в очереди 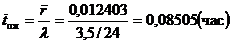
общее время, затраченное на
обслуживание