|
xi
|
1.24
|
3.5
|
1.14
|
|
yi
|
1.7530
|
1.8308
|
1.0620
|
Узагальнимо метод Лагранжа для знаходження значень в
будь-яких точках заданого відрізка. Напишемо файл-функцію Lagrange.m і тестову
програму TestLagran.m
Файл lagrange.m
yy=lagrange(x,y,xx)
% обчислення інтерполяційного полінома у формі Лагранжа
% х - масив координат вузлів
% в - масив значень інтерпольованої функції
% xx - масив значень аргументу, для яких треба обчислити
значення полінома
% yy - масив значень полінома в точках xx
% обчислюємо число вузлів інтерполяції (N=n+1)=length(x);
% створюємо нульовий масив значень інтерполяційного
полінома=zeros(size(xx));
% в циклі рахуємо суму по вузлахk=1:N
% обчислюємо добутки=ones(size(xx)); %створення масиву
одиничних елементівj=[1:k-1, k+1:N]=t.*(xx-x(j))/(x(k)-x(j));
% накопичуємо суму= yy + y(k)*t;
Файл TestLagran.m
% TestLagran.m= [1.1 1.6 2.1 2.6 3.1 3.6]; = [1.03 1.39 1.65
1.80 1.85 1.82];=[2.4 3.5 1.14];
[yy]= lagrange(x,y,xx)
% побудова графіків
% виведення вузлів інтерполяції(х)(x, y, 'ko')on
% виведення графіка полінома(xx,yy,'r')
Виконуємо файл TestLagran.m у Матлабі та отримуємо.
>> TestLagran
yy = 1.7529 1.8314 1.0618
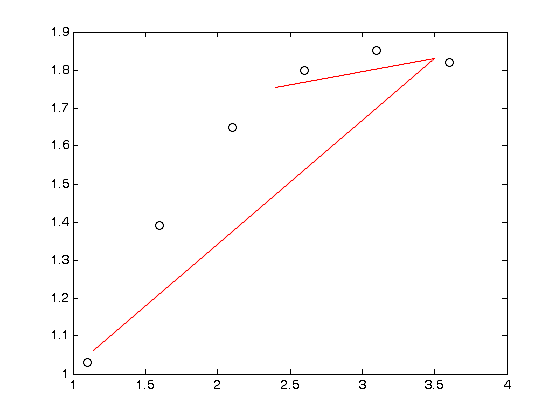
Рис. 4
. Інтерполяційний поліном Ньютона
Інтерполяційний поліном Ньютона ступеня <n, який проходить
через точки (xk, yk ) можна представити в наступній
загальній формі:
(х)=d0,0+d1,1(х-х0)+….+dn,n(х-х0)(х-х1)(х-xn-1)
де dk,k= d[х0,х1,....,xk]
- скінчені різниці
k,0 = yk і dk,j= (dk,j-1
- dk-1,j-1)/(xk - xk-j)
Для побудови і обчислення полінома Ньютона напишемо функцію
[C,D] = newpoly(х,у) і збережемо її у файлі newpoly.m
Файл newpoly.m
function [C,D]=newpoly(x, y)
%Вхід х - вектор абсцис
% y - вектор ординат
%Вихід C - вектор коефіцієнтів полінома Ньютона
% D - таблиця скінчених різниць=length(x);=zeros(n,n);(:,1)=y';
%транспонування рядка в стовпець
%Формування таблиці скінчених різниць
Dj=2:nk=j:n(k,j)=(D(k,j-1)-D(k-1,j-1))/(x(k)-x(k-j+1));
% Обчислення коефіцієнтів полінома
Ньютона=D(n,n);k=(n-1):-1:1=conv(C,poly(x(k)));=length(C);(m)=C(m)+D(k,k);
Тест-програма, в якій задаються вхідні дані, викликається
функція newpoly і обчислюються значення полінома в заданих точках.
Файл Testnewpoly.m
%Тест TestNewpoly =[1.1 1.6 2.1 2.6 3.1 3.6]; =[1.03 1.39
1.65 1.80 1.85 1.82];
[C,D]=newpoly(x,y)
%Значения полінома в заданих
точках=polyval(C,2.4)=polyval(C,3.5)=polyval(C,1.14)
Виконаємо TestNewpoly в робочому середовищі Matlab
>> TestNewpoly
 = 1.7529= 1.8314= 1.0618
= 1.7529= 1.8314= 1.0618
. Інтерполяція сплайнами
Найпростішим способом інтерполяції є наближення даних
сплайном нульового порядку (на кожній ділянці ступінь полінома дорівнює нулю),
при якому значення в кожній проміжній точці приймається рівним найближчому
значенню, заданому в таблиці. В результаті дані наближаються східчастою
функцією, а саме наближення називається інтерполяцією по сусідніх точках.
Лінійна інтерполяція заснована на з'єднанні сусідніх точок відрізками прямих -
табличні дані наближаються ламаною лінією. Для отримання більш гладкої функції
слід застосовувати інтерполяцію кубічними сплайнами. Всі ці способи реалізовані
у функції Matlab interpl, у якості вхідних аргументів якої указуються
координати абсцис і ординат табличної функції, координати абсцис проміжних
точок, в яких обчислюються значення полінома і спосіб інтерполяції. Текстові
константи, які задають спосіб інтерполяції:
‘nearest’ - наближення по сусідніх елементах;
‘linear’ - лінійна інтерполяція;
‘spline’ - інтерполяція кубічними сплайнами.
Вихідним аргументом interp1 є вектор значень полінома в
проміжних точках.
Напишемо файл-програму, яка демонструє всі ці способи
інтерполяції і обчислює значення функції в заданих точках.
Файл interplSpline.m=[1.1 1.6 2.1 2.6 3.1 3.6]; =[1.03 1.39
1.65 1.80 1.85 1.82];
%проміжні точки інтерполяції =[x(1):0.01:x(length(x))];
%задані точки інтерполяції =[2.4 3.5 1.14];
% побудова графіків
% виведення вузлів інтерполяції(х) на графік(x,y,'ko')on
% обчислення східчастої функції в проміжних
точках=interp1(x,y,xi,'nearest');
% обчислення кусково-лінійної функції в проміжних
точках=interp1(x,y,xi,'linear');
% обчислення кубічного сплайна в проміжних
точках=interp1(x,y,xi,'spline');(xi,ynear,'k',xi,yline,'k:',xi,yspline,'k-.')
%title ('Способи інтерполяції функцій')('\itx')('\ity')
%legend ('таблична функція','по сусіднім
елементам','лінійна','кубічними сплайнами')
%Обчислення значень функції в заданих
точках=interp1(x,y,xx,'nearest')=interp1(x,y,xx,'linear')=interp1(x,y,xx,'spline')
Виконуємо файл interplSpline.m у Матлабі та отримуємо
значення та малюнок.
>> interplSpline
ynear = 1.8000 1.8200 1.0300= 1.7400 1.8260 1.0588= 1.7529
1.8314 1.0621
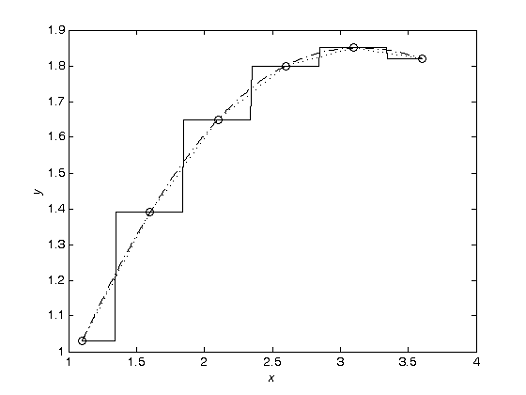
Рис. 7 'Способи інтерполяції функцій'
Представимо знайдені результати в таблиці.
Таблиця 6
|
Спосіб згладжування
|
xi
|
2.4
|
3.5
|
1.14
|
|
По найближчих
точках (nearest)
|
yi
|
1.8000
|
1.8200
|
1.0300
|
|
Лінійна
інтерполяція (linear)
|
yi
|
1.7400
|
1.8260
|
1.0588
|
|
Кубічним сплайном
(spline)
|
yi
|
1.7529
|
1.8314
|
1.0621
|
поліном інтерполяція диференціювання функція
Практична робота №2
Диференціювання полінома
Нехай функція f(х) задана на відрізку [a,b] =[1,1.5] вузлами
інтерполяції, поданими в таблиці 7
Таблиця
7
|
xi
|
1.1
|
1.6
|
2.1
|
2.6
|
3.1
|
3.6
|
|
yi
|
1.03
|
1.39
|
1.65
|
1.80
|
1.85
|
1.82
|
Необхідно побудувати інтерполяційні поліноми і обчислити з їх
допомогою значення f’(xi) в заданих точках xi.
х1=2.4
х2=3.5
х3=1.14
. Введемо два вектори і заповнимо їх початковими даними:
х=[1.1 1.6 2.1 2.6 3.1 3.6];
у=[1.03 1.39 1.65 1.80 1.85 1.82];
Як ми знаємо, в MATLAB поліноми представляються у вигляді
вектора своїх коефіцієнтів. Скористаємося функцією polyfit=(х,у,n) для
знаходження коефіцієнтів полінома 4-го ступеню.
polyfit=(х,у,n)
де х - вектор значень абсцис;
у- вектор значень ординат;ступінь полінома.
>> x = [1.1 1.6 2.1 2.6 3.1 3.6];
>> y = [1.03 1.39 1.65 1.80 1.85 1.82];
>> p4=polyfit(x, y, 4);
Відповідь: >> p4= 0.0100 -0.0844 0.0472 0.9578 0.0169
Якщо n - ступінь полінома, то аналітичний запис його буде
наступним:
.0100x4 - -0.0844x3 + 0.0472x2
- 0.9578x + 0.0169
Для обчислення похідної полінома призначена функція polyder.
Виклик цієї функції з одним аргументом - вектором коефіцієнтів полінома,
приводить до обчислення вектора коефіцієнтів похідної полінома.
Знайдемо коефіцієнти вектора першої похідної полінома р4
>> d1 = polyder(p4)
Відповідь:= 0.0400
-0.2531 0.0944 0.9578
Отже, ми отримали
коефіцієнти полінома 3-й ступеню:
.0400x3 - 0.2531x2 +
0.0944x + 0.9578
Переконатися в
правильності отриманої відповіді можна “вручну” продиференціювавши поліном р4.
Знайдемо значення
похідної в заданих точках:
>> df1 =
polyval(d1, 2.4)
Відповідь:= 0.2794
>> df2 =
polyval(d1, 3.5)
Відповідь:= -0.0973
>> df3 =
polyval(d1, 1.14)
Відповідь:
= 0.7957
Знайдемо похідні
вищих порядків.
>> d2 =
polyder(d1)= 0.1200 -0.5062 0.0944
>> d3 =
polyder(d2)= 0.2400 -0.5062
>> d4 =
polyder(d3)= 0.2400
Геометричний зміст похідної
Побудуємо графік інтерполяційного полінома на відрізку
інтерполяції.
=1.0:0.05:1.5
>> t=1.0:0.05:3.6
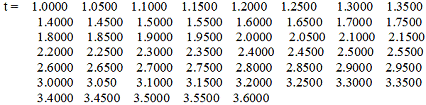
>> P4 = polyval(p4, t)
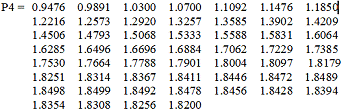
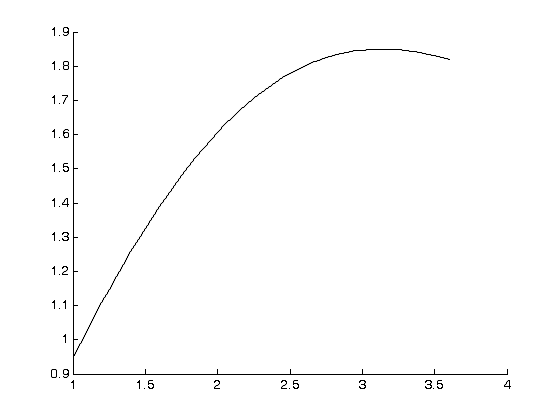
Рис. 8
У тому самому вікні побудуємо графік дотичної в т. х1=1.26.
Похідна
>> df1 = polyval(d1,2.4)
df1 = 0.2794
Рівняння дотичної, яка проходить через задану точку x0:
y0=y’(x-x0)
Для нашого прикладу це буде рівняння:
= 1.7530+0.2794*(t-2.4)
>> Y = 1.7530+0.2794*(t-2.4)
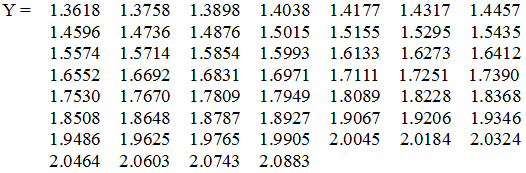
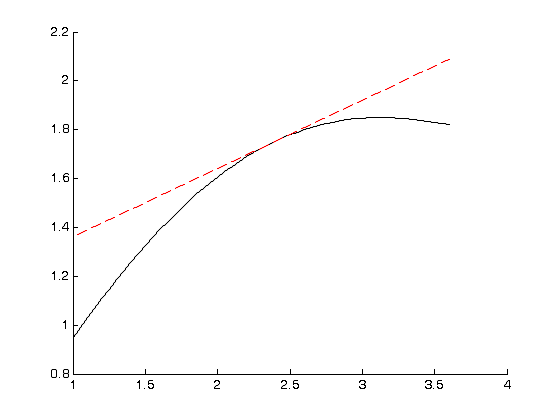
Рис. 9 Наближення табличної функції та дотична
Скінчені різниці
Диференціал функції дорівнює df(x) = f’(х)dx
i = Dxi = xi+1-xi - прирост аргументу(xi)=
Dyi = yi+1 - yi
- прирост функції
Геометричний зміст диференціала
Диференціал функції графічно зображається приростом ординати
дотичної, проведеної до заданої точки.
Прирости функцій називаються скінчені різниці.
Знайдемо різниці між точками нашої табличної функції
Таблиця 8
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
|
xi
|
1.1
|
1.6
|
2.1
|
2.6
|
3.1
|
3.6
|
|
Yi
|
1.03
|
1.39
|
1.65
|
1.80
|
1.85
|
1.82
|
Побудуємо таблицю різниць її значень
Таблиця 9
|
Dx1= x2-x1
|
Dx2=x3-x2
|
Dx3=x4-x3
|
Dx4=x5-x4
|
Dx5=x6-x5
|
0.1
|
0.1
|
0.1
|
0.1
|
0.1
|
|
Dy1= y2-y1
|
Dy2=y3-y2
|
Dy3=y4-y3
|
Dy4=y5-y4
|
Dy5=y6-y5
|
|
Dyi
|
0.02
|
0.03
|
0.03
|
0.04
|
0.05
|
Якщо відстані між вузлами однакові Dx1=Dx2=Dx3 = h.., то доцільно
побудувати різниці другого та третього порядків для значень функції D2yk, D3yk.
Таблиця 10
|
D2y1= Dy2-Dy1
|
D2y2=y3-y2
|
D2y3=y4-y3
|
D2y4=y5-y4
|
|
D3y1=D2y2
- D2y1
|
D3y2=D2y3
- D2y3
|
D3y3=D2y4
- D2y3
|
|
Для знаходження вектора різниць вказаного порядку в Matlab
призначена функція diff, яка може викликатися з одним або двома аргументами:
=diff(x) - обчислення
різниць 1-го порядку,nx=diff(x,n) - обчислення різниць n-го порядку.
Знайдемо різниці 1-го
та 2-го порядку для векторів табличної функції та диференціали dy/dx d2y/dx
в цих точках.
Напишемо програму
myDif.m у вигляді файл-програми.
% myDif.m - знаходження диференціала табличної функції
Файл myDif.m=[1.1 1.6
2.1 2.6 3.1 3.6];=[1.03 1.39 1.65 1.80 1.85
1.82];=diff(x)=diff(y)=dy./dxy=diff(y,2)
Отримаємо значення за
допомогою нашої функції nyDif
>> myDif
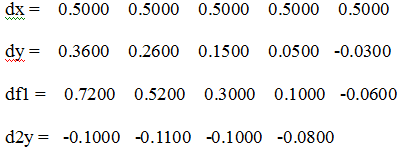
Результати обчислень запишемо в таблицю
Таблиця 11
|
x
|
dx
|
y
|
dy
|
dy/dx
|
d2y
|
|
1.1
|
0.5
|
1.03
|
0.36
|
0.72
|
- 0.1
|
|
1.6
|
0.5
|
1.39
|
0.26
|
0.52
|
- 0.11
|
|
2.1
|
0.5
|
1.65
|
0.15
|
0.3
|
- 0.1
|
|
2.6
|
0.5
|
1.80
|
0.05
|
0.1
|
- 0.08
|
|
3.1
|
0.5
|
1.85
|
- 0.03
|
- 0.06
|
|
|
3.6
|
|
1.82
|
|
|
|
Диференціювання полінома Ньютона
Таблиці різниць використовуються для знаходження похідної
табличної функції, для наближення якої використовується інтерполяційний поліном
Ньютона.
Поліном Ньютона має наступний загальний вигляд:
n(x)=d0,0+d1,1(x-x0)+…+dn,n(x-x0)(x-x1)…(x-xn-1),
где dk,k=
d[x0,x1,…xk] - скінчені різниці. k,0 =
yk и dk,j= (dk,j-1 - dk-1,j-1)/(xk
- xk-j)
Для знаходження
похідної функції в точках xi (1<i<n) використовується формула
(отримана шляхом диференціювання півсум формул Ньютона 1-го порядку):
'(xi) = (Dyi-1 + Dyi)/2)/h
Ця формула непридатна
для диференціювання в граничних точках відрізку. Для цього скористаємося
наступними формулами другого порядку:
'(x1) = (Dy1 - D2y1)/2)/h '(xn) = (Dyn-1 - D2yn-2)/2)/h
Файл-програма
myDiff.m демонструє використання різниць для знаходження першої похідної у
вузлових точках.
Файл myDiff.m=[1.1
1.6 2.1 2.6 3.1 3.6];=[1.03 1.39 1.65 1.80 1.85
1.82];=length(x);=x(2)-x(1);=zeros(n);=diff(x);=diff(y);=dy./dx;y=diff(y,2);(1)=((dy(1)-d2y(1))/2)/h;
(6)=((dy(5)-d2y(4))/2)/h;k=2:(n-1)(k)=((dy(k-1)+ dy(k))/2)/h;
Запускаємо програму і
отримаємо:
>> myDiff
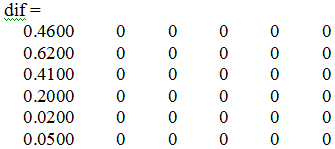
Крім цього, для
знаходження похідної інтерполяційного полінома Ньютона можна використати раніше
розроблену функцію newpoly.
Скористаємося
функцією [C,D] = newpoly(x,y), яка знаходить коефіцієнти інтерполяційного
полінома Ньютона.
[C,D]=newpoly(x,y)
%Вхід x - вектор
абсцис
% y - вектор ординат
%Вихід C - вектор
коефіцієнтів полінома Ньютона
% D - таблиця
різниць=length(x);=zeros(n,n);(:,1)=y'; %транспонування рядка в столбець
%Формування таблиці
різниць Dj=2:nk=j:n(k,j)=(D(k,j-1)-D(k-1,j-1))/(x(k)-x(k-j+1));
%Знаходження
коефіцієнтів полінома
Ньютона=D(n,n);k=(n-1):-1:1=conv(C,poly(x(k)));=length(C);
C(m)=C(m)+D(k,k);
end
Тест-програма TestdiffNew, в якій задаються вхідні дані,
викликається функція newpoly, обчислюються значення полінома і похідної в
заданих точках.
Файл TestdiffNew.m
%Тест TestdiffNew =[1.1 1.6 2.1 2.6 3.1 3.6];=[1.03 1.39 1.65
1.80 1.85 1.82];
%Знаходження коефіцієнтів полінома Ньютона і таблиці
скінечних різниць
[C,D]=newpoly(x,y);
%Знаходження
коефіцієнтів першої похідної полінома Ньютона=polyder(C)
%Знаходження значення
першої похідної у вузлових точках= polyval(d1,x)
%Знаходження значення
першої похідної в заданих точках=
polyval(d1,2.4)=polyval(d1,3.5)=polyval(d1,1.14)
Запускаємо файл-програму
>> TestdiffNew
Результат виконання програми :
Вектор коефіцієнтів
похідної полінома Ньютона:= -0.0133 0.1653 -0.6788 0.7109 0.6382
Значення похідної у
вузлових точках:= 0.7993 0.6277 0.4093 0.1943 0.0127 -0.1257
Значення похідної в
заданих точках:= 0.2776= -0.1013= 0.7888
Висновок
Ми знайшли наближені значення похідної трьома різними
способами. Всі три результати дещо відрізняються між собою. При відсутності
точного аналітичного виразу функції неможливо зробити висновок, який з методів
кращий.
Практична робота №3
Мета роботи: Чисельне інтегрування функцій
Знаходження невизначених інтегралів для табличних функцій.
Обчислення визначених інтегралів для табличних функцій. Інтегрування функцій,
заданих аналітично.
1 Знаходження невизначених інтегралів для табличних функцій
Якщо підінтегральна функція задана поліномом, то для її
інтегрування можна скористатися функцією
=polyint (p,c)
де c - константа інтегрування (вільний член первісної
функції). Якщо с не задано, то вважається за 0.
>> q=polyint (p)
Функція повертає вектор коефіцієнтів первісної.
Приклад.
Нехай функція f(х) задана на відрізку [a,b] =[1,3.6] вузлами
інтерполяції, поданими в таблиці.
Таблиця 12
|
xi
|
1.1
|
1.6
|
2.1
|
2.6
|
3.1
|
3.6
|
|
yi
|
1.03
|
1.39
|
1.65
|
1.80
|
1.85
|
1.82
|
. Знайдемо її інтерполяційний поліном.
Введемо два вектори і заповнимо їх початковими даними: =[1.1
1.6 2.1 2.6 3.1 3.6]=[1.03 1.39 1.65 1.80 1.85 1.82]
Знайдемо вектори полінома
p4=polyfit(x,y,4)
>> p4=polyfit(x,y,4)
Відповідь:
p4 = 0.0100 -0.0844 0.0472 0.9578 0.0169
Якщо n - ступінь полінома, то аналітичний запис його буде
наступним:
.0100x4 - 0.0844x3 + 0.0472x2
+ 0.9578x + 0.0169
2. Знайдемо інтеграл полінома за допомогою функції polyint
=polyint(p4)
>> q=polyint(p4)
q = 0.0020 -0.0211 0.0157 0.4789 0.0169 0
Аналітичний запис первісної
= 0.002x5 - 0.0211x4 + 0.0157x3
+ 0.4789x2 + 0.0169x
Якщо тепер зайти похідну від q, то отримаємо наш поліном р4.
Функцію polyint можна використовувати для знаходження
невизначеного інтеграла, тобто для відтворення первісної функції від табличної.
2. Обчислення визначених інтегралів для табличних функцій
Візьмемо ту саму функцію f(х) яка задана на відрізку [a,b]
=[1,3.6] вузлами інтерполяції
Таблиця 13
|
xi
|
1.1
|
1.6
|
2.1
|
2.6
|
3.1
|
3.6
|
|
yi
|
1.03
|
1.39
|
1.65
|
1.80
|
1.85
|
1.82
|
Обчислимо інтеграл табличної функції за допомогою
квадратурних формул та порівняємо результат.
Введемо два вектори і заповнимо їх початковими даними: =[1.1
1.6 2.1 2.6 3.1 3.6]=[1.03 1.39 1.65 1.80 1.85 1.82]
Знайдемо відрізок h=0.1
Обчислення за формулою прямокутників
Файл my_rectangle.m
function my_rectangle
%h=(b-a)/(n-1)
x=[1.1 1.6 2.1 2.6 3.1 3.6];=[1.03 1.39 1.65 1.80 1.85 1.82];
n=6;=(x(n) - x(1))/(n-1);=0;i=1:n-1=sy+y(i);=h*sy
Виконаємо програму в робочому вікні Matlab.
>> my_rectangle= 3.8600
Обчислення
за формулою трапецій
Для цього можна скористатися функцією trapz(x,y)
>> x=[1.1 1.6 2.1 2.6 3.1 3.6];
>> y=[1.03 1.39 1.65 1.80 1.85 1.82];
>> In = trapz(x,y)
Результат:= 4.0575
Можна написати просту файл програму, яка обчислює формулу
трапецій
Файл my_trapz.m
%my_trapz.m
%h=(b-a)/n крок інтегрування=[1.1 1.6 2.1 2.6 3.1 3.6];
=[1.03 1.39 1.65 1.80 1.85 1.82];=6;=(x(n)-
x(1))/(n-1);=0;i=2:n-1=sy+y(i);=h*((y(n)+y(1))/2+sy)
Результат виконання програми:
>> my_trapz
In = 4.0575
Знайдений розв’язок не відрізняється від отриманого за
допомогою функції trapz(x,y).
Оцінка точності обчислень
Знайдемо залишковий член формули трапецій для оцінки похибки
обчислення інтеграла.
Для табличної функції залишковий член формули трапецій можна
обчислити за наближеною формулою:
Rтр = -((b-a)2/12)mean(D2y)
де mean - середнє значення на відрізку інтегрування,
D2y - вектор скінчених різниць другого
порядку.
В Matlab для обчислення скінчених різниць використовується
функція diff з двома вхідними аргументами: вектором значень функції і порядку
різниці.
Обчислимо залишковий член формули трапецій для нашого прикладу.
Виконаємо :
>> d2y=diff(y,2)
Отримаємо :y =
-0.1000 -0.1100 -0.1000 -0.0800
Виконаємо :
>>
Rtr=-((0.5^2)/12)* mean(d2y)
Отримаємо := 0.0020
Додамо обчислене
значення залишкового члена до обчисленого інтеграла:
>> In+Rtr
Уточнене значення
інтегралу:= 4.0595
Інтегрування функцій,
заданих аналітично
Інтерполяційний
поліном нашої табличної функції має вигляд
0.0100x4 -
0.0844x3 + 0.0472x2 + 0.9578x + 0.0169x;=0.0100*x^4 -
0.0844*x^3 + 0.0472*x^2 + 0.9578*x + 0.0169
Виконуємо у Матлабі :
>> P=0.01*x.^4
- 0.0844*x.^3 + 0.0472*x.^2 + 0.9578*x + 0.0169
Отримуємо значення P.
= 1.0299 1.3900
1.6493 1.7998 1.8488 1.8185
>>Ip=int(P)
>>
Ip=double(P);
>> Ip= 1.0299
1.3900 1.6493 1.7998 1.8488 1.8185
Висновок. Порівняємо
значення інтеграла на відрізку [1.1,3.6], отримані різними способами
Таблиця 13
|
Спосіб
|
Значення інтегралу
|
|
За формулою
прямокутників
|
3.8600
|
|
За формулою
трапецій з урахуванням похибки обчислень
|
4.0595
|
|
З допомогою функції
trapz(x,y)
|
4.0575
|
|
З допомогою функції
int(P,1.1,3.6)
|
Не знайшов
|
Практична робота №4
Розв’язування диференційних рівнянь
Знайти розв’язок диференційного рівняння першого порядку
[0,1]
'=cos(1.5x+y)+(x-y), y(0)=0
Розв’язок
Оскільки це рівняння першого порядку, немає потреби у
приведенні до системи рівнянь. Просто запишемо рівняння у вигляді допоміжної
функції
Файл oscil2.m:
Dif=oscil2(x,y)=[cos(1.5*x+y)+(x-y)];
Для знаходження розв’язку рівняння скористаємося солвером
ode113. Напишемо файл-функцію difur2
файл difur2.mdifur2=[0];
[X,Y]=ode113(@oscil2,[0,1],y0)(X,Y(:,1),'r.-')on('x')('y')
Виконаємо файл difur2 у командному рядку Matlab
>> difur2=
.0000
.0000
.0001
.0001
.0002
.0005
.0010
.0020
.0040
.0081
.0162
.0324
.0648
.1295
.2295
.3295
.4295
.5295
.6295
.7295
.8295
.9295
.0000=
.0000
.0000
.0001
.0001
.0002
.0005
.0010
.0020
.0040
.0081
.0162
.0323
.0645
.1274
.2181
.2978
.3645
.4175
.4575
.4861
.5050
.5162
.5205
Результати запишемо в таблицю і виведемо на графік
Таблиця наближених значень інтегралу рівняння
'=cos(1.5x+y)+(x-y), y(0)=0, x= [0,1]
Таблиця 14
|
x
|
y
|
|
0
|
0
|
|
0.0000
|
0.0000
|
|
0.0000
|
0.0000
|
|
0.0001
|
0.0001
|
|
0.0001
|
0.0001
|
|
0.0002
|
0.0002
|
|
0.0005
|
0.0005
|
|
0.0010
|
0.0010
|
|
0.0020
|
0.0020
|
|
0.0040
|
0.0040
|
|
0.0081
|
0.0081
|
|
0.0162
|
0.0162
|
|
0.0324
|
0.0323
|
|
0.0648
|
0.0645
|
|
0.1295
|
0.1274
|
|
0.2295
|
0.2181
|
|
0.3295
|
0.2978
|
|
0.4295
|
0.3645
|
|
0.5295
|
0.4175
|
|
0.6295
|
0.4575
|
|
0.7295
|
0.4861
|
|
0.8295
|
0.5050
|
|
0.9295
|
0.5162
|
|
1.0000
|
0.5205
|
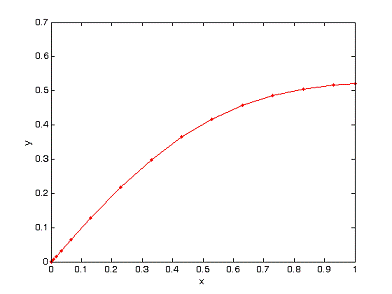
Рис. 10