Термодинамика
Законы классической термодинамики
Опишите адиабатически изолированную систему.
Адиабатный процесс - происходящий без
теплообмена с окружающей средой.
Промежуточным случаем между закрытой и
изолированной системой является Адиабатически изолированная система, которая не
обменивается с окружающей средой энергией в форме теплоты. Однако изменение
внутренней энергии такой системы возможно за счёт производимой над ней работы,
причём количество работы равно изменению энергии. Всякий процесс в
адиабатически изолированной системе называется адиабатическим процессом.
Адиабатически изолированная система - это система, в которой изменения её
состояния могут происходить только благодаря механическим перемещениям частей
системы и её оболочки (окружающих тел) и не могут происходить путём теплообмена
с окружающими телами. Любое изменение состояния адиабатически изолированной
системы называют адиабатическим процессом, а оболочку, окружающую такую систему
- адиабатической оболочкой.
Назовем оболочку адиабатической, если при изменении
температуры окружающих тел и поддержании постоянными значений внешних
параметров (например, давления) состояние заключенной в неё системы остается
неизменным.
Другими словами, изменить состояние системы в
адиабатической оболочке можно только путем изменения внешних параметров.
Система, заключенная в адиабатическую оболочку,
называется адиабатически изолированной. Примером адиабатической оболочки
является сосуд Дьюара.
Если адиабатически изолированная система
переходит из состояния 1 в состояние 2, то обратный адиабатический переход
может оказаться невозможным.
Какими свойствами должна обладать система, чтобы
ее можно было назвать термодинамической
Во-первых, это - системы большого числа частиц.
Во-вторых, для каждой термодинамической системы
существует состояние термодинамического равновесия. Это и есть нулевое начало
термодинамики.
В-третьих, по отношению к термодинамической
системе имеет место термодинамический принцип аддитивности.
В-четвертых, по отношению к термодинамической
системе справедливы I, II и III начала термодинамики. По традиции их считают
основными аксиомами термодинамики. Принятие их приводит к формулировке
макроскопического аппарата термодинамики.
термодинамика
адиабатический раствор
Задача № 1
Газовая смесь задана процентным составом
компонентов смеси СО2, Н2, СО, Н2О, О2, N2, SO2 в массовых долях (табл. 1).
Давление смеси равно Рсм (табл. 1, строка 8). Объем смеси равен Vсм (табл. 1,
строка 9). Температура смеси равна tсм (табл. 1, строка 10). В интервале
температур t (табл. 1, строка 11) смесь нагревается.
Данные для соответствующего варианта берутся из
табл. 1.
Определить:
. Объемный состав смеси.
. Газовые постоянные компонентов Ri и смеси Rсм,
кДж/(кг∙К).
. Среднюю молярную массу смеси mсм
через объемные и массовые доли, кг/кмоль.
. Парциальные давления компонентов через
объемные и массовые доли.
. Массу смеси Мсм, кг и массы компонентов Мi ,
кг.
. Парциальные объемы компонентов Vi , м3 .
. Плотности компонентов и смеси при нормальных
физических условиях через объемные и массовые доли.
. Массовые теплоемкости с, кДж/(кг К) при
рсм=соnst; Vсм=const; для температуры смеси tсм, 0С, (строка 10).
. Количество теплоты, необходимое для нагревания
(охлаждения) 7 кг смеси в интервале температур (строка 11) при р=const.
|
вариант
|
СО2,
%
|
Н2,
%
|
СО,
%
|
N2,
%
|
Н2О,
%
|
SО2,
%
|
О2,
%
|
рсм,
МПа
|
Vсм,
м3
|
t,
0С
|
Δt, 0С
|
|
16
|
18
|
-
|
1
|
65
|
-
|
16
|
-
|
1,2
|
8
|
1200
|
850-350
|
Дано:
Газовая смесь имеет следующий массовый состав:
CO2 = 18 %
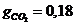 = 1 %
= 1 % 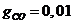 = 65 %
= 65 % 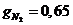 = 16 %
= 16 % 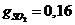
Всего:100 % 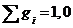 .
.
давление смеси рсм=1,2 МПа=1,2·106
Па
объем смеси Vсм=8 м3
температура смеси t=1200 0С, (Т=1473
К)
Интервал температур, для которого определяется
средняя температура теплоемкость смеси:=350 0С , (Т1=623 К)=850 0С, (Т2=1123 К)
Проверить правильность выписанных
данных по составу газовой смеси: 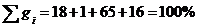 ;
;
. Определить состав смеси:
Вначале определяются массовые доли
компонентов - 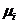 , кг/кмоль:
, кг/кмоль:
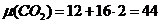 ;
;
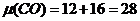 ;
;
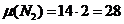 ;
;
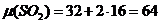 ;
;
Определение объемного состава смеси:
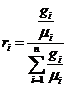
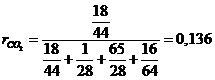
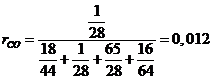
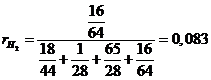
 - верно
- верно
. Определение газовых постоянных
компонентов и смеси:
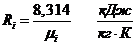
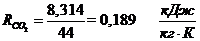
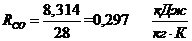
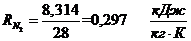
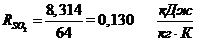
Определение газовой постоянной
смеси:
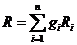
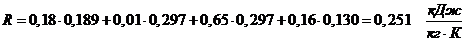
. Определение средней молекулярной массы смеси:
а) через объемные доли:
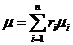 ;
;
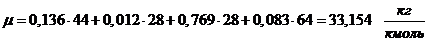
б) через массовые доли:
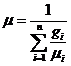
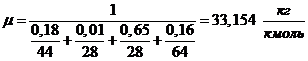 - верно.
- верно.
4. Определение парциальных давлений компонентов:
а) через объемные доли:
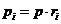
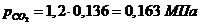
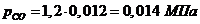
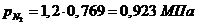

Проверить вычисления:
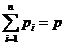
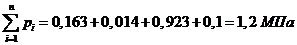 - верно
- верно
б) через массовые доли:
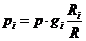
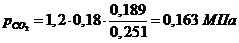
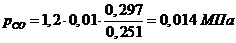
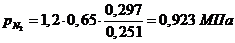
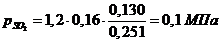
Проверить вычисления:
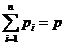
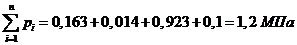 - верно
- верно
. Определение массы смеси:
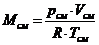
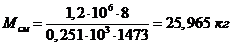
Определение массы компонентов:
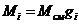
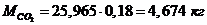
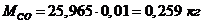
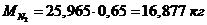
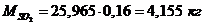
Проверить вычисления:
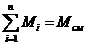
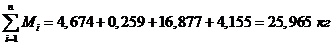 - верно.
- верно.
. Парциальные объемы компонентов Vi
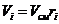
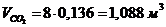
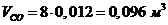
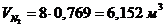
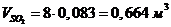
Проверить вычисления:
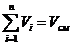
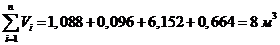 - верно.
- верно.
. Плотности компонентов и смеси при
нормальных физических условиях (р0=105 Па, t0=0 0C) через объемные и массовые
доли.
Определение плотности компонентов при нормальных
физических условиях
(р0=1,013·105 Па, t0=0 0C):
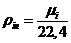
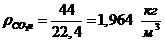
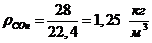
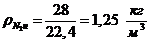

а) через объемные доли:
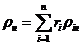
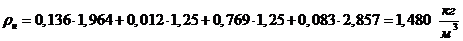
б) через массовые доли:
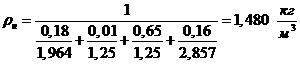
Проведем проверку:
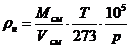
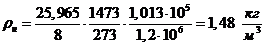 - верно
- верно
. Массовые теплоемкости с, кДж/(кг
К) при рсм=соnst; Vсм=const; для температуры смеси tсм, 0С
а) мольная теплоемкость при постоянном давлении:
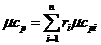 ;
;
где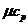 и
и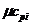 - истинные мольные теплоемкостей
смеси и компонентов при p = const, которые необходимо взять из любого
термодинамического справочника, например [3]:
- истинные мольные теплоемкостей
смеси и компонентов при p = const, которые необходимо взять из любого
термодинамического справочника, например [3]:
Истинные теплоемкости компонентов при заданной
температуре t = 1200 0C:
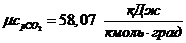
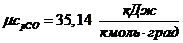
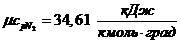
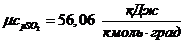
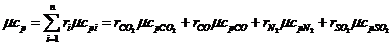
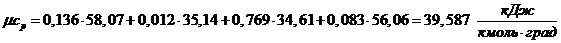
б) мольная теплоемкость при
постоянном объеме:
Используя уравнение Майера,
определить мольную теплоемкость при v = const:
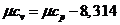
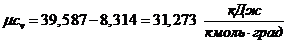
в) массовая теплоемкость смеси при постоянном
давлении:
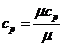 ;
;
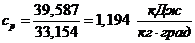
г) массовая теплоемкость смеси при постоянном
объеме:
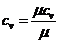 ;
;
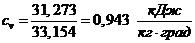
. Количество теплоты, необходимое
для нагревания 7 кг смеси в интервале температур от t1=350 0С до t2=850 0С при
р=const.
Для 7 кг смеси количество теплоты
равно:
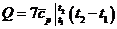
Где 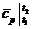 - средняя массовая теплоемкость
смеси при постоянном давлении в данном интервале температур:
- средняя массовая теплоемкость
смеси при постоянном давлении в данном интервале температур:
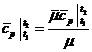
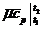 - средняя мольная теплоемкость
смеси при постоянном давлении
- средняя мольная теплоемкость
смеси при постоянном давлении
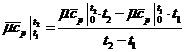
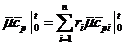
Примечание: в последующие вычисления температуру
подставлять только в градусах Цельсия (0C).
Средние теплоемкости компонентов при заданных
температурах из [3]:
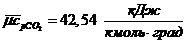
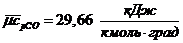
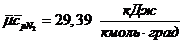
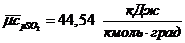
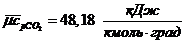
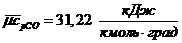
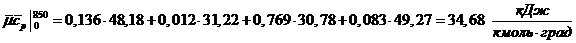
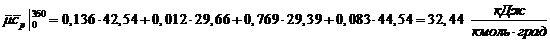
средняя мольная теплоемкость смеси
при постоянном давлении:
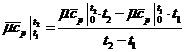
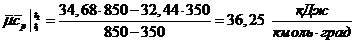
средняя массовая теплоемкость смеси при
постоянном давлении в данном интервале температур:
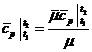
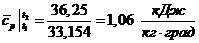
Для 7 кг смеси количество теплоты
равно:
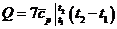
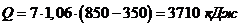
Задача № 2
Определить изменение энтропии ΔS
для М=3,4 кг азота в изохорном процессе, имеющему температуру от t1=130 0С до
t2=500 0С, если подводится 100 кДж тепла. Теплоемкость азота считать постоянной,
СV=0,75 кДж/(кг К).
Дано:
М=3,4 кг
µ=28·10-3 кг/моль=130 0С (Т1=403 К)
Q=100 кДж=105 Дж
СV=0,75
кДж/(кг К)
ΔS-?
Получим общее выражение для изменения энтропии.
Для этого воспользуемся формулой 2-го начала термодинамики
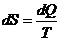
в которую подставим выражение 1-го
начала термодинамики
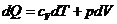
Объединяя эти выражения, получаем:
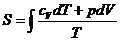 (1)
(1)
Для преобразования выражения (1), воспользуемся
уравнение состояния идеального газа для одного моля:
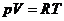
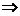
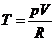
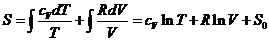 (2)
(2)
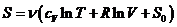
Тогда изменение энтропии будет равно
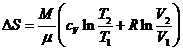 (3)
(3)
Для изохорного процесса ΔV=0,
следовательно
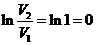
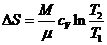
Температуру найдем из первого начала
термодинамики, при изохорном процессе работа не совершается, следовательно, все
подводимая теплота идет на изменение внутренней энергии, т.е. с учетом
уравнения Майера 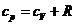 , а
, а 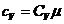
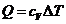
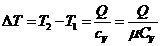
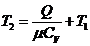
Подставляем в (3) получаем
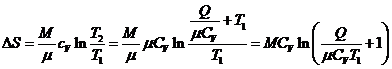
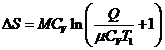
Подставляем числовые значения
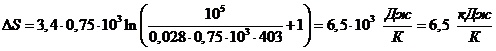
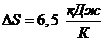
Фазовые равновесия и фазовые переходы.
Термодинамические свойства
Условие фазового равновесия
Важнейшим вопросом в учении о фазах является
выяснение условий, при которых система, состоящая из двух или нескольких фаз, находится
в равновесии.
Пусть имеются две фазы, но один компонент
Тогда условие равновесия:
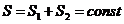 или
или 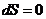
Уравнения Гиббса для фаз:
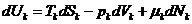
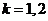 - номер фазы
- номер фазы
Система изолированная:
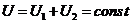
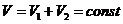
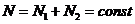
следовательно
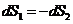 ,
, 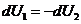 ,
, 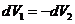 ,
, 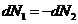
из (1) выразим 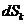 и
воспользуемся (2):
и
воспользуемся (2):
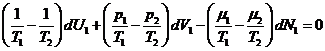
Последнее равенство возможно, если
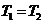 ,
, 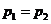 ,
, 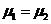
или
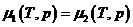 - условие равновесия фаз
- условие равновесия фаз
Две фазы находятся в равновесии, то температуры,
давления и химические потенциалы этих фаз равны между собой. Аналогичным путем
такой же результат может быть получен для системы, в которой количество
сосуществующих фаз превышает две.
. Найдите свободную энергию одного киломоля газа
Ван-дер-Ваальса и покажите, что убыль её при изотермических процессах равна
работе изотермического расширения газа.
Дано:=const, b?,
ΔF-?,
A-?
Воспользуемся формулой, с помощью которой
вводится свободная энергия:
F=U-TS
Для преобразования формулы (1) применим формулу
2-го начала термодинамики:
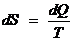
Подставляя значение 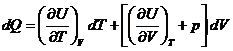 в (2) и
учитывая, что имеем дело с газом Ван-дер-Ваальса, т.е.
в (2) и
учитывая, что имеем дело с газом Ван-дер-Ваальса, т.е. 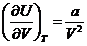 , получаем:
, получаем:
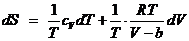
Проинтегрируем полученное выражение:
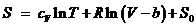
Cоставим
выражение для внутренней энергии реального газа:
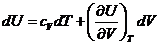
где для газа Ван-дер-Ваальса 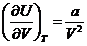 .
.
Тогда, после интегрирования,
получаем:
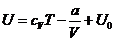
Подставим выражения (4) и (5) в
формулу (1):
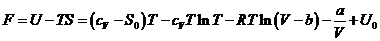
Выражение (6) можно написать дважды
для начального и конечного состояния газа, который расширяется в изотермическом
процессе. Тогда
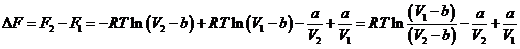
Далее подсчитаем работу газа при
изотермическом расширении:
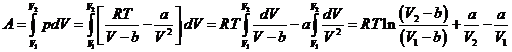
где использовано уравнение
Ван-дер-Ваальса.
Из сравнения выражений (7) и (8)
устанавливаем, что при изотермическом расширении реального газа работа
совершается за счет уменьшения свободной энергии. Именно по этой причине часть
внутренней энергии термодинамической системы исторически получила название
“свободная энергия”.
Ответ:
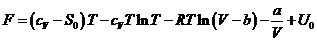
. Найдите термическое уравнение состояния
вещества и внутреннюю энергию, если его свободная энергия известна в виде
характеристической функции:
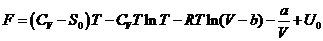
где CV, S0, a, b, U0 - постоянные величины.
Дано:
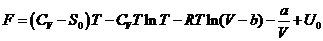
, S0, a, b, U0 - постоянные величины
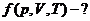
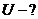
Решение
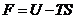
Или дифференциал
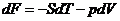
С другой стороны
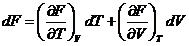
Сравнивая эти соотношения, получаем
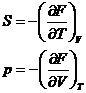
Найдем давление продифференцировав
уравнение свободной энергии по объему
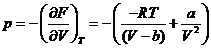
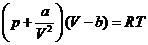 - термическое уравнение состояния
вещества
- термическое уравнение состояния
вещества
Внутренняя энергия вещества будет
определяться по формуле:
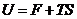
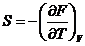 , имеем
, имеем 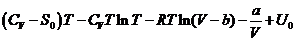
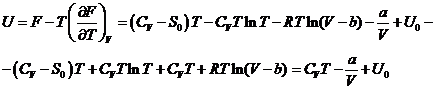
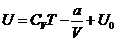
Ответ:
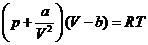
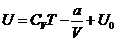
Элементы технической термодинамики. Введение в
химическую термодинамику
Понятие об идеальных и неидеальных растворах
Идеальным называется раствор, общее давление
паров которого является линейной функцией его мольного состава в жидкой фазе и
при смешении компонентов которого не происходит сжатия или расширения объема,
не выделяется и не поглощается теплота.
Идеальный раствор - это раствор образован двумя
неограниченно растворимыми друг в друге жидкостями, близкими по свойствам, то
силы взаимодействия между частицами в растворе существенно не отличаются от
таковых в чистых жидкостях. При этом образование раствора не сопровождается
тепловым эффектом и объем его равен сумме объемов компонентов
Различают идеальные и реальные (неидеальные)
растворы. В идеальных растворах компоненты смешиваются, как идеальные газы, без
изменения объема и энтальпии. Увеличение энтропии таких растворов рассчитывают
по уравнениям для идеальных газов. Растворы, подчиняющиеся законам идеальных
растворов при всех концентрациях, называют совершенными, если это условие
соблюдается лишь при сильном разбавлении, то их называют бесконечно разбавленными.
Чем меньше концентрация раствора, тем ближе его свойства к свойствам идеального
раствора. Изучение свойств идеальных растворов (давление насыщенного пара,
температура кипения, температура кристаллизации) используют для определения
молекулярного веса, степени диссоциации растворенных веществ.
Отклонения реальных растворов от свойств
идеального раствора являются следствием таких химических явлений, как
сольватация, ассоциация и диссоциация компонентов, а также следствием чисто
физических факторов таких, как влияние различных молекулярных объемов и
силового поля молекул.
Цикл Сти́рлинга -
термодинамический цикл
<https://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D1%80%D0%BC%D0%BE%D0%B4%D0%B8%D0%BD%D0%B0%D0%BC%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D1%86%D0%B8%D0%BA%D0%BB>,
описывающий рабочий процесс машины Стирлинга
<https://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%88%D0%B8%D0%BD%D0%B0_%D0%A1%D1%82%D0%B8%D1%80%D0%BB%D0%B8%D0%BD%D0%B3%D0%B0>,
запатентованной в 1816 г. шотландским изобретателем Робертом Стирлингом
<https://ru.wikipedia.org/wiki/%D0%A1%D1%82%D0%B8%D1%80%D0%BB%D0%B8%D0%BD%D0%B3,_%D0%A0%D0%BE%D0%B1%D0%B5%D1%80%D1%82>,
приходским священником по профессии.
Помимо рабочего тела, нагревателя и
холодильника абстрактная машина Стирлинга содержит ещё регенератор -
устройство, отводящее тепло от рабочего тела на некоторых этапах цикла, и
отдающее это тепло рабочему телу на других этапах. Идеальный цикл Стирлинга
состоит из процессов:
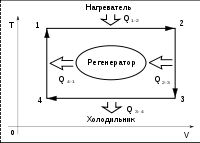 <https://commons.wikimedia.org/wiki/File:%D0%A6%D0%B8%D0%BA%D0%BB_%D0%A1%D1%82%D0%B8%D1%80%D0%BB%D0%B8%D0%BD%D0%B3%D0%B0_T-V.svg?uselang=ru>V
диаграмма идеального цикла Стирлинга с регенератором.
<https://commons.wikimedia.org/wiki/File:%D0%A6%D0%B8%D0%BA%D0%BB_%D0%A1%D1%82%D0%B8%D1%80%D0%BB%D0%B8%D0%BD%D0%B3%D0%B0_T-V.svg?uselang=ru>V
диаграмма идеального цикла Стирлинга с регенератором.
-2 изотермическое
<https://ru.wikipedia.org/wiki/%D0%98%D0%B7%D0%BE%D1%82%D0%B5%D1%80%D0%BC%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%BF%D1%80%D0%BE%D1%86%D0%B5%D1%81%D1%81>
расширение рабочего тела с подводом тепла от нагревателя;
-3 изохорный
<https://ru.wikipedia.org/wiki/%D0%98%D0%B7%D0%BE%D1%85%D0%BE%D1%80%D0%BD%D1%8B%D0%B9_%D0%BF%D1%80%D0%BE%D1%86%D0%B5%D1%81%D1%81>
отвод тепла от рабочего тела к регенератору;
-4 изотермическое сжатие рабочего
тела с отводом тепла к холодильнику;
-1 изохорический нагрев рабочего
тела с подводом тепла от регенератора.
По определению 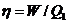 . В цикле
Стирлинга
. В цикле
Стирлинга
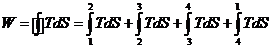

Считая рабочее тело идеальным газом,
находим
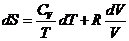
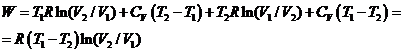
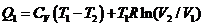
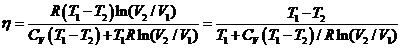
Отсюда видно, что
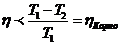
Т.е. КПД цикла Стирлинга меньше КПД
цикла Карно в тех же температурных пределах. Кроме того, в отличие от цикла
Карно КПД цикла Стирлинга зависит от природы рабочего вещества.
. Рассчитайте величину 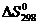 для
процесса Na2O(т) + H2O(ж) → 2NaOH(т), используя значения стандартных
энтропий веществ (табл. 3)
для
процесса Na2O(т) + H2O(ж) → 2NaOH(т), используя значения стандартных
энтропий веществ (табл. 3)
Решение
величину 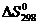 определяется
по формуле
определяется
по формуле
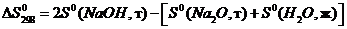 =
=
Используя справочные данные:
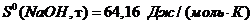
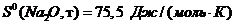
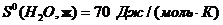
Имеем
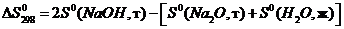
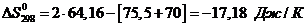
Ответ:
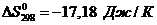
. Идеальный двухатомный газ,
содержащий 1 моль вещества, совершает цикл, состоящий из двух изохор и двух
изобар. Наименьший объем 10 л, наибольший 20 л, наименьшее давление 246 кПа,
наибольшее 410 кПа. Построить график цикла. Определить температуру газа для
характерных точек цикла и КПД.
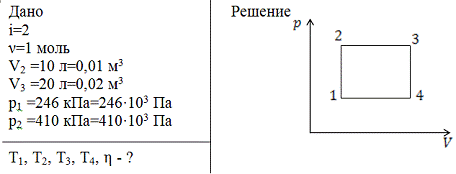
Процессы 1-2 и 3-4 - изохорный,
процессы 2-3 и 4-1 - изобарные. Тогда имеем т.к. 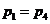 ,
, 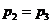 и
и 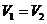 ,
, 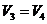 имеем из уравнения состояния
идеального газа
имеем из уравнения состояния
идеального газа
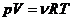
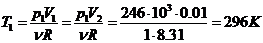
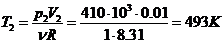
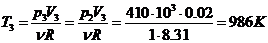
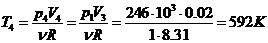
КПД цикла определяется по формуле
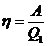
где Q1 -
количество теплоты , полученное от нагревателя; А - работа , совершаемую газом
за цикл. Из первого начала термодинамики имеем
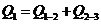
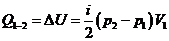
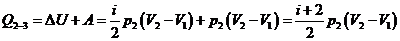
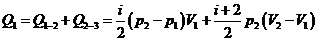
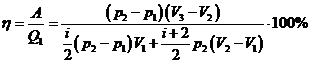
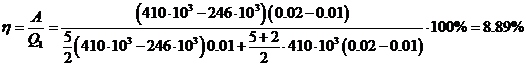
Ответ:
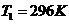
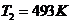
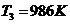
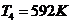
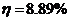
. Идеальный газ совершает цикл
Карно, 2/3 количества теплоты, полученного от нагревателя, отдает холодильнику.
Температура холодильника 280 К. Определить температуру Т1 нагревателя.

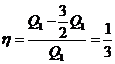
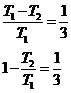
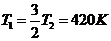
Ответ:

Список рекомендуемой литературы
1. Базаров И.П. Термодинамика.- М.:
Высшая школа, 1991. - 376с.
. Кудинов В.А. Техническая
термодинамика: учеб. пособие для вузов/Кудинов В.А., Карташов Э.М. - М.: Высш.
школа, 2007. - 261 с.
. Задачник по технической
термодинамике и теории тепломассообмена//В.Н. Афанасьев, С.И. Исаев и др.- под
ред. В.И. Крутова и Г.Б. Петражицкого/Учебное пособие для машиностроительных
вузов: Рекомендован УМО Мин. Образования РФ. С-Петербург: БХВ-Петербург 2011. -
384 с.
. Серова Ф.Г. Сборник задач по
термодинамике: учебное пособие для студентов/ Ф.Г. Серова, А.А. Янкина.- М.:
«Просвещение», 1976.-160 с.
. Термодинамика: конспект лекций
(презентаций) / сост. А.Г. Князева.- Томск: Изд-во ТПУ, 2014.