Релятивистская кинетическая теория

Контрольная работа

Релятивистская кинетическая теория

Содержание

1. Направления и сериалы в релятивистской кинетической теории

2. Макроскопические величины

2.1 Вектор потока частиц

2.2 Тензор энергии - импульса

2.3 Вектор потока энтропии

3. Релятивистское кинетическое уравнение

3.1 Случай без столкновения

3.2 Кинетическое уравнение

3.3 Дифференциальное сечение и скорость перехода

3.4 Внешняя сила

4. Краткий обзор основных результатов релятивистской кинетической теории

4.1 Макроскопические законы термодинамики

4.2 Локально - равновесное состояние

5. Эффект Комптона - Геттинга в двух сериалах

6. Заключение

Список литературы

1. Направления и сериалы в релятивистской кинетической теории

Физика окончательно сформировалась как наука и получила мощный импульс для своего развития, когда ученые смогли создавать сериалы об окружающем их мире. Эти сериалы, как указывает выдающийся российский математик В.П. Маслов [1], имеют лишь примерное соответствие с используемым в них математическим аппаратом и примерное соответствие с приборной базой, используемой наукой на данном этапе своего развития. Поэтому, применение уже созданных сериалов к реальной действительности сопровождается многочисленными правилами, условностями и оговорками. Такая сложная ситуация в физике всегда приводила к конфликтам и недопониманию, особенно при получении принципиально нового знания о природе. Исторически первым сериалом был сериал, написанный И. Ньютоном, в виде 3 законов динамики и закона всемирного тяготения. Сегодня он подвергается беспримерному по силе натиску, который имеет как экспериментальную [2], так и идеологическую [3-5] основу. Курьезные ситуации возникают там, где различные по своему математическому аппарату и физическому содержанию теории претендуют на описание сходных и даже близких явлений. Простое перечисление этих теорий в справочниках и энциклопедиях не позволяет сделать между ними критический выбор, а экспериментаторам не позволяет сколько-нибудь однозначно интерпретировать результаты эксперимента. Сопоставление и сравнение сведенных в сериалы направлений является элементом физического творчества и требует от исследователей определенных навыков, которые вырабатываются годами работы их в науке. Как это ни парадоксально, возникшая ситуация стала залогом бурного развития физики в 21 веке.

Все только что сказанное полностью относится к разным по своей сути сериалам, которые объединены общим названием "Релятивистская кинетическая теория". Простое их перечисление весьма затруднительно, а авторы, зачастую, претендуют на создание наиболее совершенной теории. Не претендуя на общность, попробуем перечислить некоторые вполне независимые и слабо связанные направления под названием РКТ:

)        релятивистская кинетическая теория в специальной теории относительности (СТО) с интегралами столкновений для квантовых процессов [6];

2)      слаборелятивистская статистическая механика N тел с парными интегралами столкновений [7];

)        релятивистская кинетическая теория Больцмана в искривленном пространстве - времени общей теории относительности ОТО [8-10];

)        релятивистская кинетическая теория в 8 - мерном пространстве - времени опорных элементов с 2-мя независимыми временами - собственным и мировым [11].

Перечисленные выше сериалы являются независимыми и неоконченными. Они имеют также непересекающиеся области применения. Затруднения с идентификацией возникают в том случае, когда авторы пользуются различными понятиями и различными переменными. Идентификация путем прямого сравнения членов уравнений возможна только тогда, когда при выводе использовались одни и те же фазовые пространства и в этих пространствах вводились одни и те же меры. 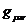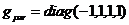Самым простым способом сравнения уравнений и их решений является например выбор в 3) метрики  виде метрики пространства - времени Минковского  совместно с выбором подходящего интеграла столкновений. Наиболее значительны претензии сериала 4). Например, в работах А.А. Власова, выполненных в рамках этих идей, есть попытки описания конденсации твердого тела из молекул в процессе самосборки кристалла. Существуют и совпадения результатов различных сериалов, связанные с выбором приближения, в котором выполнены расчеты. Простейший пример такого типа будет приведен ниже.

релятивистская кинетическая теория термодинамика

Со времен Л. Больцмана, успешной кинетической моделью вещества является разреженный газ с простейшими микроскопическими свойствами. Теория такого газа, в последние годы, находит применение в физике от астрофизики до афилированных с физикой областей техники и технологии. Формулировка этой теории важна для развития релятивистской механики. Здесь уместна аналогия с основополагающими трудами Н.Н. Боголюбова и Ю.Л. Климантовича, которые вывели нерелятивистские кинетические уравнения из уравнений механики частиц.

В настоящей лекции мы будем придерживаться простейших вариаций схемы 1), что позволяет обеспечить относительную простоту и физическую ясность изложения. В то же время, предлагаемая схема открыта для обобщений и учета сил различной физической природы, иным путем вводимых в вариантах 2) - 4). К сожалению, любой, даже полукачественный вывод релятивистских кинетических уравнений приводит к математически сложным выражениям. Поэтому, мы попытаемся избежать самых больших сложностей такого рода, формулируя простые физические принципы, которым будет следовать изложение.

2. Макроскопические величины

2.1 Вектор потока частиц

Для описания неоднородной системы вводится локальная плотность 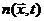, являющаяся функцией пространственных координат 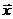 и времени t. Эта величина определяется таким образом, что произведени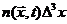е  дает среднее число частиц, находящихся в элементе 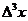в точке  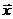в момент времени t. Подобным образом определяется и вектор потока частиц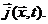

В теории относительности две локальные величины, плотность частиц и вектор потока частиц, образуют 4 - вектор потока частиц, который мы обозначим следующим образом:

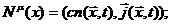 (1)

где 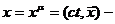пространственно - временная точка, c - скорость света, а индекс 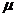принимает значения: 0,1,2,3.

Теперь представим себе простую систему, состоящую из релятивистских частиц. Массу, импульс энергию частицы обозначим соответственно через 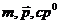, причем

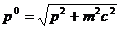 (2)

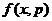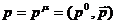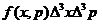Если число частиц велико, то можно ввести функцию распределения (ФР) , которая дает распределение 4-импульсов  в каждой пространственно - временной точке. Она определена таким образом, что произведение дает среднее число частиц, которые в момент времени t находятся в элементе объема 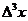 с центром в точке  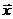и имеют импульсы в пределах  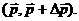При таком определении предполагается, во - первых, что число частиц, находящихся в элементе объема 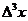, велико и во - вторых, что с макроскопической точки зрения элемент 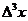 имеет малые размеры.

С помощью такой функции распределения плотность потока числа частиц определяется как

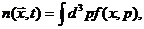 (3)

где интегрирование ведется по всем импульсам. Таким же образом определяется вектор потока частиц:

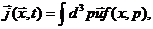 (4) где  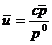(5)

представляет собой скорость релятивистской частицы с импульсом 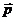. С учетом (3), (4) можно записать 4 - вектор потока частиц (1) в виде

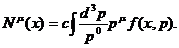 (6)

Для того, чтобы убедиться, что функция распределения является скалярной величиной, достаточно воспользоваться тождеством

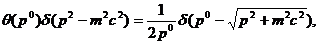 (7)

где  единичная ступенчатая функция, а 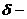дельта - функция Дирака. Символом  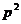обозначен квадрат 4 - импульса  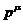[12]: 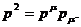 Здесь и вплоть до особых оговорок мы будем пользоваться метрикой с сигнатурой Уиллера 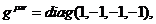[8]

 (8)

в которой времениподобные векторы имеют положительный модуль, в частности,

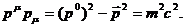 (9)

С учетом тождества (7), 4 - вектор потока (6) можно записать в виде: 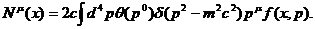 (10) В этом выражении задана мера интегрирования в 4-м пространстве так, что 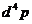представляет собой скаляр, так как якобиан преобразований Лоренца равен единице,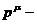4 вектор, скаляр, поток 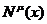 - 4 - вектор.

Кроме того, величина 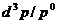 является скаляром в силу этих же соображений.

2.2 Тензор энергии - импульса

Рассмотрим плотность потока энергии. Так как энергия на одну частицу равна 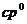, среднее значение можно записать следующим образом:

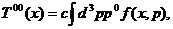 (11)

где макроскопическую плотность энергии мы обозначили символом 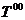, причем поток энергии есть 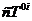и

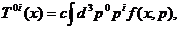 i=1,2.3, (12)

где величин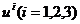а  представляет собой декартовы компоненты скорости. Плотность импульса 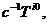 который является средним значением от импульсов частиц 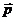, определяется следующей формулой:

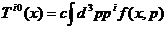, i=1,2,3. (13)

Наконец, поток импульса (или тензор давлений) определяется как поток i - компоненты импульса в направлении j:

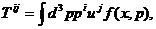 где i,j=1,2,3. (14)

Введенные 16 величин можно объединить в один 4 - тензор. В самом деле, с учетом соотношений (5), связывающих микроскопическую скорость частиц с их импульсом, формулы (11) - (14) можно записать в более компактной ковариантной форме:

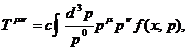  (15)

где 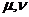=0,1,2,3. Следовательно, в РКТ тензор энергии - импульса (ТЭИ) определяется как второй момент функции распределения, и представляет собой симметричную величину.

Запомним, что в формуле (15) для ТЭИ учитываются лишь энергия покоя и кинетическая энергия частиц. То есть, предполагается, что система является разреженной, а энергия взаимодействия частиц мала по сравнению с энергией покоя. В противном случае ТЭИ следовало бы дополнить энергией взаимодействий частиц (ее нерелятивистский аналог - потенциальная энергия частиц).

2.3 Вектор потока энтропии

С помощью введенной Больцманом H - функции локальная плотность энтропии определяется так:

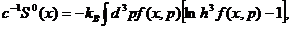 (16)

где 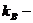постоянная Больцмана, h - произвольная постоянная, выбранная так, чтобы стоящая под знаком логарифма комбинация 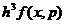 была безразмерной величиной. В качестве h удобно выбрать постоянную Планка, а из логарифма вычесть единицу, как это сделано в формуле (16). Поток энтропии, соответствующий формуле (16) имеет вид:

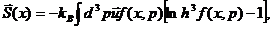 (17)

где 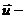скорость частиц.

В релятивистской теории для плотности и потока энтропии можно применять те же самые выражения (16), (17), поскольку с учетом (5) они объединяются в единый релятивистский 4 - вектор:

который называется 4 - вектором потока энтропии. С помощью этого выражения будет сформулирован закон возрастания энтропии.

3. Релятивистское кинетическое уравнение

Кинетическое уравнение, или уравнение переноса, является замкнутым уравнением, описывающим поведение одночастичной функции распределения в пространстве и времени [13].

Конкретный вид этого уравнения определяется рядом условий. Одно из них состоит в том, что рассматриваются только двухчастичные столкновения. Кроме того, изменения функции распределения в микроскопическом масштабе длины и времени должны быть пренебрежимо малы, ввиду того, что только при этих условиях и возможно микроскопическое описание.

В этом параграфе мы дадим вывод релятивистского кинетического уравнения (РКУ), основываясь на ряде "очевидных" гипотез, проверяемых экспериментально.

Чтобы получить уравнение, которому должна удовлетворять функция 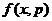в релятивистской кинетической теории наряду с требованиями ковариантности делаются такие же предположения, как и в нерелятивистском подходе [13].

1)      Учитываются лишь двухчастичные столкновения

2)      Используется гипотеза молекулярного хаоса. Эта гипотеза представляет собой статистическое предположение о числе двойных столкновений. Предполагается, что число таких столкновений пропорционально произведению функций распределения сталкивающихся частиц, а также скорости перехода, являющейся мерой вероятности процесса столкновения.

)        Предполагается, что функция распределения медленно меняется в пространств - времени, то есть ее изменения на характерной длине взаимодействия и в течение характерного времени взаимодействия пренебрежимо малы

3.1 Случай без столкновения

В этом случае, наряду с формулой (6) для вектора потока числа частиц 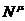, можно построить скалярную величину

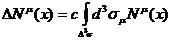, (19)

где времениподобный вектор 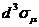 есть ориентированная элементарная площадка плоской пространственно - подобной поверхности 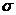,  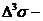малый сегмент в окрестности точки x.

Иначе, это выражение можно переписать с использованием (5), (6) в системе отсчета, где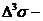чисто пространственно-подобная величина в виде

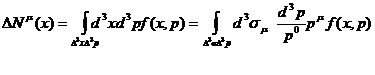 (20)

Эта величина представляет собой число классических мировых линий, пересекающих сегмент 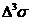и направленных вдоль импульсов p в элементе 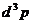в окрестности .

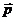Несколько позже эти же мировые линии частиц пересекут элемент поверхности 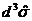. Следовательно, справедливо равенство

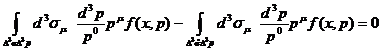. (21)

Теперь рассмотрим элемент 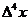 пространства Минковского, заключенный между поверхностями 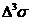,  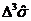и поверхностью трубки, образуемой рассматриваемыми мировыми линиями. Так как нас интересует случай без столкновений, ни одна мировая линия не должна пересечь поверхность трубки. Поэтому, равенство (21) выражает собой равенство нулю общего потока через поверхность 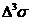 элемента  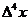пространства Минковского:

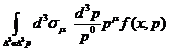=0 (22)

C помощью теоремы Гаусса (которая справедлива для пространства любой размерности) это соотношение можно переписать в виде 4 - дивергенции:

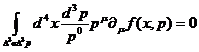 (23)

где 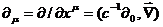 - оператор дифференцирования по пространственно - временным координатам. В силу произвольности интервалов 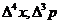, из (23) следует, что

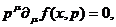 (24)

Это и есть РКУ в отсутствии столкновений.

В трехмерных обозначениях оно перепишется как

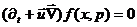 (25)

3.2 Кинетическое уравнение

Для получения полного кинетического уравнения необходимо учесть влияние столкновений. В результате столкновений число частиц в области изменения переменных 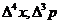меняется на величину, которую можно записать как

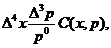 (26)

причем С (x, p) - инвариантная функция, которую необходимо определить. Для нахождения ее вида, обратимся к предположениям, сделанным вначале параграфа 3.

Рассмотрим столкновения между 2-мя частицами, которые до столкновений имели импульсы 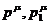, а после столкновения 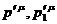. Согласно гипотезе молекулярного хаоса, среднее число таких столкновений в элементе объема 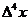 в пространстве Минковского вблизи точки x (в интервале 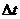времени t) и в элементе объема 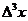 вблизи точки x пропорционально следующим величинам:

)        среднему числу частиц на единицу объема с 3 - импульсами в интервале 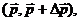а именно,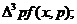

)        среднему числу частиц на единицу объема с 3 - импульсами в интервале 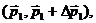а именно,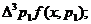

)        интервалам .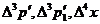

Коэффициент пропорциональности обозначим как .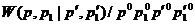

Определенная таким образом величина 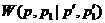 называется скоростью перехода. Она зависит лишь от 4 - импульсов частиц до и после столкновения и представляет собой лоренцев скаляр. Очевидно, что оба аргумента до и после вертикальной черты могут располагаться в произвольном порядке.

В соответствии с условием медленного изменения функции распределения на расстояниях и временах порядка характеристических длин и времен взаимодействий предполагается, что разностью пространственно - временных координат сталкивающихся частиц до и после столкновения можно пренебречь. Таким образом, зависимость от пространственно - временных координат 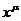означает, что в функциях распределения  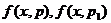фигурирует одно и то же значение x, но оно отсутствует в скорости перехода .

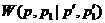В итоге, благодаря гипотезе молекулярного хаоса, мы можем сделать следующее утверждение: среднее число частиц в элементе объема 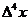 пространства Минковского с импульсами в окрестности 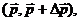выбывающих за счет столкновений, определяется посредством интегрирования описанного выше числа столкновений по всем значениям 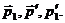Кроме того, добавим множитель ½, чтобы учесть тот факт, что нельзя различить конечные состояния с импульсам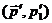и и .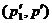

Истинное изменение числа частиц в элементах 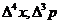 равно разности количества частиц приходящих в эти элементы и уходящих из них:

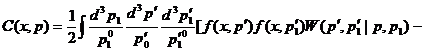
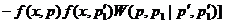 (27)

Это как раз то истинное изменение числа частиц, которое выражается формулой (27). Величина 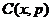 выражается через функцию распределения и скорость перехода, то есть определяется динамикой системы.

Выпишем теперь РКУ с учетом эффекта столкновений, согласно сформулированным предположениям. Так, вместо уравнения (23) получим

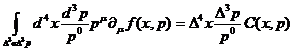 (28)

В силу произвольности интервалов 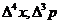, из (28) следует, что

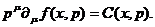 (29)

С учетом выражения (27) релятивистское кинетическое уравнение переноса запишется так:

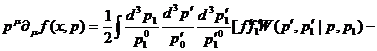
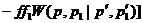, (30)

где использованы сокращенные обозначения 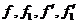 для функций  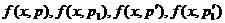соответственно.

Как и в нерелятивистской теории левую часть уравнения (30) часто называют потоковым членом (streaming term), а правую - членом столкновения (collision term).

Сходство с нерелятивистской теорией становится еще более очевидным, если последнее уравнение представить в нерелятивистской записи

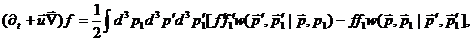 (31)

где

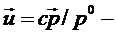скорость, а  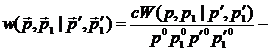скорость перехода.

Как следует из смысла выражений (27), (31), величина 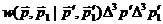 представляет собой отнесенную к единице объема и единице времени вероятность перехода для двух частиц, которые имели до рассеяния импульсы 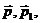а после рассеяния имеют импульсы, лежащие в пределах (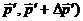 и ().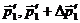

3.3 Дифференциальное сечение и скорость перехода

Скорость перехода 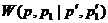, по определению, является скаляром.

Таким образом, она является функцией десяти скалярных инвариантов, которые можно построить из 4-импульсов .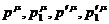

Четыре из этих скаляров заданы в силу нормировок 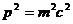и т.д. Кроме того, должен выполняться закон сохранения импульса

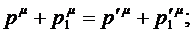 (32)

Таким образом, число свободных параметров сводится к двум. Эти 2 переменные можно выбрать по - разному, например как переменные Мандельштамма - s и t:

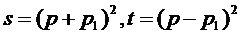
  (33)

Инвариант s, умноженный на 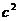, представляет собой квадрат энергии в системе центра импульсов, то есть в лоренцевой системе, в которой пространственные компоненты полного 4 - импульса 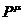 есть:

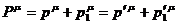 (34)

и обращаются в нуль: .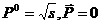

Параметр t связан с с углом рассеяния в системе центра импульсов

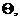 который определяется следующей формулой:

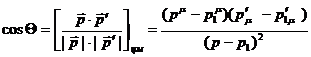 (35)

С помощью (32,33), (35) можно доказать связь между переменными рассеяния

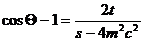 (36)

Из приведенных рассуждений и того, что при переходе энергия и импульс сохраняются, вытекает, что мы можем написать следующее выражение:

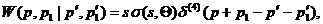
Обычно дифференциальное сечение определяется таким образом, чтобы его произведение на поток частиц в начальном состоянии было равно вероятности перехода в единице объема в единицу времени. В лоренцевой системе отсчета, где скорости падающих частиц параллельны или антипараллельны, или в системе, где одна из частиц покоится, этот поток равен произведению плотности числа частиц и относительной скорости:

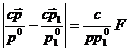 (37) Величина  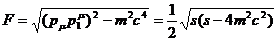(38)

называется инвариантным потоком. Далее, вероятность перехода на единицу объема и единицу времени 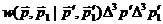, введенная в конце предыдущего пункта, должна быть нормирована на одну пару частиц в расчете на единицу объема. Следовательно, чтобы получить выражение для сечения, нужно лишь разделить ее на относительную скорость. Тогда имеем с учетом определений в (31) выражение для дифференциального сечения рассеяния:

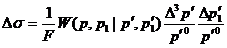 (39)

Из последнего соотношения после громоздких, но несложных вычислений следует стандартное математическое выражение для :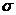

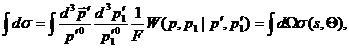 (40)

где 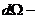элемент телесного угла в системе центра импульсов. Из этой формулы видно, что 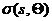 представляет собой дифференциальное сечение рассеяния в обычном определении.

Иногда бывает полезно выразить член столкновений в кинетическом уравнении (30) через дифференциальное сечение. В результате получается релятивистское уравнение переноса

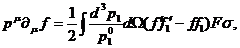 (41)

где F - инвариантный поток (38).

В трехмерной записи это уравнение имеет вид:

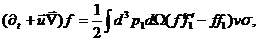 (42)

где v - скорость Меллера: .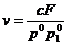

Оно полностью аналогично нерелятивистскому уравнению Больцмана [12].

3.4 Внешняя сила

В релятивистском уравнении переноса можно учесть влияние внешней силы при условии, что отклонение траекторий частиц, обусловленное этой силой, между столкновениями мало. Это условие гарантирует нам то, что непосредственно перед столкновениями частицы по-прежнему приближаются друг к другу по прямой линии. В противном случае, описание процесса столкновения с помощью понятия скорости перехода было бы бессмысленным. Поскольку по предположению внешняя сила не влияет на процесс столкновений, далее ограничимся рассмотрением случая без столкновений. При наличии внешнего силового поля 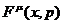 нужно видоизменить формулу (21), поскольку теперь за время прохождения частицы от элемента трехмерной поверхности 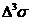 до 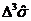 ее импульс  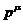изменится и станет равным 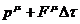. Здесь  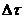- собственное время релятивистской частицы, которое связано с4-м объемом равенством

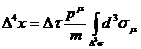 (43)

где 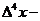четырехмерный объем.

После коррекции на действие внешней силы формула (21) принимает вид:

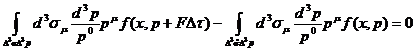 (44)

Учитывая (43), используя разложение в ряд Тейлора и теорему Гаусса, получаем

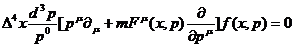 (45)

Здесь учтено, что функция распределения f является дифференцируемой и достаточно гладкой (это утверждение относительно f может быть ослаблено [9]). В силу произвольности промежутков объема и времени, из последнего равенства следует дифференциальное уравнение

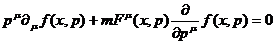 (46)

Для случая столкновительного газа, получаем полное РКУ

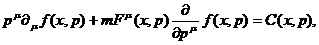 (47)

где член столкновений определяется выражением (27).

При выводе последнего уравнения предполагалось также, что внешняя сила является механической и не изменяет массу покоя частицы:

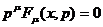 (48)

Кроме того, было сделано предположение, что частицы с импульсами, лежащими в области 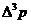в начале интервала собственного времени 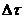, занимают такую же область импульсов в конце этого интервала.

Это предположение не является самоочевидным и заведомо выполняется только для консервативных сил [9]:

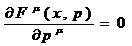 (49)

Очевидно, что этим свойством обладают, например силы Лоренца

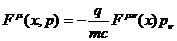, (50)

где q - заряд, 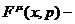антисимметричный тензор электромагнитного поля. Несколько более сложные рассуждения

приводят к аналогичному выводу и для другого классического поля - гравитационного [10].

Полезно рассмотреть РКУ в трехмерной записи.

В этом случае путем деления на  получаем

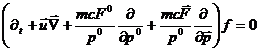 (51)

Из (48) следует, что 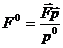. (52)

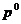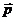Величины  и  мы до сих пор рассматривали, как независимые относительно операции 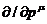, что и отражено в уравнении (53).

Можно стать на другую точку зрения и свести дифференцирование в кинетическом уравнении только к дифференцированию по импульсу

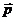. Тогда, согласно правилу дифференцирования сложной функции,

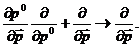 (53)

Эта замена и равенство (48) позволяют записать уравнение (51) в виде

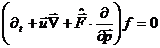 (54)

Величин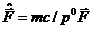а  представляет собой обычную трехмерную силу, которая равна производной по времени от трехмерного импульса.

При 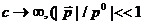все полученные релятивистские уравнения переходят в стандартные уравнения нерелятивистской кинетической теории [12].

4. Краткий обзор основных результатов релятивистской кинетической теории

4.1 Макроскопические законы термодинамики

Кинетическая теория дает подтверждение второго начала термодинамики. Это положение известно, как H - теорема Больцмана.

Так, для реагирующей смеси, состоящей из N частиц (с номерами i, j, k, l…) можно вывести закон возрастания энтропии. Этот закон следует из точного выражения для локального прироста энтропии релятивистской среды: 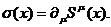 Здесь  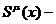4 вектор тока энтропии, математическое выражение для ее локального прироста есть:

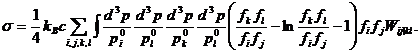 (55)

Поскольку функция 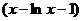положительна для положительных значений x и обращается в нуль только при x=1, прирост энтропии никогда не бывает отрицательным,

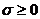 (56)

Законы сохранения для РКУ принимают вид

1)      Закон сохранения числа частиц

Равенство 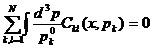 (57)

c учетом РКУ (29) можно записать в виде макроскопического уравнения

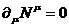 (58)

Отсюда же следует закон сохранения макроскопического тока (например, электрического)

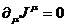 (59)

где 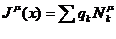, 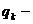соответствующий заряд.

) Сохранение энергии и импульса

Равенство 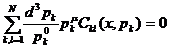 (60)

c учетом РКУ (29), (60) можно записать в виде макроскопического закона сохранения

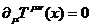 (61)

4.2 Локально - равновесное состояние

Локально - равновесное состояние определяется, как состояние в окрестности точки x, прирост энтропии в котором отсутствует

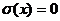 (62)

Из (69) следует единственное решение для функций распределения в этом состоянии

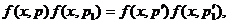 (63)

Функции распределения, удовлетворяющие этому условию, называются локально - равновесными.

Из (63) следует функциональное соотношение для таких функций

где h - постоянная Планка (64). Решением (64), следовательно, является локально - равновесная функция распределения

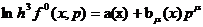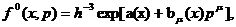 или  (65)

Если система находится под действием внешних электромагнитных сил, то параметры этой функции жестко фиксируются и она принимает вид:

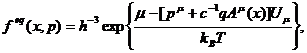 (66)

где 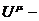макроскопическая 4 - скорость, T - температура, µ - химический потенциал среды. В случае, когда внешнее поле отсутствует, (66) принимает вид:

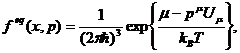 (67)

Эта равновесная функция распределения была открыта Юттнером в 1911 году и носит название "функция Юттнера" [9,10].

Из РКУ также следуют уравнения состояния идеального газа безмассовых частиц

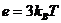 (68)

и обычное термическое уравнение состояния идеального газа

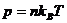 (69)

Из последних 2 - х уравнений следует хорошо известное уравнение состояние черного излучения

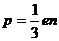 (70)

Для определения коэффициентов переноса любого релятивистского газа, в том числе газа квантовых частиц, в релятивистской кинетической теории развивается теория кинетических скобок, изложение которой выходит за рамки настоящего краткого обзора.

5. Эффект Комптона - Геттинга в двух сериалах

Одной из характерных черт космического первичного излучения является почти полная изотропия его распределения по небесной сфере.

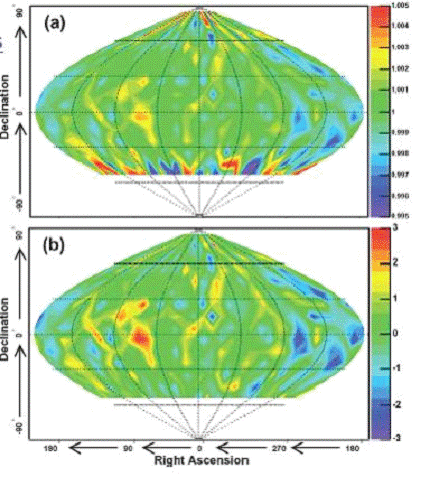
Рис. 1. Карта потока космических лучей в мюоном свете по данным установки Супер-Камиоканда. Интенсивность потока в условных единицах представлена на 1 (a). На 1 (b) представлено стандартное отклонение 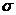. Области анизотропии обозначены контрастом серого и черного тонов.

Степень анизотропии не превышает нескольких процентов и зависит от направления. Наблюдаемую анизотропию обычно выражают, как вариацию потока j. Степень анизотропии характеризуется величиной

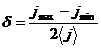 (71)

где 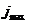, , 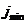 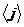- максимальная, минимальная и средняя интенсивности потока.

Эффект анизотропии, возникающий при движении Солнечной системы относительно галактических космических лучей называется эффектом Комптона - Геттинга (КГ) по имени его первооткрывателей [14,15]. Пусть дифференциальный спектр первичных частиц представлен степенным законом, зависящим только от энергии E:

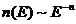, (72)

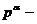импульс релятивистских частиц, 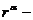их координаты в собственной системе отсчета. Тогда для достаточно разреженных бесстолкновительных потоков в отсутствии внешних полей, кинетическое уравнение в 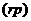пространстве будет иметь вид, аналогичный (24), (54):

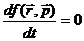 (73)

Дифференциальный поток 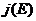и плотность частиц 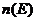можно связать с функцией распределения следующим образом. Величина

 есть число частиц в интервале 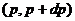внутри элемента телесного угла 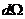. Эти частицы за время dt пересекают поверхность dS, расположенную перпендикулярно 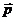. Элемент объема в 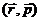пространстве равен .

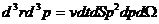Полное количество зарегистрированных под всеми углами частиц является инвариантом и фигурирует в обеих частях нижеследующего равенства:

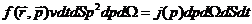 (74)

где 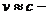скорость регистрируемых частиц.

С учетом связи между полной энергией и импульсом частиц (9) получаем связь между дифференциалами а связь между потоком и фазовой скоростью принимает вид:

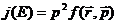. (75)

Дифференциальная плотность частиц для изотропного распределения

примет вид:

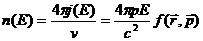 (76)

Сериал 1. Эффект Комптона - Геттинга в СТО [15].

Если рассматривать частицы в системе координат, которая движется со скоростью 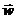, то импуль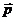с частицы в системе покоя преобразуется в импульс 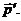 Согласно СТО, преобразования Лоренца для импульсов имеют вид:

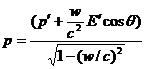 (77)

Так как скорость движения системы отсчета является нерелятивистской 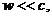радикал в знаменателе можно заменить единицей.

Тогда, выражение для функции распределения в движущейся системе координат можно разложить в степенной ряд:

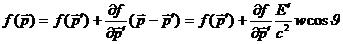 (78)

Рассчитаем дополнительную часть потока частиц, связанную с движением системы координат, через поверхность, перпендикулярную 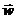, с помощью формул (75), (76):

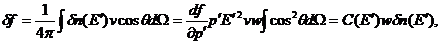 (79)

где С (E) - коэффициент анизотропии Комптона-Геттинга. Из последних формул следует, что поток частиц под углом 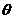 к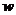 про - порционален  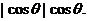Если интегральный поток частиц, пересекающих поверхность, перпендикулярную 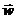, равен 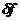, то дифференциальная интенсивность, обусловленная потоком частиц под углом 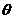, равна

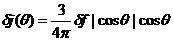 (80)

Складывая (80) с интенсивностью фона изотропно распределенных частиц плотности n, которая равна 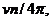получаем

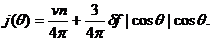
Поток 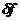связан с плотностью через КГ - коэффициент

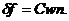 (81)

Для степенного спектра частиц (72) отсюда следуют выражения для коэффициентов анизотропии потока

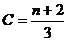 (82)

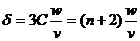 (83)

Сериал 2. Эффект Комптона - Геттинга в неинерциальной системе отсчета ОТО. Будем считать, что наблюдатель вращается либо вместе с Галактикой, либо в солнечной системе.

Рассчитаем анизотропию 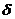с помощью бесстолкновительной кинетической теории ОТО [10]:

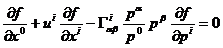 (84)

Здесь и далее примем скорость света с=1. При 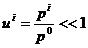 (84) упрощается:

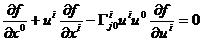 (85)

При вращении Галактики и звездных систем сила Кориолиса значительно больше других неинерциальных сил [16]:

Поэтому, отличные от нуля компоненты метрики вращающейся

системы отсчета примут вид:

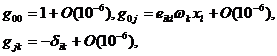 (86)

где 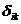 - тензор Кронекера, 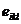-тензор Леви - Чивита,  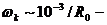- угловая скорость вращения, 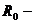характерный масштаб исследуемой системы (например, галактики или солнечной системы). Метрика (87) позволяет рассчитать символы Кристоффеля, играющие роль классических сил в кинетическом уравнении (85)

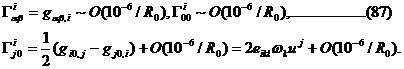
По определению компонент 4 - импульса (9), в искомом прибли - жении 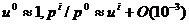. Тогда кинетическое уравнение (85) примет вид:

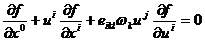 (88)

Из (88) видно, что сила Кориолиса является в этом уравнении аналогом магнитной части силы Лоренца в уравнении электромагнитного поля.

Решение (88) для стационарного (не зависящего от времени) и однородного (не зависящего от координат) состояния 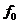 принимает вид:

 (89)

Его решением является функция

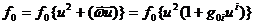, (90)

где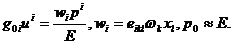

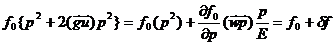 (91)

здесь 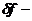анизотропная часть функции распределения, связанная с движением наблюдателя.

Соответствующие 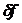плотность 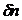и поток 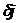имеют вид:

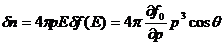 (92)

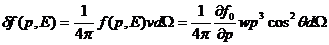 (93)

Интегрирование (93) дает

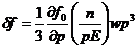. (94)

Подставляя в (94) степенной спектр (72), получим коэффициент КГ

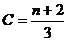, (95)

анизотропную часть потока

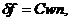 (96)

полный поток

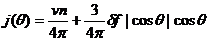 (97)

и анизотропию космических лучей

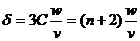. (98)

Из (83), (98) вытекает, что оба рассмотренных сериала по расчету анизотропии космического излучения за счет движения наблюдателя эквивалентны и приводят к одинаковым числовым значениям. Анизотропия за счет вращения Галактики 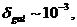анизотропия за счет собственного вращения Солнца .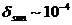

6. Заключение

Кинетическая теория предоставляет удобные методы расчета неравновесных процессов в объектах различной физической природы. Астрофизические процессы, описываемые РКТ должны иметь максимально высокую энергетику и сопровождаться явлениями взрывного характера. Например, в физике космических лучей до сих пор нет объяснения значения показателя "n" для первичного спектра космических лучей. Сегодня известны только общие указания на характер объектов, которыми он может быть создан. Любой объект конечных размеров должен быть прозрачен для лучей высоких энергий и, поэтому, его спектр должен обрезаться на некоторой большой энергии E. В то же время, в космических лучах присутствуют ядра железа и других тяжелых элементов. Эти элементы выбрасываются сверхновыми звездами и остаются в Галактике при расширении оболочек сверхновых. Релятивистские ударные волны в космическом пространстве, создаваемые расширением этих оболочек неоднократно рассчитывались ранее [6] и рассчитываются до сих пор [17]. Однако, остается надежда на то, что изменение и взаимопроникновение сериалов, описывающих релятивистские процессы в Галактике когда - нибудь приведет к надежно установленным и общепризнанным результатам и в этой области физики.

Список литературы

1.      В.П. Маслов // Квантование термодинамики и ультравторичное квантование Москва - Ижевск, Регулярная и хаотическая динамика, 2006.

2.      D. Bekenstein // astro - ph /0701848

3.      A. Yu. Ignatiev // Phys. Rev. Lett., v.98, 101101,, 2007.

.        C. Scordis et al. / /Phys. Rev. Lett. v.96 011301, 2006.

5.      D. Bekenstein, J. Magueijo // Phys. Rev. D.73, 103513, 2006.

6.      Ю.П. Очелков, О.Ф. Прилуцкий, И.Л. Розенталь, В.В. Усов // Релятивистская кинетика и гидродинамика, М: Атомиздат, 1979.

.        И.Н. Павлоцкий // Начала слаборелятивистской статистической механики. М: Высшая школа, 1983.

.        Ч. Мизнер, Дж. Уиллер, К. Торн // Гравитация, т.2., М.: Мир, 1977.

.        С. де Гроот и др. Релятивистская кинетическая теория. // М.: Мир, 1983.

.        А.В. Захаров // Макроскопическая гравитация. // М.: Янус - К, 2010.

.        А.А. Власов // Нелокальная статистическая механика. М: Наука, 2008.

.        Л.Д. Ландау, Е.М. Лифшиц // Теория поля, М.: Наука, 1973.

.        Е.М. Лифшиц, Л.П. Питаевский // Физическая кинетика, М: Наука, 1979.

14.    A. H.compton, I. A. Getting // Phys. Rev. v.47, 817, 1935.

15.    С. Хаякава // Физика космических лучей, ч.2, М: Мир, 1974.

16.    Bailey Q. G., Kostelecky A. V. // Phys. Rev. D 74, 045001, 2006.

17.    M. Liebendorfer et. al. // Phys. Rev. D 63, 103004, 2002.