Постулаты теории относительности. Связь между массой и энергией
Курсовая
работа на тему:
«Постулаты
теории относительности. Связь между массой и энергией».
Содержание
Введение
Раздел
1. Теоретическая часть
Раздел
2. Расчётная часть
Раздел
3. Практическая часть
Заключение
Список
литературы
Введение
Теория относительности - общепринятая
официальной наукой теория о том, как устроен мир (на макроуровне), объединяющая
механику, электродинамику и гравитацию. Содержанием теории относительности
является физическая теория пространства и времени, учитывающая существующую
между ними взаимосвязь геометрического характера.
Специальная теория относительности (СТО; также
частная теория относительности) - теория, описывающая движение, законы механики
и пространственно-временные отношения при произвольных скоростях движения,
меньших скорости света в вакууме, в том числе близких к скорости света. В
рамках специальной теории относительности классическая механика Ньютона
является приближением низких скоростей. Обобщение СТО для гравитационных полей
называется общей теорией относительности.
Описываемые специальной теорией относительности
отклонения в протекании физических процессов от предсказаний классической
механики называют релятивистскими эффектами, а скорости, при которых такие
эффекты становятся существенными, - релятивистскими скоростями.
Эквивале́нтность
ма́ссы
и эне́ргии
- физическая концепция, согласно которой масса тела является мерой энергии,
заключённой в нём. Энергия тела равна массе тела, умноженной на размерный
множитель квадрата скорости света в вакууме: 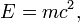 где
E - энергия тела, m - его масса, c - скорость света в вакууме, равная 299 792
458 м/с.
где
E - энергия тела, m - его масса, c - скорость света в вакууме, равная 299 792
458 м/с.
С одной стороны, концепция означает, что масса
неподвижного тела (так называемая масса покоя) является мерой внутренней
энергии этого тела;
С другой стороны, можно утверждать, что любому
виду энергии соответствует некая масса. Например, было введено понятие
релятивистской массы как характеристики кинетической энергии движущегося тела.
Раздел 1. Теоретическая часть
Постулаты теории относительности.
Постулат в физике соответствует аксиоме в
математике. Два постулата лежат в основе теории относительности. Для объяснения
опытов, не обнаруживших движение Земли относительно эфира, делались разные
предположения, пытаясь понять почему не находится преимущественная система
отсчета, которой не было, как выяснили потом. Эйнштейн решал данную проблему,
не пытаясь найти различие между инерциальными системами. Он считал, что все
инерциальные системы равноправны не только для механических, но и электромагнитных
явлений. Нет разницы между равномерным и прямолинейным движением и состоянием
покоя. Главный постулат теории Эйнштейна - это принцип относительности: все
процессы природы протекают одинаково во всех инерциальных системах отсчета.
Этот закон позволил распространить принцип относительности механики на
электромагнитные, да и вообще на все законы природы. Второй постулат теории
относительности гласит: скорость света в вакууме одинакова для всех
инерциальных систем отсчета. Она не зависит ни от скорости источника, ни от
скорости приемника светового сигнала. Из постулатов теории относительности
вытекает: скорость света имеет особое положение; скорость света в вакууме
является предельно возможной скоростью передачи взаимодействий в природе.
Большая научная смелость нужна была Эйнштейну, чтобы опубликовать постулаты,
которые противоречили представлениям о пространстве и времени. Рассмотрим
инерциальные системы К и К₁, которые
движутся друг относительно друга со скоростью Ѵ̄, когда начала
координат совпадают, происходит вспышка света. Обозначим: Ѵ·t - смещение
систем относительно друг друга за время - t; c·t - радиус сферической
поверхности.
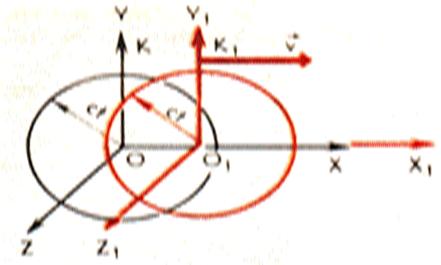
Рис. 1
Системы К и К₁
- равноправны, имеют одинаковую скорость.
Один наблюдатель связан с системой К и центр
сферы для него расположен в точке О. Для второго наблюдателя, который связан с
системой К₁ центр сферы будет находиться в
точке О₁.
Постулаты относительности приводят к противоречию, так как одна и та же
сферическая поверхность не может иметь центры в О и О₁.
Но это противоречие связано лишь с классическими представлении о пространстве и
времени, которые при скоростях, близких к скорости света, - несправедливы.
. Возникновение теории относительности
В классической механике считается, что длина и
время являются величинами абсолютными, а скорость и перемещение -
относительными. Механический принцип относительности (принцип Галилея)
заключается в том, что все механические явления протекают одинаково в любой
инерциальной системе отсчета (форма записи механических законов не изменяется
при переходе от одной ИСО к другой). В инерциальной системе отсчета невозможно
отличить покой от равномерного прямолинейного движения. Для любых механических
явлений все инерциальные системы отсчета оказываются равноправными. Галилей не
задумывался о других явлениях, т.к. в те времена механика составляла, по
существу, всю физику. До середины XIX в. считали, что все физические явления
можно объяснить на основе механики Ньютона.
В середине XIX в. была создана теория
электромагнитных явлений (теория Максвелла). Оказалось, что уравнения Максвелла
изменяют свой вид при галилеевских преобразованиях перехода от одной ИСО к
другой. Возник вопрос о том, как влияет равномерное прямолинейное движение на
все физические явления. Перед учеными встала проблема согласования теорий
электромагнетизма и механики.
Задача была трудной, т.к. законы классической
механики прекрасно подтверждались в обширной области явлений (от статики до
небесной механики), замечательно служили практике, и изменять это казалось
абсурдным. Поэтому многие ученые пытались построить теорию электродинамики так,
чтобы она соответствовала классической механике.
Согласно теории Максвелла свет распространяется
со скоростью 300 000 км/с. Спрашивается, относительно чего свет движется с
такой скоростью? (Если самолет летит по направлению ветра, скорость которого
100 км/ч, а его собственная скорость относительно воздуха 500 км/ч, то
относительно Земли самолет летит со скоростью 600 км/ч).
Относительно чего свет движется со скоростью c?
Ответ на этот вопрос не содержится ни в теории Максвелла, ни в теории Юнга.
Если свет - волна, и если волна распространяется в среде, то свет движется со
скоростью c относительно среды. Эта светоносная среда получила название эфира.
Дебаты, касающиеся светоносного эфира к концу XIX в. достигли особой остроты.
Интерес к эфиру возрос, когда стало ясно, что созданная Максвеллом теория
оказалась успешной и вроде бы свидетельствует о том, что эфир можно наблюдать.
Если эфир существует, то должен быть обнаружен
эфирный ветер. Опыт по обнаружению эфирного ветра был поставлен в 1881 г.
американскими учеными А. Майкельсоном и Р. Морли с помощью оригинального
интерферометра. Наблюдения проводились в течение длительного времени. Опыт
многократно повторяли. Результат оказался отрицательным: никакого движения
Земли относительно эфира обнаружить не удалось. Различные эфирные теории завели
физику в тупик.
В 1905 г. А. Эйнштейн, отвергнув гипотезу эфира,
предложил специальную (частную) теорию относительности, на основе которой можно
совместить механику и электродинамику. В 1905 г. вышла его работа «К
электродинамике движущихся тел». В ней Эйнштейн сформулировал два принципа
(постулата) теории относительности.постулат: все законы природы имеют одинаковую
форму во всех инерциальных системах отсчета.постулат: скорость света в вакууме
одинакова во всех инерциальных системах отсчета. Она не зависит ни от скорости
источника, ни от скорости приемника светового сигнала.
Чтобы сформулировать эти постулаты, нужна была
большая научная смелость, т.к. они, очевидно, противоречили классическим
представлениям о пространстве и времени.
Итак, современная физика подразделяется на:
классическую механику, которая изучает движение
макроскопических тел с малыми скоростями (v<< c);
релятивистскую механику, которая изучает
движение макроскопических тел с большими скоростями (v < c);
квантовую механику, которая изучает движение
микроскопических тел с малыми скоростями (v << c);
релятивистскую квантовую физику, которая изучает
движение микроскопических тел с произвольными скоростями (v Ј c).
СЛЕДСТВИЯ ИЗ ПОСТУЛАТОВ СТО
. Относительность одновременности событий
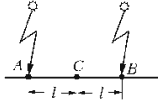
Рис. 2
Принято считать, что события в точках A и B
произошли одновременно, если световые сигналы, испущенные ими, приходят
одновременно в точку C, находящуюся посередине между точками A и B.
Допустим, что в точке C находится покоящийся
относительно A и B фотоэлемент, соединенный с осциллографом. При включении ламп
световые сигналы к фотоэлементу приходят одновременно через некоторый
промежуток времени 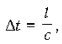 , и на экране
осциллографа наблюдается один всплеск.
, и на экране
осциллографа наблюдается один всплеск.
Пусть фотоэлемент с осциллографом движется
равномерно со скоростью v влево, тогда световая волна от правой лампы должна
будет пройти до фотоэлемента большее расстояние (l + s), чем волна от левой
лампы (l - s), где s = vDt. Это приведет к тому, что световая волна от левой
лампы дойдет до фотоэлемента раньше, чем от правой, и на экране появятся два всплеска.
Следовательно, события, одновременные в одной инерциальной системе отсчета, не
являются одновременными в другой системе отсчета, т.е. одновременность событий
относительна.
. Относительность промежутков времени.
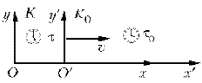
Рис. 3
Пусть инерциальная система отсчета K покоится, а
система отсчета K0 движется относительно системы K со скоростью v.
Пусть интервал времени между двумя событиями,
происходящими в одной и той же точке инерциальной системы K0, равен t0.
Тогда интервал времени между этими же событиями
в системе K будет выражаться формулой:
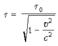 .
.
Это эффект замедления времени в движущихся
системах отсчета. Если v << c, то величиной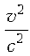 можно пренебречь, тогда
можно пренебречь, тогда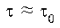 и никакого
замедления в движущихся системах можно не учитывать.
и никакого
замедления в движущихся системах можно не учитывать.
Замедление времени позволяет, в принципе,
осуществить «путешествие с будущее». Пусть космический корабль, движущийся со
скоростью v относительно Земли, совершает перелет от Земли до звезды и обратно.
За время t0 свет проходит путь от Земли до звезды: l0 = c • t0.
Продолжительность полета по часам земного
наблюдателя равна:
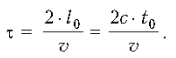
Настолько постареют люди на Земле к моменту возвращения
космонавтов. По часам, установленным на космическом корабле, полет займет
меньше времени:
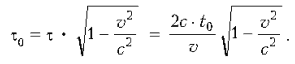
По принципу относительности, все процессы на
космическом корабле, включая старение космонавтов, происходят так же, как и на
Земле, но не по земным часам, а по часам, установленным на корабле.
Следовательно, к моменту возвращения на Землю космонавты постареют только на
время t0.
Если, например, t0 = 500 лет и v2/c2 = 0,9999,
то формулы дают t = 1000,1 года, t0 = 14,1 года.
Космонавты возвратятся на Землю по земным часам
спустя 10 веков после вылета и постареют лишь на 14,1 года.
. Относительность расстояний.
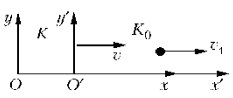
Рис. 4
Классический закон сложения скоростей не может
быть справедлив, т.к. он противоречит утверждению о постоянстве скорости света
в вакууме. Если поезд движется со скоростью v и в вагоне в направлении движения
поезда распространяется световая волна, то ее скорость относительна Земли все
равно c, а не v + c.
Рассмотрим две системы отсчета.
В системе K0 тело движется со скоростью v1.
Относительно же системы K оно движется со скоростью v2. Согласно закону
сложения скоростей в СТО:
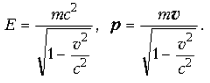
Если v << c и v1 << c, то слагаемым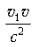 можно пренебречь, и тогда получим классический закон сложения скоростей: v2 =
v1 + v.
можно пренебречь, и тогда получим классический закон сложения скоростей: v2 =
v1 + v.
При v1 = c скорость v2 равна c, как этого
требует второй постулат теории относительности:
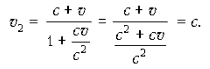
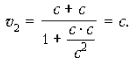
Замечательным свойством закона сложения является
то, что при любых скоростях v1 и v (не больше c), результирующая скорость v2 не
превышает c. Скорость движения реальных тел больше, чем скорость света,
невозможна. Допустим, что два тела движутся навстречу друг другу со скоростями
200 000 км/с, тогда по классической формуле сложения скоростей получим:= 200
000 км/c + 200 000 км/c = 400 000 км/с, а по закону сложения скоростей в СТО v2
= 277 000 км/с.
. Закон Ньютона в релятивистской форме.
В классической механике основным законом
динамики является второй закон Ньютона:
= m • a.
Этот закон можно записать и в другом виде через
изменение импульса:
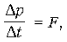
где p = m Ч v - импульс тела.
Основной закон релятивистской механики
записывается в прежней форме:
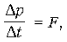 но теперь
но теперь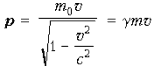 -
релятивистский импульс.
-
релятивистский импульс.
Связь между массой и энергией.
Связь между энергией и массой.
А. Эйнштейн установил основную формулу,
связывающую энергию, импульс и массу движущегося тела: E2 = p2c2+m2c4.
В эту формулу входят релятивистские энергия и
импульс:
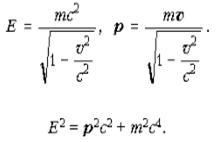
Из основной формулы следует связь массы тела с
его энергией покоя E0:
= mc2.
Эту формулу можно записать и в обратную сторону:

Эта формула позволяет перевести изменения
энергии взаимодействующих тел при нагревании, химических реакциях или
радиоактивных превращениях в эквивалентное изменение массы тел. Так как
коэффициент 1/с2 очень мал, то заметные изменения массы возможны лишь при очень
больших изменениях энергии. При химических реакциях или при нагревании тел в
обычных условиях изменения энергии невелики, поэтому изменение массы обнаружить
не удается.
В 1905 г. Эйнштейн опубликовал статью под
названием «Зависит ли инерция тела от содержащейся в нем энергии?». В ней он
пророчески заключил: «Не исключена возможность того, что теорию удастся
проверить для веществ, энергия которых меняется в большой степени (например для
солей радия)». При превращениях атомных ядер и элементарных частиц изменения энергии
оказываются весьма большими. Соответственно велики и эквивалентные изменения
массы. Лучшим примером может служить наше Солнце. В его центре происходят
термоядерные реакции синтеза водорода с образованием гелия. При этом выделяется
колоссальная энергия, малая доля которой дает нам жизнь. По формуле Эйнштейна
об эквивалентности массы и энергии можно вычислить, какая часть массы Солнца
ежесекундно превращается в излучение, и дать прогноз, что запасов термоядерного
топлива на Солнце хватит еще примерно на 10 млрд лет.
Рассмотрим важнейшее следствие, вытекающее из
теории относительности: универсальная связь между энергией и массой.
Из закона сохранения энергии и факта, что масса
тела зависит от скорости движения, вытекает связь между массой и энергией. Рассмотрим
такой пример: нагревая воду в чайнике, мы передаем определенную энергию.
Скорость движения молекул зависит от температуры и увеличивается по мере
нагревания жидкости. Согласно формуле
= QUOTE 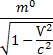
увеличение скорости молекул ведет к увеличению
массы всех молекул. Значит масса воды в чайнике увеличивается при возрастании
ее внутренней энергии, т.е. между массой жидкости и ее энергией существует
связь.
Формула Эйнштейна.
Используя, постулаты теории относительности Эйнштейн
установил универсальную связь между массой и энергией.
E= mc² = QUOTE 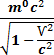 -
энергия тела или системы тел равна массе, умноженной на квадрат скорости света.
-
энергия тела или системы тел равна массе, умноженной на квадрат скорости света.
Из этой формулы можно найти массу:
𝚫m = QUOTE 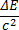 ;
;
Коэффициент очень мал, поэтому только при
больших изменениях энергии, возможны заметные изменения массы. Нагревание тел,
химические реакции дают незначительные изменения энергии, поэтому заметить
изменение массы невозможно. Горячая вода в сосуде имеет большую массу, чем
холодная вода, но даже самые чувствительные весы не могут этого обнаружить.
Изменения энергии достаточно большие, что
становится заметным изменение массы, происходят при превращениях элементарных
частиц и атомных ядер. Например, при взрыве атомной бомбы выделяется количество
энергии, сравнимое с электроэнергией, выработанной всеми электростанциями Земли
за несколько дней. Выделившаяся энергия улетает вместе с излучениями. Энергия
излучений имеет массу, которая составляет 0,1 % массы от исходного материала.
Энергия покоя.
На основании формулы:
относительность теория эйнштейн
формула
Е= mc² = QUOTE 
делаем вывод, что тело обладает энергией,
находясь в состоянии покоя, т.е. при Ѵ. Е₀=m₀c²
- энергия
покоя.
Любое тело обладает энергией уже благодаря факту
существования; энергия пропорциональна массе покоя m₀
Существует экспериментальное доказательство
энергии покоя. Если элементарная частица обладает массой покоя и превращается в
другие частицы, у которых масса покоя равна нулю (m₀=0),
то вся энергия покоя превращается в кинетическую энергию вновь образовавшихся
частиц.
Е = mc² -одна
из двух формул во всей физике, такая краткая по форме и всеобъемлющая по
содержанию.
После того, как Эйнштейн предложил принцип
эквивалентности массы и энергии, стало очевидно, что понятие массы может
использоваться двояко. С одной стороны, это та масса, которая фигурирует в
классической физике, с другой - можно ввести так называемую релятивистскую
массу как меру полной (включая кинетическую) энергии тела. Эти две массы
связаны между собой соотношением:
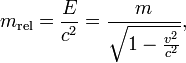
где 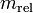 -
релятивистская масса, m - «классическая» масса (равная массе покоящегося тела),
v - скорость тела. Введённая таким образом релятивистская масса является
коэффициентом пропорциональности между импульсом и скоростью тела:
-
релятивистская масса, m - «классическая» масса (равная массе покоящегося тела),
v - скорость тела. Введённая таким образом релятивистская масса является
коэффициентом пропорциональности между импульсом и скоростью тела: 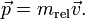
Аналогичное соотношение выполняется для
классических импульса и массы, что также приводится как аргумент в пользу
введения понятия релятивистской массы. Введённая таким образом релятивистская
масса в дальнейшем привела к тезису, что масса тела зависит от скорости его
движения.
В процессе создания теории относительности
обсуждались понятия продольной и поперечной массы частицы. Пусть сила,
действующая на частицу, равна скорости изменения релятивистского импульса.
Тогда связь силы 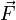 и ускорения
и ускорения 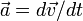 существенно
изменяется по сравнению с классической механикой:
существенно
изменяется по сравнению с классической механикой:
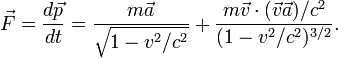
Если скорость перпендикулярна силе, то
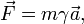
а если параллельна, то
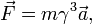
где 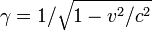 -
релятивистский фактор. Поэтому
-
релятивистский фактор. Поэтому 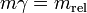 называют
продольной массой, а
называют
продольной массой, а 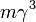 - поперечной.
- поперечной.
Утверждение о том, что масса зависит от
скорости, вошло во многие учебные курсы и в силу своей парадоксальности
приобрело широкую известность среди неспециалистов. Однако в современной физике
избегают использовать термин «релятивистская масса», используя вместо него
понятие энергии, а под термином «масса» понимая массу покоя. В частности,
выделяются следующие недостатки введения термина «релятивистская масса»:
Не инвариантность релятивистской массы
относительно преобразований Лоренца;
синонимичность понятий энергия и релятивистская
масса, и, как следствие, избыточность введения нового термина;
наличие различных по величине продольной и
поперечной релятивистских масс и невозможность единообразной записи аналога
второго закона Ньютона в виде
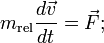
методологические сложности преподавания
специальной теории относительности, наличие специальных правил, когда и как следует
пользоваться понятием «релятивистская масса» во избежание ошибок;
путаница в терминах «масса», «масса покоя» и
«релятивистская масса»: часть источников просто массой называют одно, часть -
другое.
Несмотря на указанные недостатки, понятие
релятивистской массы используется и в учебной[12], и в научной литературе.
Следует, правда, отметить, что в научных статьях понятие релятивистской массы
используется по большей части только при качественных рассуждениях как синоним
увеличения инертности частицы, движущейся с около световой скоростью.
Раздел 2. Расчётная часть
Задача 1. Две частицы движутся в вакууме вдоль
прямой навстречу друг другу со скоростями 0,5 с и 0,75 с. Определите их
относительную скорость.
Дано:= 0,5 с= 0,75 с' - ?
Решение:
Свяжем с первой частицей неподвижную систему
отсчета K, относительно которой она движется со скоростью u. Со второй частицей
свяжем систему K', движущуюся вдоль оси x со скоростью v относительно
неподвижной системы K в направлении, противоположном оси x, то есть противоположном
скорости u. Используя релятивистский закон сложения скоростей и учитывая, что
проекция скорости v на ось x отрицательна, запишем выражение для скорости в
неподвижной системе отсчета:
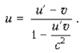
Отсюда находим относительную скорость частиц u':
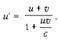
Подставляем численные значения:
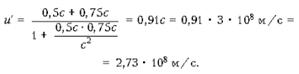
Ответ: u'=2,73 • 108м/с.
Задача 2. При осуществлении термоядерной реакции
синтеза ядра гелия из ядер изотопов водорода - дейтерия и трития - по схеме
освобождается энергия 17,6 МэВ. Какая энергия
освободится при синтезе 1 г гелия? Сколько каменного угля потребовалось бы
сжечь для получения такой же энергии?
Решение:
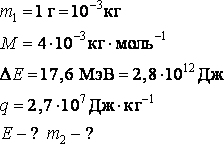
Для нахождения энергии, выделяющейся при синтезе
1г гелия, нужно умножить выход ядерной реакции 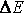 на
число осуществленных реакций, равное числу атомов гелия
на
число осуществленных реакций, равное числу атомов гелия 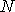 в
1 г:
в
1 г: 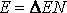
Число атомов гелия равно:
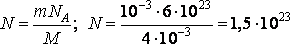
Поэтому для энергии получим:
Е = 2,8·10-12·101,5·1023 Дж = 4,2·1011 Дж.
Из условия 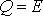 следует:
следует:
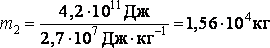
Ответ: m2 = 1,56 • 104кг.
Раздел 3. Практическая часть
Лабораторная работа на тему:
«Исследование столкновения шаров»
ЦЕЛЬ РАБОТЫ: проверка выполнения законов
сохранения энергии и импульса при упругом и неупругом ударах.
ПРИБОРЫ И МАТЕРИАЛЫ: лабораторная установка,
набор шаров.
ОБЩИЕ УКАЗАНИЯ
Примером применения законов сохранения импульса
и энергии при решении реальной физической задачи является удар абсолютно
упругих и неупругих тел.
Удар (или соударение) - это столкновение двух
или более тел, при котором взаимодействие длится очень короткое время. Силы
взаимодействия между сталкивающимися телами (ударные или мгновенные силы) столь
велики, что внешними силами, действующими на них, можно пренебречь. Это
позволяет систему тел в процессе их соударения приближенно рассматривать как
замкнутую систему и применять к ней законы сохранения.
Тела во время удара претерпевают деформацию.
Сущность удара заключается в том, что кинетическая энергия относительного движения
соударяющихся тел на короткое время преобразуется в энергию упругой деформации.
Во время удара имеет место перераспределение энергии между соударяющимися
телами. Отношение кинетических энергий тел после Wп и до Wд удара называется
коэффициентом восстановления ε:
ε =Wп /Wд.
Если для сталкивающихся тел ε<1,
то
такие тела называются абсолютно неупругими, если ε =1 - абсолютно
упругими. На практике для всех тел
0< ε<1 (например,
для стальных шаров ε =0,56, для
шаров из слоновой кости ε=0,89, для
свинца ε
=О).
Однако в некоторых случаях тела можно с большой степенью точности рассматривать
либо как абсолютно упругие, либо как абсолютно неупругие.
Прямая, проходящая через точку соприкосновения
тел и нормальная к поверхности их соприкосновения, называется линией удара.
Удар называется центральным, если тела до удара движутся вдоль прямой,
проходящей через их центры масс.
Абсолютно упругий удар - столкновение двух тел,
в результате которого в обоих взаимодействующих телах не остается никаких
деформаций, т.е. наблюдается упругая деформация и вся кинетическая энергия,
которой обладали тела до удара, после удара снова превращается в кинетическую
энергию (подчеркнем, что это идеализированный случай).
Деформация называется упругой, если после
прекращения действия внешних сил тело принимает первоначальные размеры и форму.
Деформации, которые сохраняются в теле после прекращения действия внешних сил,
называются пластическими (или остаточными). Деформации реального тела всегда
пластические, так как они после прекращения действия внешних сил никогда
полностью не исчезают.
Для абсолютно упругого удара выполняются закон
сохранения импульса и закон сохранения кинетической энергии.
Абсолютно неупругий удар - столкновение двух
тел, в результате которого тела объединяются, двигаясь дальше как единое целое.
Продемонстрировать абсолютно неупругий удар можно с помощью шаров из пластилина
(глины), движущихся навстречу друг другу.
При центральном абсолютно неупругом ударе шаров
между ними действуют силы, зависящие не от самих деформаций, а от их скоростей,
то мы имеем дело с силами, подобными силам трения, поэтому закон сохранения
механической энергии не должен соблюдаться. Вследствие деформаций происходит
«потеря» кинетической энергии, перешедшей в тепловую или другие формы энергии.
Совокупность материальных точек (тел),
рассматриваемых как единое целое, называется механической системой. Силы
взаимодействия между материальными точками механической системы называются
внутренними. Силы, с которыми на материальные точки системы действуют внешние
тела, называются внешними. Механическая система тел, на которую не действуют
внешние силы, называется замкнутой (или изолированной). Если мы имеем
механическую систему, состоящую из многих тел, то, согласно третьему закону
Ньютона, силы, действующие между этими телами, будут равны и противоположно
направлены, т. е. геометрическая сумма внутренних сил равна нулю.
Векторная величина 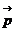 = m·
= m·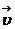 численно
равная произведению массы материальной точки на ее скорость и имеющая
направление скорости, называется импульсом (количеством движения) этой
материальной точки.
численно
равная произведению массы материальной точки на ее скорость и имеющая
направление скорости, называется импульсом (количеством движения) этой
материальной точки.
Закон сохранения импульса: импульс
замкнутой системы сохраняется, т.е. не изменяется со временем.
Математическое выражение этого закона
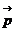 =
=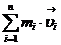 =const,
=const,
где mi, 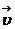 i -масса и
скорость i- го тела системы, состоящей из n тел.
i -масса и
скорость i- го тела системы, состоящей из n тел.
Энергия - универсальная мера
различных форм движения и взаимодействия. С различными формами движения материи
связывают различные формы энергии: механическую, тепловую, электромагнитную,
ядерную и др.
Кинетическая энергия механической
системы - это энергия механического движения этой системы.
Потенциальная энергия - механическая
энергия системы тел, определяемая их взаимным расположением и характером сил
взаимодействия между ними.
Пусть взаимодействие тел
осуществляется посредством силовых полей (например, поля упругих сил, поля
гравитационных сил), характеризующихся тем, что работа, совершаемая
действующими силами при перемещении тела из одного положения в другое, не
зависит от того, по какой траектории это перемещение произошло, а зависит
только от начального и конечного положений. Такие поля называются потенциальными,
а силы, действующие в них, - консервативными. Если же работа, совершаемая
силой, зависит от траектории перемещения тела из одной точки в другую, то такая
сила называется диссипативной; ее примером является сила трения.
Закон сохранения энергии: в замкнутой
системе тел, между которыми действует только консервативные силы, механическая
энергия сохраняется, т.е. не изменяется со временем.
Законы сохранения энергии и импульса
принадлежат к фундаментальным законам природы, и их экспериментальная проверка
представляет особый интерес. При изучении удара шаров это можно проделать
простым и наглядным способом.
Рассмотрим упругий и неупругий удар
для двух шаров.
Случай упругого удара. До
столкновения сумма импульсов системы шаров равна сумме импульсов после удара:
 +
+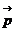 =
=  +
+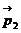 .
.
или для модулей импульсов:
m1· υ0 + m2 ·υ = m1 ·υ1 +
m2 ·υ2,
где m1 и υ0 , υ1 - масса
и скорость ударяющего шара;и υ, υ2 - масса
и скорость ударяемого шара.
Пусть до удара второй шар находится в покое: υ
= 0 и
р = 0, тогда импульс до удара
р0 = m1 ·υ0 .
(1)
После упругого удара для модулей импульсов
шаров:
р = m2 ·υ2
±
m1 ·υ1 , (2)
при отклонении шаров в одну сторону берется знак
«+», а в противоположные знак «-».
С учетом направления вектора скорости импульс до
и после удара определяется как
m1 ·υ0 = m2
·υ2
-
m1 ·υ1,
где υ1
и υ2
-скорости
ударяющего и ударяемого шаров сразу после удара.
Для определения величин скоростей шаров
воспользуемся следующим соображением.
В начальном положении отклоним ударяющий шар на
угол α0.
При
этом центр шара поднимается на высоту
h = l-l·cos α0
= l(1- cos α0
) =2 ·l· sin2 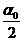 ,
,
где l- длина нити на которой
подвешен шар.
Шар получит потенциальную энергию:
Wр
= m1 ·g·h = 2·m1 ·g·l· sin2 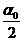 .
.
Согласно закону сохранения энергии,
потенциальная энергия в нижней точке перейдет в кинетическую энергию:
Wк
= Wр
= 2·m1 ·g·l ·sin2 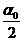 .
.
Используя определение кинетической
энергии, получим формулу для скорости:
Wк
= 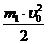 = 2·m1 ·g·l
·sin2
= 2·m1 ·g·l
·sin2 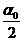 ,
,
υ0 = 2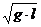 · sin
· sin 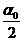 . (3)
. (3)
Значит, скорость ударяющего шара в
нижней точке траектории зависит от начального угла отклонения α0.
Соответственно скорости шаров после
ударов:
υ1 = 2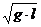 · sin
· sin 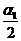 , (4)
, (4)
υ2 = 2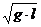 · sin
· sin 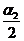 , (5)
, (5)
α2 - угол отклонения ударяемого
шара после удара.
Случай неупругого удара. Импульс
шаров после неупругого удара
р3 = (m1 + m3) · υ3 .
(6)
Так как до удара второй шар находится в покое: υ
= 0 и
р = 0, тогда импульс до удара
р0 = m1 ·υ0 ,
и импульс до и после удара будет равен
m1 υ0 = (m1
+ m3) υ3,
где υ3
- скорость шаров, движущихся вместе после неупругого удара.
Общая скорость шаров
υ3 = 2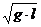 ·sin
·sin 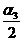 , (7)
, (7)
где α3 - угол, на
который отклонятся оба шара после неупругого удара.
Энергия шаров до удара равна
кинетической энергии первого шара, поскольку второй неподвижен:
к = 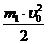 = 2·m1 ·g·l ·sin2
= 2·m1 ·g·l ·sin2 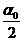 . (8)
. (8)
После упругого удара энергия шаров
W = W1 + W2 . (9)
W1 = 2·m1
·g·l· sin2 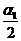 . (10)=2·m2
·g·l· sin2
. (10)=2·m2
·g·l· sin2 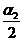 . (11)
= 2·g·l· (m1 ·sin2
. (11)
= 2·g·l· (m1 ·sin2 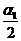 + m2 ·sin2
+ m2 ·sin2 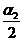 ).
).
После неупругого удара энергия шаров
= 2(m1 + m3) · g·l ·sin2 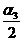 , (12)
, (12)
Коэффициент восстановления энергии
для упругого удара
ε =Wк /W. (13)
Коэффициент восстановления энергии
для неупругого удара
ε =Wк /W3. (14)
Заключение
Общая теория относительности, в
настоящее время - самая успешная теория, хорошо подтверждённая наблюдениями.
Первый успех общей теории относительности состоял в объяснении аномальной
прецессии перигелия Меркурия. Затем, в 1919 году, Артур Эддингтон сообщил о
наблюдении отклонения света вблизи Солнца в момент полного затмения, что
качественно и количественно подтвердило предсказания общей теории
относительности. С тех пор многие другие наблюдения и эксперименты подтвердили
значительное количество предсказаний теории, включая гравитационное замедление
времени, гравитационное красное смещение, задержку сигнала в гравитационном поле
и, пока лишь косвенно, гравитационное излучение. Кроме того, многочисленные
наблюдения интерпретируются как подтверждения одного из самых таинственных и
экзотических предсказаний общей теории относительности - существования чёрных
дыр.
Так же, как и в случае квантовой
механики, многие предсказания теории относительности противоречат интуиции,
кажутся невероятными и невозможными. Это, однако, не означает, что теория
относительности неверна. В действительности, то, как мы видим (либо хотим
видеть) окружающий нас мир и то, каким он является на самом деле, может сильно
различаться. Уже больше века учёные всего мира пробуют опровергнуть СТО. Ни
одна из этих попыток не смогла найти ни малейшего изъяна в теории. О том, что
теория верна математически, свидетельствует строгая математическая форма и
чёткость всех формулировок.
О том, что СТО действительно
описывает наш мир, свидетельствует огромный экспериментальный опыт. Многие
следствия этой теории используются на практике. Очевидно, что все попытки
«опровергнуть СТО» обречены на провал потому, что сама теория опирается на три
постулата Галилея (которые несколько расширены), на основе которых построена
ньютонова механика, а также на дополнительный постулат о постоянстве скорости
света во всех системах отсчета. Все четыре не вызывают какого-либо сомнения в
пределах максимальной точности современных измерений: лучше 10 − 12, а в
некоторых аспектах - до 10 − 15.
Список литературы
1.
Учебник по физике для 11 класса (Богданов К.Ю.), 2012.
.
Понятие массы в классической и современной физике (Джеммер М.), 2009.
.
История физики (Кудрявцев П.С.), 2014.