Расчёт электрических фильтров по рабочим параметрам

"Расчёт электрических фильтров по рабочим параметрам"

Оглавление

1. Постановка задачи синтеза электрического фильтра

2. Переход к ФНЧ - прототипу и нормирование по частоте

3. Аппроксимация частотной характеристики рабочего ослабления фильтра

4. Реализация схемы фильтра ФНЧ

5. Переход от схемы ФНЧ-прототипа к нормированной схеме заданного фильтра

6. Денормирование и расчёт элементов схемы фильтра

7. Расчёт частотных характеристик фильтра

8. Расчёт частотных характеристик фильтра на ЭВМ

9. Расчет спектра последовательности прямоугольных импульсов на входе и на выходе фильтра

10. Расчет переходной характеристики фильтра h(t)

Вывод

Список литературы

электрический фильтр частота спектр

1. Задание к курсовой работе

Согласно варианту требуется рассчитать фильтр верхних частот (ФВЧ), удовлетворяющий следующим техническим требованиям:

·   граничная частота полосы пропускания (ПП) 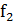=21900 (Гц);

·   граничная частота полосы непропускания (ПН) 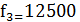(Гц);

·   коэффициент отражения 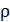=36%;

·   минимально-допустимое значение рабочего ослабления в ПН 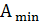=20 (дБ);

·   сопротивление нагрузки 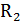 =450 (Ом).

Аппроксимацию требуется выполнить по Чебышеву, а реализацию - по Дарлингтону. (Значения взяты из старой методички с вариантами заданий)

2. Постановка задачи синтеза электрического фильтра

Синтез электрического фильтра по рабочим параметрам (рабочему ослаблению или рабочей фазовой постоянной) состоит из двух этапов: аппроксимации и реализации.

На этапе аппроксимации необходимо получить аналитическое выражение рабочей передаточной функции H(р) фильтра, удовлетворяющей условиям физической реализуемости по заданным требованиям.

На этапе реализации по найденной рабочей передаточной функции определяется схема фильтра и величины составляющих ее элементов.

В синтезе фильтров используется преобразование частоты и нормирование сопротивлений и частот.

Использование преобразования частоты позволяет свести расчет всех классов фильтров к расчету фильтра нижних частот (ФНЧ) и производить синтез любого фильтра в следующем порядке: сначала преобразовать заданную характеристику рабочего ослабления в низкочастотную, потом синтезировать ФНЧ, далее обратным частотным преобразованием перейти от элементов схемы ФНЧ к элементам (или комбинациям элементов) заданного фильтра. Нормирование заключается в том, что вместо абсолютных значений частот и сопротивлений элементов цепи ФНЧ берутся их относительные величины. Нормирование осуществляется по отношению к нагрузочному сопротивлению и граничной частоте полосы пропускания для ФНЧ и ФВЧ (или среднегеометрической частоте полосы пропускания для ПФ).

Техническими требованиями к фильтру являются:

·   граничные частоты полосы пропускания (ПП) 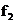 или  , ;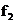

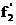·   граничные частоты полосы непропускания (ПН) 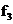 или  , ;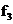

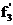·   максимально-допустимое значение рабочего ослабления в ПП ΔА (дБ) или коэффициент отражения 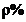, которые связаны соотношением:

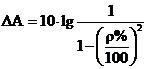
·   минимально-допустимое значение рабочего ослабления в ПН 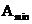(дБ);

·   сопротивление нагрузки 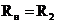 (Ом).

Синтез фильтра производится в следующем порядке:

1. Переход к ФНЧ-прототипу и нормирование частот;

2. Аппроксимация рабочей передаточной функции Т(р) и характеристики рабочего ослабления фильтра ;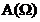

3. Реализация схемы ФНЧ (ФНЧ-прототипа);

4. Переход от схемы ФНЧ к схеме заданного фильтра и денормирование ее элементов;

5. Расчет и построение денормированных частотных характеристик рабочего ослабления А(f) и рабочей фазы В(f) фильтра.

3. Переход к ФНЧ - прототипу и нормирование по частоте

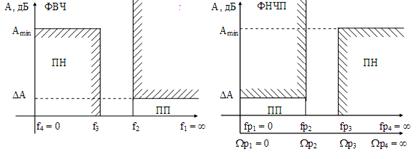
Рис. 1 Частотные характеристики фильтра верхних частот и фильтра нижних частот прототипа

При расчете ФВЧ переходим к требованиям для ФНЧ - прототипа. Частотная характеристика ФВЧ переходит в частотную характеристику ФНЧ - прототипа при использовании преобразования частоты вида:

, , , .

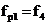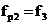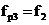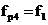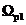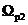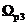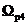, , ,  - нормированные граничные частоты ФНЧП.

=,= ,= , =

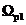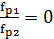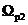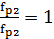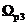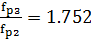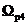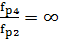
4. Аппроксимация частотной характеристики рабочего ослабления фильтра

На данном этапе по заданным техническим требованиям к ФНЧ - прототипу необходимо получить математические выражения рабочей передаточной функции H(р) и рабочего ослабления фильтра А(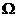). Известно, что частотное свойство фильтров определяется функцией фильтрации φ.

Следовательно, задача сводится к выбору аналитического выражения этой функции и расчету ее коэффициентов. В качестве аппроксимирующих удобно использовать полиномиальные функции, среди которых наибольшее распространение имеют полиномы Баттерворта и Чебышева.

При выборе полинома Чебышева в качестве аппроксимирующего функция фильтрации определяется выражением:

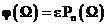, где .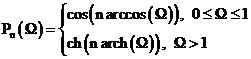

Для расчёта коэффициента неравномерности рабочего ослабления ,мне понадобится рассчитать максимально-допустимое значение рабочего ослабления в ПП ΔA [дБ], с помощью коэффициента отражения 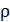 [%], который был задан, по формуле:

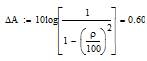
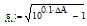 - коэффициент неравномерности рабочего ослабления в полосе пропускания.

Рабочее ослабление определяется как: 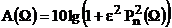. 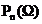- полином Чебышева, определяемый рекуррентной формулой 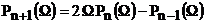, n- порядок фильтра:

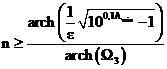
Итак, n=3.943. Округляя в большую сторону, возьмем n=4, тогда

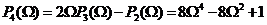
Аппроксимация по Чебышеву получила название равноволновой.

Сформируем рабочую передаточную функцию:

.

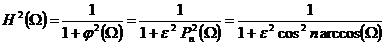С другой стороны модуль рабочей передаточной функции можно представить как:

.

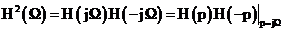Таким образом:

,т.е.

,

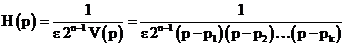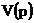 - полином Гурвица.

Решая уравнение 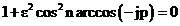, определим корни полинома Гурвица:

, .

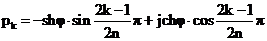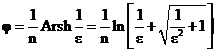Имеем:

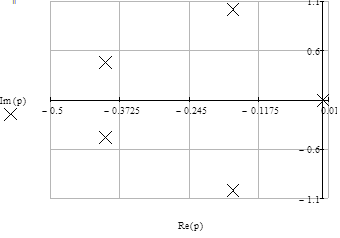
Рис. 2 Изображение корней уравнения  на комплексной плоскости

Формируем рабочую операторную передаточную функцию :

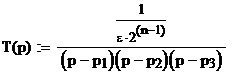
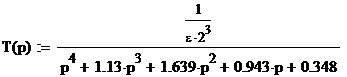
Подставляя 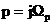, определим рабочее ослабление как:

.

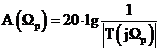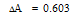
Выполним проверку функции 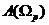 на частотах: , ,.

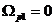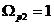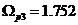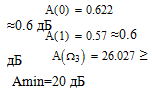
Аппроксимированное рабочее ослабление удовлетворяет техническим требованиям.

5. Реализация схемы фильтра ФНЧ

На данном этапе по найденной ранее функции H(р) необходимо получить схему ФНЧ .

Реализация по Дарлингтону основана на формировании функции 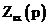 по 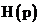. Тогда получение схемы нагруженного фильтра можно свести к реализации двухполюсника путем разложения функции Z_вх(р) в цепную дробь (по Кауэру).

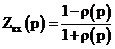, где 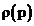 - коэффициент отражения

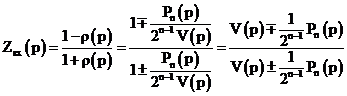, где

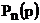 определяется по рекуррентной формуле  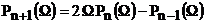заменой 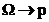, при этом все слагаемые берутся со знаком "+".

,

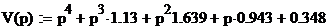
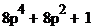Составим Z_вх(р), выбирая знак " - " у функции ρ(р):

Нормированное значение входного сопротивления в этом случае выражено в виде цепной дроби:

.

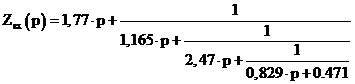Нормированные значения ёмкостей и индуктивностей будут равны:

, , , , , .

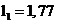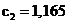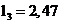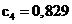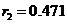Схема фильтра начинается с последовательно включенного элемента.

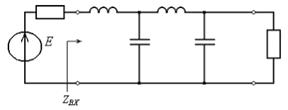
Схема. 1 Нормированная схема ФНЧ-прототипа

Если выбрать знак "+" у функции ρ(р), то получим дуальную схему фильтра:

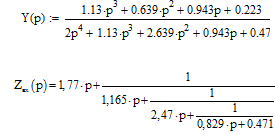
Нормированные значения ёмкостей и индуктивностей будут равны:

, , , , .

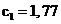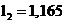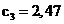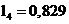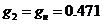Схема фильтра начинается с параллельно включенного элемента.

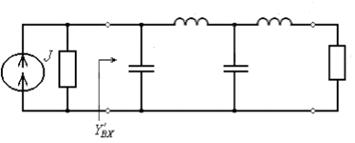
Схема. 2 Дуальная нормированная схема ФНЧ-прототипа

В дальнейшем выбираем схему 2, так как через 1 схему при замене, ток течь не будет .

6. Переход от схемы ФНЧ-прототипа к нормированной схеме заданного фильтра

Осуществим переход от нормированной схемы ФНЧ-прототипа к схеме ФВЧ по таблице 1, согласно которой нормированные элементы схемы ФНЧ-прототипа заменяются на нормированные элементы схемы ФВЧ.

Таблица 1

, , ,  .

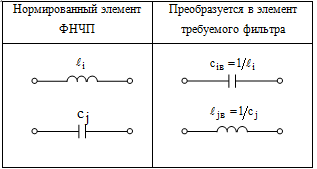
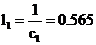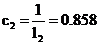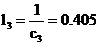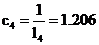7. Денормирование и расчёт элементов схемы фильтра

Для перехода от нормированной схемы к денормированной схеме с заданными нагрузочным сопротивлением 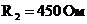 и граничной частотой  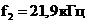осуществляем изменение уровня сопротивления и масштаба частоты с помощью следующих множителей:

а) преобразующий множитель сопротивления:

.

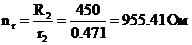б) преобразующий множитель частоты

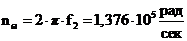
Коэффициенты денормирования индуктивности и емкости определяем по формуле:

, .

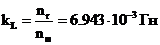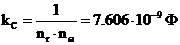Таким образом, истинные значения элементов фильтра можно определить как:

, , , , , .

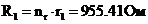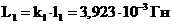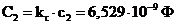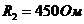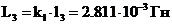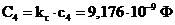Окончательно получим схему:

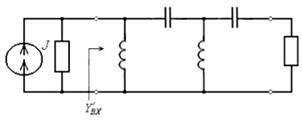
Схема. 3 Денормированная схема фильтра верхних частот пятого порядка

8. Расчёт частотных характеристик фильтра

С помощью расчёта частотных характеристик фильтра проверяется соответствие фильтра техническим требованиям:

1.      Рабочее ослабление в ПП не должно превышать заданной величины :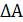

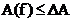
2.   Рабочее ослабление в ПН не должно быть ниже заданного значения

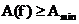
3.      Рабочая фаза B(f) позволяет судить о выполнении требований к её линейности в пределах ПП.

Выполним расчёт частотных характеристик A(f) и B(f) по аппроксимированной функции H(p). Построим графики А(f) и B(f) ФВЧ.

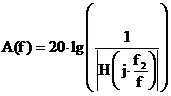
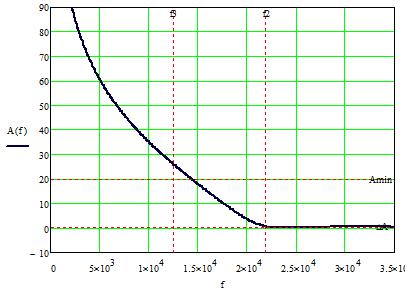
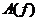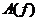Рис. 3 График зависимости рабочего ослабления  ФВЧ и  в ПП

(),  ().

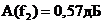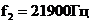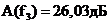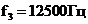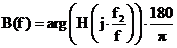
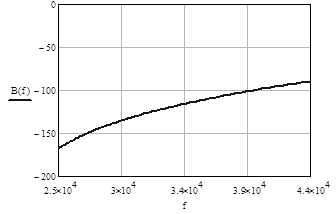
Рис. 4 График зависимости рабочей фазы B(f) ФВЧ в ПП

, .

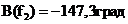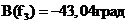Проверка технических требований по графикам зависимостей рабочего ослабления и рабочей фазы. подтверждает соответствие аппроксимированной передаточной функции Т(р) техническому заданию. Это свидетельствует о правильности выполнения этапа аппроксимации.

9. Расчёт частотных характеристик фильтра на ЭВМ

После выполнения синтеза электрического фильтра важно убедиться в его соответствии техническим требованиям. Наиболее полной проверкой правильности расчета спроектированного фильтра является расчет частотных зависимосте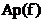й  и 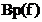 по передаточной функции Tp(jw), выраженной через элементы фильтра.

Фильтр представляет собой реактивный четырехполюсник лестничной структуры. С учетом источника сигнала с внутренним сопротивлением R₁ и сопротивления нагрузки R₂

Рабочая передаточная функция такой схемы может быть определена следующим образом:

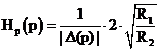, где 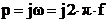 - комплексная частота.

, , .

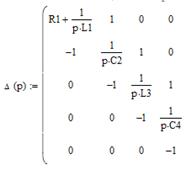
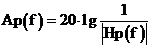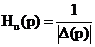Представим графики зависимости рабочего ослабления 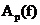 и рабочей фазы .

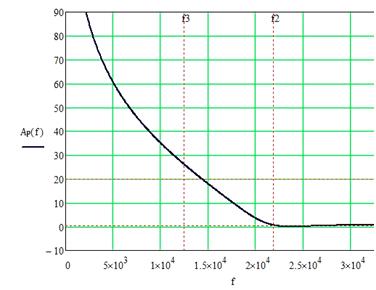
Рис. 6 Частотная зависимость рабочего ослабления  в ПП

, .

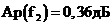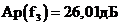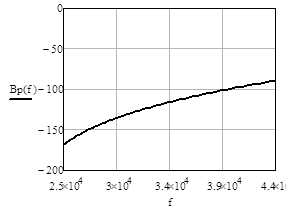
Рис.7 Частотная зависимость рабочей фазы 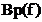 в ПП

, .

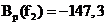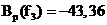По графикам видно, что фильтр полностью удовлетворяет всем техническим требованиям, значит значения элементов схемы фильтра вычислены верно.

10. Расчет спектра последовательности прямоугольных импульсов на входе и на выходе фильтра

Рассчитаем спектр последовательности прямоугольных импульсов на входе фильтра с параметрами: 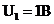, скважность 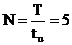, частота следования импульсов  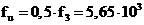по формуле 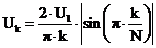, 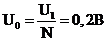. Вычислив, получим:

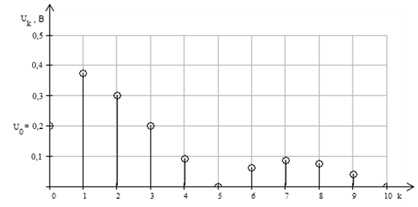
Рис. 8 Спектр последовательности прямоугольных импульсов на входе фильтра

Спектр фаз последовательности на входе при выборе начала координат в середине импульса определяется выражением:

;

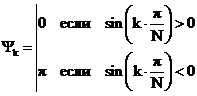Рис. 9 Спектр фаз последовательности на входе

Выходные спектры амплитуд и фаз определяются выражениями:

, , .

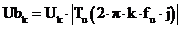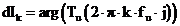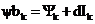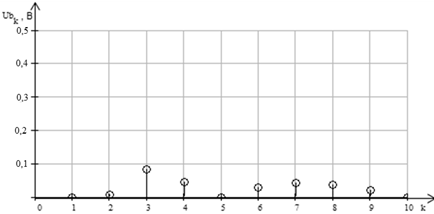
Рис. 10 Спектр амплитуд последовательности на выходе

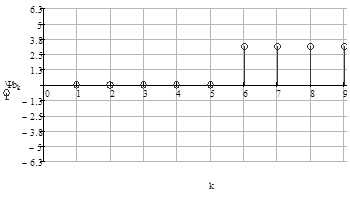
Рис.11 Спектр фаз последовательности на выходе

Сигнал на входе ФВЧ рассчитывается по формуле: 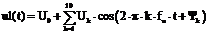, а на выходе по формуле: , .

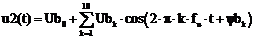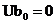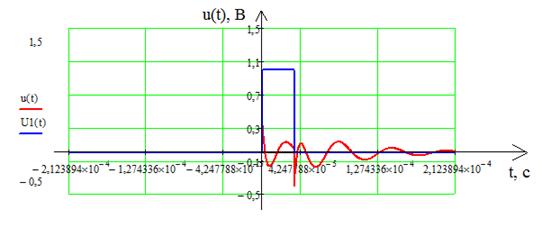
Рис. 12 Графики напряжения на входе и на выходе фильтра

11. Расчет переходной характеристики фильтра h(t)

Для вычисления переходной характеристики используем следующее выражение: 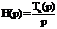. Применив обратное преобразование Лапласа, получим:

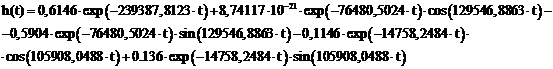
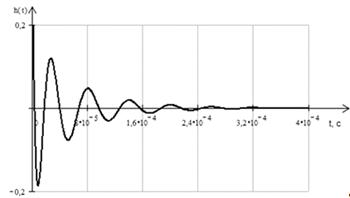
Рис.13 График переходной характеристики h(t)

Используя переходную характеристику, можно выполнить расчет отклика ФВЧ на прямоугольный импульс с амплитудой 1В и длительностью

.

 ,

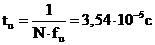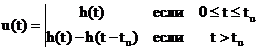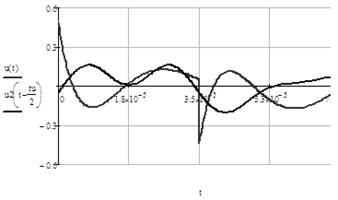
Рис.14 Импульс на выходе фильтра 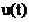, построенный с помощью 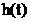, в сравнении с выходным импульсом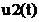

Вывод

В данной работе произведен синтез электрического фильтра в два этапа: аппроксимация и реализация. На первом этапе были получены математические выражения рабочей передаточной функции Т и рабочего ослабления A, удовлетворяющие условиям технической реализуемости. На втором этапе по найденной рабочей передаточной функции Т определили схему фильтра и величины составляющих её элементов.

Произведен расчёт и построение частотных характеристик фильтра, подтвердивших соответствие аппроксимированной функции Т техническому заданию

Были построены частотные зависимости, подтвердившие высокую точность фильтра.

На ЭВМ были получены переходная характеристика, спектры сигналов на входе и выходе фильтра и реакция фильтра на последовательность прямоугольных импульсов.

Список литературы

1. Конспект лекций по ОТЦ.

. Методическая разработка к курсовой работе.

. В.П. Бакалов, В.Ф. Дмитриков, Б.И. Крук. Основы теории цепей 2000г.

. А.Ф. Белецкий . Теория линейных электрических цепей, 1986г.

. Н. Н. Цаплин . Электрические фильтры, 2004г.