Расчет основных характеристик вынужденного рассеяния Мандельштама-Бриллюэна в конденсированных средах
министерство высшего и среднего специального образования республики
узбекистан
самаркандский государственный университет имени алишера навои
Физический факультет
Направление - физика
Кафедра «теоретическая физика и квантовая электроника»
Выпускная квалификационная
работа
Расчет основных характеристик вынужденного рассеяния
мандельштама-бриллюэна в конденсированных средах
Исполнитель: Узаков Хайдар
Самарканд -
2012
Введение
Изучение спектров рассеянного света начато более
сорока лет назад, и еще до появления различных лазерных источников возбуждения
основные черты разнообразных спектров теплового рассеяния были выяснены
Изучались спектры комбинационного рассеяния
света и спектры рассеяния, вызванного временным изменением флуктуации диэлектрической
проницаемости вследствие тепловых флуктуации давления рассеяние
Мандельштама-Бриллюэна, флуктуации энтропии центральная компонента тонкой
структуры линии Рэлея и флуктуации анизотропии крыло линии Рэлея.
Рассеянием Мандельштама-Бриллюэна, названного в
честь Мандельштама Леонида Исааковича и Леона Бриллюэна, называют рассеяние
оптического излучения конденсированными средами твердыми телами и жидкостями в
результате его взаимодействия с собственными упругими колебаниями этих сред.
Оно сопровождается изменением набора частот (длин волн, характеризующих
излучение, - его спектрального состава. Например, рассеяние
Мандельштама-Бриллюэна монохроматического света приводит к появлению шести
частотных компонент рассеянного света, в жидкостях - трёх (одна из них -
неизмененной частоты). Сравнительно сильное взаимодействие между частицами
конденсированных сред (оно связывает их в упорядоченную пространственную
решётку) приводит к тому, что эти частицы не могут двигаться независимо - любое
их возбуждение распространяется в среде в виде волны. Однако при любой отличной
от абсолютного нуля температуре частицы находятся в тепловом движении. В
результате по всевозможным направлениям в среде распространяются упругие волны
различных частот (Гиперзвук). Наложение таких волн друг на друга вызывает
появление т. н. флуктуаций плотности среды (малых локальных отклонений
плотности от её среднего значения), на которых и рассеивается свет. Рассеяние
Мандельштама-Бриллюэна показывает, что световые волны взаимодействуют непосредственно
с упругими волнами, обычно не наблюдаемыми по отдельности.
Из представления о стоячих волнах - сгущениях и
разрежениях плотности, модулирующих световую волну, - исходил Л.И. Мандельштам,
теоретически предсказавший рассеяние Мандельштама-Бриллюэна. Независимо те же
результаты получил [1] Л. Бриллюэн, рассматривая рассеяние света на бегущих
навстречу друг другу упругих волнах в среде. При его подходе к явлению
физической причиной "расщепления" монохроматических линий оказывается
эффект Доплера.
Первые попытки наблюдать рассеяние
Мандельштама-Бриллюэна, произведенные Л.И. Мандельштамом и Г.С. Ландсбергом
позволили лишь наблюдать уширение линий Рамановского рассеяния. Первые удачные
эксперименты и детальные исследования проведены Е.Ф. Гросс. В частности, он
обнаружил, что рассеяние Мандельштама - Бриллюэна расщепляет монохроматическую
линию на шесть компонент (это объясняется тем, что скорость звука v различна
для разных направлений, вследствие чего в общем случае в нём существуют три -
одна продольная и две поперечные - звуковые волны, одной и той же частоты,
каждая из которых распространяется со своей скоростью v). Он же изучил
рассеяние Мандельштама-Бриллюэна в жидкостях и аморфных твёрдых телах, при
котором наряду с двумя "смещенными" наблюдается и "несмещенная"
компонента исходной частоты f. Теоретическое объяснение этого явления
принадлежит Л.Д. Ландау и Г. Плачеку, показавшим, что, кроме флуктуаций
плотности, необходимо учитывать и флуктуации температуры среды.Предложено и
экспериментально реализовано низко пороговое вынужденное рассеяние
Мандельштама-Бриллюэна с распределенной обратной связью в сероуглероде, которая
осуществлялась благодаря дифракции Брегга излучения вынужденное рассеяние
Мандельштама-Бриллюэна пространственно-периодической решетке показателя
преломления, наведенной в оптически нелинейной среде в результате интерференции
падающего и отраженного от зеркала пучков возбуждающего света.
Получена одночастотная генерация излучения
вынужденное рассеяние Мандельштама-Бриллюэна с малой угловой расходимостью и
большой энергетической эффективностью. Развита теория, позволяющая рассчитать
нелинейный коэффициент конверсии накачки в излучение вынужденное рассеяние
Мандельштама-Бриллюэна и определить оптимальное направление генерации.
Сопоставление теории и опыта указывает на хорошее согласие между ними.
На основании таких исследований можно определить
характерные расчеты процессов, что имеет большое научное и практическое
значение ввиду широкого применения вынужденное рассеяние Мандельштама-Бриллюэна
возникает вследствие нелинейного взаимодействия интенсивного возбуждающего
света с материальной средой[2]. Вынужденное рассеяние Мандельштама-Бриллюэна
отвечает процессу распада возбуждающей световой волны на другую, рассеянную
световую волну и волну гиперзвука. При этом в предположении заданной
интенсивности возбуждающего света интенсивность рассеянного излучения растет
экспоненциально в пространстве (конвективная неустойчивость). Заметная
интенсивность рассеянного излучения в таких условиях может быть достигнута лишь
при весьма больших значениях коэффициента экспоненциального усиления ~20ч30.
Порог вынужденное рассеяние
Мандельштама-Бриллюэна может быть существенно снижен, если создать в процессе
возбуждения вынужденное рассеяние Мандельштама-Бриллюэна положительную обратную
связь; при этом имеет место экспоненциальный рост интенсивности рассеянного
излучения во времени (абсолютная неустойчивость). Как правило, это достигается
возбуждением Вынужденное рассеяние Мандельштама-Бриллюэна в оптическом
резонаторе типа интерферометра Фабри-Перо, где имеет место так называемая
«сосредоточенная обратная связь» - взаимодействие встречных волн осуществляется
в фиксированных сечениях пространства. Необходимым условием высокой
энергетической эффективности вынужденное рассеяние Мандельштама-Бриллюэна
является насыщение усиления. В резонаторе оно может сопровождаться каскадным
рождением компонент вынужденное рассеяние Мандельштама-Бриллюэна [4],
значительно ухудшающим монохроматичность генерируемого излучения.
Режим абсолютной неустойчивости может возникать
п при безрезона-торном возбуждении рассеяния, например, когда вынужденное
рассеяние Мандельштама-Бриллюэна возбуждается двумя антипараллельными пучками
света[5-7]. В последнем случае абсолютная неустойчивость привынужденное
рассеяние Мандельштама-Бриллюэна возникает только благодаря одновременному
возбуждению стоксовых и антистоксовых компонент рассеянного поля. По этой
причине порог такой параметрической генерации не намного, ниже порога обычного
конвективного вынужденное рассеяние Мандельштама-Бриллюэна. Значительно более
низкие пороги генерации осуществляются в том случае, когда параметрическая
связь может быть реализована без участия антистоксовых компонент[8]. В
настоящей работе впервые предложено и экспериментально реализовано низко
пороговое вынужденное рассеяние Мандельштама-Бриллюэна с распределенной
обратной связью для случая почти антипараллельных пучков накачки и развита
теория этого явления.
Распределение обратной связью осуществлялась
благодаря дифракции Брэгга излучения вынужденное рассеяние
Мандельштама-Бриллюэна на пространственно-периодической решетке показателя
преломления, наведенной в оптически нелинейной среде в результате интерференции
двух пучков света. Вследствие того что распределение обратной связью обладает
существенно более высокой спектральной селективностью по сравнению с
«сосредоточенной обратной связью» [9], использование такой схемы возбуждения
вынужденное рассеяние Мандельштама-Бриллюэна позволило нам получить
одночастотную генерацию вынужденное рассеяние Мандельштама-Бриллюэна,
обладающую высокой энергетической эффективностью и малой угловой расходимостью.
Развитая здесь теория этого явления позволяет рассчитать коэффициент
преобразования энергии накачки в излучение вынужденное рассеяние Мандельштама-Бриллюэна,
определить оптимальное направление генерации и распределение амплитуд
взаимодействующих в нелинейной среде волн. Сопоставление результатов опыта с
теоретическими результатами указывает на хорошее согласие между ними, но во
всех этих экспериментах не учитывают анти-стокс, а в нашем эксперименте
будем учитывать, и конечно результаты будут другие.
Цель: Изучение свойств рассеяния оптического
излучения конденсированных средах в результате его взаимодействия собственными
упругими колебаниями. Освоение навыков расчета основных параметров вынужденного
рассеивания Мандельштама-Бриллюэна в конденсированных средах.
Задачи исследования: В ходе выполнения работы
были рассмотрены уравнения полей и уравнение гидродинамики, решены укороченные
уравнения полей совместно уравнением гидродинамики.
излучение гидродинамика стрикционный
Глава I.
Вынужденное рассеяние Мандельштама-Бриллюэна в конденсированных средах
.1 Обзор литературы и постановки задачи
Рассеяние Мандельштама-Бриллюэна
рассеяние света на адиабатических флуктуациях плотности конденсированной
средсопровождающееся изменением частоты. В спектре рассеяние
Мандельштама-Бриллюэна монохроматичности света наблюдаются
дискретные, расположенные симметрично относительно частоты возбуждающего света
спектральные компоненты, называемые компонентами Мандельштама - Бриллюэна или
компонентами тонкой структуры линии Рэлея. Рассеяние предсказано Л.И.
Мандельштамом и Л.H. Бриллюэном обнаружено при рассеянии в кристалле кварца и в
жидкости E.Ф. Гроссом и впоследствии им же подробно исследовано. При
экспериментальном и теоретическом изучении спектров теплового рассеяния света
принимается в расчет влияние теплового движения в среде на световую волну, но
пренебрегается действием световой волны на движение в среде. Ситуация меняется,
если рассеяние возбуждается мощным световым импульсом лазера. В этом случае
напряженность электрического поля возбуждающей световой волны оказывается
настолько большой (<~104-108 в/см), что это поле вместе с полем
первоначально слабого теплового рассеяния начинает существенно влиять на
характер движения в среде. Вследствие эффекта электрострикции эти поля будут
приводить при определенных условиях к увеличению интенсивности звуковой волны,
возникшей из-за флуктуации давления. Эти поля могут также приводить вследствие
ориентации анизотропных молекул (квадратичный эффект Керра) к увеличению
ориентационных неоднородностей и, например, вследствие электро калорического
эффекта - к увеличению температурных неоднородностей в среде.
Для решения задачи о вынужденном молекулярном
рассеянии необходимы уравнения, описывающие влияние световых волн на р, S и ж
вследствие указанных выше эффектов стрикции, электрокалорического эффекта и
ориентации молекул.
Все три перечисленных эффекта, лежащих в основе
вынужденного молекулярного рассеяния света, являются квадратичными по полю, и в
результате смешения возбуждающей и рассеянной световых волн, различающихся по
частоте и волновому числу, воздействие света будет происходить в первую очередь
нате Фурье составляющие флуктуации, которые вызвали первоначальное тепловое
рассеяние. Указанное выше увеличение неоднородностей в среде приведет в свою
очередь к увеличению интенсивности рассеянного света, что вызовет увеличение
неоднородностей, и т. д. Интенсивность рассеянного света будет нарастать
нелинейно по мере распространения его в области нелинейного взаимодействия
света и вещества. Прохождение интенсивного света в нелинейной среде вызывает
вынужденное рассеяние и ряд других явлений, таких, как самофокусировка и
дефокусировка света, разрушение твердых прозрачных диэлектриков, кавитация в
жидкостях, возникновение плазмы и т. д. В какой мере вынужденное рассеяние
связано со всеми названными явлениями пока неясно, но этот вопрос продолжает
исследоваться.
В качестве спектральных приборов обычно
используются интерферометры Фабри-Перо, дифракционные спектрографы большой
разрешающей силы, а в особых случаях, когда требуется очень большая разрешающая
сила, применяется метод гетеродинирования или квадратичного детектирования
света.
1.2 Теория вынужденного рассеяние
Мандельштама-Бриллюэна в жидкостях
Адиабатические флуктуации плотности можно
представить как результат интерференции распространяющихся в среде по
всевозможным направлениям упругих волн различной частоты со случайными фазами и
амплитудами (т. н. дебаевских волн, которые рассматриваются в Дебая законе
теплоёмкости). Плоская световая волна, распространяющаяся в такой среде,
диафрагмирует (рассеивается) во всех направлениях на этих упругих волнах,
модулирующих диэлектрическая проницаемость среды. Каждая из упругих волн
создаёт пери-одиночную решётку, на которой и происходит дифракция света
аналогично дифракции света на ультразвуке. Максимум интенсивности света,
рассеянного на упругой волне с длиной волны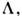 наблюдается
в направлении
наблюдается
в направлении 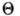 отвечающем Брэгга-
Вульфа условию
отвечающем Брэгга-
Вульфа условию
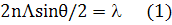
где n- показатель преломления,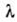 длина
волны света в вакууме.
длина
волны света в вакууме.
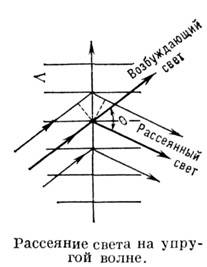
Рис. 1
Поскольку каждой упругой волне,
распространяющейся в некотором направлении со скоростью v, соответствует волна
той же частоты, бегущая навстречу, можно считать, что в среде имеются стоячие
упругие волны, временное изменение плотности в которых с частотой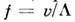 вызывает
модуляцию рассеянного света.
вызывает
модуляцию рассеянного света.
Следовательно, в рассеянном свете появятся
дискретные компоненты с частотой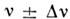 (стоксова-антистоксова),
где
(стоксова-антистоксова),
где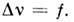 ,Условие
(1) приводит к выражению для относительного изменения частоты света,
рассеянного в направлении
,Условие
(1) приводит к выражению для относительного изменения частоты света,
рассеянного в направлении
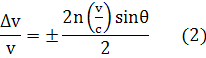
где с - скорость света в вакууме. Рассмотрение
отражения света от бегущих упругих волн в направлении, соответствующем условию
(1), приводит к такому же результату. Изменение частоты в этом случае
обусловлено Доплера эффектом. Ширина компонент Мандельштама -Бриллюэна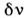 определяется коэф. Затухания
определяется коэф. Затухания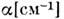 упругих волн
упругих волн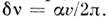
Поскольку обычно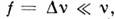 смещение
частоты прирассеяние Мандельштама-Бриллюэна
относительно невелико:
смещение
частоты прирассеяние Мандельштама-Бриллюэна
относительно невелико: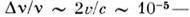 Такие величины
измеряются интерферометрия, методами, например: интерферометром Фабри-Перо.
Существенным и хорошо наблюдаемым оказывается рассеяние
Мандельштама-Бриллюэна видимого света
Такие величины
измеряются интерферометрия, методами, например: интерферометром Фабри-Перо.
Существенным и хорошо наблюдаемым оказывается рассеяние
Мандельштама-Бриллюэна видимого света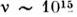 на
гиперзвуке(
на
гиперзвуке(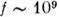 ) В жидкостях
наблюдаются 2 компоненты Мандельштама - Бриллюэна, в твёрдом аморфном теле - 4
компоненты, 2 из которых вызваны продольными и 2 - поперечными гиперзвуковыми
волнами при
) В жидкостях
наблюдаются 2 компоненты Мандельштама - Бриллюэна, в твёрдом аморфном теле - 4
компоненты, 2 из которых вызваны продольными и 2 - поперечными гиперзвуковыми
волнами при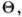 отличном от нуля. В
кристалле в общем случае вследствие анизотропии скоростей распространения
гиперзвука (3 различные скорости для каждого направления) и анизотропии
распространения возбуждающего и рассеянного света 4 возможные комбинации для состояний
поляризации падающего и рассеянного света должно наблюдаться 24 компоненты
Мандельштама-Бриллюэна. Кроме того, во всех случаях наблюдается также
несмещённая по частоте центр тонкой структуры, вызванная рассеянием на
изобарических флуктуациях энтропии. При обычных (не лазерных) источниках света
световая волна не влияет на состояние среды и вызывающие рассеяние упругие
волны обусловлены только тепловым движением молекул. Такое рассеяние света наз.
тепловым. Когда интенсивность световой волны достаточно велика (напряжённость
электрического поля волны ~106-108 в/см. сравнима с внутриатомным полем),
развивается процесс вынужденного рассеяния Мандельштама-Бриллюэна. В этом
случае бегущая интерференции картина электрических полей возбуждающей и
рассеянной световых волн усиливает те упругие волныкоторого, вызвали
первоначальное тепловое рассеяние.
отличном от нуля. В
кристалле в общем случае вследствие анизотропии скоростей распространения
гиперзвука (3 различные скорости для каждого направления) и анизотропии
распространения возбуждающего и рассеянного света 4 возможные комбинации для состояний
поляризации падающего и рассеянного света должно наблюдаться 24 компоненты
Мандельштама-Бриллюэна. Кроме того, во всех случаях наблюдается также
несмещённая по частоте центр тонкой структуры, вызванная рассеянием на
изобарических флуктуациях энтропии. При обычных (не лазерных) источниках света
световая волна не влияет на состояние среды и вызывающие рассеяние упругие
волны обусловлены только тепловым движением молекул. Такое рассеяние света наз.
тепловым. Когда интенсивность световой волны достаточно велика (напряжённость
электрического поля волны ~106-108 в/см. сравнима с внутриатомным полем),
развивается процесс вынужденного рассеяния Мандельштама-Бриллюэна. В этом
случае бегущая интерференции картина электрических полей возбуждающей и
рассеянной световых волн усиливает те упругие волныкоторого, вызвали
первоначальное тепловое рассеяние.
Механизм усиления обусловлен силами
электрострикции, втягивающими вещество в места с большим локальным значением
напряжённости электрического поля и усиливающими таким образом упругие волны.
Рост амплитуды упругих волн приводит к соответствующему увеличению
эффективности рассеяния, а это в свою очередь усиливает упругие волны. В
результате интенсивность рассеянной волны нелинейно возрастает по мере
распространения в среде. В процессе вынужденного рассеяние
Мандельштама-Бриллюэнавозникает интенсивный гиперзвук, верх,
граница частоты которого ~105 МГц для твёрдого тела и ~103-104 МГц для
жидкости.Исследование рассеяние
Мандельштама-Бриллюэна позволяет получать ценную информацию
о свойствах рассеивающей среды. Практическая ценность явления вынужденного рассеяние
Мандельштама-Бриллюэна связана с возможностью управлять.
Глава II.
Двойное вынужденное рассеяние мандельштама-бриллюэна в жидкостях
.1 Поля, уравнение полей и уравнение
гидродинамики вжидкостях
В жидкой среде имеются 4 волны
1. Лазерная падающая
. Лазерная отраженная
. Рассеянная падающая
. Рассеянная отраженная
Система координат:
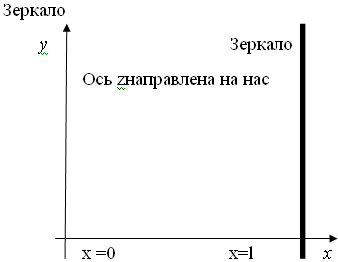
Рис. 2
Жидкость находится между x=0
и x=L
Напряженность электрического поля всех световых
волн имеют проекции только на оси zт.е.
электрические поля перпендикулярны плоскости рисунка.
Обозначения:
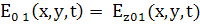 Лазерная падающая
Лазерная падающая
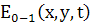 Лазерная
отраженная
Лазерная
отраженная
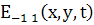 Рассеянная
падающая
Рассеянная
падающая
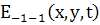 Рассеянная
отраженная
Рассеянная
отраженная
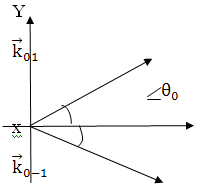
Рис. 2
Запишем эти волны в комплексной форме
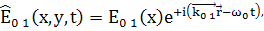 (1)
(1)
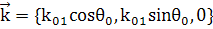 (2)
(2)
 ; (3)
; (3)
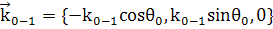 ; (4)
; (4)
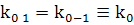 ; (5)
; (5)
Запись 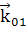 и
и
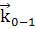 можно
представить в общей форме:
можно
представить в общей форме:
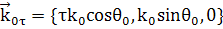 ; (6)
; (6)
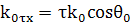 ; (7)
; (7)
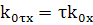 ; (8)
; (8)
Комплексные амплитуды всех волн предполагаются
зависящими только от глубины x.Аналогично
для рассеянных волн:
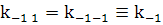 (9)
(9)
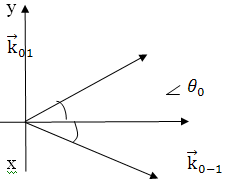
Рис. 3
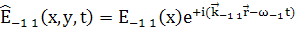 (10)
(10)
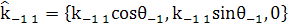 (11)
(11)
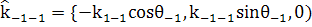 ; (12)
; (12)
Вообще
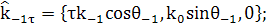 (13)
(13)
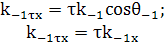
Суммарное поле:
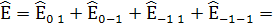
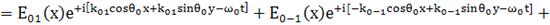
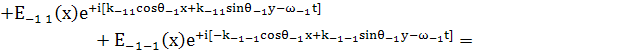
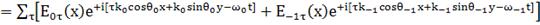 (14)
(14)
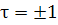 при
при 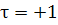 волна
идет вдоль +х
волна
идет вдоль +х
При 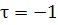 вдоль
-х
вдоль
-х
Внесем скобку множитель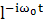
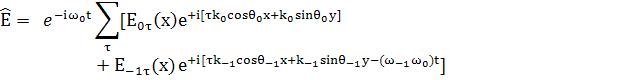 (15)
(15)
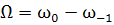 (16)
(16)
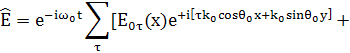
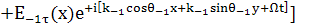 (17)
(17)
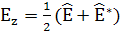 ; (18)
; (18)
Граничные условия:
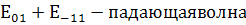 ,
,
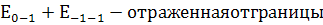 ;
;
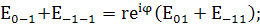 x=l; (19)
x=l; (19)
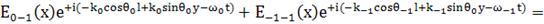
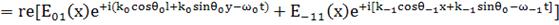
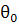 мало, поэтому
мало, поэтому 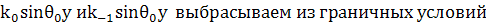 ;
;
Граничные условия должны выполняться при любом t
, поэтому
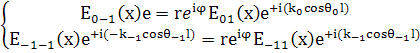 (20)
(20)
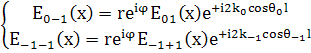 (21)
(21)
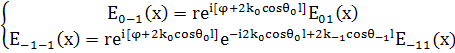 (22)
(22)
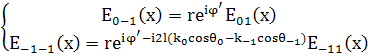 (23)
(23)
Где 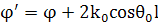
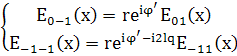 (24)
(24)
где 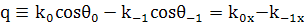
Волновое уравнение имеет вид (так как все поля
имеют составляющую только по оси z)
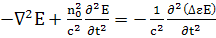 (25)
(25)
Полное действие поле
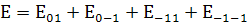 (26)
(26)
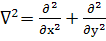 (27)
(27)
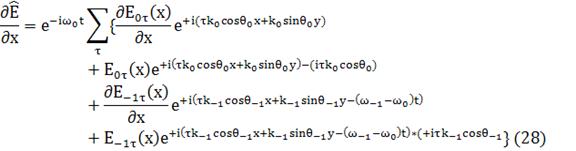 (28)
(28)
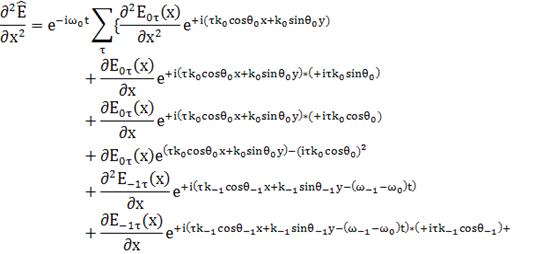
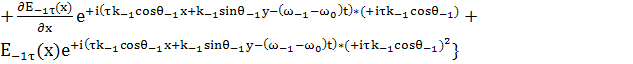 (29)
(29)
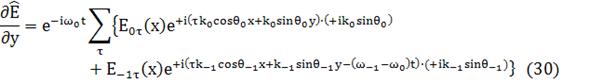 (30)
(30)

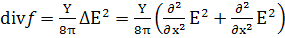 ; (32)
; (32)
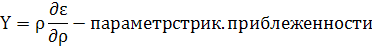
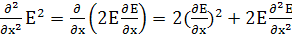 ; (33)
; (33)
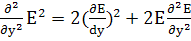 ; (34)
; (34)
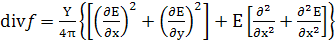 (35)
(35)
Здесь следует выбрать (т.е оставить) только
члены со звуковой частотой 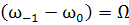
E-действительности
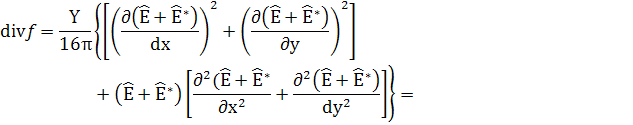
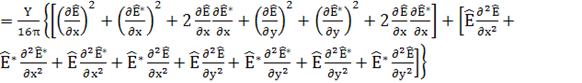 (36)
(36)
Только подчеркнутые члены содержат 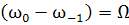 т.е
т.е
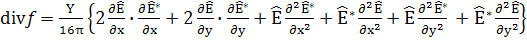 (37)
(37)
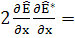 (16 членов: оставим
только члены, содержащие ї) =
(16 членов: оставим
только члены, содержащие ї) =
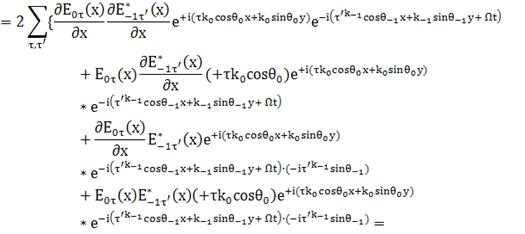
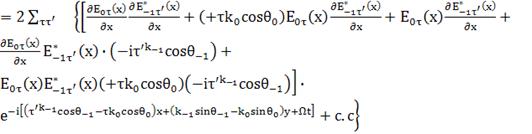 (38)
(38)
.2 Решение укороченных уравнений совместно с
уравнением гидродинамики
Члены с производными отбросим: это будем делать
лишь при решении
гидродинамики. Уравнения т.е. при отыскании
плотности:
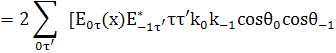
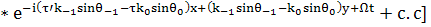 (39)
(39)
 малы: положим
малы: положим 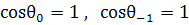
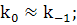
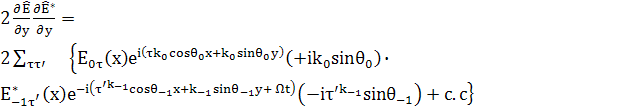 (40)
(40)
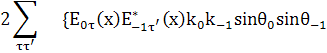
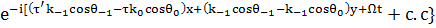 (41)
(41)
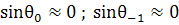 поэтому этот член
отбросим
поэтому этот член
отбросим
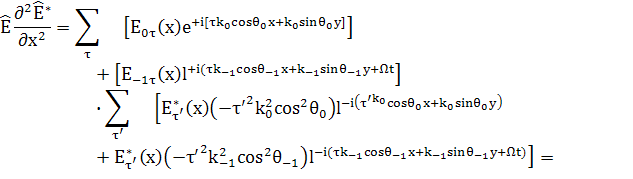
Оставляем члены с Щ:
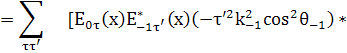
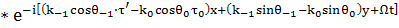 (42)
(42)
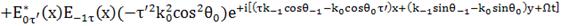
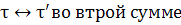
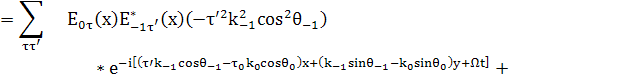
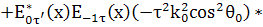
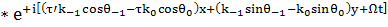 (43)
(43)
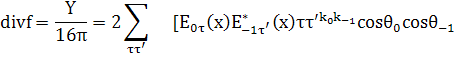
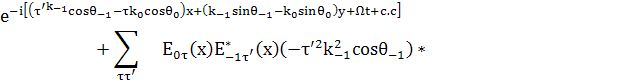
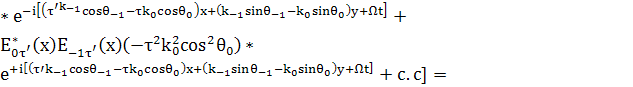
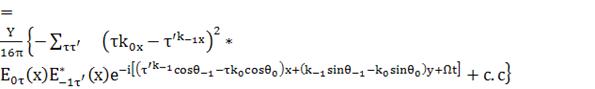 (44)
(44)
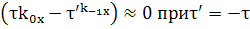
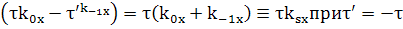
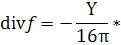
 (45)
(45)
 (46)
(46)
Или
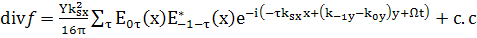 (47)
(47)
Для 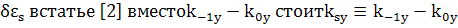
Далее будем следовать методу Tang
Для напряжения по Tang
имеем место уравнение
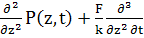 (48)
(48)
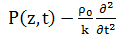 (49)
(49)
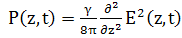 (50)
(50)
2.3 Решение укороченных уравнений с учетом
стрикционной нелинейности
Здесь все величины действительны уTang
волны распространялись вдоль осиz
у нас же волны распространяются в плоскости x,y
.Поэтому уравнение для P=P(x,y,z)
будет иметь вид
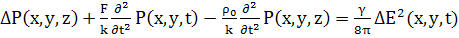 (51)
(51)
В дальнейшем следует выяснить, как г связано с Y
возможно, что совпадают.
К - упругая константа, она определяется
уравнением:
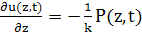 (52)
(52)
Это для задачи Tang.
Надо понять, что значит 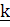 в нашей задачи.
в нашей задачи.

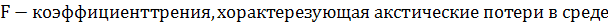
У нас 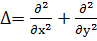 (53)
(53)
Перепишем основные формулы:
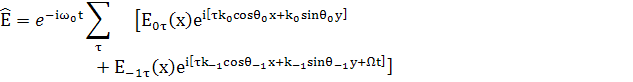
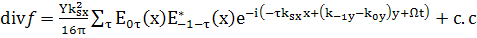 (54)
(54)
т.е. имеем тоже , что и в [2]. Следуя методу Tang,
положим
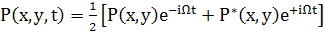 (55)
(55)
У Tang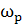 и
есть наше ї
и
есть наше ї
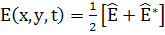 (56)
(56)
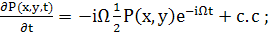 (57)
(57)
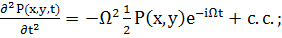 (58)
(58)
Подставим в основное уравнение и приравняем
коэффициент при 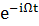

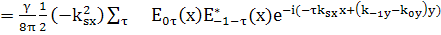 (59)
(59)
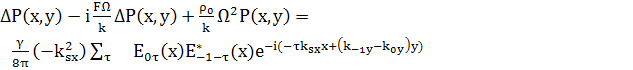 (60)
(60)
т.е. полученное уравнение является правильным
вводим обозначения:
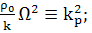 (61)
(61)
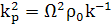 (62)
(62)
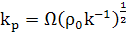 (63)
(63)
Отсюда ясно, откуда взялось
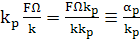 (64)
(64)
Здесь обозначено
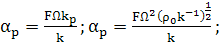 (65)
(65)
Если связать 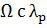 получим
уравнение Tang, но как это
сделать не ясно, итак
получим
уравнение Tang, но как это
сделать не ясно, итак
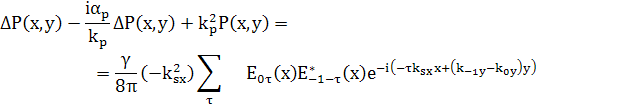 (66)
(66)
Вид уравнения подсказывает в каком виде искать P(x,y),
(P(x,y)
- комплексное). Если бы не было 2-го члена слева, а также в правой части , то
это было бы уравнение свободных колебаний. Поэтому P(x,y)
ищется в виде
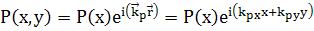 (67)
(67)
Запишем, учитывая сказанное, сразу P(x,y,t)
(это - действительно) и подставим в исходное уравнение.
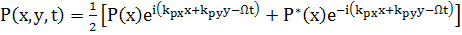 (68)
(68)
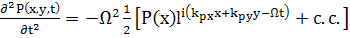 (69)
(69)
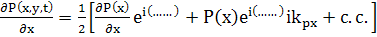 (70)
(70)
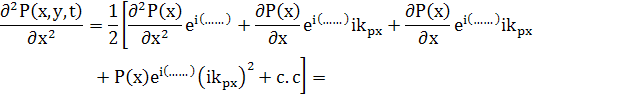
Если пренебречь,
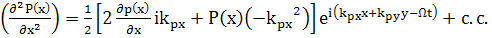 (71)
(71)
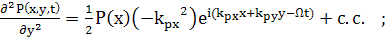 (72)
(72)
Если пренебречь 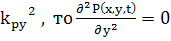 (73)
(73)
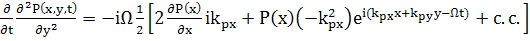 (74)
(74)
Подставляем произведение в уравнение и
приравниваем коэффициент при 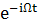
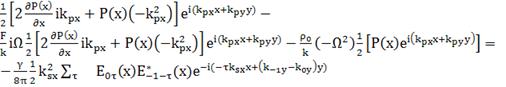 (75)
(75)
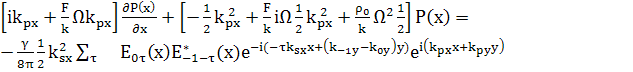 (76)
(76)
У Tang
Щ обозначалось
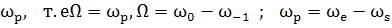
по Tang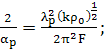 (77)
(77)
Введём сюда 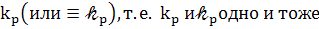
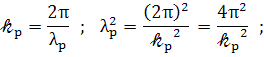
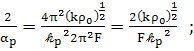 (78)
(78)
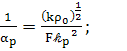 (79)
(79)
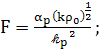 (80)
(80)
В уравнении будем считать, что 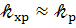 также
в правой части изменим
также
в правой части изменим 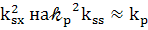 вследствие условия
согласования
вследствие условия
согласования
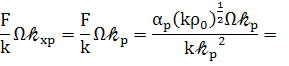
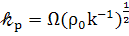 (81)
(81)
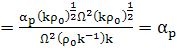 т. е.
т. е. 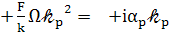 (82)
(82)
Далее , так как 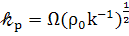 ;
;
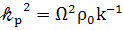 (83)
(83)
т.е. зная 5 член, слева в уравнении взаимно
уничтожаются
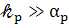 (84)
(84)
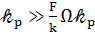 (85)
(85)
Поэтому вторым членом слева пренебрегаем
т.е. уравнение принимает вид:
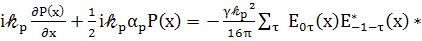
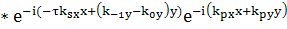 (86)
(86)
Или
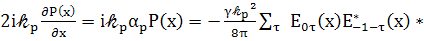
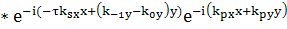 (87)
(87)
т.е.
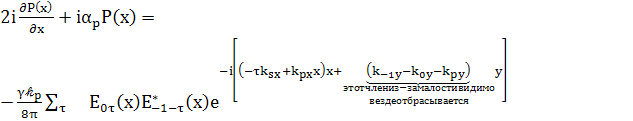 (88)
(88)
Итак,
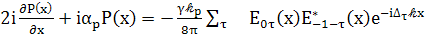 (89)
(89)
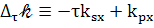 или
или
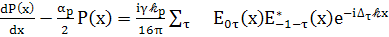 (90)
(90)
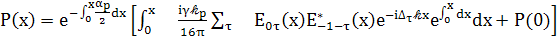 (91)
(91)
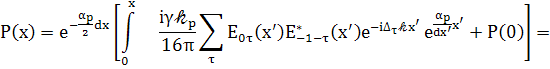
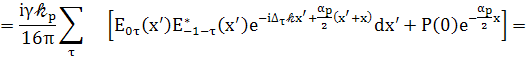
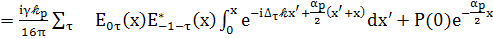 (92)
(92)
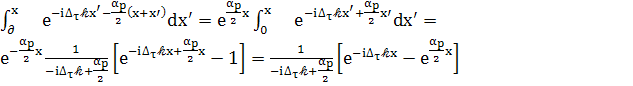 (93)
(93)
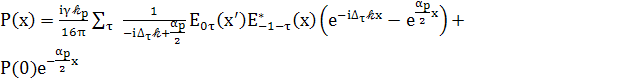 (94)
(94)
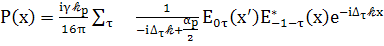 (95)
(95)
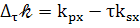 (96)
(96)
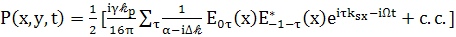 (97)
(97)
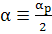 (98)
(98)
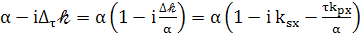 (99)
(99)
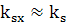
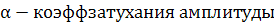
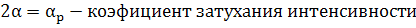
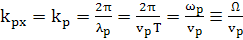 (100)
(100)
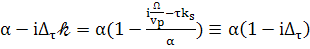 (101)
(101)
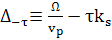 (102)
(102)

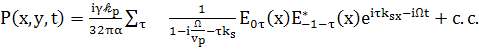 (103)
(103)
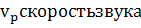
Полученное P(x,y,t)
- решения уравнения данного Tangт.е
для кристаллов. Нам же необходимо иметь P(x,y,t)
для жидкостей . Чтобы получить P(x,y,t)
для жидкостей выпишем уравнение , имеющие отношение к делу, и сравним их.
Уравнение Tang
которое решалось здесь :
 (104)
(104)
Обозначения оставленные по Tang
;
Умножим это уравнение на 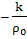
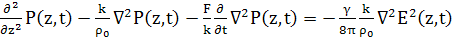 (A)
(105)
(A)
(105)
Выпишем теперь уравнение гидродинамики (Key,
Harrison)
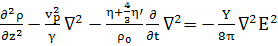 (B)
(106)
(B)
(106)
Уравнение гидродинамики по книге Зельдовича
(ОВФ), с.31, имеет вид:
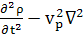 p-
и т.д., (С) (107)
p-
и т.д., (С) (107)
т.е. во втором слагаемом, в отличие от (В) нет
г=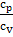 .
.
Почему - это неясно. Запись (С) видимо,
существует.
Будем следовать (С), т.е. уравнение
гидродинамики запишем в виде:
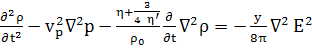 ; (D) (108)
; (D) (108)
У 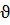 поставлен
индекс р (фонон)- phonon.
поставлен
индекс р (фонон)- phonon.
Очевидно, что если имеется решение для (А)
следует положитьP(x,y,t)=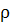 (x,y,t),
и
(x,y,t),
и
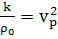 ,
, 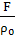 =
=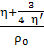 ,
,
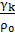 =Y;
=Y;
Отсюда
k=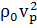 и
и 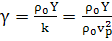 =
=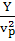 ;
т.о.
;
т.о.
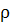 (x,y,t)=
(x,y,t)=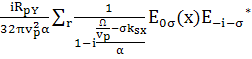 (x)
(x) +c.c.
т.к. (109)
+c.c.
т.к. (109)
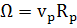 , то
, то 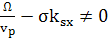
Положим 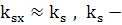 модуль
волнового вектора для суммарной световой волны.
модуль
волнового вектора для суммарной световой волны.
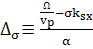 =
=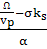 ; (110)
; (110)
В статье Заскалько и др. 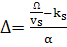 называется
отстройкой, но это лишь в том случае будет справедливо, когда
называется
отстройкой, но это лишь в том случае будет справедливо, когда 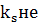 является
волновым числом звуковой волны.
является
волновым числом звуковой волны.
Что такое 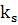 в
числителе(3) . В числителе
в
числителе(3) . В числителе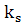 должно быть
волновым числом звуковой волны.
должно быть
волновым числом звуковой волны.
Это точно вытекает из решения уравнения
гидродинамики.
Похоже, что здесь происходит смешение понятий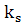 - волнового число звуковой волны и
- волнового число звуковой волны и 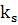 -
волновое число суммарной световой волны. S-
отsound и . S-
отsummary
-
волновое число суммарной световой волны. S-
отsound и . S-
отsummary
Если считать , что 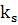 в
в
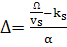 есть
волновые число световой волны, то ясно, что оно не будет совпадать с тем
есть
волновые число световой волны, то ясно, что оно не будет совпадать с тем 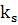 ,
что стоит в числителе (3).
,
что стоит в числителе (3).
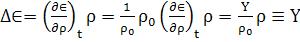
из гидродинамического уравнения.
= 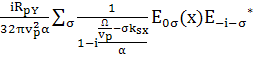 (x)
(x)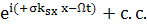 (111)
(111)
Что такое 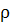 ?
По видимому, это отклонение плотности от равновесного значения:
?
По видимому, это отклонение плотности от равновесного значения:
Гидродинамические уравнения содержит от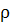 ,
так что это уравнение можно рассматривать как для плотности, так как и для
отклонения плотности.
,
так что это уравнение можно рассматривать как для плотности, так как и для
отклонения плотности.
Ещё раз поясним это.
Имеется гидродинамические уравнение для 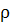 и
формула
и
формула 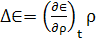 .
Что понимать под влиянием поля. Действительно, решение гидродинамические
уравнения определяется там правой части и
.
Что понимать под влиянием поля. Действительно, решение гидродинамические
уравнения определяется там правой части и 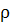 -
изменение.
-
изменение.
Тогда 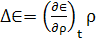 понятна.
понятна.
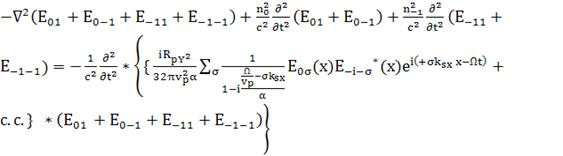 ; (112)
; (112)
 =
= 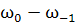
Это уравнение имеет вид:
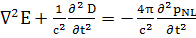 ;
;
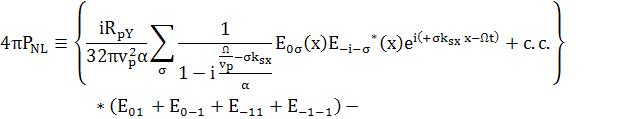
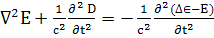 ; (113)
; (113)
р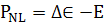 ;
;
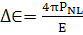 -
действия,
-
действия,
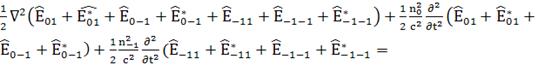
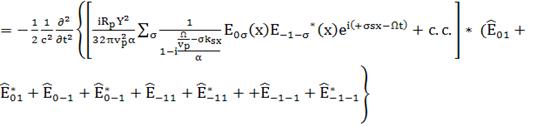 ;(114)
;(114)
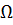 =
= 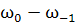 ,
,
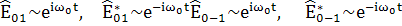
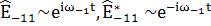 (115)
(115)
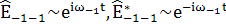 (116)
(116)
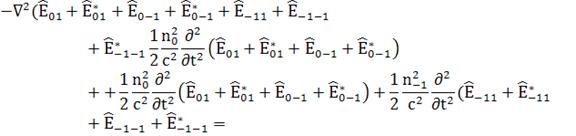
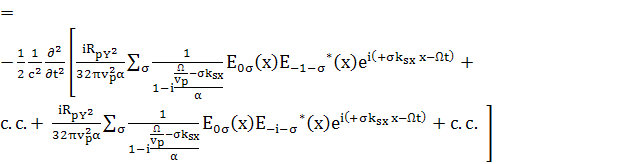 *
*
*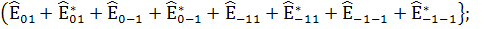 (117)
(117)
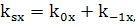 ;
; 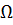 =
=
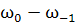 ;
;
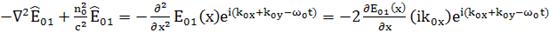 =
=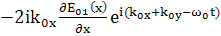 ;
(118)
;
(118)
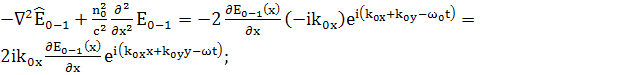 (119)
(119)
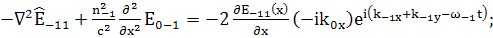 (120)
(120)
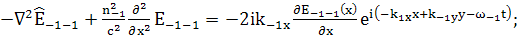 (121)
(121)
Положим,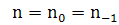
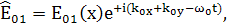 (122)
(122)
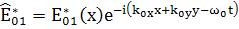 , (123)
, (123)
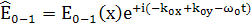 , (124)
, (124)
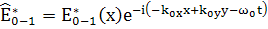 , (125)
, (125)
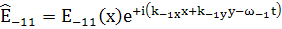 , (126)
, (126)
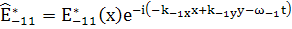 , (127)
, (127)
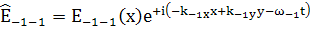 , (128)
, (128)
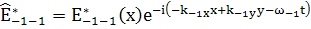 ; (129)
; (129)
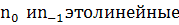 со
со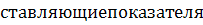 преломления, соответственно,
для волн с индексами 0 и 1, т.е. для лазерных и рассеянных волн,
преломления, соответственно,
для волн с индексами 0 и 1, т.е. для лазерных и рассеянных волн, 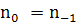 ,
т.к. линейный показатель не зависит от поля.
,
т.к. линейный показатель не зависит от поля.
Соответственно, величинам 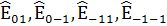 получится
четыре компонент сопряженных им.
получится
четыре компонент сопряженных им.
Приравняем коэффициенты при 
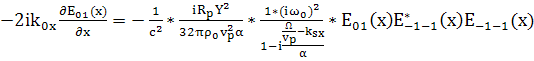 (130)
(130)
И при
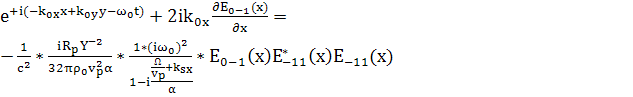
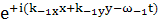
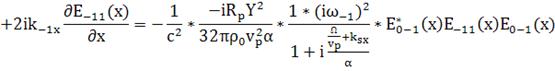
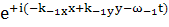
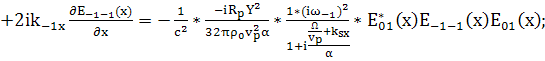 (131)
(131)
2.4 Учет Керровской нелинейности
В этих 4-х уравнениях ещё не учитывались 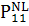 в
правой части, связанное с ориентацией молекул, т.е. с эффектом Керра. Перейдем
к рассмотрению эффекта Керра. Согласно,
в
правой части, связанное с ориентацией молекул, т.е. с эффектом Керра. Перейдем
к рассмотрению эффекта Керра. Согласно,
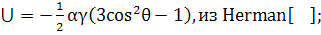 (132)
(132)
В качестве 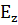 сейчас
берем
сейчас
берем
 (133)
(133)
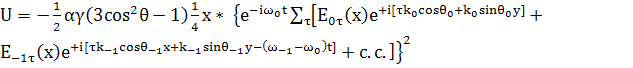 ; (134)
; (134)
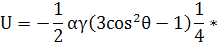
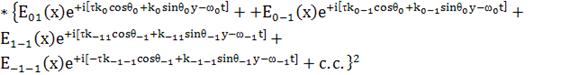 (135)
(135)
высоко частотный отброшены; Пока ничего
отбрасывать не будем.
Запишем U в виде:
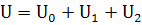 (137)
(137)
где 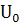 не
зависит от t
не
зависит от t
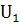 содержит
содержит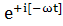
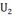 содержит
содержит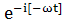
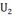
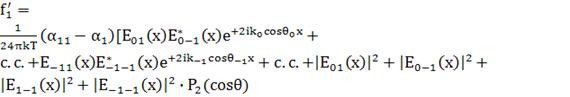 (138)
(138)
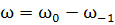
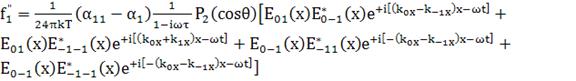 (139)
(139)
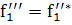
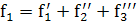
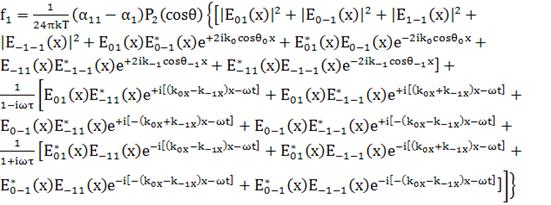 (140)
(140)
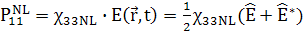 (141)
(141)
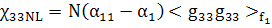 (142)
(142)
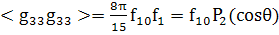 (143)
(143)
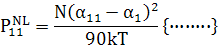
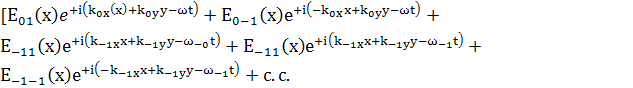 (144)
(144)
Члены , содержащие 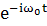
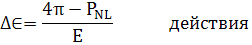
Пусть 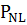 -
ориентация
-
ориентация
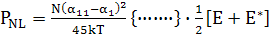 (145)
(145)
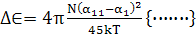 (146)
(146)
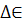 соответствует
соответствует 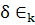 в
статье Заскалько и др.
в
статье Заскалько и др.
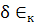 в статье Заскалько
и др.
в статье Заскалько
и др.
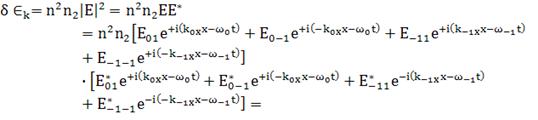
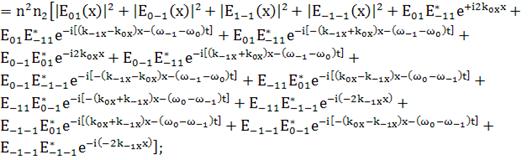 (147)
(147)
Сравним 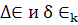
Очевидно , что при 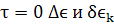 точно
совпадают причем
точно
совпадают причем
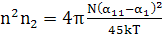 (148)
(148)
Т.е 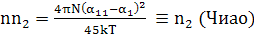 все
верно.
все
верно.
Т.е чтобы перевести наше выражение в
соответствующее 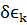 надо
надо 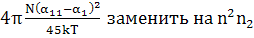
Важно,
что наше выражение для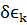 годится и при
годится и при 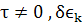 в
статье Заскалько и др. не применимо при
в
статье Заскалько и др. не применимо при 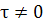
Перепишем произведение А на В:
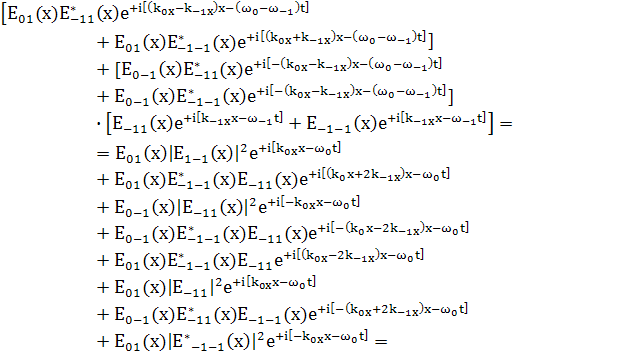
Вставим только подчеркнутые и отведенные члены,
остальные имеют высокие пространства частоты,
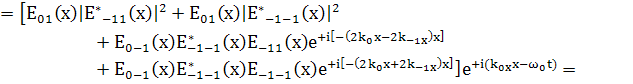
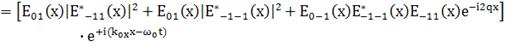 (149)
(149)
Член с 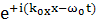 имеется
еще и в произведении
имеется
еще и в произведении 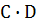
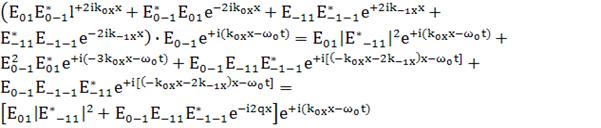 (150)
(150)
Первая часть волнового уравнения содержащая 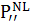
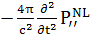 (151)
(151)
Выпишем коэффициент при 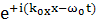 в
правой части уравнения происходящий от
в
правой части уравнения происходящий от 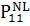
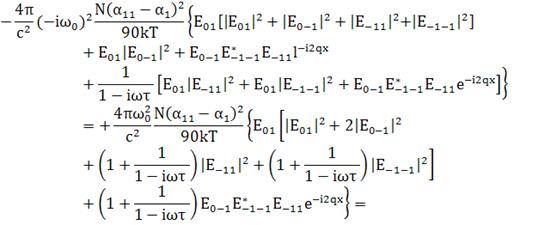
При 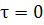
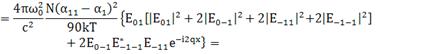
 (152)
(152)
коэффициент при 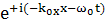
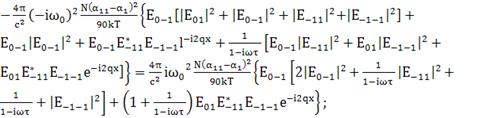 (153)
(153)
При 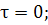
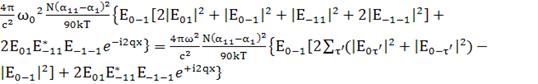 (154)
(154)
коэффициент при
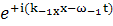 ; и
; и 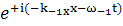 (155)
(155)
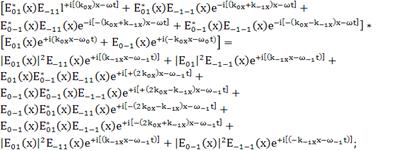 (156)
(156)
коэффициент при 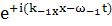
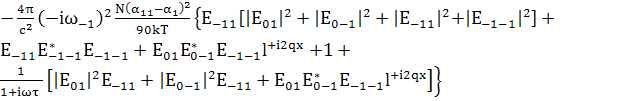 =
=
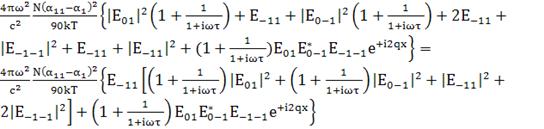 ; (157)
; (157)
При 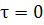 :
:
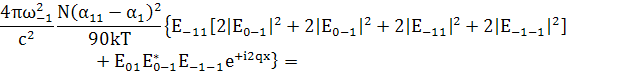
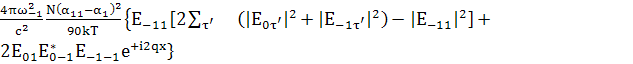 ; (158)
; (158)
коэффициент при 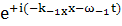
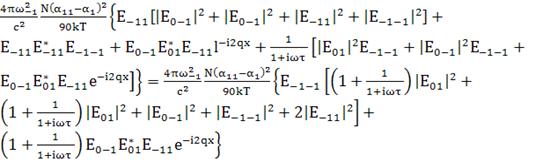 ;(159)
;(159)
При 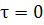 :
:
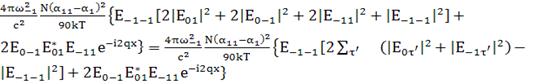 ; (160)
; (160)
Записываем укороченные волновые уравнения,
приняв во внимание и ориентационный и стрикционный вклады:
При 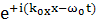 ;
(точнее, при
;
(точнее, при 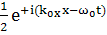 )
)
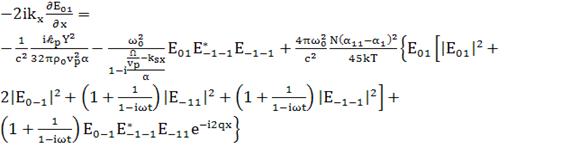 (161)
(161)
Умножим на i,
делим на 2, делим на 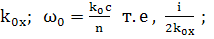
Чтобы убедиться в правильности этого уравнения
полезно сравнить его с уравнением (PQR)
в разработке к Herman.
Мы увидим, при этом, что числовой коэффициент в правой части , относящимися к ориентационному
вкладу . Именно такое сравнение помогло найти ошибку (90 исправлен на 45)
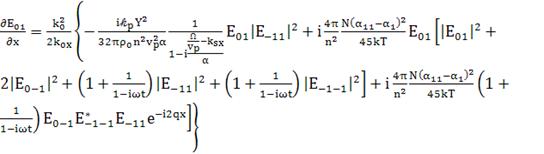 ; (162)
; (162)
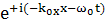 (163)
(163)
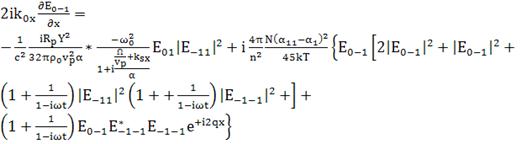 ; (164)
; (164)
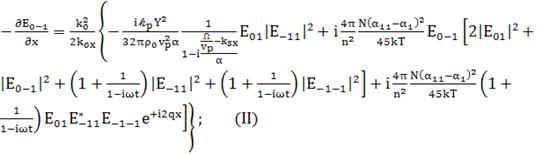 (165)
(165)
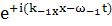 (166)
(166)
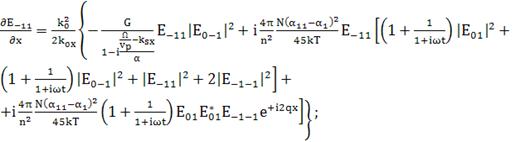 (167)
(167)
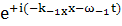 (168)
(168)
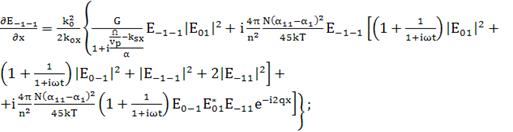 (169)
(169)
По Чиао и Годин
е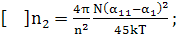
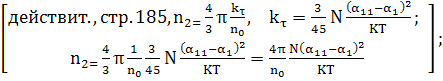 (170)
(170)
Cравнение
полученных уравнений со статьей Заскалько и др.
Положим 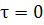
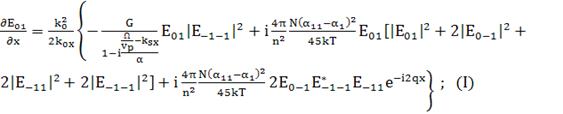 (171)
(171)
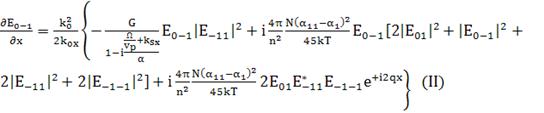 (172)
(172)
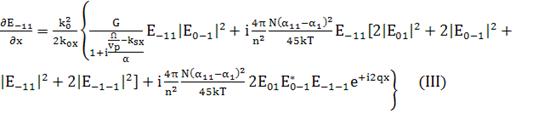 (173)
(173)
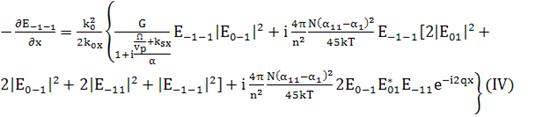 (174)
(174)
Объединим их
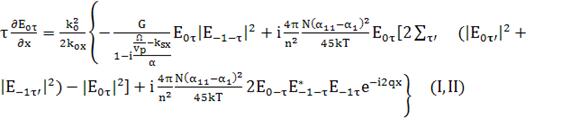 (175)
(175)
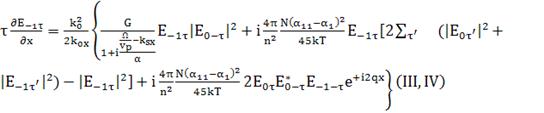 (176)
(176)
Обозначим 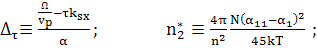 (177)
(177)
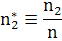
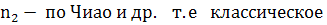
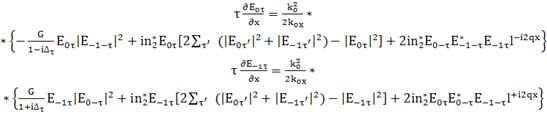
Полученное нами уравнение отличаются от
соответствующих уравнений в стать Заскалько и др.
У нас стоит 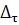 ,
в статье
,
в статье 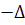 ;
;
У нас 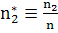 ,
в статье
,
в статье 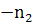 ;
;
В связи с последним фактом необходимо понять,
как определяется 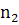 в статье,
совпадает ли оно с классическим (по Чиао), каково происхождение формулы
в статье,
совпадает ли оно с классическим (по Чиао), каково происхождение формулы 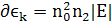 в
статье , как её понимать и , вообще , насколько она точна.
в
статье , как её понимать и , вообще , насколько она точна.
Связь между 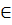 и
потенциалом Е ;Е-здесь действителен
и
потенциалом Е ;Е-здесь действителен

Случай переменного поля рассматривается дальше
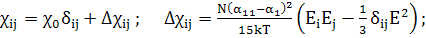 (178)
(178)
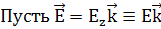 ;
; 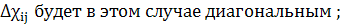
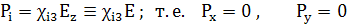
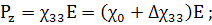 (179)
(179)
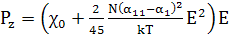 (180)
(180)
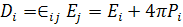 (181)
(181)
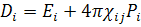 (182)
(182)
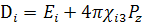 (183)
(183)
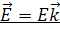 (184)
(184)
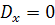 (185)
(185)
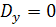 (186)
(186)
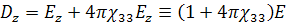 (187)
(187)
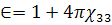 (188)
(188)
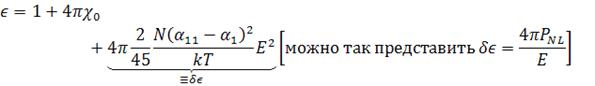
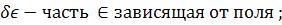
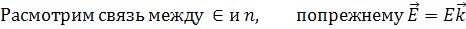
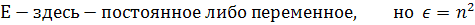
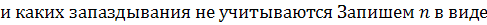
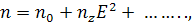
Такая запись используется в статьях с участием
Чиоа( см. Чиао, Гармайр, Таунс, Самозахват оптических пучков. Phys.
Rev. Lett.
V 13, №15, 1964,
479-482)
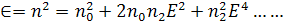 (189)
(189)
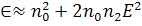 (190)
(190)
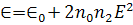 (191)
(191)
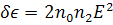 (192)
(192)
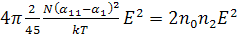 (193)
(193)
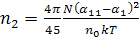 (194)
(194)
Если Е-переменное то Е здесь - мгновенное
значение , а не амплитуда.
Еще заметим, что запаздывание не учитывалось,
т.е. всё рассмотрение относится к постоянным полям, либо к переменным полям
настолько малой частоты , что их можно рассматривать как постоянные. Смысл
этого рассмотрения в том , что она даёт определение 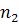
В статье Чиао и Године для 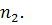 Дано
Дано
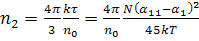 (195)
(195)
Это говорит о том что полеченное нами 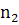 совпадает
с тем, которое даётся в классических работах.
совпадает
с тем, которое даётся в классических работах.
Найдем теперь выражение для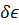 в
случае переменного поля. Можно воспользоваться выражением для
в
случае переменного поля. Можно воспользоваться выражением для 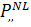 при
наличии двух полей, лазерного и рассеянного (релеейского), полученным в теории
вынужденного релеевского рассеяния (см. разработку к статье Herman)
при
наличии двух полей, лазерного и рассеянного (релеейского), полученным в теории
вынужденного релеевского рассеяния (см. разработку к статье Herman)
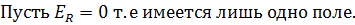
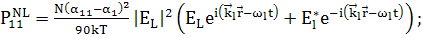 (196)
(196)
 (197)
(197)
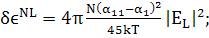 (198)
(198)
 (199)
(199)
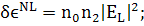 (200)
(200)
Если, однако, учесть оба поля , то
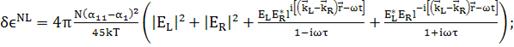 (201)
(201)
Выражение в круглых скобках не равно 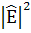
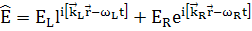 (202)
(202)
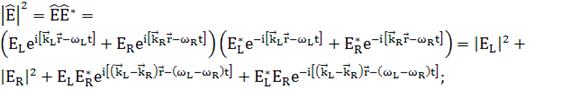 (203)
(203)
Положим в выражении для 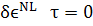 тогда
тогда
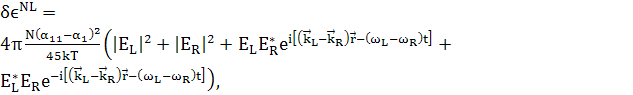 (204)
(204)
Т.е
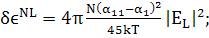 (205)
(205)
Опять
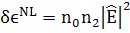 (206)
(206)
Т.е последнее выражение имеет место, когда
релаксацией пренебрегаем 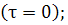 при этом
при этом 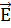 в
нём комплексное полное поле (точнее, квадрат его модуля ).
в
нём комплексное полное поле (точнее, квадрат его модуля ).
Выводы:
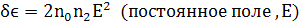 (207)
(207)
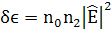 (208)
(208)
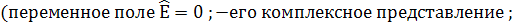
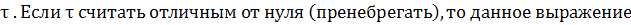
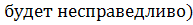
В статье Заскалько и др. записано
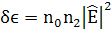 (209)
(209)
Можно думать, что они записывают 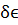 для
переменного поля при
для
переменного поля при
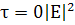 это и есть
это и есть 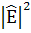
Обратим внимание еще на 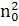 в
формуле из статьи. Ясно, что
в
формуле из статьи. Ясно, что
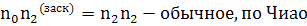
В наших укороченных уравнениях стоит 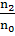 т.е
т.е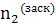 или
или
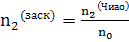 т.о
т.о
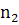 Заскалько
и др. и
Заскалько
и др. и 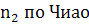 не
совпадают (отличаются множителем
не
совпадают (отличаются множителем 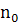 )
)
Обсудим такой вопрос:
Если поле постоянно, то  ;
(*) (210)
;
(*) (210)
Если же переменное, то 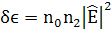 (**)
(211)
(**)
(211)
Как приблизить эти формулы друг к другу, нельзя
ли одну из другой получить, хотя бы нестрого, или некорректно?
Можно так рассуждать : пусть Е медленно
меняется; тогда, повидимому, (*) будет ещё справедливо:
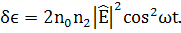 (212)
(212)
Усредним по t:
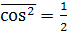 и
получается (**):
и
получается (**):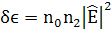 . (213)
. (213)
Ещё замечание.
Для постоянного поля 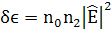 ,
и следовательно
,
и следовательно 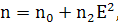
т.к.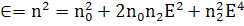 ; (214)
; (214)
Осуществим переход к переменному полю и
усредним:
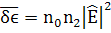 , а для
, а для 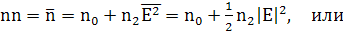
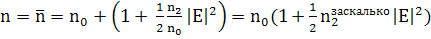 (215)
(215)
Эта запись для n
дана в статье на стр 1583.
Распишем уравнения подробно.
Везде далее будем использовать
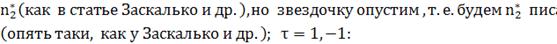
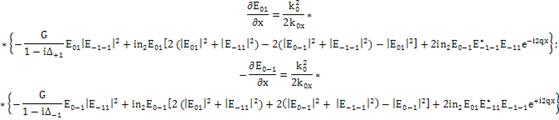
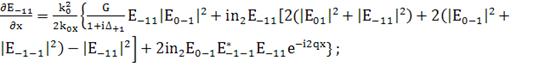 (216)
(216)
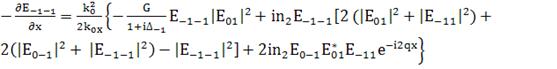 ; (217)
; (217)
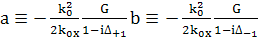 . (218)
. (218)
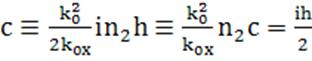 (219)
(219)
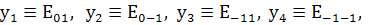 (220)
(220)
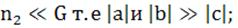 (221)
(221)
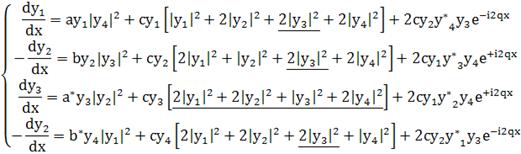 (222)
(222)
Будем искать решение в предложении , что 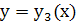 мало
. Ввиду этого подчёркнутые члены отбросим как малые : они содержат либо
мало
. Ввиду этого подчёркнутые члены отбросим как малые : они содержат либо 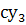 (с
- тоже мало ) либо
(с
- тоже мало ) либо 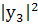 либо
либо 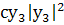
Граничные условия
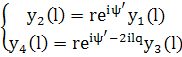 (223)
(223)
Или
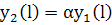 ;
; 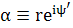
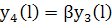 ;
; 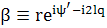
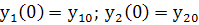
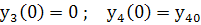
Решение должно содержать 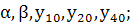
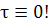
 (224)
(224)
Берем 1-ое и 4-ое уравнения отбрасываем в них
члены содержащие с, т.е, находим нулевая приближение .
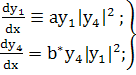 (225)
(225)
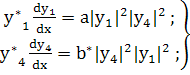 (226)
(226)
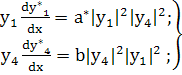 (227)
(227)
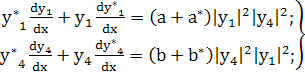 (228)
(228)
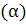
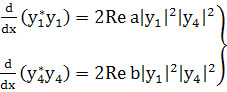 (229)
(229)
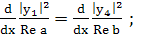 (230)
(230)
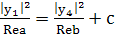 (231)
(231)
Пусть:


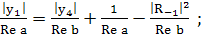 (232)
(232)
Обратимся к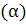
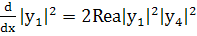 (233)
(233)
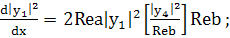 (234)
(234)
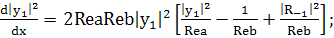 (235)
(235)
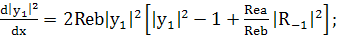 (236)
(236)
 (237)
(237)
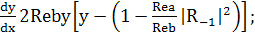 (238)
(238)
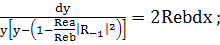 (239)
(239)
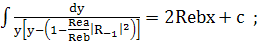 (240)
(240)
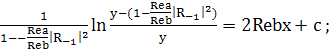 (241)
(241)
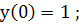 (242)
(242)
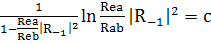 (243)
(243)
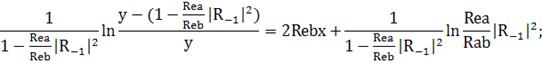
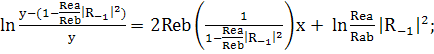 (244)
(244)
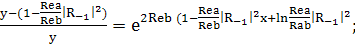 (245)
(245)
 (246)
(246)
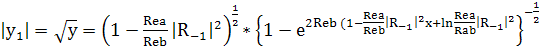 ;(247)
;(247)
Или
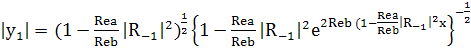 ; (248)
; (248)
Видно, что при х=0 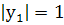 ;
;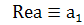 ;
; 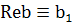 ;
(249)
;
(249)
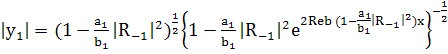 ; (250)
; (250)
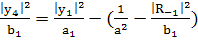 ; (251)
; (251)
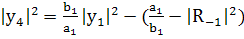 ; (252)
; (252)
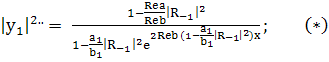 ; (253)
; (253)
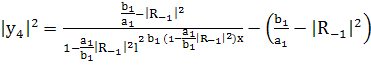 (254)
(254)
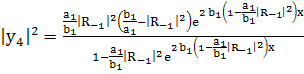 (255)
(255)
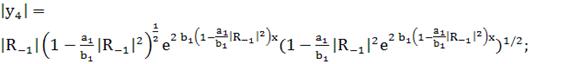 (256)
(256)
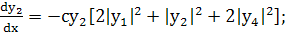 (257)
(257)
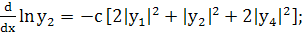 (258)
(258)
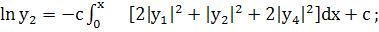 (259)
(259)
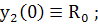 (260)
(260)
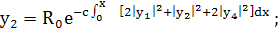 (261)
(261)
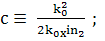 т.е. с -чисто
мнимое
т.е. с -чисто
мнимое
Следовательно,
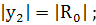 (262)
(262)
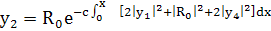 (263)
(263)
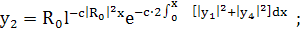
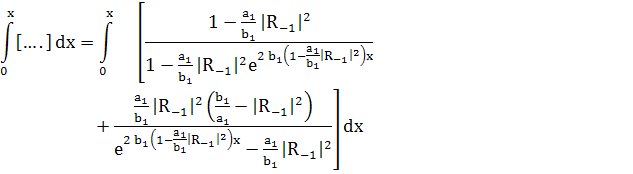
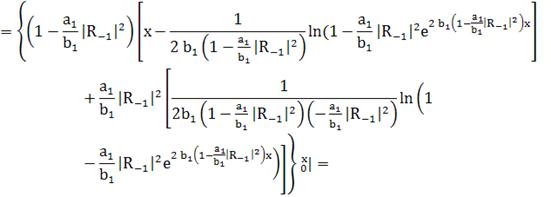
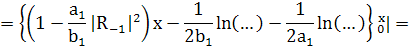
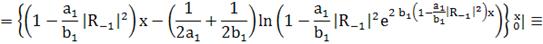
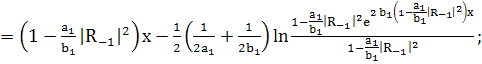 (264)
(264)
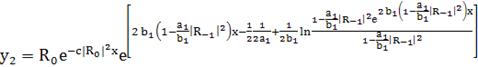 (265)
(265)
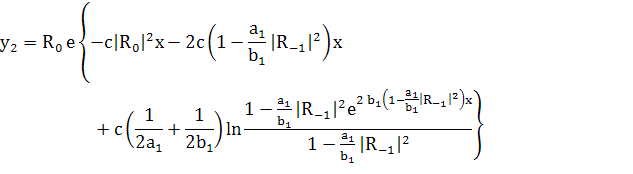 (266)
(266)
Ищем теперь 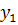 в
первом приближении
в
первом приближении
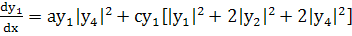 (267)
(267)
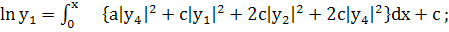 (268)
(268)
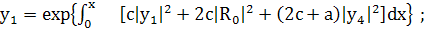 (269)
(269)
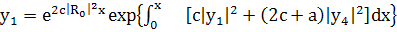 (270)
(270)
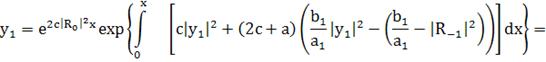
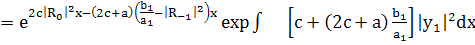 =
=
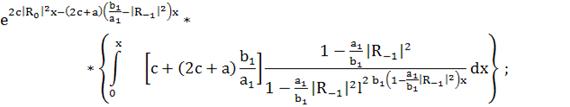 (271)
(271)
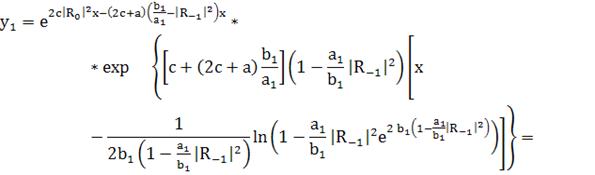
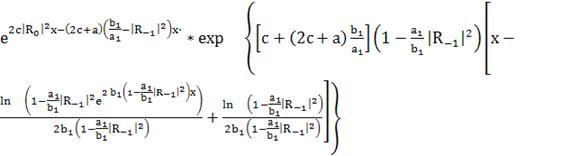 (272)
(272)
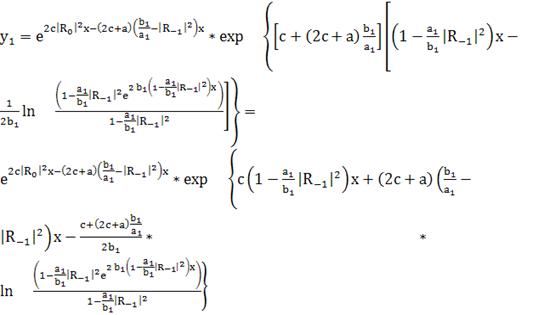 ; (273)
; (273)
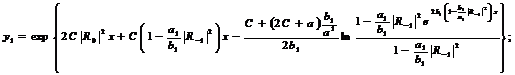 (274)
(274)
Для проверки положим С=0 и найдём 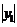 :
:
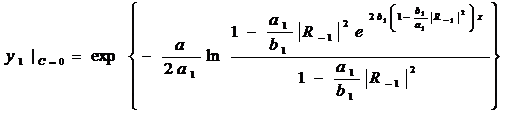 (275)
(275)
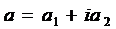 ;
;
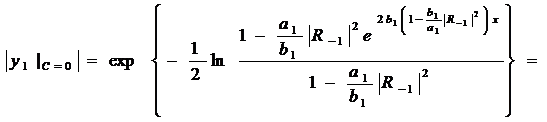
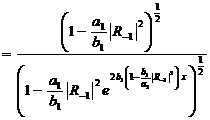 (276)
(276)
Это совпадает, как и должно быть, С(*).
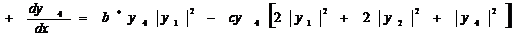 (277)
(277)
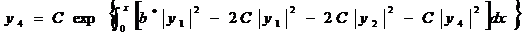 (278)
(278)
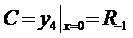 (279)
(279)
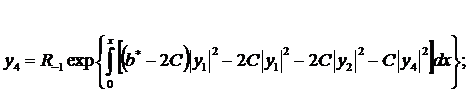 (280)
(280)
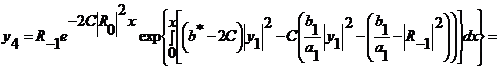
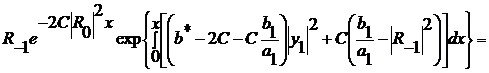
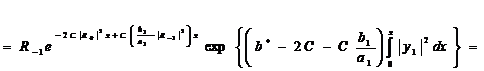
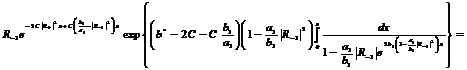
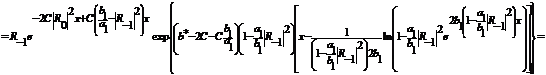
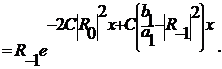
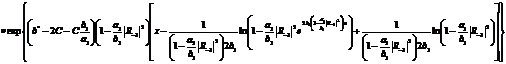 (281)
(281)
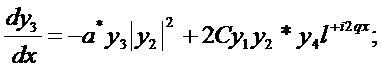 (282)
(282)
Если отбросить член c.c.
, то:
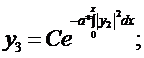 (283)
(283)
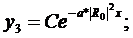 (284)
(284)
Будем искать 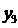 в
таком же виде и для полного уравнения, но считая, что
в
таком же виде и для полного уравнения, но считая, что
C=C(x);
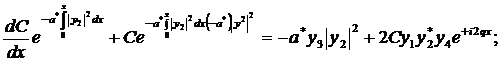 (285)
(285)
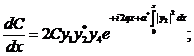 (286)
(286)
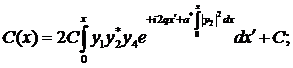 (287)
(287)
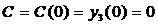 (288)
(288)
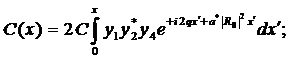 (289)
(289)
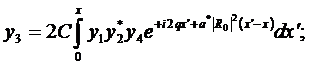 (290)
(290)
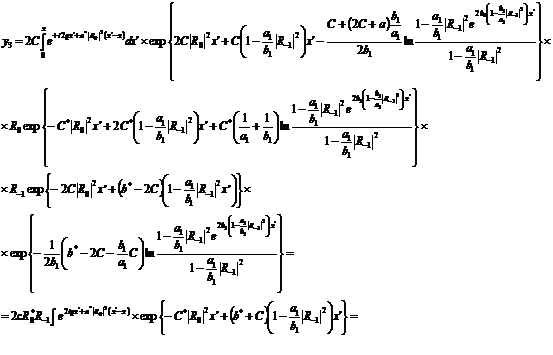

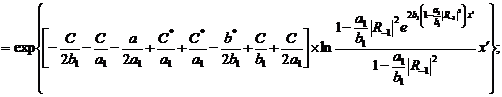 (291)
(291)
C содержит n2;
a1,
b1 содержат
G;
Но 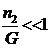 ;
отбросим в квадратной скобке
;
отбросим в квадратной скобке 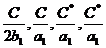 ;
;
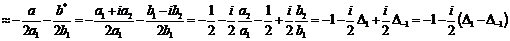 (292)
(292)
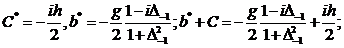 (293)
(293)
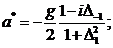 (294)
(294)
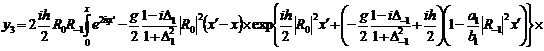
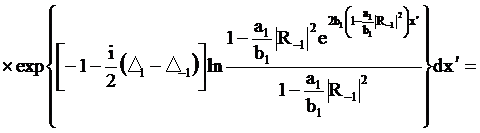
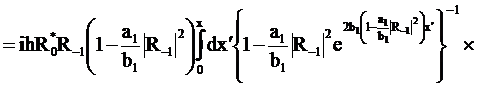
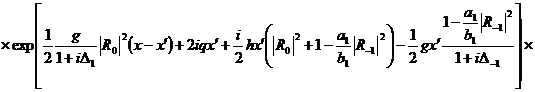
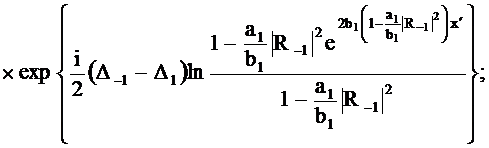 (295)
(295)
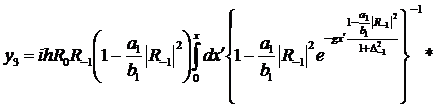
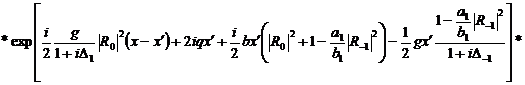
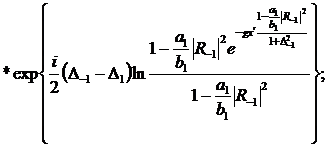 296)
296)
Если положить, что a1=b1,
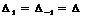 ,
то получится y3
в виде, который получается из статьи Заскалько.
,
то получится y3
в виде, который получается из статьи Заскалько.
Естественно, имеется отличие y3
(при
рассматриваемых условиях) от e-11:
знаки в показателе exp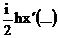 в
этих функциях разные.
в
этих функциях разные.
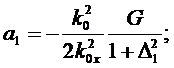 (297)
(297)
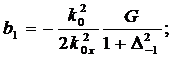 (298)
(298)
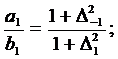 (299)
(299)
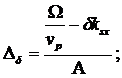 (300)
(300)
(когда вводилась величина 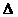 (см.намного
выше), то было принято обозначение:
(см.намного
выше), то было принято обозначение: 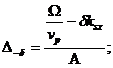 этим
определением не будем пользоваться)
этим
определением не будем пользоваться)
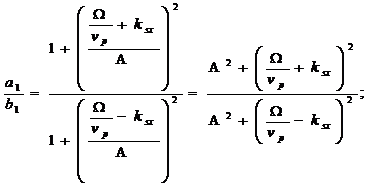 (301)
(301)
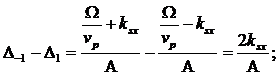 (302)
(302)
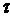 -конечное
-конечное
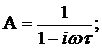 (303)
(303)
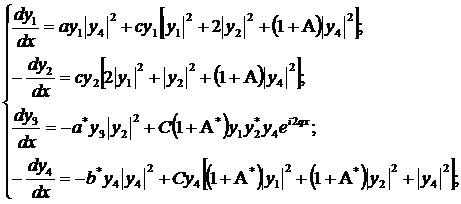 (304)
(304)
Берём 1ое и 4ое уравнения, отбрасываем в них
члены, содержащие C, т.е.
находим нулевые приближения.
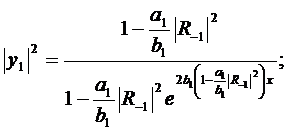 (305)
(305)
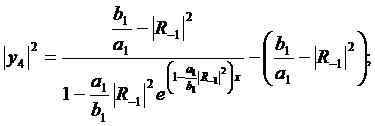 (306)
(306)
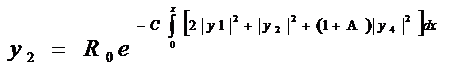 (307)
(307)
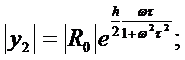 (308)
(308)
 (309)
(309)
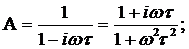 (310)
(310)
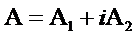 (311)
(311)
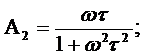 (312)
(312)
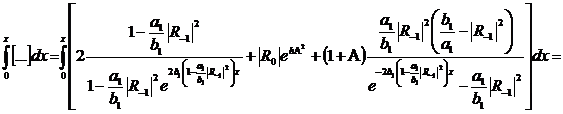
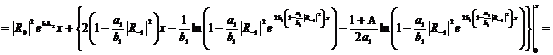
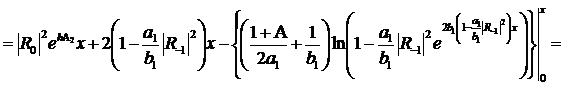
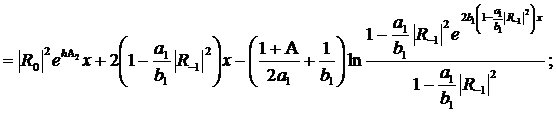
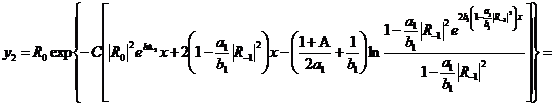
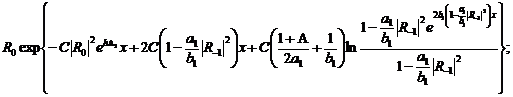 (313)
(313)
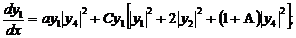 (314)
(314)
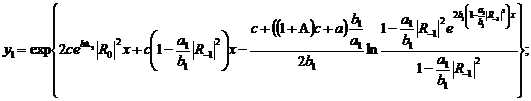 (315)
(315)
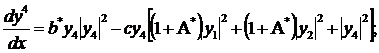 (316)
(316)
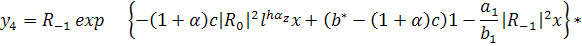
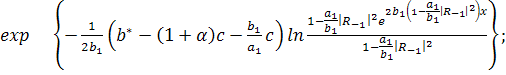 (317)
(317)
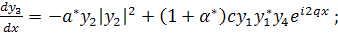 (318)
(318)
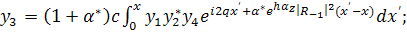 (319)
(319)
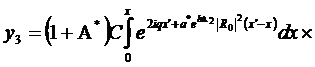
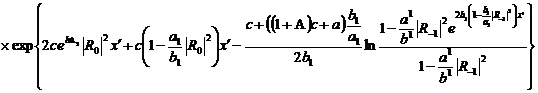
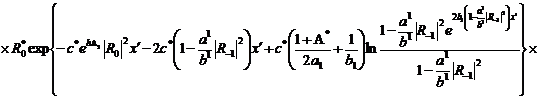
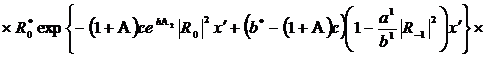
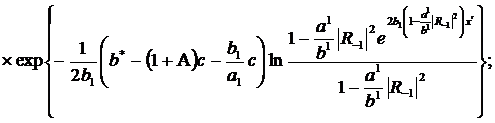 (320)
(320)
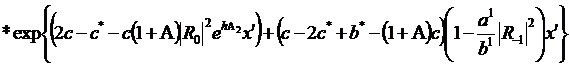
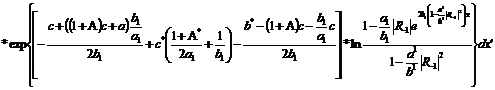 (321)
(321)
будет такой же, как и при 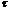 =
0 (ясно, что при
=
0 (ясно, что при 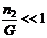 ), т.е. члены типа
), т.е. члены типа 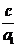 ,
,
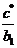 ,
… отброшены.
,
… отброшены.
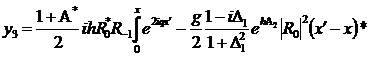
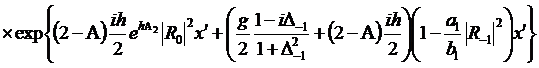
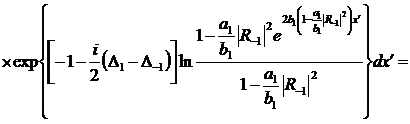
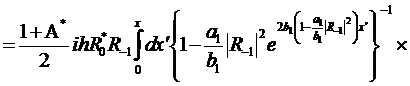
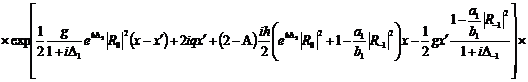
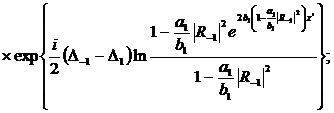 (322)
(322)
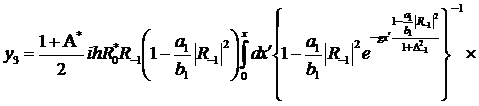 (323)
(323)
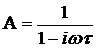 ; (324)
; (324)
При 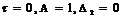 y3
совпадёт с y3
при
y3
совпадёт с y3
при 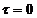 .
.
Обобщение уравнения (9) на случай 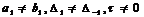
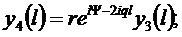
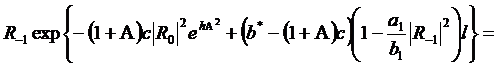

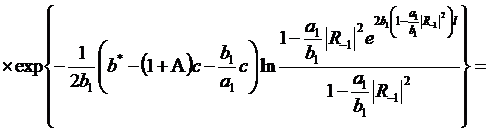
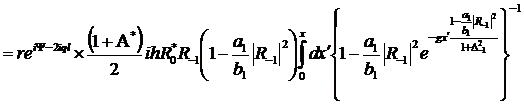
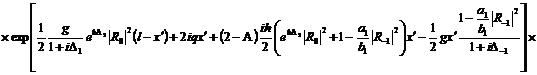

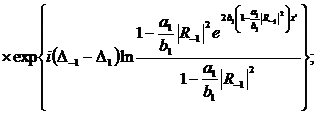 (325)
(325)
. 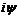 зачеркивается
в этом уравнении вместе с -
зачеркивается
в этом уравнении вместе с - 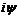 в
в 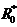 :
:
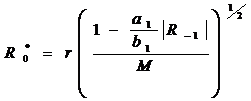
4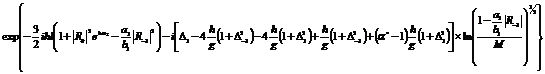
Преобразовывать уравненные не будем, а фазу
положим в нём 
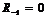 :
:
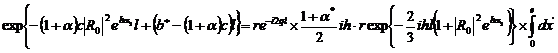
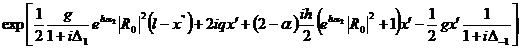 (326)
(326)
Рассмотрим случай, соответствующий статье, 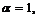
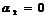 ,
, 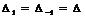 ;
;
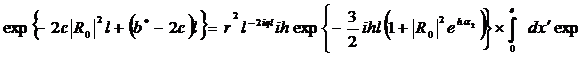
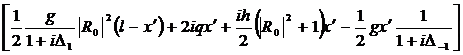 ;(
;(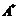 )
(327)
)
(327)
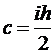 ;
;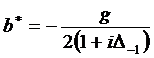
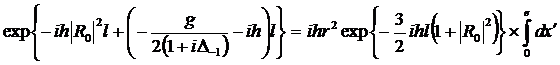
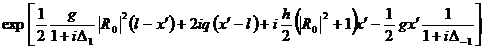 (328)
(328)
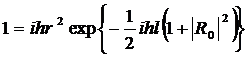
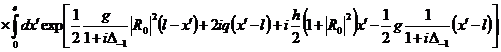 (329)
(329)
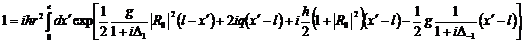 ; (330)
; (330)
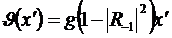 ; (331)
; (331)
но как положено 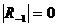 ,
,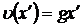 ;
;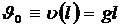 ;,
;,
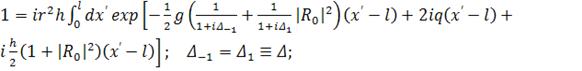 (332)
(332)
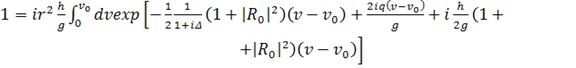 ; (333)
; (333)
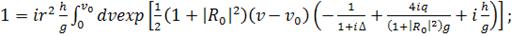 (334)
(334)
Это должно соответствовать уравнению (9) при 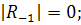 или
или
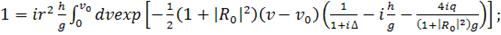 (335)
(335)
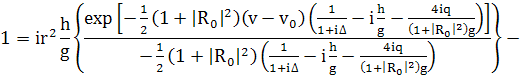
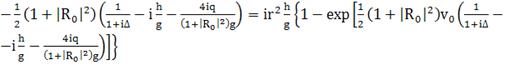 (336)
(336)
Учтем, что 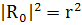 при
при
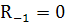
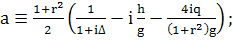 (337)
(337)
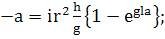 (338)
(338)
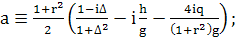 (339)
(339)
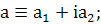 (340)
(340)
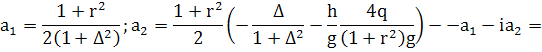
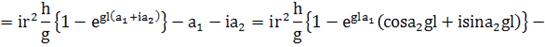
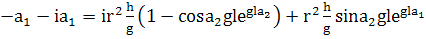 (341)
(341)
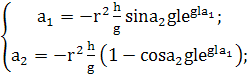 (342)
(342)
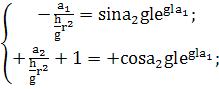 (343)
(343)
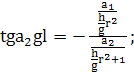 (344)
(344)
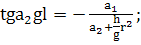 (345)
(345)
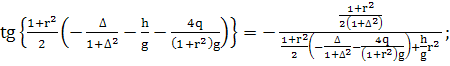 (346)
(346)
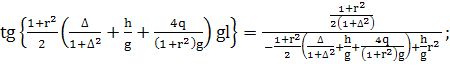 (347)
(347)
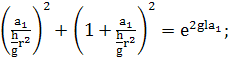 (348)
(348)
Или опять обратимся к исходному уравнению:
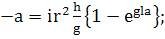 (349)
(349)
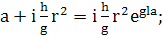 (350)
(350)
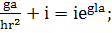 (351)
(351)
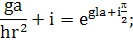
 (352)
(352)
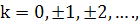 (353)
(353)
Отсюда для границы абсолютной
неустойчивости-генерации ДВРМГ получаем
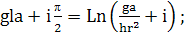 (354)
(354)
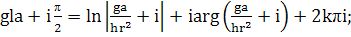 (355)
(355)
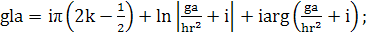 (356)
(356)
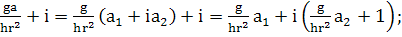 (357)
(357)
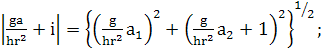 (358)
(358)
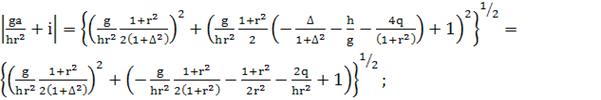 (359)
(359)
Считаем 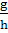 большим, тогда
этими членами можно пренебречь:
большим, тогда
этими членами можно пренебречь:
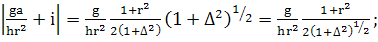 (360)
(360)
Этот же результат получиться сразу, если
отбросить i
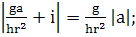 (361)
(361)
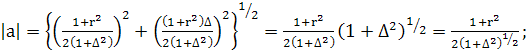 (362)
(362)
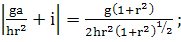 (363)
(363)
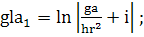 (364)
(364)
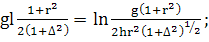 (365)
(365)
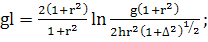 (366)
(366)
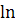 , вероятно, слабо
меняется с
, вероятно, слабо
меняется с 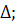 так что
зависимость
так что
зависимость  от
от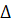 определяется коэффициентом
определяется коэффициентом 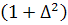 перед
перед 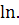 При
При
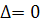 будет
минимальное
будет
минимальное 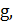 т.е. , порог
абсолютной неустойчивости.
т.е. , порог
абсолютной неустойчивости.
Рассмотрим 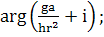
Опять отбросим i
:
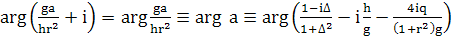 (367)
(367)
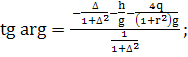 (368)
(368)
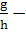 большое; в
резонансных условиях
большое; в
резонансных условиях 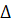 близко к нулю ;
так что
близко к нулю ;
так что
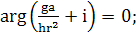 (369)
(369)
Приравниваем теперь мнимые части уравнения:
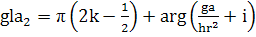 ; (370)
; (370)
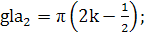 (371)
(371)
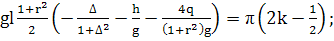 (372)
(372)
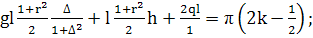 (373)
(373)
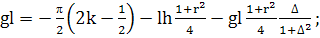 (374)
(374)
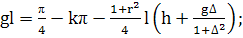 (375)
(375)
Легко проследить, что если а взять как в статье,
т.е.
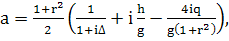 (376)
(376)
Где перед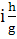 стоит «+», а не минус как у нас, то
стоит «+», а не минус как у нас, то
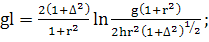 (осталось без
изменении)
(осталось без
изменении)
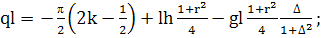 (во втором члене
теперь «+»).
(во втором члене
теперь «+»).
Теперь 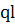 точно
совпадает с (13) статьи. В этих выкладках мы использовали (АА), где в отличие
от (9) в
точно
совпадает с (13) статьи. В этих выкладках мы использовали (АА), где в отличие
от (9) в 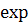 перед
перед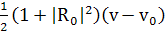 стоит
минус. Полученные результаты подтверждают, что минус должен бить. Для выражения
для а у нас стоит
стоит
минус. Полученные результаты подтверждают, что минус должен бить. Для выражения
для а у нас стоит 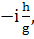 а в статье
а в статье 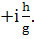 Так
как
Так
как  мало,
различия в результатах будет незначительным; так как второе слагаемое в (СС)
мало по сравнению с третьим; поэтому (СС) мало отличается от нашего (ВВ).
Лучше, последовательнее, было бы совсем выбросить член
мало,
различия в результатах будет незначительным; так как второе слагаемое в (СС)
мало по сравнению с третьим; поэтому (СС) мало отличается от нашего (ВВ).
Лучше, последовательнее, было бы совсем выбросить член 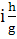 в
а.
в
а.
Имеющиеся существенные отличия наших результатов
от статьи.
У нас: 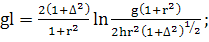 (377)
(377)
В статье: 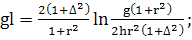 (378)
(378)
Причина пока неясна, м.б., это отпечатка в
статье, причём эта отпечатка перекочёвывает и в выражение (15).
Вернемся к уравнению (А*): пусть 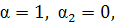 но
но
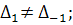
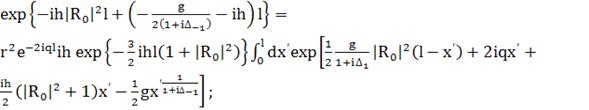 (379)
(379)
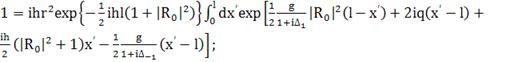 (379)
(379)
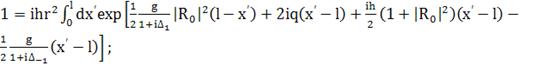 (380)
(380)
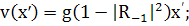 (381)
(381)
Но, так как 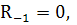 то
то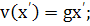 (382)
(382)
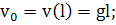 (383)
(383)
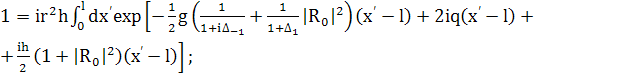 (384)
(384)
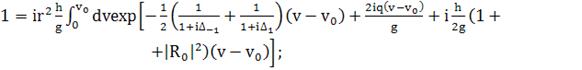 (385)
(385)
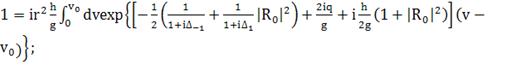 (386)
(386)
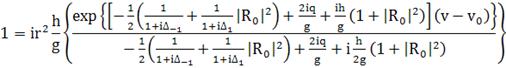 (387)
(387)
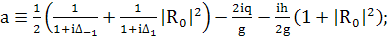 (388)
(388)
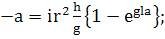 (389)
(389)
Получился такой же вид уравнения, что и при 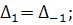
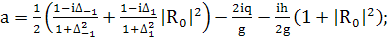 (390)
(390)
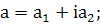 (391)
(391)
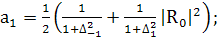 (392)
(392)
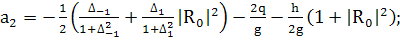 (393)
(393)
 (394)
(394)
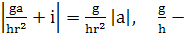 большие
большие
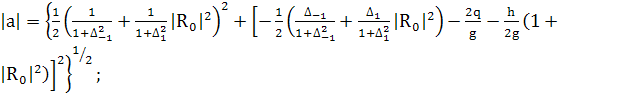 (395)
(395)
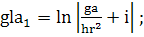 (396)
(396)
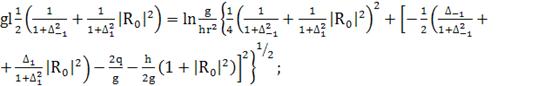 (397)
(397)
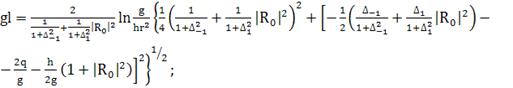 (398)
(398)
В рассматриваемом случае можно также писать 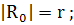
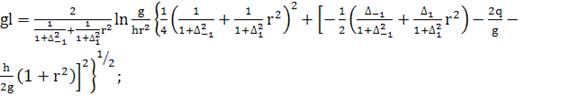 (399)
(399)
Пусть 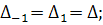
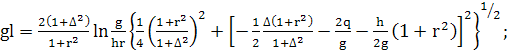 (400)
(400)
Отбросим 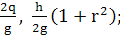 (401)
(401)
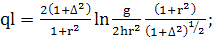 (402)
(402)
Т.е. уже ранее полученное выражения; будем
писать 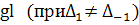 в
виде (после отбрасывания
в
виде (после отбрасывания 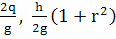 ):
):
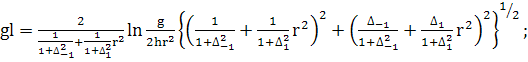 (403)
(403)
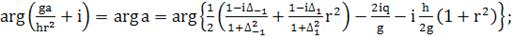 (404)
(404)
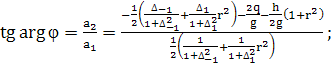 (405)
(405)
По видимому, здесь нельзя положить 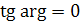 ;
;
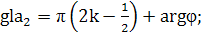 (406)
(406)
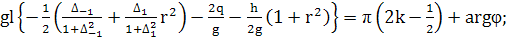 (407)
(407)
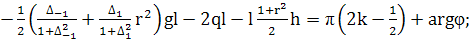 (408)
(408)
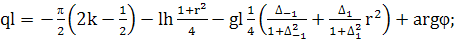 (409)
(409)
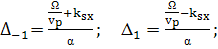 (410)
(410)
Пусть 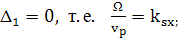 При
этом условии
При
этом условии 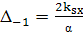 ;
;
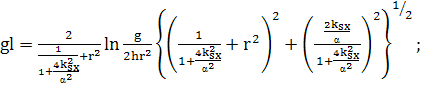 (411)
(411)
Пусть теперь 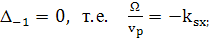 (412)
(412)
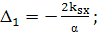 (413)
(413)
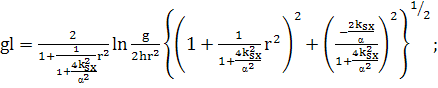 (414)
(414)
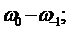 (415)
(415)
Стокс, 
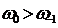 ,
,
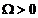
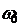 - фиксированной
антистокс,
- фиксированной
антистокс, 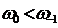 ,
,
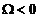
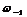 - свободная. Если
- свободная. Если 
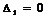 , т.е.
, т.е. 
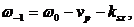 то
то 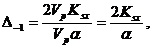 т.е.
т.е.
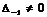 ;
т.е. переход от наших расчетов к стать Заскалько состоит в процедуре
;
т.е. переход от наших расчетов к стать Заскалько состоит в процедуре 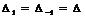 ,
что делать на самом деле нельзя; т.е нельзя полагать
,
что делать на самом деле нельзя; т.е нельзя полагать 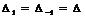 ,а
значит и нельзя перейти к уравнениям Заскалько , и следовательно, эти уравнения
не существует , неверны . Уточним
,а
значит и нельзя перейти к уравнениям Заскалько , и следовательно, эти уравнения
не существует , неверны . Уточним 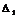 и
и
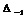 будут
, однако совпадать друг с другом лишь при очень большом
будут
, однако совпадать друг с другом лишь при очень большом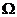 т.е
вдали от резонансов , а это не представляет интереса.
т.е
вдали от резонансов , а это не представляет интереса.
Литература
1. Заскалько О.П., Сердюченко
Ю.Н., Фабелинский И.Л. Письма в ЖЭТФ,1980,31.103
2. Старунов В.С., Фабелинский
И.Л. УФН, 1969,98,441.
. Фабелинский И.Л.
«Молекулярное рассеяние света».
4. Вукс М.Ф. «Рассеяние света в
газах, жидкостях и растворах»
5. Ефимов В.Ф., Зубарев И.Г.,
Котов А.В., Миронов А.Б., Михайлов С.И. «Квантовая Электроника» 1981,
. Физическая акустика. (под.
ред. У.Мэзона) т. 4.
. Зозуля А.А. Силин. В.П.
Тихончук В.Т. письма ЖЭТФ 1983,38,48
. Волькенштейн М.В.
«Молекулярная оптика»
. Вукс М.Ф. «Электрические и
оптические свойства молекул»
. Капустин А.П. «Акустика
жидких кристаллов»
. де Жен П. «Физика жидких
кристаллов»
. Блинов И.П. «Экспериментальные
исследования жидких кристаллов».
13. Вынужденное рассеяние
Мандельштама-Бриллюэна, уфн,1969.98,с. 441
. Рассеяние_Мандельштама
. Л.Д. Лaндау, Е.М. Лифшиц,
Электродинамика сплошных сред
16. Л.Д. Ландау, Е.М. Лившиц,
Механика сплошных сред, 1953.
17. Б.Б Маиов, Р.В. Хохлов,
Проблемы нелинейной оптики, 1964