Механика сплошных сред
Оглавление
Введение.
Задача
№1. Определение напряжений на координатных площадках.
Задача
№2. Графическое изображение компонент тензора напряжений.
Задача
№3. Расчет инвариантов тензора напряжений.
Задача
№4. Определение направляющих косинусов новых осей в старой системе координат.
Задача
№5. Преобразование компонент тензора напряжений к новой системе координат.
Задача
№6. Вычисление нормальных и главных касательных напряжений.
Задача
№7. Построение главного куба напряжений.
Задача
№8. Построение эллипсоида напряжений.
Задача
№9. Вычисление интенсивности напряжений и угла вида напряженного состояния.
Задача
№10. Построение треугольника напряжений.
Задача
№11. Построение звезды напряжений.
Задача
№12. Определение положения главных осей тензора напряжений.
Задача
№13. Построение главных осей тензора напряжений.
Задача
№14. Нахождение острых углов между осями x, y, z и главными осями.
Задача
№15. Проверочные расчеты.
Задача
№16. Построение диаграмм Мора. Графическое решение задач.
Список
использованных источников:
Введение
Механика
сплошных сред - раздел механики
<#"867641.files/image001.gif"> (1)
Эта матрица симметрична, т.е. σij=σji, или подробно: σху= σух, σyz= σzу, σzx= σxz. Напряжения 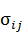 действуют на координатных площадках x, y, z.(рис.1)
действуют на координатных площадках x, y, z.(рис.1)
Касательные напряжения τx, τy, τz, действующие на координатных площадках, находим как
геометрические суммы напряжений σij с различными индексами i и j:
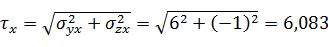
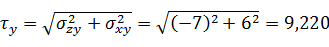 (2)
(2)
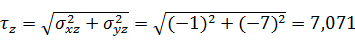
Задача №2.
Графическое изображение компонент тензора напряжений
напряжение координатный диаграмма ось
Показать на рисунке напряжения, действующие на координатных площадках x, y, z, с учетом их
знака и величины.
Выбираем элементарный объем в виде прямоугольного параллелепипеда
(рис.1). его ребра параллельны осям координат x, y, z.
Напряжения показываем по трем видимым граням параллелепипеда. Внешние
нормали к этим граням направлены в положительных направлениях координатных
осей. Поэтому положительные напряжения также направляем в положительных
направлениях координатных осей. Отрицательные напряжения направляем в
отрицательных направлениях координатных осей.
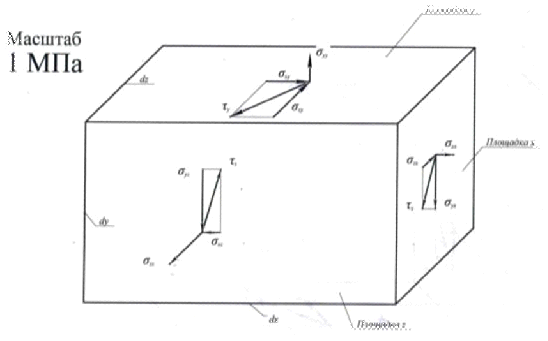
Рис.1. Напряжения, действующие координатных площадках x,y,z.
Задача №3.
Расчет инвариантов тензора напряжений
Вычислить инварианты тензора напряжений:
Первый, или линейный инвариант, равен следу матрицы тензора напряжений,
т.е. сумме компонент, расположенных на главной диагонали:
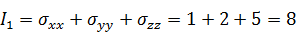 (3)
(3)
Второй или квадратичный инвариант равен сумме миноров определителя
матрицы тензора напряжений det(σij)=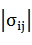 при разложении его по главной
диагонали:
при разложении его по главной
диагонали:
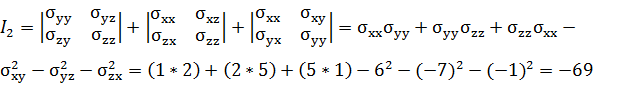 (4)
(4)
Третий, или кубический, инвариант равен определителю матрицы тензора
напряжений det(σij)=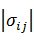 , или подробно:
, или подробно:
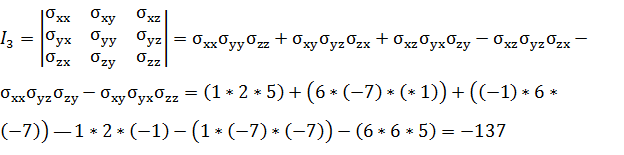 (5)
(5)
Задача №4.
Определение направляющих косинусов новых осей в старой системе координат
Задать три угла Эйлера и вычислить направляющие косинусы новых осей в
старой системе координат.
Старые оси обозначены x, y, z. Новые оси обозначим x’, y’, z’. Положение новых осей, относительно старых, однозначно
определяется тремя углами Эйлера θ, ψ, φ (рис 2).
Угол нутации θ - угол между положительными направлениями осей Oz’ и Oz (π>θ≥0).
Угол прецессии ψ - угол, между осью Ох и линией пересечения ОА
плоскостей хОу и х’Oy’. На линии ОА положительное направление
выбрано так, что ОА, Oz и Oz’ образуют правую тройку векторов. Угол ψ отсчитывается в направлении от оси
Ох к оси Оу (2π>ψ≥0).
Угол чистого вращения φ - угол между Ох’ и Оа.
Угол φ отсчитывается в направлении от Ox’ к Oy’ (2π>φ≥0).
Обозначим:
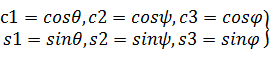 (6)
(6)
Обозначим далее направляющие косинусы новых осей в старой системе
координат так:
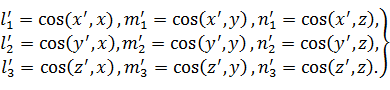 (7)
(7)
Тогда эти направляющие косинусы равны:
 (8)
(8)
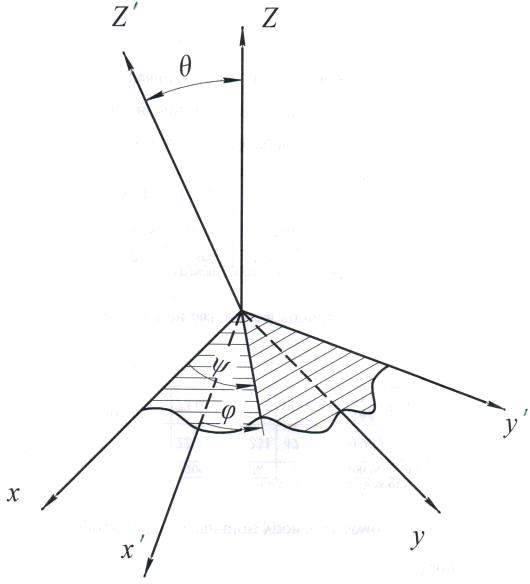
Рис.2. Взаимное расположение старых x, y, z, и новых x’, y’, z’ осей координат. Углы Эйлера.
Задача №5.
Преобразование компонент тензора напряжений к новой системе координат
Найти компоненты тензора напряжений в новой системе координат. Убедится в
правильности расчетов, высчитав инварианты тензора напряжений через его
компоненты в новой системе координат.
Компоненты тензора в старой системе координат x, y, z обозначены σij(σ11=σxx, σ12=σху и так далее).
Компоненты тензора напряжений в новой системе координат x’, y’, z’ обозначим 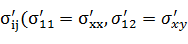 и так далее). Они выражаются через компоненты тензора
напряжений в старой системе координат так:
и так далее). Они выражаются через компоненты тензора
напряжений в старой системе координат так:
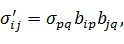 (9)
(9)
Где по индексам p и q производится суммирование от 1 до 3.
В подробной записи имеем девять формул, так как свободных индексов два - i и j.
Элементы матрицы преобразования B=(bij) равны частным производным новых
координат по старым:
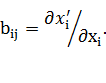 (10)
(10)
При жестком повороте осей координат новые координаты выражаются через
старые так:
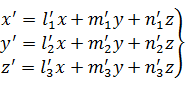 (11)
(11)
Тогда элементы матрицы преобразования В равны:
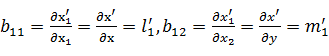 и так далее.
и так далее.
Итак, элементы матрицы преобразования В равны направляющим косинусам
новых осей x’, y’, z’ относительно старых осей x, y, z:
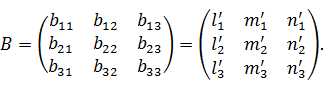 (12)
(12)
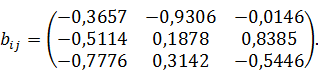
Тогда, например, по формуле (9) найдем:
 (13)
(13)
Формулу (9) можно записать в матричной, безиндексной форме:
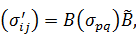 (14)
(14)
Где 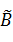 - транспонированная матрица. Матрицу
- транспонированная матрица. Матрицу 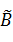 получим поменяв местами строки и
столбцы в матрице В.
получим поменяв местами строки и
столбцы в матрице В.
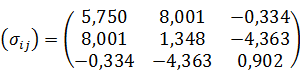
Инварианты тензора напряжений  через его компоненты в новой системе
координат вычислим по формулам (3) - (5) заменив в них σij на σ’ij.
через его компоненты в новой системе
координат вычислим по формулам (3) - (5) заменив в них σij на σ’ij.

Вычисления по формулам (9) верны, так как 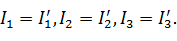
Задача №6.
Вычисление нормальных и главных касательных напряжений
Вычислить главные нормальные и главные касательные напряжения. Убедиться
в правильности расчетов, вычислив инварианты тензора напряжений через главные
нормальные напряжения.
Напряжения, действующие на три взаимно перпендикулярные главные площадки,
перпендикулярные главным осям тензора напряжений, называют главными нормальными
напряжениями.
Главные нормальные напряжения 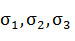 найдем, решив кубическое уравнение:
найдем, решив кубическое уравнение:
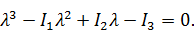 (15)
(15)
Кубическое уравнение решим методом тригонометрических подстановок.
Вначале приведем его к каноническому виду, когда коэффициент при квадрате
неизвестного равен нулю. С этой целью заменим:
λ=t+I1/3, (16)
где t - новая переменная.
Получим
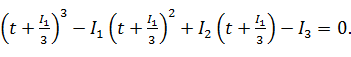 (17)
(17)
Раскроем скобки и сформируем коэффициенты при t3(он равен единице), при t (обозначим его 3р), а так же свободный член (обозначим его 2q). Итак, получим кубическое
уравнение:
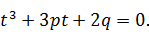 (18)
(18)
p=-30,1111
q=-42,4630
Вычислим 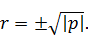 Знак r
должен совпадать со знаком q
Знак r
должен совпадать со знаком q
r=165,2305
cosφ=q/r3 . (19)
φ=1,3109
Тогда корни кубического уравнения равны:
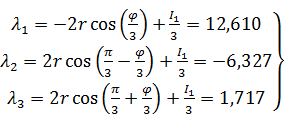 (20)
(20)
Так как 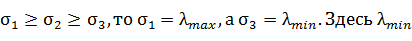 - минимальный, а
- минимальный, а 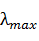 - максимальный корни кубического
уравнения.
- максимальный корни кубического
уравнения.
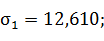
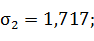
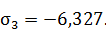
Главные касательные напряжения равны полуразностям главных нормальных
напряжений, и действуют на площадках, параллельных главным осям и
равнонаклоненых к ним:
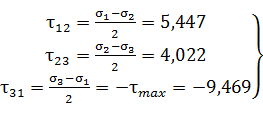 (21)
(21)
где 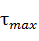 - максимальное главное касательное напряжение.
- максимальное главное касательное напряжение.
Инварианты тензора напряжений через главные нормальные напряжения
вычислим по формулам:
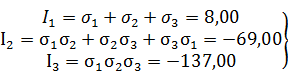 (22)
(22)
Эти инварианты совпадают с инвариантами, найденными в задаче №3 по
формулам (3)-(5), главные нормальные напряжения вычислены правильно.
Задача №7.
Построение главного куба напряжений
Записать матрицу тензора напряжений в главных осях. Показать на рисунке
главные нормальные напряжения с учетом их знака и величины по граням главного
куба вокруг рассматриваемой точки.
Матрица тензора напряжений в главных осях имеет диагональный вид:
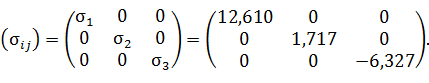 (23)
(23)
Вокруг рассматриваемой точки деформируемого тела выбираем элементарный
объем в виде куба, ребра которого параллельны главным осям тензора напряжений η1, η2, η3. Это главный куб (рис 3). На его гранях и показываем
главные нормальные напряжения. Положительные напряжения σ1, σ2 являются растягивающими, а отрицательные σ3 - сжимающими.
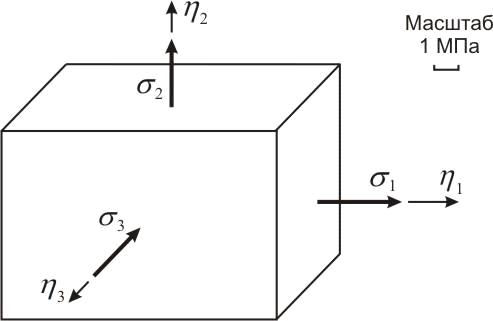
Рис. 3. Главный куб и главные нормальные напряжения.
Задача №8.
Построение эллипсоида напряжений
Построить эллипсоид напряжений.
Эллипсоид напряжений - это объемный геометрический образ напряженного
состояния (рис.4). Если провести через рассматриваемую точку М деформируемого
тела площадку с нормалью  , то конец вектора полного сопряжения
, то конец вектора полного сопряжения  , действующего на этой площадке,
находится на поверхности эллипсоида.
, действующего на этой площадке,
находится на поверхности эллипсоида.
Выбираем одну из пяти аксонометрических проекций:
) Прямоугольную изометрическую проекцию,
) Прямоугольную диметрическую проекцию,
) Косоугольную фронтальную изометрическую проекцию,
) Косоугольную горизонтальную изометрическую проекцию,
) Косоугольную фронтальную диметрическую проекцию.
Выбираем такую проекцию, чтобы плоское изображение эллипсоида было
наиболее наглядным.
Рассмотрим последовательность построения эллипсоида. Через точку М
проводим три главные оси тензора напряжений  . Они взаимно перпендикулярны, но
углы между ними на рисунке зависят от выбора аксонометрической проекции.
. Они взаимно перпендикулярны, но
углы между ними на рисунке зависят от выбора аксонометрической проекции.
На осях  по обе стороны от начала координат (точки М) в выбранном
масштабе и с учетом коэффициентов искажения по осям откладываем отрезки,
соответственно равные
по обе стороны от начала координат (точки М) в выбранном
масштабе и с учетом коэффициентов искажения по осям откладываем отрезки,
соответственно равные  . Получаем три сопряженных диаметра эллипсоида AB, CD, EF.
. Получаем три сопряженных диаметра эллипсоида AB, CD, EF.
Строим три эллипса, которые являются линиями пересечения поверхности
эллипсоида с координатными плоскостями. В координатной плоскости 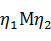 эллипс строим по двум сопряженным
диаметрам AB и CD. В координатной плоскости
эллипс строим по двум сопряженным
диаметрам AB и CD. В координатной плоскости 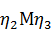 эллипс строим по двум сопряженным
диаметрам CD и EF. В координатной плоскости
эллипс строим по двум сопряженным
диаметрам CD и EF. В координатной плоскости 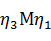 эллипс строим по сопряженным
диаметрам EF и АВ.
эллипс строим по сопряженным
диаметрам EF и АВ.
Проводим четвертый эллипс, огибающий три уже построенные эллипса в
координатных плоскостях. Он и является аксонометрической проекцией эллипсоида.
В заключении выделяем видимые и невидимые линии эллипсов, расположенных в
координатных плоскостях.
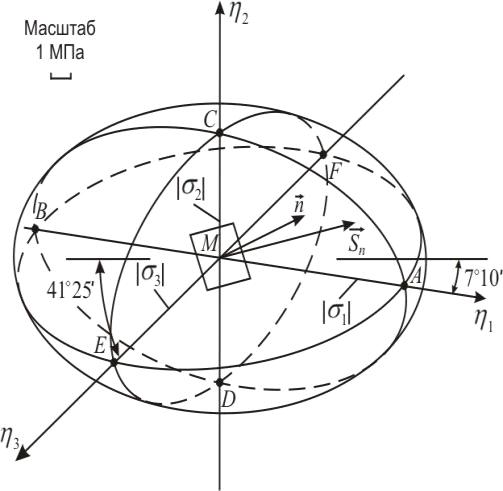
Рисунок 4. Эллипсоид напряжений(прямоугольная диметрическая проекция)
Задача №9.
Вычисление интенсивности напряжений и угла вида напряженного состояния
Вычислить интенсивность напряжений, интенсивность касательных напряжений
и угол вида напряженного состояния.
Интенсивность напряжений равна:
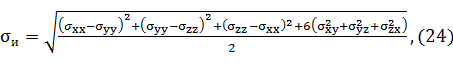
где индекс «и» означает «интенсивность».
Для контроля вычисляем  также и через главные нормальные напряжения:
также и через главные нормальные напряжения:
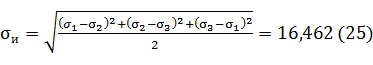
Интенсивность касательных напряжений Т (тау) равна
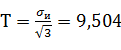 (26)
(26)
Угол вида напряженного состояния 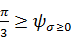 равен:
равен:
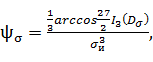 (27)
(27)
Где третий инвариант девиатора напряжений 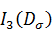 находим по формуле:
находим по формуле:
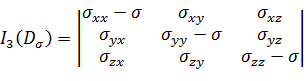 (28)
(28)
В формуле (28) среднее напряжение, или гидростатическое давление равно:
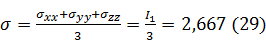
Для контроля вычисляем ψσ также и через главные нормальные
напряжения:
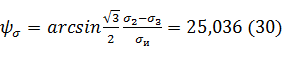
Задача №10.
Построение треугольника напряжений
Построить треугольник напряжений. Графически найти интенсивность
напряжений и угол вида напряженного состояния. Сравнить с результатами расчетов
в задаче №9.
Выбрав масштаб, строим равносторонний треугольник АВС, стороны которого
равны (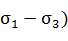 (рис 5). Сторону АВ делим на 2 части
точкой D: AD=(
(рис 5). Сторону АВ делим на 2 части
точкой D: AD=(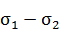 ) и DB=
) и DB=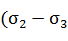 ). Точку D соединяем прямой линией с противоположной вершиной
треугольника С. Тогда длина отрезка прямой CD в выбранном масштабе равна интенсивности напряжений σи.
). Точку D соединяем прямой линией с противоположной вершиной
треугольника С. Тогда длина отрезка прямой CD в выбранном масштабе равна интенсивности напряжений σи.
Угол BCD равен углу вида напряженного
состояния ψσ. Применяя теорему синусов к
треугольнику BCD, получим формулу (30):
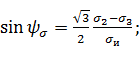
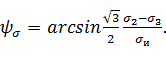
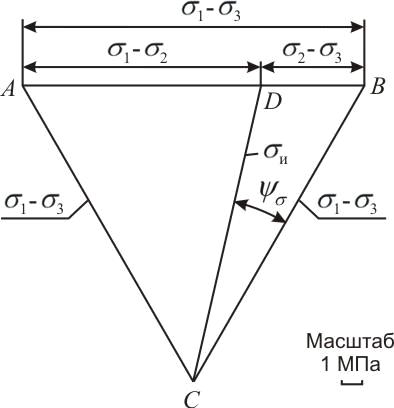
Рисунок 5. Треугольник напряжений.
Задача №11.
Построение звезды напряжений
Построить звезду напряжений. Графически найти главные нормальные и
главные касательные напряжения. Сравнить с результатами расчета главных
напряжений в задаче №6.
Звезду напряжений строим в координатах σn (нормальные напряжения), τn (касательные напряжения) (рис. 6).
Центр звезды - точка М находится на оси Оσn. Координата центра звезды численно
равна среднему напряжению σ (см. формулу 29). С центром в точке
М проводим две окружности. Радиус большей окружности равен 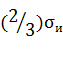 . Радиус меньшей окружности равен
интенсивности касательных напряжений Т (см. формулу 26).
. Радиус меньшей окружности равен
интенсивности касательных напряжений Т (см. формулу 26).
Из точки М проводим три луча, которые собственно образуют звезду. Углы
между лучами равны по 120о. угол между первым лучом МА и осью Оσn равен углу вида напряженного
состояния ψσ.
С учетом выбранного масштаба абсциссы точек пересечения лучей с большой
окружностью равны главным нормальным напряжениям σ1, σ2, σ3. Ординаты точек пересечения лучей с малой окружностью
равны главным касательным напряжениям τ12,
τ23,
τ31.
σ1=12,610, σ2=1,717, σ3=-6,327
τ12=5,447, τ23=4,022, τ31=-9,469
Полученные данные согласуются с результатами расчетов в задаче №6.
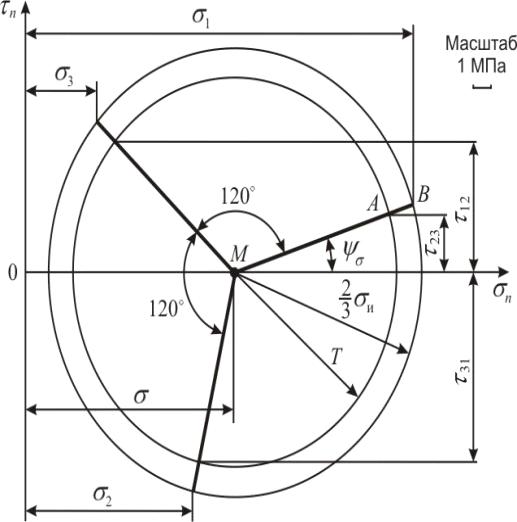
Рисунок 6. Звезда напряжений.
Задача №12.
Определение положения главных осей тензора напряжений
Найти направляющие косинусы главных осей тензора напряжений в старой
системе координат. Найти углы между главными осями и осями x,y,z.
Направляющие косинусы главных осей тензора напряжений η1, η2, η3 в старой системе координат x, y, z обозначим так:
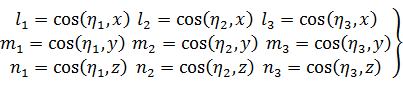 (31)
(31)
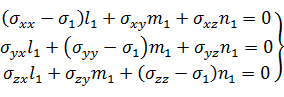 (32)
(32)
При условии:
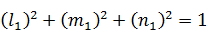 (33)
(33)
Из первых двух уравнений (32) выражаем l1 и m1 через n1 например по формулам Крамера:
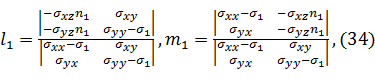
Полученные выражения l1 и m1 через n1 подставляем в уравнение (33).
Получаем квадратное уравнение относительно n1. Решая его, находим n1. При этом принимаем 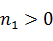 . Затем находим l1 и m1. Случай, если принять
. Затем находим l1 и m1. Случай, если принять 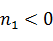 рассмотрен в задаче №13.
рассмотрен в задаче №13.
Аналогично находим направляющие косинусы l2 ,m2, n2 главной оси η2.
Направляющие косинусы l3, m3, n3 главной оси η3 находим из условия, что направляющий вектор 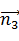 главной оси η3 есть векторное произведение направляющих векторов
главной оси η3 есть векторное произведение направляющих векторов 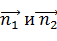 главных осей η1 и η2, т.е.:
главных осей η1 и η2, т.е.:
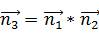 , (35)
, (35)
Так как главные оси η1, η2, η3 образуют правую прямоугольную декартову систему
координат. Запишем формулу (35) через направляющие косинусы главных осей:
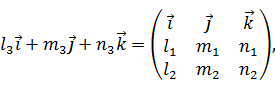 (36)
(36)
откуда найдем:
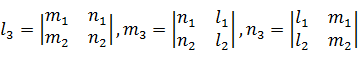 . (37)
. (37)
Результаты расчета направляющих косинусов (31) записываем в столбец 1
таблицы 2
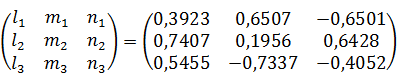
Угол между главными осями η1, η2, η3 и осями x,y,z обозначим и вычислим так:
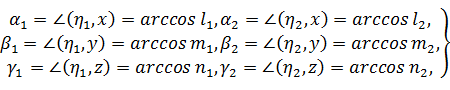
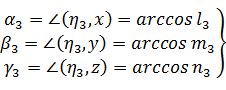 (38)
(38)
При этом нужно иметь в виду, что arccos(-x)=π-arccos x. Найденные значения углов между главными осями и осями x, y, z записываем в столбец
2 таблицы 2.
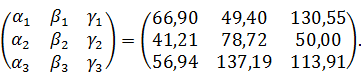
Задача №13.
Построение главных осей тензора напряжений
Показать на рисунке взаимное расположение главных осей 𝜂1, 𝜂2, 𝜂3 и осей x, y, z.
Выбираем аксонометрическую проекцию и проводим оси x, y, z (рис 7).
Выбираем масштаб. Главную ось η1 проводим через точку М(0,0,0) и через точку А с
координатами (l1, m1, n1). Главную ось η2 проводим через точку М и через точку с координатами (l2, m2, n2). Главную ось η3 проводим через точку М и через точку с координатами (l3, m3, n3)
Замечания:
Если при решении задачи 12 принять n1<0 и n2<0, то ось η3 сохранит прежнее направление. Действительно, если в
формулах (37) поменять знаки всех величин, стоящих в определителях, получи и те
же значения направляющих косинусов l3, m3, n3.
Если принять n1>0, a n2<0, то ось η1 сохранит свое направление, а оси η2 и η3 изменят свои направления на противоположные.
Если принять n1<0, a n2>0, то ось η2 сохранит свое направление, а оси η1 и η3 изменят свое направление на противоположные.
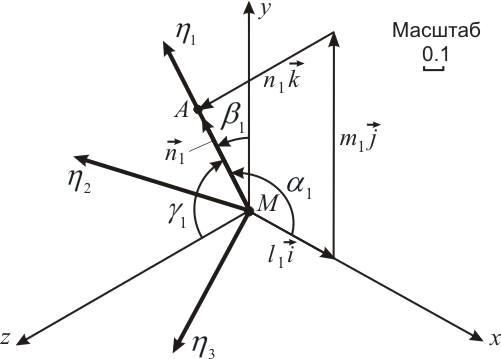
Рисунок 7. Взаимное расположение главных осей η1, η2, η3 и осей x, y, z.
Задача №14.
Нахождение острых углов между осями x, y, z и главными осями
Вычислить направляющие косинусы осей x, y, z в главной системе координат. Найти
острые углы между осями x, y, z и главными осями 𝜂1, 𝜂2, 𝜂3.
Обозначим направляющие косинусы осей x, y, z в главной системе координат так:
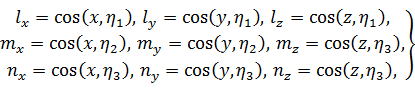 (39)
(39)
Направляющие косинусы оси х в главной системе координат, т. е. lx, mx, nx, найдем по формулам:
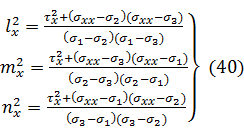
Обратим внимание на то, что формулы (40) получаются одна из другой
круговой заменой индексов 1, 2, 3. Извлекая квадратные корни, берем
положительные значения lx, mx, nx.
Направляющие косинусы оси у в главной системе координат, т.е. ly, my, ny, найдем по тем же формулам (40),
заменив в них все индексы х на у.
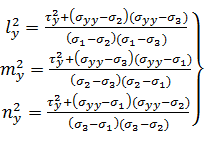
Направляющие косинусы оси z в
главной системе координат, т.е. lz, mz, nz, найдем по тем же формулам (40),
заменив в них все индексы х на z.
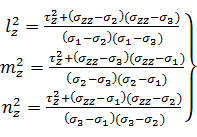
Вычисленные направляющие косинусы (39) записываем в столбец 3 таблицы 2.
Если вычисления сделаны правильно, то с точностью до знака они совпадают с
направляющими косинусами в столбце 1.
Острые углы между осями x, y, z и главными осями η1, η2, η3 обозначим и вычислит так:
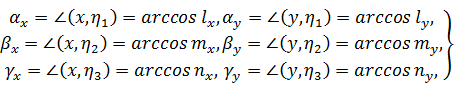
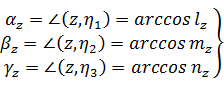 (41)
(41)

Значения этих углов записываем в столбец 4 таблицы 2. Если вычисления
сделаны правильно, то эти углы:
Совпадают с углами в столбце 2, если углы в столбце 2 меньше 90о,
т.е. также являются острыми;
Являются дополнениями углов в столбце 2 до 180о, если углы в
столбце 2 больше 90о, т.е. являются тупыми.
Задача №15. Проверочные расчеты
Проверить правильность вычислений главных нормальных напряжений 𝜎1, 𝜎2, 𝜎3 в задаче №6 и направляющих косинусов в задаче №14. С
этой целью, рассматривая площадки x, y, z как наклонные по отношению к главным осям 𝜂1, 𝜂2, 𝜂3, найти нормальные 𝜎хх, 𝜎уу, 𝜎zz и касательные 𝜏х, 𝜏y, 𝜏z напряжения на этих площадках.
Нормальные напряжения на координатных площадках x, y, z соответственно равны:
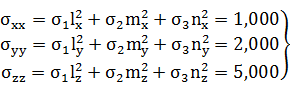 (42)
(42)
Сравним рассчитанные по этим формулам нормальные напряжения с заданными в
таблице 1. Они совпадают, значит решение выполнено правильно.
Касательные напряжения на координатных площадках x, y, z соответственно равны:
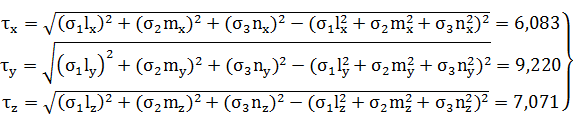 (43)
(43)
Сравниваем рассчитанные по этим формулам касательные напряжения со
значениями τx, τy, τz, полученными по формулам (2) в задаче №1. Они должны
совпасть.
Задача №16.
Построение диаграмм Мора. Графическое решение задач
С помощью диаграмм Мора графически проверить правильность вычисления в
задаче №14 углов между осями x, y, z и главными осями 𝜂1, 𝜂2, 𝜂3.
Вначале найдем графически острые углы αх, βх, γх между осью х и главными осями η1, η2, η3, см. формулы (41).
Имея главные нормальные напряжения σ1, σ2, σ3 и выбрав масштаб, строим диаграмму Мора для
напряжений (рис.8). Отмечаем на ней точку Ах, соответствующую
площадке х, по ее координатам: на площадке х нормальное напряжение равно σn=σxx, а касательное напряжение равно τn=τx.
Чрез точку Ах проводим три дуги окружностей α=const, β=const, γ=const с центрами соответственно в точках О1, О2,
О3, являющимися центрами главных кругов Мора I, II, III. Точки
пересечения этих окружностей с главными окружностями I, II, III соединяем с радиусами с центрами О1,
О2, О3.
Около центров О1, О2, О3 измеряем углы 2αх, 2βх, 2γх по или против часовой стрелки как показано на рис 8.
Найденные с помощью диаграммы Мора углы αх, βх, γх записываем в столбец 5 таблицы 2. С точностью до 30’
они должны совпасть с одноименными углами, найденными расчетом в задаче №14(см.
столбец 4 таблицы 2)
Острые углы αу, βу, γу между осью у и главными осями η1, η2, η3 найдем, построив второй раз диаграмму
Мора и отметив на ней точку Ау, соответствующую площадке у, по ее
координатам σn=σyy, τn=τy.
Острые углы αz, βz, γz между осью z и главными осями η1, η2, η3 найдем, построив третий раз диаграмму
Мора и отметив на ней точку Аz, соответствующую площадке z, по ее координатам σn=σzz, τn=τz.
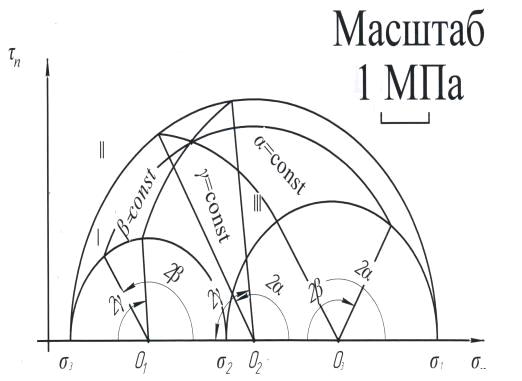
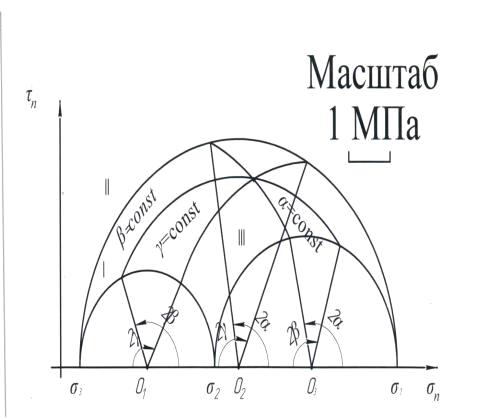
Рисунок 8. Диаграммы Мора
Таблица 2
|
Направляющие косинусы главных осей η1
η2
η3 относительно осей x, y, z
|
Углы между главными осями η1
η2
η3 и осями x, y, z
|
Направляющие косинусы осей x, y, z относительно главных осей η1
η2
η3
|
Острые углы между осями x, y, z и главными осями η1
η2
η3, полученные
|
|
|
|
расчетом
|
|
1
|
2
|
3
|
4
|
5
|
|
l1=0,3923
|
α1=66,90
|
lx=0,3923
|
αx=66,90
|
αx=66,74
|
|
m1=0.6507
|
β1=49,40
|
ly=0,6507
|
αy=49,40
|
αy=49,47
|
|
n1=-0,6501
|
γ1=130,55
|
lz=0,6501
|
αz=49,45
|
αz=49,29
|
|
l2=0,7407
|
α2=41,21
|
mx=0,7407
|
βx=42,21
|
βx=42,14
|
|
m2=0,1956
|
β2=78,72
|
my=0,1956
|
βy=78,72
|
βy=78,92
|
|
n2=0,6428
|
γ2=50,00
|
mz=0,6428
|
βz=50,00
|
βz=50,12
|
|
l3=0,5455
|
α3=56,94
|
nx=0,5455
|
γx=56,94
|
γx=56,41
|
|
m3=-0,7337
|
β3=137,19
|
ny=0,7337
|
γy=42,81
|
γy=42,67
|
|
n3-0,4052
|
γ3=119,91
|
nz=0,4052
|
γz=66,09
|
γz=66,19
|
|
|
|
|
|
|
Список
использованных источников
1. Дорогобид
В.Г., Пивоварова К.Г. Механика сплошной среды: учебное пособие - Магнитогорск:
ГОУ ВПО «МГТУ», 2006. - 256 с.
. Дорогобид
В.Г., Москвин В.М. Исследование напряженного состояния: методическое пособие -
Магнитогорск: МГТУ, 2003. 38 с.
. Зубчанинов
В. Г. Основы теории упругости и пластичности: Учебник для вузов - М.: Высш.
шк., 1990.
. Колмогоров
В.Л. Механика обработки металлов давлением: Учебник для вузов. - М.: Металлургия,
1986. - 456 с.
. Аркулис
Г.Э., Дорогобид В.Г. Теория пластичности: Учебное пособие для вузов. М.:
Металлургия, 1987. - 352с.