Цифровые частотные фильтры

Контрольная работа

Цифровые частотные фильтры

Содержание

1. Цифровая система обработки сигналов

2. Расчёт нерекурсивных ЦФ общего вида

3. Схемы и характеристики фильтров с линейной фазой

4. Общие свойства фильтров с линейной фазой

5. ЦФ с линейной фазой. Метод взвешивания

6. Метод частотной выборки

7. Расчет рекурсивных фильтров. Метод билинейного преобразования

Литература

1. Цифровая система обработки сигналов

Процесс обработки дискретных сигналов можно представить в следующей последовательности. Каждому отсчёту ставится в соответствие двоичное кодовое слово, а действия над отсчётами заменяются на действия над кодовыми словами. Дискретная цепь становится цифровой цепью, цифровым фильтром (ЦФ). Перевод отсчётов в двоичные кодовые слова происходит в аналогово-цифровом преобразователе (АЦП). На выходе ЦФ (рис.1) осуществляется обратная операция: кодовые слова в цифро-аналоговом преобразователе превращаются в отсчёты дискретного сигнала и, наконец, на выходе, синтезирующего фильтра (СФ) формируется обработанный аналоговый сигнал.

Рис. 1

Дискретная и цифровая цепи описываются одинаковыми уравнениями. Отличие состоит в приближённом характере представления отсчётов сигнала кодовыми словами конечной размерности (ошибки квантования). Поэтому сигнал на выходе цифровой цепи отличается от идеального варианта на величину погрешности квантования.

Цифровая техника позволяет получить высокое качество обработки сигналов, несмотря на ошибки квантования. Ошибки (шумы) квантования нормируются путем увеличения разрядности кодовых слов. Рациональные способы конструирования цифровой цепи также способствуют минимизации уровня шумов квантования.

цифровой частотный фильтр билинейный

Расчёт цифровой цепи по заданным требованиям к её характеристикам имеет ряд принципиальных особенностей в зависимости от наличия обратной связи.

Нерекурсивные фильтры содержат большое число элементов цепи, но вместе с тем имеют целый ряд важных достоинств: нерекурсивные ЦФ всегда устойчивы, позволяют строить фильтры с минимальной линейной фазой, отличаются простой настройкой. Методы расчёта нерекурсивных ЦФ и рекурсивных цифровых фильтров принято рассматривать отдельно.

2. Расчёт нерекурсивных ЦФ общего вида

Цель расчёта нерекурсивных цифровых фильтров (рис.2, а) заключается в расчёте значений коэффицентов  и их числа N по допускам на системные характеристики, а так же в расчёте разрядности кодовых слов и выборе оптимального динамического диапазона ЦФ по нормам на помехозащищённость сигнала и вероятность перегрузки системы, что определяется эффектами конечной разрядности кодовых слов.

Требования к системным характеристикам чаще задаются относительно одной из них: импульсной или частотной. Поэтому различают расчёт ЦФ во временной области и расчёт ЦФ в частотной области.

Расчёт ЦФ во временной области

Требуемая импульсная характеристика в общем случае имеет бесконечную протяжённость во времени. Поэтому вначале необходимо задаться конечным числом N первых отсчётов требуемой импульсной характеристики

.

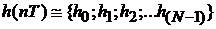Оставшиеся отсчёты по причине их малости отбрасывают и определяют погрешность приближения, которую можно оценить, например, по среднеквадратичному критерию близости.

Коэффициенты фильтра  принимаются равными соответствующим отсчётам требуемой импульсной характеристики. После расчёта разрядности коэффицентов, шумов квантования и масштабирующих коэффицентов остаётся оценить погрешность реализованной импульсной характеристики по отношению к требуемой и принять решение о необходимости повторного расчёта.

Расчёт ЦФ в частотной области

Вначале необходимо продолжить требуемую частотную характеристику на диапазон [0,5ww_д; ww_д] по правилам комплексно-сопряжённой симметрии (рис.2, б), что определяется вещественным характером импульсного отклика. По характеристикам следует определить N комплексных частотных отсчётов

,

где число N выбирается ориентировочно с таким расчётом, чтобы плавным соединением точек  и  требуемые кривые восстановились без заметных искажений.

Рис. 2

Расчёт коэффициентов фильтра выполняется по формуле обратного ДПФ

 (1)

Затем необходимо рассчитать реализованные частотные характеристики по формулам, которые следуют из выражения для передаточной функции фильтра.

, или . (2)

Остаётся сравнить требуемые и реализованные характеристики и принять решение о необходимости повторного расчёта.

Расчёты по учёту эффектов конечной разности кодовых слов остаются прежними.

3. Схемы и характеристики фильтров с линейной фазой

Нерекурсивный фильтр позволяет получить четную или нечетную импульсную характеристику и, как результат, линейную ФЧХ при произвольной АЧХ.

Фильтры с четными импульсными характеристиками называются симметричными, с нечетными - антисимметричными. Каждый из отмеченных типов фильтров имеет свои особенности в зависимости от четности числа отводов N, что удобно рассмотреть на конкретных примерах.

Симметричные фильтры с нечетным N

На рис. 3, а приведена схема и импульсная характеристика симметричного фильтра для случая N = 5. Передаточная функция такой цепи:

H (z) = a₂ + a₁ z - ¹ + a₀ z - ² + a₁ z - ³ + a₂ z - ⁴ = z - ² [a₀ + a₁ (z + z - ¹) + a₂ (z² + z - ²)]

Отсюда, после подстановки z = e ^jwwT и с учетом формулы Эйлера

H (jww) = e - ^{j2wwT (}a₀ + 2a₁ cos wwT + 2a₂ cos 2wwT)

следовательно, формулы АЧХ и ФЧХ

H (w) = a₀ + 2a₁ cos wT + 2a₂cos 2wT, j (w) = - 2wT

График АЧХ и графики поясняющие характер АЧХ - cos wwT, cos 2wwT - приведены на рис.4, а.

Симметричные фильтры с четным N

На рис. 3, б приведены схема и импульсная характеристика симметричного фильтра для случая N=4.

Передаточная функция фильтра

H (z) = a₂ + a₁ z - ¹ + a₁ z - ² + a₂ z - ³ = z - ^1,5 [a₁ (z^0,5 + z^-0,5) + a₂ (z^1,5 + z - ^1,5)]

Отсюда

H (jww) = e - ^{j 1,5 ww T (}2a₁ cos (0,5 wwT) + 2a₂ cos (1,5wwT))

Соответствующие формулы АЧХ и ФЧХ

H (w) = 2a₁ cos 0,5 wT + 2a₂ cos 1,5wT, j (w) = - 1,5wT

Характер АЧХ и поясняющие графики - на рис. 4, б.

Антисимметричные фильтры с нечетным N

На рис. 5а приведены схема и импульсная характеристика антисимметричного фильтра для случая N = 5.

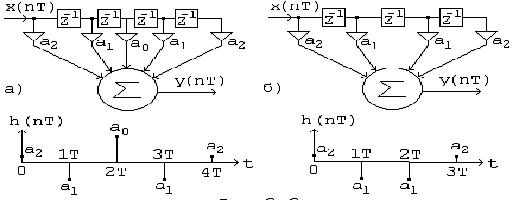
Рис. 3

Рис. 4

Передаточная функция фильтра

H (z) = a₂ + a₁ z - ¹ + 0 z - ² - a₁ z - ³ - a₂ z - ⁴ = z - ² [a₁ (z - z - ¹) + a₂ (z ² - z - ²)]

отсюда

H (jww) = e - ^{j2 ww T} j (2a₁ sin wwT + 2a₂ sin2wwT)

Поэтому формулы АЧХ и ФЧХ

H (ww) = 2a₁ sin wwT + 2a₂ sin 2wwT, jj (ww) = -2wwT

Антисимметричные фильтры с четным N

Схема и импульсная характеристика для случая N = 4 приведены на рис.5, б. Передаточная функция

H (z) = a₂ + a₁ z - ¹ - a₁ z - ² - a₂ z - ³ = z - ^1,5 [a₁ (z ^0,5 - z^0,5) + a₂ (z^1,5 - z^-1,5)]

Отсюда

H (jww) = e - ^{j1,5 ww T} j (2a₁ sin 0,5 wwT + 2a₂ sin 1,5wwT)

Формулы АЧХ и ФЧХ

H (ww) = 2a₁ sin 0,5 wwT + 2a₂ sin 1,5wwT, jj (ww) = -1,5wwT

Характер АЧХ и поясняющие графики - на рис. 6, б.

Рис. 6

4. Общие свойства фильтров с линейной фазой

Анализ рассмотренных вариантов фильтров с линейной фазой позволяет сделать выводы общего характера.

. Симметричные фильтры.

H (0) №№ 0, jj (ww) = -  wwT (3)

А. Если N - нечетное, то АЧХ - четная функция

H (w) = а₀ + 2 а_m cos (mwT) (4)

Применяется при условии H (0,5ww_д) №№ 0

Б. Если N - четное, то АЧХ - нечетная функция

H (w) = 2 а_m cos [ (m - 0,5) wT] (5)

Применяется при условии H (0,5ww_д) = 0

. Антисимметричные фильтры

 (0) = 0, jj (ww) = -wwT (6)

А. Если N - нечетное, то АЧХ - нечетная функция

H (w) = 2 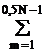а_m sin m wT (7)

Применяется при условии H (0,5ww_д) = 0

Б. Если N - четное, то АЧХ - четная функция

H (w) = 2 а_m sin [ (m - 0,5) wT] (8)

Применяется при условии H (0,5ww_д) №№ 0

Рис. 7

На рис. 7, а, б приведены графики, поясняющие отмеченные выше свойства.

Если требуемая передаточная функция имеет в качестве множителя мнимую единицу, то применяются исключительно антисимметричные фильтры. Например, передаточная функция дифференциатора или интегратора

H (jw) = jw, H (jw) = 1/jw

В этом случае условия

Н (0) = 0, или H (0,5ww_д) = 0, или H (0,5ww_д) №№ 0

при необходимости следует воспроизвести искусственно.

5. ЦФ с линейной фазой. Метод взвешивания

Расчет фильтров с линейной фазой начинается с выбора типа фильтра (симметричный, антисимметричный) и четности N в соответствии с общими свойствами фильтров с линейной фазой и требуемой АЧХ.

А. Если Н (0) №№ 0, то фильтр симметричный. Отсюда:

N - нечетное, если H (0,5ww_д) №№ 0;

N - четное, если H (0,5ww_д) = 0;

Б. Если Н (0) = 0, то фильтр антисимметричный. Отсюда:

N - нечетное, если H (0,5ww_д) = 0;

N - четное, если H (0,5ww_д) №№ 0

После выбора типа фильтра и четности N необходимо продолжить требуемую АЧХ на диапазон [0,5ww_д; ww_д] в соответствие с графиками на рис.7, а, б. Выбор расчетной формулы для ФЧХ, т.е. (3) или (6), определяется типом фильтра.

После выполненных процедур расчет фильтра осуществляется по общим правилам расчета не рекурсивных ЦФ.

Пример. Рассчитать ФНЧ с линейной фазой по следующим исходным данным:

Полоса пропускания равна [0; 200] Гц, переходной области соответствует диапазон частот [200; 300] Гц.

Решение

Выбираем f_д = 800 Гц. Отсюда после нормирования частот WW =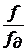

Полоса пропускания ® [0; 0,25], полоса непропускания ®® [0,375; 0,5].

Здесь Н (0) №№ 0, поэтому фильтр симметричный.

H (0,5ww_д) = 0, поэтому N - четное.

Требуемую АЧХ необходимо продолжить на диапазон [0,5ww_д; ww_д] нечетным образом (рис.8, а).

Пусть N = 8. Отсюда интервал между выборками WW₁ = = 0,125.

Формула для ФЧХ (3.3):

(ww) = - wwT.

Отсюда

(WW) = - 7ppWW,

или для частот выборки jj (kWW₁) = - 7ppWW

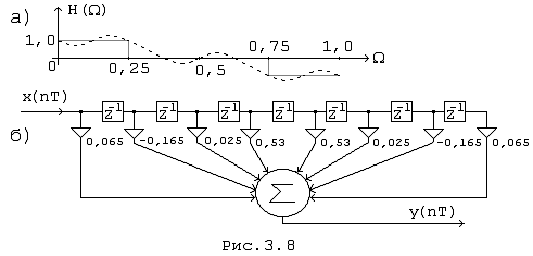
Рис. 8

Отсчеты АЧХ показаны на графике рис.8, а.

Следовательно, комплексные частотные отсчеты равны:

Н (jkWW₁) = {1e ^j0; 1e - ^j0,875pp; 1e - ^j1,75pp; 0; 0; 0; - 1e - ^j5,25pp; - 1e - ^j6,125pp }

Отсюда расчет импульсной характеристики по формуле обратного ДПФ

h [nT] = 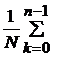H (jkWW₁) e ^{j (2pp/N) kn} =

={0,065; - 0,165; 0,025; 0,53; 0,53; 0,025; - 0,165; 0,065},

что соответствует схеме фильтра на рис.8, б.

По формуле (5) рассчитаем АЧХ фильтра

Н (W) = 1,06 cos pW + 0,05 cos 3pW - 0,33 cos 5pW + 0,13 cos 7pW.

Результаты расчета реализованной АЧХ приведены на графике рис.8, а (штриховая линия).

В окрестности точек разрыва требуемой АЧХ (частоты 0,25 и 0,75) отклонение от нормы реализованных характеристик получается значительным вследствие влияния эффекта Гиббса. Ослабить влияние эффекта Гиббса удается введением весовой функции (метод взвешивания) к импульсной характеристике.

Новая импульсная характеристика формируется по правилу:

h' (nT) = w (nT) * h (nT)

где w (nT) - весовая функция или "сглаживающее окно".

Воспользуемся весовой функцией Хэмминга:

w (nT) = 0,54 + 0,46 cos [2p ], (9)

где n = 0, 1, 2,. (N - 1)

Для рассматриваемого примера

w (nT) = {0,08; 0,244; 0,64; 0,96; 0,96; 0,64; 0,244; 0,08},

h' (nT) = {0,005; - 0,04; 0,016; 0,51; 0,51; 0,016; - 0,04; 0,005}

Отсюда новые коэффициенты фильтра и новая передаточная функция

' (z) = 0,005 - 0,04z - ¹ + 0,016z - ² + 0,51z - ³ + 0,51z - ⁴ + 0,016z - ⁵ - 0,04z - ⁶ + 0,005z - ⁷.

График АЧХ с учетом сглаживающего окна приведен на рис. 9. Расчетная функция получена из формулы для Н' (z) после подстановки

Рис. 9

z = e^jwT = e^j2pW.

Сравнивая реализованные АЧХ на рис.8, а и рис.9, можно убедиться в улучшении качества аппроксимации требуемой АЧХ при введении весовой функции. С ростом N положительный эффект возрастает.

6. Метод частотной выборки

Коэффициенты нерекурсивного ЦФ (рис.2, а) соответствуют отсчетам импульсной характеристики. Схему нерекурсивного ЦФ можно преобразовать таким образом, чтобы коэффициенты фильтра соответствовали отсчетам другой системной характеристики - передаточной функции. Новая схема ЦФ является основой конструирования фильтров по методу частотной выборки.

Схема фильтра

Схема фильтра формируется по результатам эквивалентных преобразований передаточной функции не рекурсивного ЦФ

H (z) = a_n z - ⁿ

где в соответствии с формулой обратного ДПФ

a_n = h [nT] = 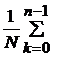H (jkww₁) e^{j (2pp / N) k n}

следовательно

Н (z) = 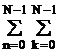 H (jkw₁) e^{j (2pp / N) k n} z - ⁿ =  (e^{j (2pp / N) k n} z - ¹) ⁿ

Применяя здесь формулу суммы N первых членов геометрической прогрессии

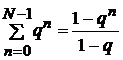
Получаем

H (z) = = P (z)  (10)

где

z (z) = 1 - d z - ^N, F_k (z) = 1/ (1 - b_k z - ¹), d = e^{j2pp k}, b_k = e ^{j2pp k / N} (11)

Рис. 10

Схема фильтра, соответствующего (10), приведена на рис.10, а. Схемы звеньев фильтра, соответствующих (11), приведены на рис.10, б.

Нули и полюсы H (Z) (3.10), т.е. корни уравнений

1 - e^{j2 pp k} z - ^N = 0, 1 - e ^{j2pp k / N} z - ¹ = 0

Расположены на единичной окружности плоскости Z в точках

z_k = e ^{j2p k / N}

и взаимно компенсируется. Но компенсация получается неполной по причине конечной разрядности кодовых слов, что приводит к скачкам частотной характеристики фильтра и, более того, не исключена вероятность самовозбуждения цепи.

Поэтому рекомендуется смещать точки z_k внутрь единичного круга на малую величину, т.е.

z_k = e - ^{aa T / N} e ^{j2pp k / N},

где aaТ < 10^-5,что соответствует коэффициентам фильтра

Небольшая поправка коэффициентов фильтра (3.12) практически не отразится на характеристиках фильтра.

Частотная характеристика фильтра

Частотная характеристика фильтра по методу частотной выборки получается подстановкой

Z = e^{jw T},

в (10). Отсюда, с учетом формулы Эйлера,

(jww) =

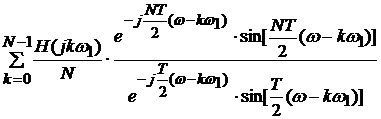
следовательно

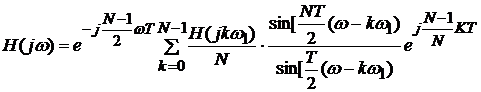 (13)

что соответствует ряду Котельникова для спектров дискретных сигналов.

Частотную характеристику нерекурсивного ЦФ можно представить как в форме ряда Фурье, так и в форме ряда Котельникова.

Каждая из отсчетных функций в (13)

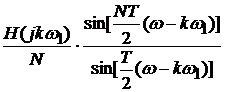 (14)

на частоте ww = kww₁ принимает значение частотной выборки H (jkw₁); остальные отсчетные функции на этой частоте обращаются в нуль. На графике рис. 11 показана в качестве примера некоторая АЧХ и ее составляющие - равносмещенные отсчетные функции для случая N = 8, где отсчетные функции представлены главным лепестком, кроме модуля отсчетной функции при К=0, которая изображена полностью.

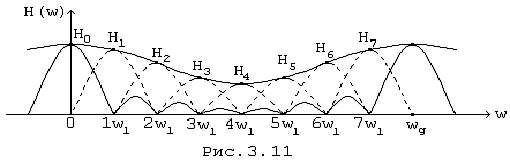
Рис. 11

Регулировка частотных отсчетов фильтра по методу частотной выборки является взаимонезависимой подобно взаимонезависимой регулировке отсчетов импульсной характеристики нерекурсивного ЦФ по схеме на рис. 2, а.

Расчет фильтра начинается с ориентировочного выбора величины N. Коэффициенты фильтра приравнивают к соответствующим отсчетам требуемой частотной характеристики.

В переходной области (точках разрыва характеристики), отсчеты необходимо выбирать с таким расчетом, чтобы получить удовлетворительное приближение реализованной характеристики к требуемой в диапазоне частот, прилегающем к переходной области. Наиболее часто в переходную область попадает 1 или 2 отсчетных частоты. В этом случае удовлетворительный результат аппроксимации можно получить простым подбором модуля отсчетов в переходной области.

После проверочного расчета частотных характеристик по формуле 10 или 13 принимается решение о необходимости повторного расчета.

Схема фильтра с вещественными отводами

Реализация фильтров по схеме на рис.10, а сопряжена с некоторыми особенностями, обусловленными комплексным характером коэффициентов в отводах. На практике получил распространение еще один вариант схемы такого фильтра, отличающийся вещественным характером коэффициентов.

Фильтр с вещественными коэффициентами получается за счет объединения каждой пары отводов с индексами К и (N-K), которая является комплексно-сопряженной по причине комплексно-сопряженной симметрии частотных характеристик фильтра относительно частоты 0,5ww_д. В результате

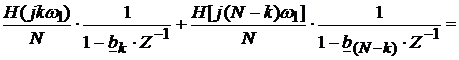
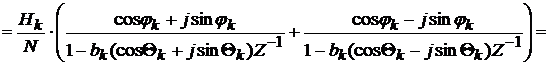
 (15)

где a_0k = cos jj_k, a_1k = - b_k cos (jj_k - qq_k), b_1k = - 2b_k cos qq_k, b_2k = b²_k

Схема фильтра, соответствующего (15), приведена на рис. 12.

Рис. 12

В схеме отсутствуют звенья, соответствующие нулевым значениям требуемой АЧХ. В результате, например, схема частотно-селективного фильтра существенно упрощается, сохраняя при этом возможность получения линейной фазы.

7. Расчет рекурсивных фильтров. Метод билинейного преобразования

Методы расчета рекурсивных ЦФ можно разделить на прямые и косвенные. Прямые методы предполагают расчет непосредственно рекурсивного ЦФ, косвенные используют в качестве промежуточного этапа расчет аналогового фильтра (АФ).

К числу косвенных методов относится метод билинейного преобразования, основанный на таком преобразовании частот, при котором частотная ось сжимается до конечных размеров. Формула частотного преобразования

 или

где ww - реальная частота, т.е. частота проектируемого ЦФ, 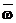 - расчетная частота, т.е. частота вспомогательного АФ, ,  - соответствующие комплексные частоты.

На рис. 13, а приведен график зависимости расчетной частоты от реальной частоты, на рис. 13, б - пример соответствия кривых АЧХ фильтров АФ и ЦФ.

Связь комплексных переменных вспомогательного АФ и реального ЦФ, т.е.  и Z определяется равенством

 (17)

Формула (17) получается подстановкой в (16) z = e^pT. В результате

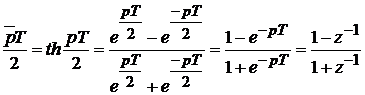
Перечислим последовательность этапов расчета ЦФ методом билинейного преобразования.

. Перевести требуемые характеристики и нормы ЦФ в соответствующие требования к АФ, применяя формулу

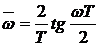
. Рассчитать передаточную функцию АФ , применяя методы расчета аналоговых фильтров.

. Определить передаточную функцию ЦФ H (z) по известной

. Построить схему ЦФ по H (z).

. Выполнить необходимые расчеты по учету эффектов конечной разрядности.

Пример. Рассчитать рекурсивный ЦФ нижних частот методом билинейного преобразования по следующим исходным данным:

Полоса пропускания равна [0; 200] Гц, переходная область равна [200; 300] Гц, DDА = 3 дБ, А_min = 15 дБ.

Решение

Выбираем f_д = 800 Гц.

Рис.13

Контрольные частоты для перевода норм ЦФ в нормы АФ:

; 200 Гц; 300 Гц.

Расчетная формула для преобразования частот

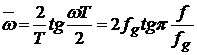
В результате

= 0 ®® 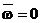®® WW_н = 0= 200 Гц ®® 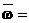1600 ®® WW_н = 1= 300 Гц ®® 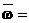3840 ®® WW_н = 2,4

где WW_н = 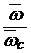 - нормированная частота ФНЧ, = 1600 - частота среза ФНЧ.

Основная формула расчета АФ

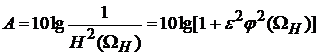
В данном случае достаточно ограничиться аппроксимирующим полиномом Баттерворта второго порядка. Учитывая что Е = 1 для DDА = 3 дБ, получаем

,

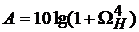Следовательно

Отсюда полюсы

р_{н 1,2} = - 0,707 ±± j 0,707,что соответствует нормированной передаточной функции

,

получаем ненормированную передаточную функцию АФ

.

После подстановки (17), получаем передаточную функцию рекурсивного ЦФ

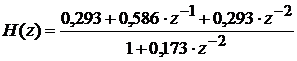
Что соответствует схеме рекурсивного ЦФ, приведенной на рис. 14, а.

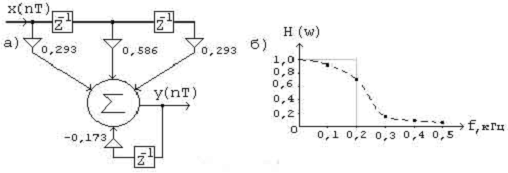
Рис. 14

График реализованной АЧХ приведен на рис.3.14, б.

Нелинейная зависимость частотного преобразования (16) определяет как недостатки, так и достоинства метода билинейного преобразования. С одной стороны линейная фаза после преобразования (16) становится нелинейной. С другой стороны - при переходе АФ ®® ЦФ отсутствуют ошибки наложения, что позволяет получить высокие уровни ослабления в ПН при конструировании частотно-селективных фильтров.

Литература

А.Т. Бизин. Введение в цифровую обработку сигналов. Сибирская Государственная Академия телекоммуникаций и информатики. Новосибирск 1998 г.

Гольденберг Л.М. и др. Цифровая обработка сигналов. - Учебное пособие для вузов. - М.: Радио и Связь, 1990 г.

Гольденберг Л.М. и др. Цифровая обработка сигналов. - Задачи и упражнения. Учебное пособие для вузов. - М.: Радио и Связь, 1992 г.

. Карташев В.Г. Основы теории дискретных сигналов и цифровых фильтров. - М.: Высшая школа, 1982 г.

. Лэм Г. Аналоговые и цифровые фильтры. Расчет и реализация. - М.: Радио и связь, 1982.

. Антонью А. Цифровые фильтры: анализ и проектирование. - М.: Радио и связь, 1983г.