Расчет тепловых процессов при сварке
Контрольная работа
РАСЧЕТ ТЕПЛОВЫХ ПРОЦЕССОВ ПРИ СВАРКЕ
Содержание
1. Методы расчета теплопроводности при сварке
. Тепловые схемы и классификация источников
нагрева
. Метод источников при решении задач
теплопроводности
.Фундаментальное решение уравнения
теплопроводности
.1 Мгновенный точечный источник
.2 Мгновенный линейный источник в пластине
.3 Мгновенный плоский источник в стержне
.4 Мгновенный точечный источник на поверхности
плоского слоя
. Расчет температурного поля движущихся источников
нагрева
.1 Движущийся точеный источник на поверхности
полубесконечного тела
.2 Движущийся линейный источник в пластине
.3 Движущийся по поверхности плоского слоя
точечный источник
.4 Движущийся плоский источник в стержне
.5Периоды теплонасыщения и выравнивания
температур
. Расчет температурного поля мощных
быстродвижущихся источников нагрева
.1 Быстродвижущийся точечный источник на
поверхности полубесконечного тела
.2 Линейный мощный быстродвижущийся источник в
пластине
. Расчет температурного поля непосредственным
интегрированием
.1 Расчет температурного поля при сварке методом
интегрирования
.2Расчет периодов теплонасыщения и выравнивания
температур
Литература
1. Методы расчета теплопроводности
при сварке
При заданном дифференциальном
уравнении теплопроводности (1.14) и наличии краевых условий поставленная задача
определения T=T(x,y,z,t),
как говорят математики, имеет решение, причем единственное. Однако получение
этого решения представляет собой существенную проблему.
Для решения задач теплопроводности
применяют аналитические и численные методы. Аналитические методы состоят в
подборе уравнения процесса, удовлетворяющего дифференциальному уравнению
теплопроводности и краевым условиям. Из аналитических методов наиболее часто
применяются методы интегральных преобразований (преобразования Ханкеля,
Лапласа, Фурье) и метод источников. Методы интегральных преобразований являются
мощным инструментом решения уравнений математической физики (к которым
относится и уравнение теплопроводности), но их использование требует уверенных
навыков в разделах математики, которые выходят за рамки курса математического
анализа машиностроительных специальностей технических университетов. Поэтому в
дальнейшем мы будем применять только метод источников как наиболее простой и, с
достаточной для практических задач сварочного производства точностью,
описывающий распределение температуры во большинстве случаях нагрева металла
при сварке.
Существующие аналитические
методы дают возможность получать решения только для процессов, описываемых
линейными дифференциальными уравнениями при линейных граничных условиях, т. е.
для тех случаев, когда теплофизические свойства можно считать не зависящими от
температуры. Аналитические методы приводят к общим уравнениям процессов,
действительным при разнообразных числовых значениях параметров, характеризующих
данную задачу: геометрических размеров, тепловых характеристик режима нагрева и
физических свойств металла. В простейших задачах удается получить решение в
замкнутой форме, т. е. выразить уравнение процесса через известные функции от
времени, пространственных координат и постоянных параметров процесса. В более
сложных задачах решения описываются определенными интегралами или бесконечными
рядами.
Численные методы в отличии от
аналитических позволяют решать задачу теплопроводности в сложной постановке, то
есть с учетом реальной геометрии сварной конструкции, температурной зависимости
теплофизических свойств, распределенности источника нагрева и т.д. В настоящее
время наиболее распространенным является численный метод конечных элементов
(МКЭ или FEM). Современные программные продукты, например ANSYS, предоставляют
широкие возможности расчета теплопроводности при сварке [3,4,5]. Численные
расчеты сообщают информацию только для данных условий задачи при определенных
значениях всех постоянных параметров. Численный метод не дает, подобно
аналитическому, общего решения задачи, но его целесообразно применять для
инженерных расчетов в тех случаях, когда получение аналитического решения ввиду
сложности условий задачи становится крайне трудоемким или вообще недоступным.
Чем проще условия задачи, тем
легче получить простое и ясное аналитическое решение, описывающее процесс в
общем виде и дающее возможность полного анализа процесса. Для получения такого
решения часто оказывается необходимым упрощать постановку задачи. Но,
схематизируя явление, нужно осознать и правильно оценить главные особенности
изучаемого процесса, пренебрегая второстепенными. Ошибки в схематизации
процесса сварочного нагрева приводят к принципиально не верному результату.
2. Тепловые схемы и
классификация источников нагрева
Геометрическая форма
свариваемых изделий в реальных условиях является сложной. Учет действительной
формы может значительно усложнить решение температурных задач сварочных процессов.
Поэтому реальную форму в тепловых расчетах идеализируют, сводя ее к одной из
следующих тепловых схем, для которых решение уравнения теплопроводности можно
получить в аналитическом виде.
Бесконечное тело - это такой
объект, в котором теплопроводность происходит во всех пространственных
направлениях T=T(x,y,z,t).
При этом реальные его границы в условиях локального сварочного нагрева не
оказывают существенного влияния на величину температуры. Эта схема предполагает
действие источников нагрева внутри рассматриваемого объема - q3 в
уравнении (1.14).
Полубесконечное тело занимает
область по одну сторону плоскости в бесконечном теле (рис. 1, а). В данном
случае температурное поле также трехмерное T=T(x,y,z,t). Подобная схема
реализуется, например, при сварке листов значительной толщины, когда
температура на обратной относительно сварки поверхности повышается
незначительно.
Пластина характеризуется
двумерным (плоским) температурным полем T=T(x,y,t). Геометрически это
пространство, ограниченное двумя параллельными плоскостями, в направлении
нормали к которым внутри тела теплопроводность отсутствует, то есть температуры
точек по толщине пластины одинаковы (рис. 1,в).
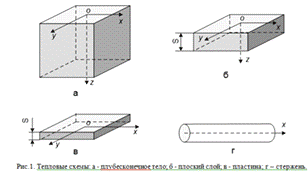
Плоский слой представляет собой
промежуточный между полубесконечным телом и пластиной случай. В этой схеме
также тело ограничено двумя параллельными плоскостями, но температура в
направлении толщины значительно изменяется T=T(x,y,z,t) (рис. 1, б).
Стержень есть тело, в котором
теплопроводность происходит только в одном направлении T=T(x,t)
(рис. 1, г).
Приведенная схематизация
нагреваемых тел условна. Например, полубесконечное тело можно рассматривать как
плоский слой бесконечной толщины, пластину - как плоский слой малой толщины,
когда можно пренебречь перепадом температуры по толщине, стержень - как цилиндр
без перепада температуры по сечению. Более того, одному и тому же
толстостенному свариваемому изделию могут соответствовать различные схемы тел:
бесконечное тело - при выполнении корневых проходов при многопроходной сварке в
узкий зазор (тепловые потоки существуют во все стороны); полубесконечное тело -
при выполнении на поверхности последнего прохода сварного шва (тепловые потоки
направлены вглубь металла); плоский слой - при электронно-лучевой сварке с несквозным
проплавлением, но со сквозным прогревом изделия (оказывает влияние тепловая
изоляция нижней поверхности изделия) и пластина - при плазменной резке толстых
листов (тепловые потоки направлены практически только поперек оси плазмы).
Только понимание физической модели может позволить грамотно выбрать
соответствующую тепловую схему.
Характерным признаком всех
способов сварки является локальный нагрев изделия, для чего используются
разнообразные концентрированные источники теплоты с высокой плотностью теплового
потока.
Обычно при расчете тепловых
процессов все сварочные источники (электрическая дуга, газовое пламя,
электронный и лазерный лучи, электрошлаковая ванна и т. д.) идеализируют.
Идеализированные источники можно классифицировать по длительности выделения
теплоты на мгновенные (время выделения теплоты tw
= 0) и непрерывно действующие (tw
> 0). Непрерывно действующие источники могут быть неподвижными (скорость
движения v = 0) и движущимися
(v > 0). Из
движущихся источников в свою очередь выделяют быстродвижущиеся источники
теплоты и вводят их в расчетную схему тогда, когда можно пренебречь тепловыми
потоками вдоль оси движения источника, что значительно упрощает расчет. По
пространству источники нагрева при сварке подразделяются на сосредоточенные и распределенные.
Сосредоточенные источники характерны тем, что при их действии тепло вводится в
область, не имеющую физического размера. Так, при трехмерной теплопроводности
сосредоточенным будет точечный источник, при котором тепло вводится в точку с
координатами x,y,z. Двумерному температурному полю соответствует линейный
источник, у которого тепловыделение равномерно по линии, перпендикулярной
плоскости температурного поля. Если температурное поле одномерно, то
сосредоточенным будет плоский источник нагрева, в котором тепло равномерно
выделяется в плоскости, перпендикулярной единственной координате. Таким
образом, источники сосредоточены по координатам рассматриваемого температурного
поля. При этом мерность пространства (dim) точечных источников = 0, линейных dim=l
и плоских dim = Далее
индексами i = 0; 1; 2; 3 у
теплоты Qi
Дж/см3, мощности qi
Вт/см3 будем указывать мерность источника.
Математически сосредоточенные
источники описываются с помощью 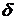 - функции (дельта - функции Дирака):
- функции (дельта - функции Дирака):
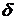 (u)= ∞
при u = 0,
(u)= ∞
при u = 0, 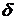 (u)= 0 при u ≠ 0,
причем
(u)= 0 при u ≠ 0,
причем
 .
.
В этих обозначениях мгновенный
точечный источник с тепловыделением Q
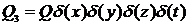 .
.
Применение вида сосредоточенного
источника нагрева должно быть согласовано с принятой тепловой схемой расчета теплопроводности.
Так, на поверхности полубесконечного тела и плоского слоя действует точечный, в
пластине - линейный, а в стержне - плоский источники тепла.
В действительности при сварочном
нагреве тепловой поток распределен в некотором компактном пространстве, то есть
действует распределенный источник нагрева. Например, для поверхностных
источников (электрическая дуга, газовое пламя, электронный или лазерный луч и
т.п.) экспериментально установлено, что удельный тепловой поток описывается
кривой Гаусса (закон нормального распределения)
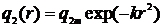 , (1)
, (1)
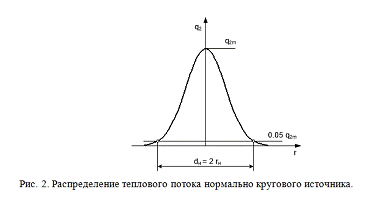
где q2m - удельный
тепловой поток в центре нагрева (при r = 0), Вт/см2; k - коэффициент
сосредоточенности теплового потока, см- Соответствующий формуле (1)
источник называется нормально круговым (рис.2).
Величины q2m и k зависят
от метода и режима сварки. При дуговой сварке эффективная тепловая мощность
дуги, вводимая в изделие q = UIη (Вт), где U - напряжение, I - ток
дуги, η
- эффективный
КПД процесса нагрева. Связь эффективной мощности дуги с параметрами
распределения q2(r) устанавливается путем интегрирования выражения
(1) с использованием подстановки u = kr2:
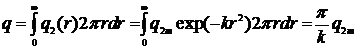 .
.
Согласно формуле (1) источник
действует на всей поверхности (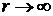 ). В практических расчетах вводится
понятие условного пятна нагрева диаметром dн = 2 rн, на
границе которого удельный тепловой поток q2 = 0.05q2m. Тогда
). В практических расчетах вводится
понятие условного пятна нагрева диаметром dн = 2 rн, на
границе которого удельный тепловой поток q2 = 0.05q2m. Тогда
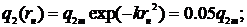
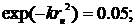
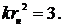 (2)
(2)
В результате условный диаметр пятна
нагрева 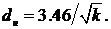 Сравним
распределение удельных тепловых потоков для различных методов сварки - газовой
и дуговой, считая, что эффективная тепловая мощность источников одинакова и
равна 5000 Вт. По данным работы [6] для газовой сварки коэффициент
сосредоточенности k = 0.3 см-2, для
аргонодуговой k = 1см-2,
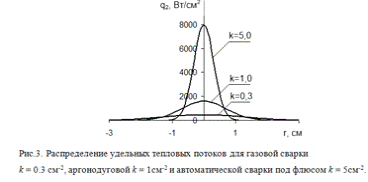
для автоматической сварки под слоем флюса k = 5см-2 (рис. 3). Чем
выше коэффициент сосредоточенности источника нагрева, тем меньше диаметр
условного пятна нагрева и больше значение максимального теплового потока.
Сравним
распределение удельных тепловых потоков для различных методов сварки - газовой
и дуговой, считая, что эффективная тепловая мощность источников одинакова и
равна 5000 Вт. По данным работы [6] для газовой сварки коэффициент
сосредоточенности k = 0.3 см-2, для
аргонодуговой k = 1см-2,
для автоматической сварки под слоем флюса k = 5см-2 (рис. 3). Чем
выше коэффициент сосредоточенности источника нагрева, тем меньше диаметр
условного пятна нагрева и больше значение максимального теплового потока.
Значительной сосредоточенностью
могут обладать электронный и лазерный лучи при соответствующей фокусировке их
на поверхности свариваемого тела. Концентрация энергии может быть настолько
существенной, что теплопроводность металла оказывается недостаточной для отвода
теплоты в глубину тела и металл закипает, испаряясь с поверхности. Это тепловая
разделительная резка материала. В предельном случае, когда 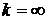 источник
становится сосредоточенным:
источник
становится сосредоточенным:
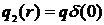 .
.
Существуют источники теплоты при
сварке со сложной формой распределения теплового потока, например,
электрошлаковый. Теплота может распределяться по толщине металла по различным
законам. В случае наплавки на массивное тело распределенностью теплоты в
направлении оси z можно пренебречь и считать источник
точечным, находящимся на поверхности тела.
При необходимости учесть
распределенность теплоты, например от сварочной дуги по глубине металла, можно
принять нормальный закон распределения по аналогии с формулой (1). В общем
случае использования различных сварочных источников теплоты вопрос о
распределенности теплового потока по толщине металла должен решаться конкретно
в зависимости от свойств самого источника и его взаимодействия со свариваемым
металлом. В первом приближении о характере распределения вводимой энергии можно
судить по форме проплавления материала.
3. Метод источников
при решении задач теплопроводности
Специфическим для задач
теплопроводности при сварке является то, что в области высокой температуры на
температурное поле оказывают влияние в большей степени особенности ввода
теплоты (особенности сварочных источников) и в меньшей степени граничные
условия.
Существуют различные
аналитические методы решения задач теории теплопроводности (метод разделения
переменных, операционные методы, метод источников и др.). Предложенный еще
лордом Кельвином метод источников (в математической физике называемый методом
функций Грина) является предпочтительным в силу своей наглядности, простоты
учета особенностей сварочных источников теплоты; вместе с тем он обладает
математической строгостью. Все это и обусловило его популярность при расчете
температурных полей в сварных изделиях.
Дифференциальное уравнение
теплопроводности (1.14) является линейным. Одним из следствий линейности
уравнения является принцип суперпозиции: результат суммы воздействий равен
сумме результатов каждого воздействия отдельно. Физическая сущность метода
источников заключается в том, что любой процесс распространения теплоты в теле
можно представить в виде суммы процессов выравнивания температуры от множества
элементарных источников теплоты, распределенных как в пространстве, так и во
времени. Подчеркнем, что заложенный в метод источников принцип суперпозиции
(наложения) решений применим только в случае, когда краевая задача линейна (в
уравнении теплопроводности и граничных условиях 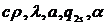 не зависят от температуры, а q3
есть линейная функция T).
не зависят от температуры, а q3
есть линейная функция T).
Ранее введено понятие мгновенных
сосредоточенных источников. Любой реальный постоянно действующий, движущийся и
произвольно распределенный в пространстве источник можно, пользуясь принципом
суперпозиции, представить в виде совокупности мгновенных сосредоточенных
источников и получить решение задачи, суммируя температурное поле от каждого из
них [6].
В общем виде метод источников при
решении дифференциального уравнения теплопроводности выглядит следующим
образом. Пусть выполняется сварное соединение конструкции с помощью
локализованного в некоторой области V
(ξ,η,ς,τ) движущегося источника
нагрева. Представим этот источник в виде совокупности мгновенных
сосредоточенных источников, каждый из которых действует в момент времени τ. Приращение
температуры от одного источника в точке конструкции (x,y,z) в данный момент
времени равно 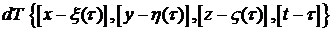 . Суммируя
значения температуры от каждого мгновенного сосредоточенного источника
движущегося объема V, получим
. Суммируя
значения температуры от каждого мгновенного сосредоточенного источника
движущегося объема V, получим
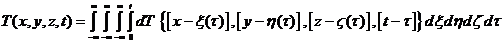 . (3)
. (3)
Таким образом, для расчета
температурных полей в сварочных процессах необходимо в первую очередь решить
уравнение теплопроводности при действии мгновенных сосредоточенных источников
нагрева.
4. Фундаментальное
решение уравнения теплопроводности
4.1 Мгновенный
точечный источник
Для бесконечного тела, в начале
координат которого действует мгновенный точечный источник, решение
дифференциального уравнения теплопроводности следующее:
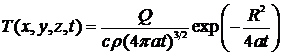 , (4)
, (4)
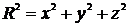 ,
,
где T - температура точки с
координатами x,y,z; Q - количество тепла, выделившееся в момент t = 0 в начале
координат; t - время, прошедшее с момента введения тепла; R - расстояние от
начала координат, где действует источник, до рассматриваемой точки (радиус -
вектор). У равнение (4) является фундаментальным решением уравнения
теплопроводности при действии мгновенного точечного источника в бесконечном
теле.
В любой момент t
≠
0 температура самого источника (R
= 0) отлична от нуля и с течением времени уменьшается по закону t-3/2,
оставаясь выше температур других точек тела. Вместе с удалением от источника
температура понижается по закону нормального распределения exp(-R2/4at).
Изотермическими поверхностями являются сферы с центром в источнике, и
температурное поле в данный момент времени зависит лишь от радиуса. В начальный
момент времени (t = 0) температура не определена (T
= ∞), что связано со схемой сосредоточенного источника, в котором в
бесконечно малом объеме в начальный момент времени содержится конечное
количество тепла Q.
На основе решения для
бесконечного тела (4) можно вывести уравнение температурного поля для схемы
полубесконечного тела, которая применяется для описания тепловых процессов в
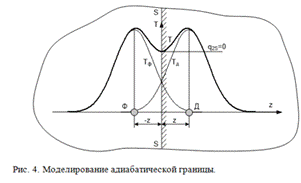
массивных изделиях. Пусть в полубесконечном теле, ограниченном поверхность S -
S действует мгновенный точечный источник Д (рис. 4). Для массивных тел тепловые
потоки внутри значительно больше потока теплоотдачи с поверхности. Поэтому
поверхность полубесконечного тела можно считать адиабатической границей, для
которой (см.п. 1.4)
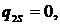
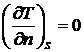 . (5)
. (5)
Дополним полубесконечную область z
> 0 до бесконечной, дбавив область z < 0. В образовавшемся объеме введем
дополнительный (фиктивный) источник нагрева Ф(-z), идентичный действительному
источнику Д(z), но расположенный симметрично по другую сторону границы S. На
рис. 4 приведено распределение температур в бесконечном теле отдельно для
действительного (TД) и фиктивного (Tф) источников.
Суммарная температура от обоих источников T = TД + Tф.
При этом на границе 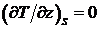 , что
соответствует определению адиабатической границы (5). Если действительный
источник находится на поверхности полубесконечного тела, то фиктивный с ним
совпадает, и T=2TД. Тогда температурное поле мгновенного точечного
источника на поверхности полубесконечного тела
, что
соответствует определению адиабатической границы (5). Если действительный
источник находится на поверхности полубесконечного тела, то фиктивный с ним
совпадает, и T=2TД. Тогда температурное поле мгновенного точечного
источника на поверхности полубесконечного тела
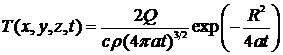 . (6)
. (6)
По такой же схеме моделируется и
изотермическая граница (граничное условие 1-го рода) TS=0, но в
этом случае T = TД - TФ. Следует
подчеркнуть, что источник нагрева не может действовать на изотермической
поверхности.
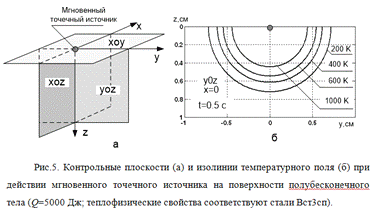
Графическое изображение
температурного поля (6) требует четкого понимания пространственного положения
поверхности, на которой строится распределение температуры. В декартовой
системе координат (x, y, z) контрольными сечениями полубесконечного тела при действии
точечного источника являются плоскости xy, xz и yz (рис. 5, а). Для
полубесконечного тела изотермические поверхности являются полусферами
(температура зависит от радиуса - вектора R). В
плоскости xy изотермы,
как сечение поверхности плоскостью
z=const, являются
окружностями, а в других плоскостях - полуокружностями (рис. 5, б).
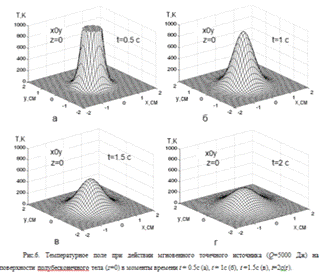
Температурное поле мгновенного точечного источника в разные моменты времени
представлено на рис. (6) (см. П 1.1.). На рисунке температура графически
ограничена значением T=1000K|.
Температура в любой точке вне
источника сначала возрастает, а затем убывает (рис.1.3). Момент достижения
максимального значения температуры в данной точке найдется из условия 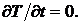
Дифференцируя выражение (6) по
времени, получаем формулу для определения времени, когда температура
максимальна
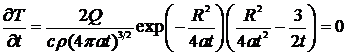 ,
,
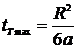 ,
, 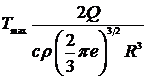 . (7)
. (7)
Максимальные темперы точек
полубесконечного тела при действии точечного источника уменьшаются с
расстоянием как R3.
4.2 Мгновенный линейный источник в
пластине.
теплопроводность сварка нагрев температурный
При сварке «на проход», то есть
когда металл в зоне действия сварочного источника нагрева расплавляется на всю
толщину, например при сварке листов на флюсо - медной подкладке, разделительной
тепловой резке и подобных процессах, температуру по толщине металла T(z)
можно считать постоянной. В этом случае реализуется тепловая схема - пластина,
и температурное поле является двумерным (плоским) T=T(x,y,t), (см. п. 1).
Выведем фундаментальное уравнение теплопроводности для этого случая, используя
предыдущие результаты.
В линейный элемент
теплопроводящего тела, имеющий форму бесконечно длинной призмы малым основанием
dxdy, в начальный
момент времени t = 0 внесем
тепло, распределенное равномерно по длине этой призмы с интенсивностью Q1
Дж/см. Температурное поле, получающееся от действия мгновенного линейного
источника, в силу линейности задачи, можно получить наложением температурных
полей бесконечного числа мгновенных точечных источников, распределенных вдоль
оси z, совпадающей с
осью призмы, и вносящих в элемент длиной dz
тепло
dQ
= Q1
dz.
При этом для температуры любой
точки тела в соответствии с формулой (4) получим
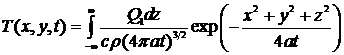 ,
,
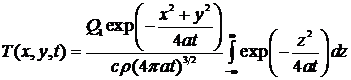 . (8)
. (8)
Введя новую переменную
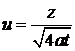 ,
,
будем иметь
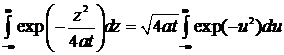 .
.
Известно [7], что
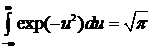 .
.
При этом формула (8) примет вид
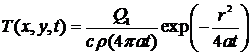 , (9)
, (9)
где 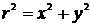 .
.
Если из теплопроводящего тела
вырежем пластину толщиной s двумя плоскостями, нормальными к
оси z, и в его
элемент sdxdy в начальный
момент времени внесем тепло Q Дж, то в соответствии с уравнением
(9) мгновенный линейный источник тепла с интенсивностью
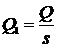 Дж/см
Дж/см
создает плоское температурное поле
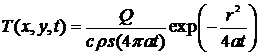 . (10)
. (10)
Это выражение и есть фундаментальное
решение уравнения теплопроводности при действии мгновенного линейного источника
в пластине.
Температурное поле мгновенного
линейного источника в данный момент времени зависит лишь от плоского
радиуса-вектора
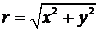 ,
,
и его изотермические поверхности - круговые
цилиндры, ось которых совпадает с осью источника. При этом изотермические линии
в плоскости yz
представляют собой прямые (рис.7) (см. П1.), а в плоскости xy - окружности.
Максимальная в данной точке
температура в момент времени, определяемый из условия 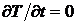 , приводит к
результату
, приводит к
результату
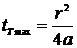 ,
, 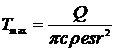 . (11)
. (11)
Максимальные температуры линейного
источника в пластине уменьшаются с расстоянием как r
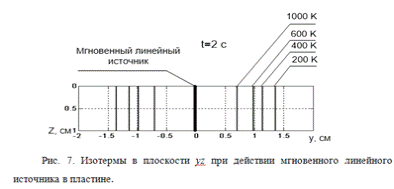
Нагрев пластины (рис.8) по сравнению
с полубесконечным телом (рис.6) при аналогичном тепловложении происходит до
больших температур, и процесс выравнивания температурного поля медленнее. Это
связано с тем, что теплопроводность в пластине происходит только в двух
направлениях - x и y, в то время как для
полубесконечного тела теплопередача трехмерна, а значит, более интенсивна.
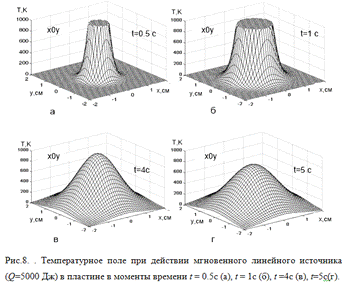
При расчете процессов
распространения тепла в пластинах необходимо учитывать влияние их теплообмена с
окружающей средой через поверхность. Пусть на поверхностях пластины толщиной s задана
теплоотдача по правилу Ньютона с коэффициентом α Дж/см2сK
(см. п.1.4) в окружающую среду нулевой температуры. В этом случае удельный
тепловой поток теплоотдачи q2S=αT. Пусть в
начальный момент температура пластины площадью F постоянна по всему ее объему и
равна Тн. Начиная с момента t=0, пластина
свободно охлаждается за счет поверхностной теплоотдачи. Тогда температура T(t) в
процессе свободного охлаждения будет оставаться одинаковой по всему объему
пластины. За время dt с двух сторон пластины 2F будет отдано в окружающую среду
количество теплоты
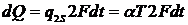 . (12)
. (12)
Температура пластины объемом sF за время dt
понизится на величину
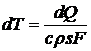 . (13)
. (13)
После подстановки (12) в (13)
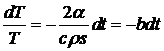 . (14)
. (14)
Величина 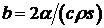 с-1
называется коэффициентом температуроотдачи для пластины. Интегрируя уравнение
(14), находим
с-1
называется коэффициентом температуроотдачи для пластины. Интегрируя уравнение
(14), находим
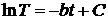 .
.
Постоянную интегрирования определим
из условия T=Tн при t=0:
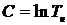 .
.
Таким образом, изменение температуры
при свободном охлаждении пластины
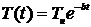 . (15)
. (15)
В начале процесса темп охлаждения
наиболее высок. По мере снижения температуры уменьшается и пропорциональная ей
скорость охлаждения. С течением времени и температура, и скорость охлаждения
асимптотически стремятся к нулю.
Если в качестве начальной считать
температуру в пластине без теплоотдачи, то подставив вместо Tн
выражение (10), получим температурное поле мгновенного линейного источника в
пластине с учетом теплоотдачи
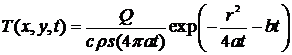 . (16)
. (16)
Интенсивность теплоотдачи
существенно зависит от толщины пластины s. Определим 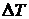 как разность
между значениями температуры при нагреве пластины мгновенным линейным
источником без учета (10) и с учетом (16) теплоотдачи с поверхности
как разность
между значениями температуры при нагреве пластины мгновенным линейным
источником без учета (10) и с учетом (16) теплоотдачи с поверхности
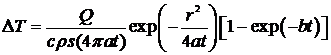 . (17)
. (17)
На рис. 9. приведены геометрическая
схема и результаты этого сравнения. Из рис. 9, а следует, что чем меньше толщина
пластины, тем большее влияние на значение температуры оказывает поверхностная
теплоотдача. Влияние теплоотдачи усиливается с ростом времени (рис. 9, б). Как
следует из формулы (17), зависимость 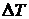 от толщины пластины s гиперболическая.
Для толщин, больших, чем 5мм, влиянием теплоотдачи с поверхности пластины можно
пренебречь.
от толщины пластины s гиперболическая.
Для толщин, больших, чем 5мм, влиянием теплоотдачи с поверхности пластины можно
пренебречь.
.3 Мгновенный плоский источник в
стержне
При одномерном процессе
теплопроводности температура изменяется только по одной координате: T=T(x,t).
Соответствующая этому случаю тепловая схема - стержень. Поперечное сечение
стержня может быть произвольным. Возьмем бесконечное теплопроводящее тело и в
его элемент, представляющий бесконечный плоский слой толщиной dx, вырождающийся
в пределе в плоскость yz, в начальный момент внесем
тепло, равномерно распределенное по его площади с интенсивностью Q2 в Дж/см
Температурное поле, вызываемое этим плоским источником, можно найти
суммированием полей мгновенных точечных источников, распределенных по всей
плоскости уz. Полагая
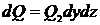
и используя формулу температурного
поля мгновенного точечного источника (6), получим
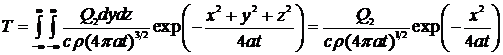 . (18)
. (18)
Таким образом, температурное поле
мгновенного плоского источника зависит лишь от расстояния 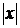 до плоскости
уz источника и
изотермическими поверхностями являются плоскости, параллельные плоскости уz. Например,
если возьмем теплопроводящее тело в форме бесконечно длинной прямоугольной
призмы с площадью поперечного сечения F, боковые
грани которой непроницаемы для тепла и в элемент его объема Fdx в начальный
момент внесем тепло с интенсивностью Q2 Дж/см2,
то температура в любом его поперечном сечении
до плоскости
уz источника и
изотермическими поверхностями являются плоскости, параллельные плоскости уz. Например,
если возьмем теплопроводящее тело в форме бесконечно длинной прямоугольной
призмы с площадью поперечного сечения F, боковые
грани которой непроницаемы для тепла и в элемент его объема Fdx в начальный
момент внесем тепло с интенсивностью Q2 Дж/см2,
то температура в любом его поперечном сечении 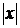 будет постоянна и определится по
формуле (18). Общее количество тепла, выделившееся в сечении F Q=Q2F Дж. В
результате фундаментальное решение уравнения теплопроводности мгновенного
плоского источника в стержне
будет постоянна и определится по
формуле (18). Общее количество тепла, выделившееся в сечении F Q=Q2F Дж. В
результате фундаментальное решение уравнения теплопроводности мгновенного
плоского источника в стержне
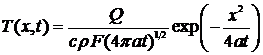 . (19)
. (19)
При этом наибольшая температура в
любом сечении |х| будет иметь место в момент времени
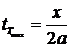 ,
,
и для нее получим
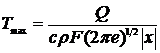 . (20)
. (20)
Распределение температуры в
различные моменты времени приведено на рис. 10.
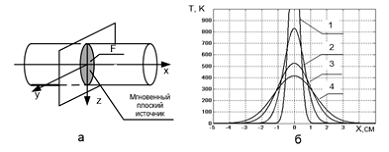
Рис. 10. Тепловая схема (а) и
распределение температуры (б) при действии мгновенного плоского источника в
стержне в моменты времени t=0.5с
(1), t= 2с (2), t
=5с (3) и t =8с (4).
По аналогии с предыдущим
случаем линейного источника в пластине, для плоского источника в стержне
учитывается поверхностная теплоотдача:
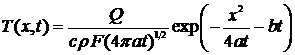 , (21)
, (21)
где коэффициент температуроотдачи
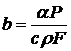 ,
,
P- периметр
сечения, F- его
площадь.
4.4 Мгновенный точечный источник на
поверхности плоского слоя
Расчет температурного поля при
сварке основывается на корректной схематизации реального процесса. Рациональный
выбор тепловой схемы позволяет получить результаты расчета температурного плоя
с достаточной для практической реализации точностью. Определение тепловой схемы
в первом приближении можно вычислить следующим образом. Пусть необходимо
сварить встык два одинаковых стальных листа толщиною s. Проведем расчет по
схеме точечного источника на поверхности полубесконечного тела и по формуле (7)
вычислим максимальную температуру при z=s. Если максимальная температура на
нижней стороне листа z=s составляет десятки градусов, то данный случай
моделируется схемой полубесконечного тела. Когда максимальная температура в
полубесконечном теле при z=s достигает температуры плавления материала ( при
сварке в жидкой фазе) - это пластина. В случае значений максимальной
температуры в сотни градусов при z=s мы имеем дело с плоским слоем.
Плоский слой - это тело,
ограниченное двумя параллельным плоскостями (z=const) на расстоянии s друг от
друга (рис.1, б). Как было отмечено выше (рис.9), при значительных толщинах
свариваемых лиcтов,
соответствующих этому случаю, теплоотдача с поверхности незначительна, поэтому
для плоского слоя обе поверхности считаются адиабатическими. Моделирование
одной адиабатической границы для мгновенного точечного источника представлено
на рис. 4. Наличие двух адиабатических границ при действии точечного источника
Д на поверхности плоского слоя приводит к необходимости введения в бесконечном
теле V системы
фиктивных источников Ф, которые обеспечивают путем отражения от адиабатических
поверхностей формирование температурного поля плоского слоя. Схема
распределения действительного и фиктивных источников приведена на рис. 11.
Температура в точке A(x,y,z)
от точечного источника Д на адиабатической поверхности S1
полубесконечного
тела определяется формулой (6). Наличие адиабатической границы плоского слоя S2
приводит к необходимости введения фиктивного источника Ф1,
расположенного симметрично относительно границы S
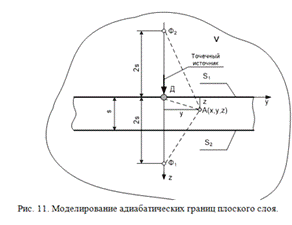
Но при действии источника Ф1
нужно смоделировать границу S1, установив источник Ф2 и
т.д., что приводит к бесконечному ряду фиктивных источников по оси z.
Температура в контрольной точке в соответствии с методом источников (принцип
суперпозиции) является суммой всех действительных и фиктивных источников. Чем
больше номер фиктивного источника, тем дальше он находится от контрольной точка
А(x,y,z) и тем меньше его вклад в результирующее значение температуры. Поэтому
этот ряд быстро сходится как 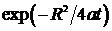 , где
, где 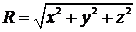 - расстояние от действительного
источника до контрольной точки А(x,y,z). Присвоив знак «+» i - тым источникам
при z > 0 и знак «-» при z < 0, на основе формулы (6), получим искомое
температурное поле мгновенного точечного источника на поверхности плоского слоя
- расстояние от действительного
источника до контрольной точки А(x,y,z). Присвоив знак «+» i - тым источникам
при z > 0 и знак «-» при z < 0, на основе формулы (6), получим искомое
температурное поле мгновенного точечного источника на поверхности плоского слоя
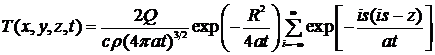 , (22)
, (22)
где i - номер источника.
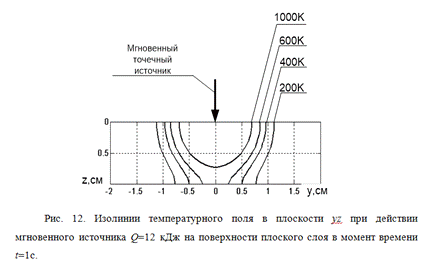
Форма изотерм в плоском слое (рис.
12) подчеркивает наличие второй адиабатической границы с обратной стороны
источника нагрева, в районе которой температура повышается за счет отражения от
границы.
5. Расчет
температурного поля движущихся источников нагрева
Для вывода уравнение процесса
распространения тепла при движущемся непрерывно действующем источнике,
применяют принцип суперпозиции (см. п. 3). Для этого весь период действия
источника разбивают на бесконечно малые элементы и рассматривают отдельные
элементарные воздействия источника на теплопроводящее тело. Эти элементарные
тепловые воздействия приложены к поверхности тела в последовательные моменты
времени в точках, расположенных по оси перемещения источника. Процессы
распространения тепла от элементарных воздействий источника можно рассматривать
вне зависимости друг от друга. Суммированием таких элементарных процессов можно
получить уравнение процесса распространения тепла при непрерывном действии
подвижного источника [6].
Принцип наложения применим,
если дифференциальные уравнения, описывающие процесс, линейны, т. е. если их
коэффициенты не зависят от искомой функции, в данном случае от температуры.
Дифференциальное уравнение теплопроводности (1.14) содержит коэффициент
температуропроводности а, изменяющийся с температурой; однако, принимая его
постоянным, можно получить приближенные решения, достаточные для практических
расчетов.
По принципу наложения изменение
температуры в какой-либо точке теплопроводящего тела представляется суммой
изменений температуры при распространении тепла от отдельных элементарных
воздействий источника с учетом времени и места их приложения. Так как источник
действует непрерывно, можно интегрировать элементарные приращения температуры dT, вызванные
действием источника в течение бесконечно малых промежутков времени, т. е. полагать
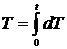 . При
простых расчетных схемах оказывается возможным выразить получаемые при
рассмотрении непрерывного процесса интегралы через известные функции.
. При
простых расчетных схемах оказывается возможным выразить получаемые при
рассмотрении непрерывного процесса интегралы через известные функции.
В дальнейшем выведем уравнения
процессов распространения тепла для трех основных расчетных схем подвижных
источников: точечного источника на поверхности полубесконечного тела, линейного
источника в неограниченной пластине, точечного источника на поверхности
плоского слоя и плоского источника в неограниченном стержне, соответствующих
практически важным типам сварочного нагрева металла.
5.1 Движущийся точеный источник на
поверхности полубесконечного тела
По поверхности массивного тела
равномерно (т. е. с постоянной скоростью v) и
прямолинейно перемещается непрерывно действующий точечный источник тепла
постоянной мощности q. Тело будем считать полубесконечным
с адиабатической плоскостью xy (рис. 13).
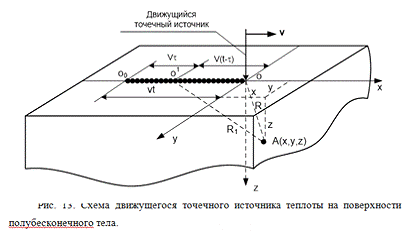
Начало связанной с телом неподвижной
(физической) системы координат o0 совместим с
положением точечного источника в момент t=0 начала
его действия; ось o0 x совместим с
направлением перемещения источника со скоростью v. Введем
подвижную систему координат xyz, начало которой o связано с
движущимся источником нагрева. В любой момент времени t температура
в точке А(x,y,z) будет
являться суммой температур от мгновенных точечных источников o1,
действовавших в моменты времени t
(t =0…t) на
расстоянии vt от начала
движения. Длительность распространения тепла мгновенного источника, введенного
в точке o1, составляет t-t. От одного мгновенного источника с
тепловложением Q=qdt, где q - мощность
источника, Вт, приращение температуры на основе выражения (6)
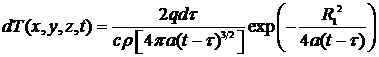 ,
,
где 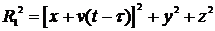 .
.
Просуммируем приращение температуры
от всех элементарных источников, действовавших в течение времени t на
дистанции o0 o:
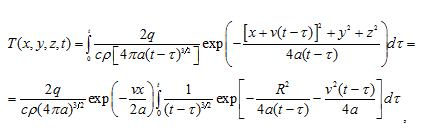 (23)
(23)
где 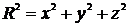 .
.
Дальнейшее преобразование
сводится к вычислению интеграла (23) при различных значениях входящих в него
параметров. Интегралы подобного типа не всегда берутся, и тогда приходится
вычислять их по приближенным формулам, например Симпсона, или разлагать решение
в ряд. В рассматриваемом случае интеграл можно выразить через известные
функции.
Предельное состояние. Если
следить за подвижным температурным полем, связанным с дугой или другим
сосредоточенным источником тепла, то можно заметить, что возникающая в начале
нагрева область повышенных температур с течением времени увеличивается и
достигает определенных предельных размеров. Подвижное температурное поле, как
бы насыщенное теплом сосредоточенного источника, только перемещается вместе с
ним, оставаясь неизменным. Такое состояние процесса называется предельным или
установившимся. Таким образом, процесс нагрева источником постоянной мощности
делится на два периода:
I период -
теплонасыщение, когда размеры связанной с источником нагретой зоны
увеличиваются; II период - предельное или
установившееся состояние процесса распространения тепла, когда температурное
поле остается постоянным. При неподвижном источнике тепла неподвижное поле
предельного состояния называют стационарным. При подвижном источнике (v=const; q=const) связанное
с ним температурное поле предельного состояния называют квазистационарным.
Процесс распространения тепла стремится к предельному состоянию при
неограниченно длительном действии источника постоянной мощности, то есть при
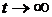 . При ручной
дуговой сварке в начале процесса сварщик не начинает движение вдоль оси
соединения до тех пор, пока не образуется сварочная ванна необходимых размеров.
При автоматической сварке система управления сварочным автоматом имеет
устройство (реле времени), осуществляющее задержку включения привода движения
автомата со скоростью сварки на время, необходимое для прогрева металла и
образования сварочной ванны. Эти приемы исключают период теплонасыщения, и
процесс сварки характеризуется предельным состоянием температурного поля при
постоянстве параметров режима сварки.
. При ручной
дуговой сварке в начале процесса сварщик не начинает движение вдоль оси
соединения до тех пор, пока не образуется сварочная ванна необходимых размеров.
При автоматической сварке система управления сварочным автоматом имеет
устройство (реле времени), осуществляющее задержку включения привода движения
автомата со скоростью сварки на время, необходимое для прогрева металла и
образования сварочной ванны. Эти приемы исключают период теплонасыщения, и
процесс сварки характеризуется предельным состоянием температурного поля при
постоянстве параметров режима сварки.
Уравнение предельного состояния
процесса распространения тепла при нагреве поверхности полубесконечного тела
подвижным точечным источником тепла, отнесенное к подвижной системе координат,
получим из уравнения (23), полагая 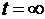 . Интеграл в уравнении (23), взятый
между пределами 0 и
. Интеграл в уравнении (23), взятый
между пределами 0 и 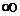 , можно
привести подстановкой
, можно
привести подстановкой
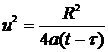
к известному несобственному
интегралу [7]
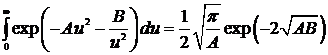
После ряда преобразований уравнение
предельного состояния процесса распространения тепла точечного источника
постоянной мощности, движущегося с постоянной скоростью v по
поверхности полубесконечного тела, отнесенное к подвижным координатам xyz, принимает
вид:
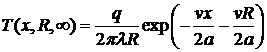 , (24)
, (24)
здесь R-
пространственный радиус-вектор в подвижной системе координат, т. е.
расстояние рассматриваемой точки А(x,y,z) от начала o подвижной
системы; х - абсцисса точки А(x,y,z).
Следует обратить внимание на то, что
температурное поле (24) не зависит от времени. Это непосредственно следует из
схемы квазистационарного температурного поля в подвижной системе координат.
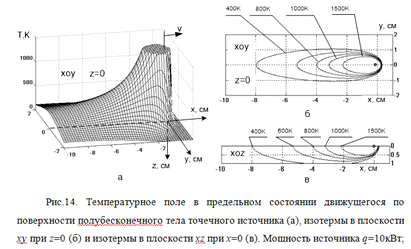
Температурное поле движущегося
источника не симметрично относительно оси y (рис. 14) (см. П 1.3). Источник
нагрева как бы «догоняет» теплопроводность по оси движения x. Градиент
температуры по оси x 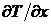 впереди
источника увеличивается, а позади уменьшается с ростом скорости его движения.
При этом в плоскости yz (сечение поперек оси x движения источника)
изотермические линии так же, как и для мгновенного источника (рис. 5, б)
остаются полуокружностями (в обоих случаях схема полубесконечного тела). Из
формулы (24) и рис. 14 видно, что поле симметрично относительно продольной оси
х, то есть изотермические поверхности являются поверхностями вращения вокруг
оси х. Чем дальше точка нагреваемого тела от источника, тем меньше максимальная
температура и тем позже она достигается. Позади источника компоненты вектора
градиента температуры вдоль оси движения источника x меньше, чем в поперечном
направлении y, а это значит, что тепловые потоки, пропорциональные градиенту
температуры по закону Фурье (1.5), вдоль оси х намного меньше, чем в поперечном
направлении y, то есть теплота преимущественно распространяется в направлении у
и z. Это
утверждение тем справедливее, чем больше асимметричность поля относительно оси
у (чем больше скорость сварки v), и оно будет использовано далее
при построении схемы быстродвижущихся источников.
впереди
источника увеличивается, а позади уменьшается с ростом скорости его движения.
При этом в плоскости yz (сечение поперек оси x движения источника)
изотермические линии так же, как и для мгновенного источника (рис. 5, б)
остаются полуокружностями (в обоих случаях схема полубесконечного тела). Из
формулы (24) и рис. 14 видно, что поле симметрично относительно продольной оси
х, то есть изотермические поверхности являются поверхностями вращения вокруг
оси х. Чем дальше точка нагреваемого тела от источника, тем меньше максимальная
температура и тем позже она достигается. Позади источника компоненты вектора
градиента температуры вдоль оси движения источника x меньше, чем в поперечном
направлении y, а это значит, что тепловые потоки, пропорциональные градиенту
температуры по закону Фурье (1.5), вдоль оси х намного меньше, чем в поперечном
направлении y, то есть теплота преимущественно распространяется в направлении у
и z. Это
утверждение тем справедливее, чем больше асимметричность поля относительно оси
у (чем больше скорость сварки v), и оно будет использовано далее
при построении схемы быстродвижущихся источников.
Неподвижный источник. Рассмотрим
случай предельного состояние процесса нагрева поверхности полубесконечного тела
точечным неподвижным непрерывно действующим источником тепла постоянной
мощности q=const. Подобная
схема в сварочном производстве реализуется, например, при сварке пробочными
швами, при ремонте локальных дефектов поверхности и в т.п. случаях.
При длительном нагреве (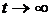 )процесс
распространения тепла стремится к предельному состоянию, температурное поле
которого можно получить, полагая в общем выражении (24) скорость v=0:
)процесс
распространения тепла стремится к предельному состоянию, температурное поле
которого можно получить, полагая в общем выражении (24) скорость v=0:
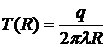 .
.
Температура зависит только от
радиуса R. Поле
симметрично относительно точки начала координат, а изотермические поверхности
являются концентрическими полусферами.
По мере приближения к началу
координат, т. е. при 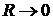 ,
температура бесконечно возрастает, как 1/R. По мере
удаления от источника температура уменьшается пропорционально радиусу-вектору R.
Температура на данном расстоянии R прямо пропорциональна мощности
источника q и обратно
пропорциональна коэффициенту теплопроводности
,
температура бесконечно возрастает, как 1/R. По мере
удаления от источника температура уменьшается пропорционально радиусу-вектору R.
Температура на данном расстоянии R прямо пропорциональна мощности
источника q и обратно
пропорциональна коэффициенту теплопроводности 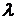 .
.
5.2 Движущийся
линейный источник в пластине
Расчет температурного поля при
движении линейного источника со скоростью v в пластине подобен предыдущей схеме
движения точечного источника на поверхности полубесконечного тела. В
соответствии с тепловой схемой - пластина - температура по оси z постоянна, и 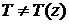 (рис. 15).
(рис. 15).
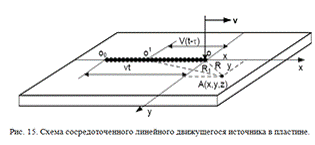
Приращение температуры от каждого
мгновенного линейного источника (16)
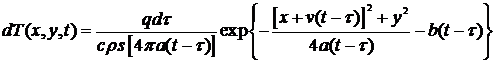 .
.
Суммируя значения температур от
мгновенных линейных источников при движении по оси x, плучаем:
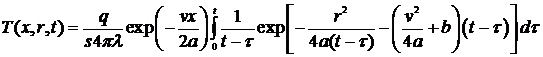 .
.
Не представляет трудности численно
рассчитать по приведенной формуле температурное поле, например в пакете Matlab,
где есть достаточно корректные функции интегрирования (см. П 1.5.). Тем не
менее, понятие предельного состояния, когда 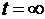 позволяет получить решение в
аналитических функциях. С помощью подстановки
позволяет получить решение в
аналитических функциях. С помощью подстановки
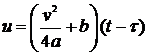
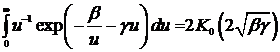
температурное поле линейного
источника, движущего в пластине со скоростью v при наличии теплообмена с
окружающей средой с коэффициентом температуроотдачи b
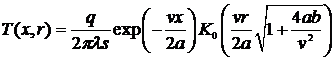 , (25)
, (25)
где K0 - функция Бесселя
первого рода нулевого порядка.
Как видно, даже упрощение расчетной
схемы предельного состояние процесса нагрева дает в результате выражение, в
котором используется специальная математическая функция, что затрудняет
качественный анализ формулы (25).
5.3 Движущийся по поверхности
плоского слоя точечный источник
Температурной поле движущегося по
поверхности плоского слоя толщиной s точечного источника можно вывести,
используя формулу для движущегося точечного источника на поверхности
полубесконечного тела (24). Считая поверхности плоского слоя адиабатическими, с
помощью метода отражения (рис. 11) получим следующее выражение для искомого
температурного поля в предельном состоянии:
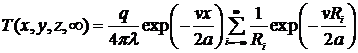 , (26)
, (26)
где 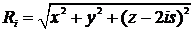 ; i - номер фиктивного источника в
системе отражений от адиабатических границ.
; i - номер фиктивного источника в
системе отражений от адиабатических границ.
При нагреве плоского слоя движущимся
источником можно различить три зоны, отличающиеся характером распространения
тепла (17). В зоне I, непосредственно прилегающей к
источнику тепла, распределение температуры в листе мало отличается от
распределения в массивном теле (рис. 14). По мере удаления от источника влияние
ограниченности тела по толщине сказывается все более заметно на распределении
температуры. В зоне II температура листа заметно повышена
по сравнению с температурой массивного тела. С удалением от источника тепловой
поток искажается не пропускающей тепла нижней плоскостью листа, и температура
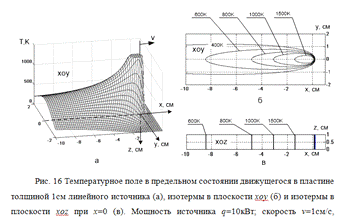
по толщине выравнивается. В зоне III, удаленной от источника
тепла, температура по толщине выравнена, и температурное поле в листе
приближается к полю линейного источника в пластине (рис. 16).
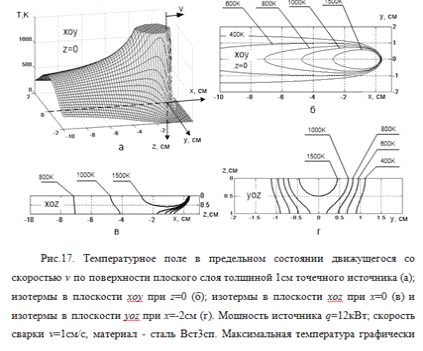
Влияние ограниченности размеров
изделия по ширине и длине на процесс распространения тепла можно учесть так же,
как и влияние ограниченности по глубине, введением дополнительных источников,
представляющих отражения основного источника в ограничивающих плоскостях,
которые предполагаются не пропускающими тепла. Таким способом можно
рассчитывать температурные поля в листах различной толщины, в полосах различной
ширины и у двугранных прямых углов, ограничивающих массивное тело. Наличие
непроницаемых для тепла граничных плоскостей стесняет поток тепла,
распространяющийся от источника, и повышает температуру тем больше, чем
значительнее стеснен тепловой поток.
5.4 Движущийся плоский источник в
стержне
Аналогично случаям полубесконечного
тела и пластины определяется температурное поле в стержне (рис. 18). Используя
(21), получим
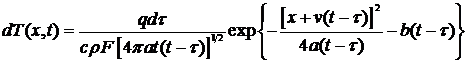 ;
;
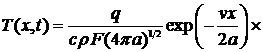
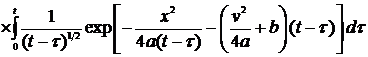 . (27)
. (27)
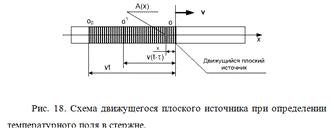
При 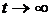 , используя подстановку u2 = t - τ и интеграл
[7]
, используя подстановку u2 = t - τ и интеграл
[7]
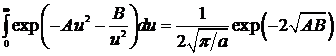 ,
,
получим
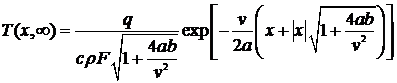 . (28)
. (28)
Видно, что в стержне без
поверхностной теплоотдачи (при b = 0) температура перед источником
падает по закону exp(-vx/a), а позади
него постоянна и равна q/(acpv). Теплоотдача
уменьшает температуру.
Структура формул для
полубесконечного тела (24), пластины (25), плоского слоя (26), и стержня (28)
одинакова: в первый сомножитель входит плотность мощности(q, q/s, q/F), далее в
показатель входят безразмерная продольная координата (критерий Пекле Ре) vx/(2a),
характеризующая асимметричность температурного поля, и функция, зависящая от
безразмерного радиус-вектора vR/(2a), vr/(2a) или
v|х|/(2а)). Влияние поверхностной теплоотдачи характеризуется безразмерным
критерием 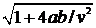 .
Однотипность структуры формул и определяет однотипность температурных полей в
различных телах.
.
Однотипность структуры формул и определяет однотипность температурных полей в
различных телах.
5.5 Периоды теплонасыщения и
выравнивания температур
Период теплонасыщения. Наступление
предельного состояния процесса проявляется в том, что связанное с источником
тепла подвижное температурное поле не изменяется со временем и только
перемещается вместе с источником. Такое предельное состояние процесса наступает
не сразу. В момент зажигания тепло дуги вводится в холодный металл, начальная
температура которого постоянна во всем объеме изделия. По мере горения дуги
тепло постепенно прогревает металл изделия. При этом размеры (длина, ширина,
глубина) прилегающей к источнику нагретой зоны увеличиваются. Когда
размеры зоны, нагретой выше определенной температуры Тт, перестают
увеличиваться, считают, что процесс распространения тепла в этой зоне
практически достиг предельного установившегося состояния. В более удаленных от
источника тепла зонах предельное состояние наступает позже, чем в зонах,
близких к источнику.
При действии неподвижного источника
постоянной мощности процесс распространения тепла стремится к предельному
стационарному состоянию, при котором температуры во всем поле остаются
постоянными. При действии источника постоянной мощности, перемещающегося
прямолинейно с постоянной скоростью, процесс распространения тепла
стремится к предельному квазистационарному состоянию, при котором
температуры остаются постоянными в подвижной системе координат, связанной с
источником тепла.
Пусть в начальный момент t=0 тело
находится при постоянной температуре, принимаемой за ноль отсчета. В момент t=0 начинает
действовать источник постоянной мощности q,
неподвижный (v=0) или
перемещающийся прямолинейно с постоянной скоростью v. Период
процесса распространения тепла от момента t=0 начала
действия источника до установления предельного состояния (стационарного или
квазистационарного) называется периодом теплонасыщения. В этом периоде
температура T(t) любой
точки тела, отнесенной к координатной системе, связанной с источником
тепла (т. е. подвижной или неподвижной, в зависимости от того, движется или
неподвижен источник), возрастает от начальной температуры Т(0)=0 до температуры
предельного состояния 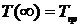 ,
наступающей теоретически при бесконечно длительном действии источника,
,
наступающей теоретически при бесконечно длительном действии источника, 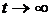 .
.
Температуру Т(t) данной точки (x,y,z) в периоде
теплонасыщения, т.е. при 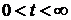 выражают в
разобранных нами ранее случаях общие уравнения процесса распространения тепла:
(23) - при точечном источнике на поверхности полубесконечного тела; (25) - при
линейном источнике в пластине с теплоотдачей.
выражают в
разобранных нами ранее случаях общие уравнения процесса распространения тепла:
(23) - при точечном источнике на поверхности полубесконечного тела; (25) - при
линейном источнике в пластине с теплоотдачей.
Для удобства расчета целесообразно
представить температуру Т(t) в периоде теплонасыщения произведением
температуры Тпр той же точки в предельном состоянии на коэффициент
теплонасыщения 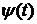 для той же
точки
для той же
точки
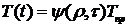 . (29)
. (29)
Коэффициент теплонасыщения,
очевидно, возрастает от нуля в начальный момент, 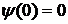 , до единицы в предельном состоянии,
, до единицы в предельном состоянии,
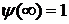 .
Возрастание этого коэффициента со временем характеризует интенсивность процесса
насыщения теплом данной точки тела.
.
Возрастание этого коэффициента со временем характеризует интенсивность процесса
насыщения теплом данной точки тела.
Коэффициенты теплонасыщения для трех
основных схем процесса распространения тепла при сварке представлены на рис. 19
в зависимости от безразмерных критериев τ пропорциональных времени t, и
критериев ρ,
пропорциональных
расстоянию рассматриваемой точки от источника тепла.
Для пространственного процесса
распространения тепла точечного источника постоянной мощности, перемещающегося
со скоростью v по
поверхности полубесконечного тела (рис. 13), коэффициент теплонасыщения 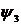 представлен
в зависимости от безразмерных критериев расстояния и времени (рис.19, а)
представлен
в зависимости от безразмерных критериев расстояния и времени (рис.19, а)
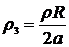 ;
; 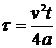 .
.
Для плоского процесса
распространения тепла от линейного источника постоянной мощности,
перемещающегося со скоростью v в пластине толщиной s с
теплоотдачей, характеризующейся коэффициентом 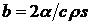 , коэфициент теплонасыщения
, коэфициент теплонасыщения 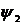 представлен
в зависимости от безразмерных Критериев расстояния и времени (рис.19, б)
представлен
в зависимости от безразмерных Критериев расстояния и времени (рис.19, б)

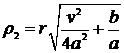 ;
; 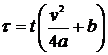 .
.
Для линейного процесса
распространения тепла от плоского источника постоянной мощности,
перемещающегося со скоростью v в стержне с поперечным сечением F и
периметром р с теплоотдачей, характеризующейся коэффициентом 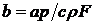 ,
коэффициент теплонасыщения
,
коэффициент теплонасыщения 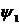 представлен в зависимости от
безразмерных критериев расстояния и времени (рис. 19, в)
представлен в зависимости от
безразмерных критериев расстояния и времени (рис. 19, в)
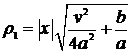 ;
; 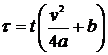 .
.
С возрастанием
продолжительности t действия сосредоточенного источника
температура во всем объеме нагреваемого тела возрастает, стремясь к предельной
температуре. Чем ближе расположена к источнику рассматриваемая точка
нагреваемого тела, т. е. чем меньше ее расстояние R, r или x; от
источника, тем раньше начинает возрастать температура, тем быстрее она
возрастает и тем раньше приближается к предельной. Таким образом, в близкой к
источнику области, нагреваемой до высоких температур, период теплонасыщения
заканчивается раньше, чем в удаленной области низких температур. В пластине
плоский поток тепла, распространяющегося от источника, более стеснен, чем
пространственный поток в полубесконечном теле, а линейный поток в стержне -
более, чем плоский поток в пластине. Чем более стеснен поток тепла, тем
медленнее насыщается теплом область, находящаяся на данном расстоянии от
источника тепла, т. е. тем ниже коэффициент ψ при данных значениях 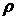 и
и 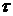 .
.
Период выравнивания температуры. По
окончании действия сосредоточенного источника введенное. им тепло продолжает
распространяться по металлу изделия вследствие теплопроводности. Неравномерное
распределение температуры, поддерживавшееся сосредоточенным источником, по
прекращении его действия выравнивается, и температура нагретой области
стремится к средней температуре тела. Период процесса распространения тепла,
начиная от момента t=tk прекращения
действия источника, называется периодом выравнивания температуры.
Пусть сосредоточенный источник
постоянной мощности q= const неподвижный
или перемещающийся прямолинейно с постоянной скоростью v=const начинает
действовать в момент t=0 и прекращает действие в момент t=tk (рис.20).
Изменение температуры определенной точки нагреваемого тела в периоде
теплонасыщения и предельного состояния, вычисленное по уравнению (29),
представлено схематически кривыми (1), (2) (рис. 20).
Расчет процесса распространения
тепла в периоде выравнивания температуры по окончании действия источника
постоянной мощности приведем к уже известному расчету процесса теплонасыщения,
применяя фиктивные источники и стоки тепла. Рассчитаем температуру в процессе
выравнивания в некоторый момент времени t (рис.20).
Пусть источник, в действительности отключенный в момент tk, продолжает
фиктивно действовать и дальше. Для моделирования этой ситуации в продолжение к
действительному источнику, существовавшему в течение времени tk, введем
фиктивный источник той же мощности (рис. 20). Для того, чтобы не изменить
теплового состояния тела, введем в момент tk фиктивный
сток тепла мощностью (-q), приложенный к тем же участкам
тела, что и фиктивный источник (+q) Очевидно, что действия равных по
мощности источника и стока, приложенных одновременно к тем же участкам тела,
взаимно уничтожаются. Таким образом, введение фиктивного источника и фиктивного
стока не изменяет теплового состояния тела, которое в действительности по
прекращении в момент tk действия
источника более тепла не получает.
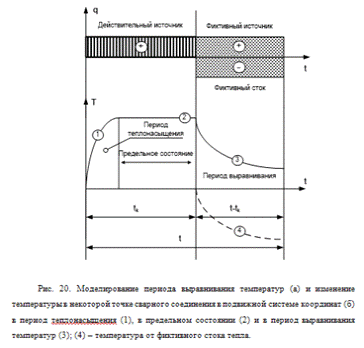
Температуру Тв (t)
в периоде выравнивания после прекращения в момент tk
действия источника постоянной мощности q
можно рассматривать как алгебраическую сумму температуры Т (t)
от продолжающего действовать источника q
и температуры Т (tk-t)
от начавшего действовать в момент tk
стока тепла (-q) (рис. 20).
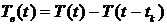 . (30)
. (30)
Заметим, что обе температуры в
правой части уравнения (30), как температуры в периоде теплонасыщения при
непрерывном действии источника q, можно выразить по уравнению (29)
через температуру предельного состояния Тпр и соответствующие
коэффициенты теплонасыщения
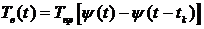 . (31)
. (31)
Таким образом, расчет температуры в
момент t в периоде
выравнивания сводится к расчету температур в периоде теплонасыщения.
Для трех основных схем процесса
распространения тепла при сварке удобно вести расчет, пользуясь графиками рис.
19. При расчете процесса распространения тепла в периоде выравнивания после
прекращения действия подвижного сосредоточенного источника следует иметь в
виду, что фиктивные источник и сток движутся так же, как двигался бы и
действительный источник, а с ними перемещается и начало подвижной системы
координат.
6. Расчет температурного поля мощных
быстродвижущихся источников нагрева
Температурные поля источников,
движущихся с любой скоростью v тем более вытянуты вдоль оси
движения х, чем выше скорость движения изотермы позади источника (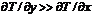 ) и,
следовательно, тем меньше продольные тепловые потоки относительно поперечных (
) и,
следовательно, тем меньше продольные тепловые потоки относительно поперечных (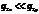 ). Схемы
быстродвижущихся источников построены на дополнительном допущении, что
продольные потоки отсутствуют (
). Схемы
быстродвижущихся источников построены на дополнительном допущении, что
продольные потоки отсутствуют (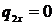 ), что, в свою очередь, позволяет
уменьшить мерность температурной задачи на единицу и, следовательно, значительно
упростить расчетные схемы. Это достоинство быстродвижущихся источников
обусловило их популярность для расчетов температурных полей при сварке. В
пределе скорость движения источника и его мощность неограниченно возрастают, а
их отношение остается постоянным:
), что, в свою очередь, позволяет
уменьшить мерность температурной задачи на единицу и, следовательно, значительно
упростить расчетные схемы. Это достоинство быстродвижущихся источников
обусловило их популярность для расчетов температурных полей при сварке. В
пределе скорость движения источника и его мощность неограниченно возрастают, а
их отношение остается постоянным:
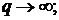
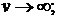
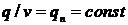 , (32)
, (32)
где 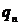 имеет размерность Дж/см и носит
название погонной энергии.
имеет размерность Дж/см и носит
название погонной энергии.
.1 Быстродвижущийся точечный источник
на поверхности полубесконечного тела
Уравнение температурного поля для
рассматриваемого случая можно получить на основе формулы (24) для предельного
состояния процесса нагрева плубесконечного тела движущимся точечным источником
подстановкой условия (32) и заменой x=-vt. С учетом 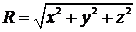 из
выражения (24) получаем:
из
выражения (24) получаем:
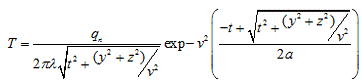 , (33)
, (33)
где t - время, отсчитываемое от
момента, когда источник теплоты пересек перпендикулярную оси x плоскость, в
которой расположена рассматриваемая точка (рис. ).
При 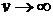 значение выражения
значение выражения 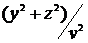 мало по
сравнению с
мало по
сравнению с 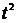 . Тогда
. Тогда
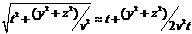 .
.
На основании формулы (24) и
приведенных рассуждений температурное поле при действии мощного
быстродвижущегося точечного источника на поверхности полубесконечного тела
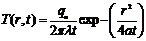 , (34)
, (34)
где 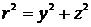 .
.
В данном выражении отсутствует
координата x, что следует из принятой схемы мощного быстродвижущегося точечного
источника, при которой тепло в направлении этой оси не распространяется (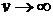 ). Уравнение
(34) может быть использовано для технических расчетов в случае больших, но
ограниченных скоростей сварки. Введя замену
). Уравнение
(34) может быть использовано для технических расчетов в случае больших, но
ограниченных скоростей сварки. Введя замену 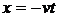 получим выражение, позволяющее
построить изолинии температурного поля в плоскости xy:
получим выражение, позволяющее
построить изолинии температурного поля в плоскости xy:
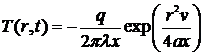 . (35)
. (35)
Если данное выражение удобно для
построения изолиний температурного поля, то формула (34) позволяет рассчитать
термические циклы точек сварного соединения T(r,t). При расчете температур по
приведенным формулам (34), (35) следует учитывать, что при t=0 и x 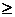 0 корректное
решение отсутствует.
0 корректное
решение отсутствует.
Допущение о незначительности
теплопроводности вдоль оси x и наличии теплового потока в основном в плоскости
yz позволяет
вывести уравнение (34) другим, более наглядным способом. Выделим в
полубесконечном теле тонкий поперечный слой (толщиной s=1), в
который внесена погонная энергия Q1=q/v (Дж/cм) в момент
пересечения слоя источником теплоты (рис. 21).
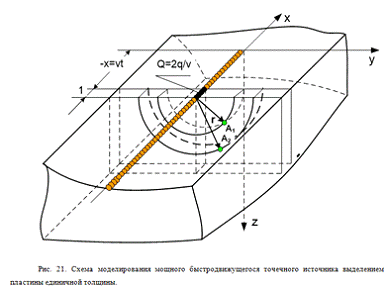

Сравним температурные поля
движущегося точечного источника в предельном состоянии (рис. 14) и в
рассматриваемом случае (рис. 21). Оказывается, что геометрические
характеристики изотерм практически одинаковы за исключением малой области в
начале координат. Следует отметить, что распределение температуры по
отрицательной части оси x в указанных случаях идентично.
6.2 Линейный мощный
быстродвижущийся источник в пластине
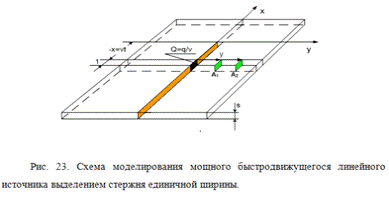
Вывод формулы температурного
поля для линейного мощного быстродвижущегося источника в пластине основывается
на схеме, аналогичной предыдущему случаю точечного источника (рис. 23).
Выделим в бесконечной пластине
тонкий поперечный слой с единичной шириной. Полагаем, что тепло вдоль оси x не
распространяется при 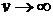 , но, в
соответствии с тепловой схемой «пластина» оно не распространяется и вдоль оси
z. Поэтому в выделенном слое теплопроводность будет одномерной вдоль оси y, что
соответствует тепловой схеме мгновенного плоского источника в стержне (21).
Проведя в этом выражении замену
, но, в
соответствии с тепловой схемой «пластина» оно не распространяется и вдоль оси
z. Поэтому в выделенном слое теплопроводность будет одномерной вдоль оси y, что
соответствует тепловой схеме мгновенного плоского источника в стержне (21).
Проведя в этом выражении замену 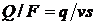 , получим
, получим
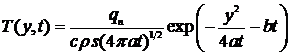 , (36)
, (36)
где в данном случае коэффициент
температуроотдачи 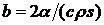 соответствует
схеме линейного источника. Изотермы температурного поля мощного
быстродвижущегося линейного источника в пластине приведены на рис. 24. Как и в
предыдущем случае быстродвижущегося точечного источника, нагрев при
положительных значениях координаты x отсутствует, так как тепло в этом
направлении не распространяется.
соответствует
схеме линейного источника. Изотермы температурного поля мощного
быстродвижущегося линейного источника в пластине приведены на рис. 24. Как и в
предыдущем случае быстродвижущегося точечного источника, нагрев при
положительных значениях координаты x отсутствует, так как тепло в этом
направлении не распространяется.

Сравнение рис. 16,б и рис. 24,а
показывает, что результаты расчета температурного поля по схеме предельного
состояния процесса нагрева и по схеме мощного быстродвижущегося источника
отличаются незначительно, что дает возможность применять для расчета тепловых
процессов при сварке более простое выражение (36).
7. Расчет
температурного поля непосредственным интегрированием
7.1 Расчет
температурного поля при сварке методом интегрирования
Метод источников в расчетах тепловых
процессов при сварке основан, в связи с линейностью дифференциального уравнения
теплопроводности, на суммировании температурных полей при действии заданной
совокупности мгновенных источников нагрева, как указано в формуле (3).
Стремление получить аналитическое выражение для температурного поля требует
введение некоторых допущений. Так, разделение термического цикла на периоды
теплонасыщения и предельного состояния дает возможность вывести аналитические
формулы для расчета температурного поля при сварке в предельном состоянии
процесса нагрева в подвижной системе координат (24), (25). Дальнейшее упрощение
аналитических формул расчета температурного поля связано со схемой мощных
быстродвижущихся источников, как показано в формулах (35), (36). При этом оказывается,
что наиболее простые зависимости, характерные для мощных быстродвижущихся
источников, приводят к расчетным результатам, практически адекватным схеме
предельного состояния. Это существенно, например, для расчета температурного
поля линейного источника в пластине, когда результирующая формула предельного
состояния процесса нагрева (25) содержит интегральную функцию Бесселя, а схема
быстродвижущегося источника (36), не содержащая специальных интегральных
функций и доступна для качественного анализа.
Аналитические формулы расчета
тепловых процессов при сварке обладают неоспоримым достоинством возможности
оперативного определения влияния параметров режима сварки и теплофизических
свойств свариваемых материалов на характеристики температурного поля. Однако,
корректность применения этих формул нужно доказать решением задачи без
введенных выше допущений, то есть непосредственным интегрированием совокупности
мгновенных сосредоточенных источников.
Пусть по поверхности
полубесконечного тела от начала неподвижной системы координат (x=0,
y=0) движется по оси
x (y=0) точечный
источник сварочного нагрева со скоростью v (рис. 25). Пройдя расстояние xf,
источник отключается в точке F. Необходимо определить температуру в точке А в
момент времени t. Предположим, что источник в это время находится в точке С.
Представим движение источника от точки О до точки С совокупностью мгновенных
точечных источников В, действующих в момент времени , расстояние точки
А от каждого из которорых - R.
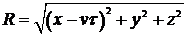 .
.
На рис 25 схема процесса
представлена в плоскости xy, поскольку координаты y и z при интегрировании от
времени не зависят. Приращение температуры от каждого мгновенного точечного
источника нагрева
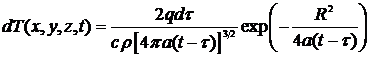 . 37
. 37
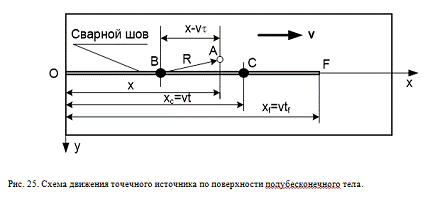
Источник нагрева имеет
ограниченное время действия tf. Если время определения температуры t
меньше tf, то интегрирование выражения (37) нужно осуществить в
пределах tin = t. Если же время t больше, чем время
действия источника, то tin = tf. Таким образом, выражение
для определения температурного поля движущегося по поверхности полубесконечного
тела точечного источника тепла в неподвижной системе координат следующее:
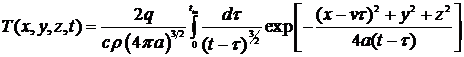 . 38
. 38
Формула (38) готова для численного
интегрирования, например с помощью математического обеспечения пакета MatLab (см. П
1.5.). На рис. 26 приведены изотермы температурного поля движущегося точечного
источника, рассчитанные путем непосредственного интегрирования выражения (38).
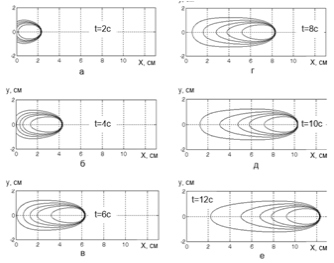
Как видно из приведенного рисунка,
непосредственное интегрирование позволяет рассчитать температурное поле в
начале действия источника, что является существенным при анализе
теплопроводности коротких сварных швов, например, при выполнении сборочных
прихваток. С увеличением времени действия источника результаты расчета,
полученные интегрированием (рис.26, е) и применением схемы предельного
состояния процесса нагрева (рис. 14) становятся близкими. Отличие температурных
полей для указанных схем расчета в начальные моменты времени (рис. 26, а, б, в,
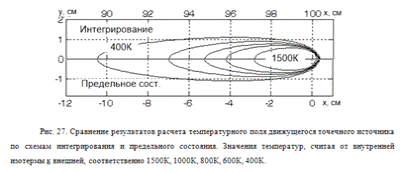
г, д) обусловлено процессом теплонасыщения. Сравнительные результаты расчета по
этим двум схемам при времени действия источника 100с даны на рис. 27. Здесь в
верхней части рисунка построены изотермы, рассчитанные непосредственным
интегрированием по выражению (38), а в нижней - по формуле предельного
состояния процесса нагрева при движении точечного источника по поверхности
полубесконечного тела. Результаты идентичны, поскольку достигнуто предельное
состояние процесса нагрева.
Для линейного источника, движущегося
в пластине, расчет температурного поля методом непосредственного интегрирования
расчетная схема соответствует рис. 25, где вместо R необходимо использовать
радиус
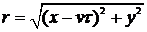 .
.
На основе формулы для мгновенного
линейного источника в пластине с теплоотдачей (16) получаем:
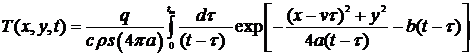 . 39
. 39
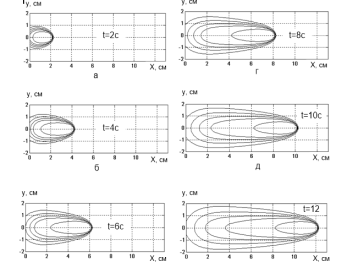
Результаты расчета температурного
поля движущегося линейного источника в различные моменты времени показаны на
рис. 28. Видно, что изотермы в начальный период движения источника имею более
ярко выраженную особенность, чем для точечного источника. Эта особенность
выражается в большей полноте изотермических линий в хвостовой части
температурного поля по сравнению со случаем предельного состояния процесса
нагрева (рис. 16). Причиной такого характера температурного поля является
относительно длительный период теплонасыщения и, соответственно, более позднее
наступление предельного состояния, при достижении которого результаты расчета
по обеим схемам совпадают.
7.2 Расчет периодов теплонасыщения и
выравнивания температур
Периоды теплонасыщения и
выравнивания температуры для точек сварного соединения можно также рассчитать
методом непосредственного интегрирования. Для этого удобно воспользоваться
выражением температурного поля в подвижной системе координат. Например, для
движущегося по поверхности полубесконечного тела точечного источника (рис.13)
это формула (23):
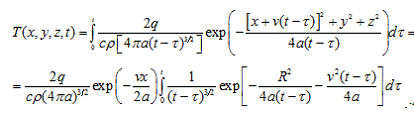 . 40
. 40
Подстановка в эту формулу конкретных
координат исследуемой точки и диапазона значений времени позволяет путем
интегрирования, например в MatLab, получить необходимые зависимости. Например,
пусть по поверхности полубесконечного тела со скоростью v=1см/с вдоль оси x
движется точечный источник мощностью q=10000 Вт. Через время tf=10с
источник отключается. Отметим несколько точек по оси x в подвижной системе
координат на расстоянии y от оси сварного шва (рис.28).
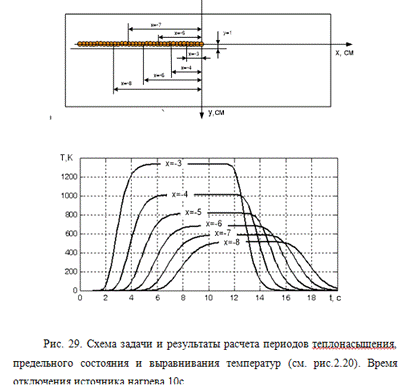
На рис. 20 приведена качественная
картина периодов сварочного нагрева. Метод непосредственного интегрирования
(рис. 28) позволяет получить конкретные результаты, на основе которых можно
сделать вывод о корректности схемы расчета периода выравнивания температур
заданием фиктивного источника и стока тепла в соответствии с формулой (30).
Итак, выше рассмотрены три схемы
расчета температуры при сварке: расчет в предельном состоянии процесса нагрева;
расчет по схеме мощного быстродвижущегося источника и расчет методом
непосредственного интегрирования. Из приведенных результатов видно, что
указанные схемы расчета температурного поля при сварке в условиях предельного
состояния процесса нагрева приводят к очень близким результатам, и для
практических расчетов при анализе сварочных процессов в указанных условиях
рационально пользоваться схемой мощных быстродвижущихся источников. В случае
необходимости анализа температуры в начальный период движения сварочного
источника, при сварке коротких швов и т.п. необходимо определить степень
законченности периода теплонасыщения по номограммам рис. 19. и скорректировать
расчет по формуле (31) или, что более рационально, воспользоваться методом
непосредственного интегрирования.
Литература
Вакатов
А.В. Исследование процесса и разработка технологии контактной точечной сварки
оцинкованной стали: Дис. канд. техн. наук: Спец. 05.03.06 / А. В. Вакатов;
Науч. руководитель Ю.В. Казаков. - Тольятти: ТПИ, 1996. - 136 с. - Библиогр.:
с. 93-101. - На правах рукописи.
Ельцов
В.В. Ремонтная сварка и наплавка изделий из сплавов магния и алюминия
трехфазной дугой: Дис. д-ра техн. наук: Спец. 05.03.06 / В. В. Ельцов. -
Тольятти: ТГУ, 2012. - 311 с. - Библиогр.: с. 300-310. - На правах рукописи.
Еремичев
А.А. Кинетика коррозионно-механического разрушения сварных соединений
биметаллических котлов для варки целлюлозы: Дис. канд. техн. наук: Спец.
05.03.06 / А. А. Еремичев; Науч. руководители Б.Н. Перевезенцев, С.Х. Петерайтис.
- Тольятти: ТПИ, 2003. - 180 с. - Библиогр.: с. 159-170. - На правах рукописи.
Медведев
А.Ю. Повышение стойкости вольфрамового активированного стержневого катода при
аргоно-дуговой сварке: Автореферат дис. канд. техн. наук: Спец. 05.03.06 / А.
Ю. Медведев; Науч. руководитель В.В. Атрощенко. - Тольятти: ТГУ, 2013. - 20 с.:
ил. - Библиогр.: с. 20. - На правах рукописи.
Цепенев
Р.А. Автоматическое управление процессом сварки: Учеб. пособие / Р. А. Цепенев;
ТолПИ, Каф. "Оборуд. и технология сварочного пр-ва". - Тольятти:
ТолПИ, 2011. - 76 с.: ил.
Кусков
Ю.В.
"Бег
к вершинам мастерства..." или классический маркетинг на рынке сварочных
материалов / Ю. В. Кусков; АО СпецЭлектрод; Моск. регион. отд-ние рос.
науч.-техн. свароч. о-ва. - М.: Б.и., 2010; Чикаго. - 88 с.: ил. - (Б-ка
"СпецЭлектрод", Вып. 5).
Малышев
Б.Д. Безопасность труда при выполнении сварочных работ в строительстве: Учеб.
пособие для сред. проф.-техн. училищ / Б. Д. Малышев, И. Г. Гетия. - М.:
Стройиздат, 1988. - 96 с.: ил. - ISBN 5-274-00033-9: 6р.
Вопросы
сварочного производства: Темат. сб. науч. тр.№ 207 / М-во высш. и сред. спец.
образования СССР, Челяб. политехн. ин-т им. Ленин. комсомола, каф. сварочн.
пр-ва. - Челябинск: Челяб. ин-т им. Ленин. комсомола, 1979. - 155 с.: ил.
Контактная
точечная сварка: Метод. указания к курсовой работе для студ. спец.
120500-120600"Оборуд. и технология сварочного пр-ва",
"Восстановление деталей машин". / Сост. А.С. Климов; ТГУ. Каф."
Оборуд. и технология сварочного пр-ва". - Тольятти: ТГУ, 2012. - 26 с.:
ил.
Конспект
лекций по разделу "Дефекты сварных соединений и контроль качества
сварки" для подготовки к аттестации на специалиста по сварочному
производству. - Тольятти: ТГУ, 2012. - 46 с.: ил.
Программа
и контрольная работа по дисциплине "Автоматизация сварочных
процессов": Учеб. пособие / Цепенев Р.А.; ТолПИ. Каф. "Оборуд. и
технология сварочного пр-ва". - Тольятти: ТолПИ, 2011. - 61 с.
Практика
работы электродной фирмы: Сб. докл. / Сост. Г.Н. Полищук и др.; Ассоц.
"Электрод" стран СНГ; АО СпецЭлектрод. - М.: Б.и., 2010; СПб. - 87
с.: ил.