Сучасні методи автоматичного керування
Сучасні методи автоматичного
керування
1. Метод простору станів
автоматичний управління зв’язок
Традиційний класичний метод дослідження динаміки систем
автоматичного управління (САУ) полягає у тому, що по рівняннях ланок системи
складається загальна структурна схема системи та визначається загальна
передавальна функція замкненої системи, що пов’язує вхідну та вихідну величини.
З передавальної функції можна одержати одне загальне диференційне рівняння
замкненої системи n-го порядку. Проте поведінку системи у часі можна
характеризувати не тільки вихідною величиною системи, але й проміжними змінними
у ланцюзі системи, число яких дорівнює порядку системи n. Ці проміжні змінні
треба обирати так, щоб після завдання початкових значень цим n змінним ми могли
б визначити значення змінної виходу у будь-який подальший момент часу, тобто
визначити стан системи у будь-який момент часу. Цей n-мірний вектор змінних
називається тому вектором стану системи, вся сукупність можливих значень цього
вектору складає простір станів системи.
В просторі станів властивості системи управління описуються
не одним диференційним рівнянням n-го порядку, а системою з n диференційних
рівнянь 1-го порядку у нормальній формі. Вибрати змінні стану та перейти до
системи рівнянь у нормальній формі можна різними способами.
Розглянемо три найбільш розповсюджених способи.
Нехай загальне диференційне рівняння замкненої системи має
вид:
(pn + an-1pn-1 + ... + a1p + a0)y = (bnpn + bn-1pn-1 + ....
+ b1p + b0)u , (1.1)
де y - вихідна величина , а u - вхідний вплив.
Тут покладена зворотна нумерація коефіцієнтів рівняння, в
порівнянні до загально прийнятої, для зручності запису подальших формул, а
також враховано, що якщо дійсний порядок m правої частини (1.1) менше порядку
лівої частини n (m<n), то всі коефіцієнти bi=0 при i=n-m+1,...,n.
Перший спосіб. Введемо змінні станів x1, ..., xn наступним чином:
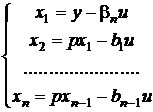 ,
(1.2)
,
(1.2)
де bi- деякі постійні коефіцієнти. Тоді рівняння (1.1) набере вигляд:
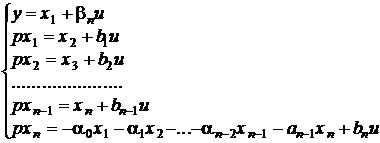 .
(1.3)
.
(1.3)
Можна довести, що розв’язок системи (1.3) буде збігатися з розв’язком
рівняння (1.1), якщо коефіцієнти bi будуть вирахуванні за рекурентними
формулами:
=bn-1 - an-1bn,=bn-2 - an-2bn - an-1b1,=bn-3 - an-3bn - an-1b2 - an-2b1,
.........................................=b0 - a0bn - an-1bn-1 - an-2bn-2 - ... - a2b2 - a1b1,
а початковими умовами будуть (згідно з (1.2)):(0)=y(0) - bnu(0);(0)=py(0) - bn pu(0) -
b1u(0);................. (1.4)(0)=pn-1y(0) - b0 pn-1u(0) - b1 pn-2u(0) -
... - bn-2 pu(0) - bn-1 u(0),
де 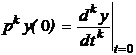 і
і 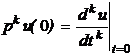 .
.
У матричній формі система (1.3) буде мати вид:
р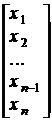 =
=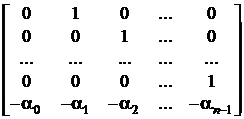 *
*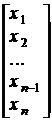 +
+ u.
u.
Вибір змінних стану згідно формул (1.2) застосовується при розв’язанні
ряду задач оптимального управління, а також при моделюванні процесів у САУ на
аналогових обчислювальних машинах (АОМ). Дійсно, система рівнянь (1.3) може
бути змодельована з використанням тільки інтеграторів та підсилювачів. Їй
відповідає структурна схема, показана на рис.1.1. Вона виходить з (1.3), якщо
останню поділити на p.
Другий спосіб. Віднімемо від правої частини (1.1) ліву та врахуємо,
що звичайно порядок правої частини n вище порядку лівої частини m:
ypn - pn-1yan-1 - ... - am+1pm+1y + pm(bmu - dmy) + ... +
+ p2(b2u - a2y) + p(b1u - a1y) + b0u - a0y = 0.
Розділимо все на pn та будемо виносити 1/p за дужки:
-y +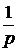 (-yan-1 +
(-yan-1 +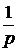 (-an-2y +...+
(-an-2y +...+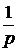 (-amy+bmu+
(-amy+bmu+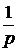 (...+
(...+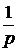 (b1u-a1y+
(b1u-a1y+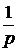 (b0u-a0y)))...))=0.
(b0u-a0y)))...))=0.
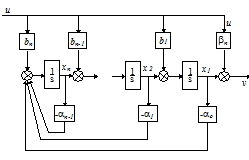
Рис. 1.1
За x1 приймемо вираз у дужках найглибшого рівня, поділений на p:
=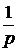 (b0u - a0y).
(b0u - a0y).
Вираз у дужках наступного рівня входження, поділений на p, буде x2:
=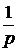 (b1u - a1y+
(b1u - a1y+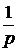 (b0u - a0y)),
(b0u - a0y)),
і так далі, поки не буде вичерпано усі дужки. Звідси видно, що xn=y. А
рівнянню (1.1) буде відповідати така система рівнянь 1-го порядку:
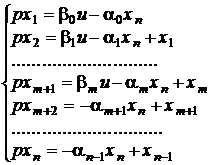 ;
(1.5)=xn .
;
(1.5)=xn .
Тут змінні xi мають інший зміст, в порівнянні з (1.3), але ця
система також відповідає повністю рівнянню (1.1) (при m<n).
Другий спосіб вибору змінних стану також застосовується при
моделюванні САУ на АОМ. Також як і 1-й спосіб він дозволяє побудувати
електронну модель з мінімальним числом підсилювачів.
Системі рівнянь (1.5) відповідає структурна схема на рис.1.2.
Вадою систем рівнянь (1.3) та (1.5) є те, що вибрані в них
змінні стану, взагалі кажучи, не збігають з реально існуючими у системі
управління фізичними величинами (змінними) (напругами, струмами, швидкостями
обертання і т.п.).
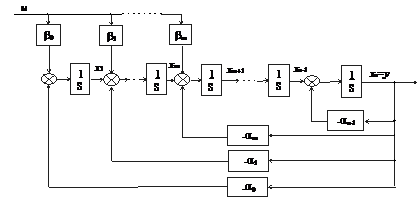
Рис. 1.2
Для розв’язання цих систем рівнянь необхідно знати, як видно з (1.4),
початкові значення (n-1)-ої похідної вихідної величини. Визначення цих значень
через фізичні початкові умови системи керування при великому порядку рівняння
(1.1) є трудомісткою задачею, і навіть при нульових фізичних початкових умовах
початкові значення похідних y можуть опинитись ненульовими.
Третій спосіб полягає у тому, що у якості змінних станів обирають
реально існуючі у САУ фізичні змінні. В електричних ланцюгах - це напруги на
ємностях та струми в індуктивностях (або відповідно величини зарядів та
потокозчеплень). В механічних системах - це узагальнені координати та узагальнені
швидкості (у декартовій системі координат - це координати та швидкості їх
зміни, у центральних кутових координатах - це кути повороту та кутові
швидкості). При такому виборі змінних рівняння ланок системи природнім чином
одержуються у нормальній формі.
Наприклад, розглянемо електричний ланцюг з послідовно з’єднаних R, L і
С (див. рис.1.3).
Виберемо у якості змінних стану напругу на ємності x1=uc та струм в
індуктивності x2=i. Тоді рівняння системи
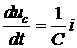

 та
та
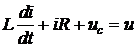
наберуть вигляд
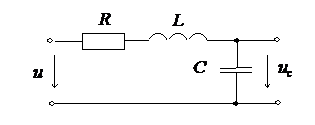
Рис. 1.3
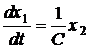 ;
;
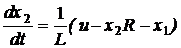 .
.
Представивши в аналогічному виді рівняння всіх ланок САУ та
з’єднавши їх в одну систему, у загальному випадку одержимо (якщо у нас тільки
один вхідний вплив u):

 . (1.6)
. (1.6)
Причому у праві частини не обов’язково входять всі n змінних та u,
тобто багато з коефіцієнтів будуть дорівнювати нулю. Не дивлячись на це
структурна схема, відповідна цій системі рівнянь, буде мати, як правило, більшу
кількість підсилювачів та суматорів, ніж попередні дві схеми. Це є вадою такого
способу вибору змінних стану при моделюванні на АОМ.
В матричної формі система (1.6) має вид
p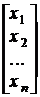 =
= +
+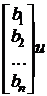 . (1.7)
. (1.7)
Вихідна змінна y може залежати від декількох змінних стану,
тому система (1.7) має бути доповнена виразом для розрахунку вихідної змінної:
y = [c1 c2 ... cn]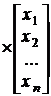 , (1.8)
, (1.8)
де ci - постійні коефіцієнти, що пов’язують внесок xi в y.
Частина з них може дорівнювати нулю.
2.
Багатовимірні системи управління. Стандартна форма рівнянь стану

Рис. 2.1
Багатовимірними називаються системи управління, які мають дві
або декілька величин, що задають впливу, та дві або декілька величини y, що
регулюються. При цьому може матись також будь-яке число збурювальних впливів.
Таку систему можна зобразити чином, показаним на рис. 2.1, де u1, ..., um -
вхідні впливи (задавальні та збурювальні); y1,...,yr - вихідні (регульовані)
змінні.
Система управління має n змінних стану та описується системою
диференційних рівнянь 1-го порядку:
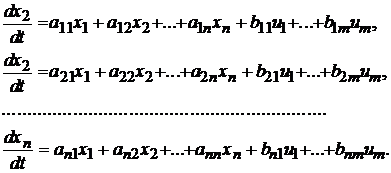

Вона доповнюється r алгебраїчними рівняннями виходу:
=c11x1+c12x2+...+c1nxn ,
.........................................=cr1x1+cr2x2+...+c1nxn
.
Ці рівняння можуть бути записані у матричній формі: (p =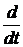 )
)
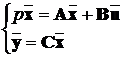 (2.1)
(2.1)
Це стандартна форма запису рівнянь стану.
Тут 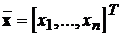 - вектор змінних стану;
- вектор змінних стану; 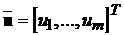 - вектор вхідних впливів;
- вектор вхідних впливів; 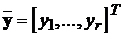 - вектор вихідних змінних. Через А, В, С позначені:
- вектор вихідних змінних. Через А, В, С позначені:
власна параметрична матриця системи
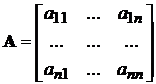 ;
;
вхідна матриця системи (або матриця входу)
=  ;
;
вихідна матриця системи (або матриця виходу)
= 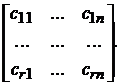
Характеристичне рівняння цієї системи має вигляд det[lI - A] = 0, де I - одинична матриця n-го порядку.
3.
Аналіз САУ в просторі станів
Отже САУ у просторі станів описуються системою диференційних
рівнянь першого порядку:
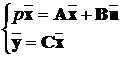 (3.1)
(3.1)
Розв’язок системи (3.1) може бути одержано різними методами
чисельного інтегрування (Ейлера, Рунге-Кутта, Хемінга та ін.). Окрім того,
розв’язок векторного диференційного рівняння (3.1) можна одержати за допомогою
такого ж методу, який застосовують для розв’язання рівняння першого порядку.
Дійсно, розглянемо таке рівняння:
 (3.2)
(3.2)
Перетворюючи (3.2) за Лапласом, отримаємо
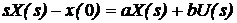
або 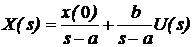 . (3.3)
. (3.3)
Взявши зворотне перетворення Лапласа від рівняння (3.3),
будемо мати:
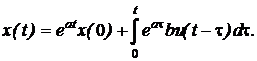 (3.4)
(3.4)
Розв’язок векторно-матричного рівняння (3.1) отримаємо
аналогічним чином:
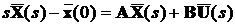
або 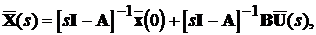
де I - одинична матриця; 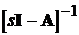 -
матриця, зворотна матриці
-
матриця, зворотна матриці 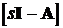 .
.
По аналогії з розв’язком (3.4) записуємо
 (3.5)
(3.5)
де eAt = L-1{[sI - A]-1}- матрична функція, матрична експонента.
Загальним розв’язком однорідного рівняння (3.1) при 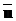 (t)=0, що описує вільні коливання системи при
ненульових початкових умовах, є:
(t)=0, що описує вільні коливання системи при
ненульових початкових умовах, є:
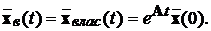 (3.6)
(3.6)
Функцію 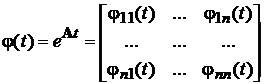 називають перехідною або фундаментальною матрицею.
називають перехідною або фундаментальною матрицею.
В розгорненій формі вираз (3.6) має вигляд:

Звідки:
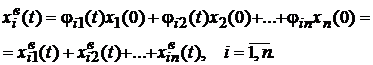
 (3.7)
(3.7)
Вираз (3.7) описує зміну i-ї складової вектору стану 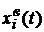 , що викликається початковими умовами
, що викликається початковими умовами 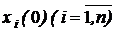 , а кожен з членів виразу у правій частині (3.7)
, а кожен з членів виразу у правій частині (3.7) 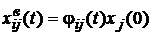 представляє собою зміну i-ї складової вектору стану
представляє собою зміну i-ї складової вектору стану 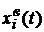 , що викликається j-ю початковою умовою.
, що викликається j-ю початковою умовою.
Отже, кожен з елементів 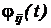 перехідної
матриці j(t) можна розглядати, як реакцію i-ї змінної
стану при xj(0)=1 та нульових початкових значеннях всіх інших змінних стану.
перехідної
матриці j(t) можна розглядати, як реакцію i-ї змінної
стану при xj(0)=1 та нульових початкових значеннях всіх інших змінних стану.
Вираз (3.6) є першим доданком у формулі (3.5). Другий доданок у виразі
(3.5) описує реакцію системи на вектор управління 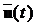 і утримує у собі змушений рух системи
і утримує у собі змушений рух системи 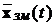 та вільну складову при нульових початкових умовах.
та вільну складову при нульових початкових умовах.
Враховуючи друге рівняння системи (3.1) та рівняння (3.5) для вихідного
вектору отримаємо:
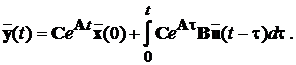 (3.8)
(3.8)
4.
Методи обчислення перехідної матриці
Обчислення перехідної матриці 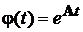 у
випадку, коли матриця А не залежить від часу, можна виконати одним з наступних
способів.
у
випадку, коли матриця А не залежить від часу, можна виконати одним з наступних
способів.
1 спосіб. Обчислення за допомогою зворотного перетворення Лапласа.
=L-1{[sI - A]-1} ,
де [sI - A]-1=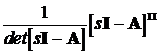 , (4.1)
, (4.1)
а символ п означає приєднану матрицю. Вона складається з
алгебраїчних доповнень відповідних елементів транспонованої вихідної матриці
[sI - A]T. Після обчислення зворотної матриці (4.1) знаходять власні числа
матриці А як корені рівняння det[sI -A]=0, та визначають оригінали кожного
члена матриці [sI - A]-1. При невисокому порядку матриці А це можна зробити за
допомогою таблиць перетворень Лапласа, у загальному ж випадку можна використати
теорему розкладання.
Приклад 1. Нехай маємо систему рівнянь
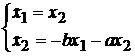 Þ
Þ 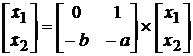 ,
,
тоді 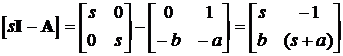 .
.
В результаті обертання матриці отримаємо:
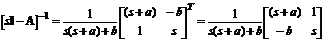 .
.
Характеристичне рівняння та його корені мають вигляд
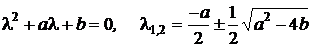 .
.
Знаходимо оригінали кожного члена матриці по теоремі
розкладання. Тоді:
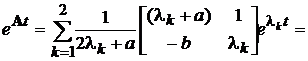
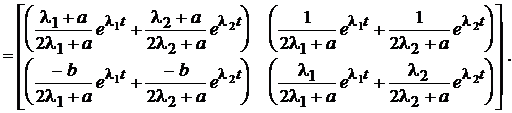
спосіб. Використання теореми (формули) Сільвестра.
Згідно теоремі Сільвестра
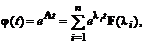 (4.2)
(4.2)
де li власні числа матриці А 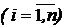 ; F(li) матриця,
що вираховується за формулою
; F(li) матриця,
що вираховується за формулою
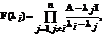 (4.3)
(4.3)
- одинична матриця.
Приклад 2. Нехай
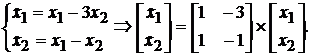
В цьому випадку характеристичне рiвняння має вигляд:
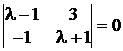 .
.
Звiдки маємо:
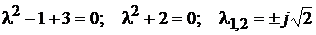 .
.
За формулою (4.3) отримаємо
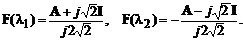
Підставляємо знайдені матриці в формулу (4.2):
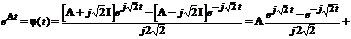
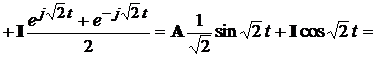
=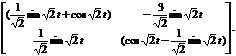
спосіб. Обчислення за допомогою степеневого ряду.
Матрична експонента може бути представлена у вигляді ряду:
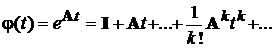 .
.
Можна обмежитись деякою кiлькiстю членів та одержати
приблизне значення j(t). Із збільшенням t приходиться враховувати все більше та
більше членів. Тому при обчисленні значення для конкретного t за допомогою ЕОМ
можна рекомендувати алгоритм, що витікає з наступної тотожності:
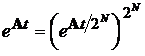 ,
,
де N - довільне ціле число. Воно завжди може бути взято
настільки великим, що наближення
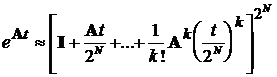 (4.4)
(4.4)
при фіксованому k ³ 1 стане задовільним. Звичайно k = 3
- 6.
Якщо нам треба вирахувати значення eAt на деякому інтервалі часу [0, T]
з кроком Dt, то вираховують спочатку 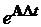 по формулі (4.4), а потім знаходять послідовно
значення матричної експоненти у всіх точках часового інтервалу по рекурентній
формулі:
по формулі (4.4), а потім знаходять послідовно
значення матричної експоненти у всіх точках часового інтервалу по рекурентній
формулі:
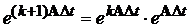 ,
k=
,
k=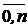 ,
,
де  .
.
5.
Матрична передавальна функція. Матрична вагова і матрична перехідна функції та
їх використання для розрахунку перехідних процесів
САУ у просторі станів описується системою диференційних
рівнянь першого порядку:
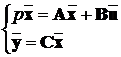 (5.1)
(5.1)
Застосуємо до цієї системи перетворення Лапласа. Отримаємо
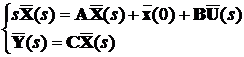 .
.
Кладучи початкові умови нульовими 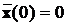 ,
знайдемо
,
знайдемо
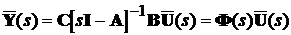 .
(5.2)
.
(5.2)
Матрицю Ф(s) називають матричною передавальною функцією
системи. Згідно з (5.2) вона дорівнює
Ф(s)=C[sI - A]-1B (5.3)
і пов’язує вектор входу 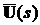 з
вектором виходу
з
вектором виходу 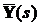 . Якщо m - розмірність вхідного вектору
. Якщо m - розмірність вхідного вектору 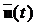 , а r - розмірність вектору виходу
, а r - розмірність вектору виходу 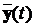 , то матрична передавальна функція представляє собою
матрицю розміру (r´m), елементи jij(s) якої представляють передавальні функції, що
пов’язують зображення i-ї вихідної змінної та j-го вхідного впливу, тобто:
, то матрична передавальна функція представляє собою
матрицю розміру (r´m), елементи jij(s) якої представляють передавальні функції, що
пов’язують зображення i-ї вихідної змінної та j-го вхідного впливу, тобто:
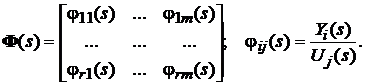
Оригінал матричної передавальної функції Ф(s), також є
матрицею і називається матричною ваговою функцією:
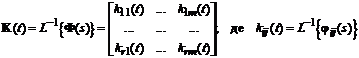 .
(5.4)
.
(5.4)
Кожна вагова функція kij(t) є реакцією i-ї вихідної змінної
на j-й вхідний вплив у вигляді d-функції і нульових інших впливах.
Згідно формули (5.3) маємо:
(t)=L-1{C[sI - A]-1B} = CL-1{[sI - A]-1}B = CeAtB . (5.5)
Матрична перехідна функція вводиться наступним чином
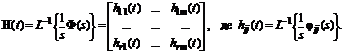 (5.6)
(5.6)
Тут кожна елементарна перехідна функція hij(t) є реакцією i-ї вихідної
змінної на j-й вхідний вплив у вигляді одиничної ступінчатої функції 1(t) і
нульових інших впливах.
Реакція системи управління на сукупність вхідних впливів довільної
форми при нульових початкових умовах може бути знайдена за допомогою інтеграла
Дюамеля, який у матричній формі має такий же вигляд, як і для скалярних
функцій:
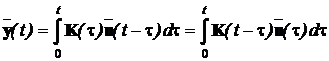 .
(5.7)
.
(5.7)
Для розрахунку складових yi(t) вектору виходу необхідно перемножити
матриці під знаком інтеграла і взяти інтеграл від кожного рядка результату
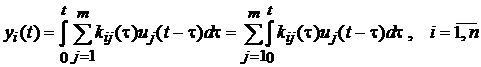 .
(5.8)
.
(5.8)
Слід завважити, що кожна з компонент матричної вагової функції є сумою
експоненціальних складових
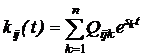 ,
,
де sk - корені характеристичного рівняння системи, що співпадають з
власними числами матриці А; Qijk - числові (в загальному випадку комплексні)
коефіцієнти, що залежать від sk і можуть бути обчислені з використанням формули
Сільвестра. Тому вираз (5.8) можна переписати у вигляді
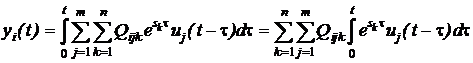 .
(5.9)
.
(5.9)
Якщо вхідні впливи ui(t) мають не дуже складний вигляд, інтеграли в
останньому виразі можуть бути зведені до табличних і взяті аналітично. І, як видно
з цього виразу, аналітично доводиться брати не більше m інтегралів (за рахунком
різних вхідних впливів), а потім виконується їх розрахунок для різних коренів
sk.
Приклад 1. Нехай uj(t) = Umjsinwjt.
Знайдемо, чому дорівнює у цьому випадку інтеграл у виразі (5.9). Позначимо його
через І, тоді
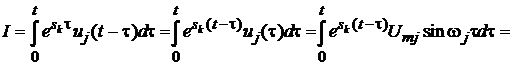
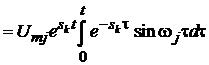 .
.
Останній інтеграл є табличним і згідно таблиці інтегралів одержуємо, що
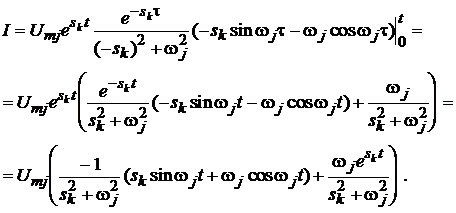
Далі зостається підставити цей результат у формулу (5.9) і вирахувати
відповідні складові при різних sk.
Найпростіше виконується розрахунок реакції САУ на сукупність постійних
впливів, коли усі впливи uj(t) дорівнюють uj×1(t) або нульові. Для вагової функції справедливо
K(t)=dH(t)/dt, тому згідно формули (5.7) вектор вихідних змінних у цьому
випадку буде дорівнювати
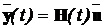 .
(5.10)
.
(5.10)
Тут необхідно тільки вирахувати матричну перехідну функцію і помножити
її на вектор постійних впливів.
З формул (5.3) - (5.6) видно, що як для розрахунку матричної
передавальної функції, так і матричних вагової і перехідної функцій,
вимагається здійснювати обертання матриці [sI - A]. Один з способів цього
обертання був показаний у попередньому розділі у п.1. Проте при великій розмірності
матриці А такий шлях може викликати деякі труднощі.
Один з засобів розв’язання цієї задачі заснований на
використанні так званого алгоритму Левер’є, згідно якому
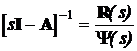 ,
(5.11)
,
(5.11)
де 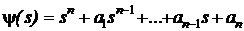 характеристичний полiном системи;(s)=sn-1
I+sn-2R1+...+sRn-2+Rn-1 - матриця розміром (n´n); I - одинична матриця розміром (n´n); R1, R2,..., Rn-1 - матриці розміром (n´n).
характеристичний полiном системи;(s)=sn-1
I+sn-2R1+...+sRn-2+Rn-1 - матриця розміром (n´n); I - одинична матриця розміром (n´n); R1, R2,..., Rn-1 - матриці розміром (n´n).
Згідно алгоритму Левер’є коефіцієнти 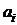 та
матриці Ri можна вирахувати за наступними рекурентними формулами:
та
матриці Ri можна вирахувати за наступними рекурентними формулами:
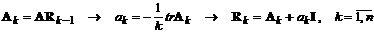 ,
(5.12)
,
(5.12)
де Ai матриці розміром (n´n); 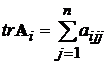 - слід матриці Ai , що дорівнює сумі її діагональних
елементів; матриця R0=I, а матриця Rn розраховується з ціллю перевірки
правильності виконання алгоритму. Якщо алгоритм виконано без помилок, то Rn
буде нульовою. В зворотному випадку вона буде утримувати ненульові елементи.
- слід матриці Ai , що дорівнює сумі її діагональних
елементів; матриця R0=I, а матриця Rn розраховується з ціллю перевірки
правильності виконання алгоритму. Якщо алгоритм виконано без помилок, то Rn
буде нульовою. В зворотному випадку вона буде утримувати ненульові елементи.
Цей алгоритм легко програмується та може бути використаний при аналізі
САУ на ЕОМ. Але при цьому обов’язкова перевірка умови Rn=0, тому що він за
великої розмірності матриці А та великого розкиду абсолютних значень її
елементів може приводити до помилок через похибки округлення чисел у машині.
Звичайно на практиці розраховують квадратичну норму матриці Rn і порівнюють її
з максимально допущенною похибкою:
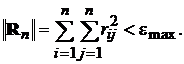
Як показує практика, алгоритм Левер’є добре працює в системах
рівнянь приблизно до десятого порядку при відсутності великих розкидів (у сотні
разів) значень коефіцієнтів матриці А, а також при цілочисельних коефіцієнтах,
і може з успіхом використовуватись у цих випадках.
Підставляючи (5.11) в (5.3) отримаємо, що
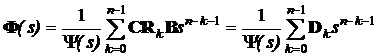 ,
(5.13)
,
(5.13)
де Dk=CRkB - (r´m) матриці, які
утримують коефіцієнти поліномів чисельників елементарних передавальних функцій jij(s) при різних ступенях s, так що
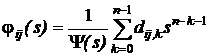 ,
,
де dij,k - елемент i-го рядка та j-го стовпця матриці Dk.
Приклад 2. Знайдемо матричну передавальну функцію системи (5.1), якщо
її матриці коефіцієнтів мають вид
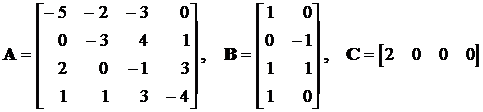 .
.
Згідно алгоритму Левер’є маємо:
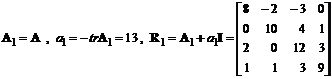 ,
,
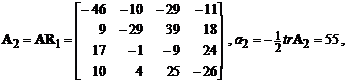
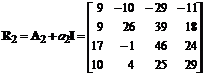 ,
,
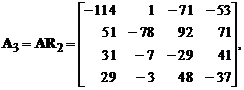
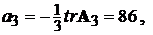
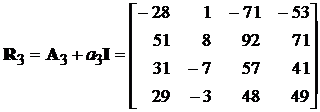 ,
,
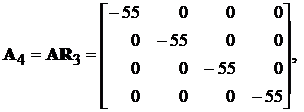
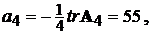 \
\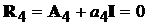 .
.
Матриця R4 нульова, що свідчить про правильність виконання алгоритму.
Далі підставляючи матриці Ri у формулу (5.13) і помножуючи їх на матриці С і В
отримуємо
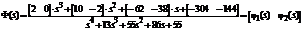 ,
,
де j1(s) і j2(s)
- елементарні передавальні функції, що пов’язують змінну виходу з першим і
другим вхідним впливом:
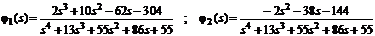 .
.
Підставляючи (5.13) у формулу (5.6) і застосовуючи формулу розкладання,
для матричної перехідної функції можна записати
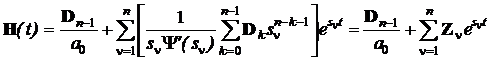 ,
(5.14)
,
(5.14)
де sn - корені характеристичного рівняння системи Y(s)=0; Zn - (r´m) матриці, що обчислюються
згідно виразу у квадратних дужках і утримують коефіцієнти zij,n елементарних перехідних
функцій hij(t) при відповідних експонентах:
 .
.
Час розрахунку вектора вихідних змінних можна істотно скоротити, якщо
підставити вираз (5.14) у формулу (5.10) і помножити матриці, що входять у
суму, на вектор вхідних впливів. При цьому треба ураховувати, що кожний такий
добуток дасть вектор-стовпець розміром r, а саме
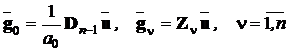 .
(5.15)
.
(5.15)
Тому в результаті такої підстановки отримаємо для вектору виходу вираз
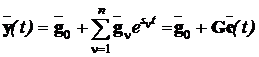 ,
(5.16)
,
(5.16)
де 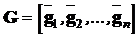 - матриця розміру (r´n);
- матриця розміру (r´n); 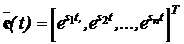 -
вектор-стовпець експоненціальних складових перехідного процесу.
-
вектор-стовпець експоненціальних складових перехідного процесу.
Як видно з останньої формули, треба один раз вирахувати вектор 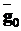 , що утримує сталі значення змінних виходу, та матрицю
комплексних коефіцієнтів G і потім за формулою (5.16) можна визначити значення
вектору виходу для будь-якого моменту часу. Це є явною перевагою перед методами
чисельного інтегрування, де для визначення yi(t), наприклад, на третій секунді
необхідно провести інтегрування рівнянь на всьому цьому інтервалі часу з
кроком, який повинен бути менше найменшої постійної часу в системі.
, що утримує сталі значення змінних виходу, та матрицю
комплексних коефіцієнтів G і потім за формулою (5.16) можна визначити значення
вектору виходу для будь-якого моменту часу. Це є явною перевагою перед методами
чисельного інтегрування, де для визначення yi(t), наприклад, на третій секунді
необхідно провести інтегрування рівнянь на всьому цьому інтервалі часу з
кроком, який повинен бути менше найменшої постійної часу в системі.
6.
Стійкість багатовимірних систем
Вектор вихідних змінних у багатовимірній системі може бути
вирахувано за формулою:
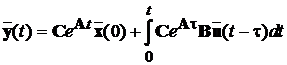 ,
(6.1)
,
(6.1)
де 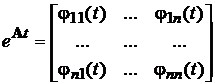 - матрична експонента, яка називається перехідною
матрицею.
- матрична експонента, яка називається перехідною
матрицею.
Можна показати (згадайте формулу Сільвестра), що компоненти jij(t) цієї матриці можуть бути представлені у вигляді
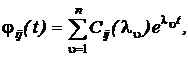 (6.2)
(6.2)
де Cij(ln) коефіцієнти, що залежать від конкретного
значення ln; ln - власні
числа матриці 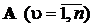 , що є коренями характеристичного рівняння
, що є коренями характеристичного рівняння
det[lI - A]=0.
Для стійкості багатовимірної системи необхідно, щоб перехідний процес
по всім змінним 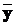 згасав у часі, тобто при t®¥ повинна пpагнути до нуля вільна (або власна) складова
перехідного процесу:
згасав у часі, тобто при t®¥ повинна пpагнути до нуля вільна (або власна) складова
перехідного процесу:
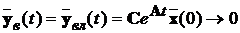 при
t®¥ ,
при
t®¥ ,
що зводиться до умови
jij(t)
® 0 при 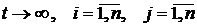 .
(6.3)
.
(6.3)
Умова (6.3) буде виконуватись, як видно з (6.2), якщо всі власні числа
матриці А будуть мати негативні дійсні частини, тобто будуть лежати у лівій
комплексній напівплощині.
Тому аналіз стійкості багатовимірних систем практично зводиться до
визначення власних чисел матриці А системи диференційних рівнянь САУ. Зараз
існують стандартні пакети програм обчислення власних чисел матриць на ЕОМ. При
не дуже великих розмірностях матриць ця задача не становить труднощів.
7.
Заміна базису. Канонічна форма рівнянь
Система управління описується системою диференційних рівнянь
у стандартній формі:
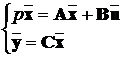 .
(7.1)
.
(7.1)
Введемо у рівняннях (7.1) заміну змінних: 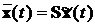 , де S - неособлива (тобто detS¹0) постійна матриця, розміру (n´ n).
, де S - неособлива (тобто detS¹0) постійна матриця, розміру (n´ n).
Тоді рівняння (7.1) наберуть вид:
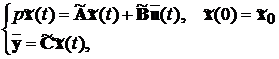 ,
(7.2)
,
(7.2)
де введено позначення
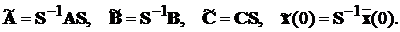
Перехід від вихідних рівнянь (7.1) до (7.2) прийнято називати заміною
базису внутрішнього опису, а матрицю S - матрицею переходу до нового базису. Перетворені
рівняння еквівалентні вихідним.
Знаючи 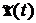 легко знайти
легко знайти 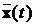 .
Більш того, матриця
.
Більш того, матриця 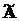 має той же характеристичний поліном D(l) , що і матриця А, тобто
має той же характеристичний поліном D(l) , що і матриця А, тобто

де I - одинична матриця.
Приклад 1. Найпростішим прикладом заміни базису є поворот осей
координатної площини навколо початку координат на деякий кут a (дивись рис. 7.1). Знайдемо зв’язок між координатами
точки А у двох системах координат:
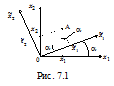
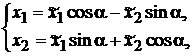 або
або
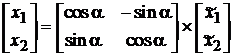 .
.
Таким чином, матриця 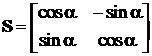 .
.
Очевидно, що зв’язок “вхід-вихід” ніяк не залежить від заміни базису: у
(7.2) входять ті ж вхідні та вихідні змінні 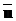 та
та
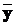 , що і в (7.1).
, що і в (7.1).
Дійсно, матрична передавальна функція у (7.1) дорівнює:
Ф(p)=C[pI - A]-1B,
тут, щоб відрізнити по написанню від матриці S, оператор
Лапласа позначений літерою p.
Помножимо цю формулу два рази на SS-1=I - це не змінить
результат.
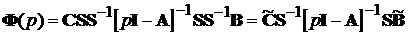 .
.
З теорії матриць відомо, що зворотна матриця з добутку трьох
матриць дорівнює:
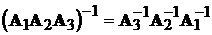 .
.
Використовуючи цю властивість, можна записати:
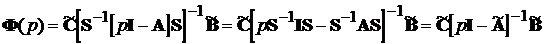 ,
,
що і вимагалось довести.
Нові змінні, тобто новий базис, можна вибрати так, щоб рівняння (7.2)
мали більш просту структуру. Припустимо, що всі власні числа li матриці А (а отже, і 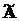 )
є простими (тобто не кратними). З алгебри відомо, що тоді матриця
)
є простими (тобто не кратними). З алгебри відомо, що тоді матриця
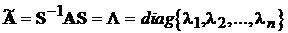
буде діагональною матрицею, якщо стовпчиками матриці S є власні
вектори, відповідні власним числам матриці А. Перехід до такого базису будемо
називати діагоналізацією, а відповідні змінні 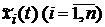 - основними формами (або модами).
- основними формами (або модами).
Власним вектором, відповідним власному числу li матриці А, називається вектор 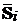 , що є розв’язком однорідного матричного рівняння:
, що є розв’язком однорідного матричного рівняння:
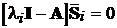 .
(7.3)
.
(7.3)
Рівняння (7.2) у нових змінних приймають вид
 ,
(7.4)
,
(7.4)
де 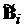 - i-й рядок матриці
- i-й рядок матриці 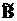 ,
а
,
а 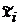 - i-та змінна з вектору
- i-та змінна з вектору 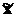 .
.
Така форма запису рівнянь (7.4) називається канонічною. Тут
кожна мода визначається своїм рівнянням, не пов’язаним з іншими. Ці рівняння
легко інтегруються:
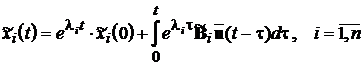 .
.
Перепишемо ці рівняння у матричній формі:
 .
.
Повернемось тепер до вихідного базису:
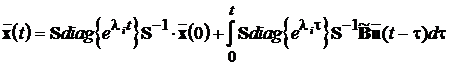 .
.
Але згідно з (3.5) вектор змінних стану дорівнює

тобто матрична експонента може бути записана у вигляді:
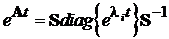 .
(7.5)
.
(7.5)
Це спектральне представлення матричної експоненти. Воно
широко використовується на практиці.
Приклад 2. Система автоматичного управління описується
диференційними рівняннями
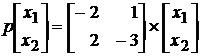 .
.
Знайти перехідний процес у системі при початкових умовах
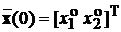 .
.
Розв'язок цієї системи рівнянь має вигляд 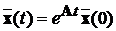 . Знайдемо
. Знайдемо 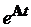 за
допомогою її спектрального представлення (7.5).
за
допомогою її спектрального представлення (7.5).
Визначимо власні числа матриці А:
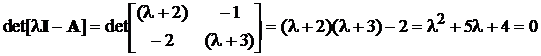 ,
,
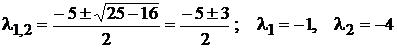 .
.
Визначимо тепер власні вектори матриці А з рівняння (7.3)
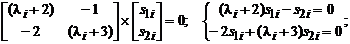
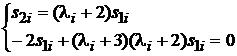 .
.
З останнього рівняння маємо 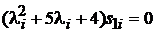 ,
але цей добуток дорівнює нулю при любому
,
але цей добуток дорівнює нулю при любому  ,
бо дорівнює нулю вираз у дужках. Тому приймаємо
,
бо дорівнює нулю вираз у дужках. Тому приймаємо 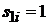 .
Тоді
.
Тоді  і s11=1, s21=1, s12=1, s22= -2. Матриці S та S-1 мають вид
і s11=1, s21=1, s12=1, s22= -2. Матриці S та S-1 мають вид
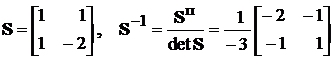 .
.
Перевіримо, чи виконається рівняння 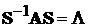 :
:
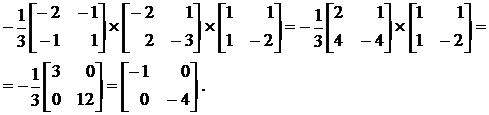
Згідно формули (7.5) для матричної експоненти будемо мати
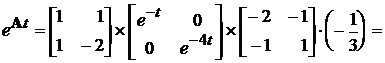

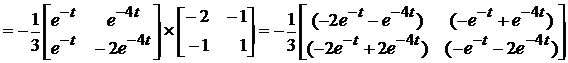 .
.
Помноживши 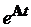 на вектор початкових умов отримаємо
на вектор початкових умов отримаємо
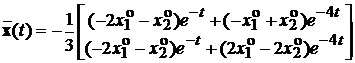 .
.
8.
Керованість та спостережуваність
Попередній етап розвитку теорії автоматичного керування
(ТАК), до широкого використання в ній поняття змінних стану, був пов’язаний з
описом САУ за допомогою змінних “вхід-вихід”. Цей спосіб математичного опису
зручний для інженерних розрахунків, але розвиток методу змінних стану показав,
що метод “вхід-вихід” має й істотні обмеження. Ці обмеження пов’язані у
основному з поняттям керованості та спостережуваності, які не враховувались
раніше. При отриманні передавальної матриці складної системи по передавальних
матрицях або функціях окремих її підсистем (елементів) можливо скорочення
однакових полюсів та нулів, що істотно впливають на динаміку системи.
Нехтування цим скороченням при розрахунку систем управління, як показує досвід,
може привести до помилкових результатів.
Управляти станом системи 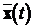 можна
змінюючи вектор входу
можна
змінюючи вектор входу 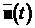 , а спостерігати її стан можна, вимірюючи вектор
виходу
, а спостерігати її стан можна, вимірюючи вектор
виходу 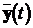 . У зв’язку з цим виникають два питання, що мають
кардинальне значення для ТАК. Чи можна, обравши відповідним чином входи
. У зв’язку з цим виникають два питання, що мають
кардинальне значення для ТАК. Чи можна, обравши відповідним чином входи 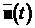 , перевести об’єкт управління з деякого довільного
стану
, перевести об’єкт управління з деякого довільного
стану 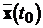 у інший довільний стан
у інший довільний стан 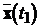 ?
А також, чи можна, спостерігаючи вектор виходу
?
А також, чи можна, спостерігаючи вектор виходу 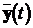 протягом
досить довгого проміжку часу, визначити початковий стан об’єкта
протягом
досить довгого проміжку часу, визначити початковий стан об’єкта 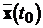 ?
?
Відповідь на перше питання пов’язана з поняттям керованості, а на друге
- з поняттям спостережуваності.
Пояснимо ці поняття на такому прикладі. Нехай система управління
описується рівняннями:
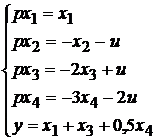
 (8.1)
(8.1)
Їй відповідає структурна схема, показана на рис. 8.1.

З рисунка видно, що змінна x1 не з’єднана з входом u, тому він не може
впливати на її змінювання у часі. Таку змінну стану називають некерованою.
Змінна x2 не з’єднана з виходом y, і тому по спостереженню виходу y неможливо
визначити x2. Таку змінну стану називають неспостережуваною.
Більш загальне визначення керованості таке: “Систему називають повністю
керованою, якщо для будь-яких моментів часу  та
та
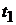 ,
, 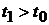 ,
та будь-яких заданих станів
,
та будь-яких заданих станів  та
та
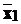 існує управління
існує управління 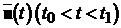 ,
що переводить систему з початкового стану
,
що переводить систему з початкового стану  у
кінцевий
у
кінцевий 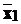 “.
“.
Судити про те, чи є система керованою по виду її рівнянь стану у
загальному випадку дуже важко. Проте, якщо рівняння системи
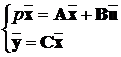 (8.2)
(8.2)
приведені до канонічної форми
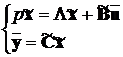 ,
(8.3)
,
(8.3)
де L - діагональна матриця, то по їх вигляду можна судити про
керованість системи.
Представимо перше матричне рівняння з (8.3) у розгорненій
формі:
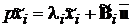 ,
,
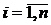
де 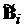 - i-й рядок матриці
- i-й рядок матриці 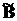 .
Ці рівняння показують, що керуючі сигнали
.
Ці рівняння показують, що керуючі сигнали 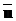 не
будуть надавати якого-небудь впливу на змінну
не
будуть надавати якого-небудь впливу на змінну 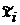 ,
якщо всі елементи i-го рядку матриці
,
якщо всі елементи i-го рядку матриці 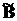 дорівнюють
нулю.
дорівнюють
нулю.
Таким чином, система (8.3) є керованою, якщо матриця 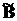 не утримує рядків, всі елементи яких дорівнюють нулю.
не утримує рядків, всі елементи яких дорівнюють нулю.
Якщо система рівнянь (8.2) не приведена до канонічної форми, то про її
керованість можна судити за допомогою наступної теореми Калмана.
Теорема 1. “Необхідна та достатня умова для керованості системи (8.2)
складається в тому, щоб пара матриць А та В була невиродженою, тобто щоб
матриця
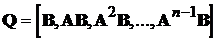 (8.4)
(8.4)
мала ранг, що дорівнює n, де n - порядок системи рівнянь (8.2)”.
Рангом матриці Q називається число, що дорівнює найбільшому з порядків
відмінних від нуля мінорів, тобто детермінантів квадратних підматриць, які
можна виділити у матриці Q.
Якщо який-небудь з мінорів порядку r не дорівнює нулю, а всі мінори
більш високого порядку дорівнюють нулю, то число r і буде рангом матриці Q.
Якщо всі мінори матриці Q дорівнюють нулю, тобто r = 0, то система повністю
некерована. Якщо r < n, то система буде неповністю керованою.
Визначення спостережуваності:
“Систему (8.2) називають спостережуваною, якщо за даними вимірювання
або спостереження векторів 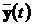 та
та
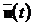 на кінцевому інтервалі часу
на кінцевому інтервалі часу 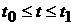 можна однозначно визначити початковий стан
можна однозначно визначити початковий стан  . Систему (8.2) називають повністю спостережуваною,
якщо спостережувані всі її стани у будь-які моменти часу”.
. Систему (8.2) називають повністю спостережуваною,
якщо спостережувані всі її стани у будь-які моменти часу”.
Судити про спостережуваність системи легко, якщо її рівняння приведено
до канонічної форми (8.3). Змінна стану (мода) 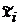 не
буде потрапляти на вихід системи
не
буде потрапляти на вихід системи 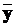 ,
якщо матриця виходу
,
якщо матриця виходу 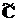 буде мати нульовий i-й стовпець. Тобто для повної
спостережуваності системи (8.3) потрібно, щоб матриця
буде мати нульовий i-й стовпець. Тобто для повної
спостережуваності системи (8.3) потрібно, щоб матриця 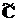 не мала нульових стовпців.
не мала нульових стовпців.
У загальному випадку рівнянь (8.2) необхідні та достатні умови
спостережуваності визначаються наступною теоремою Калмана.
Теорема 2. “Необхідні та достатні умови для повної спостережуваності
полягають у тому, щоб пара матриць 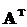 та
та
 була невиродженою, тобто щоб матриця
була невиродженою, тобто щоб матриця
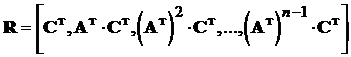
мала ранг, що дорівнює n.”
Тут 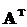 та
та  це
транспоновані матриці. Якщо ранг матриці R дорівнює r та менше n, то система
неповністю спостережувана.
це
транспоновані матриці. Якщо ранг матриці R дорівнює r та менше n, то система
неповністю спостережувана.
Приклад. Задана система рівнянь: 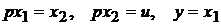 .
.
Тут 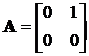 ;
; 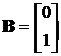 ;
;
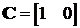 .
.
Матриця  , її ранг rangQ = 2, бо detQ = -1 ¹ 0. Тому система є повністю керованою.
, її ранг rangQ = 2, бо detQ = -1 ¹ 0. Тому система є повністю керованою.
Матриця 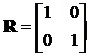 ; detR = 1 ¹ 0, rangR
= 2. Тому система є повністю спостережуваною.
; detR = 1 ¹ 0, rangR
= 2. Тому система є повністю спостережуваною.
Якщо ж у цій системі замінити останнє рівняння на 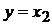 , то
, то
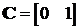 ;
;
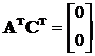 ;
; 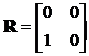 ,
detR = 0.
,
detR = 0.
Тут є один тільки мінор першого порядку (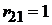 ),
відмінний від нуля. Значить rangR=1, а система неповністю спостережувана.
),
відмінний від нуля. Значить rangR=1, а система неповністю спостережувана.
9.
Декомпозицiя системи рівнянь
Будь-яка система, що описується рівняннями стану
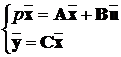 ,
(9.1)
,
(9.1)
може бути представлена у вигляді структурної схеми, показаної на рис.
9.1.
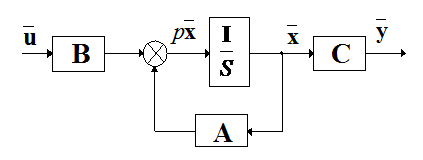
Рис. 9.1
Верхня частина схеми відповідає некерованій частині системи, бо вектор 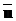 не впливає на цю підсистему. Цій структурній схемі
відповідає система рівнянь
не впливає на цю підсистему. Цій структурній схемі
відповідає система рівнянь
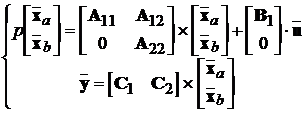
Тут підсистема 1 також не впливає на підсистему 2, тому
підматриця A21=0.
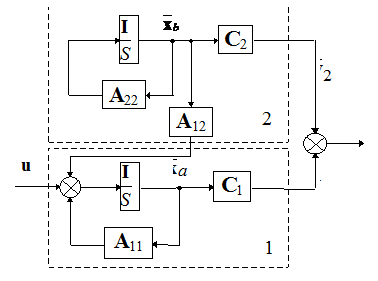
Рис. 9.2
Якщо система неповністю спостережувана, то шляхом заміни базису в ній
також можна виділити дві підсистеми: спостережувану та неспостережувану. У
цьому випадку структурна схема буде мати вигляд рис. 9.3. Підсистема 2 (нижня)
тут є неспостережуваною, бо у неї немає зв’язку з виходом 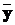 .
.
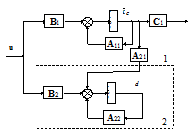
Рис. 9.3
Цій схемі відповідає система рівнянь стану:
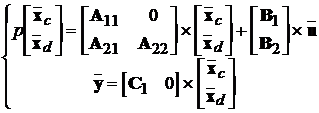 .
.
Тут підматриця 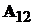 дорівнює нулю, бо підсистема 2 не впливає на
підсистему 1.
дорівнює нулю, бо підсистема 2 не впливає на
підсистему 1.
Таке виділення з системи управління (рівнянь) керованої та некерованої,
спостережуваної та неспостережуваної підсистем називається декомпозицією
системи.
У загальному ж випадку система може бути декомпозована на чотири
підсистеми (рис. 9.4): керовану, що не спостерігається  ; керовану, що спостерігається
; керовану, що спостерігається 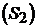 ; некеровану, що не спостерігається
; некеровану, що не спостерігається 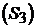 , і некеровану, що спостерігається
, і некеровану, що спостерігається 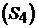 .
.
Наявність зв’язків між підсистемами визначається з наступних міркувань:
·
якщо S1
неспостережувана, то вона не може впливати на S2 та S4, які є спостережуваними;
·
якщо S1
та S2 керовані, то вони не можуть впливати на некеровані підсистеми S3 і S4;
·
якщо S3
неспостережувана, то вона не може впливати на спостережувані підсистеми S2 та
S4;
·
S4
некерована, але спостережувана, тому вона може впливати на всі підсистеми.
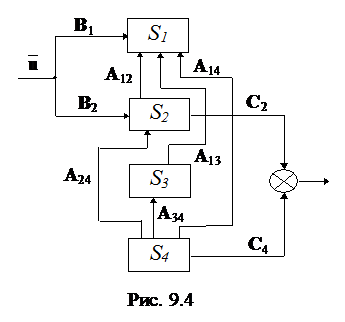
На рис. 9.4 буквами A12,…, А34, B1, B2, C2, C4 позначено
підматриці коефіцієнтів передачі.
Можливість такої декомпозицiї була доведена Калманом. Він
сформулював теорему, яка надалі одержала назву структурної теореми Калмана.
Структурна теорема Калмана: “Існує неособлива заміна координат 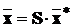 така, що система (9.1) еквівалентно може бути
перетвореною до вигляду:
така, що система (9.1) еквівалентно може бути
перетвореною до вигляду:
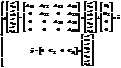 ,
(9.2)
,
(9.2)
причому 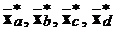 - підвектори
- підвектори 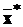 ,
такі, що сумарний розмір
,
такі, що сумарний розмір
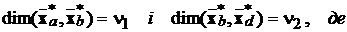
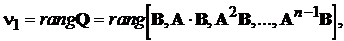
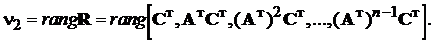
Пари матриць 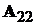 та
та 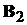 ,
,
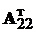 та
та 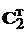 є
невиродженими і передавальна матриця системи дорівнює
є
невиродженими і передавальна матриця системи дорівнює
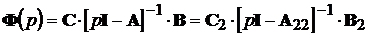 ,
(9.3)
,
(9.3)
тобто визначається тільки повністю керованою та спостережуваною
частинами системи”.
Підвектор 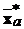 відповідає підсистемі
відповідає підсистемі 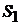 ,
а
,
а 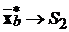 ;
; 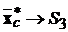 ;
;
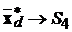 .
.
Доказ цієї теореми у частині рівнянь (9.2) досить громіздкий і ми його
опустимо. Справедливість же формули (9.3) досить легко показати.
Дійсно, враховуючи структуру матриць А, В та С можна записати:
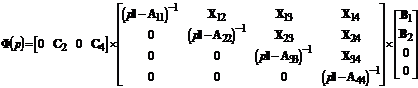 ,
,
тут  ,… ,
,… ,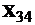 - деякі підматриці, які одержуються при обертанні матриці
- деякі підматриці, які одержуються при обертанні матриці 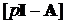 , де А має структуру (9.2). Їх структура та значення,
як побачимо далі, нас не цікавлять, тому що
, де А має структуру (9.2). Їх структура та значення,
як побачимо далі, нас не цікавлять, тому що
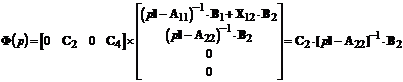 ,
,
що і вимагалось довести.
З структурної теореми Калмана таким чином витікає, що некеровані та
неспостережувані частини системи не впливають на властивість перетворення
“вхід-вихід”. Компоненти некерованої, але спостережуваної, частини 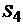 виявляються на виході, але при цьому не несуть ніякої
інформації про вхідні впливи.
виявляються на виході, але при цьому не несуть ніякої
інформації про вхідні впливи.
10. Значення
понять керованості та спостережуваності
На початку розділу 8 “Керованість та спостережуваність” ми
розглянули приклад системи, що описується рівняннями у канонічній формі:
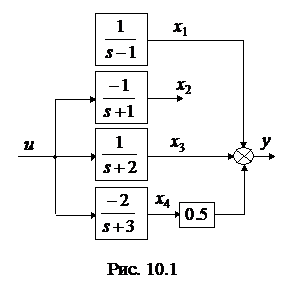
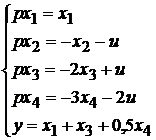 . (10.1)
. (10.1)
Їм відповідала структурна схема, показана на рис. 10.1.
З неї було видно, що мода x1 з власним числом  є некерованою, а мода
є некерованою, а мода 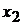 з
власним числом
з
власним числом 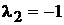 неспостережуваною.
неспостережуваною.
Проте на практиці майже ніколи система не буває одразу описана
канонічними рівняннями. Як правило, система управління складається з декількох
підсистем (ланок), відповідним чином з’єднаних та описаних своїми рівняннями
або передавальними функціями. При визначенні спільної передавальної функції
інформація про частини системи, що не спостерігаються і не керуються, як
витікає з структурної теореми Калмана, може бути загубленою. Наприклад, система
рівнянь (10.1) у канонічній формі відповідає системі (див. рис. 10.2), що
складається з послідовно з’єднаних двох ланок з передавальними функціями:
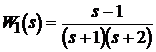 і
і
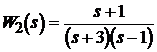 .
.
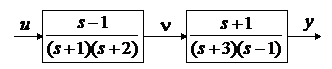
Рис. 10.2
Ланка W1 є немінімально-фазовою, у неї позитивний нуль 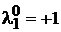 . Ланка W2 є нестійкою, у неї позитивний полюс
. Ланка W2 є нестійкою, у неї позитивний полюс  . Спільна передавальна функція системи дорівнює
. Спільна передавальна функція системи дорівнює
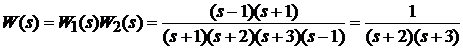 .
.
Ця передавальна функція, відповідає вже стійкій системі (здавалось би),
оскільки позитивний полюс  скоротився з таким же нулем. Скоротився також і один
негативний полюс
скоротився з таким же нулем. Скоротився також і один
негативний полюс 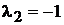 з нулем
з нулем 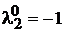 .
.
Проте таке скорочення нуля та полюса можливо тільки теоретично. В дійсності
ж таке скорочення не враховує створення диполя “нуль-полюс” (рис. 10.3), який
створюється тому, що на практиці неможливо здійснити абсолютно точний збіг нуля
і полюса.

Рис. 10.3
Якщо цей диполь “нуль-полюс” розташований у лівій напівплощині біля
точки -a1, то йому у перехідному процесі буде
відповідати член виду 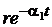 , де r - лишок W(s), пов’язаний з полюсом. Останній
дуже малий, оскільки біля полюса розташований нуль. В більшості випадків цим
членом можна знехтувати. Якщо ж диполь розташований у правій напівплощині, то
він дасть нестійкий член
, де r - лишок W(s), пов’язаний з полюсом. Останній
дуже малий, оскільки біля полюса розташований нуль. В більшості випадків цим
членом можна знехтувати. Якщо ж диполь розташований у правій напівплощині, то
він дасть нестійкий член 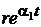 яким би малим не було r.
яким би малим не було r.
Нулі та полюса, що скоpочуються, відповідають присутнім у системі
некерованим або неспостережуваним модам. Причому, якщо по стрілці (від входу до
виходу) спочатку розташований нуль, а потім аналогічний полюс, як, наприклад, у
вказаній САУ 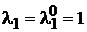 , то має місце некерованість відповідної моди. Якщо ж
по стрілці спочатку розташований полюс, а потім аналогічний нуль, як,
наприклад, у даному випадку при
, то має місце некерованість відповідної моди. Якщо ж
по стрілці спочатку розташований полюс, а потім аналогічний нуль, як,
наприклад, у даному випадку при 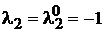 ,
то має місце неспостережуваність відповідної моди. У випадку багатовимірних
систем з багатьма входами та виходами, коли скорочення може відбуватись у
результаті властивостей детермінантів, виявлення некерованості та
неспостережуваності значно складніше. Проте у всіх випадках це відбувається
з-за тих або інших скорочень між підсистемами. Слід підкреслити розбіжність між
некерованими (або неспостережуваними) полюсами залежно від того, розташовані
вони у лівій або правій напівплощині.
,
то має місце неспостережуваність відповідної моди. У випадку багатовимірних
систем з багатьма входами та виходами, коли скорочення може відбуватись у
результаті властивостей детермінантів, виявлення некерованості та
неспостережуваності значно складніше. Проте у всіх випадках це відбувається
з-за тих або інших скорочень між підсистемами. Слід підкреслити розбіжність між
некерованими (або неспостережуваними) полюсами залежно від того, розташовані
вони у лівій або правій напівплощині.
Якщо відповідний полюс стійкий (лежить у лівій напівплощині), то
система є працездатною.
Припустимо тепер, що у системі мається спостережуваний, але некерований
нестійкий полюс. Оскільки він спостерігається, то вихід нестійкий. Він не може
бути не поміченим, але його некерованість виключає можливість управління
системою. В цьому випадку виходом з положення може бути не зміна закону
регулювання, а зміна структури системи.
Припустимо тепер, що у системі мається неспостережуваний нестійкий
полюс. Оскільки цей полюс не пов’язаний з виходом, то вихід буде
спостерігатись, як стійкий. Але, проте, внутрішня нестійкість системи може
привести до аварії, коли нестійка змінна досягне відповідної амплітуди, або до
появи ефекту насичення з-за виходу системи з лінійної зони.
Таким чином неврахування некерованості або неспостережуваності при
введенні системи управління до експлуатації, навіть коли розрахунки дають гарні
результати, може привести до негараздів у дійсності.
11.
Розміщення власних чисел та стабілізація. Модальне управління
Вид перехідного процесу (аперіодичний або коливальний) та
якiсть процесу регулювання (спектр частот, час затухання, перерегулювання) залежить
від розташування полюсів передавальної функції замкненої системи. Зокрема, для
стійкості системи, вимагається розміщення полюсів у лівій напівплощині.
Одним з методів синтезу регуляторів для лінійних стаціонарних
систем є метод, що забезпечує задане розташування полюсів передавальної функції
на комплексній площині. Він одержав всебічний розвиток у 80-х роках і став
іменуватись методом модального управління.
Будь-яка система управління описується рівняннями стану виду:
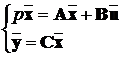 ,
,
де А - матриця коефіцієнтів рівнянь розміру (n´n); В - матриця входу розміру (n´m); С - матриця виходу розміру (r´n); 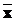 -
вектор стану і
-
вектор стану і 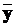 - вектор вихідних змінних.
- вектор вихідних змінних.
Полюса передавальної функції збігають у даному випадку з власними
числами матриці А, які можуть бути визначені з рівняння
 .
(11.1)
.
(11.1)
Таким чином, задача модального управління прямо пов’язана з
задачею розміщення власних чисел квадратної матриці.
Проблема розміщення власних чисел
Розглянемо спочатку чисто алгебраїчну задачу, що називається
проблемою розміщення власних чисел. Задані (n´n)-матриця А та (n´m)-матриця В; вимагається
знайти (m´n)-матрицю К таку, що (n´n)-матриця
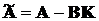 (11.2)
(11.2)
мала б довільно заданий набір власних чисел 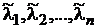 .
.
Умови, при яких дана задача має розв’язок, регламентуються наступною
теоремою.
Теорема 1. “Необхідною та достатньою умовою розв’язності проблеми
розміщення власних чисел є невиродженість пари матриць А та В, тобто виконання
умови
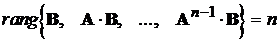 “.
(11.3)
“.
(11.3)
Доказ даної теореми вельми громіздкий і тому ми його не приводимо.
Дана теорема стверджує, що при виконанні умови (11.3), тобто якщо ранг
даної матриці дорівнює порядку матриці А, то матриця K у формулі (11.2) може
бути визначена. З практичної точки зору виконання умови (11.3) означає, що САУ
повинна бути повністю керованою.
Однозначний розв’язок проблема розміщення власних чисел має тільки при
m=1, тобто коли матриця В представляє собою стовпчик 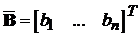 , а матриця K - рядок
, а матриця K - рядок 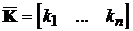 . Умова невиродженості при цьому має вигляд:
. Умова невиродженості при цьому має вигляд:  Розв’язок цей може бути знайдено за наступним
алгоритмом.
Розв’язок цей може бути знайдено за наступним
алгоритмом.
Алгоритм 1. Визначення матриці K при m = 1.
Нехай задані (n´n)-матриця А та (n´1)-стовпчик 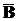 .
Нехай відомі коефіцієнти
.
Нехай відомі коефіцієнти 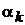 (
(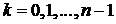 )
характеристичного полінома (11.1) матриці А та потрібні власні числа
)
характеристичного полінома (11.1) матриці А та потрібні власні числа 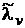
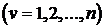 матриці
матриці 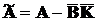 .
Тоді для знаходження
.
Тоді для знаходження 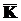 слід виконати наступні операції.
слід виконати наступні операції.
. Вирахувати потрібні коефіцієнти характеристичного полінома матриці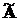 , розташувавши по ступеням l добуток
, розташувавши по ступеням l добуток
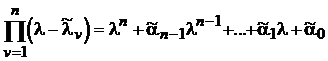 .
.
. Вирахувати величини 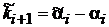 ,
,
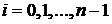 та скласти з них рядок
та скласти з них рядок 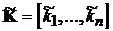 .
.
. Побудувати матрицю 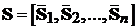 ,
де
,
де 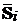 - i-й стовпчик матриці S, за наступними рекурентними
формулами:
- i-й стовпчик матриці S, за наступними рекурентними
формулами:
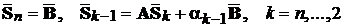 .
.
. Вирахувати 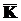 , розв’язавши рівняння
, розв’язавши рівняння 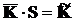 .
У розгорненій формі воно має вигляд
.
У розгорненій формі воно має вигляд
 ,
,
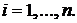
де 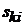 елементи i-го стовпчика матриці S.
елементи i-го стовпчика матриці S.
Це система n алгебраїчних рівнянь з n невідомими і має єдиний
розв’язок.
Приклад 1. Нехай 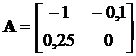 ,
, 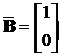 ,
,
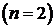 .
.
Вимагається знайти 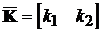 такий,
що матриця
такий,
що матриця 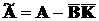 має власні числа
має власні числа 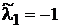 ,
,
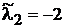 .
.
Характеристичний поліном матриці А дорівнює:
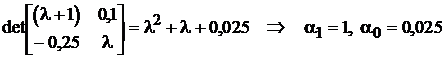 .
.
Тоді, діючи по алгоритму 1, одержуємо:
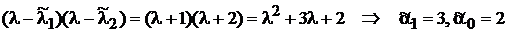 1.
.
1.
.
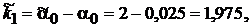 2.
2.
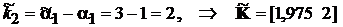 .
.
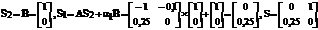 3.
.
3.
.
Розв’язуємо систему рівнянь 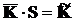 :
:
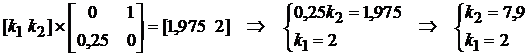 .
.
У загальному випадку, коли m > 1 задача розміщення власних
чисел не має єдиного розв’язку, тобто може бути визначена множина матриць K,
які приводять до одного й того ж результату. Процес розв’язання тут
ускладнюється і у загальному випадку досить громіздкий. Існують різні способи
розв’язання даної задачі при m > 1. Ми розглянемо найпростіший з них, який,
втім, може бути застосований у більшості практично виникаючих ситуацій.
Будемо розшукувати бажану (m´n)-матрицю K у вигляді
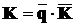 , (11.4)
, (11.4)
де 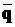 - вектор-стовпець,
- вектор-стовпець,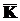 - вектор-рядок.
- вектор-рядок.
Тоді 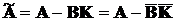 , де
, де 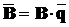 -
вектор-стовпець.
-
вектор-стовпець.
Задамося тепер довільним 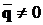 ,
для якого виконується умова
,
для якого виконується умова
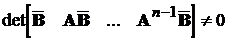 .
(11.5)
.
(11.5)
Тоді, використовуючи вище згаданий алгоритм для матриці А та 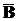 , знайдемо рядок
, знайдемо рядок 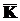 ,
що забезпечує будь-яке задане розташування власних чисел, після чого бажана
матриця K обчислюється за формулою (11.4).
,
що забезпечує будь-яке задане розташування власних чисел, після чого бажана
матриця K обчислюється за формулою (11.4).
Єдине ускладнення у цій процедурі полягає в тому, як підібрати 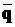 , що забезпечує виконання умови (11.5) невиродженості
матриць А та
, що забезпечує виконання умови (11.5) невиродженості
матриць А та 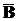 . Можна проте довести, що у випадку, коли матриця А
має прості власні числа (а це типова ситуація для САУ), такий
. Можна проте довести, що у випадку, коли матриця А
має прості власні числа (а це типова ситуація для САУ), такий 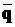 існує і, більш того, при майже будь-якому навмання
взятому
існує і, більш того, при майже будь-якому навмання
взятому 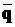 умова (11.5) буде виконаною, якщо звичайно виконано
вихідне припущення (11.3).
умова (11.5) буде виконаною, якщо звичайно виконано
вихідне припущення (11.3).
Приклад 2. Нехай n = 3, m = 2 і
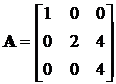 ,
,
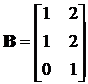 .
.
Перевіримо виконання умови (11.3):
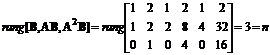 ,
бо
,
бо 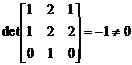 .
.
Приймемо 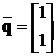 , тоді
, тоді 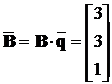 .
Перевіримо виконання умови (11.5):
.
Перевіримо виконання умови (11.5):
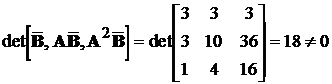 ,
,
тобто вона виконана і можна застосовувати алгоритм 1 для визначення 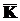 , а потім матриці K за формулою (11.4).
, а потім матриці K за формулою (11.4).
12. Стабілізація
Покажемо тепер практичну корисність тих викладок, які ми
провели, для розв’язання задач управління.
Теорема 2. “Нехай об’єкт описується основною моделлю
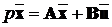 ,
,
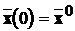 ,
,
причому пара матриць А та В невироджена. Нехай у будь-який момент часу
t³0 є доступним для вимірювання вектор стану 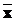 . Тоді може бути побудований зворотний зв’язок
. Тоді може бути побудований зворотний зв’язок
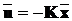 ,
(11.6)
,
(11.6)
такий, що замкнена система стійка”.
Доказ
елементарний. Підставляючи (11.6) у основну модель об’єкта, отримаємо, що
замкнена система описується рівнянням:
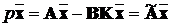 ,
де
,
де  ,
,
а матриця коефіцієнтів рівняння K, згідно теореми 1, може бути обрана
так, щоб всі власні числа матриці 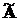 виявились
у лівій напівплощині.
виявились
у лівій напівплощині.
Дана теорема стверджує, що якщо нам доступні для вимірювання всі змінні
стану багатовимірної системи і система нестійка, то шляхом введення
неодиничного зворотного зв’язку (11.6), ми можемо стабілізувати систему, тобто
перетворити її у стійку з заданим розташуванням полюсів передавальної функції.
Структурна схема САУ з таким зворотним зв’язком показана на рис.11.1.
Тут враховано, що на вхід системи можуть надходити окрім сигналів зворотного
зв’язку 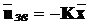 також і зовнішні керуючі впливи
також і зовнішні керуючі впливи 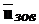 і загальний керуючий вплив на об’єкт буде дорівнювати
і загальний керуючий вплив на об’єкт буде дорівнювати
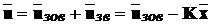 .
.

Рис. 11.1
13.
Оцінка стану
Перейдемо тепер до більш складної постановки задачі. Нехай нам
недоступно вимірювання всіх змінних стану, а доступно тільки вимірювання
змінних виходів 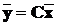 у будь-який момент часу t ³ 0. Можна показати, що у випадку невиродженості пари
матриць
у будь-який момент часу t ³ 0. Можна показати, що у випадку невиродженості пари
матриць 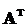 та
та  ,
тобто якщо
,
тобто якщо
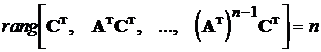 ,
,
стан системи 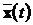 може бути відбудовано по спостереженнях виходу. Це
витікає з теореми спостережуваності. Наступна теорема вказує шлях для цього.
може бути відбудовано по спостереженнях виходу. Це
витікає з теореми спостережуваності. Наступна теорема вказує шлях для цього.
Теорема про систему асимптотичної оцінки:
“Нехай вектор стану 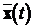 об’єкта
визначається як розв’язок рівняння
об’єкта
визначається як розв’язок рівняння
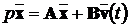 ,
,
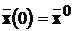 . (12.1)
. (12.1)
Тоді може бути побудовано пристрій, який називається системою
асимптотичної оцінки і використовує у якості вхідних впливів вихід об’єкта, що
вимірюється:
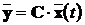 ,
,
та його вхід 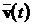 , і виробляє оцінку
, і виробляє оцінку 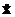 як
розв’язок рівняння
як
розв’язок рівняння
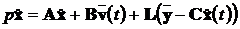 ,
,
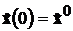 . (12.2)
. (12.2)
При невиродженості пари 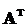 та
та
 матриця L може бути обрана так, що помилка оцінювання
матриця L може бути обрана так, що помилка оцінювання
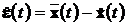
пpагне до нуля при 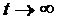 при
будь-якій обмеженій початковій помилці
при
будь-якій обмеженій початковій помилці 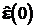 “.
“.
Доказ.
Віднімаючи (12.2) з (12.1), отримаємо рівняння, що визначає зміни
помилки оцінювання
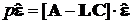 .
.
Для того, щоб помилка пpагнула до нуля, досить вибрати L так, щоб
матриця [А-LC] мала власні числа з негативними дійсними частинами. Але власні
числа цієї матриці збігають з власними числами транспонованої матриці
 .
.
Очевидно, що задача вибору матриці L (або  ) відрізняється від вже розглянутої задачі розміщення
власних чисел матриці [A - BK] тільки позначеннями і може бути розв’язаною за
допомогою вже вивчених алгоритмів, якщо пара
) відрізняється від вже розглянутої задачі розміщення
власних чисел матриці [A - BK] тільки позначеннями і може бути розв’язаною за
допомогою вже вивчених алгоритмів, якщо пара 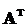 і
і
 невироджена.
невироджена.
Пояснимо отриманий результат. При побудові системи оцінки
використовуються ті ж матриці А, В, С, що і в описі об’єкта, і вводиться той же
самий зовнішній вплив 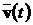 . Тому, якщо початкові умови
. Тому, якщо початкові умови 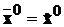 збігають, збігають і подальші траєкторії
збігають, збігають і подальші траєкторії 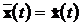 при t ³ 0,
тобто система оцінки працює як модель об’єкта.
при t ³ 0,
тобто система оцінки працює як модель об’єкта.
Головна ж перевага системи оцінки полягає у тому, що вона дозволяє
оцінити стан об’єкта і тоді, коли його початковий стан невідомо. Cаме для цієї
цілі служить останній доданок, що вводить у систему оцінки сигнал зворотного
зв’язку, пропорційний різниці між істинним, безпосередньо виміряним виходом 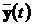 та його прогнозом
та його прогнозом 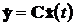 .
.
При цьому треба підкреслити, що співвідношення (12.2) визначає
структуру пристрою, який може бути безумовно реалізованим, наприклад,
побудованим за допомогою стандартних інтеграторів та підсилювачів.
Схема системи асимптотичної оцінки показана на рис. 12.1.
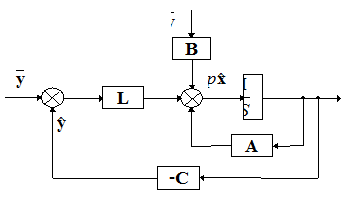
Рис. 12.1
14.
Стабілізуючий зворотний зв’язок по спостереженнях виходу
З використанням системи асимптотичної оцінки можна повністю
розв’язати задачу побудови зворотного зв’язку по спостереженнях виходу, що має
строгу реалізацію.
Теорема. “Нехай об’єкт, що описується рівняннями
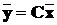 ,
,
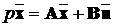 ,
,  ,
(13.1)
,
(13.1)
замкнений зворотним зв’язком виду
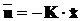 ,
(13.2)
,
(13.2)
де 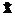 знаходиться по вимірюваннях виходу
знаходиться по вимірюваннях виходу 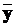 за допомогою системи асимптотичної оцінки:
за допомогою системи асимптотичної оцінки:
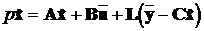 ,
, 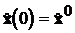 .
(13.3)
.
(13.3)
Тоді при невиродженості пар матриць А і В та 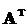 і
і 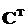 можливий
вибір матриць коефіцієнтів підсилення K та L таких, що замкнена система є
стійкою”.
можливий
вибір матриць коефіцієнтів підсилення K та L таких, що замкнена система є
стійкою”.
Доказ.
Вилучивши змінні 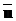 та
та 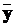 запишемо
рівняння замкненої системи у вигляді
запишемо
рівняння замкненої системи у вигляді
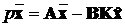 ,
(13.4)
,
(13.4)
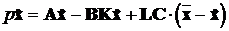 .
(13.5)
.
(13.5)
Динаміка системи характеризується двома векторними змінними 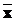 та
та 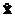 ,
що мають однакову розмірність. Перейдемо до нових змінних
,
що мають однакову розмірність. Перейдемо до нових змінних 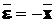 і
і 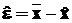 ,
що характеризують помилку управління (відхилення
,
що характеризують помилку управління (відхилення 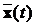 від
бажаного стану
від
бажаного стану 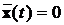 ) та помилку оцінювання. Таке перетворення координат є
неособливим і не міняє характеристичне рівняння системи. Маємо тепер
) та помилку оцінювання. Таке перетворення координат є
неособливим і не міняє характеристичне рівняння системи. Маємо тепер
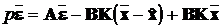
для рівняння (13.4), а друге рівняння отримаємо шляхом
віднімання (13.5) з (13.4):
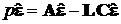
і остаточно одержуємо
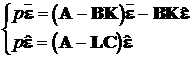 або
або
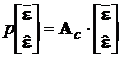 , (13.6)
, (13.6)
де 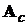 - матриця, що характеризує властивості замкненої
системи і має блочно-трикутну структуру:
- матриця, що характеризує властивості замкненої
системи і має блочно-трикутну структуру:
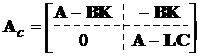 .
.
Її власні числа збігають з власними числами блоків, що стоять на
головній діагоналі, тобто матриць [A - BK] та [A - LC]. Разом з тим було
доведено нами раніше, що при виконанні умов невиродженості пар матриць А і В та
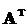 і
і 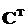 матриці
K та L можуть бути обрані так, щоб довільно розмістити власні числа цих
матриць. Тим самим доведена можливість (та вказано алгоритм) стабілізації
замкненої системи у цілому.
матриці
K та L можуть бути обрані так, щоб довільно розмістити власні числа цих
матриць. Тим самим доведена можливість (та вказано алгоритм) стабілізації
замкненої системи у цілому.
Теорема стверджує, що, якщо система (13.1) є нестійкою, але є повністю
керованою і повністю спостережуваною, то існує можливість побудови зворотного
зв’язку (13.2) за допомогою системи асимптотичної оцінки (13.3) такого, що
замкнута система буде стійкою, причому з любим наперед заданим набором власних
чисел, тобто з любою наперед заданою якістю перехідного процесу. Структурна
схема замкненої системи, описаної у даній теоремі, має вигляд, показаний на
рис. 13.1.
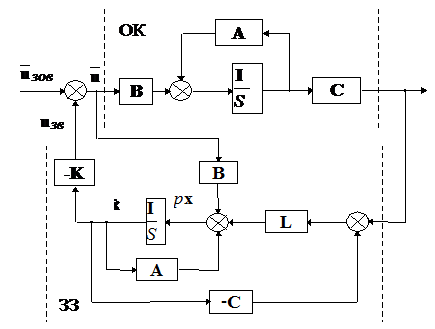
Рис. 13.1
Система асимптотичної оцінки входить як частина у конструкцiю
зворотного зв’язку (ЗЗ) від вимірювань виходу  до
управління
до
управління 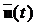 , причому зворотний зв’язок є динамічним, що задається
не алгебраїчним співвідношенням, а системою диференційних рівнянь, яка має той
же порядок, що й рівняння об’єкта. На рис.13.1 також враховано, що у загальному
випадку сигнал управління
, причому зворотний зв’язок є динамічним, що задається
не алгебраїчним співвідношенням, а системою диференційних рівнянь, яка має той
же порядок, що й рівняння об’єкта. На рис.13.1 також враховано, що у загальному
випадку сигнал управління 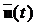 на вході об’єкту керування (ОК) буде складатися не
тільки з сигналу зворотного зв’язку
на вході об’єкту керування (ОК) буде складатися не
тільки з сигналу зворотного зв’язку 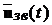 (вираховується
за формулою (13.2)), а й з зовнішнього керуючого впливу
(вираховується
за формулою (13.2)), а й з зовнішнього керуючого впливу 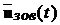 . Це не змінює положень приведеної вище теореми, бо
по-перше, для лінійної САУ виконується принцип суперпозиції, а по-друге,
стійкість САУ розглядається як властивість її вільного руху, коли
. Це не змінює положень приведеної вище теореми, бо
по-перше, для лінійної САУ виконується принцип суперпозиції, а по-друге,
стійкість САУ розглядається як властивість її вільного руху, коли 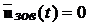 .
.
Вияснимо, якою у цьому випадку виявиться матрична передавальна функція
замкненої системи, що пов’язує вхід системи 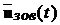 з
її виходом
з
її виходом  . Для цього підставимо
. Для цього підставимо 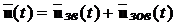 в рівняння (13.1), врахуємо, що
в рівняння (13.1), врахуємо, що 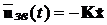 , і знов введемо змінну
, і знов введемо змінну 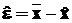 .
В результаті отримаємо
.
В результаті отримаємо
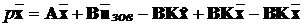 ,
,
або 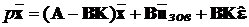 .
.
Друге рівняння системи отримується аналогічно другому рівнянню з (13.6)
і має такий же вид. Таким чином замкнена САУ описується системою рівнянь
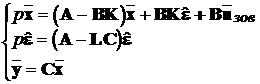 .
.
Звідси видно, що зовнішні управління 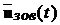 ніяк
не впливають на похибку оцінювання і тому некерована частина системи (
ніяк
не впливають на похибку оцінювання і тому некерована частина системи (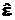 ) згідно структурній теоремі Калмана “випадає” з
перетворення “вхід-вихід”. В результаті матрична передавальна функція замкненої
системи дорівнює
) згідно структурній теоремі Калмана “випадає” з
перетворення “вхід-вихід”. В результаті матрична передавальна функція замкненої
системи дорівнює
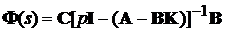 .
.
Вона не залежить від властивостей системи оцінки (ця система оказується
некерованою по відношенню до 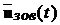 )
і має точно такий же вигляд, як і у випадку, коли можлива організація
зворотного зв’язку безпосередньо по вимірам стану
)
і має точно такий же вигляд, як і у випадку, коли можлива організація
зворотного зв’язку безпосередньо по вимірам стану 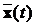 , тобто при
, тобто при 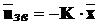 .
Ця важлива властивість описаної конструкції зворотного зв’язку дозволяє
незалежно використовувати вибір коефіцієнтів матриці K для формування
передавальної функції від зовнішнього управління до виходу, а вибір коефіцієнтів
матриці L - для зменшення впливу похибок оцінювання.
.
Ця важлива властивість описаної конструкції зворотного зв’язку дозволяє
незалежно використовувати вибір коефіцієнтів матриці K для формування
передавальної функції від зовнішнього управління до виходу, а вибір коефіцієнтів
матриці L - для зменшення впливу похибок оцінювання.
15.
Оптимізація стабілізуючого зворотного зв’язку
Якiсть стабілізації та розміщення власних чисел
Вернемось ще раз до постановки задачі стабілізації: даний
об’єкт, що описується матричним рівнянням
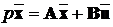 ,
,
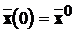 . (14.1)
. (14.1)
Вимагається вибрати зворотний зв’язок
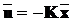 (14.2)
(14.2)
так, щоб забезпечити стійкість замкненої системи
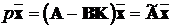 . (14.3)
. (14.3)
Нами було раніше встановлено, що при невиродженості пари матриць А та В
коефіцієнти зворотного зв’язку K можуть бути обрані так, щоб власні числа
матриці
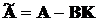 (14.4)
(14.4)
розміщувались у лівій напівплощині. Окрім того, ми встановили, що
власні числа можна розміщувати де завгодно, а отже, необмежено збільшувати і
ступінь стійкості.
Таким чином, вибір даного зв’язку може забезпечити не тільки стійкість,
але й якiсть процесу стабілізації, тобто якiсть перехідного процесу у системі
(14.3). Вільна складова перехідного процесу у системі (14.3) буде дорівнювати:
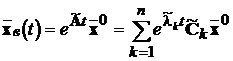 ,
(14.5)
,
(14.5)
де 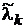 власні числа матриці
власні числа матриці 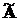 ,
а
,
а 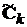 - матриці, що складаються з постійних елементів, якщо
всі
- матриці, що складаються з постійних елементів, якщо
всі 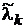 різні.
різні.
Всі елементи матриць 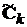 є
дробно-раціональними функціями
є
дробно-раціональними функціями 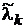 і
при великих величинах
і
при великих величинах 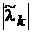 вони ростуть не швидше, ніж
вони ростуть не швидше, ніж 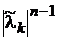 . При збільшенні
. При збільшенні 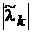 експоненціальний
співмножник у (14.5) зменшується швидше, ніж росте
експоненціальний
співмножник у (14.5) зменшується швидше, ніж росте 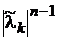 . Звідси витікає наступна теорема.
. Звідси витікає наступна теорема.
Теорема 1. “З можливості довільного вибору 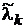 витікає, що для будь-якого Т > 0 та e > 0 можна забезпечити виконання умови
витікає, що для будь-якого Т > 0 та e > 0 можна забезпечити виконання умови
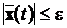 при
при
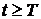 .”
.”
Таким чином, зміщуючи власні числа досить далеко “вглиб” лівої
напівплощини, можна забезпечити скільки завгодно швидке досягнення рівноваги з
будь-якою потрібною точністю. Цей формальний оптимістичний результат приховує,
проте, деякі деталі, неурахування яких може приводити до істотних помилок.
По-перше, тенденція до великого зміщення у ліву напівплощину власних
чисел замкненої системи може приводити до великих “закидів” значень деяких
змінних, перш ніж вони входять у бажаний допуск. Якiсть такого процесу
стабілізації не можна вважати прийнятною. По-друге, забезпечення довільного
розташування власних чисел може потребувати дуже великого рівня керуючих
впливів.
Твердження перше може бути проілюстровано кривими на рис. 14.1.
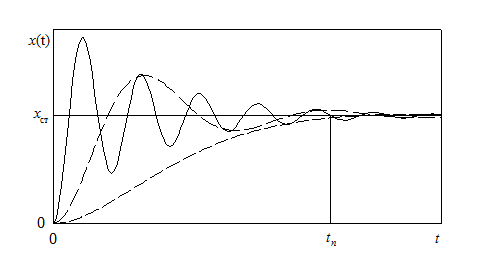
Рис. 14.1
Тут показані перехідні процеси, відповідні різним наборам власних
чисел. Всі вони мають одну й ту ж тривалість tп, проте істотно відрізняються по
якості. Отже, не можна вважати час практичного затухання прийнятною мірою
якості процесу стабілізації. Важливо, щоб протягом всього процесу стабілізації
відхилення від бажаного стану були невеликі. Тривалість перехідного процесу tп
залежить від віддалення власних чисел від удаваної осі, якість же його - від їх
взаємного розташування.
Твердження друге говорить про те, що для забезпечення скільки завгодно
великої швидкодії, тобто для зміщення власних чисел матриці 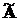 (14.4) далеко вглиб лівої напівплощини, можуть
вимагатись дуже великі коефіцієнти зворотних зв’язків, утримувані у матриці K,
а отже на вході системи можуть виникнути неприпустимо великі керуючі впливи, що
вираховуються по формулі (14.2). Таким чином при виборі зворотного зв’язку
важливо також враховувати обмеження на припустимий рівень керуючих впливів.
(14.4) далеко вглиб лівої напівплощини, можуть
вимагатись дуже великі коефіцієнти зворотних зв’язків, утримувані у матриці K,
а отже на вході системи можуть виникнути неприпустимо великі керуючі впливи, що
вираховуються по формулі (14.2). Таким чином при виборі зворотного зв’язку
важливо також враховувати обмеження на припустимий рівень керуючих впливів.
Інтегральний показник якості та його мінімізація
Обидві вище вказані тенденції можна формалізувати, вводячи
інтегральний енергетичний показник якості процесу стабілізації у вигляді:
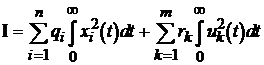 ,
(14.6)
,
(14.6)
де 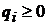 ,
, 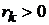 -
задані коефіцієнти.
-
задані коефіцієнти.
Доданки виду
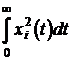
характеризують “енергію” i-ої компоненти вектору стану, тобто норму її
відхилення від нуля; доданки
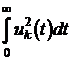
характеризують “енергію” k-ої компоненти вектору управління.
Коефіцієнти 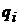 задають відносну важливість відхилень по кожній
координаті (деякі з них можуть бути неістотними і тоді
задають відносну важливість відхилень по кожній
координаті (деякі з них можуть бути неістотними і тоді 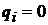 ), коефіцієнти
), коефіцієнти 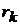 визначають
важливість “енергетичних витрат” по різних керуючих впливах.
визначають
важливість “енергетичних витрат” по різних керуючих впливах.
Питання вибору коефіцієнтів сумірності 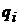 та
та
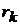 розглянемо декілька пізніше. А зараз розглянемо, при
якому стабілізуючому зворотному зв’язку досягається мінімальне значення
енергетичного показника. Перепишемо його у матричній формі:
розглянемо декілька пізніше. А зараз розглянемо, при
якому стабілізуючому зворотному зв’язку досягається мінімальне значення
енергетичного показника. Перепишемо його у матричній формі:
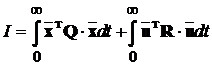 ,
(14.7)
,
(14.7)
де Q = diag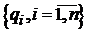 , R = diag
, R = diag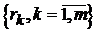 -
діагональні матриці.
-
діагональні матриці.
У загальному випадку припустимо вважати Q довільною не негативно
визначеною матрицею, а R - довільною позитивно визначеною. При цьому викладки і
докази ускладнюються незначно.
Якщо Q - симетрична матриця з дійсними елементами, то 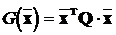 називається квадратичною формою відносно вектору
називається квадратичною формою відносно вектору 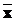 . Якщо
. Якщо 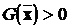 при
при
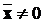 , то форма G та матриця Q називаються позитивно
визначеними. Якщо
, то форма G та матриця Q називаються позитивно
визначеними. Якщо 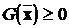 при
при 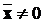 ,
то форма G та матриця Q називаються не негативно визначеними. Коротко вони
позначаються відповідно Q > 0 та Q ³
0.
,
то форма G та матриця Q називаються не негативно визначеними. Коротко вони
позначаються відповідно Q > 0 та Q ³
0.
По критерію Сільвестра (n´n)-матриця
Q > 0 тоді та тільки тоді, якщо позитивні всі детермінанти її діагональних
блоків:
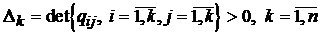 .
.
Сформульовану проблему мінімізації показника (14.7) шляхом
вибору стабілізуючого зворотного зв’язку K прийнято іменувати задачею
оптимальної стабілізації, або лінійно-квадратичною проблемою оптимального
управління. Особливістю задачі оптимальної стабілізації є те, що в ній вдається
вказати вид зворотного зв’язку, що дає найкращий результат при будь-яких
початкових умовах.
Шлях знайдення такого зворотного зв’язку вказується наступною
теоремою.
Теорема 2. “Нехай існує позитивно визначена матриця Р*, що є
розв’язком матричного квадратного рівняння
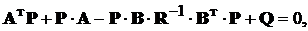 (14.8)
(14.8)
та матриця K*, пов’язана з P* співвідношенням
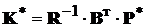 .
(14.9)
.
(14.9)
Тоді при будь-яких початкових умовах 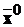 оптимальна
стабілізація забезпечується управлінням
оптимальна
стабілізація забезпечується управлінням
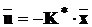 (14.10)
(14.10)
причому мінімальне значення показника якості дорівнює
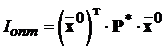 .”
(14.11)
.”
(14.11)
Рівняння (14.8) прийнято називати (у вітчизняній літературі) рівнянням
А.І.Лур’є (1951 р.) або (у закордонній) алгебраїчним рівнянням Ріккаті (на два
століття раніше). Можливість розв’язання рівняння Ріккаті (Лур’є) залежить від
вигляду матриць, що входять у нього. Умови, при яких воно має розв’язок,
обумовлюються теоремою 3.
Теорема 3. “Для існування єдиного позитивно визначеного розв’язку
матричного квадратного рівняння (14.8) досить, щоб пара матриць А та В була
невиродженою, R > 0 (тобто була позитивно визначеною) та, окрім того,
виконана одна з двох умов:
а) або Q > 0 (позитивно визначена);
б) або Q ³ 0 (не негативно визначена) і може бути
зображена у вигляді 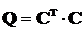 , причому так, що пара матриць
, причому так, що пара матриць 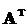 та
та 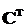 невироджена.”
невироджена.”
Описана теорія зводить задачу оптимальної стабілізації до чисто
алгебраїчної задачі пошуку розв’язку матричного квадратного рівняння Ріккаті
(Лур’є) (14.8). Якщо розмірність вектору стану 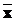 дорівнює
n, то розмір шуканої матриці P* дорівнює (n´n). Але матриця P* є симетричною, тому число невідомих
елементів дорівнює n(n+1)/2, для визначення яких маємо систему такого ж числа
скалярних квадратних рівнянь. Розв’язання цієї системи саме по собі є складною
обчислювальною задачею. Тільки при n = 2 її можна спробувати розв’язати “у
лоб”.
дорівнює
n, то розмір шуканої матриці P* дорівнює (n´n). Але матриця P* є симетричною, тому число невідомих
елементів дорівнює n(n+1)/2, для визначення яких маємо систему такого ж числа
скалярних квадратних рівнянь. Розв’язання цієї системи саме по собі є складною
обчислювальною задачею. Тільки при n = 2 її можна спробувати розв’язати “у
лоб”.
Приклад. Нехай для системи, що описується скалярними рівняннями
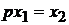 ,
,
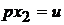 ,
,
вимагається знайти стабілізуючий зворотний зв’язок 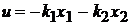 , причому такий, що у перехідних процесах замкненої
системи при будь-яких початкових умовах досягається мінімум інтегрального
показника
, причому такий, що у перехідних процесах замкненої
системи при будь-яких початкових умовах досягається мінімум інтегрального
показника
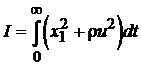 ,
,
де r - позитивний параметр.
Задачу можна переписати у стандартній матричній формі (14.7),
якщо позначити:
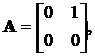
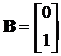 ,
, 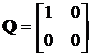 ,
R=r .
,
R=r .
Потім треба розв’язати рівняння Ріккаті (Лур’є), яке у даному
випадку буде мати вид:
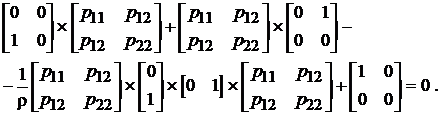
Тут враховано, що матриця Р симетрична і р21=р12 .
Після перемноження матриць отримаємо
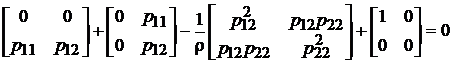 ,
,
або 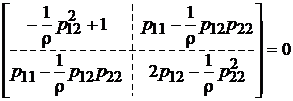 .
.
З рівності нулю всіх елементів матриці одержуємо:
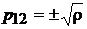 ;
;
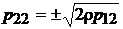 ;
;  .
.
Розв’язок має бути позитивно визначеним, причому завідоммо 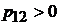 , що дає правило вибору знаків
, що дає правило вибору знаків
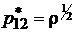 ,
,
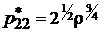 ,
,  .
.
Оптимальні коефіцієнти зворотного зв’язку шукаються по
формулі (14.9):
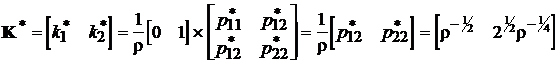 .
.
Замкнена система описується рівняннями
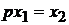 ,
,
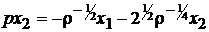
і буде вже мати власні числа у лівій напівплощині, які
забезпечують мінімум показника І.
Для систем більш високого порядку існують спеціальні
алгоритми розв’язання рівняння Ріккаті (Лур’є). Один з таких алгоритмів
наводиться нижче.
В силу симетрії матриць P і R (і R-1) для матриці K (14.9)
можна записати
Т = PTB(R-1)T = PBR-1,
окрім того із (14.9) отримуємо, що RK = BTP. Підставляючи ці
вирази в рівняння Ріккаті (Лур’є) (14.8) зводимо його до виду
+ PA - KTRK + Q = 0 . (14.12)
Можна показати [1], що рівняння (14.12) повністю еквівалентне
рівнянню
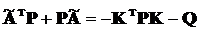 ,
де
,
де 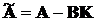 .
.
Послідовні наближення матриці K далі будуються по наступному алгоритму:
задамося якою-небудь матрицею KО такою, що матриця 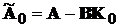 є гурвіцевою (тобто має всі власні числа у лівій
напівплощині);
є гурвіцевою (тобто має всі власні числа у лівій
напівплощині);
1
на кожній
i-й ітерації розв’язують систему лінійних алгебраїчних рівнянь
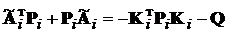
відносно компонентів матриці Pi. Визначивши їх, обчислюють нове
наближення матриць K і 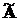
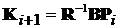 і
і
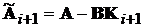 , і = 0, 1, 2, ... .
, і = 0, 1, 2, ... .
Збіжність алгоритму забезпечена у рамках умов теореми 3, причому всі 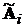 гурвіцеві. Початкове ж наближення KО може бути
знайдено, наприклад, за допомогою алгоритмів, що були розглянуті у розділі 11.
гурвіцеві. Початкове ж наближення KО може бути
знайдено, наприклад, за допомогою алгоритмів, що були розглянуті у розділі 11.
Побудова критерію. Завдання ступеню стійкості
Вид оптимального зворотного зв’язку залежить від вибору
коефіцієнтів матриць Q і R, що входять у показник якості (14.7) і визначають
характер “сумірності” енергії різних компонентів векторів стану та управління.
Проблема зведення різних вимог, що пред’являються до системи, у єдиний показник
якості (14.7) не має однозначного розв’язку. Все залежить від конкретного
призначення та умов роботи системи.
На практиці звичайно використовують засіб приведення до відносних
величин (або нормування). Нехай відомі величини 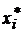 та
та
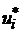 , перевищення яких відповідними компонентами векторів
стану та управління небажане.
, перевищення яких відповідними компонентами векторів
стану та управління небажане.
Тоді рекомендується складати критерій якості у вигляді:
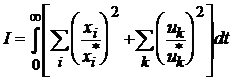 ,
,
тобто приймають 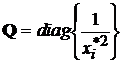 ,
, 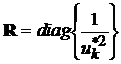 .
.
Такий підхід, у всякому разі, гарантує сумірність внеску всіх
компонентів, хоч, звичайно, не можна стверджувати, що оптимальна стабілізація
по вказаному критерію дійсно гарантує невихід за обмеження 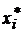 тa
тa 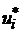 .
Окрім того, розподіл власних чисел матриці оптимальної замкненої системи також
істотно залежить від Q та R. Тому, намагаючись гарантувати себе від поганого
розподілу власних чисел, часто вводять додаткові вимоги при пошуку оптимального
стабілізуючого зворотного зв’язку - він повинен забезпечити ступінь стійкості
замкненої системи не нижче заданої величини
.
Окрім того, розподіл власних чисел матриці оптимальної замкненої системи також
істотно залежить від Q та R. Тому, намагаючись гарантувати себе від поганого
розподілу власних чисел, часто вводять додаткові вимоги при пошуку оптимального
стабілізуючого зворотного зв’язку - він повинен забезпечити ступінь стійкості
замкненої системи не нижче заданої величини 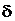 .
.
Добитися задоволення цієї вимоги нескладно. Дійсно, розв’яжемо задачу
оптимальної стабілізації, використавши у розрахунках замість матриці А матрицю 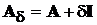 . Тоді у результаті розв’язання рівняння Ріккаті
(Лур’є) отримаємо матрицю
. Тоді у результаті розв’язання рівняння Ріккаті
(Лур’є) отримаємо матрицю 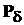 та коефіцієнти посилення
та коефіцієнти посилення 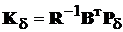 такі, що матриця
такі, що матриця 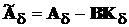 завідоммо
стійка, тобто всі її власні числа лежать зліва від удаваної осі. Але тоді
матриця
завідоммо
стійка, тобто всі її власні числа лежать зліва від удаваної осі. Але тоді
матриця
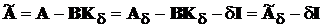
буде мати всі власні числа зліва від прямої, зсунутої відносно удаваної
осі на 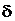 (див. рис. 14.2), оскільки
(див. рис. 14.2), оскільки
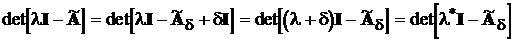 .
.
Якщо l= a+jb, то l*= a+d+jb = a*+jb*, де a*= a+d, b*= b. Це означає
зсув удаваної осі уліво на величину 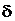 .
.
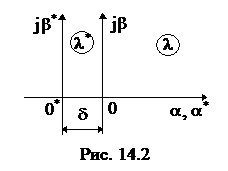
Таким чином ми можемо сформулювати наступне правило:
“Для побудови оптимального стабілізуючого зворотного зв’язку, що
забезпечує заданий ступінь стійкості 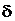 замкненої
системи, досить знайти позитивно визначений розв’язок
замкненої
системи, досить знайти позитивно визначений розв’язок 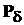 рівняння
рівняння
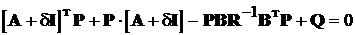
та прийняти 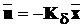 , де
, де 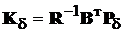 “.
“.
Список
літератури
1.
Первозванский
А.А. Курс теории автоматического управления. - М.: Наука, 2006. - 615 с.
2.
Справочник
по теории автоматического управления / Под ред. А.А. Красовского. - М.: Наука, 2007. - 712 с.
3.
Солодовников
В.В., Плотников В.Н., Яковлев А.В. Основы теории и элементы систем
автоматического регулирования. - М.: Машиностроение, 2005. - 536 с.
4.
Попов
Е.П. Теория линейных систем автоматического регулирования и управления. - М.:
Наука, 2009. - 304 с.
5.
Теория
автоматического управления. - Ч.1 / Под ред. А.А. Воронова. - М.: Высшая школа,
2005. - 270 с.
6.
Кузовков
Н.Т. Модальное управление и наблюдающие устройства. - М.: Машиностроение, 2006. - 185 с.
7.
Авдеев
В.В. Алгоритмы модального управления: Учеб. пособие. - Днепpопетpовск: ДГУ, 2009. - 36 с.