Подъем инвариантов классических групп
Подъем инвариантов классических групп
А.Н. Зубков, Омский государственный педагогический
университет, кафедра алгебры
Пусть
G простая алгебраическая группа одного из трех классических типов - B, C, D,
над алгебраически замкнутым полем K произвольной характеристики. Группа G=G(n)
канонически вложена в GL(n) для подходящего n [8]. Рассмотрим диагональное
действие группы G на 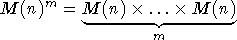 -
m экземплярах пространства
-
m экземплярах пространства 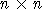 матриц
M(n) сопряжениями. Возникает интересная задача - описать кольцо инвариантов
In,m=K[M(n)m]G(n) . В предлагаемой работе будет доказано, что имеет место
естественный эпиморфизм
матриц
M(n) сопряжениями. Возникает интересная задача - описать кольцо инвариантов
In,m=K[M(n)m]G(n) . В предлагаемой работе будет доказано, что имеет место
естественный эпиморфизм 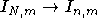 ,
который индуцирован каноническим отображением
,
который индуцирован каноническим отображением 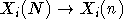 , где
, где 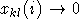 тогда и только тогда, когда
тогда и только тогда, когда 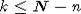 , или
, или 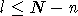 (для симплектического случая определение другое,
здесь зануляются все элементы вне "центрального"
(для симплектического случая определение другое,
здесь зануляются все элементы вне "центрального"  -блока). На остальных местах
отображение тождественно.
-блока). На остальных местах
отображение тождественно.
Все
необходимые сведения о модулях с хорошей фильтрацией (кратко модули с ХФ),
можно найти в [5].
Мы
будем использовать идею доказательства теоремы 2 из [5]. Пусть 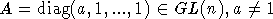 .
.
Cлучай
B, D. Мы будем предполагать, что 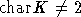 . Подходящим образом изменяя базис, мы можем
считать, что
. Подходящим образом изменяя базис, мы можем
считать, что 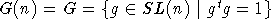 . Более
того, так как действие сопряжениями, то можно полагать даже, что
. Более
того, так как действие сопряжениями, то можно полагать даже, что 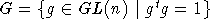 .
.
Пара
аффинных G-многообразий 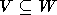 (G
- произвольная редуктивная группа) называется хорошей, если K[W] и IV - G-
модули с ХФ. Здесь IV - это идеал
(G
- произвольная редуктивная группа) называется хорошей, если K[W] и IV - G-
модули с ХФ. Здесь IV - это идеал 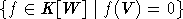 . Пусть W=M(n), V= C(A)=CG(A), где
. Пусть W=M(n), V= C(A)=CG(A), где 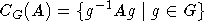 . Наша задача сейчас -
показать, что
. Наша задача сейчас -
показать, что 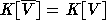 и, что
и, что 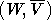 - хорошая пара.
- хорошая пара.
Нетрудно
проверить, что g-1Ag = En + (a-1)(xij), где xij = g1ig1j, g=(gij), En -
единичная матрица. Обозначим через M(n)r множество матриц ранга 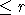 , а через S - подпространство
симметрических матриц в M(n).
, а через S - подпространство
симметрических матриц в M(n).
Лемма
1. Класс сопряженности V совпадает с 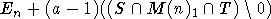 , где T - это множество всех матриц,
удовлетворяющих условиям
, где T - это множество всех матриц,
удовлетворяющих условиям 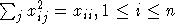 .
.
Обозначим
множество 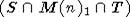 через L
через L
Доказательство.
Легко проверить непосредственно, что M(n)1 совпадает с множеством матриц вида
(xiyj), где 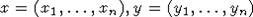 независимо
пробегают все векторы из n-мерного векторного пространства E(n). Пусть
независимо
пробегают все векторы из n-мерного векторного пространства E(n). Пусть 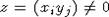 и лежит в
и лежит в 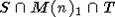 . Тогда xiyj = yixj. Найдутся xi0 и
yj0 не равные нулю, ведь
. Тогда xiyj = yixj. Найдутся xi0 и
yj0 не равные нулю, ведь 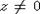 .
Тогда из xi0yj0 = yi0xj0 следует, что
.
Тогда из xi0yj0 = yi0xj0 следует, что 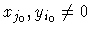 . Далее, если xi =0, тогда xi0yi= yi0xi =0, то
есть yi=0 и наоборот. Другими словами, xi =0 тогда и только тогда, когда yi =0.
Более того, для ненулевых коэффициентов отношение xi/yi является константой.
Обозначим ее t. Переходя к параметрам xi'=t-1/2xi=yi'=t1/2yi, можно
предполагать, что xi=yi для всех i. Подставляя в уравнения определяющие T и
используя то, что
. Далее, если xi =0, тогда xi0yi= yi0xi =0, то
есть yi=0 и наоборот. Другими словами, xi =0 тогда и только тогда, когда yi =0.
Более того, для ненулевых коэффициентов отношение xi/yi является константой.
Обозначим ее t. Переходя к параметрам xi'=t-1/2xi=yi'=t1/2yi, можно
предполагать, что xi=yi для всех i. Подставляя в уравнения определяющие T и
используя то, что 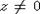 , мы
получим, что
, мы
получим, что 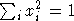 . Достроим
cистему из одного вектора x до ортонормированного базиса пространства E(n) и
расположим векторы этого базиса столбцами (причем x - первый) в матрице g.
Ясно, что
. Достроим
cистему из одного вектора x до ортонормированного базиса пространства E(n) и
расположим векторы этого базиса столбцами (причем x - первый) в матрице g.
Ясно, что 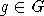 , и g-1Ag = En
+ (a-1)z. Таким образом,
, и g-1Ag = En
+ (a-1)z. Таким образом, 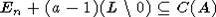 .
Обратное включение очевидно.
.
Обратное включение очевидно.
Поскольку
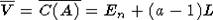 , то мы можем
воспользоваться леммой 1 (
, то мы можем
воспользоваться леммой 1 (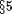 )
[7] и заключить, что
)
[7] и заключить, что 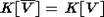 ,
если докажем, что
,
если докажем, что 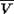 нормальное
многообразие. Cдвиг и умножение на (ненулевой) скаляр - гомеоморфизмы, поэтому
достаточно показать, что нормально L. Пусть Sn - единичная сфера в E(n). Из
сказанного выше ясно, что отображение из Sn в L по правилу
нормальное
многообразие. Cдвиг и умножение на (ненулевой) скаляр - гомеоморфизмы, поэтому
достаточно показать, что нормально L. Пусть Sn - единичная сфера в E(n). Из
сказанного выше ясно, что отображение из Sn в L по правилу 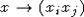 является доминантным. В частности, мы
имеем вложение
является доминантным. В частности, мы
имеем вложение 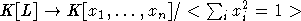 . Образ
этого вложения порожден элементами xixj. Алгебра
. Образ
этого вложения порожден элементами xixj. Алгебра 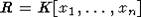 имеет градуировку
имеет градуировку 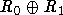 , где R0 - подпространство, натянутое на мономы
четной степени, а R1 - нечетной. Элемент
, где R0 - подпространство, натянутое на мономы
четной степени, а R1 - нечетной. Элемент 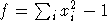 однороден относительно этой градуировки, поэтому
однороден относительно этой градуировки, поэтому
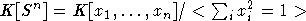 "наследует"
градуировку R. Будем обозначать ее теми же символами. Заметим еще, что K[L]=R0.
Ранг якобиана
"наследует"
градуировку R. Будем обозначать ее теми же символами. Заметим еще, что K[L]=R0.
Ранг якобиана 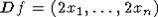 равен 1
по крайней мере на
равен 1
по крайней мере на 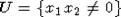 , и
, и 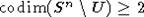 . По критерию Серра ([6]
. По критерию Серра ([6] 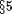 , теорема 5.8.6), K[Sn]
нормально (
, теорема 5.8.6), K[Sn]
нормально (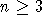 ). Пусть
теперь
). Пусть
теперь 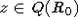 - целый над R0.
Так как
- целый над R0.
Так как 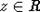 , то
, то 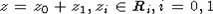 и
и 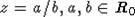 . Следовательно,
. Следовательно, 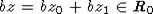 , то есть
, то есть 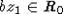 , откуда z1=0.
, откуда z1=0.
Согласно
предложению 6.7 [2], чтобы доказать, что 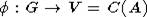 (
(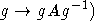 отождествляется с
отождествляется с 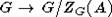 , где ZG(A) - централизатор элемента A,
достаточно проверить, что дифференциал
, где ZG(A) - централизатор элемента A,
достаточно проверить, что дифференциал  сюръективен. Однако
сюръективен. Однако 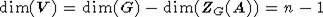 . Используя формализм с двойными числами [8],
имеем:
. Используя формализм с двойными числами [8],
имеем: 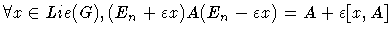 . Таким образом,
. Таким образом,
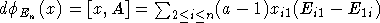 . Отсюда ясно, что
образ
. Отсюда ясно, что
образ 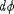 имеет ту же
размерность n-1. Итак,
имеет ту же
размерность n-1. Итак, 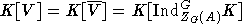 .
Отметим еще для дальнейшего, что ZG(A) состоит из матриц, у которых правый
"нижний"
.
Отметим еще для дальнейшего, что ZG(A) состоит из матриц, у которых правый
"нижний" 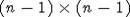 -угол
- это произвольная матрица из G(n-1), а в первом столбце и первой строке везде
стоят нули, кроме начала, где коэффициент равен
-угол
- это произвольная матрица из G(n-1), а в первом столбце и первой строке везде
стоят нули, кроме начала, где коэффициент равен 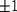 .
.
По
тем же соображениям, что и выше, осталось показать, что (M(n), L) - хорошая
пара. Согласно лемме 1.3(a) [4], можно рассмотреть "башню" 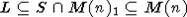 и проверить каждый
"скачок". Рассмотрим сначала
и проверить каждый
"скачок". Рассмотрим сначала 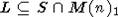 . Мы имеем коммутативную (все морфизмы
G-эквивариантны) диаграмму:
. Мы имеем коммутативную (все морфизмы
G-эквивариантны) диаграмму:
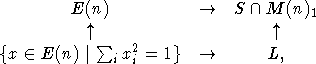 где вертикальные стрелки -
это просто включения. Переходя к координатным алгебрам, мы получим
"дуальную" диаграмму:
где вертикальные стрелки -
это просто включения. Переходя к координатным алгебрам, мы получим
"дуальную" диаграмму:
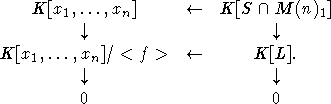
В
первой диаграмме горизонтальные стрелки - G-доминантные морфизмы, поэтому во
второй - вложения. Отсюда ясно, что 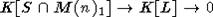 можно отождествить с
можно отождествить с 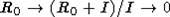 (в принятых выше обозначениях). Здесь I - идеал,
порожденный элементом f. Из тех же градуировочных соображений ясно, что
(в принятых выше обозначениях). Здесь I - идеал,
порожденный элементом f. Из тех же градуировочных соображений ясно, что 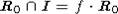 . Осталось отметить, что f
G-инвариант и, следовательно, G-модуль
. Осталось отметить, что f
G-инвариант и, следовательно, G-модуль 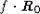 изоморфен R0. То, что R0 с ХФ, будет следовать
из того, что
изоморфен R0. То, что R0 с ХФ, будет следовать
из того, что 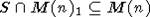 - хорошая
пара.
- хорошая
пара.
Пусть
теперь 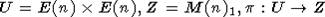 по правилу
по правилу 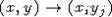 . Ясно, что
. Ясно, что 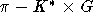 -эквивариантное отображение, где K* =
GL(1) действует по правилу
-эквивариантное отображение, где K* =
GL(1) действует по правилу 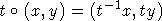 . Напомним, что отображение G-многообразий
. Напомним, что отображение G-многообразий 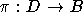 называется факторным, если
называется факторным, если  сюръективно и
сюръективно и 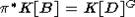 . Хорошо известно, что
. Хорошо известно, что  K*-факторное отображение [4]. Обозначим
через
K*-факторное отображение [4]. Обозначим
через 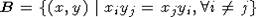 . Покажем, что
(U, B) - хорошая пара. Функтор ограничения переводит GL(n)-модули с ХФ в
G-модули с ХФ. Алгебра
. Покажем, что
(U, B) - хорошая пара. Функтор ограничения переводит GL(n)-модули с ХФ в
G-модули с ХФ. Алгебра 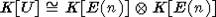 изоморфна
изоморфна
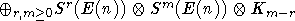 как
как 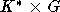 -модуль (Kl - это одномерный K*-модуль
с весом l). Хорошо известно, что GL(n)-модуль Sk(E(n)) с ХФ [9]. По теореме
Донкина-Матье, K[U]
-модуль (Kl - это одномерный K*-модуль
с весом l). Хорошо известно, что GL(n)-модуль Sk(E(n)) с ХФ [9]. По теореме
Донкина-Матье, K[U] 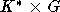 -модуль
с ХФ. Заметим, что достаточно доказывать наличие ХФ только относительно G.
Представим алгебру K[U] в виде
-модуль
с ХФ. Заметим, что достаточно доказывать наличие ХФ только относительно G.
Представим алгебру K[U] в виде 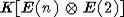 . Отождествление происходит по правилу
. Отождествление происходит по правилу 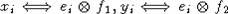 , где
, где 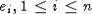 - стандартный базис E(n), а f1,f2 -
E(2). Cогласно [1],
- стандартный базис E(n), а f1,f2 -
E(2). Cогласно [1], 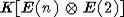 имеет
имеет
 -фильтрацию c факторами
-фильтрацию c факторами
 , где
, где 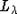 - функтор Шура,
- функтор Шура, 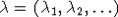 пробегает все разбиения с
пробегает все разбиения с  . Нетрудно заметить, что
идеал, порожденный xiyj-xjyi, совпадает с той частью фильтрации, где
. Нетрудно заметить, что
идеал, порожденный xiyj-xjyi, совпадает с той частью фильтрации, где 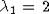 . Поскольку
. Поскольку 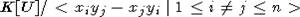 без кручения [3], то
без кручения [3], то 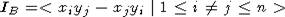 . В частности, IB с ХФ как G-модуль, а
значит, и как
. В частности, IB с ХФ как G-модуль, а
значит, и как 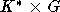 -модуль. В
итоге многообразия U, B, Z удовлетворяют условиям предложения 1.4(a) из [4]. А
это значит в частности, что
-модуль. В
итоге многообразия U, B, Z удовлетворяют условиям предложения 1.4(a) из [4]. А
это значит в частности, что 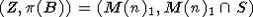 - хорошая пара. Осталось заметить, что (M(n),
M(n)1) - хорошая GL(n)-пара по [4]. Согласно сказанному выше, это также хорошая
G-пара. В частности, хорошей G-парой будет
- хорошая пара. Осталось заметить, что (M(n),
M(n)1) - хорошая GL(n)-пара по [4]. Согласно сказанному выше, это также хорошая
G-пара. В частности, хорошей G-парой будет 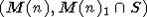 , что и требуется.
, что и требуется.
Случай
C. Здесь доказательство аналогично ортогональному случаю. Мы только вкратце
повторим основные моменты, указав отличие от рассмотренного выше. Матрица A
остается той же самой. При этом у элементов группы ZG(A) первые и последние
строки и столбцы нулевые, кроме элементов на диагонали, которые взаимно обратны
и пробегают K*. Кроме того, "серединный" 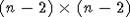 -квадрат лежит в G(n-2)=Spn-2(K). Далее, легко
проверить, что класс сопряженности C(A) совпадает с En + (a-1)L, где
-квадрат лежит в G(n-2)=Spn-2(K). Далее, легко
проверить, что класс сопряженности C(A) совпадает с En + (a-1)L, где 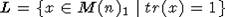 . В частности, он уже
замкнут. Проверка того, что
. В частности, он уже
замкнут. Проверка того, что 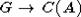 отождествляется с факторным
отождествляется с факторным 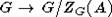 совершенно аналогична. Здесь
совершенно аналогична. Здесь 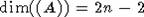 , образ Lie(G) состоит из
матриц того же вида, что и в ортогональном случае, только коэффициенты первой
строки и первого столбца никак не связаны друг с другом и поэтому размерность
образа тоже равна 2n-2. Наконец, (M(n), L) - очевидно хорошая пара. Достаточно
рассмотреть башню
, образ Lie(G) состоит из
матриц того же вида, что и в ортогональном случае, только коэффициенты первой
строки и первого столбца никак не связаны друг с другом и поэтому размерность
образа тоже равна 2n-2. Наконец, (M(n), L) - очевидно хорошая пара. Достаточно
рассмотреть башню 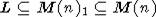 и
использовать то, что tr(x)-1 - G-инвариант! Заметим еще, что в симплектическом
случае характеристика поля произвольна.
и
использовать то, что tr(x)-1 - G-инвариант! Заметим еще, что в симплектическом
случае характеристика поля произвольна.
Пусть
теперь G - любая группа типа B, D, C. Дословно повторяя доказательство теоремы
2 из [5], мы получим эпиморфизм 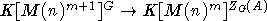 , индуцированный
, индуцированный 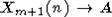 (на остальных общих матрицах отображение
тождественно). Разбив матрицы из M(n) на блоки в соответствии с блочным
"строением" группы ZG(A), мы видим, что пространство M(n) изоморфно
(так как ZG(A)-многообразие)
(на остальных общих матрицах отображение
тождественно). Разбив матрицы из M(n) на блоки в соответствии с блочным
"строением" группы ZG(A), мы видим, что пространство M(n) изоморфно
(так как ZG(A)-многообразие) 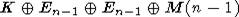 в ортогональном случае и
в ортогональном случае и 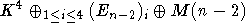 в симплектическом. Здесь K и K4
тривиальные модули, а на En-1 (соответственно на En-2) ZG(A) действует как
G(n-1) (G(n-2)) c точностью до умножения на скаляр. Отсюда ясно, что
каноническое отображение
в симплектическом. Здесь K и K4
тривиальные модули, а на En-1 (соответственно на En-2) ZG(A) действует как
G(n-1) (G(n-2)) c точностью до умножения на скаляр. Отсюда ясно, что
каноническое отображение 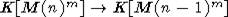 (
(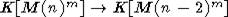 ), даст эпиморфизм
), даст эпиморфизм 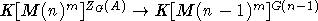 (
(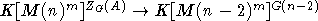 ). Пусть Rn,m - Q-алгебра, порожденная следами
от всевозможных произведений общих матриц, или транспонированных к ним (в
случае C - симплектически транспонированных).
). Пусть Rn,m - Q-алгебра, порожденная следами
от всевозможных произведений общих матриц, или транспонированных к ним (в
случае C - симплектически транспонированных).
Доказательство.
К сожалению, размеры статьи, допустимые в данном журнале, не позволяют нам
привести полное доказательство. Поэтому мы просто отметим здесь, что In,m
порождается элементами из 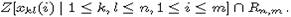 После этого утверждение леммы очевидно, ведь
произведение матрицы A на матрицы Xi(n), у которых приравнены нулю коэффициенты
левого верхнего "угла" (или "окаймления" в случае C), дает
тот же результат, что и произведение единичной матрицы.
После этого утверждение леммы очевидно, ведь
произведение матрицы A на матрицы Xi(n), у которых приравнены нулю коэффициенты
левого верхнего "угла" (или "окаймления" в случае C), дает
тот же результат, что и произведение единичной матрицы.
В
силу сделанного выше замечания о порождающих In,m специализация 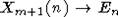 отображает In,m+1 в In,m. Отсюда уже
легко получается основная теорема.
отображает In,m+1 в In,m. Отсюда уже
легко получается основная теорема.
Теорема.
Каноническое отображение алгебры K[M(n)m] в K[M(n-1)m] (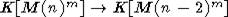 в случае C) индуцирует эпиморфизм
колец инвариантов.
в случае C) индуцирует эпиморфизм
колец инвариантов.
Список литературы
Akin K., Buchsbaum D.A., Weyman J. Shur functors and Shur
complexes// Adv. in Math. Vol.44. P.207-278 (1982).
Борель
А. Линейные алгебраические группы. M.: Мир., 1972.
De Concini C., Procesi C. A characteristic free approach to
invariant theory// Adv. in Math. 1976. Vol.21. P. 330-354.
Donkin S. The normality of conjugacy classes of matrices// Inv.
Math., Vol.101. P.717-736 (1990).
Donkin S. Invariants of several matrices// Invent. Math. Vol.110.
P.389-401 (1993).
Grotendick A., Dieudonne J. Elements de geometrie algebriques//
Inst. Hautes Etudes Sci.Publ.Math. 4. 1960-1967.
Grosshans F. Observable subgroups and Hilbert's fourteenth problem//
Am.J. Math. 95. P.229-253 (1973).
Humphreys J.E. Linear algebraic groups/ Springer Verlag. 1975.
Zubkov A.N. Endomorphisms of tensor products of exterior powers and
Procesi hypothesis// Commun. in Algebra. 22(15). 6385-6399 (1994).
Для
подготовки данной работы были использованы материалы с сайта http://www.omsu.omskreg.ru/