Об одном обобщении логистической модели динамики популяций с ограниченным временем жизни особей
Об одном обобщении логистической модели динамики
популяций с ограниченным временем жизни особей
Н.В. Перцев, Омский государственный педагогический
университет, кафедра математического анализа
1. Введение
Одной
из классических моделей динамики популяций является логистическая модель или
модель Ферхюльста-Пирла, которая описывается дифференциальным уравнением
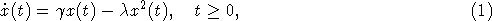
с
начальным условием 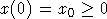 ,
где параметры
,
где параметры 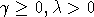 характеризуют
интенсивности рождения и гибели особей популяции. Решение уравнения (1), как
известно, имеет вид
характеризуют
интенсивности рождения и гибели особей популяции. Решение уравнения (1), как
известно, имеет вид
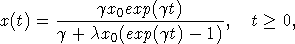
а
график x(t) представляет собой так называемую логистическую кривую. Модель (1)
и ее различные модификации подробно изучены в ряде работ, см.,например, [1, с.
14], [2, с. 11].
В
настоящей работе рассматривается один из вариантов модели (1), в котором
учитывается ограниченность времени жизни особей популяции. Будем предполагать,
что особи популяции, родившиеся в момент времени t, в течение некоторого
периода 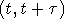 могут
производить новых особей популяции (с интенсивностью
могут
производить новых особей популяции (с интенсивностью 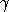 ), либо могут погибать (с интенсивностью
), либо могут погибать (с интенсивностью 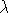 ). Особи, дожившие до момента
времени
). Особи, дожившие до момента
времени 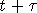 , погибают, не
оставляя потомства. Параметр
, погибают, не
оставляя потомства. Параметр 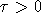 означает предельное время жизни особей
популяции. Начальное распределение особей по возрасту будем задавать
неотрицательной, непрерывной функцией
означает предельное время жизни особей
популяции. Начальное распределение особей по возрасту будем задавать
неотрицательной, непрерывной функцией 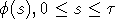 . При сделанных предположениях численность x(t)
популяции описывается интегро-дифференциальным уравнением [3]
. При сделанных предположениях численность x(t)
популяции описывается интегро-дифференциальным уравнением [3]
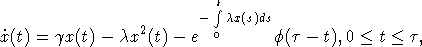
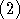
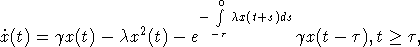
с
начальным условием

Ниже
исследуются свойства решений уравнения (2) с начальным условием (3).
2. Основные результаты
В
уравнении (2) при 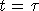 под
под 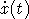 понимается правосторонняя
производная. Сделаем замену
понимается правосторонняя
производная. Сделаем замену 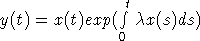 . Тогда x(t) удовлетворяет соотношению
. Тогда x(t) удовлетворяет соотношению
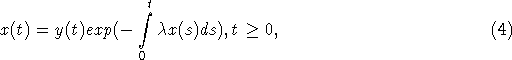
в
котором y(t) является решением следующего линейного дифференциального уравнения
с запаздыванием:
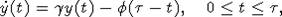
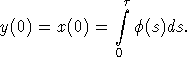
При
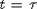 под
под  понимается правосторонняя производная.
Уравнение (5) может быть проинтегрировано по отрезкам вида
понимается правосторонняя производная.
Уравнение (5) может быть проинтегрировано по отрезкам вида 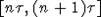 ,n = 0,1,2,...,. Отсюда следует, что
уравнение (5) имеет единственное решение y(t), определенное на
,n = 0,1,2,...,. Отсюда следует, что
уравнение (5) имеет единственное решение y(t), определенное на 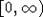 . Нетрудно заметить, что y(t) является
неотрицательной функцией, причем, если x(0)>0, то y(t)>0, если же x(0)=0,
то y(t)=0 при всех
. Нетрудно заметить, что y(t) является
неотрицательной функцией, причем, если x(0)>0, то y(t)>0, если же x(0)=0,
то y(t)=0 при всех 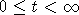 .
Применяя к уравнению (4) принцип сжимающих отображений [4, с. 11], получаем,
что уравнение (2) с начальным условием (3) имеет единственное неотрицательное
решение x(t), определенное на
.
Применяя к уравнению (4) принцип сжимающих отображений [4, с. 11], получаем,
что уравнение (2) с начальным условием (3) имеет единственное неотрицательное
решение x(t), определенное на  . Из (4) следует, что x(t)>0, если x(0)>0
и x(t)=0, если x(0)=0,
. Из (4) следует, что x(t)>0, если x(0)>0
и x(t)=0, если x(0)=0, 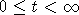 .
Исследуем далее зависимость свойств решений x(t) от параметров модели (ниже
везде принято, что x(0)>0).
.
Исследуем далее зависимость свойств решений x(t) от параметров модели (ниже
везде принято, что x(0)>0).
Примем,
что параметры таковы: 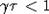 ,
, 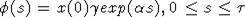 , где
, где  - единственный положительный корень уравнения
- единственный положительный корень уравнения 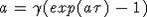 . Тогда функция
. Тогда функция 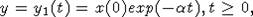 является решением уравнения
(5). Из неравенства
является решением уравнения
(5). Из неравенства 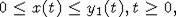 следует,
что
следует,
что 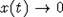 при
при 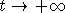 . Пусть теперь
. Пусть теперь 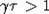 и
и 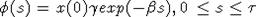 , где
, где 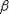 - единственный положительный корень уравнения
- единственный положительный корень уравнения 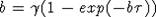 . Функция
. Функция  является решением уравнения (5).
Подставляя y2(t) в (4) и дифференцируя обе части, получаем, что x(t)
удовлетворяет уравнению
является решением уравнения (5).
Подставляя y2(t) в (4) и дифференцируя обе части, получаем, что x(t)
удовлетворяет уравнению
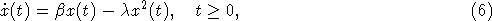
которое
с точностью до обозначений совпадает с уравнением (1). Имеем, что x(t) -
монотонная функция и 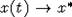 при
при
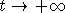 , где
, где 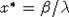 , причем x* - единственный
положительный корень уравнения
, причем x* - единственный
положительный корень уравнения 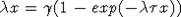 . Если
. Если 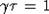 и
и  , то уравнение (5) имеет решение
, то уравнение (5) имеет решение 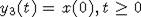 . Тогда x(t) удовлетворяет уравнению
. Тогда x(t) удовлетворяет уравнению 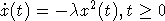 , откуда следует, что
, откуда следует, что 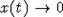 при
при 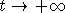 . Заметим, что во всех этих случаях решение x(t)
модели (2) может быть записано в явном виде.
. Заметим, что во всех этих случаях решение x(t)
модели (2) может быть записано в явном виде.
Для
дальнейшего исследования используем результаты работы [5], в которой изучены
асимптотические свойства решений дифференциального уравнения  . Применяя эти результаты к уравнению
(5), будем иметь: 1) если
. Применяя эти результаты к уравнению
(5), будем иметь: 1) если  ,
то
,
то 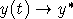 при
при 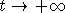 , 2) если
, 2) если 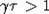 , то при
, то при 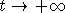 функция y(t) эквивалентна экcпоненте
функция y(t) эквивалентна экcпоненте 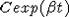 , где
, где 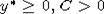 - некоторые константы. Указанные
свойства y(t) не зависят от вида функции
- некоторые константы. Указанные
свойства y(t) не зависят от вида функции 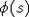 . Отсюда непосредственно вытекает, что для
. Отсюда непосредственно вытекает, что для  и y*=0 существует
и y*=0 существует 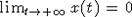 . Для остальных случаев
используем следующее соотношение.
. Для остальных случаев
используем следующее соотношение.
Зафиксируем
h>0. Из уравнения (4) имеем, что при всех 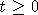 верно
верно
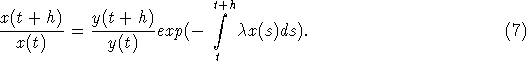
Примем,
что  и y*>0.
Соотношение (7) может быть записано в виде
и y*>0.
Соотношение (7) может быть записано в виде 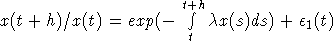 , где
, где 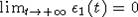 . Учитывая положительность x(t), из последнего
равенства получаем, что при достаточно больших t для любого h>0 верно
неравенство x(t+h)/x(t) < 1 и, следовательно, существует
. Учитывая положительность x(t), из последнего
равенства получаем, что при достаточно больших t для любого h>0 верно
неравенство x(t+h)/x(t) < 1 и, следовательно, существует 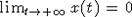 .
.
Пусть
теперь 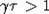 . Тогда из (7)
получим, что
. Тогда из (7)
получим, что 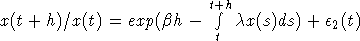 , где
, где 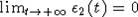 . Последнее равенство можем
переписать в виде
. Последнее равенство можем
переписать в виде
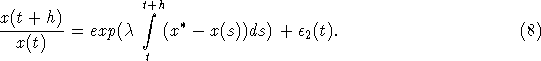
Из
(8) видно, что поведение x(t) на некотором конечном полуинтервале [0,T), T>0
может носить как монотонный, так и колебательный характер. Действительно, пусть
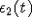 достаточно мало,
достаточно мало, 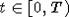 . Если
. Если 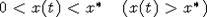 при всех
при всех 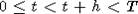 , то имеем, что
, то имеем, что 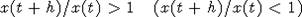 и x(t) - возрастающая ( убывающая ) функция,
и x(t) - возрастающая ( убывающая ) функция, 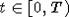 . Если учитывать влияние
слагаемого
. Если учитывать влияние
слагаемого 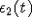 , то,
очевидно, возможны случаи, когда x(t) пересекает уровень x = x* при некоторых
, то,
очевидно, возможны случаи, когда x(t) пересекает уровень x = x* при некоторых 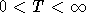 . Покажем далее, что
существует
. Покажем далее, что
существует  . Пусть t
достаточно велико и x(t) < x*. Может оказаться, что при всех h>0 верно
. Пусть t
достаточно велико и x(t) < x*. Может оказаться, что при всех h>0 верно 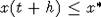 . Тогда x(t+h)/x(t) > 1
и, следовательно, указанный предел существует. Предположим теперь противное.
Обозначим через t+h1 момент первого пересечения функцией x(t) уровня x = x*,
иначе,
. Тогда x(t+h)/x(t) > 1
и, следовательно, указанный предел существует. Предположим теперь противное.
Обозначим через t+h1 момент первого пересечения функцией x(t) уровня x = x*,
иначе, 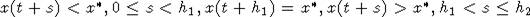 , где h2 -
некоторое число. Из (8) получаем, что x(t+h2)/x(t+h1) =
, где h2 -
некоторое число. Из (8) получаем, что x(t+h2)/x(t+h1) =
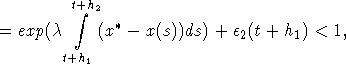
откуда
приходим к противоречию: x(t+h2) < x(t+h1)=x*. Аналогично рассматривается
случай x(t) > x*. Следовательно, если при достаточно больших t верно 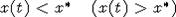 , то при всех
, то при всех 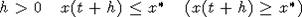 . Отсюда вытекает
существование
. Отсюда вытекает
существование 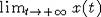 ,
который, очевидно, равен x*. Если же при некотором достаточно большом t
окажется, что x(t) = x*, то либо при всех
,
который, очевидно, равен x*. Если же при некотором достаточно большом t
окажется, что x(t) = x*, то либо при всех 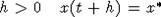 и
и  , либо найдется такой t1 > t, что x(t1) <
x* или x(t1) > x*, что сводится к ранее рассмотренным случаям.
, либо найдется такой t1 > t, что x(t1) <
x* или x(t1) > x*, что сводится к ранее рассмотренным случаям.
3. Заключение
Установленные
выше результаты показывают, что модель (2) является естественным обобщением
модели (1) в предположении, что особи популяции имеют ограниченное время жизни  . Для детального сравнения этих
моделей выделим в модели (1) слагаемое, отвечающее за гибель особей вследствие
процессов старения. Параметр
. Для детального сравнения этих
моделей выделим в модели (1) слагаемое, отвечающее за гибель особей вследствие
процессов старения. Параметр 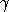 заменим на
заменим на 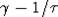 , где под
, где под  понимается среднее время жизни особей, а
понимается среднее время жизни особей, а  по-прежнему означает
интенсивность рождения особей популяции. Тогда вместо (1) будем рассматривать
уравнение
по-прежнему означает
интенсивность рождения особей популяции. Тогда вместо (1) будем рассматривать
уравнение
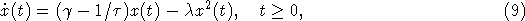
с
начальным условием x(0) = x0. Обозначим через x2(t) и x9(t) решения моделей (2)
и (9) соответственно.
При
 решения обеих моделей
стремятся к нулю при
решения обеих моделей
стремятся к нулю при 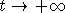 ,
иначе говоря, рассматриваемая популяция вырождается. Если
,
иначе говоря, рассматриваемая популяция вырождается. Если 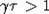 и начальное распределение особей по
возрасту в модели (2) имеет вид
и начальное распределение особей по
возрасту в модели (2) имеет вид 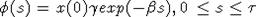 , то эта модель переходит в модель (6), которая
отличается от модели (9) только коэффициентом при x(t). Решения x6(t) модели
(6) и x9(t) носят монотонный характер и образуют логистическую кривую. Можно
показать, что
, то эта модель переходит в модель (6), которая
отличается от модели (9) только коэффициентом при x(t). Решения x6(t) модели
(6) и x9(t) носят монотонный характер и образуют логистическую кривую. Можно
показать, что 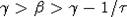 . Отсюда
следует, что в рассматриваемом случае
. Отсюда
следует, что в рассматриваемом случае 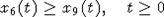 . Кроме того, при
. Кроме того, при 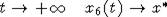 ,
, 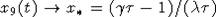 , причем x* > x*. Если по-прежнему
, причем x* > x*. Если по-прежнему 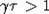 , но начальное распределение
особей по возрасту в модели (2) произвольно, то с ростом t решение x2(t)
приближается к x* либо монотонно, либо с затухающими колебаниями. Решение x9(t)
таких колебаний не имеет. Заметим, что при достаточно больших t численность
популяции будет поддерживаться на уровне x* в модели (2) и на уровне x* в
модели (9). Следовательно, в модели (2) обеспечивается более высокий предельный
уровень численности популяции, чем в модели (9).
, но начальное распределение
особей по возрасту в модели (2) произвольно, то с ростом t решение x2(t)
приближается к x* либо монотонно, либо с затухающими колебаниями. Решение x9(t)
таких колебаний не имеет. Заметим, что при достаточно больших t численность
популяции будет поддерживаться на уровне x* в модели (2) и на уровне x* в
модели (9). Следовательно, в модели (2) обеспечивается более высокий предельный
уровень численности популяции, чем в модели (9).
Таким
образом, при определенных соотношениях на параметры модели (2) ее решения
качественно совпадают с решениями классической модели (9). Вместе с тем имеются
и существенные различия в решениях этих моделей, обусловленные учетом
ограниченности времени жизни особей популяции.
Список литературы
Свирежев
Ю.М. Нелинейные волны, диссипативные структуры и катастрофы в экологии. М.:
Наука, 1987.
Динамическая
теория биологических популяций / Под ред. Р. А. Полуэктова. М.: Наука, 1974.
Перцев
Н.В. Применение одного дифференциального уравнения с последействием в моделях
динамики популяций // Фундаментальная и прикладная математика / Под ред. А.К.
Гуца: Сб. науч. тр. Омск, 1994. С. 119 - 129.
Красносельский
М.А. и др. Приближенное решение операторных уравнений. М.: Наука, 1969.
Cooke K., Yorke A. Some equations Modelling Growth Processes and
Gonorhea Epidemics // Math. Biosci., 1973. V.16. P.75 - 101.
Для
подготовки данной работы были использованы материалы с сайта http://www.omsu.omskreg.ru/