Математичне моделювання реальних процесів звичайними диференціальними рівняннями
МІНІСТЕРСТВО
ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ
БЕРДЯНСЬКИЙ
ДЕРЖАВНИЙ ПЕДАГОГІЧНИЙ УНІВЕРСИТЕТ
Інститут
фізико-математичної і технологічної освіти
Кафедра
математики та методики викладання математики
МАТЕМАТИЧНЕ
МОДЕЛЮВАННЯ реальних процесів звичайними
ДИФЕРЕНЦІАЛЬНИМИ РІВНЯННЯМИ
(Курсова
робота)
Бердянськ,
2012
ЗМІСТ
ВСТУП
РОЗДІЛ I. МАТЕМАТИЧНЕ
МОДЕЛЮВАННЯ ДИФЕРЕНЦІАЛЬНИМИ РІВНЯННЯМИ
.1 Поняття математичного
моделювання
.2 Види математичних моделей
.3 Основні поняття диференціальних
рівнянь
Висновки до розділу I
РОЗДІЛ II. ЗАСТОСУВАННЯ
МАТЕМАТИЧНОГО МОДЕЛЮВАННЯ ДИФЕРЕНЦІАЛЬНИМИ РІВНЯННЯМИ
.1 Приклади процесів, що
моделюються диференціальними рівняннями експоненціальної змінної
.2 Рівняння гармонічних
коливань
Висновки до розділу II
ВИСНОВКИ
СПИСОК ВИКОРАСТАНИХ ДЖЕРЕЛ
ВСТУП
Математичне моделювання -
метод дослідження процесів або явищ шляхом створення математичних моделей
<#"826432.files/image001.gif"> - елемент розсіювання енергії; 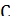
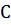 і
і 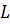 - елементи накопичення енергії.
Поєднанням цих простих елементів і джерел фазових змінних отримують
еквівалентну схему технічної системи будь-якої складності і її математичну
модель.
- елементи накопичення енергії.
Поєднанням цих простих елементів і джерел фазових змінних отримують
еквівалентну схему технічної системи будь-якої складності і її математичну
модель.
Детерміністичні моделі
описують закономірності, що виявляються в одиночному, у кожнім окремо узятому
елементі сукупності. Такій закономірності властива тверда механічна
причинність, що конкретно визначає поводження кожної одиниці сукупності. Вона
одержала назву динамічної або закономірності з твердою детермінацією. Типовими
прикладами динамічних закономірностей можуть служити закони класичної механіки.
У динамічних закономірностях зв’язок між причиною і наслідком може бути
виражений цілком точно у вигляді конкретних математичних формул. Тут кожному
наборові значень пояснюючих змінних завжди відповідає визначене значення
пояснюваної змінної. Такий зв’язок називається функціональним. Детерміністична
модель служить вираженням функціонального зв’язку.
Для моделювання
нестаціонарних імовірнісних процесів використовують стохастичні моделі. Якщо
об’єкт моделювання стаціонарний і піддається випадковим впливам, то модель
називають статистичною. Наприклад, для моделювання функцій перетворення
вимірювальних пристроїв досить скористатися детермінованим способом опису, тоді
як для аналізу похибок, оцінки інформаційних характеристик необхідно застосувати
ймовірнісно-статистичні методи.
Стохастичні моделі описують
закономірності, які обумовлені одночасною дією на об’єкт багатьох факторів і
які проявляються чітко тільки при масових спостереженнях. До найбільш
розповсюджених методів побудови стохастичних моделей відносяться методи,
об’єднані під загальною назвою - багатовимірний статистичний аналіз, зокрема -
кореляційний і регресійний аналізи. Практика показує, що стохастичні моделі,
одержані за допомогою кореляційного і регресійного аналізів, мають перевагу при
кількісному описі причинно-наслідкових відносин в економіці і соціальній сфері
в порівнянні з детерміністичними моделями. Виявлення кількісних співвідношень у
вигляді регресії дає можливість краще зрозуміти природу досліджуваного явища. А
це, у свою чергу, дозволяє впливати на виявлені фактори, втручатися у
відповідний економічний процес з метою одержання потрібних результатів.
Неперервні моделі
представляють системи з неперервними процесами, а дискретні моделі відображають
поведінку систем з дискретними станами. Дискретно-неперевні моделі
використовуються, коли на об’єкті виділяються обидва типи процесів.
Якщо при описі моделі
використовуються лише лінійні математичні конструкції (наприклад, лінійні
алгебраїчні рівняння), то модель називають лінійною, інакше - нелінійною.
Моделі з розподіленими
параметрами описують просторове поширення явищ, а моделі з зосередженими
параметрами нехтують просторовою складовою. Динамічні неперервні детерміновані
моделі з розподіленими параметрами використовують апарат диференціальних
рівнянь у частинних похідних, а з зосередженими параметрами - звичайних
диференціальних рівнянь.
Для аналітичних моделей
властиво те, що процеси функціонування об’єкта представляються у вигляді
аналітичних математичних залежностей: алгебраїчних, диференціальних,
інтегральних рівнянь або їх систем, логічних умов. Наприклад, закон Ома чи
рівняння Максвелла. Дослідження аналітичних моделей можливе за допомогою
методів:
Ø аналітичних;
Ø чисельних;
Ø якісних.
Аналітичні методи полягають у пошуку
явних залежностей між характеристиками. Однак такі залежності можливо отримати
лише для невеликої кількості простих моделей, як правило, лінійних. Інколи
виконують спрощення моделей для отримання можливості вивчити хоча б загальні
властивості об’єкта.
Чисельні методи дозволяють отримати
розв’язок аналітичних моделей, для котрих застосування аналітичних методів
неможливо або недоцільно. Розв’язок чисельними методами здійснюється для
конкретних вихідних даних і має додаткову похибку.
Якісні методи дозволяють зробити
певні висновки по моделі, не маючи розв’язку у явному вигляді. Наприклад, такі
методи використовуються у теорії автоматичного управління для оцінки
ефективності різних варіантів систем управління.
Імітаційне моделювання передбачає
представлення моделі у вигляді алгоритму та комп’ютерної програми, яка дозволяє
відтворити поведінку об’єкту. Імітаційні моделі розглядаються як експерименти,
що проводяться на комп’ютерах, з математичними моделями, що імітують поведінку
реальних об'єктів. При цьому імітуються елементарні явища, що складають процес,
зі збереженням їх логічної структури та послідовності у часі, що дозволяє
отримати відомості про стан системи у певний момент часу та оцінити
характеристики системи. Імітаційні моделі дозволяють вирішувати більш складні
задачі, ніж аналітичні. Наприклад, вони дозволяють досить легко враховувати
вплив випадкових факторів [20, c.80].
Традиційно під моделюванням на
комп’ютері розумілося лише імітаційне моделювання. Але завдяки розвитку
графічного інтерфейсу та графічних пакетів значного поширення набуло
комп’ютерне структурно-функціональне моделювання, а також розпочалося
використання комп’ютера з метою концептуального моделювання, наприклад для
побудови систем штучного інтелекту.
Під комп’ютерним моделюванням найчастіше
розуміють: умовний образ об’єкта чи деякої системи об’єктів (або процесів),
описаних за допомогою взаємозалежних комп’ютерних таблиць, схем, діаграм,
графіків, малюнків, анімаційних фрагментів, гіпертекстів і т. ін., що
відбивають структуру та взаємозв’язки між елементами об’єкта чи системи.
Комп’ютерні моделі такого типу називають структурно-функціональними; окрему
програму, сукупність програм чи програмний комплекс, що дає змогу виконанням
послідовності обчислень з подальшим графічним відображенням їх результатів
відтворювати (імітувати) процеси функціонування об’єкта (системи об’єктів), що
функціонує під впливом різних, як правило випадкових, факторів (імітаційну
модель).
Інколи застосовується комбіноване
(аналітико-імітаційне) моделювання, яке полягає в тому, що об’єкт
декомпозується на окремі підсистеми. Для тих підсистем, для яких це можливе,
використовуються аналітичні моделі, а для інших розробляються імітаційні
моделі.
Розробка моделей поєднує в собі
науку і мистецтво. На жаль, немає чіткого формального алгоритму, який би
дозволив побудувати модель для будь-якого об’єкту.
Моделі прогнозування. Існує множина
математичних моделей, за допомогою яких вирішуються ті, або інші задачі. У всіх
сферах діяльності людини важливим моментом є прогнозування наступних подій.
Зараз існує більше 100 методів і методик прогнозування. Умовно їх можна
розділити на фактографічні й експертні. Фактографічні методи засновані на
аналізі інформації про об'єкт, а експертні - на судженнях експертів, які
отримані при проведенні колективних або індивідуальних опитувань. Серед
фактографічних методів можна виділити наступні:
Ø Статистичні методи.
Ø Методи аналогії.
До статистичних методів ставляться
апроксимація, інтерполяція, , методи дослідження тимчасових рядів.
До методів аналогії ставляться
моделі планування експерименту, а також математичної, історичної й іншої
аналогії.
Серед моделей прогнозування можна
виділити наступні:
Моделі апроксимації. Методи
апроксимації застосовні до детермінованих і статистичних систем. Апроксимація -
наближення. Вибір апроксимуючої функції 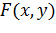 пов'язаний
з рішенням задачі. Для цього застосовується критерій мінімізації квадратичної
помилки.
пов'язаний
з рішенням задачі. Для цього застосовується критерій мінімізації квадратичної
помилки.
Постановка задачі.
Нехай проведено 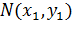 дослідів,
де
дослідів,
де 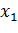 -
вхідний параметр;
-
вхідний параметр; 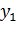 - вихідний
параметр.
- вихідний
параметр.
Необхідно підібрати модель єднальну 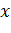 і
і
 (рис.1.1).
(рис.1.1).
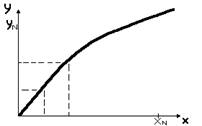
Рис.1.1.Єднальна модель  і
і
Через точки 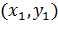 можна
провести криву, що, у свою чергу, може проходити через ці точки або перебувати
поблизу даних точок.
можна
провести криву, що, у свою чергу, може проходити через ці точки або перебувати
поблизу даних точок.
В апроксимації для одержання параметрів моделі
використовується Мнк-критерій (метод найменших квадратів). Кращою вважається та
модель, для якої сума квадратів відхилень значень, від теоретичних буде
мінімальною.
Для цього формується цільова функція або
критерій оптимізації.
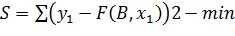
Далі треба досліджувати функцію на екстремум.
Невідомими будуть коефіцієнти моделі B. Найбільше просто перебувають параметри,
якщо 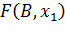 являє
собою поліном
являє
собою поліном 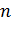 -ний ступеня. При
цьому формується система лінійних рівнянь, порядок якої на одиницю більше
степеня полінома.
-ний ступеня. При
цьому формується система лінійних рівнянь, порядок якої на одиницю більше
степеня полінома.
У загальному випадку для знаходження параметрів
формується система диференціальних рівнянь. Наприкінці формується система
лінійних рівнянь, яку можна вирішувати точними методами (метод Крамера, Гауса,
зворотної матриці). Коли система вирішена, тобто, знайдені параметри моделі,
можна виконати прогнозування значень y [4, c.16-17].
Якщо 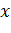
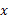 знаходиться усередині інтервалу
знаходиться усередині інтервалу 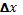
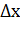 , то говорять про прогнозування в
сьогоденні. Якщо
, то говорять про прогнозування в
сьогоденні. Якщо 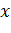 менше
менше 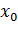 , або
, або 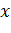 більше
більше 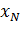 , то мова
йде про екстраполяцію.
, то мова
йде про екстраполяцію.
Моделі інтерполяції. В інтерполяції,
на відміну від апроксимації, проводиться мінімізація лінійної помилки. Також,
на відміну від апроксимації, де крива стосовно точок досліду може
розташовуватися будь-яким образом, а саме перебувати поблизу цих точок, або
проходити через деякі з них, крива інтерполяції, або інтерполяційний поліном
обов'язково проходить через всі точки кривої, які називаються вузлами.
Найбільш простий підхід до одержання
інтерполяційної моделі був запропонований Лагранжем. Тому що поліном проходить
через кожну досліджену точку, то
потрібно скласти стільки рівнянь, скільки проведено дослідів. У лівій частині
рівняння формується поліном, що проходить через 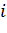
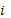 -ту точку. У правій частині
формується вектор значень
-ту точку. У правій частині
формується вектор значень 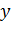
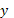 . У результаті виходить система лінійних
рівнянь
. У результаті виходить система лінійних
рівнянь 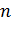 -ого
порядку, де
-ого
порядку, де 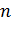 -число
дослідів, а степінь інтерполяційного полінома на одиницю менше числа дослідів.
-число
дослідів, а степінь інтерполяційного полінома на одиницю менше числа дослідів.
Кількість дослідів має бути більше
п'яти, інакше результати інтерполяції будуть не придатні для прогнозування.
Тому що метод інтерполяції вимагає проходження моделі через всі точки, то
накладаються певні умови на досліджене значення. Різниці 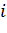 -ого порядку
повинні бути приблизно однаково малі. Добре інтерполюються монотонні функції.
-ого порядку
повинні бути приблизно однаково малі. Добре інтерполюються монотонні функції.
Обидва розглянутих методи
відносяться до методів дослідження детермінованих моделей.
1.3 Основні
поняття диференціальних рівнянь
У кінці XVII - на початку XVIII
століття різноманітні практичні і наукові проблеми привели до появи
диференціальних рівнянь. Насамперед це були диференціальні рівняння першого
порядку, інтегрування яких намагались здійснити за допомогою функцій, що
виражають скінченне число алгебраїчних дій, або таких, що включають елементарні
неалгебраїчні дії, наприклад оперування тригонометричними функціями.
Найбільш прості диференціальні
рівняння з’явились в працях Ісаака Ньютона (1643 - 1727) і Готфріда Лейбніца
(1646 - 1716), саме Лейбніцу і належить термін «диференціальне рівняння».
Диференціальні рівняння мають велике прикладне значення, вони є знаряддям
дослідження багатьох задач природознавства та техніки. Їх широко використовують
в механіці, астрономії, фізиці, хімії, біології. Це пояснюється тим, що досить
часто об’єктивні закони, яким підпорядковуються певні явища (процеси),
записують у формі диференціальних рівнянь, а самі ці рівняння є засобами для
кількісного вираження цих законів.
Наприклад, фізичні закони описують
деякі співвідношення між величинами, що характеризують певний процес, і швидкістю
змінних цих величин. Іншими словами, ці закони виражають рівностями, в яких є
невідомі функції та їх похідні.
У XVIII столітті теорія
диференціальних рівнянь відокремилась з математичного аналізу в самостійну
математичну дисципліну. Її успіхи пов’язанні з іменами швейцарського Іоганна
Бернуллі (1667 - 1748 ), французького математика Жозефа Лагранжа (1736 - 1813)
і особливо Леонарда Ейлера (1707 - 1783).
Перший період розвитку
диференціальних рівнянь був пов'язаний з успішним розв’язком деяких важливих
прикладних задач, що приводять до диференціальних рівнянь, розробкою методів
інтегрування різних типів диференціальних рівнянь і пошуку класів рівнянь,
розв’язки яких можна подати у вигляді елементарних функцій або їх первісних.
Проте дуже швидко виявилося, що інтегрованих диференціальних рівнянь зовсім
небагато. Це привело до розвитку власне теорії диференціальних рівнянь, яка
займається розробкою методів, що дають змогу за властивостями диференціального
рівняння визначити властивості і характер його розв’язку [24, c.408].
У зв’язку з потребами практики
поступово розробляються і способи наближеного інтегрування диференціальних
рівнянь. Ці методи дають зручні алгоритми обчислень з ефективними оцінками
точності, а сучасна обчислювальна техніка дає змогу економічно і швидко звести
розв’язок кожної такої задачі до числового результату.
Рівняння, яке містить невідому
функцію й її похідні, називається диференціальним рівнянням. Порядок найвищої
похідної, що входить у задане диференціальне рівняння, називається його
порядком.
Наприклад, рівняння
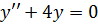
являється диференціальним рівнянням
другого порядку.
Якщо в рівняння входять незалежна
змінна, невідома функція і її перша похідна, то таке рівняння називається
диференціальним рівнянням першого порядку. Якщо, крім цього, в рівняння входить
похідна другого порядку від шуканої функції, то рівняння називається
диференціальним рівнянням другого порядку тощо [22, c.402].
Диференціальним рівнянням n-го
порядку називають рівність:
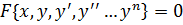
де 
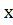 - незалежна зміна;
- незалежна зміна; 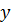 - невідома
функція;
- невідома
функція; 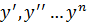 -
похідні невідомої функції.
-
похідні невідомої функції.
Будь-яку функцію, що
задовольняє диференціальному рівнянню, називають розв’язком, або інтегралом
цього рівняння, а знаходження розв’язку диференціального рівняння -
інтегруванням.
Наприклад, функція
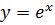
є розв’язком диференціального
рівняння
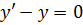 ,
,
Оскільки
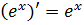 .
.
Розв’язком диференціального
рівняння називають будь-яку функцію,яка при підстановці в рівняння перетворює
його в тотожність.
Функція
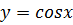
є розв’язком диференціального
рівняння (1):
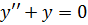 (1)
(1)
Справді, друга похідна від
функції 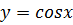 дорівнює:
дорівнює:
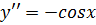 .
.
Підставляючи значення 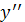
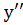 в рівняння
в рівняння
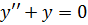 ,
,
Отримаємо
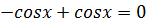
Аналогічно можна
переконатися, що функція
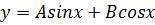
де  і
і 
 - довільні сталі, також є
розв’язком даного рівняння (1).
- довільні сталі, також є
розв’язком даного рівняння (1).
Загальним розв’язком
(загальним інтегралом) диференціального рівняння називають таку функцію, яка
перетворює дане рівняння в тотожність і містить стільки незалежних довільних
сталих, який порядок цього рівняння.
Процес знаходження загального
розв’язку називають інтегруванням диференціального рівняння.
Розв’язок диференціального
рівняння при певних, значеннях довільних сталих називається частинним
розв’язком цього рівняння.
Так, у розглянутому вище
прикладі
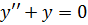
розв’язок 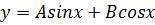 -
загальний, а розв’язок
-
загальний, а розв’язок 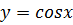 -
частинний.
-
частинний.
На практиці здебільшого
частинний розв’язок диференціальних рівнянь знаходять із загального розв’язку,
виходячи із заданих умов, яким має задовольняти окремий розв’язок даного
диференціального рівняння. Ці умови називають початковими умовами.
Задача відшукання частинного
розв’язку даного диференціального рівняння за початковими умовами називається
задачею Коші.
Приклад. Знайти окремий
розв’язок диференціального рівняння
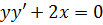 (2)
(2)
який задовольняє початковим
умовам:
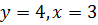 ,
,
якщо загальний розв’язок
даного рівняння задано у вигляді:
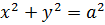 (3)
(3)
Розв’язування. Підставивши в
загальний розв’язок (3) початкові умови, дістанемо значення довільної сталої
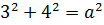
 ,
,
Звідси
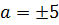
Отже, шуканий окремий
розв’язок диференціального рівняння (2) для заданих початкових умовах є функція
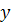
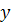 , задана рівнянням
, задана рівнянням
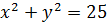
Дамо геометричну
інтерпретацію розв’язку рівняння (2).
Оскільки кожен окремий
розв’язок даного рівняння є деякою функцією однієї змінної, то в прямокутній
системі координат на площині цьому розв’язку відповідає деяка лінія. Ця лінія
називається інтегральною кривою даного диференціального рівняння [24, c.403].
Загальному розв’язку
диференціального рівняння відповідає множина всіх інтегральних кривих цього
рівняння, яка називається сім’єю інтегральних кривих.
Ми встановили, що окремим
розв’язком рівняння
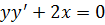
при початкових умовах
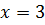 і
і 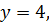
є крива
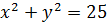 ,
,
а загальним розв’язком -
сім’я інтегральних кривих
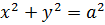 .
.
У системі координат на
площині загальний розв’язок задає множина концентричних кіл з центром у початку
координат. Початкові умови означають, що серед цієї множини кіл требо взяти те
коло, яке проходить через точку з координатами
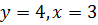 .
.
Це коло задається рівнянням
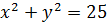 .
.
Багато фізичних законів мають
вигляд диференціальних рівнянь. Інтегрування цих рівнянь - складна справа. Одні
диференціальні рівняння вдається розв’язати в явному вигляді, тобто записати
шукану функцію у вигляді формули. Для інших ще й досі не знайдено зручних
формул. У цих випадках знаходять наближені розв’язки за допомогою комп’ютерних
програм .
Диференціальні рівняння
досить повно і просто описують виробничі процеси. Тому важливо не лише вміти їх
розв’язувати, а й складати.
Висновки
до розділу I
Математичне моделювання -
метод дослідження процесів або явищ шляхом створення їхніх математичних моделей
<#"826432.files/image054.gif">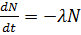 ,
,
яке означає, що число
розпадів - 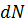 , Що
відбулося за короткий інтервал часу
, Що
відбулося за короткий інтервал часу 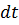 , пропорціональнo числу атомів у
зразку
, пропорціональнo числу атомів у
зразку 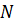
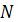 .
.
Експоненціальний закон
Рис.2.1. Експоненціальна
крива радіоактивного розпаду
Експоненціальна крива
радіоактивного розпаду (рис.2.1.): за осі абсцис ("осі 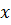 ") -
час, за осі ординат ("осі
") -
час, за осі ординат ("осі 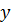 ") - кількість нераспавшихся
ядер або швидкість розпаду в одиницю часу.
") - кількість нераспавшихся
ядер або швидкість розпаду в одиницю часу.
У зазначеному вище
математичному вираженні 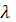
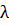 - постійна розпаду, яка
характеризує ймовірність радіоактивного розпаду за одиницю часу і має
розмірність
- постійна розпаду, яка
характеризує ймовірність радіоактивного розпаду за одиницю часу і має
розмірність 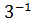 . Знак мінус
вказує на спад числа радіоактивних ядер з часом.
. Знак мінус
вказує на спад числа радіоактивних ядер з часом.
Розв’язування цього диференціального
рівняння має вигляд:
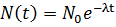 ,
,
де 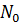 - початкове
число атомів, тобто число атомів для
- початкове
число атомів, тобто число атомів для 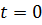 .
.
Таким чином, число
радіоактивних атомів зменшується з часом за експоненціальним законом.
Швидкість розпаду, тобто
число розпадів в одиницю часу
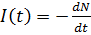
також падає експоненціально.
Диференціюючи вираз для залежності числа атомів від часу, отримуємо:
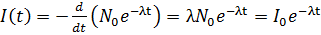
де 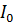 - швидкість
розпаду в початковий момент часу
- швидкість
розпаду в початковий момент часу 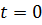 .
.
Таким чином, залежність від
часу числа нераспавшимися радіоактивних атомів і швидкості розпаду описується
однією і тією ж постійною 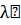 . [1, c.60].
. [1, c.60].
Період напіврозпаду
На практиці набула більшого
поширення інша тимчасова характеристика - період напіврозпаду 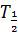 , Що
дорівнює часу, протягом якого число радіоактивних атомів або швидкість розпаду
зменшуються в 2 рази [8, c.39].
, Що
дорівнює часу, протягом якого число радіоактивних атомів або швидкість розпаду
зменшуються в 2 рази [8, c.39].
Зв'язок цієї величини з
постійною розпаду можна вивести із співвідношення
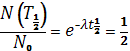
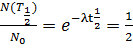 ,
,
Звідки:
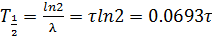
Приклади характеристик
розпаду
Існуючі в природі
радіонукліди в основному виникають в складних ланцюжках розпадів урану і торію
і мають періоди напіврозпаду в дуже широкій області значень: від 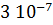 секунди для 212
секунди для 212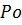 до
до 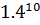 10 років
для 232
10 років
для 232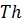 . Саме
існування в даний час багатьох природних радіоактивних елементів незважаючи на
те, що з моменту утворення цих елементів при виникненні Всесвіту пройшло дуже
багато часу, є наслідком дуже великих періодів напіврозпаду 235
. Саме
існування в даний час багатьох природних радіоактивних елементів незважаючи на
те, що з моменту утворення цих елементів при виникненні Всесвіту пройшло дуже
багато часу, є наслідком дуже великих періодів напіврозпаду 235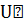 , 238
, 238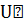
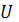 , 232
, 232 . Приміром,
ізотоп 238
. Приміром,
ізотоп 238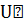 стоїть на
початку довгого ланцюжка (так званий ряд радію), що складається з 20 ізотопів,
кожен з яких виникає при -розпаді або
стоїть на
початку довгого ланцюжка (так званий ряд радію), що складається з 20 ізотопів,
кожен з яких виникає при -розпаді або 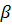 -розпаді попереднього елемента.
Період напіврозпаду 238
-розпаді попереднього елемента.
Період напіврозпаду 238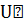 (4,5
(4,5 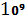 109 років) багато більше,
ніж період напіврозпаду якого з наступних елементів радіоактивного ряду, тому
розпад в цілому всього ланцюжка відбувається за той же час, що й розпад 238
109 років) багато більше,
ніж період напіврозпаду якого з наступних елементів радіоактивного ряду, тому
розпад в цілому всього ланцюжка відбувається за той же час, що й розпад 238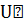 , її
родоначальника, в таких випадках кажуть, що ланцюжок знаходиться в стані
секулярного (або вікового) рівноваги [7, c.55]. Приклади характеристик розпаду
деяких речовин [16, c.105]:
, її
родоначальника, в таких випадках кажуть, що ланцюжок знаходиться в стані
секулярного (або вікового) рівноваги [7, c.55]. Приклади характеристик розпаду
деяких речовин [16, c.105]:
Таблиця 2.1
Приклади характеристик
розпаду деяких речовин
|
Речовина
|
238  235 235  234 234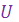 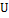 210 210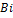 210 210 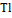
|
|
|
|
|
|
Період напіврозпаду
|
4,5 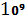 109 років7,13 108 років2,48
105 років4,97 дня1,32 хвилини 109 років7,13 108 років2,48
105 років4,97 дня1,32 хвилини
|
|
|
|
|
|
Постійна розпаду
|
4,84 10-18 c-1
|
|
8,17 10-14 c-1
|
1,61 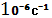 10-6 c-18,75 10-6 c-18,75
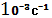 10-3
c-1 10-3
c-1
|
|
|
Частка
|

|

|

|
|
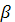
|
|
Повна енергія розпаду
|
4,2 MeB
|
4,6783
|
4,75 MeB
|
1,17 MeB
|
1,80 MeB
|
2.2 Рівняння
гармонічних коливань
Гармонічні коливання. Диференціальне
рівняння гармонічних коливань
Коливанням називається всякий рух
або зміна стану тіла, що характеризується тим чи іншим ступенем повторюваності
в часі значень фізичних величин, які визначають цей рух або стан тіла.
Коливання називаються вільними, якщо
вони здійснюються за рахунок енергії, яка була надана, за відсутності в
наступному зовнішніх впливів на коливну систему.
Коливання називаються періодичними,
якщо значення фізичних величин, які змінюються під час коливань, повторюються
через однакові проміжки часу. Найпростішим типом періодичних коливань є так
звані гармонічні коливання - коливання, при яких значення фізичної величини
змінюється з часом за законом косинуса (синуса) [17, c.20].
Нехай матеріальна точка здійснює
прямолінійні гармонічні коливання вздовж осі координат 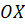 біля
положення рівноваги, яке прийняте за початок координат. Тоді залежність
координати
біля
положення рівноваги, яке прийняте за початок координат. Тоді залежність
координати 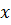 від часу
від часу 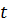 задається
рівнянням
задається
рівнянням
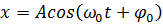
Тут 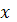
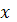 - зміщення коливної точки;
- зміщення коливної точки; 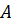 - амплітуда
коливання
- амплітуда
коливання 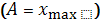
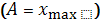 ;
; 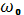
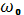 - циклічна частота;
- циклічна частота; 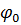 - початкова
фаза коливань в момент часу
- початкова
фаза коливань в момент часу 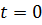 ;
;
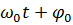 - фаза коливань в момент часу
- фаза коливань в момент часу 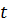 .
.
Найменший проміжок часу 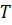 , після
проходження якого повторюються значення всіх фізичних величин, що
характеризують коливання, називається періодом коливання. За час
, після
проходження якого повторюються значення всіх фізичних величин, що
характеризують коливання, називається періодом коливання. За час 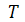
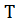 здійснюється одне повне коливання
і фаза коливань отримує приріст
здійснюється одне повне коливання
і фаза коливань отримує приріст 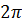 , тобто
, тобто
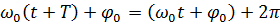 .
.
Звідси
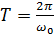 .
.
Частотою коливань називається
кількість повних коливань, що здійснюються за одиницю часу:
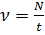 ,
,
де 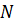 - кількість
коливань, виконаних за час
- кількість
коливань, виконаних за час 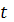
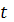 . Частота коливань - величина, яка
обернена до періоду коливань:
. Частота коливань - величина, яка
обернена до періоду коливань:
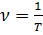 .
.
Циклічна частота
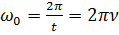 .
.
Отже, циклічна частота
дорівнює кількості повних коливань, що здійснюється за 2p с. Коливний процес
характеризується швидкістю і прискоренням коливної точки:
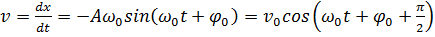 ,
,
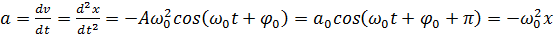
де 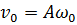 - амплітуда
швидкості, а
- амплітуда
швидкості, а 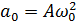 - амплітуда
прискорення. Зміщення, швидкість і прискорення точки, що гармонічно
коливається, є періодичними функціями часу з однаковими циклічною частотою
- амплітуда
прискорення. Зміщення, швидкість і прискорення точки, що гармонічно
коливається, є періодичними функціями часу з однаковими циклічною частотою 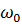 і періодом
і періодом 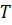 . Фаза
швидкості відрізняється від фази зміщення на
. Фаза
швидкості відрізняється від фази зміщення на  , а фаза прискорення відрізняється
від фази зміщення на
, а фаза прискорення відрізняється
від фази зміщення на 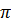 .
.
Прискорення завжди напрямлене
до положення рівноваги: віддаляючись від положення рівноваги, коливна точка
рухається сповільнено, наближаючись до нього - прискорено. Прискорення прямо
пропорційне до зміщення, а його напрямок протилежний до напрямку зміщення [6,
c.69].
Другий закон закон Ньютона
дає змогу в загальному вигляді записати зв’язок між силою і прискоренням для
прямолінійних гармонічних коливань матеріальної точки з масою 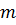 :
:
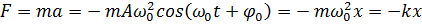
Сила, що діє на коливну
матеріальну точку прямо пропорційна до зміщення і завжди напрямлена до
положення рівноваги. Тому її називають повертальною силою. Фаза сили 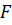 збігається
з фазою прискорення.
збігається
з фазою прискорення.
Для прямолінійних коливань
вздовж осі 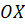 прискорення
прискорення
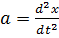 .
.
Тоді
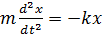 ,
, 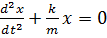
І
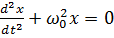 ,
, 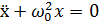 .
.
Це диференціальне рівняння
вільних прямолінійних гармонічних коливань, збуджених пружними або
квазіпружними силами.
Частковими розв’язками цього
диференціального рівняння є функції:
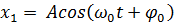
І
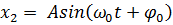
Кінетична енергія
матеріальної точки, що здійснює гармонічні коливання, дорівнює:
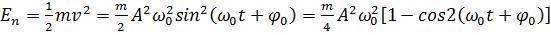 ..
..
Потенціальна енергія
матеріальної точки, що здійснює гармонічні коливання під дією квазіпружної
сили, дорівнює:
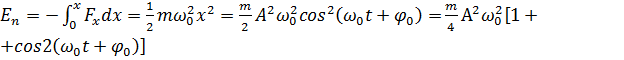
Повна механічна енергія
коливної точки:
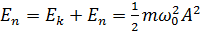 .
.
Рівняння гармонічних коливань
у контурі
Аналогія між механічними і
електромагнітними коливаннями наштовхує на припущення, що електромагнітні
коливання в контурі теж мають відбуватися за гармонічними законом.
Із закону збереження енергії
випливає, що повна електромагнітна енергія контура, що дорівнює сумі енергії
магнітного і електричного полів, з часом не змінюється, якщо опір контура 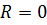 .
.
 .
.
Тому,
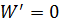 .
.
Отже,
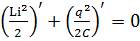
Або
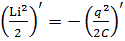 .
.
Фізичний зміст полягає у
тому, що модулем швидкості зміни енергії однакові, а знак «мінус» вказує на те,
що коли одна енергія збільшується, то друга - зменшується [20, c.45].
Беремо похідні за часом:
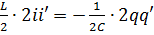 ;
; 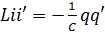 .
.
Але
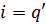 ,
,
Тому
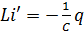 .
.
Оскільки
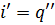 ,
,
То
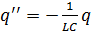
Або
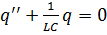 .
.
Згадаємо, що рівняння такого
виду описують гармонічні коливання фізичної величини (в даному випадку
електричного заряду). Розв’язком даного рівняння є функція
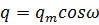 ,
,
Де
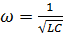 .
.
Оскільки
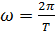 ,
,
То
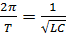 ,
,
звідки формула Томсона
 .
.
За гармонічним законом
змінюється не тільки заряд на обкладках конденсатора, а й напруга і сила струму
в контурі.
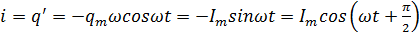 ;
;
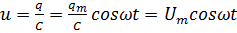 .
.
Коливання заряду (напруги) і
струму в контурі зсунуті за фазою на 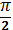
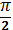 , отже струм досягає максимального
значення в ті моменти, коли заряд (напруга) на обкладках конденсатора дорівнює
нулю і навпаки.
, отже струм досягає максимального
значення в ті моменти, коли заряд (напруга) на обкладках конденсатора дорівнює
нулю і навпаки.
Висновки
до розділу II
Закон радіоактивного розпаду
- фізичний закон, що описує залежність інтенсивності радіоактивного розпаду від
часу і кількості радіоактивних атомів в зразку.
Коливанням називається всякий
рух або зміна стану тіла, що характеризується тим чи іншим ступенем
повторюваності в часі значень фізичних величин, які визначають цей рух або стан
тіла.
Найпростішим типом
періодичних коливань є так звані гармонічні коливання - коливання, при яких
значення фізичної величини змінюється з часом за законом косинуса (синуса).
ВИСНОВКИ
Математичне моделювання -
метод дослідження процесів або явищ шляхом створення їхніх математичних моделей
<http://uk.wikipedia.org/wiki/%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%BD%D0%B0_%D0%BC%D0%BE%D0%B4%D0%B5%D0%BB%D1%8C>
і дослідження цих моделей.
Математичне моделювання тією
чи іншою мірою застосовують всі природничі і суспільні науки, що використовують
математичний апарат для одержання спрощеного опису реальності за допомогою
математичних понять.
Математичне моделювання як
кількісний інструментарій дослідника по суті своїй належить не тільки математиці
- воно має самостійне значення, і свою історію. Примітно, що один і той же
математичний апарат зустрічається в описі різних об'єктів в різних наукових
дисциплінах. Тим самим математичне моделювання є міждисциплінарною категорією.
Математичні методи, що зарекомендували себе в першу чергу у фізиці і інших
природничонаукових дисциплінах, згодом з розвитком самої математики знайшли
успішне вживання і в гуманітарних науках. Економіко-математичне моделювання і
моделювання політичної сфери виявляють собою наочний приклад плідного вживання
математичної ідеї в наукових дослідженнях
Модель досліджується для
того, щоб можна було управляти досліджуваним об'єктом або системою, на підставі
отриманої по моделі інформації. Управління системи пов'язане з поліпшенням його
характеристик або її стабілізацією, тобто з можливістю прогнозування поводження
систем.
Розрізняють детерміністичне і
стохастичне моделювання. Якщо у відношенні величин, аналізованих
детерміністичними моделями, передбачається їхня стабільність, а випадковими
відхиленнями зневажають, відносячи їх тільки на рахунок помилок спостережень і
вимірів, то в основі стохастичних моделей лежить випадковий характер величин,
оцінюваний імовірними методами. Тут задача полягає у відшуканні тенденцій, що
виявляються у випадкових відхиленнях.
Фізичні закони часто описують
певні співвідношення між велечинами, що характерезують процес швідкістю та
прискоренням зміни цих величтн. Математично такі закони записують як
співвідношення між функціями та їх похідними. Якщо функція, яка описує фізичний
процес невідома, то отримуємо рівняння, яке називають диференціальним. Отже,
вивчення деяких фізичних процесів може бути замінено дослідженням розв’язків
диференціальних рівнянь.
Закон радіоактивного розпаду
- фізичний закон, що описує залежність інтенсивності радіоактивного розпаду від
часу і кількості радіоактивних атомів в зразку.
Найпростішим типом
періодичних коливань є так звані гармонічні коливання - коливання, при яких
значення фізичної величини змінюється з часом за законом косинуса (синуса).
СПИСОК ВИКОРАСТАНИХ ДЖЕРЕЛ
1. Бартоломей
Г. Г., Байбаков В. Д., Алхутов М. С., Бать Г. А. Основи теорії і методи
розрахунку ядерних енергетичних реакторів / Г.Г. Бартоломей, В. Д. Байбаков, М.
С. Алхутов, Г. А . Бать - М.: Вища школа, 1982. - 500 с.
2. Блехман
И. И., Мышкис А. Д., Пановко Н. Г., Прикладная математика: С примерами из
механики: Учебное пособие / И. И. Блехман, А. Д. Мышкис, Н. Г. Пановко. - М.
УРСС, 2006. - 376 с.
4. Губарєв
В. В. Концептуальні основи інформатики./ В. В. Губарєв - К., 2001. - 320 с.
. Івченко
Б. П., Мартищенко Л. А. Інформаційна мікроекономіка Частина 1: Методи аналізу й
прогнозування. / Б. П. Івченко, Л. А. Мартищенко,1997. - 450 с.
6. Камерон
І. Ядерні реактори / І. Камерон - К.: Вища школа, 1987. - 320 с.
7. Клімов
А. Н. Ядерна фізика і ядерні реактори / А. Н. Клімов - К.: Вища школа, 1985. -
352 с.
8. Коротаев А. В. <http://uk.wikipedia.org/wiki/%D0%9A%D0%BE%D1%80%D0%BE%D1%82%D0%B0%D1%94%D0%B2_%D0%90%D0%BD%D0%B4%D1%80%D1%96%D0%B9_%D0%92%D1%96%D1%82%D0%B0%D0%BB%D1%96%D0%B9%D0%BE%D0%B2%D0%B8%D1%87>,
Малков А. С., Халтурина Д. А. Законы истории. Математическое моделирование
исторических макропроцессов / А. В. Коротаев
<http://uk.wikipedia.org/wiki/%D0%9A%D0%BE%D1%80%D0%BE%D1%82%D0%B0%D1%94%D0%B2_%D0%90%D0%BD%D0%B4%D1%80%D1%96%D0%B9_%D0%92%D1%96%D1%82%D0%B0%D0%BB%D1%96%D0%B9%D0%BE%D0%B2%D0%B8%D1%87>,
А. С. Малков, Д. А. Халтурина - М.,2005. - 406 с.
9. Кремень
В. Г. Освіта і наука в Україні - інноваційні аспекти. Стратегія. Реалізація.
Результати./ В. Г. Кремень - К.: Грамота, 2005. - 448 с.
10. Кудрявцев
П. С. Відкриття радіоактивних преврещеній. Ідея атомної енергії / П. С.
Кудрявцев Курс історії фізики - М.: Просвещение, 1982. - 460 с.
11. Мала гірнича енциклопедія
<http://uk.wikipedia.org/wiki/%D0%9C%D0%B0%D0%BB%D0%B0_%D0%B3%D1%96%D1%80%D0%BD%D0%B8%D1%87%D0%B0_%D0%B5%D0%BD%D1%86%D0%B8%D0%BA%D0%BB%D0%BE%D0%BF%D0%B5%D0%B4%D1%96%D1%8F>.
в 3-х т.2 / За ред. В. С.Білецького
<http://uk.wikipedia.org/wiki/%D0%91%D1%96%D0%BB%D0%B5%D1%86%D1%8C%D0%BA%D0%B8%D0%B9_%D0%92%D0%BE%D0%BB%D0%BE%D0%B4%D0%B8%D0%BC%D0%B8%D1%80_%D0%A1%D1%82%D0%B5%D1%84%D0%B0%D0%BD%D0%BE%D0%B2%D0%B8%D1%87>.
- Донецьк: «Донбас», 2004. - 600 с.
. Малков С. Ю., Математическое
моделирование исторической динамики: подходы и модели / С. Ю. Малков. - М.:
РГСУ, 2004. - с. 76-188.
. Моделирование социально-политической и
экономической динамики / Ред. М. Г. Дмитриев. - М.: РГСУ, 2004. - 190 с.
. Мышкис А. Д. Элементы теории
математических моделей./.А. Д. Мышкис - М.: КомКнига, 2007. - 195 с.
15. Нічуговська
Л. І. Науково-методичні основи математичної освіти студентів економічних
спеціальностей вищих навчальних закладів / Л. І. Нічуговська - Полтава, 2004. -
464 с.
16. Раков
С. Формування математичних компетентностей випускника школи як місія
математичної освіти. / С. Раков - Математика в школі. 2007. - 369 с.
. Самарский
А. А., Михайлов А. П. Математическое моделирование. Методы. Примеры / А. А.
Самарський, А. П. Михайлов - М.: Физматлит, 2001. - 260 с.
18. Содді
Ф. Історія атомної енергії / Ф. Соддів - М.:Атомиздат, 1979. - 288 с.
19. Турчак
К. Чисельні методи / К. Турчак - К., 2002. - 300 с.
20. Фурашев В. Н., Ландэ Д. В., Брайчевский
С. М. Моделирование информационно-электоральных процессов
<http://chaos.in.ua/book/modelirovanie-informatsionno-elektoralnykh-protsessov>
/ В. Н Фурашев, Д. В. Ландэ, С.М. Брайчевский - К.: НИЦПИ АпрН Украины, 2007. -
182 с.
21. Хуторской
А. Ключевые компетенции как компонент личностно-ориентированного образования. /
А. Хуторской - Народное оброзование. 2003. - 200 с.
22. Черчмен
У., Акоф Р., Арноф Я. Введення в дослідження операцій. / У. Черчмен, Р. Акоф,
Я. Арноф - К., 2006. - 702 с.
23. Шелобаєв
С. И. Математичні методи й моделі в економіці, фінансах і бізнесі. / С. И.
Шелобаєв - К., 2000. - 325 с.
24. Шкиль
Н. И., Слепкань З. И., Дубинчук Е. С. Алгебра и начала анализа : Проб. учеб.
Для 10-11 кл. серед. шк. / Н. И. Шкиль, З. И. Слепкань, Е. С. Дубинчук. - К.:
Вежа, 1995. - 624 с.