Випадкові потоки подій. Пуассонівські потоки

Випадкові потоки подій. Пуассонівські потоки

Випадкові потоки подій. Пуассонівські потоки

В СМО під вхідним потоком подій розуміють потік вимог на обслуговування (наприклад, потік автомобілів, що прибувають на АЗС для заправки, де подією є прибуття одного, будь-якого автомобіля, моментом здійснення події - момент його прибуття на АЗС, часовий інтервал між подіями - інтервал між моментами прибуття на АЗС цього та попереднього автомобіля), а також вихідний потік обслуговування (наприклад, потік заправлених автомобілів, що покидає АЗС).

Потік подій є регулярним, якщо події відбуваються через рівні інтервали часу.

Випадковий потік характеризується нерівномірністю інтервалів часу слідування подій. Головною характеристикою випадкового потоку є ймовірність попадання інтервалу часу між подіями в задані межі.

До пуассонівського потоку подій належать ті, що задовольняють наступні умови: відсутність післядії, відсутність імовірності появи двох подій одночасно (ординарність потоку), стаціонарність потоку.

Математичні моделі послідовностей часових інтервалів між подіями у потоках Пуассона та Ерланга

Враховуючи, що Pо(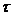) є імовірність того, що в інтервалі τ немає жодної події, тобто згідно з законом Пуассона (при m=0):

,

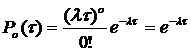можна стверджувати, що

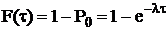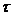, (>0)

Тоді диференційна функція розподілу (щільність розподілу) буде мати вигляд:

, ()

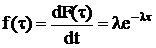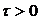Графіки F(τ) і λ(τ) для цього закону, що називається експоненціальним (показовим) законом розподілу інтервалів між сусідніми подіями в пуассонівському потоці, представлено на рис.1.

Для експоненціального закону розподілу величина Т = 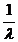 характеризує швидкість зміни імовірності появи певних інтервалів. Наприклад, за будь-якої інтенсивності λ

(T) = 0,631 ≈ 0,63; F(2T) = 0,865; F(3T) = 0,95

F(T) = 0,369λ ≈ 0,37λ; f(2T) ≈ 0,135λ; f(3T) = 0,05λ ,

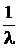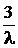що означає, що в діапазоні від 0 до Т =  знаходяться приблизно 63% всіх числових інтервалів між подіями в пуассонівському потоці, в діапазоні від 0 до 3Т =  знаходяться приблизно 95%. Практично це означає, що визначивши експериментально інтенсивність потоку λ, можна визначити також межі 95% діапазону всіх можливих значень часових інтервалів в потоці як Т0,95 =.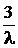

Рис.1. Графіки F(τ) і λ(τ) для експоненціального закону розподілу імовірностей.

Для опису потоків подій з післядією використовуються потоки Ерланга. При цьому замість одного інтервалу між подіями розглядають суму k інтервалів як один інтервал, враховуючи, що з ростом інтервалу взаємодія подій зменшується. Кількість інтервалів визначають порядок потоку Ерланга. Наприклад, при k = 2 в потоці, що взаємодіє, розглядають кожну другу подію (шляхом “просіювання” кожної парної або непарної події), при k = 3 - кожну третю подію і т.д. Очевидно, чим більша взаємодія подій в потоці, тим більший слід вибирати інтервал розгляду t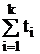j =  (j=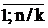), де і - відраховується кожного разу від tj. Очевидно, що найпростіший (пуассонівський) потік можна розглядати як потік Ерланга 1-го порядку (k=1, тобто без “просіювання” подій).

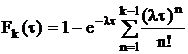
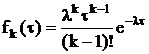
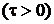
де λ - інтенсивність породжуючого потоку Пуассона (без “просіювання”).

На рис.2 показані щільності розподілу імовірностей часових інтервалів слідування подій в потоках Ерланга k-го порядку при 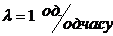 (k=1,2,3,4).       При цьому k є в певній мірі характеристикою зв’язності потоку.

Інтегральна та функція щільності розподілу мають аналітичний вираз:

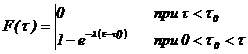
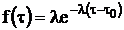
математичний модель подія інтервал

Графік f(τ) для цього розподілу представлено на рис.2 і є f(τ) експоненційного закону розподілу, переміщену на τ0.

Приклади моделей потоків подій в транспортних системах

Приклад 1.

Маємо результати 20 вимірювань часових інтервалів руху автомобілів у потоці (N=20):

 (сек) = 1,2; 2,0; 2,1; 2,0; 2,1; 3,0; 10,5; 2,1; 1,7; 1,2; 1,5; 1,5; 11,5; 11,0; 2,1; 2,0; 1,1; 1,7; 9,7; 11,8

Визначити закон розподілу інтервалів руху автомобілів у потоці.

Рішення

. Визначимо середній інтервал руху автомобілів (оцінка математичного сподівання)

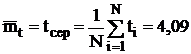сек.

. Визначаємо оцінку дисперсії інтервалів руху відносно середнього інтервалу

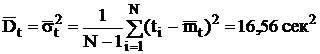
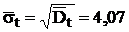сек.

. Визначаємо інтенсивність руху

.

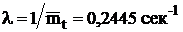. Щільність експоненціального розподілу часових інтервалів

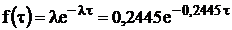
. Інтегральна функція розподілу часових інтервалів руху

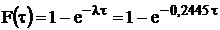
Графіки f(τ) і F(τ) представлені на рис.3.

Першим показником належності послідовності часових інтервалів до експоненціального розподілу є рівність 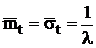 за умови ti>0.

У випадку, що розглядається, ми маємо саме рівність цих значень. Тому приймаємо у першому наближенні гіпотезу про експоненціальний закон розподілу часових інтервалів руху в потоці.

Примітка: В цьому прикладі не розглядається питання визначення репрезентативності вибірки і застосування відповідних критеріїв перевірки статистичних гіпотез. Ці питання відносяться до курсу “Прикладна статистика”.

Приклад 2.

В даному прикладі розглянемо аналогічну задачу за умови руху з підвищеною інтенсивністю, коли на режим руху починає впливати взаємодія між сусідніми автомобілями, що рухаються в потоці. Маємо результати 20 вимірювань часових інтервалів руху автомобілів у потоці (N=20):

 (сек) = 1,7; 2,0; 2,1; 2,5; 4,0; 5,0; 6,0; 3,1; 2,6; 3,2; 2,0; 6,8; 7,0; 3.2; 3,3; 5,2; 6,0; 3,8; 1,6; 2,0

Рішення

Здійснюємо статистичну обробку даних за методикою прикладу 1. В результаті визначаємо:

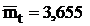сек; 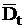= 3,075 сек2; 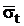= 1,753 сек.

Оскільки 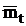≠ 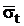при ti>0 (i=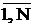) і ці значення відрізняються досить суттєво, використовуємо для опису розподілу часових інтервалів руху розподіл Ерланга.

Визначаємо інтенсивність руху (одночасно це є інтенсивність потоку Ерланга)

Враховуючи

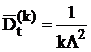
визначаємо порядок потоку Ерланга

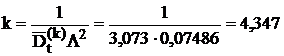
Вибираємо найближче ціле значення k=4. Таким чином, для опису часових інтервалів руху потоку, що розглядається, приймаємо потік Ерланга 4-го порядку зі щільністю імовірності розподілу часових інтервалів

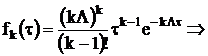
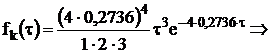
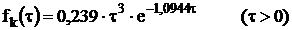
Будуємо графік цієї функції, звівши результати розрахунків fk(τ) при різних значеннях τ до таблиці 1.

Таблиця 1

Для самостійної роботи.

. Побудувати графік функцій Fk(τ) та fk(τ), застосовуючи відповідні формули потоків Ерланга.