Статистическое изучение регионов РФ
КУРСОВАЯ РАБОТА
Статистическое изучение
регионов РФ
Задание
1
Таблица 1.1. Исходные данные - социально-экономические
показатели по регионам России, 2008 год (20-49 интервал наблюдения; 8 и 10
признаки)
|
Регионы
|
Число ДТП на 100 000 населения
|
Число автобусов общего пользования на 100 000
населения, шт.
|
|
1. Архангельская обл.
|
197,6
|
38
|
|
2. Вологодская обл.
|
196,0
|
50
|
|
3. Калининградская обл.
|
145,8
|
16
|
|
4. Ленинградская обл.
|
203,2
|
26
|
|
5. Мурманская обл.
|
118,8
|
60
|
|
6. Новгородская обл.
|
287,3
|
75
|
|
7. Псковская обл.
|
220,9
|
77
|
|
8. Республика Дагестан
|
55,1
|
22
|
|
9. Кабардино-Балкарская
|
86,6
|
44
|
|
10. Краснодарский край
|
134,3
|
26
|
|
11. Ставропольский край
|
103,8
|
27
|
|
12. Астраханская обл.
|
128,0
|
30
|
|
13. Волгоградская обл.
|
122,1
|
68
|
|
14. Ростовская обл.
|
146,4
|
35
|
|
15. Респ. Башкортостан
|
132,2
|
34
|
|
16. Республика Мордовия
|
142,0
|
27
|
|
17. Республика Татарстан
|
158,2
|
62
|
|
18. Удмуртская респ.
|
117,5
|
54
|
|
19. Чувашская республика
|
148,3
|
49
|
|
20. Пермский край
|
149,9
|
46
|
|
21. Кировская обл.
|
187,8
|
45
|
|
22. Нижегородская обл.
|
179,9
|
59
|
|
23. Оренбургская обл.
|
158,1
|
47
|
|
24. Пензенская обл.
|
124,0
|
35
|
|
25. Самарская обл.
|
147,5
|
25
|
|
26. Ульяновская обл.
|
98,5
|
29
|
|
27. Курганская обл.
|
156,7
|
19
|
|
28. Свердловская обл.
|
167,9
|
38
|
|
29. Тюменская обл.
|
195,4
|
120
|
|
30. Челябинская обл.
|
147,9
|
43
|
1.1 Структурная равноинтервальная группировка
Структурная группировка по признаку - число ДТП
на 100 000 населения
Выполним структурную группировку по площади территорий, и
разобьем совокупность на 6 групп. Рассчитаем величину интервала:
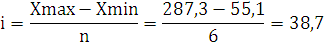
где i - величина отдельного интервала,
Xmах - максимальное значение признака в
исследуемой совокупности,
Xmin - минимальное значение признака в
исследуемой совокупности,- количество групп.
Таблица 1.2. Группировка регионов по числу ДТП на 100 000
населения
|
№ п/п
|
Число ДТП на 100 000 населения
|
Количество регионов в группе
|
Процент к итогу, %
|
|
1
|
55,1-93,8
|
2
|
7
|
|
2
|
93,8-132,5
|
8
|
27
|
|
3
|
132,5-171,2
|
12
|
40
|
|
4
|
171,2-209,9
|
6
|
20
|
|
5
|
209,9-248,6
|
1
|
3
|
|
6
|
248,6-287,3
|
1
|
3
|
|
Итого
|
30
|
100
|
Вывод: в 7% регионов число ДТП на 100 000 населения в
пределах от 55,1-93,8; в 27% регионов число ДТП на 100 000 населения в пределах
от 93,8-132,5; в 40% регионов число ДТП на 100 000 населения в пределах от
132,5-171,2; в 20% регионов число ДТП на 100 000 населения в пределах от
171,2-209,9; в 3% регионов число ДТП на 100 000 населения в пределах от
209,9-248,6; в 3% регионов число ДТП на 100 000 населения в пределах от
248,6-287.3.
Структурная группировка по признаку - число
автобусов общего пользования на 100 000 населения
Выполним структурную группировку по площади территорий, и
разобьем совокупность на 6 групп. Рассчитаем величину интервала:
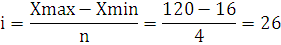
где i - величина отдельного интервала,
Xmах - максимальное значение признака в
исследуемой совокупности,
Xmin - минимальное значение признака в исследуемой
совокупности,- количество групп.
Таблица 1.3. Группировка регионов России по числу автобусов
общего пользования
|
№ п/п
|
Число автобусов общего пользования на 100 000
населения, шт.
|
Количество регионов в группе
|
Процент к итогу, %
|
|
1
|
16-42
|
14
|
47
|
|
2
|
42-68
|
11
|
37
|
|
3
|
68-94
|
4
|
13
|
|
4
|
94-120
|
1
|
3
|
|
Итого
|
30
|
100
|
Вывод: в 47% регионов число автобусов общего пользования на
100 000 населения в пределах от 16-42; в 37% регионов число автобусов общего
пользования на 100 000 населения в пределах от 42-68; в 13% регионов число
автобусов общего пользования на 100 000 населения в пределах от 68-94; в 3%
регионов число автобусов общего пользования на 100 000 населения в пределах от
94-120.
1.2 Аналитическая группировка
В качестве признака фактора выберем число автобусов общего
пользования на 100 000 населения шт., а в качестве результата - число ДТП на
100 000 населения.
Xmax = 120 Xmin = 16=
1+3,322lgN, N= 30= 1+3,322lg30= 6= Xmax - Xmin = 120 -
16=104
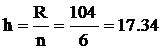
Таблица 1.4. Распределение регионов по числу автобусов общего
пользования на 100 000 населения, шт.
|
N п/п
|
Число автобусов общего пользования, шт.
|
Количество регионов в группе
|
Итого по признаку результата
|
Среднее значение по признаку результату
|
|
1
|
16-33,34
|
10
|
1314,9
|
131,49
|
|
2
|
33,34-50,68
|
12
|
1842,7
|
153,56
|
|
3
|
50,68-68,02
|
5
|
892,5
|
178,5
|
|
4
|
68,02-85,36
|
2
|
508,2
|
254,1
|
|
5
|
85,36-102,7
|
0
|
-
|
-
|
|
6
|
102,7-120,04
|
1
|
120
|
120
|
|
Итого
|
30
|
4678,3
|
837,65
|
Вывод: Исходя из данной таблицы, связь межу числом
автобусов общего пользования на 100 000 населения и числом ДТП на 100 000
населения отсутствует.
1.3 Комбинационная группировка
Таблица 1.5. Распределение регионов по числу автобусов общего
пользования на 100 000 населения
|
Число автобусов общего пользования, шт.
|
Число ДТП на 100 000 населения
|
Итого
|
|
55,1 -93,8
|
93,8 -132,5
|
132,5 -171,2
|
171,2 -209,9
|
209,9 -248,6
|
248,6 -287,3
|
|
|
16-33,34
|
1
|
3
|
5
|
1
|
0
|
0
|
10
|
|
33,34-50,68
|
1
|
2
|
6
|
3
|
0
|
0
|
12
|
|
50,68-68,02
|
0
|
3
|
1
|
1
|
0
|
0
|
5
|
|
68,02-85,36
|
0
|
0
|
0
|
0
|
1
|
1
|
2
|
|
85,36-102,7
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
102,7-120,04
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
|
Итого
|
2
|
8
|
12
|
6
|
1
|
1
|
30
|
Вывод: Т.к. наибольшие частоты не расположены вдоль
диагонали, то связь между признаками - отсутствует.
Задание
2
.1 Построение рядов распределения
Ряд распределения регионов по числу ДТП на 100
000 населения
Таблица 2.1. Распределение регионов по числу ДТП на 100 000
населения
|
№ п/п
|
Группы регионов по числу ДТП.
|
Число регионов, fi
|
Середины интервалов, хi
|
Накопленные частоты S
|
|
1
|
55,1-93,8
|
2
|
74,45
|
2
|
|
2
|
93,8-132,5
|
8
|
113,15
|
10
|
|
3
|
132,5-171,2
|
12
|
151,85
|
22
|
|
4
|
171,2-209,9
|
6
|
190,55
|
28
|
|
5
|
209,9-248,6
|
1
|
229,25
|
29
|
|
6
|
248,6-287,3
|
1
|
267,95
|
30
|
|
Итого
|
30
|
-
|
-
|

Рис. 1 Гистограмма распределения регионов по числу ДТП на 100
000 населения
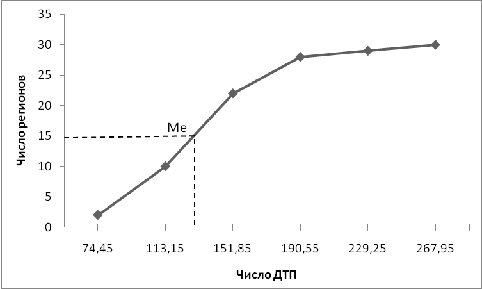
Рис. 2 Кумулятивное распределение числа ДТП на 100 000
населения.
Ряд распределения регионов по числу автобусов
общего пользования на 100 000 населения.
Таблица 2.2. Распределение регионов по числу автобусов общего
пользования на 100 000 населения
|
Группы регионов по числу автобусов
общего пользования
|
Число регионов, единиц fi
|
Середины интервалов, уi
|
Накопленные частоты, S
|
|
12-42
|
14
|
29
|
14
|
|
42-68
|
11
|
55
|
25
|
|
68-94
|
4
|
81
|
29
|
|
94-120
|
1
|
107
|
30
|
|
Итого
|
30
|
-
|
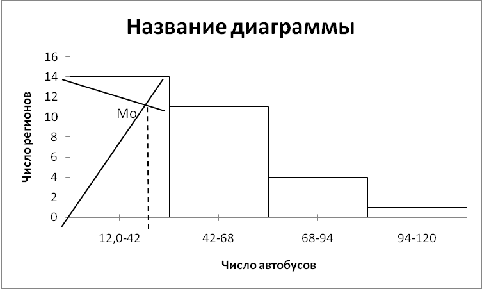
Рис. 3 Гистограмма распределения регионов по числу автобусов
общего пользования на 100 000 населения
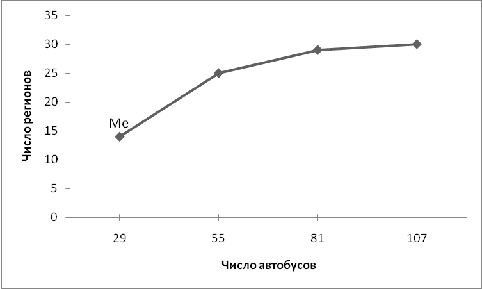
Рис. 4 Кумулятивное распределение регионов по среднемесячной
номинальной начисленной заработной плате
2.2 Анализ рядов распределения
Анализ ряда распределения регионов по числу ДТП
на 100 000 населения
Таблица 2.3. Распределение регионов по числу ДТП на 100 000
населения
|
Группы регионов по числу ДТП x
|
Число регионов, единиц fi
|
Сере дины интервалов xi
|
Накопленные частоты, S
|
xi fi
|
(xi - 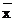 )2 fi )2 fi
|
|
55,1-93,8
|
2
|
74,45
|
2
|
148,9
|
37199,01
|
|
93,8-132,5
|
8
|
113,15
|
10
|
905,2
|
76331,06
|
|
132,5-171,2
|
12
|
151,85
|
22
|
3820,9
|
41743,68
|
|
171,2-209,9
|
5
|
190,55
|
28
|
952,75
|
2056,4
|
|
209,9-248,6
|
1
|
229,25
|
29
|
229,25
|
339,3
|
|
248,6-287,3
|
1
|
267,95
|
30
|
267,95
|
3262,7
|
|
Итого
|
30
|
-
|
-
|
6324,95
|
160932,15
|
Среднее арифметическое значение признака:
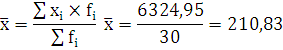
Вывод: По данным по 30 регионам в 2008 г. среднее число ДТП
на 100 000 населения составляет 210,83
Мода:
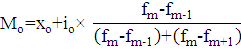
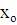 - нижняя граница модального интервала,
- нижняя граница модального интервала,
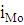 - значение модального интервала,
- значение модального интервала,
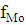 - модальная частота,
- модальная частота,
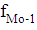 - частота предшествующая модальной,
- частота предшествующая модальной,
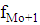 - частота следующая за модальной.
- частота следующая за модальной.

Вывод: в большинстве регионов число ДТП на 100 000 населения в
2008 г. Составляет 146.57
Медиана:
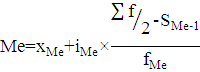
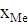 - нижняя граница медианного интервала,
- нижняя граница медианного интервала,
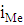 - медианный интервал,
- медианный интервал,
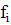 - сумма частот,
- сумма частот,
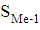 - накопленная частота,
- накопленная частота,
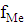 - медианная частота.
- медианная частота.
Вывод: 50% регионов имеет число ДТП на 100 000 населения в 2008
году менее 141,3., а 50% регионов - более 141,3
Квартили:
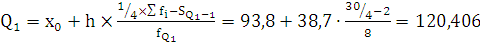 , где
, где
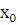 - нижняя граница интервала, содержащего нижний квартиль;-
величина интервала, где находится нижний квартиль;
- нижняя граница интервала, содержащего нижний квартиль;-
величина интервала, где находится нижний квартиль;
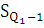 - накопленная частота интервала предшествующая нижнему квартилю.
- накопленная частота интервала предшествующая нижнему квартилю.
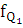 - частота интервала содержащего нижний и верхний квартиль.
- частота интервала содержащего нижний и верхний квартиль.
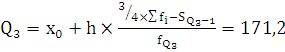 +38,7
+38,7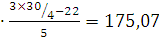 , где
, где
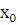 - нижняя граница интервала, содержащего верхний
квартиль;- величина интервала, где находится верхний квартиль;
- нижняя граница интервала, содержащего верхний
квартиль;- величина интервала, где находится верхний квартиль;
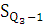 - накопленная частота интервала предшествующая
верхнему квартилю.
- накопленная частота интервала предшествующая
верхнему квартилю.
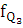 - частота интервала содержащего нижний и верхний
квартиль.
- частота интервала содержащего нижний и верхний
квартиль.
Вывод: В четверти регионов число ДТП на 100 000 населения составляет
менее 120,406 и у четверти более 175,07.
Среднеквадратическое отклонение:
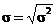
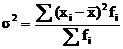
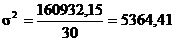
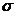 =
=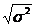 = 73,24
= 73,24
Вывод: возможное отклонение числа ДТП на 100 000 населения от
среднего значения составляет 73,24.
Коэффициент вариации:
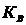 =
=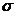 /
/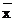 ∙100%=(73.24/ 210.83)∙100%=34,7%
∙100%=(73.24/ 210.83)∙100%=34,7%
Вывод: совокупность не однородна, так как коэффициент вариации
превышает 33%.
Анализ ряда распределения регионов по числу автобусов общего
пользования на 100 000 населения, шт.
Таблица 2.4. Распределение регионов по числу автобусов общего
пользования на 100 000 населения, шт.
Группы регионов по числу автобусов на 100 000 населения Число
регионов, единиц fi Середины интервалов xi Накопленные
частоты S xi fi (xi - 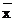 )2 ∙
)2 ∙
|
fi
|
|
|
16-42
|
14
|
29
|
14
|
406
|
5107,34
|
|
42-68
|
11
|
55
|
25
|
605
|
523,71
|
|
68-94
|
4
|
81
|
29
|
324
|
4329,64
|
|
94-120
|
1
|
107
|
30
|
107
|
3469,21
|
|
Итого
|
30
|
-
|
-
|
1442
|
13429,9
|
Среднее арифметическое значение признака:
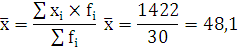
Вывод: среднее число автобусов общего пользования на 100 000
населения в регионах в 2008 г. составляет 48,1 шт.
Мода:
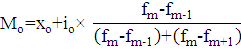
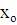 - нижняя граница модального интервала,
- нижняя граница модального интервала,
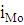 - значение модального интервала,
- значение модального интервала,
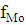 - модальная частота,
- модальная частота,
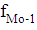 - частота предшествующая модальной,
- частота предшествующая модальной,
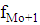 - частота следующая за модальной.
- частота следующая за модальной.
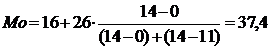 шт.
шт.
Вывод: в большинстве регионов число автобусов общего пользования
на 100 000 населения составляет 37,4
Медиана:
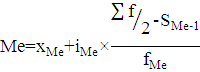
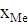 - нижняя граница медианного интервала,
- нижняя граница медианного интервала,
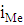 - медианный интервал,
- медианный интервал,
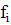 - сумма частот,
- сумма частот,
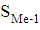 - накопленная частота,
- накопленная частота,
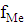 - медианная частота.
- медианная частота.
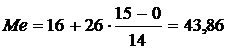 шт.
шт.
Вывод: в 50% регионов число автобусов общего пользования на 100
000 населения более 43,86 шт., а в 50% регионов менее 43,86 шт.
Квартили:
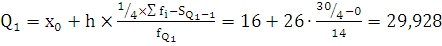 , где
, где
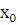 - нижняя граница интервала, содержащего нижний квартиль;-
величина интервала, где находится нижний квартиль;
- нижняя граница интервала, содержащего нижний квартиль;-
величина интервала, где находится нижний квартиль;
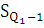 - накопленная частота интервала предшествующая нижнему квартилю.
- накопленная частота интервала предшествующая нижнему квартилю.
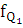 - частота интервала содержащего нижний и верхний квартиль.
- частота интервала содержащего нижний и верхний квартиль.
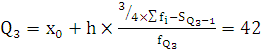 +26
+26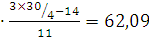 , где
, где
Вывод: В четверти регионов число автобусов общего пользования на
100 000 населения составляет менее 29,928 шт., и у четверти более 62,09 шт.
Среднеквадратическое отклонение:
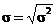
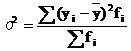
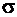 =
=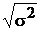 =21,16 шт.
=21,16 шт.
Вывод: возможное отклонение числа автобусов общего пользования на
100 000 населения от среднего значения составляет 21,16 шт.
Коэффициент вариации:
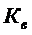 =
=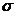 /
/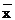 ∙100%=21,16 / 48,1 ∙100%=44%
∙100%=21,16 / 48,1 ∙100%=44%
Вывод: совокупность не однородна, так как коэффициент вариации
превышает 33%
.3 Проверка теоремы о разложении дисперсии
Правило сложения дисперсий: общая дисперсия равна сумме
межгрупповой дисперсии и средней из внутригрупповых дисперсий.
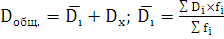 ;
; 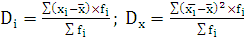
Общая дисперсия по формуле:
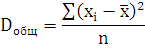
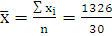 =44,2
=44,2
Таблица 2.5. Промежуточные показатели
|
№п./п.
|
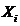 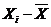 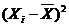
|
|
|
|
1
|
2
|
3
|
4
|
|
1
|
38
|
-6,2
|
38,44
|
|
2
|
50
|
5,8
|
33,64
|
|
3
|
16
|
-28,2
|
795,24
|
|
4
|
26
|
-18,2
|
331,24
|
|
5
|
60
|
15,8
|
249,64
|
|
6
|
75
|
30,8
|
948,64
|
|
7
|
77
|
32,8
|
1075,84
|
|
8
|
22
|
-22,2
|
492,84
|
|
9
|
44
|
-0,2
|
0,04
|
|
10
|
26
|
-18,2
|
331,24
|
|
11
|
27
|
-17,2
|
295,84
|
|
12
|
30
|
-14,2
|
201,64
|
|
13
|
68
|
23,8
|
566,44
|
|
14
|
35
|
-9,2
|
84,64
|
|
15
|
34
|
-10,2
|
104,04
|
|
16
|
27
|
-17,2
|
295,84
|
|
17
|
62
|
17,8
|
316,84
|
|
18
|
54
|
9,8
|
96,04
|
|
19
|
49
|
4,8
|
23,04
|
|
20
|
46
|
1,8
|
3,24
|
|
21
|
45
|
0,8
|
0,64
|
|
22
|
59
|
14,8
|
219,04
|
|
23
|
47
|
2,8
|
7,84
|
|
24
|
35
|
-9,2
|
84,64
|
|
25
|
25
|
-19,2
|
368,64
|
|
26
|
29
|
-15,2
|
231,04
|
|
27
|
19
|
-25,2
|
635,04
|
|
28
|
38
|
-6,2
|
38,44
|
|
29
|
120
|
75,8
|
5745,64
|
|
30
|
43
|
-1,2
|
1,44
|
|
Итого
|
1326
|
-
|
13616,8
|
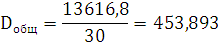
Найдем внутригрупповые дисперсии.
По 1 группе:

Таблица 2.6. Промежуточные
показатели
|
№п./п.
|
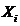 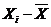 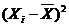
|
|
|
|
1
|
16
|
-8,7
|
75,69
|
|
2
|
26
|
1,3
|
1,69
|
|
3
|
22
|
-2,7
|
7,29
|
|
4
|
26
|
1,3
|
1,69
|
|
5
|
27
|
2,3
|
5,29
|
|
6
|
30
|
5,3
|
28,09
|
|
7
|
27
|
2,3
|
5,29
|
|
8
|
25
|
0,3
|
0,09
|
|
9
|
29
|
4,3
|
18,49
|
|
10
|
19
|
-5,7
|
32,49
|
|
Итого
|
247
|
-
|
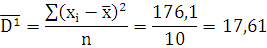
По 2 группе:
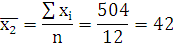
Таблица 2.7. Промежуточные показатели
|
№ п/п
|
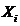 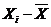 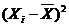
|
|
|
|
1
|
38
|
-4
|
16
|
|
2
|
50
|
8
|
64
|
|
3
|
44
|
2
|
4
|
|
4
|
35
|
-7
|
49
|
|
5
|
34
|
-8
|
64
|
|
6
|
49
|
7
|
49
|
|
7
|
46
|
4
|
16
|
|
8
|
45
|
3
|
9
|
|
9
|
47
|
5
|
25
|
|
10
|
35
|
-7
|
49
|
|
11
|
38
|
-4
|
16
|
|
12
|
43
|
1
|
1
|
|
Итого
|
504
|
-
|
362
|
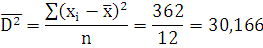
По 3 группе:
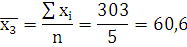
Таблица 2.8. Промежуточные
показатели
|
№ п/п
|
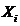 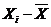 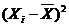
|
|
|
|
1
|
60
|
0,6
|
0,36
|
|
2
|
68
|
7,4
|
54,76
|
|
3
|
62
|
1,4
|
1,96
|
|
4
|
54
|
-6,6
|
43,56
|
|
5
|
59
|
-1,6
|
2,56
|
|
Итого
|
303
|
-
|
103,2
|
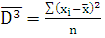 =
=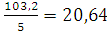
По 4 группе:
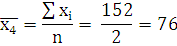
Таблица 2.9. Промежуточные
показатели
|
№п\п
|
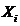 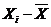 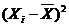
|
|
|
|
1
|
75
|
-1
|
1
|
|
2
|
77
|
1
|
1
|
|
Итого
|
152
|
-
|
2
|
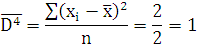
По 6 группе
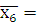
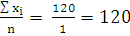
Таблица 2.10. Промежуточные показатели
|
№п\п
|
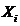 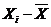 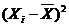
|
|
|
|
1
|
120
|
0
|
0
|
|
Итого
|
-
|
-
|
-
|
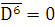
Средняя из внутригрупповых дисперсий:
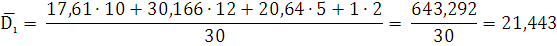
Межгрупповая дисперсия:
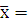 44,2
44,2
Таблица 2.11. Промежуточные показатели
|
№п/п
|
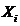 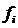 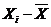 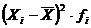
|
|
|
|
|
1
|
24,7
|
10
|
-19,5
|
3802,5
|
|
2
|
42
|
12
|
-2,2
|
58,08
|
|
3
|
60,6
|
5
|
16,4
|
1344,8
|
|
4
|
76
|
2
|
31,8
|
2022,48
|
|
5
|
0
|
0
|
0
|
0
|
|
6
|
120
|
1
|
75,8
|
5745,64
|
|
Итого
|
-
|
30
|
-
|
12973,5
|
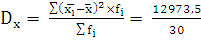 = 432,45
= 432,45
Общая дисперсия по правилу сложения:
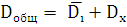 = 432,45+21,443=453,893
= 432,45+21,443=453,893
,893=453,893
Из проведённых расчётов видно, что общие дисперсии,
рассчитанные различными способами, равны, что и требовалось доказать.
.4 Расчёт коэффициента корреляции
Изобразим корреляционное поле. Построим уравнение регрессии и
определим тесноту связи между признаками, используя дисперсионный и
корреляционный анализ.
Для определения тесноты связи между признаками рассчитаем
коэффициент детерминации, который определяется как доля объясненной или
межгрупповой дисперсии в общей дисперсии признака-результата. Он показывает,
какая часть общей вариации признака-результата y объясняется влиянием
изучаемого фактора х:
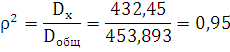
Таким образом, на 95% вариация числа ДТП на 100 000 населения
обусловлена количеством автобусов общего пользования на 100 000 населения, на
5% прочими факторами.
Корреляционное отношение определяется как отношение средних
квадратичных отклонений:
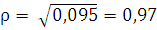
Полученное значение корреляционного отношения показывает
функциональную связь по шкале Чеддока между числом ДТП на 100 000 населения и
количеством автобусов общего пользования на 100 000 населения.
При линейной форме зависимости для измерения тесноты связи
кроме корреляционного отношения используется также коэффициент корреляции. Он
может быть исчислен по следующей формуле:
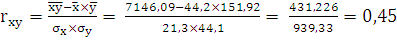 , где
, где
 среднее квадратическое отклонение по признаку x;
среднее квадратическое отклонение по признаку x;
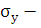 среднее квадратическое отклонение по признаку y;
среднее квадратическое отклонение по признаку y;
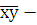 общее среднее по двум признакам;
общее среднее по двум признакам;
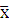 - среднее значение признака х.
- среднее значение признака х.
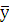 - среднее значение признака у.
- среднее значение признака у.
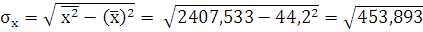 = 21,3
= 21,3
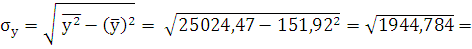 44,1
44,1
Для расчета коэффициента корреляции построим таблицу:
Таблица 2.12. Расчетная таблица для определения линейного
коэффициента корреляции
|
№ П/п
|
Число автобусов общего пользования на 100 000
населения. (x)
|
Число дорожно-транспортных происшествий на
100000 населения(y)
|
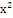
|
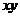 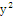 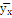 = =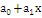
|
|
|
|
1
|
38
|
197,6
|
1444
|
7508,8
|
39045,76
|
146,03
|
|
2
|
50
|
196,0
|
2500
|
9800
|
38416
|
157,43
|
|
3
|
16
|
145,8
|
256
|
2332,8
|
21257,64
|
125,13
|
|
4
|
26
|
203,2
|
676
|
5283,2
|
41290,24
|
134,63
|
|
5
|
60
|
118,8
|
3600
|
7128
|
14113,44
|
166,93
|
|
6
|
75
|
287,3
|
5625
|
21547,5
|
82541,29
|
181,18
|
|
7
|
77
|
220,9
|
5929
|
17009,3
|
48796,81
|
183,08
|
|
8
|
22
|
55,1
|
484
|
1212,2
|
3036,01
|
130,83
|
|
9
|
44
|
86,6
|
1936
|
3810,4
|
7499,56
|
151,73
|
|
10
|
26
|
134,3
|
676
|
3491,8
|
18036,49
|
134,63
|
|
11
|
27
|
103,8
|
729
|
2802,6
|
10774,44
|
135,58
|
|
12
|
30
|
128,0
|
900
|
3840
|
16384
|
138,43
|
|
13
|
68
|
122,1
|
4624
|
8302,8
|
14908,41
|
174,53
|
|
14
|
35
|
146,4
|
1225
|
5124
|
21432,96
|
143,18
|
|
15
|
34
|
132,2
|
1156
|
4494,8
|
17476,84
|
142,23
|
|
16
|
27
|
142,0
|
729
|
3834
|
20164
|
135,58
|
|
17
|
62
|
158,2
|
3844
|
9808,4
|
25027,24
|
168,83
|
|
18
|
54
|
117,5
|
2916
|
6345
|
13806,25
|
161,23
|
|
19
|
49
|
148,3
|
2401
|
7266,7
|
21992,89
|
156,48
|
|
20
|
46
|
149,9
|
2116
|
6895,4
|
22470,01
|
153,63
|
|
21
|
45
|
187,8
|
2025
|
8451
|
35268,84
|
152,68
|
|
22
|
59
|
179,9
|
3481
|
10614,1
|
32364,01
|
165,98
|
|
23
|
47
|
158,1
|
2209
|
24995,61
|
154,58
|
|
24
|
35
|
124,0
|
1225
|
4340
|
15376
|
143,18
|
|
25
|
25
|
147,5
|
625
|
3687,5
|
21756,25
|
133,68
|
|
26
|
29
|
98,5
|
841
|
2856,5
|
9702,25
|
137,48
|
|
27
|
19
|
156,7
|
361
|
2977,3
|
24554,89
|
127,98
|
|
28
|
38
|
167,9
|
1444
|
6380,2
|
28190,41
|
146,03
|
|
29
|
120
|
195,4
|
14400
|
23448
|
38181,16
|
223,93
|
|
30
|
43
|
147,9
|
1849
|
6359,7
|
21874,41
|
150,78
|
|
Итого
|
1326
|
4557,7
|
72226
|
214382,7
|
750734,1
|
-
|
|
Ср. знач.
|
44,2
|
151,92
|
2407,533
|
7146,09
|
25024,47
|
-
|
Линейное уравнение связи, выраженное прямой линией:
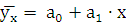 ;
;
значения параметров должны удовлетворять системе:
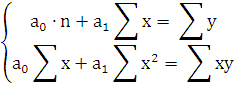
Отсюда:
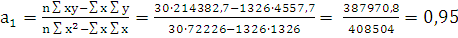 автобусов на 100 000 населения
автобусов на 100 000 населения
Вывод: При изменении количества автобусов общего
пользования на 100 000 населения на 1 штуку число ДТП на 100 000 населения
увеличится на 0,95.
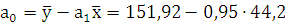 = 151,2 - 41,99 = 109,93 автобусов на 100 000
населения
= 151,2 - 41,99 = 109,93 автобусов на 100 000
населения
Найдем теоретически уравнение регрессии (y) и построим линию
регрессии.
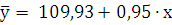
Линейный коэффициент корреляции также можно рассчитать по
формуле:
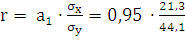 = 0,000021
= 0,000021
2.5 Изображение корреляционного поля и построение
на нём ломаной регрессии
В табл. 2.12 увидим выровненные значения результативного
признака, т.е. 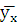 , которые показывают, какими теоретически должны
быть средние показатели числа ДТП при данных показателях числа автобусов общего
пользования.
, которые показывают, какими теоретически должны
быть средние показатели числа ДТП при данных показателях числа автобусов общего
пользования.
На основе полученных данных построим график.
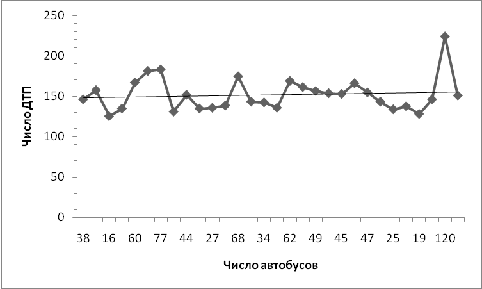
Рис. 5 Корреляционное поле зависимости числа ДТП от числа
автобусов общего пользования
Задание
3
.1Пределы, за которые не выйдет среднее значение
признака
Определим пределы, за которые с доверительной вероятностью
0,954 не выйдет среднее значение признака, рассчитанное по генеральной
совокупности;
Нам известно: 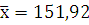 ;
; 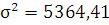 ;
;  ;
; 
Так как мы имеем собственно - случайный 36% бесповторный
отбор, то N
= 83 региона, а n = 30 регионов.
Необходимо определить среднюю ошибку выборки:
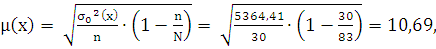 где
где
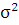 (х) - дисперсия выборочной совокупности,- объем
выборочной совокупности,- объем генеральной совокупности.
(х) - дисперсия выборочной совокупности,- объем
выборочной совокупности,- объем генеральной совокупности.
Предельная ошибка выборки определяется по формуле:
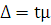 = 2
= 2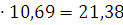
Зная выборочную среднюю величину признака и предельную ошибку
выборки, можно определить границы, в которых заключена генеральная средняя:
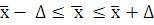
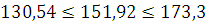
Вывод: На основании проведенного выборочного обследования с
вероятностью 0,954 можно заключить, что число ДТП на 100 000 населения
находится в пределах от 130,54 до 173,3.
Определение объема выборки для снижения
предельной ошибки средней величины на 50%
Для того чтобы снизить предельную ошибку средней величины на
50% нужно изменить объем выборки.
Нам известно: 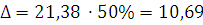 ;
; 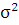 =5364,41; N = 83; t = 2
=5364,41; N = 83; t = 2
Для определения необходимого объема выборки при бесповторном
отборе используется формула:
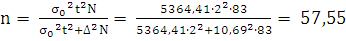 ед.
ед.
Вывод: Чтобы снизить предельную ошибку количества ДТП на 100
000 населения на 50%, необходимо увеличить объем выборки на 57,55 ед.
.2 Определение пределов, за которые в генеральной
совокупности не выйдет значение доли регионов, у которых индивидуальные
значения признака превышают моду
При помощи повторного отбора, определим пределы, за которые в
генеральной совокупности не выйдет значение доли количества автобусов общего
пользования на 100 000 населения, у которых индивидуальные значения признака
превышают моду.
Нам известно: Мо = 37,4 автобусов общего пользования на 100
000 населения. В 17 регионах число автобусов общего пользования на 100 000
населения превышает 37,4 на 100000 чел.= 2; p = 0,954
Доля признака в выборочной совокупности определим по формуле:
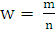 =
=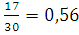 , где
, где
- число регионов, у которых индивидуальные значения признака
превышают моду;
n - число всех регионов совокупности.
Тогда средняя ошибка выборки будет вычисляться по формуле:
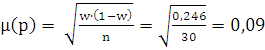 где
где
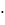 (1-w) - дисперсия доли альтернативного признака:
(1-w) - дисперсия доли альтернативного признака:
σ2 = w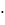 (1-w) = 0,56
(1-w) = 0,56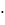 (1 - 0,56) = 0,246
(1 - 0,56) = 0,246
Предельная ошибка выборки:
∆ = tμ = 2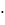 0,091 = 0,182
0,091 = 0,182
Зная выборочную долю признака и предельную ошибку выборки,
можно определить границы, в которых заключена генеральная доля:
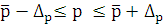
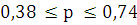
Вывод: С вероятностью 0,954 доля числа автобусов общего
пользования на 100 000 населения в регионах России находится в пределах от 0,38
до 0,74.
Определение объема выборки для снижения
предельной ошибки доли на 30%
Для того чтобы снизить предельную ошибку доли на 30%
необходимо изменить объем выборки.
Нам известно:
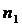 - начальный объем выборки.
- начальный объем выборки.
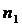 = 30 ед.
= 30 ед.
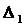 - предельная ошибка потребления овощей на душу населения в год.
- предельная ошибка потребления овощей на душу населения в год.
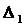 = 0,18
= 0,18
Предельная ошибка потребления снизилась на 30% (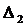 ):
):
0,18 - 100%
х - 30%
х = 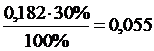
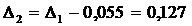
Выразим 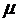 из следующей формулы:
из следующей формулы: 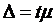
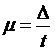
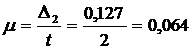
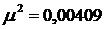
Выразим n из следующей формулы:
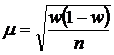
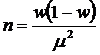
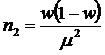 , где
, где
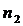 - объем выборки, при котором предельная ошибка доли снизится на
30%.
- объем выборки, при котором предельная ошибка доли снизится на
30%.
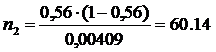 ед.
ед.
Вывод: чтобы снизить предельную ошибку доли регионов, у
которых площади территории превышают моду на 30%, нужно изменить объем выборки
до 60.14
Задание
4
.1 Данные по Псковскому району
Таблица 4.1. Данные динамики поголовья крупного рогатого
скота на конец года по Псковскому району
|
Годы
|
Поголовье крупного рогатого скота на конец
года, гол.
|
С постоянной базой сравнения
|
С переменной базой сравнения
|
|
|
К роста
|
Тр, %
|
Тпр, %
|
Δ
|
К роста
|
Тр, %
|
Тпр, %
|
Δ
|
|
2007
|
12872
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
2008
|
12538
|
0,97
|
97
|
-3
|
-334
|
0,97
|
97
|
-3
|
-334
|
|
2009
|
12204
|
0,95
|
95
|
-5
|
-668
|
0,97
|
97
|
-3
|
-334
|
|
2010
|
10911
|
0,85
|
85
|
-15
|
-1961
|
0,89
|
89
|
-11
|
-1293
|
|
2011
|
10605
|
0,82
|
82
|
-18
|
-2267
|
0,97
|
97
|
-3
|
-306
|
|
2012
|
10457
|
0,81
|
81
|
-19
|
-2415
|
0,99
|
99
|
-1
|
-148
|
|
2013
|
10309
|
0,80
|
80
|
-20
|
-2563
|
0,99
|
99
|
-1
|
-148
|
Формулы для базисных показателей: К = 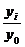 Δo = yi - yo
Δo = yi - yo
Для переменных показателей: К = 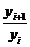 Δi = yi+1 - yi
Δi = yi+1 - yi
Абсолютное значение одного процента прироста: 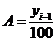
Общие показатели: 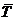 р = К∙100%
р = К∙100%
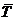 пр =
пр = 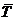 р - 100%
р - 100%
Выполним расчеты:
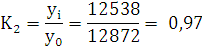
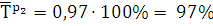
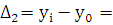 12538 - 12872 = -334
12538 - 12872 = -334
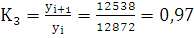
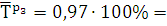 97%
97%
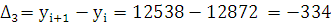
Средний уровень динамики: ряд интервальный, с равноотстающими
уровнями, следовательно, используем формулу простой средней арифметической:
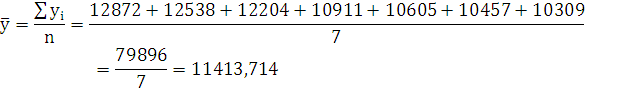
Средний абсолютный прирост:
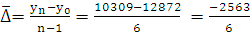 = -427,166
= -427,166
Средний темп роста:
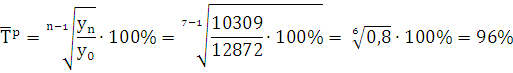
Средний темп прироста:
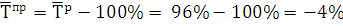
Вывод: На протяжении с 2007 по 2013 года поголовье крупного
рогатого скота на конец гота уменьшилось на 2563 головы, в среднем составило
96% от базисного периода, т.е. в среднем поголовье крупного рогатого скота на
конец года в Псковском районе уменьшилось на 4%.
Сглаживание ряда динамики трехлетней скользящей
средней
Таблица 4.2. Сглаживание показателей поголовья крупного
рогатого скота на конец года по Псковскому району
|
Годы
|
Поголовье крупного рогатого скота на конец года,
гол.
|
Трехлетняя скользящая средняя
|
|
2007
|
12872
|
-
|
|
2008
|
12538
|
12538
|
|
2009
|
12204
|
11884,333
|
|
2010
|
10911
|
11240
|
|
2011
|
10605
|
10657,667
|
|
2012
|
10457
|
10457
|
|
2013
|
10309
|
-
|
Формула для расчета трехлетней скользящей средней:
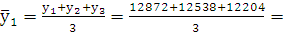 12538
12538
Отобразим графически сглаживание ряда динамики трехлетней
скользящей средней.
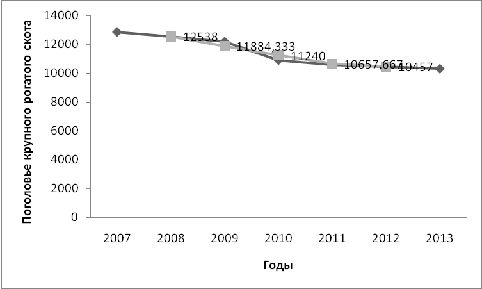
Рис. 6. Сглаживание ряда динамики трехлетней скользящей
средней
Вывод: Для поголовья крупного рогатого скота на конец года в
Псковском районе наблюдается тенденция уменьшения показателей с 2007 г. по 2013
г.
Построим табл. 4.3 для определения параметров функции
аналитического выравнивания.
Таблица 4.3. Расчетные данные для определения параметров
функции аналитического выравнивания
|
Года
|
Поголовье крупного рогатого скота на конец
года, гол.
|
tусл
|
t2усл
|
y∙ tусл
|
y
|
|
2007
|
12872
|
-3
|
9
|
-38616
|
12854,79
|
|
2008
|
12538
|
-2
|
4
|
-25076
|
12374,43
|
|
2009
|
12204
|
-1
|
1
|
-12204
|
11894,07
|
|
2010
|
10911
|
0
|
0
|
0
|
11413,71
|
|
2011
|
10605
|
1
|
1
|
10605
|
10933,35
|
|
2012
|
10457
|
2
|
4
|
20914
|
10452,99
|
|
2013
|
10309
|
3
|
9
|
30927
|
9972,63
|
|
Итого
|
79896
|
0
|
28
|
-13450
|
68482,26
|
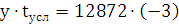 = -38616
= -38616
Так как число уровней ряда не четное, условные переменные
будут нумероваться с 0, чтобы 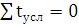
Предположим, что тренд - прямая линия, ее функция: y = ao + a1· t; значения параметров
должны удовлетворять системе:

Введем условное время так, чтобы ∑tусл = 0,
получаем систему:
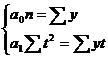
ее решение: 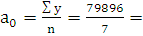 11413,71 гол.
11413,71 гол.
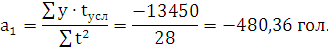
тогда: 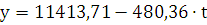
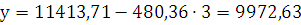
Показатель а1 = -480,36 означает, что в Псковском
районе ежегодно происходит уменьшение поголовья крупного рогатого скота на
конец года на данную величину, т.е. показывает среднюю величину абсолютного
прироста выровненного ряда динамики.
Вывод: Средний уровень динамики за 7 лет составил 11413,71
рублей
Составим прогноз среднемесячной заработной платы работников
организаций образования на 2014 г.:
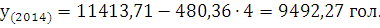
Вывод: Таким образом мы видим, что поголовье крупного
рогатого скота на конец года в 2014 году будет уменьшено до 9492,27 голов.
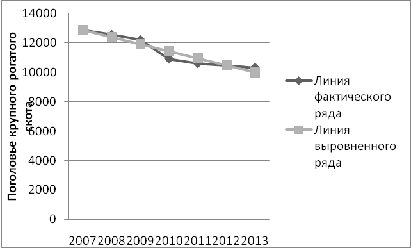
На основе полученных данных построим графически фактический и
выровненный уровни поголовья крупного рогатого скота на конец года.
4.2 Данные по Локнянскому району
Таблица 4.4. Данные динамики поголовья крупного рогатого
скота на конец года по Локнянскому району
|
Года
|
Поголовье крупного рогатого скота на конец
года, гол.
|
С постоянной базой сравнения
|
С переменной базой сравнения
|
|
|
К роста
|
Тр, %
|
Тпр, %
|
Δ
|
К роста
|
Тр, %
|
Тпр, %
|
Δ
|
|
2007
|
950
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
2008
|
3764
|
3,962
|
396,2
|
296,2
|
2814
|
3,962
|
396,2
|
296,2
|
2814
|
|
2009
|
3600
|
3,789
|
378,9
|
278,9
|
2650
|
0,96
|
96
|
-4
|
-164
|
|
2010
|
3256
|
3,427
|
342,7
|
242,7
|
2306
|
0,9
|
90
|
-10
|
-344
|
|
2011
|
3100
|
3,263
|
326,3
|
226,3
|
2150
|
0,95
|
95
|
-5
|
-156
|
|
2012
|
2697
|
2,838
|
283,8
|
283,8
|
1747
|
0,87
|
87
|
-13
|
-403
|
|
2013
|
2294
|
2,414
|
241,4
|
141,4
|
1344
|
0,85
|
85
|
-15
|
-403
|
Формулы для базисных показателей: К = 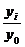 Δo = yi - yo
Δo = yi - yo
Для переменных показателей: К = 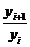 Δi = yi+1 - yi
Δi = yi+1 - yi
Абсолютное значение одного процента прироста: 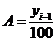
Общие показатели: 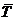 р = К∙100%
р = К∙100%
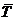 пр =
пр = 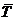 р - 100%
р - 100%
Произведем расчеты:
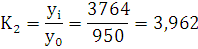
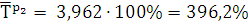
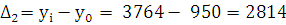
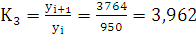
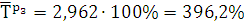
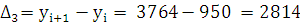
Средний уровень динамики: ряд дискретный, с равноотстающими
уровнями, следовательно, используем формулу простой средней арифметической:
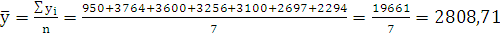 гол.
гол.
Средний абсолютный прирост:
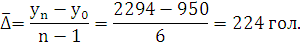
Средний темп роста:
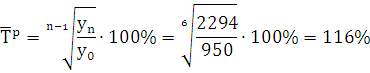
Средний темп прироста:
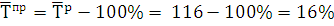
Вывод: На протяжении с 2007 по 2008 год поголовье крупного
рогатого скота увеличилось на 2814 голов. На протяжении с 2008 по 2013
наблюдалось уменьшение поголовья крупного рогатого скота. Таким образом,
средний абсолютный прирост составил 224 гол., что в среднем составляет 116% от
базисного периода.
Таблица 4.5. Сглаживание показателей поголовья крупного
рогатого скота на конец года по Локнянскому району
|
Годы
|
Поголовье крупного рогатого скота на конец
года, гол.
|
Трехлетняя скользящая средняя
|
|
2007
|
950
|
-
|
|
2008
|
3764
|
2771,33
|
|
2009
|
3600
|
3540
|
|
2010
|
3256
|
3318,66
|
|
2011
|
3100
|
3017,66
|
|
2012
|
2697
|
2697
|
|
2013
|
2294
|
-
|
Формула для расчета трехлетней скользящей средней:
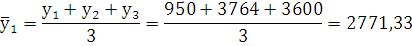
Отобразим графически сглаживание ряда динамики трехлетней
скользящей средней.
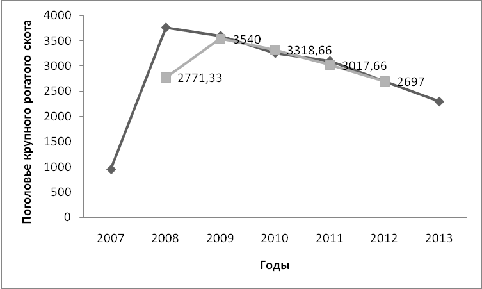
Рис. 8. Сглаживание ряда динамики трехлетней скользящей
средней
Вывод: Для поголовья крупного рогатого скота на конец года в
Локнянском районе наблюдается тенденция увеличения показателей с 2007 г. по
2008 г., а с 2008 г. по 2013 г. наблюдается тенденция уменьшения показателей.
Построим табл. 4.6 для определения параметров функции
аналитического выравнивания.
Таблица 4.6. Расчетные данные для определения параметров
функции аналитического выравнивания
|
Года
|
Поголовье крупного рогатого скота на конец года
|
tусл
|
t2усл
|
y∙ tусл
|
y
|
|
2007
|
950
|
-3
|
9
|
-2850
|
2658,92
|
|
2008
|
3764
|
-2
|
4
|
-7528
|
2708,85
|
|
2009
|
3600
|
-1
|
1
|
-3600
|
2758,78
|
|
2010
|
3256
|
0
|
0
|
0
|
2808,71
|
|
2011
|
3100
|
1
|
1
|
3100
|
2858,64
|
|
2012
|
2697
|
2
|
4
|
5394
|
2908,57
|
|
2013
|
2294
|
3
|
9
|
6882
|
2958,5
|
|
Итого
|
19661
|
0
|
28
|
1398
|
53899,38
|
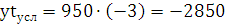
Предположим, что тренд - прямая линия, ее функция: y = ao + a1· t; значения параметров
должны удовлетворять системе:

Введем условное время так, чтобы ∑tусл = 0,
получаем систему:
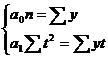
ее решение: 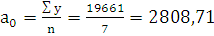 гол.
гол.
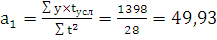 гол.
гол.
тогда: 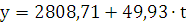
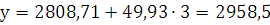
Показатель а1 = 49,93 показывает среднюю величину
абсолютного прироста выровненного ряда динамики.
Вывод: Средний уровень динамики за 7 лет составил 2808,71
голов.
Составим прогноз поголовья крупного рогатого скота на конец
года на 2014 г.:

Вывод: Таким образом, мы видим, что поголовье крупного
рогатого скота на конец года в 2014 году будет увеличено до 3008,43 гол.
На основе полученных данных построим графически фактический и
выровненный уровни поголовья крупного рогатого скота на конец года.
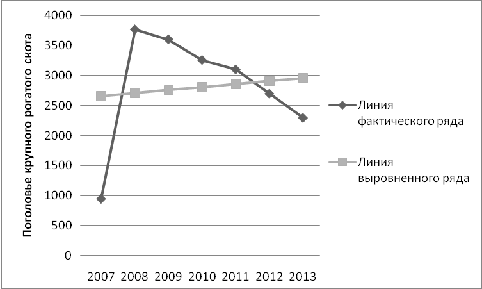
Рис. 9 Динамика поголовья крупного рогатого скота по
Локнянскому району
Задание
5
Пользуясь таблицами №4 и №5, сформируем таблицу исходных
данных.
Таблица 5.1. Данные о продаже продукции по кварталам
|
Вид продукции
|
1 квартал
|
2 квартал
|
|
Продано, тыс. шт.
|
Цена за ед., руб.
|
Стоимость продукции, тыс. руб. 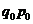 Продано, тыс. шт. Продано, тыс. шт.
|
Цена за ед., руб.
|
Стоимость продукции, тыс. руб. 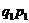
|
|
|
А
|
72
|
40
|
2880
|
102
|
36
|
3672
|
|
В
|
70
|
20
|
1400
|
85
|
28
|
2380
|
|
С
|
90
|
15
|
1350
|
110
|
15
|
1650
|
|
Итого:
|
234
|
75
|
5630
|
297
|
79
|
7702
|
Индивидуальный индекс физического объема:
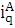 =
= 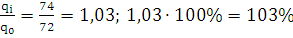
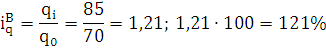
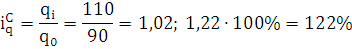
Индивидуальный индекс цены:
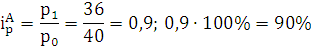
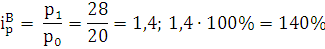

Индивидуальный индекс товарооборота:
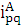 =
= 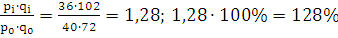
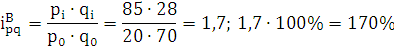
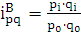 =
=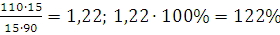
Вывод: Объем реализованной продукции в отчетном периоде
товаров А, В и С увеличился на 3%, 21% и на 22% соответственно, или в 1,03,
1,21 и 1,22 раза, по сравнению с базисным.
Цена продукции группы А снизилась на 10% или в 0,9 раз, цена
продукции группы B увеличилась на 40% или в 1,4 раз, а цена продукции группы C не изменилась.
В текущем периоде по сравнению с базисным товарооборот
продукции А увеличился в 1,28 раз. Товарооборот продукции В увеличился на 70%
или в 1,7 раз. Товарооборот продукции С увеличился на 22%, или в 1,22 раза.
Агрегатный индекс физического объема продукции:
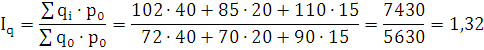
Вывод: Объемы реализации продукции, за отчетный период, имели
положительную динамику и увеличились в 1,32 раза, что составило 132%, изменения
произошли на 32%.
Агрегатный индекс цены. При определении общего индекса цен 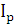 существует два подхода
при выборе соизмерителя (веса) индексируемой величины:
существует два подхода
при выборе соизмерителя (веса) индексируемой величины:
. В качестве веса приниматься физический объем работ и услуг
текущего периода:
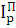 =
= 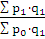 =
= 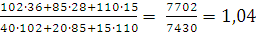
Такой агрегатный индекс цен называется индексом Пааше.
. В качестве веса принимается физический объем работ и услуг
базисного периода - индекс Ласпейреса:
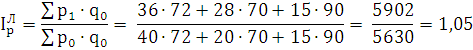
Вывод: Цена продукции за отчетный период увеличилась по
формуле Паше на 4% или в 1,04 раза, а по формуле Лайспереса изменения произошли
на 5%.
Агрегатный индекс товарооборота:
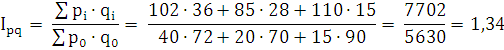
Вывод: Товарооборот продукции за отчетный период увеличился в
1,38 раза, что составило 134%, изменения произошли на 34%.
Индекс товарооборота можно рассматривать как часть некоей
системы индексов, определенной взаимосвязью между признаками. Так, если:
товарооборот продукции = количество ∙ цена, то и общий индекс
товарооборота должен быть равен произведению индекса физического объема на
индекс цен:
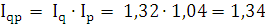
Таким образом, товарооборот продукции увеличился на 34%.
Определим абсолютное изменение товарооборота произведенной
продукции в текущем периоде по сравнению с базисным, в том числе за счет
изменения цен и за счет изменения продажи продукции.
Общее абсолютное изменение товарооборота продукции за счет
двух факторов составляет:
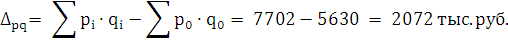
Следовательно, изменение товарооборота продукции, за счет
изменения двух факторов, произошло на 2072 тыс. руб. с перерасходом.
Абсолютное изменение общего товарооборота продукции за счет
изменения цены:
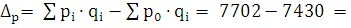 272 тыс. руб.
272 тыс. руб.
Изменение товарооборота продукции, за счет изменения цены,
произошло на 272 тыс. руб. с перерасходом.
Абсолютное изменение общего товарооборота продукции за счет
изменения физического объема:
∆q = ∑p0qi - ∑p0q0 = 7430 - 5630 = 1800
тыс. руб.
Изменение товарооборота продукции, за счет изменения
физического объема, произошло на 1800 тыс. руб. с перерасходом.
Взаимосвязь абсолютных приростов (аддитивная связь):
∆Р = ∆p + ∆q = 272 + 1800 = 2072 тыс.
руб.
Определим, как изменилась средняя цена единицы продукции
(индекс переменного состава):
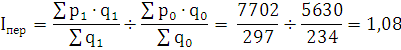
Средняя цена единицы продукции изменилась в 1,08 раз, или
увеличилась на 8% в результате практически неизменных цен на продукцию и
изменении структуры продукции.
Индекс фиксированного состава, определяющий влияние на индекс
средней величины изменения усредняемой цены:
экономический корреляция
дисперсия комбинационный
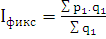
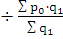 =
=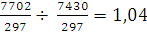
Средняя цена единицы продукции увеличилась на 4%.
Индекс структурного сдвига определяет изменение структуры
продукции:
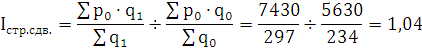
Структура продукции изменилась в 1,04 раза, увеличившись на
4%.
Индексы цен переменного, постоянного состава, индекс
структурных сдвигов образуют систему взаимосвязанных индексов:
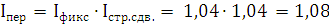
Список
используемой литературы
1. Методические
указания по выполнению курсовой работы по ред. Л.Н. Гальдикас и Л.И.
Стрикуновой., 2011 г.
2. Муниципальные
районы и городские округа Псковской области - основные характеристики: стат.
сборник в 2 томах, Псковоблкомстат, 2011. - 142 с., том 1
3. Псковский
статистический ежегодник. 2011: Cтат. сб. В 2 т. Т.1 / Псковстат - П., 2011. -
198 с.
4. Нименья
И.Н. Статистика. М: Финансы и статистика, 2005 г.
. Теория
статистики: Учебник / Под ред. проф. Р.А. Шмойловой. - 3-е изд. перераб. - М.:
Финансы и статистика, 2002. -560 с.:
. Федеральная
служба государственной статистики [Электронный ресурс] / Районы Псковской
области. / Социально-экономические показатели 2003-2011 гг. - Электронные
данные. - Режим доступа: http:// www.gks.ru, свободный.