Моделирование системы управления реакционным аппаратом на основе анализа уравнений кинетики химической реакции
Введение
Автоматизация производственных процессов представляет собой одно из
наиболее важных направлений технического прогресса, является наиболее
эффективным средством повышения производительности труда на современных
промышленных предприятиях.
Разработаны и проверены на практике схемы автоматического регулирования
отдельных узлов, агрегатов, производственных участков и цехов с использованием
серийной аппаратуры автоматизации; разработаны многочисленные
специализированные средства автоматизации (датчики, регулирующие органы и
т.д.), приспособленные для работы в условиях эксплуатации химической
промышленности.
Автоматизация дает не только непосредственный экономический эффект; ее
успехи оказывают большое влияние на общий технический уровень химической промышленности.
Высокая точность поддержания заданного режима работы, которая достигается при
использовании системы автоматического управления, позволяет значительно
интенсифицировать технологические процессы, используя более активные
катализаторы, высокие температуры и давление. Многие вновь разрабатываемые
технологические процессы оказывается возможным реализовать только как
автоматизированные, так как ручное управление не гарантирует безопасного их
ведения и получения продукции заданного качества. Применение систем
автоматического дистанционного управления позволяет широко практиковать
размещение технологического оборудования на открытых площадках.
1.Описание технологического объекта
Основным аппаратом в технологической схеме получения практически любого химического
продукта является химический реактор.
Работой реактора в значительной мере определяется производительность
установки в целом, качество и себестоимость получаемых продуктов.
Скорость химической реакции определяется уравнениями кинетики и взаимодействием
гидродинамических, массообменных и тепловых процессов в аппарате, от которых
зависит концентрация реагентов и условия протекания реакции. В свою очередь,
химические превращения в реакторе приводят к изменению тепловых и
гидродинамических процессов в нем. Этим взаимосвязям соответствуют перекрестные
связи в структурной схеме реактора. Наличие таких внутренних обратных связей
может приводить к возникновению неустойчивых режимов, автоколебаниям параметров
процесса, изменению качества получаемого продукта и должно учитываться при
построении систем автоматизации химических реакторов.
Упрощенная структурная схема реактора представлена на рис.1.
химический реакция регулятор
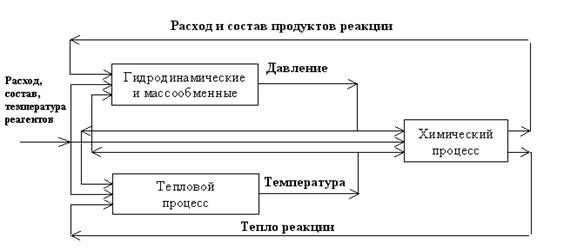
Рис.1
Структурная схема реактора.
Предполагается, что в изотермических реакторах теплообмен через стенку
идеальный, и тепло, выделяемое в результате химической реакции, мгновенно
отводится от реагирующей смеси, так что температура в реакторе не изменяется.
При полном отсутствии теплообмена через стенку реактора в нем протекает
адиабатический процесс.
Химические реакции, протекающие в реакторах разделяются на
экзотермические (с выделением тепла) и эндотермические (с поглощением тепла). В
данной работе рассматривается реактор, в котором протекает экзотермический
процесс. Этот процесс является более сложным для управления, так как
сравнительно небольшое изменение температуры в реакторе может привести к
значительным изменениям степени конверсии. В некоторых случаях это может вызвать
даже неустойчивость процесса, если изменение количества выделяемого при реакции
тепла не может быть скомпенсировано соответствующим изменением скорости отвода
тепла. Неустойчивость процесса может приводить к взрывам и аварийной остановке
реактора.
Основной задачей при управлении химическим реактором непрерывного
действия, является стабилизация заданных значений температуры и концентрации в
реакторе. Этого можно достичь регулированием по отклонению температуры в
реакторе от заданного значения воздействием на температуру. Эта система
регулирования может быть реализована путем изменения давления кипящего
хладагента, находящегося в рубашке реактора. Использование такого способа
регулирования позволяет изменять теплоотвод от реактора при изменении в нем температуры.
Так же возможно регулирование по отклонению температуры в реакторе от заданного
значения воздействием на входную температуру реакционной смеси. Этот способ
регулирования может быть реализован путем изменения режима работы специального
теплообменника, установленного на входе реакционной смеси в реакторе. Однако
такая система может оказаться очень инерционной. Можно также изменять
температуру части реакционной смеси и изменять ее входную температуру, изменяя
соотношения холодного и горячего потоков, поступающих в реактор.
2.Обоснование и выбор схемы управления объектом
Температура является показателем термодинамического состояния системы и
используется как выходная координата при регулировании тепловых процессов.
Динамические характеристики объектов в системах регулирования температуры
зависит от физико-химических параметров процесса и конструкции аппарата.
Поэтому общие рекомендации по выбору автоматической системы регулирования (АСР)
температуры сформулировать невозможно, и требуется анализ каждого конкретного
процесса.
Задача управления изменения температур экзотермических реакций в реакторе
заключается в обеспечение устойчивости процесса при заданных показателях
качества. Чаще всего применяются одноконтурные системы управления, так как они
более экономичны и просты в реализации. Технологическая схема реактора с
одноконтурной схемой регулирования имеет вид (Рис.2.):
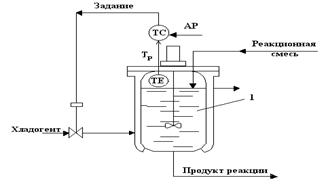
Рис.2.Схема одноконтурной АСР в химическом реакторе
где
-реактор;
ТЕ - преобразователь измерения температуры;
ТС - регулятор температуры;
Тр - температура реакционной смеси в реакторе.
Но при этом довольно таки тяжело достичь желаемого результата. С целью
обеспечения быстродействия применяются многоконтурные системы управления. С
этой целью в объекте кроме основной выходной координаты, выбираются
вспомогательные, которые подвержены тем же возмущениям, но являются менее
инерционными и имеют малое запаздывание. В принципе таких вспомогательных
величин может быть выбрано несколько, число их определяет количество контуров.
В данном случае для регулировки подачи хладагента мы используем каскадную схему
управления. Это позволит заметно улучшить показатели переходного процесса в
объекте.
Функциональная схема реактора с каскадной схемой регулирования имеет вид
(Рис.3.):
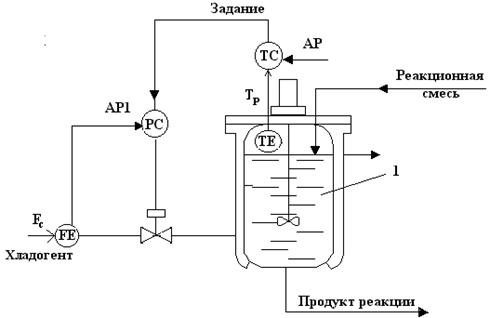
Рис.3.Схема двухконтурной каскадной АСР в химическом реакторе
где
-реактор;
ТЕ - преобразователь измерения температуры;
ТС - регулятор температуры;- регулятор расхода охлаждающей жидкости;c
- расход охлаждающей жидкости;
Тр - температура реакционной смеси в реакторе;
Тс - температура охлаждающей жидкости.
На рисунке сверху показана двухконтурная АСР температуры в химическом
реакторе посредством изменения расхода хладогента в рубашке реактора. С целью
обеспечения более высокого качества регулирования, в схему введен
стабилизирующий контур, в который входит регулятор АР1 поддерживающий
температуру охлаждающей жидкости Тс в рубашке реактора. Значение этой
температуры задается регулятором АР корректирующего контура регулирования
температуры реакционной смеси Тр в реакторе.
химический реакция
регулятор
3.Определение передаточной функции объекта управления
Построение математической модели объекта управления по экспериментальной
переходной функции (или аппроксимации экспериментальной кривой разгона)
производится в следующем порядке:
. На основании формы переходной функции и в зависимости от
динамических свойств исследуемой системы устанавливаются вид ее передаточной
функции.
. Определяются значения коэффициентов передаточной функции из
условия наилучшего приближения модели к объекту.
. Производится оценка точности аппроксимации.
В данной работе я использовал программу, которая даёт возможность быстро
рассчитывать передаточные функции объектов, ей является программа RKPF.
Программа рассчитывает коэффициенты передаточной функции объекта по введенной
кривой разгона (в виде значений выхода от времени), отображая это в виде
графиков и числовых значений. Воспользуемся этой программой. При запуске
программы необходимо указать тип переходного процесса и входные значения в
появившемся диалоговом окне. В нашем случае показания снимались 21 раз, с
интервалом времени в 12,5 сек, процесс с самовыравниванием. После этого вводим
все снятые значения в программу. Для получения результата необходимо нажать на
кнопку «Вычислить» (расположенную на панели инструментов).
Результат будет представлен в следующем виде:
Проведя вычисления, программа выводит результат:
Таблица 1
|
|
t
|
s
|
(1 s)
|
q = t /F1
|
(1 q)
|
(1 s)(1 q)
|
1 2q + q 2/2
|
(1 s)(1 2q + q 2/2)
|
|
52
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
|
52,45
|
12,5
|
0,018
|
0,982
|
0,128
|
0,889
|
0,884
|
0,784
|
0,779
|
|
52,9
|
25
|
0,036
|
0,964
|
0,2559
|
0,778
|
0,759
|
0,581
|
0,567
|
|
54,04
|
37,5
|
0,0816
|
0,9184
|
0,3839
|
0,668
|
0,623
|
0,391
|
0,364
|
|
55,86
|
50
|
0,1544
|
0,8456
|
0,5118
|
0,557
|
0,486
|
0,212
|
0,185
|
|
58,13
|
62,5
|
0,2452
|
0,7548
|
0,6398
|
0,446
|
0,36
|
0,046
|
0,037
|
|
60,4
|
75
|
0,336
|
0,664
|
0,7677
|
0,335
|
0,248
|
-0,109
|
-0,081
|
|
63,13
|
87,5
|
0,4452
|
0,5548
|
0,8957
|
0,224
|
0,148
|
-0,251
|
-0,166
|
|
65,63
|
100
|
0,5452
|
0,4548
|
1,0236
|
0,114
|
0,064
|
-0,38
|
-0,214
|
|
68,3
|
112,5
|
0,652
|
0,348
|
1,1516
|
0,003
|
0,001
|
-0,497
|
-0,237
|
|
70,86
|
125
|
0,7544
|
0,2456
|
1,2796
|
-0,108
|
-0,043
|
-0,602
|
-0,241
|
|
72,68
|
137,5
|
0,8272
|
0,1728
|
1,4075
|
-0,219
|
-0,074
|
-0,695
|
-0,236
|
|
74,04
|
150
|
0,8816
|
0,1184
|
1,5355
|
-0,33
|
-0,087
|
-0,776
|
-0,205
|
|
74,95
|
162,5
|
0,918
|
0,082
|
1,6634
|
-0,44
|
-0,088
|
-0,843
|
-0,169
|
|
75,41
|
175
|
0,9363
|
0,0636
|
1,7914
|
-0,551
|
-0,077
|
-0,899
|
-0,126
|
|
75,63
|
187,5
|
0,9452
|
0,0548
|
1,9193
|
-0,662
|
-0,056
|
-0,943
|
-0,079
|
|
76,09
|
200
|
0,9636
|
0,0364
|
2,0473
|
-0,773
|
-0,031
|
-0,974
|
-0,039
|
|
76,13
|
212,5
|
0,9724
|
0,0276
|
2,1752
|
-0,883
|
-0,021
|
-0,993
|
-0,024
|
|
76,54
|
225
|
0,9816
|
0,0184
|
2,3032
|
-0,994
|
-0,008
|
0
|
0
|
|
76,77
|
237,5
|
0,9908
|
0,0092
|
2,4312
|
-1,105
|
-0,004
|
-0,994
|
-0,004
|
|
77
|
250
|
1
|
0
|
2,5591
|
-1,216
|
0
|
-0,977
|
0
|
Результат, где показана найденная передаточная функция, и статическая
ошибка:
Передаточная
функция объекта: 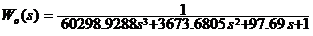
Ошибка
аппроксимации: 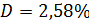
Так как программа выдала коэффициент усиления без учета в % хода
регулирующего органа, определим его следующим образом:
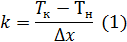
где Тн - начальная температура кривой разгона (Тк=770)
Тк - конечная температура кривой разгона. ( Тн=520)
Dх - возмущение в % хода регулирующего органа.(Dх=14%)
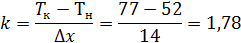
Так как программа вывела коэффициенты передаточной функции объекта
управления в секундах, переводим их в минуты, а так же учитываем значение
коэффициента усиления:
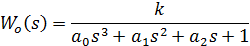
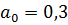
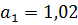
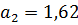
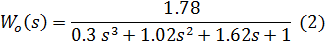
Т.к. максимальная ошибка аппроксимации не превышает 5 %, то для
дальнейших расчетов можно использовать передаточную функцию (3).
Передаточная функция объекта в стабилизирующем контуре задана
апериодическим звеном первого порядка с чистым запаздыванием:
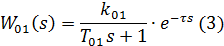
где 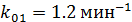 ;
; 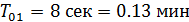 ;
; 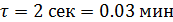 .
.
4.Выбор модели автоматического регулятора
Перед тем, как приступить к выбору автоматического регулятора составляют
схему автоматического регулирования данного химико-технологического объекта и
определяют канал регулирования. Тип автоматического регулятора выбирается с
учетом свойств объекта регулирования и заданных параметров качества переходного
процесса. В химико-технологической промышленности наиболее часто применяют
регуляторы непрерывного действия:
И-регулятор,
П-регулятор,
ПИ-регулятор,
ПИД-регулятор.
Для одноконтурной системы выберем ПИ-регулятор, а для каскадной системы в
качестве стабилизирующего регулятора используем П - регулятор, а в качестве
корректирующего ПИ - регулятор. Эти регуляторы были выбраны благодаря ряду
преимуществ. Колонна ректификации является инерционным объектом, поэтому
необходимы регуляторы, которые отличаются быстродействием и работоспособностью
на таких объектах, таким свойствами обладают П-регуляторы. Однако использование
П-регуляторов возможно при допущении остаточного отклонения параметра от
заданного. Автоматические регуляторы с пропорционально-интегральным законом
регулирования объединили преимущества П- и И-регуляторов. Статическая ошибка у
ПИ-регуляторов практически равна нулю, т.е. повышается точность регулирования.
Также ПИ-регуляторы обладают достаточным быстродействием и дают возможность
вывода параметра на заданный уровень.
У регуляторов с пропорциональным законом регулирования выходная величина
в пределах зоны регулирования изменяется пропорционально изменению входа.
Уравнение динамики П-регулятора:
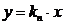 , (4)
, (4)
где
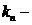 коэффициент пропорциональности.
коэффициент пропорциональности.
Передаточная
функция П-регулятора, равная отношению выходной величины к входной имеет вид:
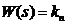 (5)
(5)
У
ПИ-регуляторов воздействие входной величины на выход тем больше, чем больше
коэффициент пропорциональности и меньше постоянная интегрирования 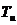 .
.
Уравнение
динамики ПИ-регулятора:
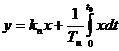 . (6)
. (6)
где с1 и с0 - параметры настройки ПИ-регулятора.
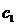 =
=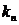 с0=
с0=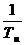 (7)
(7)
Передаточная
функция этого регулятора:
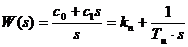 (8)
(8)
5.Определение условий устойчивости системы
Под устойчивостью системы понимается её свойство возвращаться к
равновесному состоянию после устранения возмущения.
Для того чтобы линейная САР была устойчива, необходимо и достаточно,
чтобы корни характеристического уравнения системы находились в комплексной
плоскости корней слева от мнимой оси.[1]
5.1 Определение области значения настроек регулятора для одноконтурной
системы
Структурная схема одноконтурной системы представлена на рис.4
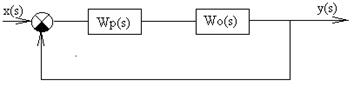
Рисунок 4. Структурная схема одноконтурной системы
где W0(s) - передаточная функция объекта управления
WP(s) - передаточная функция ПИ-регулятора
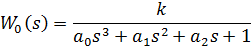
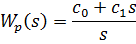
Передаточная функция разомкнутой системы:
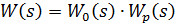
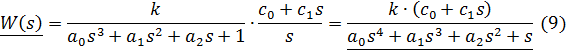
Передаточная функция замкнутой системы:
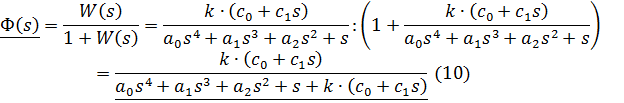
Характеристическое уравнение системы:
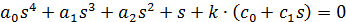
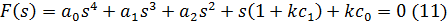
Приведем характеристическое уравнение системы к виду:
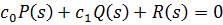
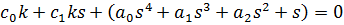
делаем подстановку: s=jω
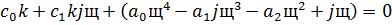
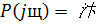
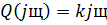
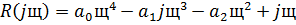
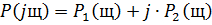
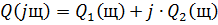
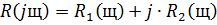
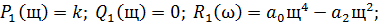
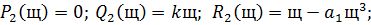
Составляем систему:
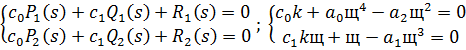
Коэффициенты 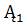 и
и 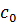 находятся по формулам:
находятся по формулам:
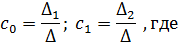
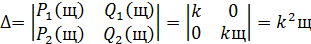
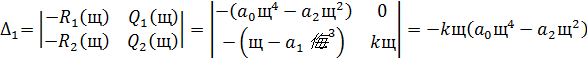
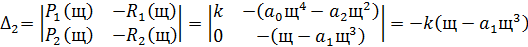
В результате получим:
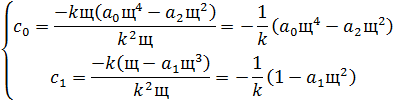
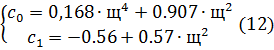
При
некотором значении частоты ω
определители 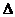 ,
, 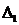 и
и 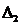 равны нулю одновременно. При этом в плоскости параметров
С0 и С1 получаются так называемые особые прямые. Т.к.
равны нулю одновременно. При этом в плоскости параметров
С0 и С1 получаются так называемые особые прямые. Т.к. 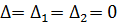 при ω=0.
при ω=0.
Найдём
уравнения особых прямых при частоте ω=0:
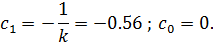
Задаваясь
значениями ω, построим в плоскости параметров с0 и с1 кривую.
D-разбиения и особые прямые (рис. 5). Расчетные данные приведены в таблице 2.
Граница Д - разбиения штрихуется слева, если при изменении ω от -∞ до +∞. Главный определитель 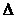 больше нуля, и справа, если
больше нуля, и справа, если 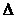 меньше нуля. В данном случаи
меньше нуля. В данном случаи 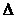 больше нуля, так как частота ω изменяется в пределах от 0 до +∞. При изменении
ω от -∞ до +∞ мы обходим кривую Д -
разбиения два раза и поэтому она штрихуется всегда двойной штриховкой.
Штриховка особых прямых производится так, чтобы вблизи точки сопряжения особой
прямой и кривой Д - разбиения заштрихованные и не заштрихованные стороны прямой
и кривой были направлены друг к другу.
больше нуля, так как частота ω изменяется в пределах от 0 до +∞. При изменении
ω от -∞ до +∞ мы обходим кривую Д -
разбиения два раза и поэтому она штрихуется всегда двойной штриховкой.
Штриховка особых прямых производится так, чтобы вблизи точки сопряжения особой
прямой и кривой Д - разбиения заштрихованные и не заштрихованные стороны прямой
и кривой были направлены друг к другу.
Таблица 2
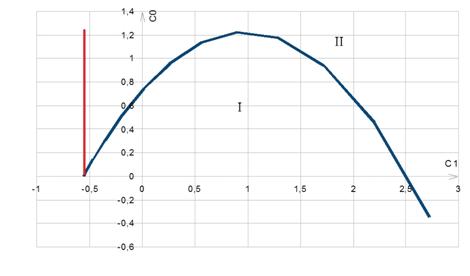
Рисунок 5. Кривая D-разбиения одноконтурной системы
Пусть в области I имеется k отрицательных корней слева от мнимой оси. При
переходе через кривую Д-разбиения два корня переходят из левой полуплоскости в
правую, т.е. в области II будет k- 2 корня. Таким образом, областью с
наибольшим количеством левых корней будет область I.
5.1.1 Проверка найденной области на устойчивость
Для проверки найденной области на устойчивость воспользуемся критерием
Рауса-Гурвица.
Согласно этому критерию, для устойчивости системы четвёртого порядка,
кроме положительности всех коэффициентов характеристического уравнения,
требуется выполнение условия.
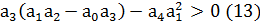
Характеристическое уравнение системы:
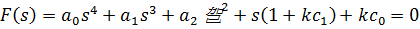
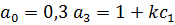
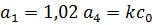
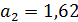
Возьмем произвольную точку из области I , ограниченной кривой D -
разбиения и особыми прямыми, в ней значения 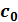 и
и 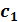 будут соответственно равны:
будут соответственно равны: 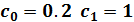 Подставим значения коэффициентов
характеристического уравнения и значения
Подставим значения коэффициентов
характеристического уравнения и значения 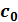 и
и 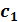 в неравенство (13) получим:
в неравенство (13) получим:
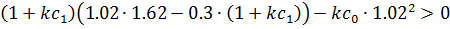
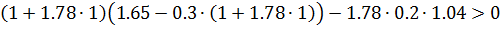
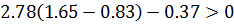
Неравенство выполняется, следовательно, область I - область устойчивости,
т.е. система устойчива
5.2 Определение области значения настроек регуляторов для
каскадной системы управления
В каскадных системах при регулировании основной технологической величины
в объекте с большим запаздыванием используют также вспомогательные величины,
реагирующие на изменение основных возмущений объекта и регулирующего
воздействия с меньшим запаздыванием.
В таких случаях стабилизация вспомогательных величин способствует более
качественному регулированию основной величины. Каскадная система состоит из
нескольких контуров регулирования, каждый из которых регулирует свою величину.
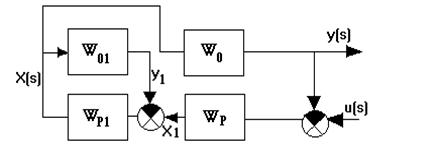
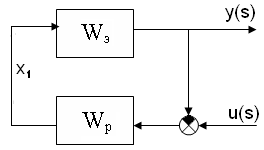
Рисунок 7. Эквивалентная схема каскадной АСР
Передаточная функция разомкнутой системы имеет вид:
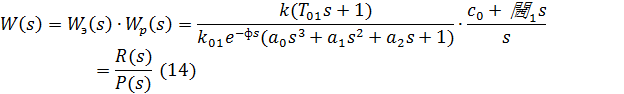
Где 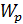 - передаточная функция ПИ - регулятора.
- передаточная функция ПИ - регулятора.
Тогда передаточная функция замкнутой системы Ф(s):
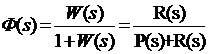
Отсюда
характеристическое уравнение системы:
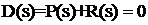
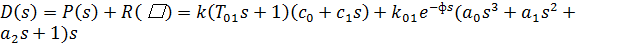 (16)
(16)
Уравнение (17) можно привести к виду:
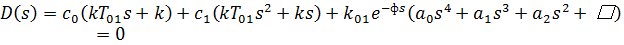
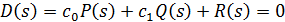
где 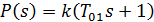
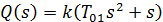
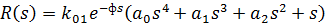
Сделаем подстановку s=jω :
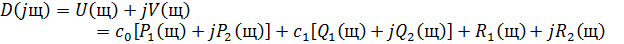
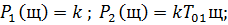
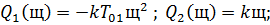
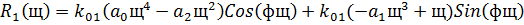
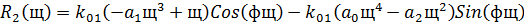
Составляем систему:
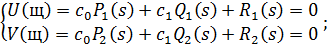
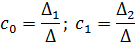
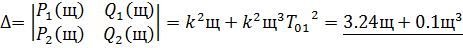
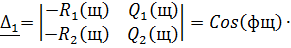
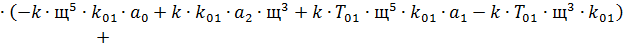
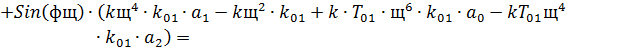
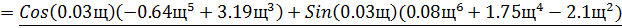
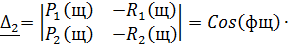
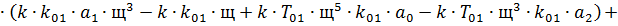
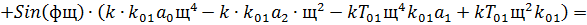
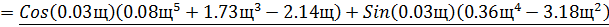
В результате получим:
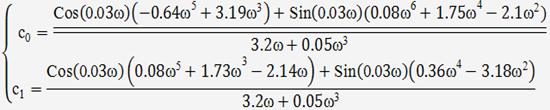
И в числителе и в знаменателе обоих уравнений системы (18) вынесем за
скобку 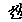 , и сократим, в результате получим:
, и сократим, в результате получим:
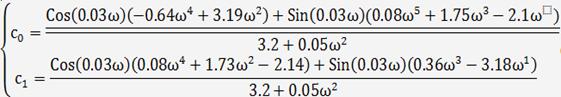
По найденным уравнениям строим кривую D - разбиения в плоскости
параметров 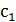 ,
, 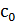 . А так же особые прямые, их уравнения находим, приравняв ω нулю:
. А так же особые прямые, их уравнения находим, приравняв ω нулю:
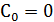 ,
, 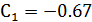 .
.
Таблица 4
|
C0
|
C1
|
w
|
|
0
|
-0,67
|
0
|
|
0,04
|
-0,65
|
0,2
|
|
0,16
|
-0,58
|
0,4
|
|
0,36
|
-0,46
|
0,6
|
|
0,62
|
-0,3
|
0,8
|
|
0,93
|
-0,08
|
1
|
|
1,28
|
0,2
|
1,2
|
|
1,65
|
0,54
|
1,4
|
|
2,01
|
0,95
|
1,6
|
|
2,34
|
1,44
|
1,8
|
|
2,62
|
2,03
|
2
|
|
2,8
|
2,7
|
2,2
|
|
2,87
|
3,49
|
2,4
|
|
2,78
|
4,41
|
2,6
|
|
2,5
|
5,45
|
2,8
|
|
2,01
|
6,65
|
3
|
|
1,25
|
8,01
|
3,2
|
|
0,2
|
9,56
|
3,4
|
|
-1,17
|
11,3
|
3,6
|
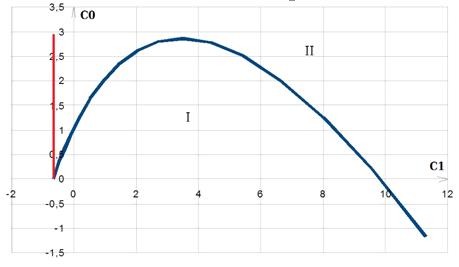
Рисунок 8. Кривая D - разбиения для ПИ-регулятора каскадной системы
Нанеся штриховку, определяем область с наибольшим количеством левых
корней, также как это было сделано для одноконтурной системы. Этой областью
будет область I. Проверим, является ли эта область областью устойчивости.
5.2.1 Проверка найденной области на устойчивость
Согласно критерию Михайлова, для устойчивости системы, характеристическое
уравнение которой имеет четвертый порядок, достаточно чтобы характеристическая
кривая последовательно проходила четыре квадранта координатной плоскости.
Передаточная функция разомкнутой системы имеет вид:
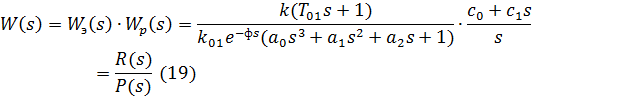
Тогда передаточная функция замкнутой системы Ф(s):
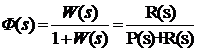 (20)
(20)
Отсюда характеристическое уравнение системы:
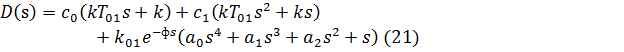
Подставив в (22) s=jω , а так же параметры настройки 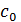 и
и 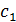 , произвольно взятые из области I (
, произвольно взятые из области I (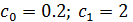 ), и отделив мнимую и действительную
части, получим:
), и отделив мнимую и действительную
части, получим:
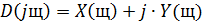
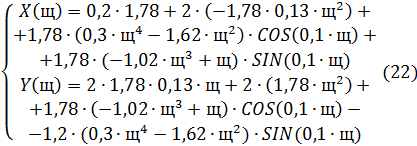
Подставляя в выражения (22) различные значения ω, найдем значения вещественной 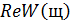 и мнимой
и мнимой 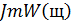 частей, по которым строим АФХ
разомкнутой системы:
частей, по которым строим АФХ
разомкнутой системы:
Таблица 5
|
X(w)
|
Y(w)
|
w
|
|
0,36
|
0
|
0
|
|
0,33
|
0,22
|
0,1
|
|
0,23
|
0,49
|
0,2
|
|
0,08
|
0,82
|
0,3
|
|
-0,14
|
1,17
|
0,4
|
|
-0,41
|
1,55
|
0,5
|
|
-0,73
|
1,95
|
0,6
|
|
-1,1
|
2,34
|
0,7
|
|
-1,52
|
2,72
|
0,8
|
|
-1,96
|
3,09
|
0,9
|
|
-2,44
|
3,42
|
1
|
|
-2,94
|
3,71
|
1,1
|
|
-3,45
|
3,95
|
1,2
|
|
-3,95
|
4,13
|
1,3
|
|
-4,45
|
4,24
|
1,4
|
|
-4,93
|
4,28
|
1,5
|
|
-5,38
|
4,25
|
1,6
|
|
-6,4
|
3,6
|
1,9
|
|
-6,59
|
3,19
|
2
|
|
-6,67
|
2,69
|
2,1
|
|
-6,64
|
2,08
|
2,2
|
|
-6,48
|
1,38
|
2,3
|
|
-6,16
|
0,57
|
2,4
|
|
-5,68
|
-0,33
|
2,5
|
|
-5,02
|
-1,32
|
2,6
|
|
-4,15
|
-2,4
|
2,7
|
|
-3,07
|
-3,56
|
2,8
|
|
-1,74
|
-4,79
|
2,9
|
|
-0,16
|
-6,09
|
3
|
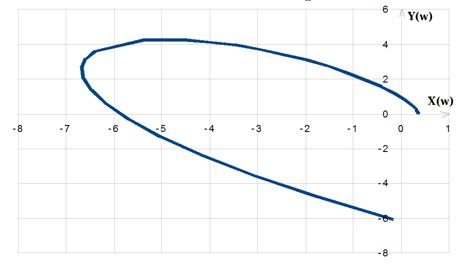
Рисунок 9. Характеристическая кривая
Характеристическая кривая последовательно проходит четыре квадранта
координатной плоскости (рис.11), следовательно, система устойчива.
Далее определим область допустимых значений стабилизирующего регулятора
(П-регулятора). Для расчета воспользуемся формулой:
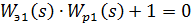 (23)
(23)
где 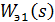 - передаточная функция эквивалентного объекта.
- передаточная функция эквивалентного объекта.
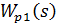 - передаточная функция П-регулятора
- передаточная функция П-регулятора
Из структурной схемы, представленной на рис.9, видно, что:
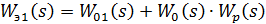 (24)
(24)
Величина W0(s)×Wp(s) оказывает незначительное влияние и поэтому
ей можно пренебречь, тогда:
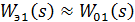 (25)
(25)
С учетом (25) выражение (23) примет вид:
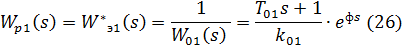
При расчёте параметров настройки П-регулятора используют следующую
расчетную формулу:
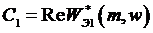 (27)
(27)
Подставив s=jw в (23) и выделив вещественную и мнимую части, получим:
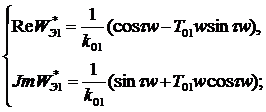
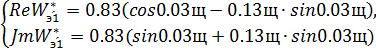
По полученным выражениям строим кривую D-разбиения П-регулятора (рис.10)
и определяем область с наибольшим количеством левых корней.
Таблица 5
|
ReW*Э1
|
JmW*Э1
|
w
|
|
0,83
|
0
|
0
|
|
0,82
|
0,27
|
2
|
|
0,77
|
0,53
|
4
|
|
0,7
|
0,79
|
6
|
|
0,6
|
1,04
|
8
|
|
0,47
|
1,28
|
10
|
|
0,32
|
1,5
|
12
|
|
0,14
|
1,72
|
14
|
|
-0,06
|
1,91
|
16
|
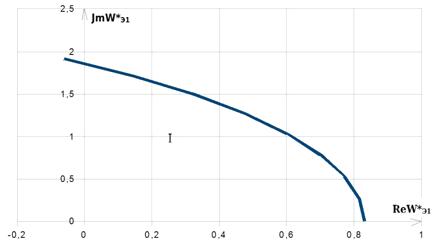
Рисунок 10 .Кривая D-разбиения для П- регулятора каскадной системы
Из графика видно, что областью допустимых значений является область I. А
параметры настройки П - регулятора лежат на оси.
6.Определение оптимальных настроек регуляторов
Рассмотрим последовательность расчета системы автоматического
регулирования на заданную степень затухания, если известны аналитические
выражения расширенных амплитудно-фазовых характеристик объектов и регулятора.
6.1 Расчет оптимальных настроек регулятора для одноконтурной
системы
Для определения оптимальных настроек ПИ-регулятора в одноконтурной
системе воспользуемся методом расширенных частотных характеристик.
Исходное уравнение расчета настройки регуляторов замкнутой автоматической
системы, как для одноконтурной, так и для каскадной системы, имеет вид:
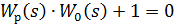
где 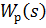 - передаточная функция регулятора;
- передаточная функция регулятора;
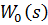 - передаточная функция объекта.
- передаточная функция объекта.
Выделим действительную и мнимую части:
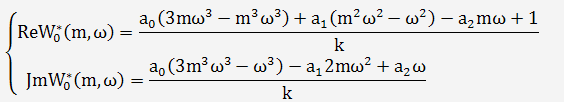
Для расчёта параметров настройки ПИ-регулятора используют расчетные
формулы(33), связывающие настроечные параметры регулятора с характеристиками W0*.
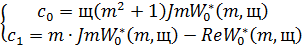
Степень затухания по условию равна: ψ=0.7
Используя формулу (34), находим значение m:
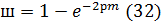
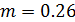
Подставив (32) и значение m в (33) получим:
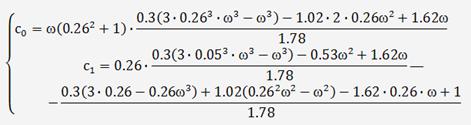
По найденным выражениям построим зависимость С0(С1),
которая при m=0 соответствует кривой D-разбиения, а при m=0.26 кривой по
которой определяются оптимальные параметры настройки ПИ-регулятора,
соответствующие заданной степени колебательности.
Таблица 6
|
w
|
C1
|
C0
|
|
0
|
-0,5
|
0
|
|
0,04
|
-0,489
|
0,001047
|
|
0,16
|
-0,25
|
0,015458
|
|
0,24
|
-0,12351
|
0,032384
|
|
0,32
|
-0,05776
|
0,052678
|
|
0,4
|
-0,00705
|
0,073674
|
|
0,48
|
0,047494
|
0,092232
|
|
0,56
|
0,104786
|
0,104736
|
|
0,64
|
0,163716
|
0,107095
|
|
0,72
|
0,223179
|
0,094744
|
|
0,768
|
0,258654
|
0,078195
|
|
0,88
|
0,33929
|
0,005275
|
|
0,887
|
0,34418
|
-0,00114
|
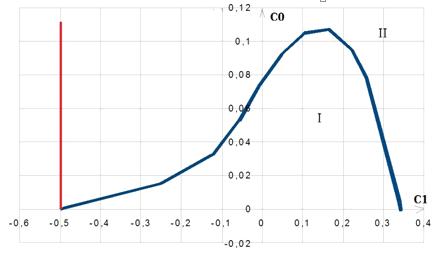
Рисунок 11. Кривая D-разбиения и кривая оптимальных настроек
одноконтурной системы
По рисунку 11 определяем оптимальные параметры настройки регулятора для
одноконтурной системы:
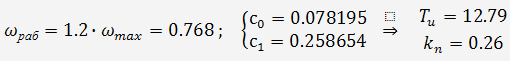
6.2 Расчет оптимальных настроек регуляторов для каскадной
системы
Также как и для одноконтурной системы воспользуемся методом расширенных
частотных характеристик. Определим оптимальные настройки корректирующего
контура. Так как в него включен ПИ-регулятор, то воспользуемся формулой (31):
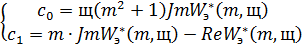
В этом случае обратная передаточная функция эквивалентного объекта:
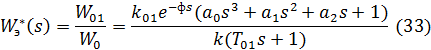
Подставим в (35) 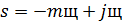 и определим вещественную и мнимую части обратной передаточной
функции эквивалентного объекта управления:
и определим вещественную и мнимую части обратной передаточной
функции эквивалентного объекта управления:
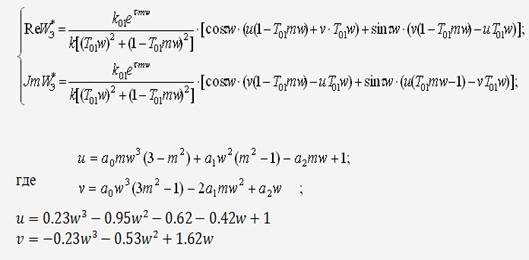
Тогда выражение (33) будет выглядеть следующим образом:
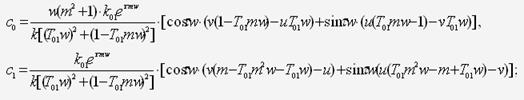

Строим зависимость с0(с1) при m=0.26:
Таблица
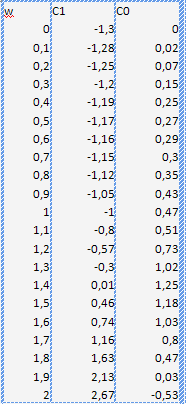
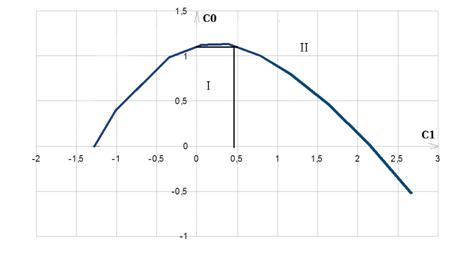
Рисунок 12 . Кривая D-разбиения и
кривая оптимальных настроек для
ПИ-регулятора каскадной системы
На
кривой оптимальной настройки в области устойчивости выбираем рабочую точку и
находим значения параметров 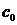 и
и 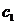 :
:
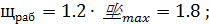
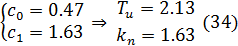
Определим оптимальные настройки стабилизирующего контура, в который
включен П-регулятор. Для этого воспользуемся формулой:
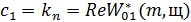 (35)
(35)
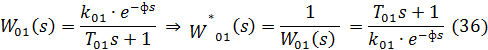
Подставив
в (35) 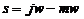 и выделив мнимую и вещественную части, получим:
и выделив мнимую и вещественную части, получим:
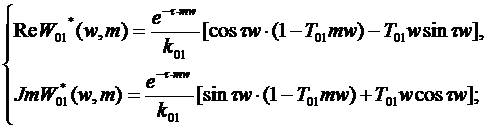
Строим
в одной координатной плоскости зависимость 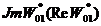 кривую
D-разбиения при m=0.26. На оси ReW01* внутри области устойчивости выбираем
настроечный параметр стабилизирующего П - регулятора:
кривую
D-разбиения при m=0.26. На оси ReW01* внутри области устойчивости выбираем
настроечный параметр стабилизирующего П - регулятора:
Таблица 8
|
w
|
JmW*Э1
|
|
0
|
0,83
|
0
|
|
1
|
0,8
|
0,13
|
|
2
|
0,75
|
0,26
|
|
3
|
0,7
|
0,38
|
|
4
|
0,64
|
0,5
|
|
5
|
0,58
|
0,61
|
|
6
|
0,51
|
0,72
|
|
7
|
0,44
|
0,83
|
|
8
|
0,36
|
0,93
|
|
9
|
0,28
|
1,02
|
|
10
|
0,19
|
1,11
|
|
11
|
0,1
|
1,19
|
|
12
|
0,01
|
1,27
|
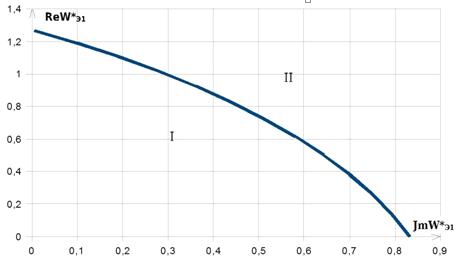
Рисунок 13. Кривая D-разбиения и кривая оптимальных настроек для П-регулятора каскадной
системы
7.Расчёт и построение переходных процессов
Для наглядности полученных результатов расчета одноконтурной и каскадной
систем, а также для определения показателей качества переходного процесса,
построим кривые переходных процессов для каждой из полученных систем. В
настоящее время существует большое количество прикладного программного
обеспечения, позволяющего моделировать любые виды переходных процессов с
заданными показателями качества, контролировать поведение системы, изменяя
любые параметры, производить проверку системы на работоспособность,
безопасность, устойчивость и т.д. К таким программам можно отнести Matlab,
пакет VisSim и т.д.
Для моделирования переходных процессов в данной курсовой работе будет
использован пакет VisSim.
7.1 Расчёт и построение переходного процесса в одноконтурной
системе управления
Как известно, для получения переходного процесса необходимо на вход
системы подать ступенчатое единичное воздействие. Переходный процесс в этом
случае определяется структурой объекта и параметрами регулятора.
На рис.15 представлена блок схема, для построения переходного процесса в
одноконтурной системе.
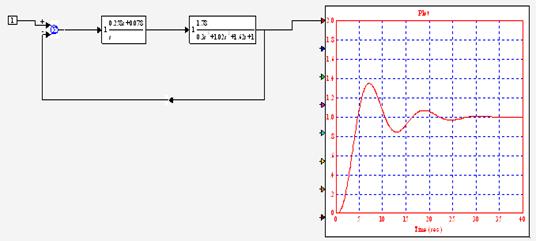
Рисунок 16. Модель одноконтурной системы
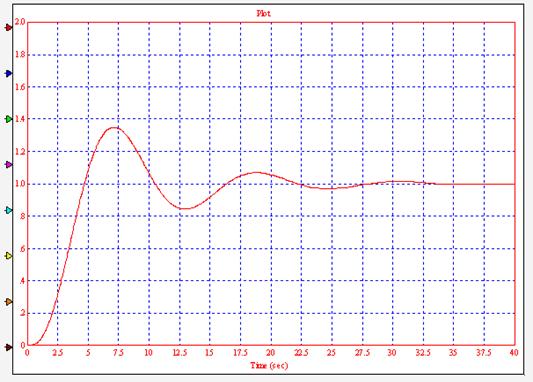
Рисунок 16. График переходного процесса в одноконтурной системе
Для оценки качества переходного процесса воспользуемся прямыми и
косвенными показателями качества.
1. Время переходного процесса tp определяется как промежуток
времени, через который величина сигнала войдет в зону допустимой ошибки 2ε, ε = 5%, по графику определяем tp
= мин;
2.
Перерегулирование 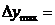 %;
%;
.
Колебательность - число колебаний за время переходного процесса - ;
4. Степень затухания;
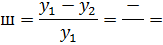
7.2 Расчёт и построение переходного процесса в каскадной
системе управления
На рис.17 представлена блок схема, для построения переходного процесса в
каскадной системе.
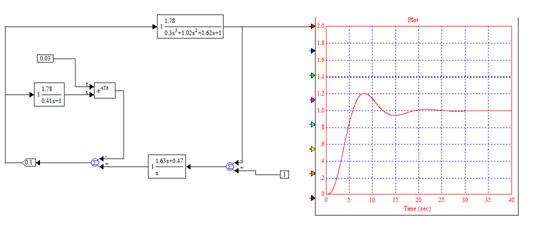
Рисунок 17. Блок-схема каскадной системы управления
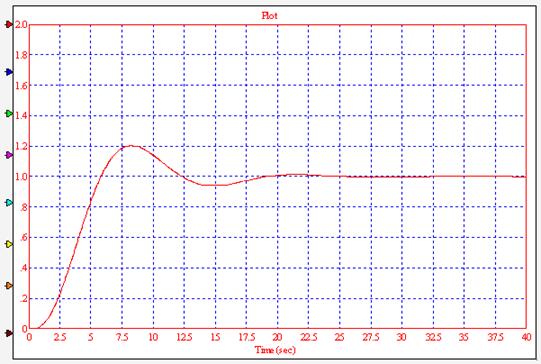
Рисунок
18. График переходного процесса в каскадной системе управления
Графически определим характеристики переходного процесса:
. Время переходного процесса tp = мин;
2.
Перерегулирование 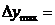 %;
%;
.
Колебательность - число колебаний за время переходного процесса - ;
.
Степень затухания
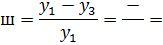
8. Выводы по результатам расчёта систем
На предприятиях химической промышленности большую роль играют
технологические установки, предназначенные для нагрева сырья , перед тем как
оно поступит на ректификацию и другие технологические процессы. Примером такого
объекта является трубчатая печь. От начальной температуры сырья зависит
качество и скорость последующих этапов переработки, что в плане экономии прежде
всего материальных ресурсов играет значительную роль.
В данной курсовой работе была разработана и рассчитана каскадная и
одноконтурная система автоматического управления температуры технологического
потока в трубчатой печи.
Для анализа систем регулирования были получены кривые оптимальных
настроек ПИ-регулятора для одноконтурной системы, ПИ- и П- регуляторов для
многоконтурной системы. В графическом виде найдены рабочие точки.
Построены графики переходных процессов с соблюдением заданной степени
затухания. По графикам переходных процессов для одноконтурной и каскадной
систем произведён сравнительный анализ качественных характеристик трубчатой
печи.
Очевидно, что по полученным данным можно с уверенностью утверждать, что
применение каскадной системы регулирования ведет к улучшению качественных
характеристик объекта регулирования, по сравнению со случаем применения
одноконтурной системы, которая по всем показателям качества уступает
многоконтурным.
К важным преимуществам каскадной системы в сравнении с одноконтурной
относятся:
· уменьшение времени переходного процесса почти в раза;
· снижение колебательности в раза;
· перерегулирования почти в раза;
· возможность более точного управления переходным процессом.
В результате полученных расчетных данных можно сделать вывод, что и
одноконтурная и каскадная системы регулирования полностью отвечают
предъявляемым к ним требованиям и имеют переходные характеристики сопоставимые
с характеристиками реально существующих систем управления.
Список использованной литературы
1. Завьялов В.Г. Методические указания к
курсовой работе по ТАУ.С.: СамГТУ, 2002г.
2. Воронова А.А. Теория линейных систем
автоматического управления. М.: Высшая школа, 1986г.
3. Полоцкий Л. М., Лапшенков Г. И.
Автоматизация химических производств. Теория, расчет и проектирование систем
автоматизации. М.: Химия, 1982.
4. Дудников Е.Г. Автоматическое
управление в химической промышленности. М.: Химия, 1987г.