Эквиваленты функций

Эквиваленты функций

Контрольная работа

Эквиваленты функций

Используя таблицу истинности, установить эквивалентность функций в формуле:

Решение:

Обозначим:

Составим таблицу истинности для правой и левой части функции:

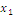
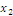
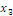
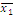
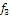
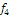
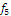
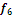
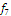
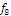
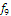
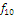
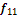
0	0	0	1	1	1	0	1	1	1	0	1	0	1	0	1	1
1	0	0	0	1	1	1	1	1	0	1	0	1	1	0	0	0
0	1	0	1	0	1	0	1	0	1	0	1	0	1	1	1	1
0	0	1	1	1	0	0	1	1	1	0	1	0	1	0	1	1
1	1	0	0	0	1	0	1	0	1	0	1	0	1	1	1	1
1	0	1	0	1	0	1	0	1	0	0	1	1	0	0	0	1
0	1	1	1	0	0	0	1	1	1	0	1	0	1	0	1	1
1	1	1	0	0	0	0	1	1	0	1	0	0	1	0	0	0

Ответ: Как видно из таблицы, значения правой и левой части равенства действительно совпадают, значит, функции в данной формуле эквивалентны.

Определить к каким классам (константы нуля, константы единицы, самодвойственных функций, монотонных функций, линейных функций, симметрических функций) относится функция следующего вида:

 

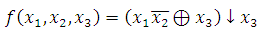
Обозначим:

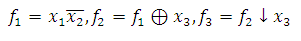
Решение:

1 Составим таблицу истинности:

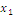
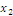
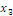
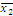
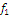
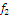
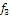
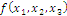
0	0	0	1	0	0	1	1
1	0	0	1	1	1	0	0
0	1	0	0	0	0	1	1
0	0	1	1	0	1	0	0
1	1	0	0	0	0	1	1
1	0	1	1	1	0	0	0
0	1	1	0	0	1	0	0
1	1	1	0	0	1	0	0

2 Т. к. f(0,0,0) ¹ 0, значит, данная функция не относится к классу константы 0.

3 Т. к. f (1,1,1) = 0, значит, данная функция относится к классу не сохраняющих константу 1.

4  Т. к. f(0,1,1) < f (0,1,0) и f(1,0,0) = f(0,1,1), значит, данная функция не относится к классу монотонных функций.

5  Т. к., например, f(0,0,0) ¹ f(1,1,1) или f(0,0,1) ¹ f(1,1,0), то данная функция относится к классу самодвойственных функций.

6 Т. к. не выполняется условие f(0,1,1) = f(1,0,1) = f(1,1,0) (значения соответственно равны 0,0,1), то данная функция не относится к классу симметрических функций.

7 Проверим принадлежность функции к классу линейных функций.

Для этого запишем ее в таком виде:

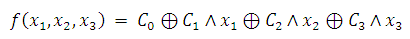
Найдем коэффициенты C_i :

f (0,0,0) = 1 (из таблицы истинности)

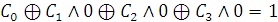, т.о., С₀ = 1.

f(1,0,0 )= 0 (из таблицы истинности)

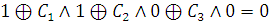, т.о., С₁ = 1.

f(0,1,0) = 1 (из таблицы истинности)

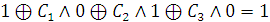, т.о., С₂ = 0.

f(0,0,1) = 0 (из таблицы истинности)

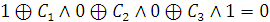,т.о., С₃ = 1.

Тогда f₁(x₁,x₂,x₃) = 1.

Сравним значения функций f и f₁ по таблице истинности:

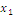
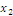
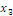
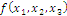
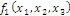
0	0	0	1	1
1	0	0	0	1
0	1	0	1	1
0	0	1	0	1
1	1	0	1	1
1	0	1	0	1
0	1	1	0	1
1	1	1	0	1

Т. к. значения функций различны для одинаковых наборов, то данная функция не относится к классу линейных функций.

Ответ: данная функция относится к классу константы 1.

Необходимо для данной ФАЛ f(x₁,x₂,x₃,x₄) найти ее ДСНФ, КСНФ, ПСНФ, ЭСНФ, ИСНФ, принимающей значение 1 на следующих наборах:

4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 15.

Решение:

1 Составим таблицу истинности:

№
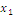
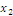
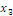
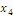
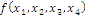
0	0	0	0	0	0
1	0	0	0	1	0
2	0	0	1	0	0
3	0	0	1	1	0
4	0	1	0	0	1
5	0	1	1	1
6	0	1	1	0	1
7	0	1	1	1	1
8	1	0	0	0	1
9	1	0	0	1	1
10	1	0	1	0	1
11	1	0	1	1	1
12	1	1	0	0	1
13	1	1	0	1	1
14	1	1	1	0	0
15	1	1	1	1	1

2 Для получения ДСНФ, ПСНФ используем термы для 1 значений функции:

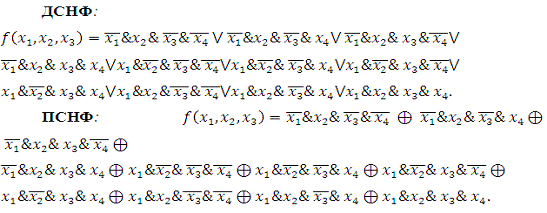
3 Для получения КСНФ, ЭСНФ используем термы для 0 значений функции:

 

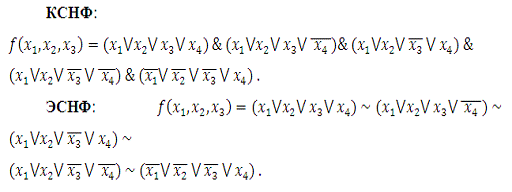
Используя метод неопределенных коэффициентов, необходимо найти МДНФ функции f(x1,x2,x3), принимающей значение 1 на наборах:

0, 3, 4, 7.

Решение:

1. Составим таблицу истинности:

№
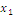
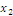
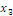
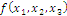
0	0	0	0	1
1	0	0	1	0
2	0	1	0	0
3	0	1	1	1
4	1	0	0	1
5	1	0	1	0
6	1	1	0	0
7	1	1	1	1

2.

К₁⁰ \/ К₂⁰ \/ К₃⁰ \/ К₁₂⁰⁰ \/ К₁₃⁰⁰ \/ К₂₃⁰⁰ \/ К₁₂₃⁰⁰⁰ = 1

К₁⁰ \/ К₂⁰ \/ К₃¹ \/ К₁₂⁰⁰ \/ К₁₃⁰¹ \/ К₂₃⁰¹ \/ К₁₂₃⁰⁰¹ = 0

К₁⁰ \/ К₂¹ \/ К₃⁰ \/ К₁₂⁰¹ \/ К₁₃⁰⁰ \/ К₂₃¹⁰ \/ К₁₂₃⁰¹⁰ = 0

К₁⁰ \/ К₂¹ \/ К₃¹ \/ К₁₂⁰¹ \/ К₁₃⁰¹ \/ К₂₃¹¹ \/ К₁₂₃⁰¹¹ = 1

К₁¹ \/ К₂⁰ \/ К₃⁰ \/ К₁₂¹⁰ \/ К₁₃¹⁰ \/ К₂₃⁰⁰ \/ К₁₂₃¹⁰⁰ = 1

К₁¹ \/ К₂⁰ \/ К₃¹ \/ К₁₂¹⁰ \/ К₁₃¹¹ \/ К₂₃⁰¹ \/ К₁₂₃¹⁰¹ = 0

К₁¹ \/ К₂¹ \/ К₃⁰ \/ К₁₂¹¹ \/ К₁₃¹⁰ \/ К₂₃¹⁰ \/ К₁₂₃¹¹⁰ = 0

К₁¹ \/ К₂¹ \/ К₃¹ \/ К₁₂¹¹ \/ К₁₃¹¹ \/ К₂₃¹¹ \/ К₁₂₃¹¹¹ = 1

3 Приравняем 0 все коэффициенты при 0 значениях функции:

К₁⁰ = К₂⁰ = К₃¹ = К₁₂⁰⁰ = К₁₃⁰¹ = К₂₃⁰¹ = К₁₂₃⁰⁰¹ = 0

К₁⁰ = К₂¹ = К₃⁰ = К₁₂⁰¹ = К₁₃⁰⁰ = К₂₃¹⁰ = К₁₂₃⁰¹⁰ = 0

К₁¹ = К₂⁰ = К₃¹ = К₁₂¹⁰ = К₁₃¹¹ = К₂₃⁰¹ = К₁₂₃¹⁰¹ = 0

К₁¹ = К₂¹ = К₃⁰ = К₁₂¹¹ = К₁₃¹⁰ = К₂₃¹⁰ = К₁₂₃¹¹⁰ = 0

4 Вычеркнем 0 коэффициенты из коэффициентов при 1 значениях функции:

К₂₃⁰⁰ \/ К₁₂₃⁰⁰⁰ = 1

К₂₃¹¹ \/ К₁₂₃⁰¹¹ = 1

К₂₃⁰⁰ \/ К₁₂₃¹⁰⁰ = 1

К₂₃¹¹ \/ К₁₂₃¹¹¹ = 1

5 Найдем минимальное покрытие: К₂₃⁰⁰ и К₂₃¹¹ ,т. е.

f₁(x₁,x₂,x₃) =

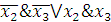
6. Проверка:

№
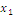
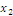
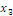
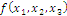
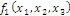
0	0	0	0	1	1
1	0	0	1	0	0
2	0	1	0	0	0
3	0	1	1	1	1
4	1	0	0	1	1
5	1	0	1	0	0
6	1	1	0	0	0
7	1	1	1	1	1

Т.к. f =f₁, то преобразования выполнены верно.

Ответ: f₁(x₁,x₂,x₃) =  .

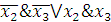Используя метод Квайна, необходимо найти МДНФ функции f(x₁,x₂,x₃,x₄), принимающей значение 1 на наборах: 3, 4, 5, 6, 13, 14, 15.

Решение:

1. Составим таблицу истинности:

 

№
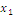
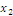
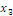
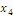
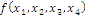
0	0	0	0	0	0
1	0	0	0	1	0
2	0	0	1	0	0
3	0	0	1	1	1
4	0	1	0	0	1
5	0	1	0	1	1
6	0	1	1	0	1
7	0	1	1	1	0
8	1	0	0	0	0
9	1	0	0	1	0
10	1	0	1	0	0
11	1	0	1	1	0
12	1	1	0	0	0
13	1	1	0	1	1
14	1	1	1	0	1
15	1	1	1	1	1

2 Выпишем термы для 1 значений функции и склеим все возможные:

1.  3.  4.  5.  6.  7.

3 Составим таблицу и найдем минимальное покрытие:

	1	2	3	4	5	6	7
		+	+
		+		+
			+		+
				+		+
					+		+
						+	+

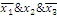
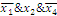
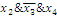
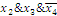
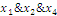
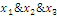
В данном случае следующие импликанты являются существенными:

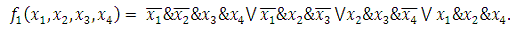
3  Проверка:

№
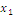
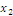
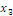
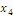
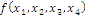
0	0	0	0	0	0	0
1	0	0	0	0	0
2	0	0	1	0	0	0
3	0	0	1	1	1	1
4	0	1	0	0	1	1
5	0	1	0	1	1	1
6	0	1	1	0	1	1
7	0	1	1	1	0	0
8	1	0	0	0	0	0
9	1	0	0	1	0	0
10	1	0	1	0	0	0
11	1	0	1	1	0	0
12	1	1	0	0	0	0
13	1	1	0	1	1	1
14	1	1	1	0	1	1
15	1	1	1	1	1	1

Т. к. f₁ = f, то преобразования выполнено верно.

Ответ:

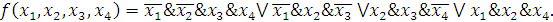
 Используя метод Квайна- Мак - Класки , необходимо найти МДНФ функции f(x₁,x₂,x₃,x₄), принимающей значение 1 на наборах: 2, 6, 7, 10 ,12 ,13 14, 15.

Решение:

1. Составим таблицу истинности:

№
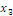
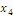
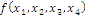
0	0	0	0	0	0
1	0	0	0	1	0
2	0	0	1	0	1
3	0	0	1	1	0
4	0	1	0	0	0
5	0	1	0	1	0
6	0	1	1	0	1
7	0	1	1	1	1
8	1	0	0	0	0
9	1	0	0	1	0
10	1	0	1	0	1
11	1	0	1	1	0
12	1	1	0	0	1
13	1	1	0	1	1
14	1	1	1	0	1
15	1	1	1	1	1

2 Составим группы по количеству единиц и выполним необходимые преобразования:

№
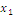
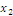
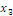
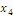
2	0	0	1	0	по 1 единице
6	0	1	1	0
10	1	0	1	0	по 2 единицы
12	1	1	0	0
7	0	1	1	1
13	1	1	0	1	по 3 единицы
14	1	1	1	0
15	1	1	1	1	по 4 единицы

1. 2. 3. 4. 5. 6. 7. 8. 9. 10.

(2,6) = 0_10 (2,10) = _010 (6,7) = 011_ (6,14) = _110 (10,14) = 1_10 (12,13) = 110_ (12,14) = 11_0 (7,15) = _111 (13,15) = 11_1 (14,15) = 111_

3 Составим таблицу и найдем минимальное покрытие:

	0010	0110	0111	1010	1100	1101	1110	1111
0_10	+	+
_010	+			+
011_		+	+
_110		+					+
1_10				+			+
110_					+	+
11_0					+		+
_111			+					+
11_1						+		+
111_							+	+

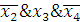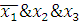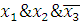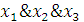Импликанты , ,  и являются существенными. Т. о., получаем:

.

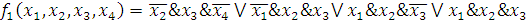4 Проверка:

№
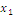
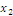
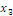
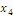
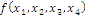
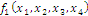
0	0	0	0	0	0	0
1	0	0	0	1	0	0
2	0	0	1	0	1	1
3	0	0	1	1	0	0
4	0	1	0	0	0	0
5	0	1	0	1	0
6	0	1	1	0	1	1
7	0	1	1	1	1	1
8	1	0	0	0	0	0
9	1	0	0	1	0	0
10	1	0	1	0	1	1
11	1	0	1	1	0	0
12	1	1	0	0	1	1
13	1	1	0	1	1	1
14	1	1	1	0	1	1
15	1	1	1	1	1	1

Т.к. f₁ = f, то преобразования выполнено верно.

Ответ:

 

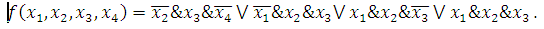
Используя метод диаграмм Вейча, необходимо найти МДНФ функции f(x₁,x₂,x₃,x₄), принимающей значение 1 на наборах: 0, 2, 4, 8, 12, 14, 15.

Решение:

1. Составим таблицу истинности:

 

№
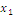
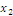
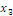
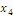
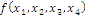
0	0	0	0	0	1
1	0	0	0	1	0
2	0	0	1	0	1
3	0	0	1	1	0
4	0	1	0	0	1
5	0	1	0	1	0
6	0	1	1	0	0
7	0	1	1	1	0
8	1	0	0	0	1
9	1	0	0	1	0
10	1	0	1	0	0
1	1	0	1	1	0
12	1	1	0	0	1
13	1	1	0	1	0
14	1	1	1	0	1
15	1	1	1	1	1

1. Для булевой функции 4-х переменных диаграмма Вейча имеет вид:

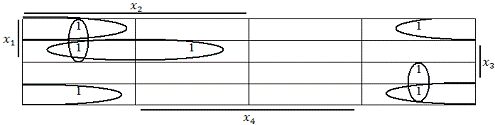
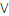
0000		0010	=	00_0
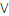
0000		0100	=	0_00
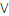
1100		1110	=	11_0
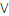
1100		1000	=	1_00
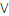
1111		1110	=	111_

Получаем:

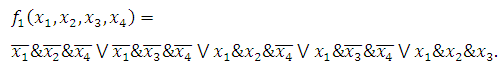
1. Проверка:

№
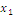
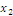
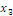
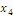
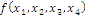
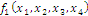
0	0	0	0	0	1	1
1	0	0	0	1	0	0
2	0	0	1	0	1	1
3	0	0	1	1	0	0
4	0	1	0	0	1	1
5	0	1	0	1	0	0
6	0	1	1	0	0	0
7	0	1	1	1	0	0
8	1	0	0	0	1	1
9	1	0	0	1	0	0
10	1	0	1	0	0	0
1	1	0	1	1	0	0
12	1	1	0	0	1	1
13	1	1	0	1	0	0
14	1	1	1	0	1	1
15	1	1	1	1	1	1

Т. к. f₁ = f, то преобразования выполнено верно.

Ответ:

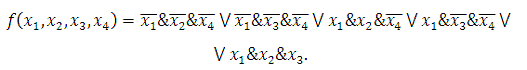
константа эквивалентность дизъюнктивная форма функция

Список использованной литературы

1.Гаврилов Г.П., Сапоженко А.А. Сборник задач по дискретной математике.- М.: Наука,1977.

.Горбатов В.А. Фундаментальные основы дискретной математики. Информационная математика. - М.: Наука. Физматлит, 2000.

.Информатика: Энциклопедический словарь для начинающих /Сост. Д.А. Поспелов. - М.: Педагогика - Пресс, 1994.

.Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. - М.: Энергоатомиздат,1988.

.Лихтарникова Л.М.,Сукачева Т.Г. Математическая логика / Курс лекций. - СПб. : Издательство «Лань», 1998.

.Логинов Б.М. Лекции и упражнения по курсу «Введение в дискретную математику». - Калуга: МГТУ им.Н.Э. Баумана, 1998.

.Нефедов В.Н., Осипова В.А. Курс дискретной математики: Учеб. пособие.-М.: Изд-во МАИ,1992.

.Савельев А.П. Прикладная теория цифровых автоматов. М.: Наука,1985.

.Фудзисава Т., Касами Т. Математика для радиоинженеров: Теория дискретных структур: Пер. с япон. - М.: Радио и связь,1984.

.Муха Ю.П., Авдеюк О.А., Скворцов М.Г. Математическая логика. Конспект лекций по теоретической информатике: Учеб. пособие/ ВолгГТУ.- Волгоград, 2001.

/ Муха Ю.П., Авдеюк О.А. Математическая логика и теория алгоритмов. Конспект лекций: Учеб. пособие/ ВолгГТУ.- Волгоград, 2005.