Развертки геометрических тел
Сибирский государственный университет
путей сообщения
Кафедра «Графика»
Развертки геометрических тел
Выполнил:
Давыденко Д.В.
Группа: Д-114
Руководитель:
Жидкова Е.В.
Новосибирск 2014
Введение
Разверткой поверхности геометрического тела называется плоская фигура,
которая получается в результате совмещения всех граней или всех поверхностей,
ограничивающих тело, с одной плоскостью.[1, электронный ресурс]
Поверхности некоторых геометрических тел криволинейной формы, например
шара и других поверхностей вращения, нельзя развернуть в одну плоскость. Для
развертки таких поверхностей используют способы приближенной развертки.
Построение разверток поверхностей представляет собой важную техническую
задачу и имеет большое практическое значение при конструировании различных
изделий из листового материала, так как в промышленности применяется много
конструкций в виде сосудов и трубопроводов, выполненных из листового материала
способом изгибания. Одним из важных этапов в проектировании таких конструкций
является построение разверток.
При этом необходимо отметить, что часто приходится изготовлять из
листового материала не только развертывающиеся, но и неразвёртывающиеся
поверхности (Поверхности, которые не могут быть наложены на плоскость без
складок и разрывов).
Признак развертываемости поверхности можно определить следующим образом:
поверхность будет развертывающейся, если касательная плоскость во всех точках
одной и той же ее прямолинейной образующей постоянна
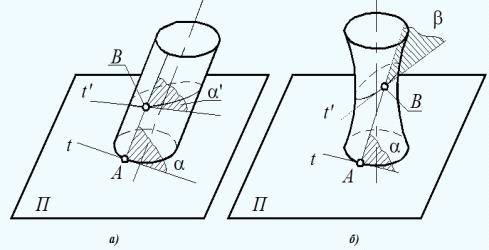
Рисунок 1 - Поверхности: а - развертывающаяся; б - неразвертывающаяся
К развертывающимся поверхностям относятся все многогранные поверхности.
Разверткой многогранной поверхности является плоская фигура, полученная
последовательным совмещением с одной и той же плоскостью всех ее граней.
Поэтому построение развертки многогранной поверхности сводится к
определению натуральной величины отдельных ее граней.
Это позволяет рассмотреть фигуру в натуральную величину со всех ракурсов
одновременно и произвести необходимые действия над ней с предельной точностью и
удобством для инженера. Именно поэтому развертки так широко применяются на
производстве.
Развертки геометрических тел
Если рассматривать поверхность и ее развертку как точечные множества, то
между этими двумя множествами устанавливается взаимно однозначное соответствие.
Значит, каждой точке на поверхности соответствует единственная точка развертки,
каждой линии соответствует линия на развертке и наоборот.[2, электронный
ресурс]
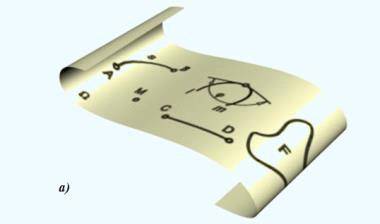
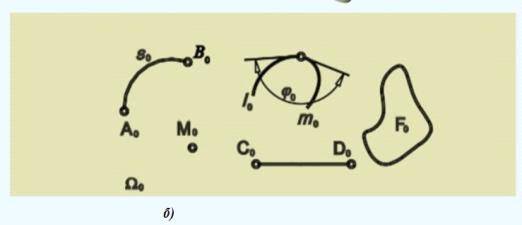
Получение развертки поверхности: а - поверхность; б - развертка
поверхности
Указанное взаимно однозначное соответствие обладает рядом весьма важных
свойств, которые заключаются в следующем:
• длины двух соответствующих линий развертки и поверхности равны между
собой;
• углы, образованные линиями на развертке, и углы между соответствующими
линиями на поверхности равны;
• замкнутая линия на поверхности и соответствующая ей линия на развертке
ограничивают одинаковую площадь.
Также необходимо отметить еще два важных свойства:
• прямая линия на поверхности переходит в прямую на развертке;
• параллельные прямые переходят тоже в параллельные прямые.
Развертка параллелепипеда
Параллелепипед и его развертка показаны на рисунке. Зная размеры: a, b, c,можно построить
развертку.(рисунок 2)
Возможны другие места присоединения сторон параллелепипеда на развертке
для экономного раскроя.
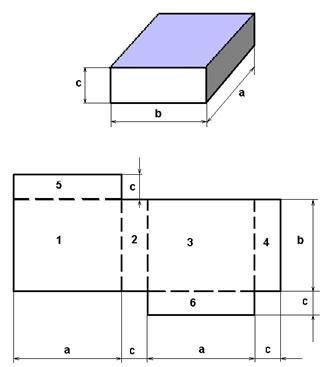
Рисунок 2
Развертка поверхности правильной пирамиды
Развертка поверхности правильной пирамиды представляет собой плоскую
фигуру, составленную из боковых граней - равнобедренных или равносторонних
треугольников и правильного многоугольника основания. Для примера взята
правильная четырехугольная пирамида.[3, электронный ресурс]
Чертеж развертки правильной пирамиды выполняется следующим образом
(рисунок. 3):
. Из произвольной точки S0, как из центра, проводят дугу окружности
радиуса L, равного длине бокового ребра пирамиды, так как в данном примере
ребра пирамиды являются линиями уровня.
. По этой дуге откладывают четыре отрезка, равных стороне основания
пирамиды, которое на ортогональном чертеже спроецировано в натуральную
величину, так как тоже является линией уровня.
. Найденные точки соединяют прямыми линиями с точкой S0.
. Получив, таким образом, развертку боковой поверхности, к основанию
одного из треугольников пристраивают квадрат, равный основанию пирамиды. .
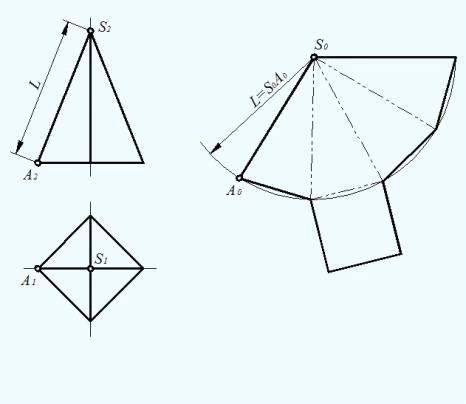
Рисунок 3
Развертка поверхности прямого кругового конуса
Развертка поверхности прямого кругового конуса представляет собой плоскую
фигуру, состоящую из кругового сектора и круга.
Чертеж развертки прямого кругового конуса выполняется следующим образом
(рисунок 4):
. Провести осевую линию и из точки S0, взятой на ней, как из центра,
проводят дугу окружности радиусом L, равным образующей конуса.
. Рассчитать угол сектора по формуле: 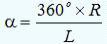 , где R - радиус окружности основания
конуса, L - длина образующей конуса.
, где R - радиус окружности основания
конуса, L - длина образующей конуса.
. Полученный угол расположить симметрично относительно осевой линии с
вершиной в точке S0.
. К полученному сектору пристроить круг с центром на осевой линии и
диаметром, равным диаметру основания конуса.
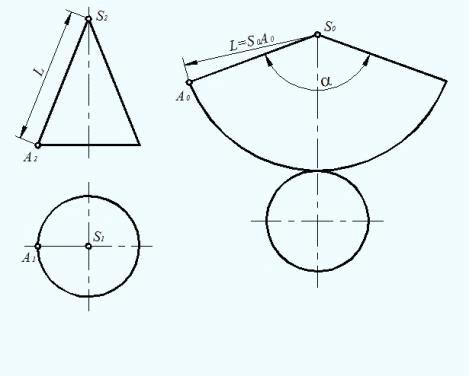
Рисунок 4
Развертка поверхности прямого кругового цилиндра
Развертка поверхности прямого кругового цилиндра представляет собой
плоскую фигуру, состоящую из прямоугольника и двух кругов (рисунок 5). Одна
сторона прямоугольника равна высоте цилиндра, другая - длине окружности
основания. Длину окружности можно определить по формуле C=πD,
где D - диаметр
окружности основания.
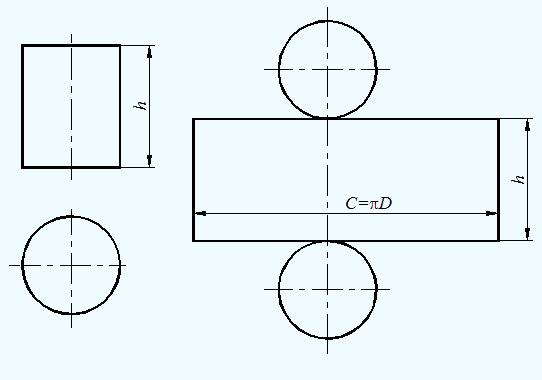
Рисунок 5
Развертка правильной призмы
Правильная призма и ее развертка показаны на рисунке. Зная размеры a, H, можно построить развертку.(рисунок 6; 6.1)
Возможны другие места присоединения оснований призмы 7, 8 на развертке
для экономного раскроя.
Основания представляют собой правильные n - угольники.
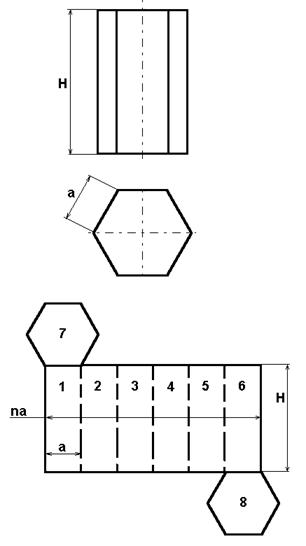
Рисунок 6

Рисунок 6.1
Развертка прямого эллиптического цилиндра
Прямой эллиптический цилиндр и его развертка показаны на рисунке. Зная
размеры H, a и b.(рисунок
7)
можно построить развертку. Основания - 2 эллипса. Развертка представляет
собой прямоугольник со сторонами H и L.
L = al1, где а - большая полуось; l1 - длина эллипса при а = 1. Значения
l1 даны в таблице в зависимости от
Отношения b/a.
Рисунок 7
Способ нормального сечения
развертка поверхность чертеж сечение
Способ нормального сечения заключается в том, что цилиндр или призма
пересекаются плоскостью, перпендикулярной образующим цилиндра или ребрам
призмы.
Способ нормального сечения применяется в том случае, если основание
призмы не является плоскостью уровня, а основание цилиндра - окружностью.
Строится сечение цилиндра или призмы этой плоскостью и определяется его
натуральная величина. Затем сечение спрямляется, и перпендикулярно спрямленному
нормальному сечению проводятся прямые, соответствующие образующим цилиндра или
ребрам призмы, и на этих прямых откладываются натуральные величины образующих
или ребер.
Соединив концы образующих или ребер плавной кривой или ломаной линией,
получают развертку боковой поверхности цилиндра или призмы.
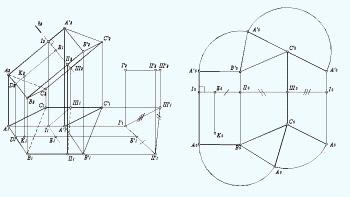
Рассмотрим применение этого способа для призматических поверхностей на
примере треугольной призмы, ребра которой являются фронтальными линиями уровня
(рис. 155).
Так как боковые ребра призмы являются фронтальными линиями уровня, они
проецируются на фронтальную плоскость проекций в натуральную величину. Тогда
фронтально - проецирующая плоскость δ(δ2), перпендикулярная к боковым ребрам,
определит нормальное сечение I-II-III призмы. Способом плоскопараллельного
движения определена его натуральная величина I'1-II'1-III'1.
Для построения развертки призмы строится спрямленное нормальное сечение
I0-II0-III0. Для этого нужно отложить на произвольной прямой натуральные
величины сторон нормального сечения, а затем через точки I0, II0 и III0 нужно
провести прямые, перпендикулярные к этой прямой. На этих прямых откладываются
натуральные величины ребер:
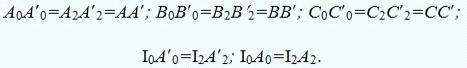
Затем точки A0, B0, C0, A0 и точки A'0, B'0, C'0, A'0 соединяются прямыми
линиями. К полученной развертке боковой поверхности призмы пристраиваются
натуральные величины двух ее оснований:
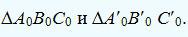
Если боковые ребра данной призмы занимают произвольное расположение
относительно плоскостей проекций, то нужно предварительно преобразовать их в
линии уровня.
Рассмотрим построение разверток цилиндрических поверхностей на примере
построения развертки боковой поверхности кругового цилиндра, ось i которого
является фронтальной линией уровня.
Так же, как и в случае призмы, построено нормальное сечение цилиндра фронтально
- проецирующей плоскостью α(α2), перпендикулярной оси цилиндра и
определена его натуральная величина - окружность радиусом r. Эта окружность
разбита на шесть равных частей точками I, II, III, IV, V и VI. Далее строится
спрямленное нормальное сечение I0-II0-III0-IV0-V0-VI0-I0, длина которого равна
2πr.
Через точки
I0,II0,III0,IV0,V0,VI0 и I0проводятся прямые, перпендикулярные спрямленному
нормальному сечению, и на них откладываются натуральные величины образующих
цилиндра:
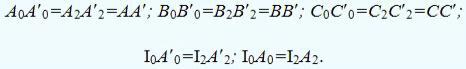
Точки A0, B0, C0…и точки A'0, B'0, C'0…соединяются плавными кривыми
линиями, которые будут развертками верхнего и нижнего оснований цилиндра.
Если образующие цилиндра являются прямыми общего положения, то следует
преобразовать их так, чтобы они стали линиями уровня.
 <#"816060.files/image016.jpg"> <#"816060.files/image017.jpg">
<#"816060.files/image016.jpg"> <#"816060.files/image017.jpg">
Натуральная
величина основания пирамиды определена способом замены плоскостей проекций:
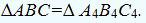
После
этого строится развертка боковой поверхности пирамиды и к ней пристраивается
треугольник основания для получения полной развертки поверхности наклонной
пирамиды. Положение точки S0 выбирается произвольно:
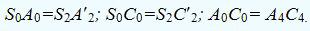
Рассмотрим
построение разверток конических поверхностей. Для построения развертки способом
триангуляции коническую поверхность заменяют вписанной в нее поверхностью
пирамиды.
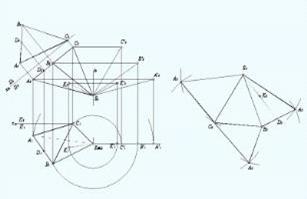
Подробнее
рассмотрим применение этого способа для построения разверток конических
поверхностей на примере эллиптического конуса с круговым основанием (рисунок
8).
 <#"816060.files/image021.jpg">
<#"816060.files/image021.jpg">
Рисунок
8
Построение
развертки наклонного конуса способом триангуляции
Коническая
поверхность заменяется поверхностью вписанной шестиугольной пирамиды. Основание
конуса точками I, II, III,… разбито на шесть частей. Так как коническая
поверхность имеет плоскость симметрии α(α1)⊥ П1, то можно построить развертку только одной
половины поверхности. Таким образом, поверхность разбита на ряд примыкающих
один к другому треугольников с общей вершиной S: ∆ S-I-II, ∆
S-II-III, ∆ S-III-IV,…Каждый из этих треугольников строится по трем
сторонам, при этом две стороны равны натуральным величинам образующих, а третья
- хорде, стягивающей дугу окружности основания между соседними точками деления.
Для определения натуральных величин этих треугольников способом вращения вокруг
оси i(i1,i2) построены натуральные величины их сторон - образующих конуса:

Стороны
I-II, II-III, III-IV,…изображаются на П1 в натуральную величину, так как основание
конуса лежит в горизонтальной плоскости уровня.
Для
построения развертки положение точки S0 выбирается произвольно, а каждый
треугольник строится по трем сторонам:
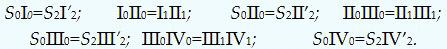
После
этого построена развертка боковой поверхности конуса - фигура S0-I0-II0-…-I0,
при этом точки I0, II0,…I0 соединены плавной кривой линией, являющейся
разверткой окружности основания.


Развертки
неразвертывающихся поверхностей
Все поверхности вращения, за исключением конуса и цилиндра вращения,
являются неразвертывающимися поверхностями, поэтому могут быть построены лишь
их условные развертки.
Общий прием построения условных разверток поверхностей вращения
заключается в следующем: поверхность разбивают, обычно плоскостями, на ряд
частей. Каждую часть заменяют приближающейся к ней наилучшим образом
развертывающейся поверхностью, обычно цилиндрической или конической.
На этом основаны два способа построения условных разверток поверхностей
вращения: способ цилиндров и способ конусов.
Способ цилиндров
Способ цилиндров состоит в том, что данную поверхность вращения разбивают
с помощью меридианов на сравнительно узкие, равные между собой доли, затем
каждую такую долю заменяют описанной цилиндрической поверхностью, которая
касается данной поверхности в точках среднего меридиана доли. Границами
цилиндрической поверхности будут плоскости меридианов, ограничивающих
рассматриваемую долю.
Рассмотрим применение этого способа для построения развертки поверхности
сферы.
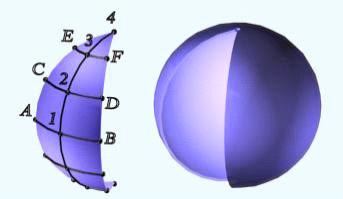
Разбить сферу при помощи меридианов на шесть равных частей (рис. 160). Каждая
из образовавшихся частей проецируется на П1 в виде сектора I1-41-II1.
Рассмотрим построение условной развертки одной части сферы, средним меридианом
которой является главный меридиан l. Прежде всего, эту часть сферы заменяют
цилиндрической поверхностью Ф(Ф1,Ф2), описанной около нее.бразующие
цилиндрической поверхности, ось которой q(q1,q2)⊥ П2, являются
фронтально-проецирующими прямыми. Горизонтальной проекцией этого
цилиндрического элемента является треугольник ∆A1B1O1, а фронтальной
проекцией - контур сферы. На рисунке показано наглядное изображение цилиндра,
заменяющего часть сферы.
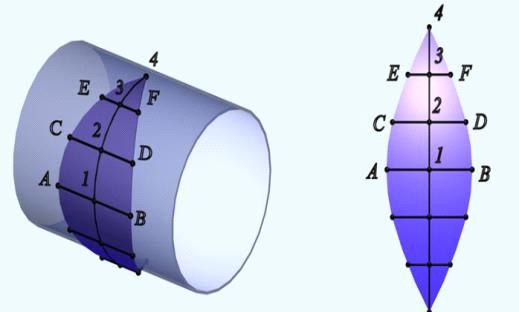
Для построения развертки этой цилиндрической поверхности (лепестка)
фронтальную проекцию l2 главного меридиана нужно разделить на шесть равных
частей точками 1, 2, 3, 4… и провести через точки деления горизонтальные
проекции образующих цилиндрической поверхности. Затем меридиан нужно
«выпрямить», то есть дуги 1-2, 2-3, 3-4 заменить хордами 12-22, 22-32, 32-42.
Для этого на плоскости П1 через точки 1, 2, 3, 4 провести дуги в пределах одной
доли и заменить длину каждой дуги соответствующей касательной A1B1, C1D1, E1F1.
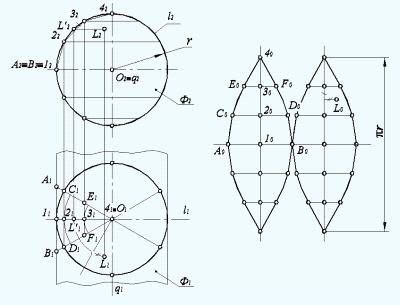
Для построения развертки одной из шести долей в произвольном месте
провести вертикальную ось симметрии и отложить на ней отрезки 12-22, 22-32,
32-42 с плоскости П2, то есть длину очерковой образующей, замененную хордами:
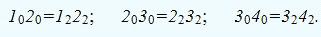
Через точки 10, 20, 30, 40 провести горизонтальные линии и отложить на
них следующие отрезки:
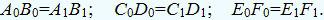
Соединив полученные точки плавной кривой линией, получают развертку одной
доли данной сферы, равной 1/6 ее части. Развертки остальных долей являются
повторением первой. Обычно сферу, как и любую другую поверхность вращения,
разбивают на двенадцать и более частей для получения более точной развертки.
 <#"816060.files/image032.jpg">
<#"816060.files/image032.jpg">
Рисунок
9
Построение
развертки кольца способом цилиндров
.
Поверхность кольца разделить фронтально-проецирующими плоскостями β(β2),δ(δ2)…
на равные части. В итоге вся поверхность
кольца разбивается на двенадцать равных частей, из которых на рис 161 показаны
только три.
Каждая
из частей заменяется поверхностью прямого кругового цилиндра, диаметр которого
равен диаметру сечения кольца.
.
Построить окружность - натуральную величину нормального сечения и разделить ее
на шесть равных частей точками 0,1, 2, 3, 4, 5, 6. Перенести эти точки на
плоскость (торец) тора и провести через них дуги окружности в пределах одной
доли (части). Заменить длины дуг длинами их касательных: AB(A2B2), CD(C2D2),
EF(E2F2), GH(G2H2), KL(K2L2), MN(M2N2) и PQ(P2Q2). Таким образом, ширина
развертки приравнивается к сумме длин касательных.
.
На произвольной вертикальной (или горизонтальной) линии отложить длины хорд
01-11=0010, 11-21=1020, 21-31=2030, 31-41=3040, 41-51=4050, 51-61=5060, то есть
ширина развертки приравнивается к сумме длин касательных.
.
Через эти точки деления 00, 10, 20, 30, 40, 50, 60 провести перпендикуляры, на
которых отложить следующие отрезки:
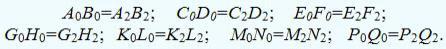
.
Соединить полученные точки, для построения развертки одной доли кольца.
Нанесение
на развертке поверхности кольца произвольных точек производится точно так же,
как и в случае нанесения точек на развертке сферы.
На
рисунке 9 показано построение на развертке точки S, принадлежащей поверхности
кольца (равенство соответствующих отрезков обозначено специальными значками).
Способ
конусов
Способ
конусов заключается в замене поверхности вращения другой поверхностью,
состоящей из конусов, вписанных в данную поверхность. Таким образом,
поверхность вращения оказывается разделенной на несколько частей (поясов),
каждая из которых заменена конусом.
Рассмотрим
построение развертки способом конусов на примере поверхности вращения
произвольного вида (рисунок 9,10).
Данную
поверхность разделить плоскостями α(α2) и α'(α'2), перпендикулярными оси поверхности, на три части - I, II, III. Заменить
каждую из них прямым конусом: I - конусом с вершиной в точке S(S2), II -
усеченным конусом с вершиной в точке O(O2), III - усеченным конусом с вершиной
в точке O'(O'2). Таким образом, построение развертки сводится к построению
разверток трех конусов.
Для
построения развертки точка S0 выбирается произвольно. Очевидно, что длины дуг,
имеющих радиусы R4 и R3 и радиусы R2 и R1 равны. Точки O0 и O'0 выбирают так,
чтобы развертки конусов касались друг друга.
Следовательно,
можно сделать вывод, что некоторые окружности на поверхности оказались линиями
разрывов на ее развертке, и, таким образом, в данном случае, нарушено одно из
основных свойств развертки. Это можно видеть на развертках всех
неразвертывающихся поверхностей.
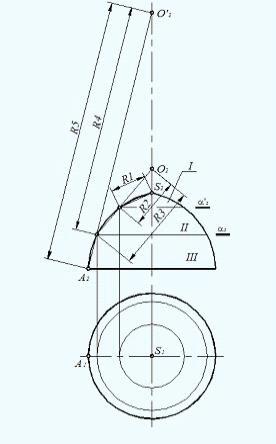
Рисунок
9
Разбиение
поверхности вращения произвольного вида на конусы
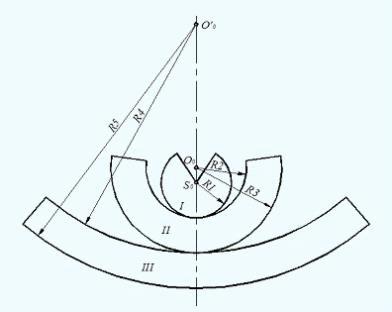
Рисунок
10
Построение
развертки кольца способом конусов
Заключение
Инженерная
графика, а следовательно и всё инженерное производство основывается на основных
видах разрабатываемого предмета [4, с.34].
Построение
основных видов предмета осуществляется при помощи разверток. Предмет мысленно
помещается внутрь куба и проецируется на 6 его граней. Далее выполняется
развертка куба и получается 6 основных видов.
Распределение
видов по ГОСТу
Основываясь на это, мы можем утверждать, что развертки геометрических тел
являются одной из важнейших частей конструирования и производства.
Список литературы
1. С.Ю
Попов Оформления чертежей и геометрические построения [Электронный ресурс] URL:
http://прораб.com.ua/19-razvertki-poverxnostej-geometricheskix-tel ( Дата
обращения 05.04.2014)
2. Архитектура
2005 [Электронный ресурс] URL: http://rx-fly.ru/architecture/drawing/22-chertezhi-razvertok-poverhnostey-geometricheskih-tel.html:(Дата
обращения 05.04.2014)
3. И.Ю.
Скоболёва Начертательная геометрия 2009 [Электронный ресурс] URL: http://cdot-nntu.ru/basebook/ng1/system/teor/teor74.html
:(Дата обращения 05.04.2014)
. Вольхин
К.А. Инновационные технологии в инженерной графике. Проблемы и перспективы.
2014 (с. 34)