Почти возрастающая функция
Почти возрастающая функция
Определение: Функция f(x) на отрезке [a, b] называется почти возрастающей на этом отрезке, если существует C>0: для любых 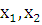 принадлежащих [a, b]:
принадлежащих [a, b]: 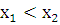 => f (
=> f ( ≤
≤ 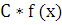
Утверждение 1. Рассмотрим монотонно убывающую и непрерывную на [a, b] функцию f(x). Функция f(x) монотонно убывает на [a, b] тогда существует постоянная константа C = 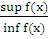 на промежутке [a, b] причем inf f(x)>0.
на промежутке [a, b] причем inf f(x)>0.
Доказательство: По определению почти возрастающей функции должна существовать C (C-const) что f (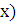 ≤
≤ 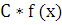 . Очевидно, что C=
. Очевидно, что C=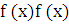 то есть, f (
то есть, f (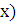 ≤
≤
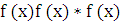 .
.
Пусть 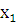 =a,
=a, 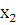 =b, так как
=b, так как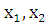 принадлежат [a, b]. Так как функция f(x) монотонно убывает на [a, b] то sup f(x) будет достигаться на левой границе [a, b], inf f(x) достигается на правой границе. => f(a)=sup f(x) на [a, b], f(b)=inf f(x), так как C=
принадлежат [a, b]. Так как функция f(x) монотонно убывает на [a, b] то sup f(x) будет достигаться на левой границе [a, b], inf f(x) достигается на правой границе. => f(a)=sup f(x) на [a, b], f(b)=inf f(x), так как C=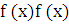 то
отсюда следует, что C =
то
отсюда следует, что C = 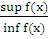 . Тем самым найдено
постоянное c.
. Тем самым найдено
постоянное c.
Докажем что inf f(x)>0. Предположим противное, пусть
inf f(x) ≤0, то и f(b) 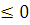 так
как f(a)=sup f(x), f(b)=inf f(x), по определению существует C>0 такое что f(
так
как f(a)=sup f(x), f(b)=inf f(x), по определению существует C>0 такое что f(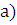 ≤
≤ 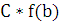 , так
как функция f(x) монотонно убывает и непрерывна на [a, b], то f(a) ≤
, так
как функция f(x) монотонно убывает и непрерывна на [a, b], то f(a) ≤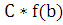 только
тогда, когда С<0. Противоречие с тем что С>0. Отсюда следует inf f(x)>0.
только
тогда, когда С<0. Противоречие с тем что С>0. Отсюда следует inf f(x)>0. 
Утверждение 2. Рассмотрим монотонно убывающую и непрерывную на интервале (a,+∞) функцию f(x). Пусть функция ограничена снизу М
такое, что f(x)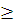 M и M>0. Тогда если функция f(x) имеет конечный предел при x
M и M>0. Тогда если функция f(x) имеет конечный предел при x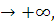 то inf f(x) будет равен этому пределу.
то inf f(x) будет равен этому пределу.
Доказательство. Допустим, что функция f(x) ограничена снизу, то есть, ограничена снизу множество {f(x)} значений функций. Тогда для этого
множества существует конечная точная нижняя грань A (A=inf f(x)). Докажем. Что это число А и будет
искомым пределом. Существует 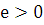 , по
свойству точной нижней грани, найдем такое значение x’>a, что f(x)<A+
, по
свойству точной нижней грани, найдем такое значение x’>a, что f(x)<A+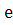 так как функция монотонная для x<x’ => f(x)< A+
так как функция монотонная для x<x’ => f(x)< A+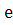 с другой стороны A-
с другой стороны A-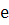 <A
<A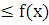 => выполняется неравенство |f(x) - A|<
=> выполняется неравенство |f(x) - A|<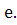
Утверждение 3. Для того чтобы монотонно убывающая и непрерывная на интервале (a,+∞) функция f(x) почти возрастала необходимо чтобы inf f(x) >0
Доказательство: Аналогично доказательству для монотонно убывающей на [a, b] функции f(x). 
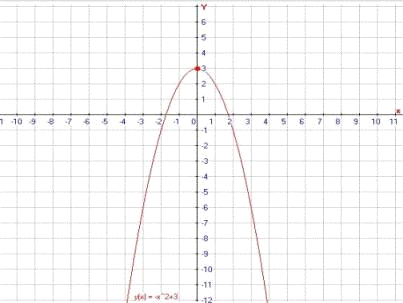
Пример 1: Рассмотрим функцию f(x)=-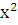 +3 на
промежутке от [0,1] существует С>0
+3 на
промежутке от [0,1] существует С>0 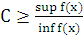 . На промежутке [0,1] sup f(x)=3, inf f(x)=2 => C
. На промежутке [0,1] sup f(x)=3, inf f(x)=2 => C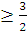
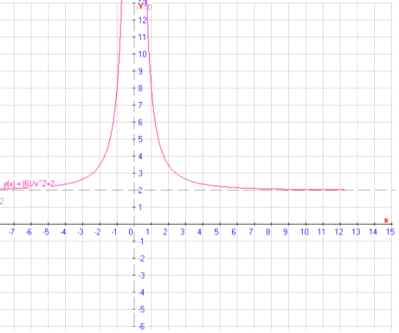
Пример 2: Рассмотрим функцию f(x)=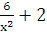 на
промежутке от (1,
на
промежутке от (1,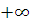 )
функция ограничена снизу М>0, так как существует предел
этой функции и M>0, то существует
)
функция ограничена снизу М>0, так как существует предел
этой функции и M>0, то существует 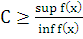 . Очевидно что на промежутке (1,
. Очевидно что на промежутке (1,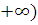 sup f(x)=8, а для того чтобы найти inf f(x) необходимо найти предел этой
функции.
sup f(x)=8, а для того чтобы найти inf f(x) необходимо найти предел этой
функции. 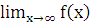 =
=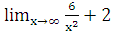 =2. inf f(x)>0 Таким образом,
=2. inf f(x)>0 Таким образом, 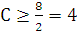 .
.
Утверждение 4. Пусть функция f(x):  непрерывна и дифференцируема на всем промежутке [a, b] путь далее существует
непрерывна и дифференцируема на всем промежутке [a, b] путь далее существует 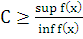 . Для того чтобы найти inf f(x) и sup f(x) на промежутке [a, b] необходимо найти точки экстремума и вычислить значения функции в
этих точках. То есть:
. Для того чтобы найти inf f(x) и sup f(x) на промежутке [a, b] необходимо найти точки экстремума и вычислить значения функции в
этих точках. То есть:
1) Найти f ′(x)
) Найти точки, в которых f ′(x)=0
или f ′(x) не существует, и отобрать из них те, что лежат внутри отрезка [a.b];
3) Вычислить значения функции f(x)
в точках, полученных в пункте 2, и на концах отрезка и выбрать из них
наибольшее и наименьшее; они и будут соответственно sup f(x) и inf f(x) для функции f(x) на отрезке [a, b].
Следствие: Для того чтобы вычислить inf f(x) и sup f(x) необходимо, чтобы существовали
точки экстремума.
Теорема. (необходимое условие существования экстремума) Если функция f(x) дифференцируема в точке х = х1
и точка х1 является точкой экстремума, то производная функции
обращается в нуль в этой точке.
Тогда при достаточно малых
положительных Dх>0 верно неравенство:
f(x1+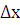 )<f(x), то есть f(x1+
)<f(x), то есть f(x1+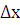 ) - f(x)<0. Тогда
) - f(x)<0. Тогда 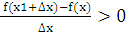 при
при 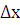 <0
<0
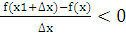 при
при 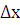 >0
>0
По определению: 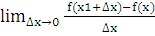 =f(x1) т.е. если х0, но х<0,
то f(x1) 0, а если х0, но х>0, то f(x1) 0.
=f(x1) т.е. если х0, но х<0,
то f(x1) 0, а если х0, но х>0, то f(x1) 0.
А возможно это только в том случае,
если при х0 f(x1) = 0.
Для случая, если функция f(x) имеет в точке х2
минимум теорема доказывается аналогично.
Теорема. (Достаточные условия существования экстремума)
Пусть функция f(x) непрерывна в интервале [a, b], и дифференцируема во всех точках
этого интервала. Если при переходе через точку х1 слева направо
производная функции f¢(x) меняет знак с «+» на «- «, то в
точке х = х1 функция f(x) имеет максимум, а если производная меняет знак с «- «на «+» - то
функция имеет минимум.
Доказательство.
Пусть 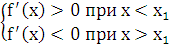
По теореме Лагранжа: f(x) - f(x1) = f¢(e) (x - x1), где x < e < x1.
Тогда: 1) Если х < x1, то e < x1; f¢(e)>0; f¢(e) (x - x1)<0, следовательно
f(x) - f(x1)<0 или f(x) < f(x1).
) Если х > x1, то e > x1 f¢(e)<0; f¢(e) (x - x1)<0, следовательно
f(x) - f(x1)<0 или f(x) < f(x1).
Т. к. ответы совпадают, то можно
сказать, что f(x) < f(x1) в любых точках вблизи
х1, т.е. х1 - точка максимума.
Доказательство теоремы для точки
минимума производится аналогично.
Утверждение 5: Пусть функция f(x): 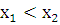 непрерывна
и дифференцируема на промежутке (a,+
непрерывна
и дифференцируема на промежутке (a,+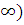 пусть, далее, функция f(x) ограничена снизу М такое, что f(x)
пусть, далее, функция f(x) ограничена снизу М такое, что f(x)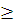 M>0. Пусть так же существует
предел этой функции при x
M>0. Пусть так же существует
предел этой функции при x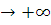 . Для того чтобы найти inf f(x) необходимо найти предел функции f(x) при x
. Для того чтобы найти inf f(x) необходимо найти предел функции f(x) при x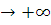 . Sup f(x) находиться из условия нахождения
точки максимума.
. Sup f(x) находиться из условия нахождения
точки максимума.
Если предел функции равняется
бесконечности, то необходимо найти точки минимума и найти наименьшее значение в
этих точках.
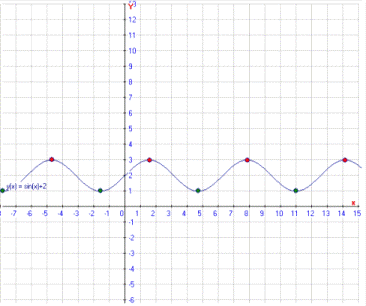
Пример 3: Рассмотрим функцию f(x)=sin x+2 на промежутке от (1,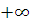 )
)
возрастающий
функция дифференцируемость
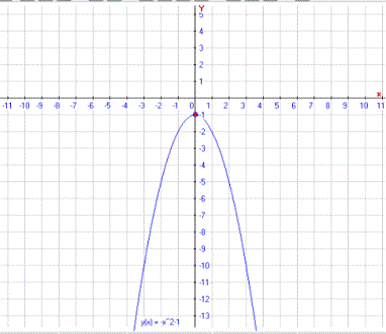
Пример 4: Рассмотрим функцию f(x)=-x2-1. На промежутке (0,+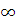 ) данная функция не является почти возрастающей, так как она не
ограничена и не существует точная нижняя грань.
) данная функция не является почти возрастающей, так как она не
ограничена и не существует точная нижняя грань.
Пример 5: Рассмотрим функцию f(x)=5. По определению почти возрастающей функции существует C>0: для любых 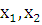 принадлежащих [a, b]:
принадлежащих [a, b]: 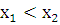 => f (
=> f ( ≤
≤ 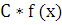 . Здесь inf f(x) = sup f(x) Очевидно, что C
. Здесь inf f(x) = sup f(x) Очевидно, что C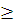 1.
Рассмотри данную функцию на промежутке от [0,3] пусть
1.
Рассмотри данную функцию на промежутке от [0,3] пусть 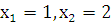 значение функции в этих точках равна 5. Отсюда следует f (
значение функции в этих точках равна 5. Отсюда следует f (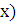 ≤
≤ 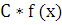 то
есть f(
то
есть f(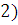 ≤
≤
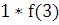 => 5=5.
=> 5=5.
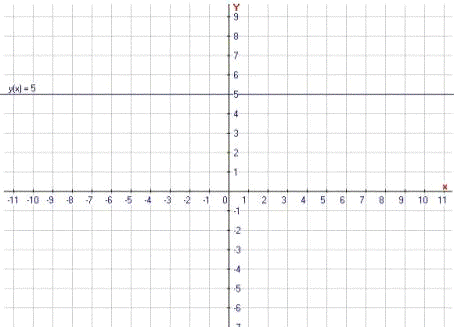
Следствие: Для того чтобы
существовала почти возрастающая функция для функции f(x) необходимо чтобы функция f(x) была ограничена снизу
положительным числом, и имел inf f(x)>0.