Дискретная математика

Дискретная математика

1. Дано: универсальное множество U и X, Y, Z Í U.

U = {a, b, c, d} X = {a, c} Y = {a, b, d} Z = {b, c};

Найти: a) (XÈZ)Ç`Y   b)`X ÇY    c) X \ (`ZÈY);

Решение:

a)`Y = U\Y          `Y = (abcd)\(abd)          `Y = c;ÈZ = (ac) È (bc) = (abc);

(abc) Ç c = c;) `X = U\X,       `X = (abcd)\(ac),  `X = (bd);

`XÇY,       (bd)Ç(abd) = bd;) `Z = U\Z, `Z = (abcd)\(bc),            `Z = ad;

`ZÈY = (ad)È(abd) = (abd)\(`ZÈY),                 (ac)\(abd) = c;

Ответ: a) c; b) bd; c) c.

2. Пусть множества A, B, C Í U;

Продемонстрировать диаграммами Эйлера - Венна что:

a) A È (B \ C) = (A È B) \ (C \ A);) A \ (B È C) = (A \ B) Ç (A \ C);

Рассмотрим левую часть равенства (а);

Найдем сперва разность множеств В и С;

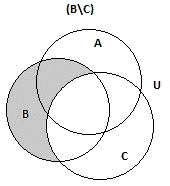
Рис.

Теперь найдем объединенное множество А È (В \ C);

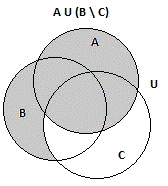
Рис.

Теперь рассмотрим правую часть равенства (а);

Найдем разность множеств С и A;

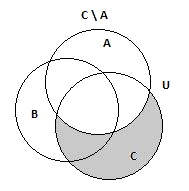
Рис.

Теперь найдем объединение А и В;

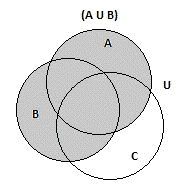
Рис.

Затем найдем разность множеств (AÈB) и (C \ A);

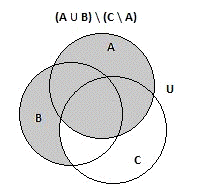
Рис.

И сравним полученные диаграммы из левой и правой части:

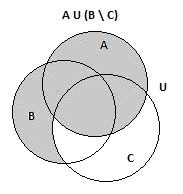
Рис.

Мы видим, что левая и правая части действительно равны.

Перейдем теперь к равенству (b) и рассмотрим его левую часть;

Покажем объединение множеств В и С:

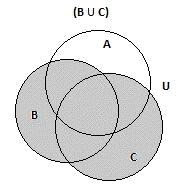
Рис.

И вычтем из множества А полученное множество (BÈC):

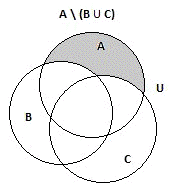
Рис.

Перейдем к правой части равенства, и найдем разности множеств (A \ B) и множеств (А \ C);

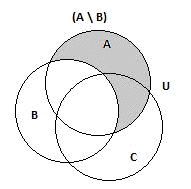
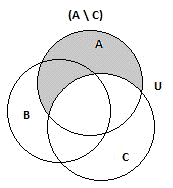
Рис.

И найдем пересечение полученных множеств;

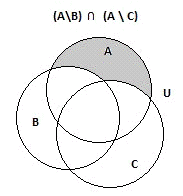
Рис.

А теперь сравним полученные диаграммы из левой и правой частей:

Рис.

И вновь мы видим равенство левой и правой частей.

. Доказать справедливость:

`A`È`B = `A Ç`B;

Доказательство:

Рассмотрим левую часть равенства;

`A`È`B = U \ AÈB = U,

поскольку другие множества не включены в универсальное множество U, то результатом вычитания из универсального множества включенных в него множеств А и В, объединенных во множество АÈВ, будет само универсальное множество U.

Теперь рассмотрим правую часть равенства;

`А = U\A = B;

`B = U\B = A;

А Ç В = U,

поскольку другие множества не включены в универсальное множество U и по условию задачи множества Аи В не имеют общих множеств, то и результатом пересечения двух имеющихся множеств будет само универсальное множество U.

И поскольку, левая и правая части равенства равны U, значит они равны друг другу, ч.т.д.

4. Это задача на перестановки с повторениями

Значит вычисляем по формуле:

Р₍n₁!n₂!...n_k!₎ = n!/ n₁!n₂!...n_k!

Тогда

Р = 17! / 5!5!4!3! = 24504480

Ответ: 24504480

. Имеем буквы с выборкой по 3 из 30 букв, и цифры с выборкой по 4 из 10.

Так как в комбинации букв цифры не входят, комбинации можно искать по отдельности, но общее количество комбинаций должно быть перемножено.

А³₃₀ = 30!/(30 - 3)! = 30 * 29 * 28 = 24360;

А⁴₁₀ = 10!/(10 - 4)! = 10 * 9 * 8 * 7 = 5040;

И найдем произведение:

* 5040 = 122774400;

Ответ: 122774400.

. Для того, чтобы число, составленное из заданных цифр, делилось на 5, достаточно, чтобы цифра 5 стояла на последнем месте. Остальные пять цифр могут стоять на оставшихся местах в любом порядке. Значит, искомое число шестизначных чисел, кратных пяти, равно числу перестановок из пяти элементов, т.е.

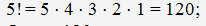
Ответ: 120.

7.составим рекуррентное соотношение:

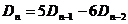
составим характеристическое уравнение:

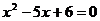
имеем корни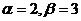

по формулам находи общее решение:

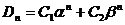, где

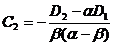
получим

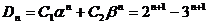
. Построим по матрице весов граф.

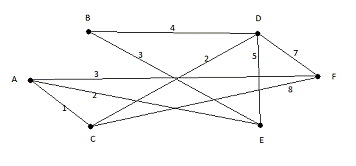
Рис.

Затем выберем начальной вершиной вершину В, и расслабим соседние вершины D и E.

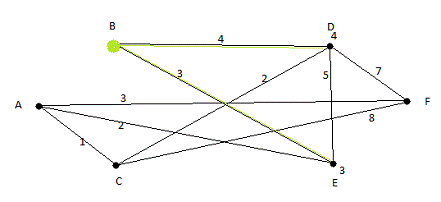
Рис.

Затем, выбираем наименьшую вершину, т.е. Е, и продолжаем выполнение алгоритма поиска минимального покрывающего дерева.

Рис.

Рис.

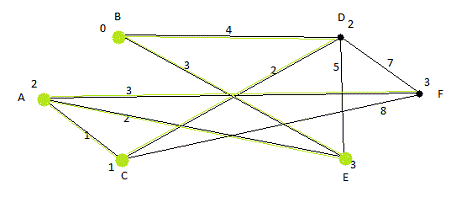
Рис.

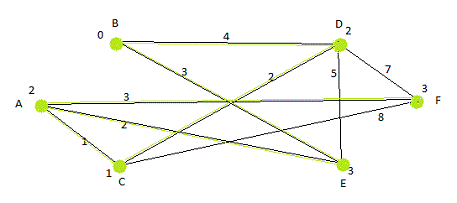
Рис.

. Построим дерево кратчайших расстояний из вершины V_0, используя алгоритм Дейкстры

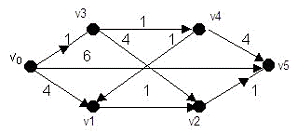
Рис.

величина задача дискретный математика

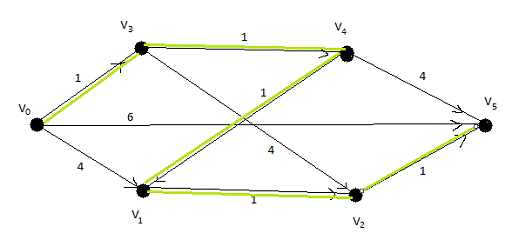
Рис.

Маршрут V₀ , V₃, V₄, V₁, V₂, V₅ является кратчайшим, т.к. его длина равняется 5, в то время как длина маршрутов V_0, V_5; V₀ , V₃ , V₄ , V₅ ; V₀ , V₁ , V₂ , V₅ ; V₀ , V₃ , V₂ , V₅ равна 6.

. Найдем величину максимального потока в сети, используя алгоритм Форда - Фалкерсона.

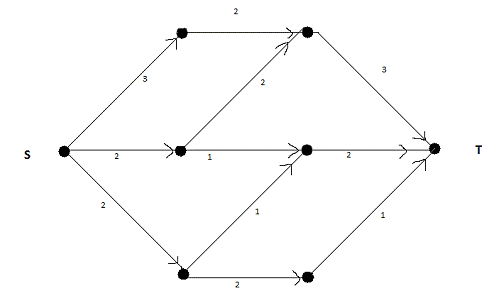
Рис.

Для начала заполним все потоки так:

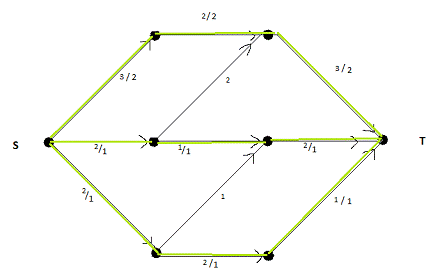
Рис.

И так:

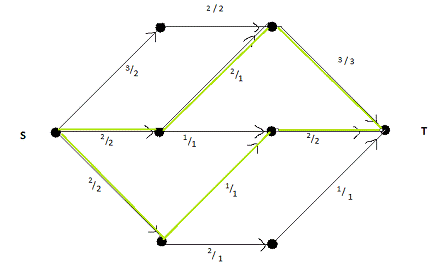
Рис.

В результате мы имеем полностью заполненную сеть, где пропускная способность инкрементых вершине Т дуг полностью истрачена, и значит больше пропустить через эту вершину уже невозможно.

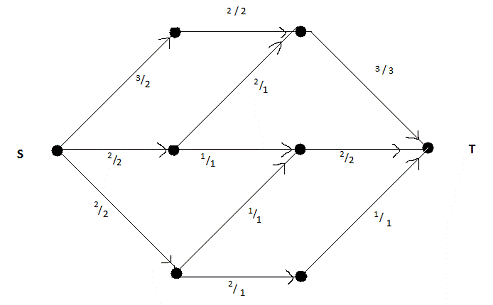
Рис.

Таким образом величина максимального потока в сети равна сумме величин потоков на дугах инкрементных выходной вершине Т, т.е. равна 6.

Если провести проверку, то мы увидим, что в каждую вершину сколько потоков вошло, столько же и вышло, как и во всей сети в целом: вошло шесть и вышло шесть.

Мое мнение об этом примере таково, что он не удачен для демонстрации работы алгоритма, поскольку вся сеть заполняется всего за один подход, и дальнейшие вычисления, которые есть суть алгоритма, становятся лишними.

3.