Разработка активного фильтра
1. Исходные
данные
Шифр: 306718/110
. Частота среза ФНЧ
f0 = (N1+3)*10 Гц = (0+3)*10 Гц = 30 Гц;
2. Коэффициент усиления в полосе пропускания ФНЧ
k0 = (N1+1)/2 = (0+1)/2 = 0,5;
3. Рабочая частота полосового фильтра -
fр= (N1+N2+5)*10 Гц = (0
+1+5)*10 Гц = 60 Гц;
4. Коэффициент усиления на рабочей частоте
Кр = (N1+N2 +2)/2 = (0 +1+2)/2 =1,5.
. Введение в теорию частотных фильтров
Активные фильтры широко используются в разнообразных автоматических
устройствах. Они представляют собой функциональные элементы, в которых в
качестве частотно-избирательных звеньев используются резисторно-конденсаторные
RC - цепочки, а в качестве активного звена - операционный усилитель (ОУ).
Благодаря наличию ОУ такие фильтры называются активными.
Активные фильтры могут использоваться как фильтры нижних частот, фильтры
верхних частот и полосовые фильтры (ПФ). На рис. 1 показаны примерные
амплитудно-частотные характеристики (АХЧ) ФНЧ и ПФ, представляющие собой
зависимость коэффициента передачи K=UВЫХ/UВХ от частоты f
подаваемого входного напряжения.

Рис. 1
На каждой из показанных АЧХ могут быть выделены 3 определенные полосы
частот: полоса пропускания, где коэффициент передачи К имеет наибольшее
значение, полоса запирания или подавления, где коэффициент передачи доходит до
минимума, и промежуточная или переходная полоса. Последняя - эта интервал
частот, в пределах которого значение коэффициента передачи К изменяется от
максимального Кmax до
минимального значения. Чем уже переходная полоса, тек блике характеристика фильтра
к идеальной. Для ФНЧ первой границей полосы пропускания является частота, при
которой коэффициент передачи становится ниже1/√2 ( при Кmax = 1 ). Эту частоту называют частотой
среза f0. Частотой подавления, являющейся
второй границей переходной полосы, считается частота f1, при которой К < 0,3 от
максимального значения.
Для полосовых фильтров характерны граничные частоты полосы пропускания f1 и f2 ,
определяемые аналогично (см. рис.1,б).
ПФ с узкой полосой пропускания П= f2- f1 порядка П=(0,1…0,2)* fp получили название узкополосных или частотовыделяюших.
Они настраиваются на рабочую (резонансную ) частоту fр , на которой происходит максимальное усиление сигнале
в Кр раз. В окрестностях частоты fp коэффициент усиления сигнала
значительно уменьшается, т.е. на рабочей частоте fр функция имеет явно подчеркнутый максимум.
При разработке частотного фильтра, так же как и любого другого элемента с
частотнозависимой характеристикой, необходимо решить две задачи. В первую
очередь следует выбрать передаточную функцию W(р) частотного фильтра. Затем решается вторая задача -
реализация выбранной передаточной функции W(p) на основе той или иной
электронной схемы.
В настоящее время разработано большое количество различных схем активных
частотных фильтров. Из множества таких схем наиболее приемлемыми для
использования в быстродействующих автоматических устройствах оказались активные
фильтры первого и второго порядков. Порядок - это степень многочлена
знаменателя передаточной функции W(p) частотного фильтра. Чем выше степень
многочлена, а, следовательно, и порядок фильтра, тем круче наклон АЧХ в
переходной полосе и лучше его фильтрующие свойства. Поэтому фильтра высоких
порядков получают последовательным соединением простейших звеньев (например,
фильтр 3-го порядка реализуется соединением звеньев первого и второго
порядков).

Рис. 2
Целью курсовой работы является проектирование активного фильтра третьего
порядка с регулируемой частотной характеристикой.
Используя в цепи отрицательной обратной связи ФНЧ параллельно соединенные
безинерционное и дифференцирующее звенья с регулируемыми коэффициентами Кж
и Кг . преобразовать исходный ФНЧ в узкополосный частотный фильтр с рабочей
частотой fp и коэффициентом усиления на этой
частоте Кр.
3.Определение
постоянных времени ФНЧ
В общем случае передаточная функция активного частотного фильтра второго
порядка имеет следующий вид:
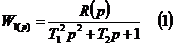
Вид
фильтра определяется степенью числителя R (р):
фильтр
нижних частот - R(р) = К1,
полосовой
фильтр -R(р) = К1р,
фильтр
низких частот 1-го порядка строится на основе передаточной функции
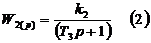
В
этих выражениях:
Т1,
Т2, Т3 - постоянные времени;
К1,К2
- коэффициенты усиления в полосе пропускания:
р
- оператор дифференцирования по времени р=d/dt
Настройка
частотных фильтров на заданные параметры - частоту среза f0 (или
рабочую частоту fр) и коэффициент усиления в полосе пропускания Ко (Кр ) -
сводится к расчету постоянных времени в выражениях (1), (2):
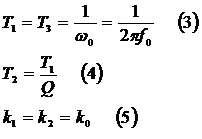
частотный фильтр передаточный
Определяем
постоянные времени и коэффициенты усиления ФНЧ 1-го и второго порядков.
Воспользуемся выражениями (3)-(5):
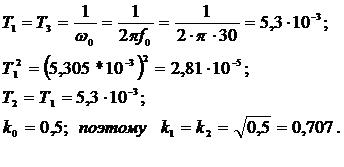
4.
Определение передаточных функций разомкнутой и замкнутой системы
Передаточная функция разомкнутой системы определяется как произведение
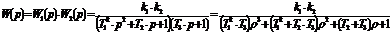
Для
определения передаточной функции замкнутой системы воспользуемся
преобразованием параллельно соединенных звеньев:
W’(p)=W3(p)+W4(p)=kж+kг∙р
В
результате получаем структурную схему представленную на (Рис. 3).

Преобразование схемы производим согласно выражения:
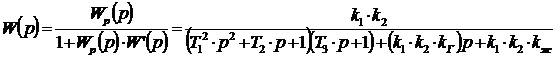
После
преобразований W(р) принимает вид:
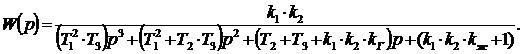
Введем
новые обозначения и вычислим их значения :
к=к1*к2=0,707*0,707=0,5;
а3=Т12Т3=2,81*
10-5*5,3*10-3 =1,489 * 10-7;
а2=Т12
+Т2 *Т3=2,81 * 10-5+(5,3*10-3
)2=5,619 * 10-5;
а1=Т2
+Т3=5,3*10-3 +5,3*10-3 =0,0106;
b=a1+kг*к;
с=кж*к+1.
С
учетом новых обозначений передаточные функции разомкнутой замкнутой системы
принимают вид:
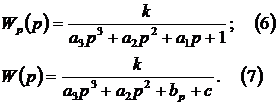
5. Нахождение
частотных характеристик разомкнутой и замкнутой системы
Если на вход системы (или отдельного звена) подавать гармонические
колебания с постоянными амплитудами и частотой, то после затухания переходных
процессов на выходе также возникают синусоидальные колебания с той же частотой,
но с другой амплитудой, и сдвинутые по фазе относительно входных колебаний.
Обычно важно знать отношение амплитуды выходного сигнала к амплитуде
входного А=U вых m /U вх m и фазовый сдвиг ц. Эти величины зависят от частоты
сигнала, т.е. А и ц является функциями щ и называются соответственно амплитудно-частотной и
фазочастотной характеристикой (ФЧХ).
Аналитические выражения для АЧХ и ФЧХ можно получить, имея передаточную
функцию. Для этого в выражение передаточной функции W(p) вместо р подставляется
jщ . При этом получается комплексная величина W(jщ), которая называется комплексной частотной
характеристикой. Модуль этой функции представляет собой амплитудно- частотную
характеристику А(щ ), а аргумент - фазочастотную характеристику ц(щ), т.е.:
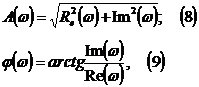
где
Re(щ), Im(щ) -соответственно действительная и мнимая
части комплексной частотной характеристики.
При
анализе схем автоматического регулирования удобно пользоваться
амплитудно-частотными характеристиками, построенными в логарифмическом
масштабе. Логарифмической единицей усиления по амплитуде принят децибел (дБ).
Величину логарифма АЧХ, выраженную в децибелах,
L(щ)=20lgA(щ)
(10)
называют
логарифмической амплитудно-частотной характеристикой (ЛАЧХ). Например, если
один сигнал больше другого в 10 раз, то отношение первого ко второму составляет
+ 20 дБ, а если один сигнал в 10 раз меньше другого, то - 20 дБ.
За
единицу частоты обычно принимают декаду. Декадой называют интервал частот между
какой-либо величиной частоты и ее десятикратным значением. В логарифмическом
масштабе частот отрезок в одну декаду не зависит от частоты и имеет длину,
равную
lg10щ-lgщ=lg10=1.
Для
разомкнутой системы, подставляя jщ вместо р в выражении (6), определяем
комплексную частотную характеристику
Для
разделения Wp(jщ) на действительную и мнимую части умножаем
числитель и знаменатель этого выражения на сопряженный комплекс.
Тогда:

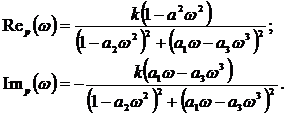



















АЧХ
разомкнутой системы определяется согласно (8).  После
несложных преобразований:
После
несложных преобразований:
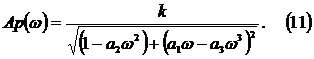
Для
расчета ФЧХ разомкнутой системы воспользуемся выражением:
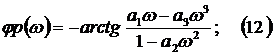
ЛАЧХ
paзoмкнутой системы определяется по (10):
Lp(щ)=20lg(Ap(щ)).
(13)
Замкнутая
система. Поступая аналогично, имеем:
комплексная
частотная характеристика замкнутой системы:
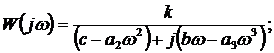
действительная
и мнимая части W(jщ):
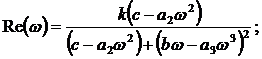
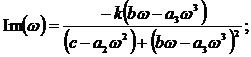
АЧХ
замкнутой системы:
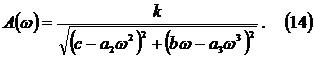
ФЧХ
замкнутой системы:

ЛАЧХ
замкнутой системы:
L(щ)=20lg(A(щ)).
(16)
6. Расчёт
коэффициентов усиления корректирующих звеньев
В соответствии с заданием на проектирование необходимо получить
узкополосный частотный фильтр, настроенный на рабочую частоту ѓр с
коэффициентом усиления на этой частоте Кр. При этом регулироваться могут только
коэффициенты усиления корректирующих звеньев Кг и Кж, а все остальные параметры
САР должны оставаться неизменными.
Одним из путей решения поставленной задачи является анализ АЧХ замкнутой
системы. АЧХ, представленная в виде (14), неудобна для анализа, поэтому ее
преобразуют к более удобной форме.
Для этого в коэффициенты АЧХ, которые определяются согласно выражения,
подставляются соответствующие выражения (3)-(5) при добротности Q=1. Тогда
коэффициенты в (14) принимают вид:
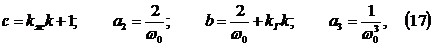
а
АЧХ замкнутой системы определяется:
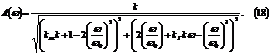
Такая
форма представления АЧХ позволяет производить независимую настройку фильтра.
Пусть с помощью коэффициента Кг осуществляется настройка ПФ на частоту ѓр,
а с помощью Кж - на заданный коэффициент усиления КР. Тогда на
рабочей частоте щ=щр=2р ѓр
правый член подкоренного выражения должен обращаться в нуль, а левый -
обеспечивать заданный коэффициент усиления, т.е.
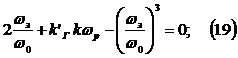
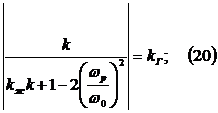
Разрешая
(19) и (20) относительно Кг и Кж, получаем:
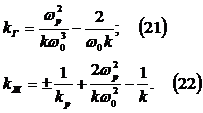
которые
обеспечивают настройку узкополосного фильтра на заданные параметры.
На
частоте щ=0 выражение (18) с учетом (22) приобретает следующий
вид:
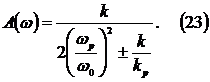
Из
(3) следует, что если пренебречь отношением К /Кр, то для получения
приемлемого коэффициента передачи на нулевой частоте выбирать рабочую частоту
ПФ ѓр в несколько раз большей частоты среза ѓ0 ФНЧ.
Расчет
производим по выражениям (21) и (22)
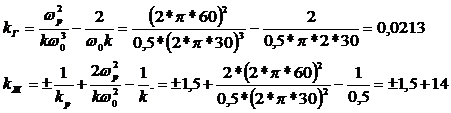
откуда
k’ж=15,5; k’’ж=12,5
7.Определение устойчивости САР с помощью критерия Михайлова
Определяем коэффициенты b и c по выражению, при k’ж=15,5, kг=0,0213:
b=a1+kг*к=0,0106+0,0213*0,5=0,02125;
с=кж*к+1=15,5*0,5+1=8,75.
характеристическое уравнение с учетом рассчитанных ранее коэффициентов a3
и а2 запишется в виде
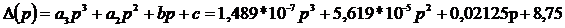
Уравнение
характеристической кривой согласно (2.4):
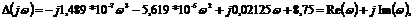
где
Re(щ) =8,75-5,619 * 10(-5)щ2
Im(щ)=
0,02125щ -1,489 * 10-7щ3
Вычисляем
точки пересечения годографа с осями координат:
Re(щ)=0
при 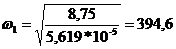 ;
;
Im(щ1)= 0,02125* 394,6-1,489 * 10-7* 394,63=-0764;
Im(щ)= 0
при щ2=0;
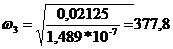 ;
;
Re(щ2) =8,75;
Re(щ3) =8,75-5,619 * 10-5*377,82=
0,73
Приведем
вычисления Re(щ) и Im(щ) для различных частот:
Re(щ3) =8,75-5,619 * 10-5*502= 8,6;
Re(щ3) =8,75-5,619 * 10-5*1002= 8,19;
Re(щ3) =8,75-5,619 * 10-5*2002= 6,5;
Re(щ3) =8,75-5,619 * 10-5*4002=
-0,24;
Re(щ3) =8,75-5,619 * 10-5*6002=
-11,48;
Im(щ)=
0,02125*50 -1,489 * 10-7*503= 1,044
Im(щ)=
0,02125*100-1,489 * 10-7*1003= 1,976
Im(щ)=
0,02125*200-1,489 * 10-7*2003= 3,059
Im(щ)=
0,02125*400-1,489 * 10-7*4003= -1,03
Im(щ)=
0,02125*600-1,489 *10-7*6003= -19,4
Таблица
1
|
щ
|
50
|
200
|
377,8
|
394,6
|
400
|
600
|
|
Re(щ)
|
8,6
|
8,19
|
6,5
|
0,73
|
0
|
-0,24
|
-11,48
|
|
Im(щ)
|
1,044
|
1,976
|
3,059
|
0
|
-0,754
|
-1,03
|
-19,4
|
Система неустойчива, т.к. кривая 1 ( pиc. 4) последовательно не проходит
три квадранта.
Воспользуемся вторым значением Кж = К’’ж = 12,5.
Тогда с=к”ж*к+1=12,5*0,5+1= 7,25.
Уравнения приобретают вид:
Re(щ) = 7,25-5,619 * 10-5щ2
Im(щ)= 0,02125щ -1,489 * 10-7щ3
Определяем точки пересечения кривой 2 с осями Re и Im:
Re(щ)=0
при 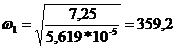 ;
;
Im(щ1)= 0,02125* 359,2-1,489 * 10-7* 359,23=
0,73;
Im(щ)= 0
при щ2=0;
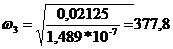 ;
;
Re(щ2) =7,25;
Re(щ3) =7,25-5,619 * 10-5*377,82=
-0,77.
Производим
аналогичные вычисления:
Re(щ3) =7,25-5,619 * 10-5*502= 7,12;
Re(щ3) =7,25-5,619 * 10-5*1002= 6,69;
Re(щ3) =7,25-5,619 * 10-5*2002= 5,00;
Re(щ3) =7,25-5,619 * 10-5*4002=
-1,74;
Re(щ3) =7,25-5,619 * 10-5*6002= -13.
Таблица
2
|
Щ
|
50
|
100
|
200
|
359,2
|
377,8
|
400
|
600
|
|
Re(щ)
|
7,12
|
6,69
|
5,00
|
0
|
-0,77
|
-1,74
|
-13
|
|
Im(щ)
|
1,044
|
1,976
|
3,059
|
0,73
|
0
|
-1,03
|
-19,4
|
Строим кривую 2 (рис. 4). Легко убедиться, что система устойчива, поскольку
годограф Михайлова последовательно обходит три квадранта. Поэтому для
дальнейших расчетов принимаем следующие значения коэффициентов усиления
корректирующих звеньев:
kг=0,0213; Кж = 12,5.
8. Построение
области устойчивости системы и определение диапазона изменения коэффициентов
усиления корректирующих звеньев
Метод Д-разбиения основан на том, что при непрерывном изменении
коэффициентов характеристического уравнения Д(р)=0 его корни непрерывно
перемещаются в плоскости корней и могут переходить из правой и левую или из
левой в правую полуплоскости, пересекая мнимую ось. Разделение плоскости
варьируемых параметров из области, в которых характеристическое уравнение
Д(р)=0 имеет определенное одинаковое количество правых корней, получило
название Д -разбиения. Области именуются по количеству правых корней, поэтому
область, в которой все правые корни отсутствуют, Д (0) является областью
устойчивости. Задача Д- разбиения заключается в отыскании границ областей с
одинаковым числом правых корней и последующем выделения из них области
устойчивости.
Представим характеристическое уравнение (24) в виде:
Д(р)=a3p3+ a2p2+(а1+Кг*К)с+(Кж*К+1)=0.
Подставляя p= jщ и решив характеристическое уравнение
относительно Кж и Кг с учетом рассчитанных ранее коэффициентов а1, а2,
а3, имеем:
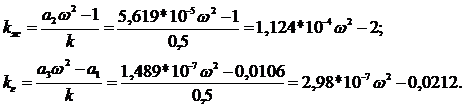
Определяем
точки пересечения графика Д-разбиения с осями координат:
kж=0 при 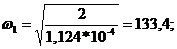
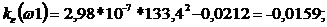
kг=0, при 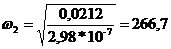 ;
;
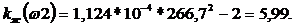
Изменяя
щ от 0 до +∞,строим границу Д-разбиения (рис. 5).
Таблица
3
|
щ
|
0
|
133,4
|
266,7
|
500
|
|
Кж
|
-2
|
0
|
6
|
28,1
|
|
Кг
|
-0,0212
|
-0,0159
|
0
|
0,0533
|
Для определения области устойчивости проверим произвольные точки в 1 и 2
области с помощью критерия Рауса. Неравенства в нашем случае приобретают вид:
а3>0; а2>0; а1+Кг*К>0;
Кж*К+1>0; (а1+Кг*К)*а2>( Кж*К+1)*а3
Так как первые четыре неравенства всегда выполняются, проверку
устойчивости осуществляем с помощью последнего выражения:
) точка в 1 области: kг=0,1 kж=20;
(0,0106+0,1*0,5)*5,619*10-5=3,41*10-6;
(20*0,5+1)*1,489*10-7=1,64*10-6;
,41*10-6 >1,64*10-6 - следовательно, область I является областью устойчивости.
) точка во 2 области: : kг=0 kж=30;
(0,0106+0*0,5)*5,619*10-5=5,96*10-7;
(30*0,5+1)*1,489*10-7=2,4*10-6;
,96*10-7 <2,4*10-6 - следовательно, область I I является областью неустойчивости.
Для сохранения устойчивости системы варьируемые параметры kг и kж должны находиться в I области, причем оба этих
коэффициента должны быть больше нуля.
Для неизменного расчетного значения kг=0,0213, определяющего рабочую частоту ПФ, можно графически
определить диапазон изменения kж (а следовательно, и пределы
изменения коэффициента усиления kг ) при котором система находится в
устойчивом состоянии. Как видно из рис. 6,устойчивость замкнутой системы
обеспечивается при 0< kж <17.
Связь величины kж с коэффициентом усиления kр на рабочей частоте ѓр можно установить из
выражения (20):
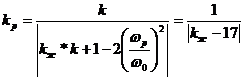
При
изменении kж от 0 до 17 коэффициент усиления kр изменяется от 1/17 до ∞. При этом система
остается устойчивой. Дальнейшее увеличение kж, от 17 до ∞ также приводит к изменению kр от ∞ до 0, однако в этом случае система будет
неустойчивой.
9. Построение
частотных характеристик (АЧХ, ЛАЧХ, ФЧХ) замкнутой и разомкнутой системы
В качестве исходных данных используем kг=0,0213, k’’ж=12,5
-для устойчивой системы и k’ж=15,5
- для неустойчивой системы.
Частотные характеристики приведены на рис. 7. АЧХ, представленные на рис.
7, а, построены по выражениям (9), (14).
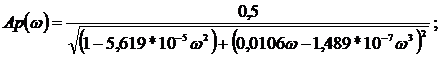
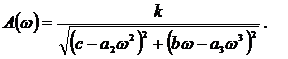
Полученные
характеристики подтверждают правильность проведенных расчетов: исходная АЧХ
низкочастотного фильтра Ар(щ) с плоской характеристикой в полосе пропускания,
частотой среза ѓ0 =30 Гц и коэффициентом усиления k0=0,5 преобразована в характеристику узкополосного
фильтра с рабочей частотой ѓр =60 Гц к коэффициентом усиления
Кр=1,5. ЛАЧХ строятся по (13) и (16). Из логарифмических АЧХ (рис. 7, б) видно,
что наклон обеих характеристик в области высоких частот составляет - 64 дБ/дек.
В низкочастотной области полосовой фильтр ослабляет выходной сигнал на - 23 дБ
и поддерживает эту величину неизменной практически до рабочей частоты. Зятем
сигнал усиливается до -15 дБ и далее ЛАЧХ замкнутой системы начинает
приближаться к Lр(щ).
На
рис. 7, в представлены ФЧХ разомкнутой системы цр(щ) рассчитанная по
(12), ФЧХ корректирующих звеньев цк(щ)=arctg(kГ /kж*щ) и
суммарная ФЧХ ц∑(щ)=цр(щ)+ цк(щ). Две
последние характеристики приведены для устойчивой (k’’ж=12,5)
и неустойчивой (k’ж=15,5) системы. Как видно из этих
графиков ФЧХ корректирующих звеньев, для устойчивой цк(щ) и
неустойчивой ц’к(щ) системы практически совпадают. Это означает, что
проектируемая система приближается к границе устойчивости, что предъявляет
жесткие требования к аппаратной реализации корректирующих элементов. Суммарная
ФЧХ устойчивой системы ц∑(щ) позволяет определить сдвиг фаз
между входным сигналом и сигналом на выходе корректирующих звеньев при
различных значениях частот, т.е. тот фазовый сдвиг, с помощью которого
поддерживается отрицательная ОС. Разница между устойчивой ц∑(щ)
и неустойчивой ц’∑(щ) характеристиками также незначительна, а
следовательно, нестабильность параметров корректирующих звеньев может привести
к переходу ОС из отрицательной к положительной и выходу системы из состояния
равновесия.
ФЧХ
замкнутой системы определяется согласно (15). На рис. 7, г приведены ФЧХ
устойчивой ц(щ) и неустойчивой ц’(щ) системы. ФЧХ устойчивой системы является
убывающей функцией, равной 0 на частоте ѓ0=0 и стремящейся к -3р/2
(270°) при частоте ѓ →∞. ФЧХ WX неустойчивой системы ц’(щ)
существенно отличается от графика ц(щ), что, как указывалось выше, позволяет
оценивать устойчивость замкнутой системы по виду ее ФЧХ.
10.Расчёт
параметров схемы активного фильтра
Реализация звеньев САР (рис. 2) осуществляется с помощью типовых схем на
операционных усилителях. ОУ - это усилитель постоянного тока с большим
коэффициентом усиления. ОУ является активным звеном, использующим энергию
постороннего источника питания. Современные ОУ представляют собой аналоговую
микросхему, имеющую два входных (инвертирующий и не инвертирующий) и один общий
выходной зажимы. Кроме них имеются зажимы для подачи напряжения питания,
которые обычно на схемах не показываются. Инвертирующий вход создаёт выходное
напряжение, полярность которого противоположна полярности входного напряжения.
Основные схемы применения ОУ строятся на использовании различных вариантов
отрицательной ОС между выходом ОУ и его инвертирующим входом. ОС в таких схемах
осуществляется через соответственно подобранные резисторы и емкости в
зависимости от характера операций, выполняемых с помощью данной схемы. Для
облегчения расчета схем реальные ОУ с достаточной степенью точности
представляются в виде идеальных усилителей. Идеальным усилителем является ОУ с
бесконечно большим коэффициентом усиления, входное сопротивление которого также
равно бесконечности. Такой усилитель должен пропускать сигналы на всех частотах
от 0 до ∞, а его выходное сопротивление должно равняться нулю.
В таблице 4 приведены принципиальные схемы, передаточные функции и
расчетные формулы для реализации всех звеньев проектируемого активного фильтра.
Фильтр нижних частот второго порядка, являющийся колебательным звеном,
осуществляется с использованием многоконтурной отрицательной ОС с R-C
-элементами. ФНЧ первого порядка представляет собой простейшее инерционное
звено. Корректирующие элементы могут быть представлены простейшими звеньями:
ЖОС -безинерционным, ГОС - дифференцирующим и реализованы также в соответствии
с таблицей 4.
Однако в этом случае требуется два ОУ. Для построения схемы с использованием
одного ОУ находится эквивалентная передаточная функция этих звеньев
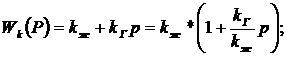
которая
осуществляется с использованием четырехполюсника в цепи ОС и резистора во
входной цепи.
Узел
суммирования может быть реализован двумя схемами - инвертирующей и
неинвертирующей. В первом случае выходной сигнал сдвинут относительно входного
на 180°, во втором - синфазен входному. Несмотря на то, что передаточные
функции реальных звеньев получены с использованием инвертирующего входа ОУ, т.е.
во всех выражениях табл. 4 присутствует знак "-", их частотные
характеристики полностью соответствуют теоретическим. Поэтому в качестве
суммирующего звена используется активный неинвертирующий сумматор.
Таблица
4
|
Передаточная функция звена и её параметры
|
Схема звена
|
Расчётные формулы
|
|
1. ФНЧ 2-го порядка  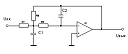 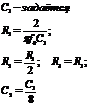
|
|
|
|
2. ФНЧ 1-го порядка 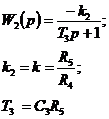 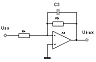 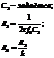
|
|
|
|
3. Корректирующие звенья 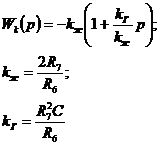 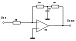 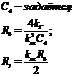
|
|
|
|
4. Суммирующее звено (для двух входных напряжений)
|
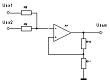 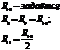
|
|
Воспользовавшись исходными данными и расчетными формулами из таблицы 4 и
положив:
С1 = С3 = С4 = 1 мкФ; R1O=2 кОм;
получаем:
для ФНЧ второго порядка
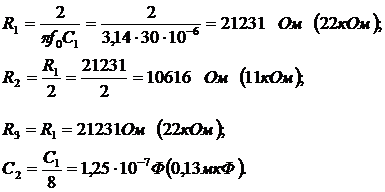
для
ФНЧ первого порядка
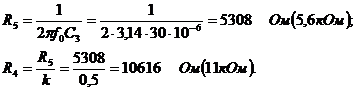
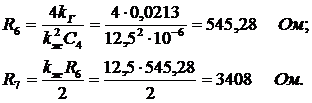
(выбираем
потенциометры с максимальным сопротивлением соответственно 1 кОм и 3,6 кОм);
суммирующее
звено
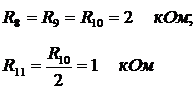
В
скобках приведены стандартные значения сопротивлений.
Литература
частотный фильтр активный
1. Методические указания к курсовому проектированию по
дисциплине «Теоретические основы автоматизации электрической части станций и
подстанций» / Составитель: В.Ю. Румянцев.- Мн.: БГПА, 1996 г.