Динамическая устойчивость энергосистемы
Реферат
Пояснительная записка содержит 21 страницы, 6 таблиц, 14
рисунков,3 источников литературы, в которой подробно расписана методика
расчёта, которая использовалась в данной работе.
Объект исследования: система электропередачи.
Цель работы: получить навыки расчёта электромеханических
переходных процессов в системе электропередачи, рассчитать предельное снижение
напряжения на шинах асинхронного двигателя, оценить статическую и динамическую
устойчивость системы.
Содержание
Введение
Исходные данные
1. Рассчитать предел передаваемой мощности генератора Г-1 в систему
при нормальном режиме работы
2. Рассчитать аварийный и послеаварийный режимы работы системы
2.1 Расчёт аварийного и послеаварийного режима при однофазном
коротком замыкании в точке К-1
2.2 Расчёт аварийного и послеаварийного режима при трёхфазном
коротком замыкание в точке К-2
3. Рассчитать предельное снижение напряжения на шинах асинхронного
двигателя
Заключение
Список используемой литературы
Введение
Устойчивость
энергосистемы - это способность ее возвращаться в исходное состояние при малых
или значительных возмущениях. По аналогии с механической системой
установившийся режим энергосистемы можно трактовать как равновесное положение
ее.
Параллельная работа генераторов
электрических станций, входящих в энергосистему, отличается от работы
генераторов на одной станции наличием линий электропередачи, связывающих эти
станции. Сопротивления линий электропередачи уменьшают снихронизирующую
мощность генераторов и затрудняют их параллельную работу. Кроме того,
отклонения от нормального режима работы системы, которые происходят при
отключениях, коротких замыканиях, внезапном сбросе или набросе нагрузки, также
могут привести к нарушению устойчивости, что является одной из наиболее
тяжелых: аварий, приводящей к перерыву электроснабжения потребителей Поэтому
изучение проблемы устойчивости очень важно, особенно применительно к линиям
электропередачи переменным током. Различают два вида устойчивости: статическую
и динамическую.
Статической устойчивостью называют
способность системы самостоятельно восстановить исходный режим при малых и
медленно происходящих возмущениях, например при постепенном незначительном
увеличении или уменьшении нагрузки.
Динамическая устойчивость энергосистемы
характеризует способность системы сохранять синхронизм после внезапных и резких
изменений параметров режима или при авариях в системе (коротких замыканиях,
отключений часта генераторов, линий или трансформаторов). После таких внезапных
нарушений нормальной работы в системе возникает переходный процесс, по
окончании которого вновь должен наступить установившийся послеаварийный режим
работы.
Именно такие внезапные нарушения в работе СЭС приводят к
тяжелым экономическим последствия для населения и промышленных объектов.
Современная энергетика уделяет очень большое внимание борьбе
с авариями на линиях, короткими замыканиями, большой вклад делает еще на стадии
проектировании СЭС городов и предприятий.
Исходные
данные
Схема для расчёта представлена на рисунке 1.

Рисунок 1 - Схема системы электропередачи
Исходные данные для расчёта первой и второй задачи принимаем
по таблице в соответствии с номером варианта.
Технические данные трансформаторов:
Тип транс форматора 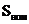 ,
,
МВАПределы регулиро
вания, %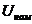 , кВ
, кВ
обмоток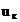 , %
, %
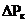 ,
,
кВт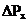 ,
,
кВт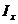 ,
,
|
%
|
|
|
|
|
|
|
|
|
|
|
В
|
Н
|
|
|
|
|
|
|
ТДЦ-250000/110
|
250
|
-
|
110
|
13.8; 15.75; 18
|
10,5
|
640
|
200
|
0.5
|
|
ТДЦ-630000/110
|
630
|
-
|
110
|
20
|
10.5
|
900
|
320
|
0.45
|
Параметры двухцепной воздушной линии электропередачи
Марка провода 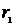 ,
,
Ом/км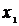 ,
,
Ом/км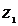 ,
,
Ом/км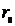 ,
,
Ом/км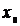 ,
,
Ом/км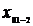 ,
,
Ом/кмДлина
|
l, кмU, кВ
|
|
|
|
|
|
|
|
|
|
АС-330
|
0.107
|
0.367
|
0.382
|
0.330
|
1.389
|
0.931
|
110
|

Рисунок 2 - Схема системы для расчёта предельного снижения
напряжения на шинах асинхронного двигателя
Исходные данные для расчёта третьей задачи принимаем ниже по
таблице в соответствии с номером варианта.
Технические данные асинхронного электродвигателя
|
Тип
|
Номинальные
данные
|
Пусковые
характеристики
|
|
|
P, кВт
|
I, А
|
N, об/мин
|
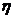 , % , %
|
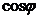 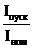 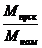 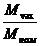 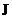 , кг*м2U, кВn0, об/мин , кг*м2U, кВn0, об/мин
|
|
|
|
|
|
|
|
ДАЗО 17-39-8/10
|
500
|
61.5
|
741
|
91.0
|
0.85
|
5.2
|
0.65
|
2.1
|
288
|
6
|
741
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Параметры КЛ:
|
Тип провода
|
Длина l,
км
|
х0,
Ом/км
|
|
АПвВ 1*300
|
0,035
|
0,099
|
1. Рассчитать
предел передаваемой мощности генератора Г-1 в систему при нормальном режиме
работы
Составляем схему замещения системы, которая представлена на
рис.1 и рассчитываем индуктивные сопротивления всех элементов:
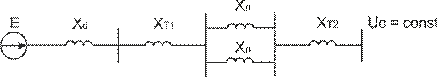
Рисунок 3 - Схема замещения системы
индуктивное сопротивлении задано,
индуктивное сопротивление трансформаторов:
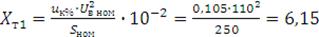
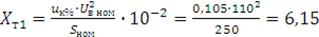 Ом,
Ом,
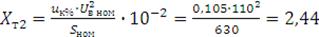
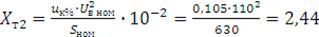 Ом,
Ом,
индуктивное сопротивление ЛЭП:
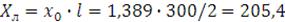
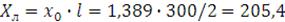 Ом.
Ом.
Все сопротивления схемы замещения приводятся к номинальному
напряжению генератора. Сопротивление трансформаторов:
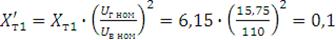
 Ом,
Ом,
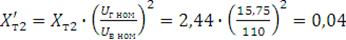
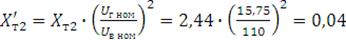 Ом,
Ом,
сопротивление ЛЭП:
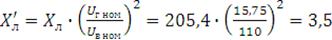
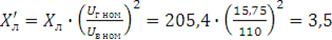 Ом.
Ом.
Определяем суммарное сопротивление системы:
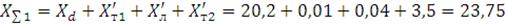
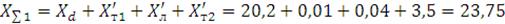 Ом.
Ом.
Рассчитываем номинальную реактивную мощность генератора:
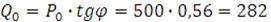
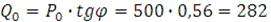 МВАр,
МВАр,
Определяем приближённое значение синхронной ЭДС генератора:
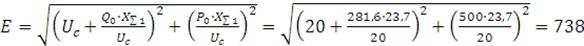
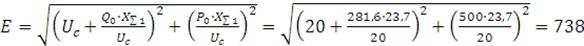 кВ.
кВ.
Определяем предел передаваемой мощности генератора в систему:
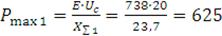
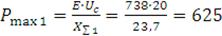 МВт.
МВт.
Определяем значение коэффициента запаса статической устойчивости:
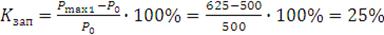
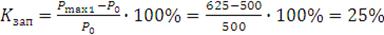 .
.
По данным расчёта строим векторную диаграмму.
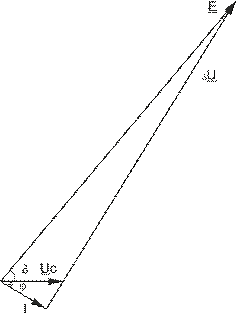
Рисунок 4 - Векторная диаграмма
Изменяя значения угла 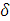
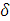 от 0 до 180 град., рассчитываем соответствующие значения мощности
отдаваемой генератором в систему по формуле:
от 0 до 180 град., рассчитываем соответствующие значения мощности
отдаваемой генератором в систему по формуле:
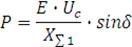
Результаты расчёта заносим в таблицу 3.
Таблица 3
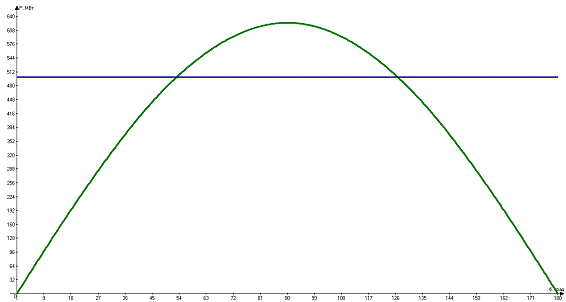
Рисунок 5 - Угловая характеристика мощности
Система является статически устойчивой, так как коэффициент запаса
больше 20%. И предел передаваемой мощности генератора в систему достигается при
угле δ = 900.
2. Рассчитать
аварийный и послеаварийный режимы работы системы
Рассчитываем режимы по очереди.
2.1 Расчёт
аварийного и послеаварийного режима при однофазном коротком замыкании в точке
К-1
.1.1 Нормальный режим
.1.2 Аварийный режим
Составляем схему замещения системы при однофазном КЗ
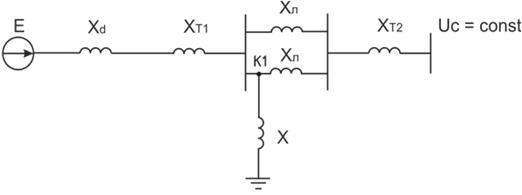
Рисунок 6 - Схема замещения для аварийного режима при
однофазном КЗ
Суммарное сопротивление КЗ Х∆ при однофазном
коротком замыкании равно сумме сопротивлению обратной последовательности и
сопротивлению нулевой последовательности.
Преобразуем схему замещения системы при однофазном КЗ из
соединения "звезда" в соединение "треугольник" со сторонами
Х1, Х2, Х3.
Сопротивление Х2 и Х3 могут быть
отброшены, т.к. поток мощности отдаваемый генератором в сеть не проходит через
эти сопротивления.
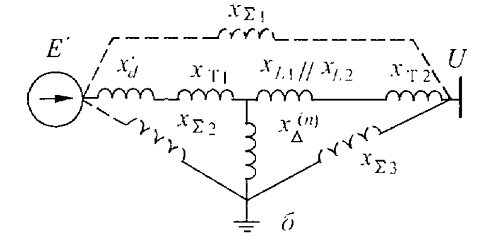
Рисунок 7 - Преобразованная схема замещения
Определим суммарное сопротивлении системы:
Хd∑II = 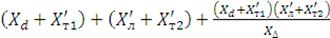
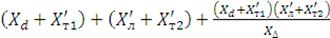 ,
,
Где X∆=X2∑+X0∑ - шунт
несимметричного КЗ, который включается между началом и концом схемы прямой и
обратной последовательности.
Определяем индуктивное сопротивление нулевой последовательности Х0∑:
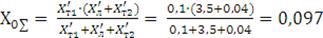
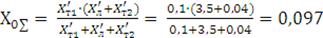 Ом.
Ом.
Определим индуктивное сопротивление обратной последовательности X2∑
2∑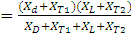
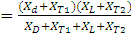 = 3 Ом
= 3 Ом
Определяем сопротивления шунта КЗ X∆:
∆=X2∑+X0∑ = 3 +0,097 = 3,097 Ом
Определяем суммарное сопротивлении системы:
Хd∑II = 20,2 + 0,1 + 3,5 +0,04 + 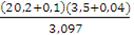
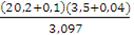 = 47Ом.
= 47Ом.
Определяем предел передаваемой мощности генератора в систему:
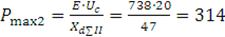
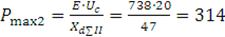 МВт.
МВт.
Изменяя значения угла 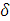
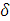 от 0 до 180 град., рассчитываем соответствующие значения мощности
отдаваемой генератором в систему по формуле:
от 0 до 180 град., рассчитываем соответствующие значения мощности
отдаваемой генератором в систему по формуле:
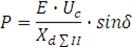
Результаты расчёта заносим в таблицу 4.
Таблица 4
|
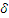 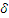 , град0153045607590105120135150165180 , град0153045607590105120135150165180
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
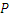 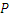 , МВт081,3157222,3271,9303,3314303,3271,9222,315781,30 , МВт081,3157222,3271,9303,3314303,3271,9222,315781,30
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.1.3 Послеаварийный режим
Составляем схему замещения системы для послеаварийного
режима.

Рисунок 8 - Схема замещения для послеаварийного режима при
однофазном КЗ
Послеаварийный режим определяется отключением одной цепи ЛЭП,
после чего сопротивление 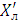
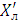 изменяется:
изменяется:
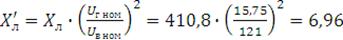
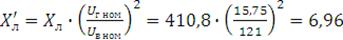 Ом.
Ом.
Определяем суммарное сопротивлении системы:
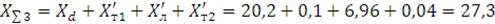
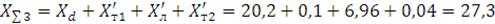 Ом.
Ом.
Определяем предел передаваемой мощности генератора в систему:
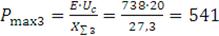
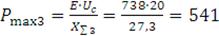 МВт.
МВт.
Рассчитываем значение углов:
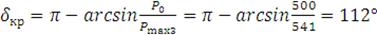
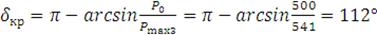 ,
,
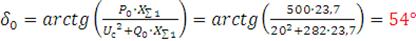
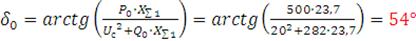 .
.
Находим предельный угол отключения КЗ δоткл:
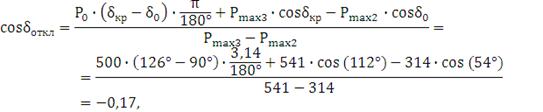
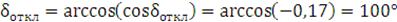
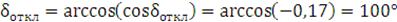 .
.
Рассчитываем предельное время отключения КЗ:
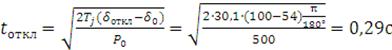
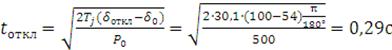 .
.
Выбираем соответствующие уставки срабатывания устройств РЗА:
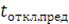
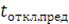 ≥ Тоткл =
≥ Тоткл = 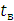
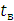 +
+ 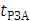
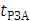
Поскольку линия имеет защиту, то через некоторое время она
отключится выключателями. Следовательно, выбираем элегазовый выключатель серии
ВГБЭ-35 - 110 с временем отключения 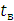
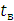 = 0,07 с. Также должно быть предусмотрены устройства релейной
защиты от КЗ. Выбираем токовое реле РТ-40 с временем уставки
= 0,07 с. Также должно быть предусмотрены устройства релейной
защиты от КЗ. Выбираем токовое реле РТ-40 с временем уставки 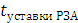
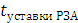 = 0,08 с.
= 0,08 с.
Время действия релейной защиты определяется:
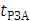
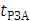 =
= 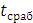
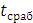 +
+ 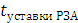
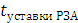 = 0,07 + 0,08 = 0,15 с,
= 0,07 + 0,08 = 0,15 с,
Находим время отключения КЗ:
Тоткл = 0,07 + 0,15 = 0,22 с.
,29 ≥ 0,22, что удовлетворяет условию 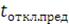
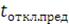 ≥ Тоткл
≥ Тоткл
Изменяя значения угла 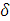
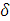 от 0 до 180 град., рассчитываем соответствующие значения мощности
отдаваемой генератором в систему по формуле:
от 0 до 180 град., рассчитываем соответствующие значения мощности
отдаваемой генератором в систему по формуле:
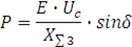
Таблица 5
Результаты расчёта заносим в таблицу 5.
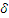
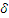 ,
,
|
град0153045607590105120135150165180
|
|
|
|
|
|
|
|
|
|
|
|
|
|
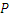
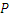 ,
,
|
МВт0140270.5382.5468.5522.6541522.6468.5382.5270.51400
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Строим в одной координатной плоскости угловые характеристики
мощности в нормальном, аварийном и послеаварийном режимах, на графике указываем
значение мощности турбины Р0. С учётом рассчитанного значения
предельного угла отключения КЗ δоткл на графике строим площади
ускорения и торможения.
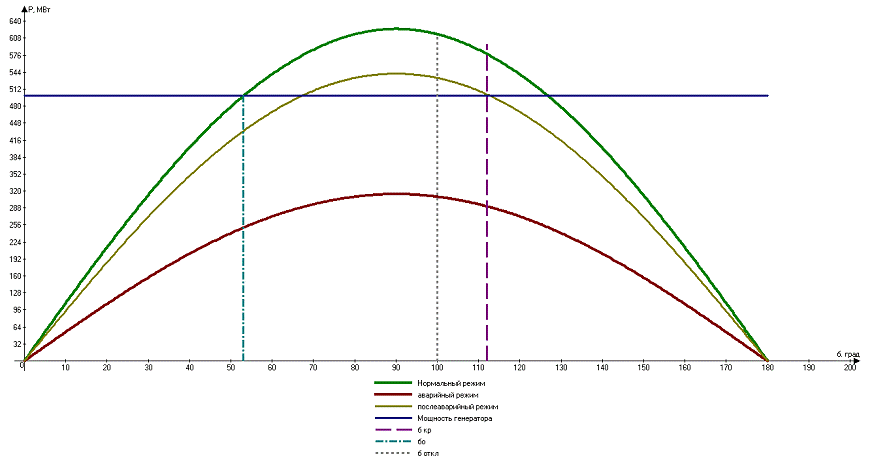
Рисунок 9 - График угловых характеристик мощностей и площади
ускорения и торможения при однофазном КЗ
Для определения динамической устойчивости системы при однофазном
КЗ необходимо рассмотреть площади ускорение Fуск и торможения Fторм.
Условием для динамической устойчивости системы является неравенство: Fуск
≤ Fторм. Невооруженным глазом видно по графику угловой
характеристики, что площадь ускорения на порядок больше площади торможения,
значит система не является динамически устойчивой. Следовательно, накопленная
кинетическая энергия не успевает превратиться в потенциальную, в результате
скорость вращения ротора и угол δ будут расти и генератор выпадет из
синхронизма. Для определения статической устойчивости системы необходимо найти
коэффициент запаса 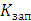
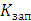 . Вычислив коэффициент запаса
. Вычислив коэффициент запаса 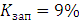
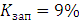 , можно сделать вывод, что система является статически устойчивой,
так как
, можно сделать вывод, что система является статически устойчивой,
так как 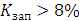
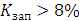 .
.
2.2 Расчёт
аварийного и послеаварийного режима при трёхфазном коротком замыкание в точке
К-2
2.2.1 Нормальный режим
Расчёт нормального режима проведён в задаче 1.
.2.2 Аварийный режим
Составляем схему замещения системы при трёхфазном КЗ
Рисунок 10 - Схема замещения системы при трёхфазном КЗ
При трёхфазном КЗ в точке К-2 взаимное сопротивление схемы
становится бесконечно большим, т.к. сопротивление шунта КЗ Х∆
(3) = 0. При этом характеристика мощности аварийного режима совпадает с
осью абсцисс.
.2.3 Послеаварийный режим
Схема замещения при трехфазном коротком замыкании и и расчет
послеаварийного режима аналогичем послеаварийному режиму, приведенному в
п.2.1.3
Рассчитываем значение углов:
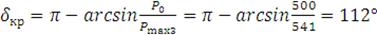
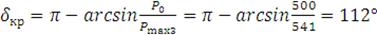 ,
,
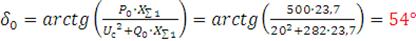
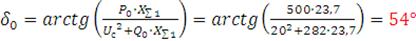 .
.
Находим предельный угол отключения КЗ δоткл:
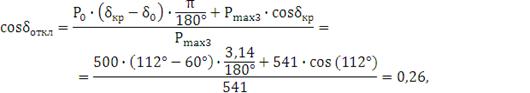
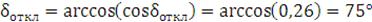
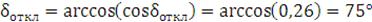 .
.
Рассчитываем предельное время отключения КЗ:
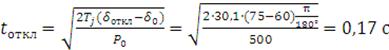
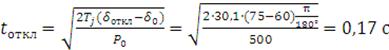 .
.
Выбираем соответствующие уставки срабатывания устройств РЗА:
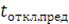
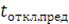 ≥ Тоткл =
≥ Тоткл = 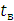
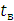 +
+ 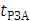
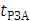
Поскольку линия имеет защиту, то через некоторое время она
отключится выключателями. Следовательно, выбираем элегазовый выключатель серии
ВГТ - 110 с временем отключения 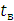
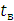 = 0,055 с. Также должны быть предусмотрены устройства релейной
защиты от КЗ. Выбираем токовое реле РТ-40 с временем уставки
= 0,055 с. Также должны быть предусмотрены устройства релейной
защиты от КЗ. Выбираем токовое реле РТ-40 с временем уставки 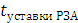
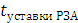 = 0,05 с.
= 0,05 с.
Время действия релейной защиты определяется:
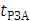
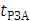 =
= 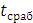
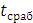 +
+ 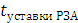
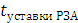 = 0,005 + 0,05 = 0,055 с,
= 0,005 + 0,05 = 0,055 с,
Находим время отключения КЗ:
Тоткл = 0,055 + 0,055 = 0,11 с.
,17 ≥ 0,11, что удовлетворяет условию 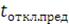
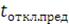 ≥ Тоткл
≥ Тоткл
Строим в одной координатной плоскости угловые характеристики
мощности в нормальном, аварийном и послеаварийном режимах, на графике указываем
значение мощности турбины Р0. С учётом рассчитанного значения
предельного угла отключения КЗ δоткл на графике строим площади ускорения и торможения.
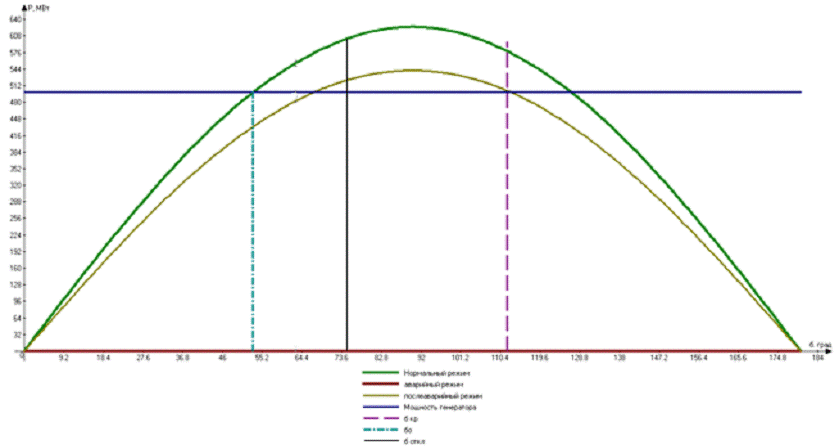
Рисунок 11 - График угловых характеристик мощностей и площади
ускорения и торможения при трёхфазном КЗ
Для определения динамической устойчивости системы при однофазном
КЗ необходимо рассмотреть площади ускорение Fуск и торможения Fторм.
Условием для динамической устойчивости системы является неравенство: Fуск
≤ Fторм. Невооруженным глазом видно по графику угловой
характеристики, что площадь ускорения на порядок больше площади торможения,
значит система не является динамически устойчивой. Следовательно, накопленная
кинетическая энергия не успевает превратиться в потенциальную, в результате
скорость вращения ротора и угол δ будут расти и генератор выпадет из
синхронизма. Для определения статической устойчивости системы необходимо найти
коэффициент запаса 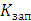
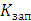 . Вычислив коэффициент запаса
. Вычислив коэффициент запаса 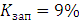
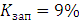 , можно сделать вывод, что система является статически устойчивой,
так как
, можно сделать вывод, что система является статически устойчивой,
так как 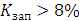
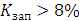 .
.
3. Рассчитать
предельное снижение напряжения на шинах асинхронного двигателя
Рассчитываем параметры элементов электропередачи и параметры
нагрузки, приведённые к базисному напряжению Uб = 6 кВ и базисной
мощности:
Sб = SАД ном = 
 ,
,
Сопротивление линии:
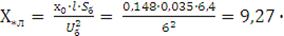
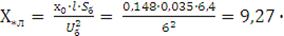 10-4
10-4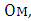
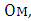
Индуктивное сопротивление рассеяния магнитной цепи двигателя:
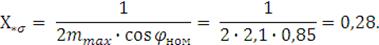
Определяем активную мощность потребляемая в исходном режиме
двигателя:
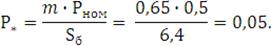
Находим активное сопротивление ротора двигателя в исходном режиме
(упрощенная схема замещения асинхронного двигателя):
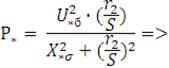
,05 = 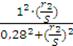
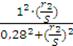 ,
,
,0392 +0,05∙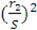
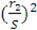 =
= 
 ,
,
произведём замену 
 на х и получим:
на х и получим:
,05х2 - х + 0,0392 = 0;
Д = в2
- 4ас = 12 - 4∙0,05∙0,0392 = 0,99216;
х1 = 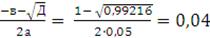
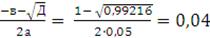 ;
;
х2 = 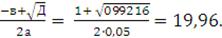
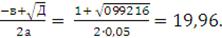
Выбираем наибольший из корней уравнения и получаем:

 = 19,96.
= 19,96.
Определяем реактивную мощность, потребляемую в исходном режиме
двигателем:
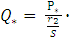
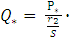
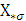
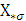 =
= 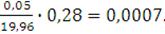
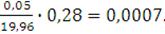
Определяем напряжение на шинах системы в исходном режиме:
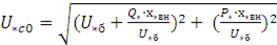
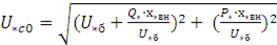
=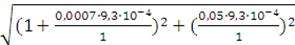
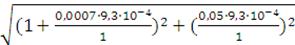 =1,где
=1,где 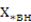
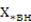 =
= 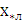
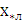 .
.
Определяем напряжение на шинах системы, при котором происходит
затормаживание двигателя:
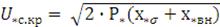
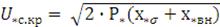 =
= 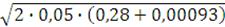
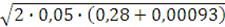 = 0,71.
= 0,71.
Определяем запас статической устойчивости двигателя по напряжению:
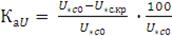
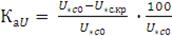 =
= 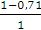
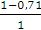 ∙
∙ 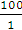
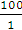 = 29%.
= 29%.
Для построения механической характеристики М = f (S) по уравнению
М = 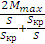
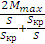 , необходимо произвести следующий расчёт:
, необходимо произвести следующий расчёт:
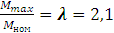
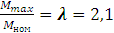
Определяем номинальную частоту вращения ротора:
ном
= n0∙ (1 - Sном) = 741∙ (1-0,01) = 734
об/мин.
Находим критическое скольжение:
кр
= Sном∙(?? +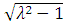
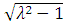 ) = 0,01∙ (2,1 +
) = 0,01∙ (2,1 + 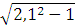
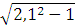 ) = 0,039.
) = 0,039.
Определяем номинальный и максимальный (критический) моменты
двигателя:
Мном = 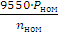
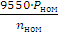 =
= 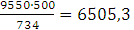
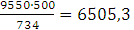 Н∙м,
Н∙м,
Мmax = ??
∙ Мном = 2,1∙6505,3 = 13661, 4 Н∙м.
Для построения механической характеристики воспользуемся формулой
Клосса:
М = 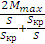
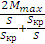 =
= 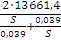
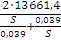
Задавшись различными значениями скольжения S, найдём
соответствующие им значения момента М. Результаты расчёта занесем в таблицу 6.
Таблица 6
|
S
|
M, Н∙м
|
|
0
|
|
0,01
|
6648
|
|
0,039
|
13661
|
|
0,06
|
12419
|
|
0,08
|
10589
|
|
0,1
|
9262
|
|
0,2
|
5126
|
|
0,3
|
3502
|
|
0,4
|
2642
|
|
0,5
|
2118
|
|
0,6
|
1763
|
|
0,7
|
1518
|
|
0,8
|
1332
|
|
0,9
|
1150
|
|
1
|
1064
|
По данным таблицы 6 строим график М = f (S):
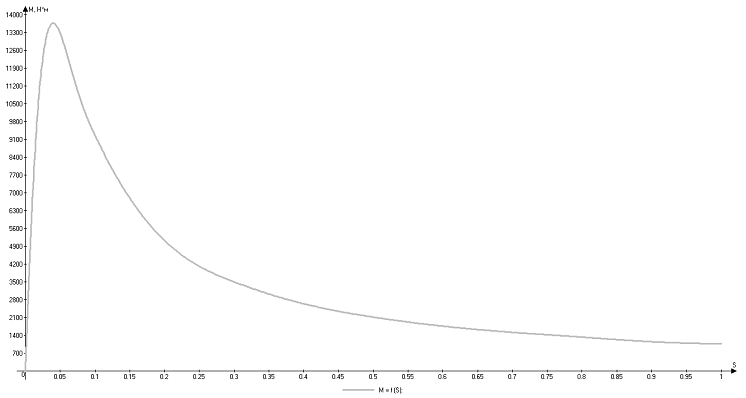
Рисунок 12 - График механической характеристики асинхронного
двигателя
Система является статически устойчивой, так как коэффициент запаса
двигателя по напряжению больше 20%
Заключение
После выполнения данной курсовой работы были отработаны и
закреплены теоретические знания, приобретенные в течение семестра по расчету
различных видов КЗ; проверки системы на статическую и динамическую устойчивать;
построения угловых характеристик мощности и механической характеристики асинхронных.
Научился выполнять анализ системы на устойчивость,
рассчитывать режимы работы системы до, после, и во время различных видов КЗ.
Можно сделать вывод, что расчет электромеханических
переходных процессов занимает одну из значимых позиций по расчету и
проектировании различных простых и сложных систем энергоснабжения.
Список
используемой литературы
1.
Куликов Ю.А. Переходные процессы в электрических системах: Учеб. пособие. -
Новосибирск: НГТУ, М.: Мир: ООО "Издательство АСТ", 2008. -
с.
.
Боровиков В.Н. и др. Электроэнергетические системы и сети - Москва:
Метроиздат., 2010. - 356 с.
.
Аполлонов А.А. Расчет и проектирование релейной защиты и автоматики - С. -
Петербург, 2009г. - 159 с.