Статические характеристики элементов криогенных систем
Курсовая работа
по теплотехническим криогенным
системам
Тема: СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ЭЛЕМЕНТОВ КРИОГЕННЫХ СИСТЕМ
Содержание
1. Моделирование статических нерасчетных режимов теплообменных
аппаратов
2. Расчет статических характеристик ступени охлаждения
3. Моделирование движения реального рабочего вещества во
вращающихся каналах
Список литературы
1.
Моделирование статических нерасчетных режимов теплообменных аппаратов
При анализе разнообразных криогенных
систем часто применяется метод структурного анализа, согласно которому
производится декомпозиция системы на ступени охлаждения.
Криогенную систему можно представить в
виде конструкции, состоящей из следующих ступеней: ступени подготовки рабочего
вещества (СПТ), на которой производятся его сжатие с отводом теплоты в
окружающую среду и очистка от примесей; ступени предварительного охлаждения
(СПО); ступени окончательного охлаждения (СОО), на которой ведется процесс
охлаждения путем преобразования внутренней энергии рабочего вещества при дросселировании,
расширении в детандере, выхлопе и т.п.; ступени использования эффекта
охлаждения (СИО), на которой обеспечивается вывод из системы субстанции либо в
виде теплоты, либо в виде конденсированного криопродукта. Структурно ступени
СИО и СОО могут частично или полностью совпадать. Часто в структурную схему
системы включается дополнительная криогенная установка, предназначенная для
получения внешнего криогенного продукта, используемого в СПО для отвода теплоты
от потока с высоким давлением [1,13, 14].
Ступени охлаждения, в свою очередь,
состоят из ряда стандартных элементов, в качестве которых широко используются
рекуперативные и радиационные теплообменные аппараты. В рекуперативных
теплообменных аппаратах может быть организовано различное взаимное направление
потоков рабочих сред. В зависимости от агрегатного состояния криоагентов они
подразделяются на жидкостно-жидкостные, газожидкостные и газо-газовые. Процесс
теплообмена в аппаратах первых двух типов может протекать с изменением
агрегатного состояния одного из криоагентов, в частности с кипением жидкости.
Процессы кипения криоагента осуществляются в ванне теплообменных аппаратов СПО
и в теплообменниках нагрузки СИО, которые являются парогенерирующими элементами
системы криогенного обеспечения.
К радиационным теплообменным аппаратам
прежде всего следует отнести элементы объекта криостатирования с радиационным
теплоподводом и внутристеночным выделением теплоты, участки криотрубопроводов и
другие элементы криогенных систем.
Современные системы криогенного
обеспечения рассчитывают с учетом последних достижений криогенной техники [13,
15]. Они способны работать при оптимальных параметрах с высокими
энергетическими показателями. Однако при эксплуатации могут возникать ситуации,
которые переводят отдельные элементы или всю систему криогенного обеспечения на
нерасчетные режимы работы. Для выявления степени влияния отдельных возмущающих
факторов на параметры потоков рабочих сред и оболочки каналов может быть
использован метод математического моделирования [10, 16, 17].
Метод математического моделирования
становится незаменимым при расчетных анализах схемных решений установок и
объектов новейшей техники.
При разработке математических моделей
элементов теплоэнергетических систем используются модели с сосредоточенными или
распределенными параметрами. В статических сосредоточенных моделях все
параметры системы не зависят от пространственных координат, и считается, что их
масса и энергия сосредоточены в материальной точке. Модели с распределенными
параметрами могут иметь одну, две и три пространственные координаты. При
моделировании реальных процессов теплообмена в элементах теплоэнергетических
систем рассматриваются модели теплообменных аппаратов с двумя, а чаще с одной
пространственной координатой. При анализе сложных структурных энергетических
систем применяются также комбинированные модели, в которых одни из элементов
представляются как системы с распределенными параметрами, другие - как системы
с сосредоточенными параметрами.
Модели теплообменных аппаратов криогенных
систем могут состоять из нескольких подсистем, например: первая - прямой поток
рабочего вещества, вторая - оболочка канала, третья - обратный поток или
термостатирующая жидкость.
Если математические модели теплообменных
аппаратов рассматриваются как одномерные в направлении оси x, тогда система
уравнений, описывающая исходный равновесный режим или новое устойчивое
состояние рекуперативного теплообменника, имеет вид:
уравнения сплошности
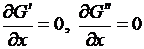 ; (2.1)
; (2.1)
уравнения энергии
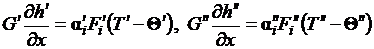 ; (2.2)
; (2.2)
уравнения состояния
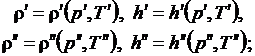
уравнения движения
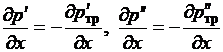 , (2.4)
, (2.4)
где G ¢, G ² - расход вещества прямого и обратного
потоков; h¢, h² - энтальпия потоков; α¢, α² -
коэффициенты теплоотдачи потоков; Fi¢, Fi² - площадь теплообменной поверхности наружной и внутренней стенок
оболочки канала; T ¢, T ² - температура прямого и обратного
потоков; Q¢, Q² - температура наружной и внутренней
поверхностей оболочки каналов; p¢, p² -
давление прямого и обратного потоков; ρ¢, ρ² - плотность потоков; 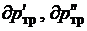 - потери давления в потоках.
- потери давления в потоках.
Из-за сложности реальных процессов, протекающих в теплообменных
аппаратах, при реализации их математических моделей численным методом
принимается ряд допущений:
1
по
расходу, давлению и внешнему тепловому потоку процесс рассматривается как
квазистационарный;
2
так
как закономерности движения реального потока определяются экспериментальным
путем и полученные при этом коэффициенты отражают реальную структуру потока,
считается, что процесс течения рабочих сред одномерный и их параметры
изменяются только в направлении движения потока по ординате x;
3
не
учитывается осевая теплопроводность материала оболочки канала и рабочих
веществ;
4
не
учитывается теплопроводность оболочки вдоль оси y, т.е. принимается, что
температура элементарного участка оболочки во всех точках данного сечения
постоянна: Qi¢= Qi²;
не учитывается теплоприток из окружающей среды, т.е. 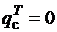 .
.
Математическая модель
противоточного рекуперативного теплообменного аппарата. На рис. 2.1 показана
физическая модель рассматриваемого теплообменного аппарата.
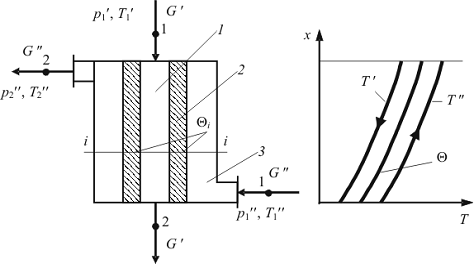
Рис. 2.1 Физическая модель рекуперативного
теплообменного аппарата: а - расчетная схема; б - распределение температуры по
высоте аппарата; 1 - прямой поток; 2 - оболочка канала; 3
- обратный поток
Рекуперативный теплообменник состоит из трех подсистем: оболочки
канала и двух рабочих сред - прямого G ¢ и обратного G ² потоков, которые имеют на входе параметры
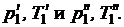 Для расчета распределения температур
вдоль ординаты x может быть применен метод элементарных
балансов [10, 18]. Для решения поставленной задачи поверхность теплообменного
аппарата разбивается на n участков Fi = F/n (рис.2.2)
и для i-го участка каждой подсистемы записываются
уравнения теплового баланса:
Для расчета распределения температур
вдоль ординаты x может быть применен метод элементарных
балансов [10, 18]. Для решения поставленной задачи поверхность теплообменного
аппарата разбивается на n участков Fi = F/n (рис.2.2)
и для i-го участка каждой подсистемы записываются
уравнения теплового баланса:
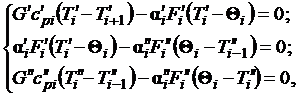
где 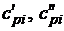 - теплоемкость в i-м сечении прямого и обратного потоков
соответственно;
- теплоемкость в i-м сечении прямого и обратного потоков
соответственно; 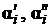 - коэффициенты теплоотдачи в i-м
сечении потоков;
- коэффициенты теплоотдачи в i-м
сечении потоков; 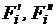 - площадь поверхности теплообмена
элементарного участка внутренней и наружной поверхностей оболочки канала.
- площадь поверхности теплообмена
элементарного участка внутренней и наружной поверхностей оболочки канала.
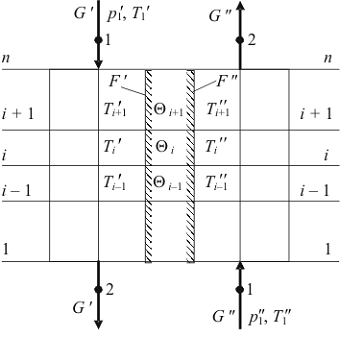
Рис. 2.2 Расчетная схема к определению статического распределения
термических параметров по высоте рекуперативного теплообменного аппарата
Выражения для расчета температуры каждой подсистемы в i-м сечении могут быть записаны следующим
образом:
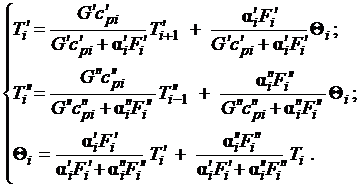 (2.6)
(2.6)
Для решения на ЭВМ система уравнений (2.6) может быть представлена
в виде
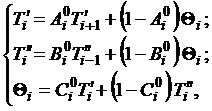 (2.7)
(2.7)
где 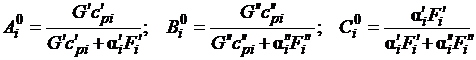 - коэффициенты, характеризующие условия
теплообмена на границах подсистем прямого и обратного потоков и оболочки
канала.
- коэффициенты, характеризующие условия
теплообмена на границах подсистем прямого и обратного потоков и оболочки
канала.
Поставленная задача является краевой; для ее решения численным
методом может быть применена либо неявная схема (когда рассматриваемая система
алгебраических уравнений, число которых равно числу участков n, представляется в виде трехдиагональной
матрицы и решается методом матричной прогонки), либо явная схема. При этом на
основании решения уравнения теплового баланса задается первоначальное
распределение параметров. Далее температуры для данного шага решения берутся на
основе предыдущей итерации.
Для решения системы уравнений (2.7) число участков выбирают таким
образом, чтобы значения коэффициентов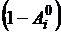 ,
, 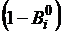 и
и 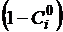 были положительными.
были положительными.
Из анализа структуры выражений для расчета значений коэффициентов 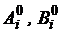 следует, что условие сходимости может
быть представлено как
следует, что условие сходимости может
быть представлено как
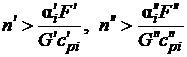 , (2.8)
, (2.8)
где n¢, n² - необходимое расчетное число участков
прямого и обратного потоков соответственно.
Истинное число участков должно быть больше или равно большему из
чисел n¢ и n².
Блок-схема реализации математической модели рекуперативного
теплообменного аппарата изображена на рис.2.3 С помощью блока 1 производится
ввод исходных данных. Блок 2 осуществляет обращение к программе расчета
термодинамического поля рабочих веществ. В блоке 3 вычисляется начальное
распределение температуры потоков рабочих сред. После задания начальных условий
счета по соответствующим процедурам в блоке 4 рассчитываются теплоемкость 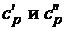 и другие теплофизические параметры
рабочих веществ, необходимые для расчета коэффициентов теплоотдачи. Локальные
коэффициенты теплоотдачи
и другие теплофизические параметры
рабочих веществ, необходимые для расчета коэффициентов теплоотдачи. Локальные
коэффициенты теплоотдачи 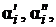 потери давления Dpi вычисляются по соответствующим
процедурам, вид которых выбирается исходя из принятой конструкции
теплообменного аппарата, геометрии каналов и условий теплообмена. В блоке 5
происходит определение коэффициентов уравнений типа (2.7), а в блоке 6 - расчет
методом итерации с заданной точностью EPS температуры в i-м сечении каждой подсистемы и давлений
потоков. В блоке 7 происходит наращивание цикла расчета и передача информации в
блоки 4 и 5. После завершения всего цикла результаты выводятся на печать или
информация передается соответствующим подпрограммам математической модели
криогенной системы (блок 8).
потери давления Dpi вычисляются по соответствующим
процедурам, вид которых выбирается исходя из принятой конструкции
теплообменного аппарата, геометрии каналов и условий теплообмена. В блоке 5
происходит определение коэффициентов уравнений типа (2.7), а в блоке 6 - расчет
методом итерации с заданной точностью EPS температуры в i-м сечении каждой подсистемы и давлений
потоков. В блоке 7 происходит наращивание цикла расчета и передача информации в
блоки 4 и 5. После завершения всего цикла результаты выводятся на печать или
информация передается соответствующим подпрограммам математической модели
криогенной системы (блок 8).
На рис. 2.4 отображены результаты расчета и
экспериментального исследования распределения температуры потоков гелия при
высоком и низком давлении в теплообменнике нижней ступени охлаждения
сателлитной гелиевой установки с избыточным обратным потоком. Показано
распределение температур в теплообменном аппарате типа "труба в
трубе" при следующих параметрах потоков: G ¢ = 0,0192 кг/с; y = (G ¢ - G ²) /G ¢=
0,08 при p1¢= 2,0 MПa, p2² = 0,13 МПа. Необходимо отметить
вполне удовлетворительное подтверждение расчетных зависимостей
экспериментальными данными [18].
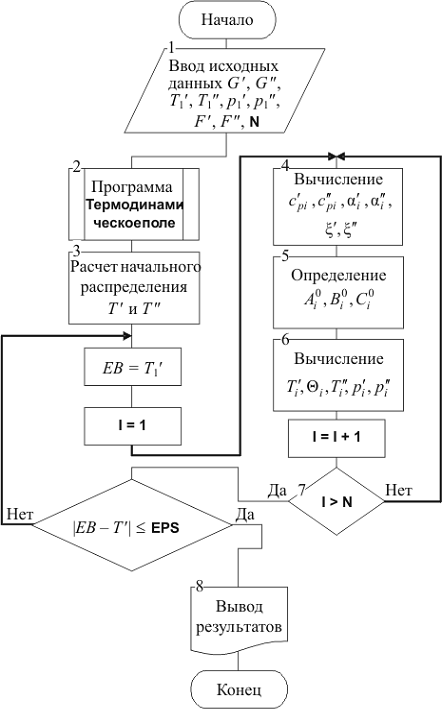
Рис. 2.3 Блок-схема алгоритма расчета рекуперативного
теплообменного аппарата
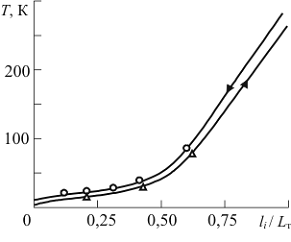
Рис. 2.4 Распределение температуры потока в теплообменном
аппарате:
- расчет; - экспериментальные точки
Математическая модель рекуперативного
теплообменного аппарата с кипением криоагента в межтрубном пространстве. На рис. 2.5 показана
физическая модель указанного аппарата.
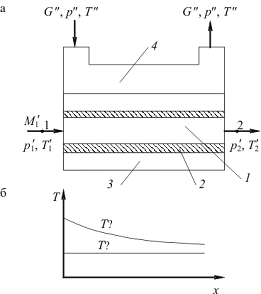
Рис. 2.5 Физическая модель рекуперативного теплообменного
аппарата с кипением криоагента: а - расчетная схема; б - распределение
температуры по длине аппарата; 1 - прямой поток; 2 - оболочка канала;
3 - кипящая жидкость; 4 - насыщенный пар
Рассматриваемый теплообменник относится к испарительным
аппаратам и состоит из трех подсистем: прямого потока, оболочки канала и
кипящего криоагента.
Тепловой баланс i-го участка для подсистем Прямой поток и Оболочка
канала может быть записан в виде (рис.2.6)
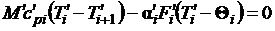 . (2.9)
. (2.9)
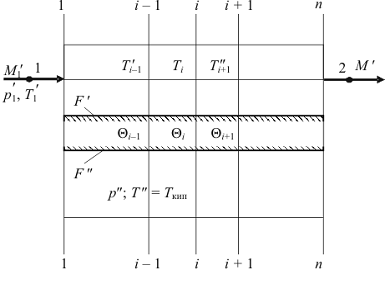
Рис. 2.6 Расчетная схема к определению статического распределения
параметров в подсистемах испарительного теплообменного аппарата
Значение коэффициента теплоотдачи 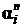 будет определяться теплофизическими свойствами кипящего
криоагента, режимом процесса кипения и условиями его осуществления. Для
пузырькового режима кипения в большом объеме коэффициент
будет определяться теплофизическими свойствами кипящего
криоагента, режимом процесса кипения и условиями его осуществления. Для
пузырькового режима кипения в большом объеме коэффициент 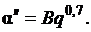 Зная, что
Зная, что 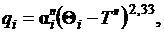 данное уравнение можно записать следующим образом [19, 20]:
данное уравнение можно записать следующим образом [19, 20]:
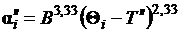 . (2.10)
. (2.10)
Тогда
из теплового баланса оболочки канала следует
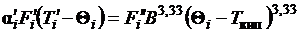 . (2.11)
. (2.11)
Поскольку теплообменные аппараты такого типа являются
парогенерирующими элементами криогенных систем, возникает необходимость в
расчете теплоты, подводимой к кипящему криоагенту. Для этого вычисляем значения
энтальпии потока M ¢ на
выходе из элементарного участка, т.е.
а затем поверхностную плотность теплового потока, подводимого к
кипящему криоагенту:
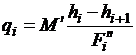 . (2.13)
. (2.13)
Давление потока M ¢ в сечении i +1 находим
по формуле
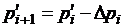 , (2.14)
, (2.14)
где Dpi - потеря давления потока M ¢ от гидравлического сопротивления канала.
Локальный коэффициент теплоотдачи 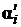 и величина xi
определяются по соответствующим расчетным процедурам. Температура потока M ¢ в сечении i
+1 может быть найдена путем
совместного решения уравнений (2.9) и (2.11) методом итерации или по двум
известным параметрам pi+1 и hi+1 с помощью процедуры ТН (Р, Н, Т).
и величина xi
определяются по соответствующим расчетным процедурам. Температура потока M ¢ в сечении i
+1 может быть найдена путем
совместного решения уравнений (2.9) и (2.11) методом итерации или по двум
известным параметрам pi+1 и hi+1 с помощью процедуры ТН (Р, Н, Т).
Блок-схема реализации алгоритма математической модели расчета
статического режима работы испарительного теплообменного аппарата изображена на
рис. 2.7.
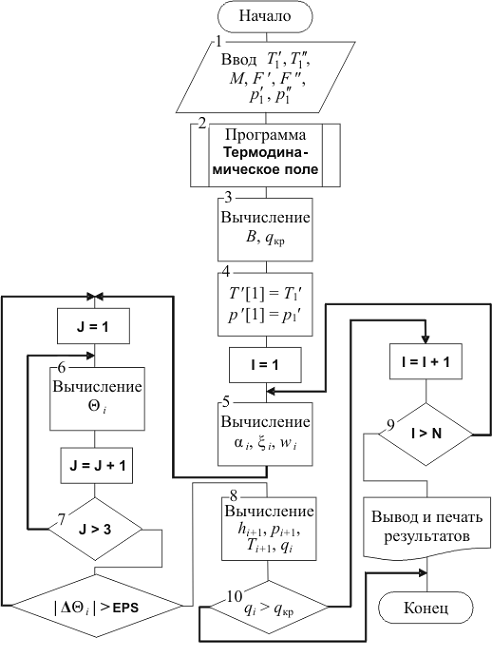
Рис. 2.7 Блок-схема расчета статического режима испарительного
теплообменного аппарата
В блоке 1 содержатся исходные данные, которые используются в
блоках 2 и 3 для расчета параметров термодинамических и теплофизических свойств
реального рабочего вещества и параметров B и qкр. В блоке 4 задаются начальные условия расчета, по которым
в блоках 5 и 6 вычисляются основные величины.
В блоке 7 происходит наращивание цикла расчета и передача
информации в блок 5 или 4. Поскольку в алгоритме расчета 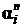 принято условие пузырькового режима
кипения криоагента, в блоке 9 происходит сравнение величин qкр и qi; в случае перехода в режим пленочного кипения решение
останавливается. После завершения всего цикла информация передается в блок 8
для вывода и печати результатов.
принято условие пузырькового режима
кипения криоагента, в блоке 9 происходит сравнение величин qкр и qi; в случае перехода в режим пленочного кипения решение
останавливается. После завершения всего цикла информация передается в блок 8
для вывода и печати результатов.
На основе приведенной блок-схемы и системы уравнений (2.9) -
(2.14) разработана и реализована подпрограмма HEX2
расчета распределенных параметров подсистем модели погружного рекуперативного
теплообменного аппарата [10].
Рекуперативные теплообменники с кипящим в межтрубном пространстве
криоагентом могут быть использованы в двухконтурных криогенных системах
термостатирования в качестве интегрального элемента, обеспечивающего связь
криогенной установки с циркуляционным контуром охлаждения объекта
криостатирования.
На рис. 2.8-2.10 отображены результаты моделирования процесса
теплообмена в теплообменнике нагрузки криогенной гелиевой установки (КГУ)
системы охлаждения ротора криотурбогенератора (КТГ) гелием при сверхкритическом
давлении. Наиболее интенсивное понижение температуры гелия (см. рис.2.8)
происходит на начальных участках. По мере движения гелия по трубе DTi уменьшается и при достаточной площади
поверхности теплообмена достигает минимального расчетного значения (DTж = 0,1 К). Локальные коэффициенты теплоотдачи
(см. рис.2.9) больше на начальных участках канала, где значения температурного
напора DTi велики, а при относительной длине li /Lт ³ 5 коэффициенты αi остаются практически постоянными. Эти
статические характеристики полностью соответствуют физической модели
теплообменника типа газ-жидкость.
В связи с тем что полное гидравлическое сопротивление
теплообменника Dp пропорционально M 2, с увеличением расхода (см. рис.2.10) наблюдается резкое
возрастание Dp (при изменении M ¢ от 0,02 до 0,1 кг/с потери давления возрастают с 0,0026 до 0,0439
МПа). В этом случае давление гелия, выходящего из теплообменника, составляет
0,256 МПа.
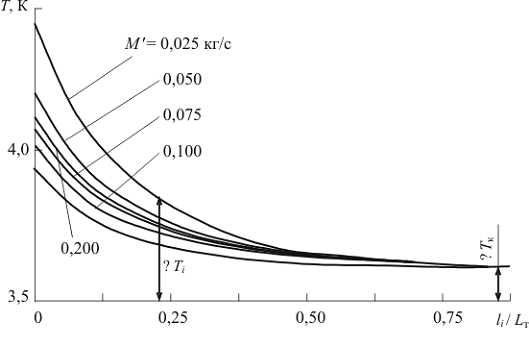
Рис. 2.8 Изменение температуры гелия при сверхкритическом давлении
по длине канала теплообменного аппарата
криогенная система теплообменный аппарат
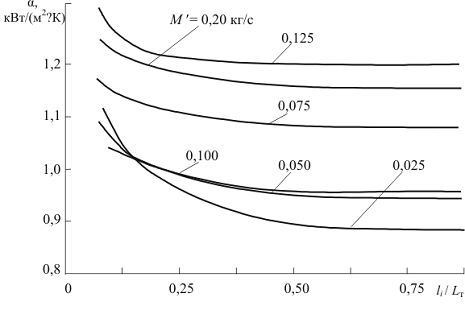
Рис. 2.9 Изменение коэффициента теплоотдачи по длине трубок
змеевика аппарата
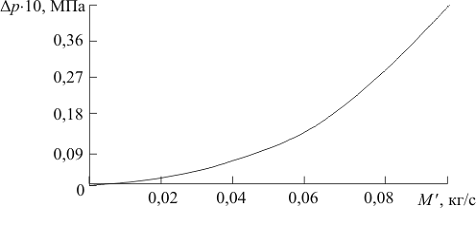
Рис. 2.10. Зависимость полного сопротивления Δp теплообменника нагрузки от расхода
переохлаждаемого потока гелия p1= 0,3 МПа
Дальнейшее увеличение расхода при данной геометрии канала
может привести к тому, что давление потока на выходе станет ниже критического.
На рис. 2.11 показана зависимость расхода испарившегося гелия
dG² от изменения количества
теплоты, подводимой циркуляционным потоком к жидкому гелию (в относительных
единицах при Ткип = 3,5 К). Очевидно, что наличие
дополнительного тепловыделения в объекте криостатирования вызывает переход на
нерасчетный режим работы парогенерирующего элемента системы, который, в свою
очередь, передает возмущение через обратный поток основному теплообменнику КГУ.
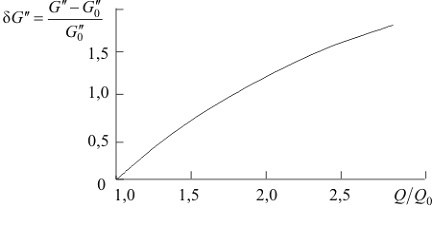
Рис. 2.11. Изменение относительной величины парового потока
от отношения Q/Q0 при Q0 = 70 Вт и G0²= 3,07·10-8 кг/с
Математическая модель радиационного
теплообменного аппарата с распределенными параметрами. На рис.2.12 показаны
физическая модель и расчетная схема аппарата, который состоит из двух подсистем
- прямого потока и оболочки канала. Внешний тепловой поток Q может иметь
различную интенсивность и произвольный характер распределения вдоль поверхности
оболочки канала и внутри ее. При разработке модели было принято, что внешний
поток равномерно распределен по наружной поверхности оболочки.
Расчет распределенного вдоль ординаты x температурного поля Ti потока M ¢ и оболочки канала Qi начинается с определения
локальных коэффициентов теплоотдачи αi при заданной в начале
расчета среднемассовой температуре потока Ti0.
Из теплового баланса элементарного участка (см. рис.2.12, б)
может быть получена зависимость для определения температуры оболочки канала Qi = Ti + qi /αi, где qi - поверхностная
плотность теплового потока.
Одновременно с определением по длине канала αi, Ti и Qi вычисляется падение
давления, вызванное гидравлическим сопротивлением трубы. Для участка канала,
заключенного между сечениями i и i + 1, падение давления
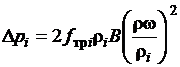 , (2.15)
, (2.15)
где fтр i - коэффициент трения; В = Lт / (dвнN), здесь dвн
- внутренний диаметр канала; 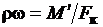 - среднемассовая скорость потока, здесь M ¢ - массовый расход; Fк - площадь проходного сечения канала.
- среднемассовая скорость потока, здесь M ¢ - массовый расход; Fк - площадь проходного сечения канала.
Тогда
давление вещества потока в сечении
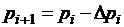 . (2.16)
. (2.16)
Энтальпия потока гелия в последующем сечении определяется из
теплового баланса элементарного участка:
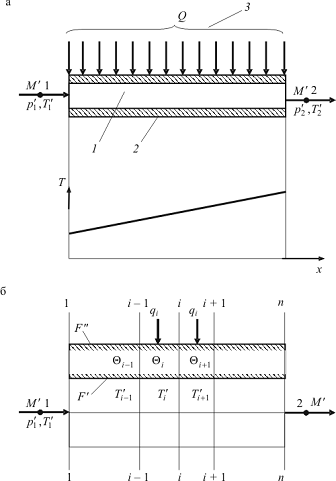
Рис. 2.12. Математическое моделирование радиационного
теплообменного аппарата: а - физическая модель; б - расчетная схема; 1 -
прямой поток; 2 - оболочка канала; 3 - тепловой поток
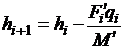 . (2.17)
. (2.17)
Среднемассовая температура потока Ti+1 рассчитывается по значениям давления pi+1 и энтальпии hi+1
с помощью процедуры TH (P,H,T).
На рис. 2.13 изображена блок-схема алгоритма расчета параметров
радиационного теплообменного аппарата.
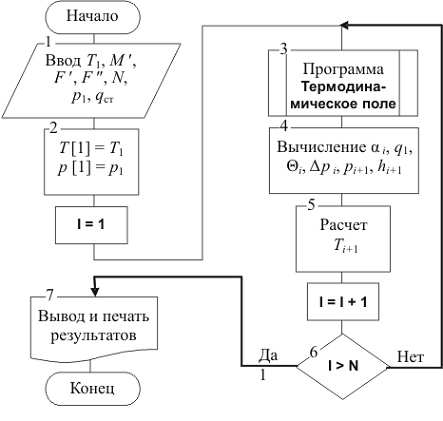
Рис. 2.13. Блок-схема алгоритма расчета параметров радиационного
теплообменного аппарата
В блоке 1 осуществляется ввод исходных данных, в блоке 2
содержатся начальные условия. В блоке 3 вызываются необходимые параметры термодинамического
поля рабочего вещества, которые используются в блоках 4 и 5 для определения
искомых величин. В блоке 6 обеспечивается полный цикл расчетов, после
завершения которых информация передается в блок 7 для печати, вывода и передачи
соответствующим подпрограммам.
Алгоритм расчета радиационного теплообменного аппарата для
охлаждения оболочки канала гелием при сверхкритическом давлении реализован в
подпрограмме HEX [21].
На рис.2.14 показаны статические
характеристики радиационного теплообменного аппарата, который представляет
собой канал сверхпроводящей обмотки возбуждения (СПОВ) ротора с равномерно
распределенным внешним теплопритоком.
Вычислительный эксперимент проводился при
поверхностной плотности тепловых потоков qст = 8,55 Вт/м и qст = 34,2 Вт/м и M ¢ = 0,1 кг/с. В обоих случаях была получена практически линейная
зависимость изменения Ti и Θi по длине канала (см.
рис.2.14, а): температуры стенки и потока монотонно возрастают. С увеличением qст возрастает и ΔTi. Для исследованных режимов теплообмена
эта разность мала: при qст = 8,55 Вт/м2 и M ¢ = 0,1 кг/с
она составляет около 0,006 K, а при qст = 34,2 Вт/м2 и том же
расходе - около 0,05 К. Вместе с тем перепад температур по длине канала равен
0,17 и 0,65 К соответственно.
Необходимо отметить, что для всех
исследованных режи- мов характерны достаточно высокие значения αi - в пределах 1,07…1,49 кВт/ (м2·К). Однако при M ¢ = const степень изменения αi относительно li / Lт незначительна, так как
среднемассовая скорость гелия по длине канала, ввиду несущественности изменения
температуры потока, остается почти постоянной и мало влияет на локальный
коэффициент теплоотдачи.
Гидравлические потери давления монотонно
возрастают по длине канала и имеют линейную зависимость. Увеличение Δpi может быть объяснено тем, что с
повышением Ti становится больше локальная скорость потока гелия из-за
уменьшения его плотности.
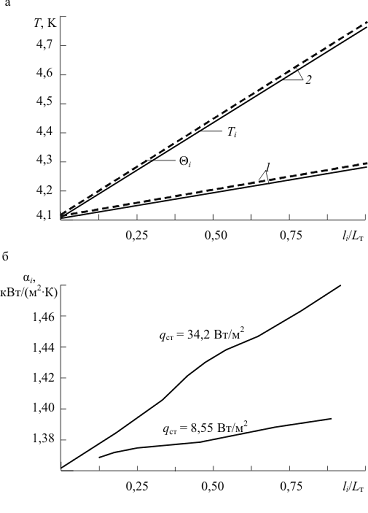
Рис. 2.14. Статические характеристики
радиационного теплообменного аппарата: а - изменение температуры потока и
стенки; б - изменение коэффициента теплоотдачи αi по длине охлаждаемых
каналов ротора при расходе гелия M ′ = 0,1 кг/с для различных
значений плотности тепловых потоков; 1 - 8,55 Вт/м2; 2
- 34,2 Вт/м2
2. Расчет
статических характеристик ступени охлаждения
В многоступенчатых криогенных установках
особое место занимает ступень использования охлаждения, особенно в
двухконтурных системах криостатирования. В этом случае СИО обеспечивает связь
энергетических и материальных потоков криогенной установки и объекта
криостатирования. Объекты криостатирования часто представляют собой сложные
криоэнергетические машины и устройства с многофакторными режимными параметрами,
изменение которых может сильно влиять на показатели работы криогенной системы
[15].
К объектам криостатирования, в частности,
относится и сверхпроводящий ротор КТГ [22], схема циркуляционного контура
охлаждения которого изображена на рис.2.15. В ротор III криотурбогенератора
подаются два потока гелия. Поток G, предназначенный для охлаждения термического
экрана, токовводов и тепловых мостов, направляется из КГУ в центральную полость
ротора, где создается разрежение под действием термосифонного эффекта
теплообменников тепловых мостов II.
Сверхпроводящая обмотка возбуждения IV криостатируется с помощью циркуляционного потока гелия M ¢, кратность циркуляции которого
обеспечивается насосом VI.
Теплообменник нагрузки I является
связующим звеном между циркуляционным контуром и криогенной
гелиевой установкой. Для снятия тепловой нагрузки из гелиевой установки подается
поток жидкого гелия 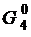 , который кипит в теплообменнике I при разрежении, создаваемом криогенным нагнетателем VII.
, который кипит в теплообменнике I при разрежении, создаваемом криогенным нагнетателем VII.
Для исследования взаимного влияния структурных элементов на
условия криостатирования ротора может быть применено математическое
моделирование.
Для расчетного анализа циркуляционного контура КТГ принимается
комбинированная математическая модель, состоящая из элементов с распределенными
(I, IV, V) и сосредоточенными (радиальные каналы
0-1, 2-3 и циркуляционный насос) параметрами. Разработана программа Контур,
блок-схема которой показана на рис.2.16. При построении модели использован
итерационный метод.
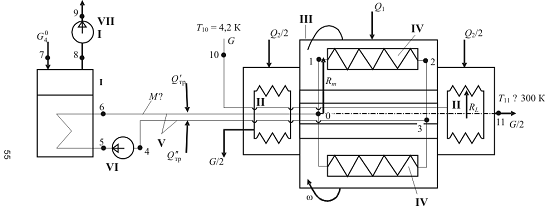
Рис. 2.15. Принципиальная схема криостатирования ротора
криотурбогенератора: I - теплообменник нагрузки; II - теплообменники тепловых
мостов; III - ротор; IV - бандаж СПОВ; V - криотрубопроводы; VI -
циркуляционный насос; VII - криогенный нагнетатель; 1-11 - характерные точки
циркуляционного контура

Рис. 2.16. Блок-схема алгоритма расчета программы Контур
Расчет начинается с точки 6, так как ее
параметры наиболее достоверно могут быть найдены из условий теплообмена в
аппарате I.
Параметры в точке 0 (p0, T0, h0) определяются с помощью
подпрограммы HEX при заданном потоке M ¢, его параметрах p6, Т6 на
входе в криотрубопровод и поверхностной плотности внешнего теплового потока qт. При расчете параметров
состояния гелия на выходе из радиального канала принимаем, что в канале 0-1 под
действием центробежных сил происходит сжатие гелиевого потока. Параметры точки
1 определяются путем совместного решения уравнений методом последовательных
приближений:
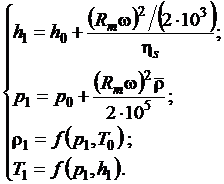
Для моделирования тепловых процессов в горизонтальном гелиевом
канале 1-2 используется подпрограмма HEX, при реализации которой определяются параметры p2, T2, h2 и т.д. При этом принимаем, что поток гелия равномерно
распределяется по всем горизонтальным каналам и имеет одинаковые параметры на
входе. Параметры точки 3 с учетом наличия центростремительного торможения
потока гелия в радиальном канале 2-3 определяем путем совместного решения
системы уравнений методом последовательных приближений:
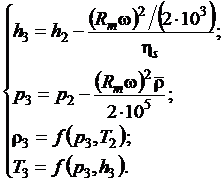
Параметры состояния гелия в точке 4 (p4, T4, h4, ρ4) перед циркуляционным насосом
рассчитываются аналогично параметрам точки 0 по программе HEX.
Параметры точки 5, расположенной после циркуляционного насоса,
определяются из условия, что насос обеспечивает изменение давления
циркуляционного потока гелия до давления в точке 0 в теплообменном аппарате I и криотрубопроводе:
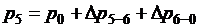 . (2.20)
. (2.20)
Тогда энтальпия в точке 5 определяется как
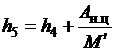 , (2.21)
, (2.21)
а температура будет найдена по давлению и энтальпии:
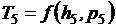 . (2.22)
. (2.22)
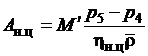 , (2.23)
, (2.23)
где
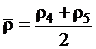 . (2.24)
. (2.24)
Уравнения (2.21) - (2.24) решаются совместно методом последовательных
приближений.
В связи с тем что ротор создает собственный напор, в ряде случаев
давление перед насосом p4 может быть больше, чем требуемое давление
р5. В таком случае параметры точки 5 определяются из
предположения о том, что в насосе происходит процесс дросселирования потока
гелия от давления р4 до p5
при h4 = h5 = const, а работа насоса Aн. ц = 0. Параметры в точке 6, т.е. на выходе теплообменника I, определяются по подпрограмме HEX2.
Расчет параметров состояния гелия в характерных точках циркуляционного
контура заканчивается вычислением теплового потока, отводимого криогенной
установкой:
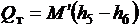 . (2.25)
. (2.25)
Параметры циркуляционного и кипящего гелия во всех характерных
точках рассчитываются с помощью программы Термодинамическое поле,
разработанной на базе подпрограмм расчета термических и калорических параметров
криогенных рабочих веществ (см. разд.1).
Численный эксперимент проводится при допущении, что все элементы
ротора (токовводы, тепловые экраны, теплообменники тепловых мостов, элементы
подвески ротора) охлаждены до рабочих температур и теплоприток в них снимается
благодаря дополнительному потоку гелия G, а циркуляционный гелий воспринимает только равномерно
распределенный по периферии ротора тепловой поток Q1.
Для расчета принимаются следующие условия: температура кипящего
гелия в аппарате I Tкип
= 3,5 К; длина криотрубопровода Lт = 10 м, а теплоприток к ним 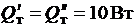 ; КПД насоса ηн. ц = 0,7; изоэнтропный КПД процессов сжатия и торможения гелия в
радиальных каналах ротора ηs = 0,9…1,0; радиус Rm = 0,34 м; длина
каналов охлаждения СПОВ lк = 2,5 м; число
каналов охлаждения Nк = 388 с внутренним
диаметром dвн = 0,002 м; частота вращения ротора n = 50-1 с.
; КПД насоса ηн. ц = 0,7; изоэнтропный КПД процессов сжатия и торможения гелия в
радиальных каналах ротора ηs = 0,9…1,0; радиус Rm = 0,34 м; длина
каналов охлаждения СПОВ lк = 2,5 м; число
каналов охлаждения Nк = 388 с внутренним
диаметром dвн = 0,002 м; частота вращения ротора n = 50-1 с.
Результаты численного эксперимента отображены на рис. 2.17.
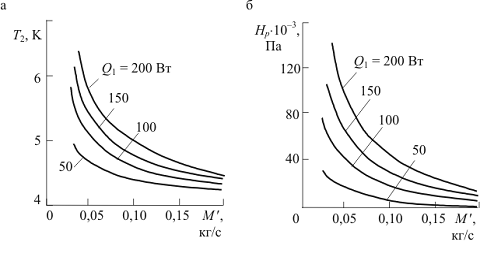
Рис. 2.17. Изменение температуры гелия при Rm = 0,34 м: а - на выходе из каналов бандажа
СПОВ; б - собственного напора ротора
Из анализа рис. 2.17, а следует, что
температура гелия на выходе из каналов на участке циркуляционного контура
интенсивно падает при изменении массы потока с 0,025 до 0,1 кг/с. Дальнейшее увеличение расхода гелия в каналах с 0,1 до 0,2 кг/с существенного уменьшения температуры циркуляционного гелия в
точке 2 (см. рис.2.15) не вызывает. При расходе вещества циркуляционного потока
гелия порядка 0,03 кг/с для принятых значений Q1 обеспечивается заданный уровень термостатирования, так как
полученные значения температуры меньше заданного значения максимально
допустимой температуры СПОВ Tmax = 6 К.
Значение собственного напора ротора в циркуляционном тракте при
определенных параметрах однофазного потока достаточно велико (см. рис.2.17, б).
Учитывая, что собственный напор ротора при постоянной линейной скорости потока
на расстоянии Rm от оси вращения зависит от разности
значений плотности гелия на участках, где движение его происходит под действием
центробежных и центро-стремительных сил, констатируем, что Hp возрастает при увеличении Q1 и уменьшении M ¢.
Компенсация гидравлических потерь давления на ряде участков
циркуляционного контура приводит к тому, что практически во всех рассмотренных
расчетных режимах давление перед насосом p4
выше требуемого p5 и Aн. ц = 0.
3.
Моделирование движения реального рабочего вещества во вращающихся каналах
В системах криогенного обеспечения
энергетических машин и устройств широко применяются поточные машины
динамического действия, называемые лопаточными или турбомашинами. К ним
относятся турбокомпрессоры, турбодетандеры, криогенные нагнетатели, а также
центробежные насосы. В лопаточных машинах главными рабочими элементами,
образующими проточную часть, служат две решетки - вращающаяся (рабочее колесо)
и неподвижная (направляющий аппарат).
Объекты криостатирования с циркуляционным
охлаждением снабжены системой каналов, в которых обеспечивается заданный режим
течения криоагента. Специфическим объектом криостатирования является ротор КТГ,
в каналах которого под действием центробежных или центростремительных сил
создаются специфические условия течения гелия. В связи с этим интерес
представляет качественная оценка характера изменения параметров потока рабочего
вещества в межлопаточных каналах рабочих колес центробежных насосов, криогенных
нагнетателей и в радиальных каналах ротора.
Основные уравнения движения
рабочего вещества с переменной массой при учете трения и подвода энергии. Рассмотрим элемент канала
(рис. 2.18), заключенный между сечениями 1-1 и 2-2.
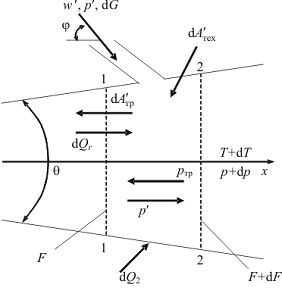
Рис. 2.18. Расчетная схема одномерного течения сжимаемого рабочего
вещества в произвольном сечении канала
Примем, что в сечении 1-1 поток рабочего
вещества и канал характеризуются следующими параметрами: ρ - плотность, T - температура, p - давление, h - энтальпия, G - массовый расход, ω - линейная скорость, F - площадь поперечного сечения канала.
В сечении 2-2 эти параметры таковы:
ρ + dρ, T + dT, p + dp, h + dh, G + dG, w + dw, F + dF.
Поток dG поступает через перфорацию суммарной
площадью 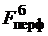 в боковой поверхности F б со скоростью w¢ и
давлением p¢. При этом степень перфорации
в боковой поверхности F б со скоростью w¢ и
давлением p¢. При этом степень перфорации
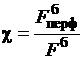 . (2.27)
. (2.27)
В общем случае угол раскрытия канала θ может быть найден из соотношения 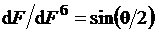 . Для цилиндрического канала θ = 0 и принимается, что рабочее вещество
подводится под углом φ.
. Для цилиндрического канала θ = 0 и принимается, что рабочее вещество
подводится под углом φ.
Уравнение количества движения для рассматриваемого случая имеет в
вид [23]
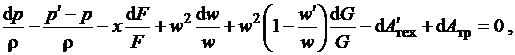 (2.28)
(2.28)
где 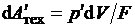 - удельная работа внешней массовой силы,
здесь p′ - удельная массовая сила,
совпадающая по знаку с вектором скорости (для насоса от лопатки рабочего
колеса);
- удельная работа внешней массовой силы,
здесь p′ - удельная массовая сила,
совпадающая по знаку с вектором скорости (для насоса от лопатки рабочего
колеса);  - удельная работа сил трения, здесь pтр - сила трения;
- удельная работа сил трения, здесь pтр - сила трения;
Дифференцируя уравнение расхода G = ρwF, уравнения состояния вида p = p (ρ, s) и T
= T (ρ, p), а также принимая, что дифференциал энтропии
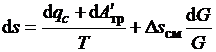 , (2.29)
, (2.29)
где Δsсм - приращение энтропии рабочего вещества
при смешении основного потока G с
подводимым потоком dG, находим зависимости для определения
изменения скорости, давления и температуры на элементарном участке dx оси канала:
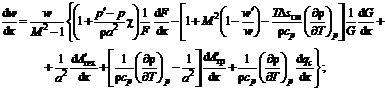
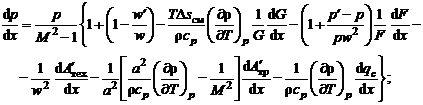
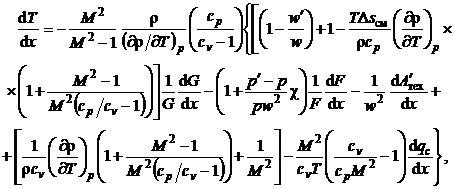
где M = w/a - число Маха; a - скорость звука; cv, cp - удельная теплоемкость
рабочего вещества при постоянном объеме и давлении соответственно.
При решении дифференциальных уравнений (2.30) - (2.32) необходимо
знать изменение энтропии Δsсм при смешении потоков ΔG и G. Для этого преобразованием уравнения сохранения количества
движения (2.28) при одном только расходном воздействии, т.е. при условии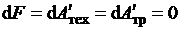 , было получено [24] для 1 кг вещества
изменение энтропии
, было получено [24] для 1 кг вещества
изменение энтропии
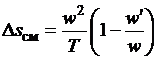 . (2.33)
. (2.33)
Определение поля скоростей и термодинамических параметров в
радиальном сечении вращающихся каналов. При анализе режимов течения рабочего вещества во
вращающихся каналах различают абсолютное, относительное и переносное движение
со скоростями c, w, u соответственно.
Таким образом, каждая частица рабочего вещества имеет скорость c = u + w, где c, u, w - векторы. Модуль этих скоростей может быть определен из
треугольника скоростей на входе и выходе канала (рис. 2.19).
Дифференциальные уравнения (2.30) - (2.32) позволяют рассчитать
распределение скорости, давления и температуры вдоль средней линии канала
произвольной конфигурации (см. рис.2.19, а). Средняя линия радиального сечения
канала проводится через центры вписанных окружностей с текущими значениями
диаметра.
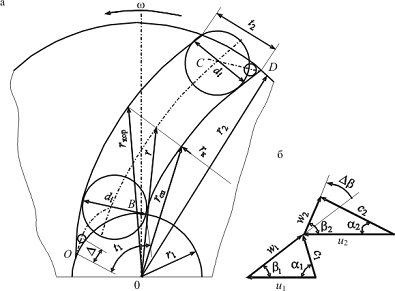
Рис. 2.19. Расчетная схема вращающегося канала: а - геометрические
параметры канала; б - треугольники скоростей
Площадь сечения канала вычисляем по формуле Fi = dibi, где bi
- диаметр окружности, вписанной в меридиальное сечение. На участках косых
срезов канала с шагами t1, t2
на входе и выходе размеры di
определяются вдоль линий, ортогональных к корыту канала. Зависимости площади
сечения F = f (x), радиусов
средней линии канала r = f (x), шагов t1 = f (x) и t2 = f (x) на расходных участках могут быть заданы в виде одномерных
массивов.
В свою очередь, производные геометрических параметров массового
расхода и теплоподвода извне, зависящие от длины средней линии канала,
определяются соотношением вида
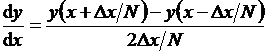 , (2.34)
, (2.34)
где x - расстояние от начала канала до
рассматриваемого сечения; Δx - шаг по длине средней линии канала; N - целое число.
Массовый расход задается в виде зависимости G = G [t (x)] на участках косого среза канала. Производные механической
работы и потерь вычисляем по формулам
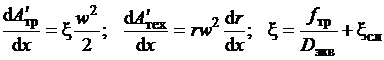 , (2.35)
, (2.35)
где ξ - коэффициент
потерь, отнесенный к единице длины канала; fтр - местный
коэффициент трения; Dэкв - эквивалентный диаметр; ξсл - коэффициент, учитывающий потери от случайных факторов.
При рассмотрении квазидвумерного течения скорости p и T на границах канала (корыте и спинке) определяем с учетом его
профиля и угловой скорости:
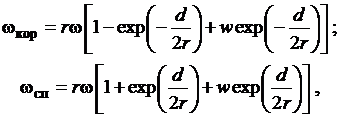
где r ≈ 0,5 (rкор+ rсп) - радиус кривизны линии
тока, здесь rкор, rсп - радиусы кривизны корыта и спинки канала; d - диаметр окружности,
вписанной в канал радиальной плоскости; w - скорость потока на
средней линии канала; ω - угловая скорость
последнего [25].
Давление и температуру находим из
предположения, что вдоль диаметра d изменение параметров потока происходит при s = const. Тогда для рассматриваемого
сечения по известной энтальпии заторможенного потока на границах канала
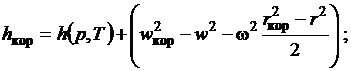 (2.38)
(2.38)
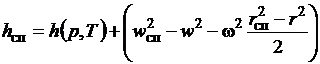 (2.39)
(2.39)
и энтропии
s = f (p,T) (2.40)
с помощью соответствующих процедур расчета параметров термодинамического
поля рабочего вещества получаем искомые величины:
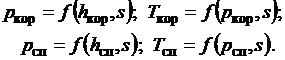 (2.41)
(2.41)
Исходная система дифференциальных уравнений решена методом
Рунге-Кутта, для реализации которого применена стандартная подпрограмма
математического обеспечения. Для использования подпрограммы разработана
процедура расчета правых частей уравнений (2.30) - (2.32), текст которой
показан на рис.2.20.
В этой подпрограмме M - число Маха; PG, PF, PLR, PLT, PQC, PCIGW, PCIGP, PCIGT - производные расхода,
площади сечения канала, удельной работы потерь, удельной подведенной работы,
удельного теплоподвода извне, скорости, давления и температуры от длины канала x соответственно.
Далее приведен пример численного эксперимента, характеризующий
параметры квазидвумерного течения гелия в каналах рабочих колес (РК)
центробежного насоса (ЦН), криогенного нагнетателя (КН) и в радиальных каналах
ротора КТГ. Эти данные получены при условии, что 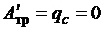 .
.
Течение однофазного потока гелия в межлопаточных каналах
рабочего колеса центробежного насоса и криогенного нагнетателя. При моделировании течения гелия в
межлопаточных каналах РК, ЦН, КН принимают следующие геометрические
характеристики: d1 = 0,028 м - входной диаметр; d2 = 0,12 м - выходной диаметр; rк = 0,0403 м - радиус
привязки лопатки РК; β1л = 32° - входной установочный угол лопатки; i = 6° - угол атаки потока; OB = 0,006 м - длина средней линии на участке входного косого среза с шагом t1 (см. рис.2.19); OC = 0,0725 м - длина средней линии канала до начала выходного косого среза с
шагом t2; OD = Lкан = 0,102 м - длина средней линии межлопаточного
канала РК; b1 = 0,009 м - ширина канала в меридиальном сечении; z1 = 12 - число лопаток.
При течении гелия со сверхкритическим давлением в межлопаточном
канале РК создаются сложные гидродинамические условия, обусловленные угловой
скоростью канала и его профилем, что может привести к образованию в канале РК
обратных вихревых потоков.

Рис. 2.20. Подпрограмма расчета правых частей уравнений (2.30) -
(2.32)
В анализируемом случае вышесказанное подтверждается отрицательными
значениями относительной скорости wсп вдоль спинки лопатки канала (рис. 2.21).
Рис. 2.21. Изменение скорости течения гелия в межлопаточном
пространстве РК ЦН при p1 = 0,26 МПа и T1 = 3,8 К: 1-3 -
при частоте вращения n = 25 c-1; 1′-3′ - при n = 75 c-1; 1, 1′
- вдоль средней линии канала; 2, 2′ - вдоль корыта лопатки;
3, 3′ - вдоль спинки лопатки
Естественно, что наиболее сложные условия
течения потока гелия создаются на участках косых срезов канала РК, поэтому при
решении уравнения (2.30) для данных участков учтены как изменение площади
проходного сечения, так и закономерность расхода гелия для входного G1 = G [t1 (x)] и выходного G2 = G [t2 (x)] косых срезов. В
численном эксперименте значение скорости потока, полученное решением уравнения
(2.30), контролируется ее значением, найденным из уравнения расхода.
Практически полное совпадение указанных величин достигается только на участке
канала между косыми срезами.
Течение гелия со сверхкритическим
давлением в межлопаточном канале РК ЦН при изменении частоты вращения от 25 до
50 с-1 происходит
в докритическом режиме (при M = 0,003…0,01) при T ≈ const. Температура потока такого гелия вдоль средней
линии межлопаточного канала РК изменяется на сотые доли градуса Кельвина. Так,
при n =
25 с-1 и
температуре на входе в РК T1 = 3,8 К она достигает значения
на выходе T2 = 3,81 К, а при n = 50 с-1 - T2 = 3,87 К.
Одновременно с этим наблюдается расслоение
температур в перпендикулярном сечении к направлению потока гелия. Так, при n = 50 с-1 и x = 0,072 м на средней линии потока
T = 3,86 К на линиях потока вдоль
спинки канала Tсп =
3,85 К, а вдоль корыта канала Tкор = 3,87 К.
Важными параметрами ЦН являются расход и
напор потока (рис. 2.22).
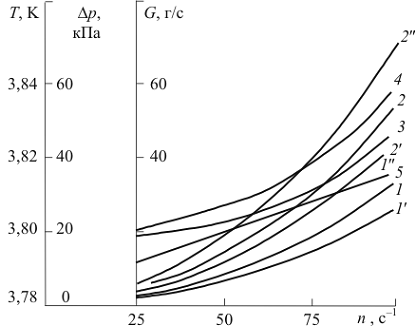
Рис. 2.22. Изменение параметров потока гелия в сечении
межлопаточного канала РК насоса при различной частоте вращения, p1 = 0,26 МПа и T1 = 3,8 K: 1, 1', 1''
и 2, 2', 2'' - перепад давления потока при x = 0,045 м и x = 0,06 м; 1, 2 -
перепад давления на средней линии канала; 1', 2' - на линии тока
вдоль спинки лопатки; 1'', 2'' - на линии тока вдоль корыта
лопатки; 3, 4 - температура потока на средней линии
канала при x = 0,045 м и x = 0,06 м; 5 - расход гелия
через полное сечение межлопаточного канала
При принятых геометрических размерах РК ЦН
уже при n =
25 с-1 обеспечивает
расход G =
118,3 г/с, а перепад давления
вдоль средней линии канала Δp = 5,84 кПа. С возрастанием
частоты вращения РК рассматриваемые параметры увеличиваются.
В системах криообеспечения криогенные
нагнетатели предназначаются для создания необходимого уровня разрежения в
межтрубном пространстве теплообменника нагрузки и сжатия удаляемых паров гелия
до давления обратного потока в аппаратах КГУ. Для качественной оценки
параметров квазидвумерного течения парообразного гелия в канале РК криогенного
нагнетателя на рис.2.23 показаны характеристики для двух режимов: n = 166,7 с-1 и n = 333,3 с-1.
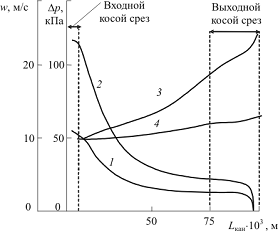
Рис. 2.23. Изменение параметров потока парообразного гелия вдоль
средней линии канала РК КН при различных частотах вращения и p1 = 0,047 МПа, T1 = 3,5 К: 1, 2 - значения скорости при n = 166,7 c-1 и n = 333,3 с-1;
3, 4 - значения давления при n = 333,3 с-1
и n = 166,7 c-
При течении парообразного гелия в межлопаточном канале РК КН имеет
место также докритический режим с числами Маха порядка 0,033…0,038 и заметным
изменением плотности потока (при n =
333,3 с-1 она увеличивается в 1,8
раза). Для принятых условий (n = 333,3 с-1) численного эксперимента получено, что расход
парообразного гелия через РК КН составляет 86,1 г/с при
параметрах потока гелия на входе в косой выходной срез (x = 0,0725 м) р = 125 кПа и Т ≈ 5,3 К.
Таким образом, при относительно больших геометрических размерах РК
КН (в реальных машинах применяются РК с d2 =
= 0,035 м и n = 833 с-1) необходимые параметры
могут быть обеспечены при n
= 333 с-1.
Течение центробежного однофазного потока гелия в радиальных
каналах КТГ. Моделирование
квазидвумерного течения в радиальных каналах КТГ проводилось на прямолинейном
канале при следующих геометрических характеристиках: d1 = 0,05 м - диаметр
подводной трубы; r2 = 0,34 м, a = 0,01 м, b = 0,015 м - длина,
глубина и ширина канала; β1л = 32°; i = 6°; OB = 0,0201; OC = 0,343 м. Характер
изменения давления и температуры вдоль средней линии канала показан на рис.
2.24.
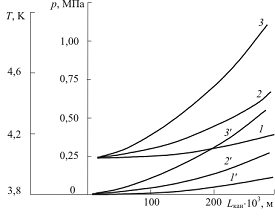
Рис.2.24. Изменение давления и температуры гелия по длине
каналов ротора КТГ в зависимости от частоты вращения при p1 = 0,26 МПа и T1 = 3,8 К: 1-3 -
значения давления; 1'-3' - значения температуры; 1, 1'
- n =
16,67 c-1; 2, 2' - n = 33,33 c-1; 3, 3' - n = 50 с-1
Было рассмотрено два режима: течение гелия
при сверхкритических параметрах и течение парообразного гелия.
При течении в прямолинейном канале гелия с
параметрами на входе T1 = 3,8 К, p1 = 0,26 МПа и n = 50 с-1 имеет
место докритический режим при числах Маха порядка 0,026…0,0195 и небольшом
изменении плотности потока. Скорости потока изменяются практически по линейному
закону; например, на участке канала длиной x = 0,150 м они имеют следующие
значения: w =
6 м/с; wсп = 3,65 м/с; wкор = 8,35 м/с.
На рис.2.25 показаны результаты расчетного
анализа течения парообразного гелия в радиальном откачном канале
теплообменников мостов КТГ.
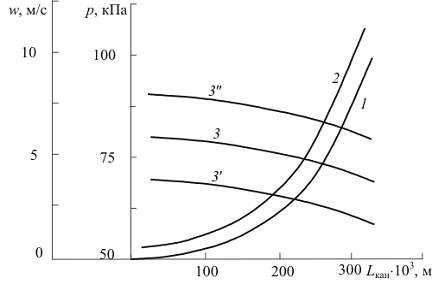
Рис. 2.25. Изменение скорости и давления потока парообразного
гелия при течении в радиальном канале теплообменников тепловых мостов КТГ: 1
- значение давления потока на средней линии канала при температуре на входе T1 = 3,55 К; 2 - то же при T1 = 3,6 К; 3, 3', 3''
- изменение скорости потока вдоль оси, спинки
и корыта канала
Анализ показал, что при радиусе канала r2 = 0,340 м достигается разрежение
на оси ротора в пределах 50…53 кПа при соответствующем изменении давления на выходе из канала от
106 до 113 кПа. При этом режим
течения парообразного гелия соответствует докритическому режиму с изменением
числа Маха от 0,061 до 0,031 и при практически линейном изменении скоростей.
Список
литературы