Расчёт одноконтурной системы автоматического регулирования
Министерство
образования и науки Российской Федерации
Федеральное
государственное бюджетное образовательное учреждение высшего профессионального
образования
"Национальный
исследовательский
Томский
политехнический университет"
Наименование
института ЭНИН
Наименование
специальности Теплоэнергетика и теплотехника
Наименование
выпускающей кафедры Автоматизация теплоэнергетических процессов
Курсовая
работа
Расчёт
одноконтурной системы автоматического регулирования
Исполнитель
студент группы 5Б1В
Броцман А.А.
Руководитель
Андык В.С.
Томск
- 2014
Содержание
Введение
.
Структурная схема одноконтурной АСР
.
Расчёт и построение границы заданного запаса устойчивости АСР
.
Определение оптимальных параметров настройки ПИ-регулятора
.
Расчёт, построение и оценка качества переходных процессов
.1
Переходный процесс по каналу регулирующего воздействия S-Y
.2.
Переходный процесс при возмущении f, идущем по каналу регулирующего воздействия
F-Y
Заключение
Список
использованных источников
регулирование автоматизированный
регулятор устойчивость
Введение
Данная курсовая работа посвящена расчёту
одноконтурной системы автоматического регулирования. Для оценки систем
регулирования необходимо определить, в каких условиях эти системы можно
использовать, какие настроечные параметры регулятора требуется установить,
чтобы процесс регулирования, осуществляемый при помощи различных регуляторов
систем, был оптимальным.
В настоящее время системы регулирования получили
широкое применение в различных отраслях промышленности. В связи с этим проблема
определения оптимальных параметров настройки регуляторов систем остаётся
актуальной, даже несмотря на то, что разработано большое количество приёмов и
методов, позволяющих решать эти проблемы. В частности, существует два
инженерных метода расчёта систем регулирования: корневой (с использованием
РАФЧХ) и частотный по максимуму АЧХ замкнутой системы (метод В.Я. Ротача).
В данной курсовой работе в первом пункте
приводятся исходные данные для расчёта заданной АСР, структурная схема которой показана
во втором пункте. Третий пункт посвящен расчёту и построению границы заданного
запаса устойчивости АСР с ПИ-регулятором и объектом регулирования корневым
методом. В четвёртом пункте определяются оптимальные параметры настройки
ПИ-регулятора. Последний пункт посвящён расчётам переходных процессов по двум
каналам: по каналу регулирующего воздействия S-Y и при возмущении f, идущем по
каналу регулирующего воздействия, здесь же представлены графики этих процессов
и произведены оценки их качества.
. Структурная схема одноконтурной АСР
Структурная схема системы регулирования,
приведенная в задании, имеет вид:
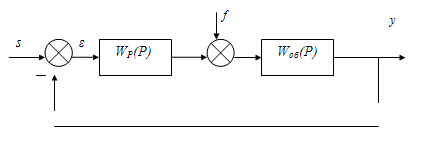
Рисунок 1 - Структурная схема
заданной системы регулирования
Учитывая исходные данные, приведенные ранее структурную
схему системы регулирования можно преобразовать к виду:
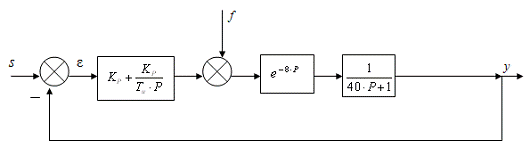
Рисунок 2 - Преобразованная структурная схема
заданной системы регулирования
. Расчёт и построение границы заданного запаса
устойчивости АСР
Для расчёта и построения границы заданного
запаса устойчивости АСР с ПИ-регулятором, представленной на рисунке 1,
воспользуемся корневым методом параметрического синтеза систем автоматического
регулирования с применением расширенных амплитудно-фазовых частотных характеристик
(РАФЧХ).
Используя исходные данные, приведенные в таблице
1, можем записать, что для заданной системы регулирования установлены следующие
требования к запасу устойчивости системы: степень затухания переходного
процесса в системе 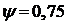 .
.
Исходя из этого, зная зависимость между степенью
затухания переходных процессов в заданной системе регулирования
ψ и
степенью колебательности переходных процессов в заданной системе регулирования
m, можно определить значение заданной степени колебательности m системы по
формуле:
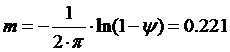 (1)
(1)
где ψ - степень
затухания переходных процессов в заданной системе регулирования.
Передаточная функция объекта регулирования
согласно исходных данных определяется по формуле:
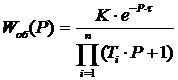 (2)
(2)
где Р - оператор Лапласа.
При n=1 выражение 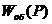 примет
вид:
примет
вид:
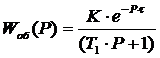 (3)
(3)
По данным таблицы 1 определяем значения
неизвестных параметров: К=1, 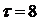 , T1=40. Тогда
после подстановки значений выше приведенных параметров получаем окончательное
выражение для передаточной функции объекта регулирования:
, T1=40. Тогда
после подстановки значений выше приведенных параметров получаем окончательное
выражение для передаточной функции объекта регулирования:
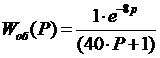 (4)
(4)
Определим расширенные частотные характеристики
объекта регулирования. Расширенные частотные характеристики какого-либо звена
можно получить подстановкой в передаточную функцию этого звена W(P) оператора 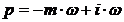 или
или
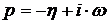 ,
в выражениях для оператора Лапласа ω - частота,
с-1. В первом случае расчётные формулы метода обеспечивают получение границы
заданной степени колебательности системы m, а во втором - получение границы
заданной степени устойчивости системы
,
в выражениях для оператора Лапласа ω - частота,
с-1. В первом случае расчётные формулы метода обеспечивают получение границы
заданной степени колебательности системы m, а во втором - получение границы
заданной степени устойчивости системы 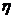 в
пространстве параметров настройки регулятора.
в
пространстве параметров настройки регулятора.
Заменим в формуле (4) оператор 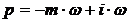 ,
в результате получаем выражение для РАФЧХ объекта регулирования:
,
в результате получаем выражение для РАФЧХ объекта регулирования:
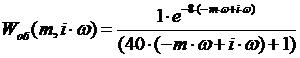 (5)
(5)
Используя математический пакет MathCad,
предварительно задав начальное значение частоты 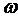 =0
с-1 и шаг по частоте
=0
с-1 и шаг по частоте 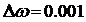 с-1, рассчитываем
расширенные частотные характеристики объекта при изменении частоты до ω=0,055
с-1.
с-1, рассчитываем
расширенные частотные характеристики объекта при изменении частоты до ω=0,055
с-1.
Расширенная вещественная частотная
характеристика (РВЧХ):
об(m,ω)=Re(Wоб(m,iω))
(6)
Расширенная мнимая частотная характеристика
(РМЧХ):
об(m,ω)=Im(Wоб(m,iω))
(7)
Расширенная амплитудно-частотная характеристика
(РАЧХ)
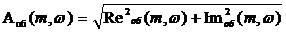 (8)
(8)
Результаты расчётов сведём в таблицу 2,
приведенную ниже.
Таблица 2 - Расширенные частотные характеристики
объекта регулирования
|
частота
ω,
с-1
|
Reоб(m,ω)
|
Imоб(m,ω)
|
Аоб(m,ω)
|
|
1,00E-09
|
1
|
-4.8e-8
|
1
|
|
0.01
|
0.9
|
-0.484
|
1.022
|
|
0.02
|
0.539
|
-0.724
|
0.903
|
|
0.03
|
0.228
|
-0.714
|
0.749
|
|
0.04
|
0.04
|
-0.621
|
0.622
|
|
0.05
|
-0.067
|
-0.522
|
0.526
|
|
0.06
|
-0.129
|
-0.436
|
0.455
|
|
0.07
|
-0.165
|
-0.365
|
0.4
|
|
0.08
|
-0.187
|
-0.306
|
0.358
|
|
0.09
|
-0.2
|
-0.256
|
0.325
|
|
0.1
|
-0.208
|
-0.214
|
0.298
|
|
0.11
|
-0.212
|
-0.177
|
0.276
|
|
0.12
|
-0.213
|
-0.145
|
0.258
|
|
0.13
|
-0.212
|
-0.116
|
0.242
|
|
0.14
|
-0.21
|
-0.091
|
0.229
|
|
0.15
|
-0.206
|
-0.068
|
0.217
|
|
0.16
|
-0.202
|
-0.046
|
0.207
|
|
0.17
|
-0.196
|
-0.027
|
0.198
|
|
0.18
|
-0.19
|
-9.296e-3
|
0.19
|
|
0.19
|
-0.183
|
7.038e-3
|
0.183
|
|
0.2
|
-0.176
|
0.022
|
0.177
|
|
0.21
|
-0.168
|
0.036
|
0.172
|
|
0.22
|
-0.159
|
0.049
|
0.167
|
|
0.23
|
-0.151
|
0.06
|
0.162
|
|
0.24
|
-0.141
|
0.071
|
0.158
|
|
0.25
|
-0.132
|
0.081
|
0.154
|
|
0.26
|
-0.122
|
0.089
|
0.151
|
|
0.27
|
-0.112
|
0.097
|
0.148
|
|
0.28
|
-0.101
|
0.104
|
0.145
|
|
0.29
|
-0.091
|
0.11
|
0.143
|
|
0.3
|
-0.08
|
0.115
|
0.14
|
|
0.31
|
-0.069
|
0.12
|
0.138
|
|
0.32
|
-0.058
|
0.123
|
0.136
|
|
0.33
|
-0.047
|
0.126
|
0.134
|
|
0.34
|
-0.036
|
0.128
|
0.133
|
|
0.35
|
-0.025
|
0.129
|
0.131
|
Расчётные формулы корневого метода для
ПИ-регулятора имеют следующий вид:
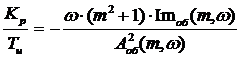 (10)
(10)
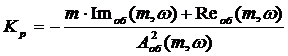 (11)
(11)
В вышеприведенных формулах (10) и (11) 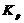 -
коэффициент передачи ПИ-регулятора,
-
коэффициент передачи ПИ-регулятора, 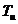 - постоянная интегрирования
ПИ-регулятора.
- постоянная интегрирования
ПИ-регулятора.
Зададим диапазон изменения частоты 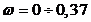 с-1
с шагом
с-1
с шагом 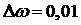 c-1,
определим настройки регулятора
c-1,
определим настройки регулятора 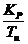 и Кр в заданном
диапазоне частот. Результаты расчётов сведём в таблицу 3.
и Кр в заданном
диапазоне частот. Результаты расчётов сведём в таблицу 3.
Таблица 3 -Результаты расчёта настройки ПИ-
регулятора в заданном диапазоне частот
|
частота
ω,
с-1
|
Кр/Ти
|
Кр
|
|
1,00E-09
|
0
|
-1
|
|
0.01
|
4.859e-3
|
-0.759
|
|
0.02
|
0.019
|
-0.465
|
|
0.03
|
0.04
|
-0.125
|
|
0.04
|
0.067
|
0.252
|
|
0.05
|
0.099
|
0.659
|
|
0.06
|
0.133
|
1.088
|
|
0.07
|
0.167
|
1.532
|
|
0.08
|
0.2
|
1.981
|
|
0.09
|
0.229
|
2.429
|
|
0.1
|
0.252
|
2.868
|
|
0.11
|
0.268
|
3.291
|
|
0.12
|
0.275
|
3.692
|
|
0.13
|
0.271
|
4.063
|
|
0.14
|
0.255
|
4.4
|
|
0.15
|
0.226
|
4.697
|
|
0.16
|
0.182
|
4.95
|
|
0.17
|
0.123
|
5.154
|
|
0.18
|
0.048
|
5.306
|
|
0.19
|
-0.042
|
5.403
|
|
0.2
|
-0.147
|
5.444
|
|
0.21
|
-0.268
|
5.426
|
|
0.22
|
-0.404
|
5.351
|
|
0.23
|
-0.553
|
5.216
|
|
0.24
|
-0.714
|
5.023
|
|
0.25
|
-0.887
|
4.773
|
|
0.26
|
-1.068
|
4.469
|
|
0.27
|
-1.257
|
4.112
|
|
0.28
|
-1.451
|
3.705
|
|
0.29
|
-1.648
|
3.252
|
|
0.3
|
-1.845
|
2.757
|
|
0.31
|
-2.04
|
2.224
|
|
0.32
|
-2.23
|
1.657
|
|
0.33
|
-2.413
|
1.063
|
|
0.34
|
-2.586
|
0.445
|
|
0.35
|
-2.747
|
-0.19
|
По данным таблицы 3 построим график зависимости 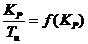 ,
т.е. укажем границу заданного запаса устойчивости системы регулирования на
рисунке 3.
,
т.е. укажем границу заданного запаса устойчивости системы регулирования на
рисунке 3.
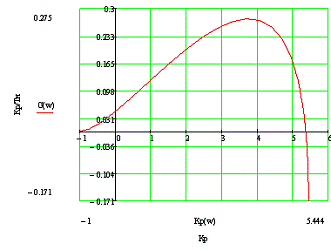
Рисунок 3 - Область параметров настройки
ПИ-регулятора
Полученная кривая является линией заданной
степени затухания Ψ=Ψзад=0,75
процесса регулирования, что соответствует степени колебательности m=0.221.
Таким образом, все значения 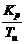 и Kp, лежащие на
этой кривой, обеспечивают определенную степень затухания (в данном случае Ψ=Ψзад=0,75).
Значения
и Kp, лежащие на
этой кривой, обеспечивают определенную степень затухания (в данном случае Ψ=Ψзад=0,75).
Значения 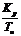 и
Kp, лежащие внутри области, ограниченной данной кривой и осями координат,
обеспечат процесс регулирования со степенью затухания больше заданного (Ψ1>Ψзад),
а лежащие вне этой области - со степенью затухания меньше заданной (Ψ1<Ψзад).
и
Kp, лежащие внутри области, ограниченной данной кривой и осями координат,
обеспечат процесс регулирования со степенью затухания больше заданного (Ψ1>Ψзад),
а лежащие вне этой области - со степенью затухания меньше заданной (Ψ1<Ψзад).
3. Определение оптимальных параметров настройки
ПИ-регулятора
Поиск оптимальных параметров настройки
регулятора осуществляется вдоль границы заданного запаса устойчивости системы
регулирования, представленной на рисунке 3, до достижения экстремума принятого
критерия качества. В задании на курсовую работу в качестве принятого критерия
качества указан первый интегральный критерий.
Минимуму второго интегрального критерия 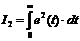 на
графике (рисунок 3) соответствует точка, в которой
на
графике (рисунок 3) соответствует точка, в которой  принимает
значение равное 0,95 от максимального в сторону увеличения частоты. Эта точка и
определит оптимальные параметры настройки ПИ- регулятора. Используя данные
таблицы 3 и рисунка 3, находим, что точке максимума соответствуют значения:
принимает
значение равное 0,95 от максимального в сторону увеличения частоты. Эта точка и
определит оптимальные параметры настройки ПИ- регулятора. Используя данные
таблицы 3 и рисунка 3, находим, что точке максимума соответствуют значения:
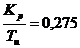 , Kp = 3.692
, Kp = 3.692
при ω = 0.12
с-1.
Поэтому оптимальные параметры настройки ПИ-
регулятора имеют значения:
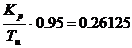 , Kp∙
0,95=3.5074,
, Kp∙
0,95=3.5074, 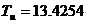 с.
с.
. Расчёт, построение и оценка качества
переходных процессов
.1 Переходный процесс по каналу регулирующего
воздействия S-Y
Для одноконтурной системы регулирования,
приведенной на рисунке 1, определим передаточную функцию замкнутой АСР по
каналу S-Y по формуле:
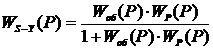 (12)
(12)
где передаточная функция объекта регулирования:
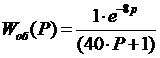 ,
,
передаточная функция ПИ- регулятора:
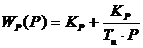 .
.
После подстановки значения 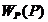 в
формулу (12), получаем окончательное выражение для передаточной функции
замкнутой АСР по каналу S-Y:
в
формулу (12), получаем окончательное выражение для передаточной функции
замкнутой АСР по каналу S-Y:
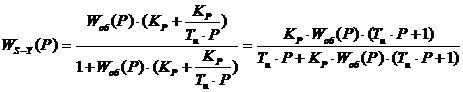 (13)
(13)
Получим выражение для АФЧХ замкнутой системы
путём замены оператора P в формуле (13) на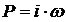 ,
в результате получаем:
,
в результате получаем:
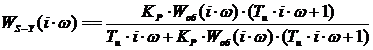 (14)
(14)
Результаты расчёта сведём в таблицу 4.
Таблица 4 - Расчёт ВЧХ замкнутой АСР при
регулирующем воздействии
|
ω,
с-1
|
Re(ω)
|
|
1,00E-09
|
1
|
|
0.01
|
1.012
|
|
0.02
|
1.047
|
|
0.03
|
1.104
|
|
0.04
|
1.182
|
|
0.05
|
1.277
|
|
0.06
|
1.381
|
|
0.07
|
1.476
|
|
0.08
|
1.517
|
|
0.09
|
1.398
|
|
0.1
|
0.913
|
|
0.11
|
-0.103
|
|
0.12
|
-1.278
|
|
0.13
|
-1.91
|
|
0.14
|
-1.954
|
|
0.15
|
-1.743
|
|
0.16
|
-1.482
|
|
0.17
|
-1.242
|
|
0.18
|
-1.039
|
|
0.19
|
-0.871
|
|
0.2
|
-0.731
|
|
0.21
|
-0.615
|
|
0.22
|
-0.518
|
|
0.23
|
-0.435
|
|
0.24
|
-0.365
|
|
0.25
|
-0.304
|
|
0.26
|
-0.251
|
|
0.27
|
-0.205
|
|
0.28
|
-0.165
|
|
0.29
|
-0.13
|
|
0.3
|
-0.098
|
|
0.31
|
-0.07
|
|
0.32
|
-0.046
|
|
0.33
|
-0.023
|
|
0.34
|
-3.53e-3
|
|
0.35
|
0.014
|
По данным таблицы 4 строим ВЧХ замкнутой АСР,
которая приведена на рисунке 4.
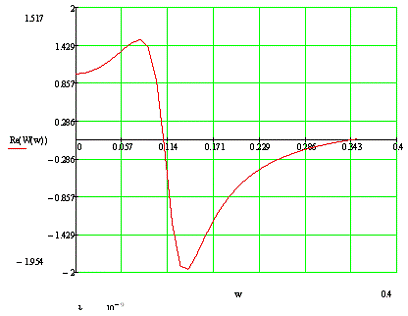
Рисунок 4 - ВЧХ замкнутой АСР при регулирующем
воздействии
Переходный процесс в замкнутой АСР по каналу S-Y
можно рассчитать, используя ВЧХ замкнутой АСР, приведенный на рисунке 4.
Установлено, что переходная характеристика
какой-либо системы y(t) связана с ВЧХ этой системы Re(ω)
выражением:
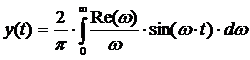 (15)
(15)
где t - время переходного процесса в замкнутой
АСР.
Для более точного расчёта в качестве верхнего
предела интеграла для y(t) принимают не 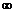 ,
а значение частоты, при которой график Re(ω) стремится
к 0, т.е. частоту среза ωСР. По
графику, приведенному на рисунке 4, определяем, ωСР
=0,34 с-1. Поэтому переходный процесс в замкнутой АСР по каналу S-Y можно
рассчитать по формуле:
,
а значение частоты, при которой график Re(ω) стремится
к 0, т.е. частоту среза ωСР. По
графику, приведенному на рисунке 4, определяем, ωСР
=0,34 с-1. Поэтому переходный процесс в замкнутой АСР по каналу S-Y можно
рассчитать по формуле:
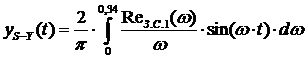 (16)
(16)
Задав диапазон изменения времени переходного
процесса 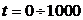 с
с шагом
с
с шагом 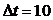 с,
рассчитываем переходный процесс в замкнутой АСР по каналу S-Y. Результаты
расчета сведём в таблицу 5.
с,
рассчитываем переходный процесс в замкнутой АСР по каналу S-Y. Результаты
расчета сведём в таблицу 5.
Таблица 5 - Расчёт переходного процесса в
замкнутой АСР по каналу S-Y
|
t
|
Y(t)
|
t
|
Y(t)
|
t
|
Y(t)
|
|
0
|
0
|
98
|
1.027
|
196
|
1.007
|
|
1
|
-0.017
|
99
|
1.015
|
197
|
1.007
|
|
2
|
-0.032
|
100
|
1.002
|
198
|
1.006
|
|
3
|
-0.041
|
101
|
0.991
|
199
|
1.006
|
|
4
|
-0.042
|
102
|
0.98
|
200
|
1.005
|
|
5
|
-0.033
|
103
|
0.97
|
201
|
1.005
|
|
6
|
-0.012
|
104
|
0.961
|
202
|
1.004
|
|
7
|
0.021
|
105
|
0.953
|
203
|
1.004
|
|
8
|
0.067
|
106
|
0.946
|
204
|
1.003
|
|
9
|
0.127
|
107
|
0.94
|
205
|
1.003
|
|
10
|
0.199
|
108
|
0.935
|
206
|
1.002
|
|
11
|
0.284
|
109
|
0.932
|
207
|
1.001
|
|
12
|
0.379
|
110
|
0.93
|
208
|
1.001
|
|
13
|
0.482
|
111
|
0.929
|
209
|
1
|
|
14
|
0.593
|
112
|
0.928
|
210
|
1
|
|
15
|
0.707
|
113
|
0.929
|
211
|
0.999
|
|
16
|
0.823
|
114
|
0.931
|
212
|
0.999
|
|
17
|
0.94
|
115
|
0.933
|
213
|
0.998
|
|
18
|
1.053
|
116
|
0.937
|
214
|
0.998
|
|
19
|
1.162
|
117
|
0.941
|
215
|
0.998
|
|
20
|
1.265
|
118
|
0.945
|
216
|
0.997
|
|
21
|
1.36
|
119
|
0.95
|
217
|
0.997
|
|
22
|
1.445
|
120
|
0.956
|
218
|
0.997
|
|
23
|
1.521
|
121
|
0.961
|
219
|
0.997
|
|
24
|
1.585
|
122
|
0.967
|
220
|
0.997
|
|
25
|
1.639
|
123
|
0.973
|
221
|
0.997
|
|
26
|
1.681
|
124
|
0.979
|
222
|
0.997
|
|
27
|
1.712
|
125
|
0.985
|
223
|
0.997
|
|
28
|
1.731
|
126
|
0.991
|
224
|
0.997
|
|
29
|
1.741
|
127
|
0.997
|
225
|
0.997
|
|
30
|
1.74
|
128
|
1.003
|
226
|
0.997
|
|
31
|
1.73
|
129
|
1.008
|
227
|
0.997
|
|
32
|
1.711
|
130
|
1.013
|
228
|
0.998
|
|
33
|
1.684
|
131
|
1.017
|
229
|
0.998
|
|
34
|
1.649
|
132
|
1.021
|
230
|
0.998
|
|
35
|
1.609
|
133
|
1.024
|
231
|
0.998
|
|
36
|
1.563
|
134
|
1.027
|
232
|
0.999
|
|
37
|
1.511
|
135
|
1.029
|
233
|
0.999
|
|
38
|
1.456
|
136
|
1.031
|
234
|
0.999
|
|
39
|
1.398
|
137
|
1.032
|
235
|
0.999
|
|
40
|
1.338
|
138
|
1.033
|
236
|
1
|
|
41
|
1.276
|
139
|
1.033
|
237
|
1
|
|
42
|
1.214
|
140
|
1.033
|
238
|
|
43
|
1.152
|
141
|
1.032
|
239
|
1.001
|
|
44
|
1.092
|
142
|
1.031
|
240
|
1.001
|
|
45
|
1.033
|
143
|
1.03
|
241
|
1.001
|
|
46
|
0.977
|
144
|
1.028
|
242
|
1.001
|
|
47
|
0.925
|
145
|
1.026
|
243
|
1.001
|
|
48
|
0.877
|
146
|
1.024
|
244
|
1.001
|
|
49
|
0.832
|
147
|
1.021
|
245
|
1.001
|
|
50
|
0.793
|
148
|
1.019
|
246
|
1.002
|
|
51
|
0.759
|
149
|
1.016
|
247
|
1.002
|
|
52
|
0.73
|
150
|
1.013
|
248
|
1.002
|
|
53
|
0.707
|
151
|
1.011
|
249
|
1.002
|
|
54
|
0.689
|
152
|
1.008
|
250
|
1.001
|
|
55
|
0.676
|
153
|
1.005
|
251
|
1.001
|
|
56
|
0.669
|
154
|
1.002
|
252
|
1.001
|
|
57
|
0.666
|
155
|
1
|
253
|
1.001
|
|
58
|
0.668
|
156
|
0.997
|
254
|
1.001
|
|
59
|
0.675
|
157
|
0.995
|
255
|
1.001
|
|
60
|
0.685
|
158
|
0.993
|
256
|
1.001
|
|
61
|
0.699
|
159
|
0.991
|
257
|
1.001
|
|
62
|
0.716
|
160
|
0.989
|
258
|
1.001
|
|
63
|
0.736
|
161
|
0.988
|
259
|
1.001
|
|
64
|
0.759
|
162
|
0.987
|
260
|
1.001
|
|
65
|
0.784
|
163
|
0.986
|
261
|
1
|
|
66
|
0.81
|
164
|
0.985
|
262
|
1
|
|
67
|
0.837
|
165
|
0.985
|
263
|
1
|
|
68
|
0.865
|
166
|
0.985
|
264
|
1
|
|
69
|
0.894
|
167
|
0.985
|
265
|
1
|
|
70
|
0.922
|
168
|
0.985
|
266
|
1
|
|
71
|
0.95
|
169
|
0.985
|
267
|
1
|
|
72
|
0.977
|
170
|
0.986
|
268
|
1
|
|
73
|
1.004
|
171
|
0.987
|
269
|
0.999
|
|
74
|
1.028
|
172
|
0.988
|
270
|
0.999
|
|
75
|
1.051
|
173
|
0.989
|
271
|
0.999
|
|
76
|
1.072
|
174
|
0.99
|
272
|
0.999
|
|
77
|
1.091
|
175
|
0.991
|
273
|
0.999
|
|
78
|
1.107
|
176
|
0.992
|
274
|
0.999
|
|
79
|
1.121
|
177
|
0.993
|
275
|
0.999
|
|
80
|
1.133
|
178
|
0.995
|
276
|
0.999
|
|
81
|
1.142
|
179
|
0.996
|
277
|
0.999
|
|
82
|
1.149
|
180
|
0.997
|
278
|
0.999
|
|
83
|
1.153
|
181
|
0.999
|
279
|
0.999
|
|
84
|
1.155
|
182
|
1
|
280
|
0.999
|
|
85
|
1.154
|
183
|
1.001
|
281
|
0.999
|
|
86
|
1.152
|
184
|
1.002
|
282
|
1
|
|
87
|
1.148
|
185
|
1.003
|
283
|
1
|
|
88
|
1.142
|
186
|
1.004
|
284
|
1
|
|
89
|
1.134
|
187
|
1.005
|
285
|
1
|
|
90
|
1.125
|
188
|
1.005
|
286
|
1
|
|
91
|
1.115
|
189
|
1.006
|
287
|
1
|
|
92
|
1.104
|
190
|
1.006
|
288
|
1
|
|
93
|
1.092
|
191
|
1.007
|
289
|
1
|
|
94
|
1.08
|
192
|
1.007
|
290
|
1
|
|
95
|
1.067
|
193
|
1.007
|
291
|
1
|
|
96
|
1.054
|
194
|
1.007
|
292
|
1
|
|
97
|
1.04
|
195
|
1.007
|
293
|
1
|
По данным таблицы 5 строим переходный процесс в
замкнутой АСР по каналу S-Y, который приведён на рисунке 5.
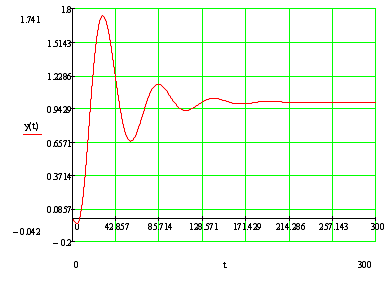
Рисунок 5 - Переходный процесс в замкнутой АСР
по каналу S-Y
Используя данные таблицы 5 и рисунка 5,
произведём оценку качества переходного процесса в замкнутой АСР по каналу S-Y.
Прямые критерии качества:
. Максимальная динамическая ошибка: А1=0,741;
. Перерегулирование:
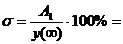 74.1% (17)
74.1% (17)
где 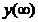 -
уровень установившегося значения регулируемой величины при времени переходного
процесса
-
уровень установившегося значения регулируемой величины при времени переходного
процесса 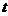 ,
равного
,
равного 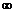 ;
;
. Динамический коэффициент регулирования Rд не определяется для такого типа
процессов;
. Степень затухания переходного процесса:
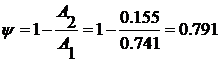 (18)
(18)
где 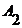 -
второй максимальный выброс регулируемой величины;
-
второй максимальный выброс регулируемой величины;
. Статическая ошибка:
 (19)
(19)
где S - сигнал регулирующего воздействия 1(t);
. Время регулирования: 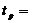 182
с. при величине
182
с. при величине 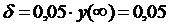 , значение которой
задают для контроля переходного процесса с заданной степенью точности.
, значение которой
задают для контроля переходного процесса с заданной степенью точности.
.2 Переходный процесс при возмущении f, идущем
по каналу регулирующего воздействия F-Y
Для одноконтурной системы регулирования,
приведенной на рисунке 1, определим передаточную функцию замкнутой АСР по
каналу F-Y по формуле:
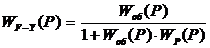 (20)
(20)
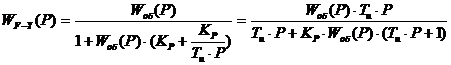 (21)
(21)
Получим выражение для АФЧХ замкнутой системы
путём замены оператора p в формуле (18) на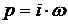 ,
в результате получаем:
,
в результате получаем:
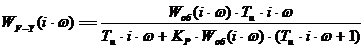 (22)
(22)
Используя математический пакет MathCad,
предварительно задав диапазон изменения частоты 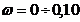 с-1
с шагом
с-1
с шагом 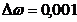 c-,
рассчитываем вещественную частотную характеристику замкнутой АСР: ReЗ.С.2(ω).
c-,
рассчитываем вещественную частотную характеристику замкнутой АСР: ReЗ.С.2(ω).
Результаты расчёта сведём в таблицу 6.
Таблица 6 - Результаты расчёта ВЧХ замкнутой АСР
при возмущении f
|
ῳ,
с-1
|
Re(ω)
|
ω,
с-1
|
R(ω)
|
ω,
с-1
|
Re(ω)
|
ω,
с-1
|
Re(ω)
|
ω,
с-1
|
Re(ω)
|
|
1,00E-09
|
0
|
0.08
|
0.416
|
0.16
|
-0.343
|
0.24
|
-0.127
|
0.32
|
-0.031
|
|
1,00E-03
|
6.604e-5
|
0.081
|
0.426
|
0.161
|
-0.341
|
0.241
|
-0.125
|
0.322
|
-0.03
|
|
2,00E-03
|
2.642e-4
|
0.082
|
0.435
|
0.162
|
-0.338
|
0.242
|
-0.124
|
0.323
|
-0.029
|
|
3,00E-03
|
5.943e-4
|
0.083
|
0.444
|
0.163
|
-0.335
|
0.243
|
-0.122
|
0.324
|
-0.028
|
|
4,00E-03
|
1.057e-3
|
0.084
|
0.453
|
0.164
|
-0.332
|
0.244
|
-0.12
|
0.325
|
-0.028
|
|
5,00E-03
|
1.651e-3
|
0.085
|
0.462
|
0.165
|
-0.329
|
0.245
|
-0.118
|
0.326
|
-0.027
|
|
6,00E-03
|
2.377e-3
|
0.086
|
0.47
|
0.166
|
-0.326
|
0.246
|
-0.117
|
0.327
|
-0.026
|
|
7,00E-03
|
3.235e-3
|
0.087
|
0.478
|
0.167
|
-0.323
|
0.247
|
-0.115
|
0.328
|
-0.025
|
|
8,00E-03
|
4.224e-3
|
0.088
|
0.486
|
0.168
|
-0.32
|
0.248
|
-0.113
|
0.329
|
-0.025
|
|
9,00E-03
|
5.346e-3
|
0.089
|
0.493
|
0.169
|
-0.317
|
0.249
|
-0.112
|
0.33
|
-0.024
|
|
1,00E-02
|
6.599e-3
|
0.09
|
0.5
|
0.17
|
-0.314
|
0.25
|
-0.11
|
0.331
|
-0.023
|
|
0.011
|
7.983e-3
|
0.091
|
0.506
|
0.171
|
-0.31
|
0.251
|
-0.109
|
0.332
|
-0.023
|
|
0.012
|
9.499e-3
|
0.092
|
0.512
|
0.172
|
-0.307
|
0.252
|
-0.107
|
0.333
|
-0.022
|
|
0.013
|
0.011
|
0.093
|
0.516
|
0.173
|
-0.304
|
0.253
|
-0.105
|
0.334
|
-0.021
|
|
0.014
|
0.013
|
0.094
|
0.52
|
0.174
|
-0.3
|
0.254
|
-0.104
|
0.335
|
-0.021
|
|
0.015
|
0.015
|
0.095
|
0.523
|
0.175
|
-0.297
|
0.255
|
-0.102
|
0.336
|
-0.02
|
|
0.016
|
0.017
|
0.096
|
0.525
|
0.176
|
-0.294
|
0.256
|
-0.101
|
0.337
|
-0.019
|
|
0.017
|
0.019
|
0.097
|
0.525
|
0.177
|
-0.29
|
0.257
|
-0.099
|
0.338
|
-0.019
|
|
0.018
|
0.021
|
0.098
|
0.524
|
0.178
|
-0.287
|
0.258
|
-0.098
|
0.339
|
-0.018
|
|
0.019
|
0.024
|
0.099
|
0.522
|
0.179
|
-0.284
|
0.259
|
-0.096
|
0.34
|
-0.017
|
|
0.02
|
0.026
|
0.1
|
0.518
|
0.18
|
-0.28
|
0.26
|
-0.095
|
0.341
|
-0.017
|
|
0.021
|
0.029
|
0.101
|
0.512
|
0.181
|
-0.277
|
0.261
|
-0.094
|
0.342
|
-0.016
|
|
0.022
|
0.032
|
0.102
|
0.505
|
0.182
|
-0.274
|
0.262
|
-0.092
|
0.343
|
-0.015
|
|
0.023
|
0.035
|
0.103
|
0.496
|
0.183
|
-0.27
|
0.263
|
-0.091
|
0.344
|
-0.015
|
|
0.024
|
0.038
|
0.104
|
0.485
|
0.184
|
-0.267
|
0.264
|
-0.089
|
0.345
|
-0.014
|
|
0.025
|
0.041
|
0.105
|
0.472
|
0.185
|
-0.264
|
0.265
|
-0.088
|
0.346
|
-0.014
|
|
0.026
|
0.044
|
0.106
|
0.457
|
0.186
|
-0.261
|
0.266
|
-0.087
|
0.347
|
-0.013
|
|
0.027
|
0.048
|
0.107
|
0.439
|
0.187
|
-0.258
|
0.267
|
-0.085
|
0.348
|
-0.012
|
|
0.028
|
0.052
|
0.108
|
0.42
|
0.188
|
-0.254
|
0.268
|
-0.084
|
0.349
|
-0.012
|
|
0.029
|
0.055
|
0.109
|
0.399
|
0.189
|
-0.251
|
0.269
|
-0.083
|
0.35
|
-0.011
|
|
0.03
|
0.059
|
0.11
|
0.376
|
0.19
|
-0.248
|
0.27
|
-0.081
|
0.351
|
-0.011
|
|
0.031
|
0.063
|
0.111
|
0.351
|
0.191
|
-0.245
|
0.271
|
-0.08
|
0.352
|
-0.01
|
|
0.032
|
0.067
|
0.112
|
0.324
|
0.192
|
-0.242
|
0.272
|
-0.079
|
0.353
|
-9.497e-3
|
|
0.033
|
0.071
|
0.113
|
0.296
|
-0.239
|
0.273
|
-0.078
|
0.354
|
-8.936e-3
|
|
0.034
|
0.076
|
0.114
|
0.266
|
0.194
|
-0.236
|
0.274
|
-0.076
|
0.355
|
-8.381e-3
|
|
0.035
|
0.08
|
0.115
|
0.236
|
0.195
|
-0.233
|
0.275
|
-0.075
|
0.356
|
-7.831e-3
|
|
0.036
|
0.085
|
0.116
|
0.204
|
0.196
|
-0.23
|
0.276
|
-0.074
|
0.357
|
-7.287e-3
|
|
0.037
|
0.09
|
0.117
|
0.172
|
0.197
|
-0.227
|
0.277
|
-0.073
|
0.358
|
-6.747e-3
|
|
0.038
|
0.095
|
0.118
|
0.14
|
0.198
|
-0.224
|
0.278
|
-0.072
|
0.359
|
-6.213e-3
|
|
0.039
|
0.1
|
0.119
|
0.108
|
0.199
|
-0.221
|
0.279
|
-0.07
|
0.36
|
-5.683e-3
|
|
0.04
|
0.105
|
0.12
|
0.076
|
0.2
|
-0.218
|
0.28
|
-0.069
|
0.361
|
-5.159e-3
|
|
0.041
|
0.11
|
0.121
|
0.044
|
0.201
|
-0.215
|
0.281
|
-0.068
|
0.362
|
-4.639e-3
|
|
0.042
|
0.116
|
0.122
|
0.013
|
0.202
|
-0.213
|
0.282
|
-0.067
|
0.363
|
-4.125e-3
|
|
0.043
|
0.121
|
0.123
|
-0.017
|
0.203
|
-0.21
|
0.283
|
-0.066
|
0.364
|
-3.615e-3
|
|
0.044
|
0.127
|
0.124
|
-0.047
|
0.204
|
-0.207
|
0.284
|
-0.065
|
0.365
|
-3.11e-3
|
|
0.045
|
0.133
|
0.125
|
-0.075
|
0.205
|
-0.204
|
0.285
|
-0.064
|
0.366
|
-2.61e-3
|
|
0.046
|
0.139
|
0.126
|
-0.101
|
0.206
|
-0.202
|
0.286
|
-0.063
|
0.367
|
-2.114e-3
|
|
0.047
|
0.145
|
0.127
|
-0.127
|
0.207
|
-0.199
|
0.287
|
-0.061
|
0.368
|
-1.623e-3
|
|
0.048
|
0.151
|
0.128
|
-0.151
|
0.208
|
-0.196
|
0.288
|
-0.06
|
0.369
|
-1.137e-3
|
|
0.049
|
0.157
|
0.129
|
-0.173
|
0.209
|
-0.194
|
0.289
|
-0.059
|
0.37
|
-6.551e-4
|
|
0.05
|
0.164
|
0.13
|
-0.194
|
0.21
|
-0.191
|
0.29
|
-0.058
|
|
|
|
0.051
|
0.17
|
0.131
|
-0.213
|
0.211
|
-0.189
|
0.291
|
-0.057
|
|
|
|
0.052
|
0.177
|
0.132
|
-0.231
|
0.212
|
-0.186
|
0.292
|
-0.056
|
|
|
|
0.053
|
0.184
|
0.133
|
-0.248
|
0.213
|
-0.184
|
0.293
|
-0.055
|
|
|
|
0.054
|
0.191
|
0.134
|
-0.262
|
0.214
|
-0.181
|
0.294
|
-0.054
|
|
|
|
0.055
|
0.198
|
0.135
|
-0.276
|
0.215
|
-0.179
|
0.295
|
-0.053
|
|
|
|
0.056
|
0.206
|
0.136
|
-0.288
|
0.216
|
-0.177
|
0.296
|
-0.052
|
|
|
|
0.057
|
0.213
|
0.137
|
-0.299
|
0.217
|
-0.174
|
0.297
|
-0.051
|
|
|
|
0.058
|
0.221
|
0.138
|
-0.309
|
0.218
|
-0.172
|
0.298
|
-0.05
|
|
|
|
0.059
|
0.228
|
0.139
|
-0.317
|
0.219
|
-0.17
|
0.299
|
-0.049
|
|
|
|
0.06
|
0.236
|
0.14
|
-0.325
|
0.22
|
-0.167
|
0.3
|
-0.048
|
|
|
|
0.061
|
0.244
|
0.141
|
-0.332
|
0.221
|
-0.165
|
0.301
|
-0.047
|
|
|
|
0.062
|
0.252
|
0.142
|
-0.337
|
0.222
|
-0.163
|
0.302
|
-0.047
|
|
|
|
0.063
|
0.261
|
0.143
|
-0.342
|
0.223
|
-0.161
|
0.303
|
-0.046
|
|
|
|
0.064
|
0.269
|
0.144
|
-0.346
|
0.224
|
-0.159
|
0.304
|
-0.045
|
|
|
|
0.065
|
0.278
|
0.145
|
-0.349
|
0.225
|
-0.156
|
0.305
|
-0.044
|
|
|
|
0.066
|
0.286
|
0.146
|
-0.352
|
0.226
|
-0.154
|
0.306
|
-0.043
|
|
|
|
0.067
|
0.295
|
0.147
|
-0.354
|
0.227
|
-0.152
|
0.307
|
-0.042
|
|
|
|
0.068
|
0.304
|
0.148
|
-0.355
|
0.228
|
-0.15
|
0.308
|
-0.041
|
|
|
|
0.069
|
0.313
|
0.149
|
-0.356
|
0.229
|
-0.148
|
0.309
|
-0.04
|
|
|
|
0.07
|
0.322
|
0.15
|
-0.357
|
0.23
|
-0.146
|
0.31
|
-0.039
|
|
|
|
0.071
|
0.331
|
0.151
|
-0.357
|
0.231
|
-0.144
|
0.311
|
-0.039
|
|
|
|
0.072
|
0.34
|
0.152
|
-0.356
|
0.232
|
-0.142
|
0.312
|
-0.038
|
|
|
|
0.073
|
0.153
|
-0.356
|
0.233
|
-0.14
|
0.313
|
-0.037
|
|
|
|
0.074
|
0.359
|
0.154
|
-0.355
|
0.234
|
-0.138
|
0.314
|
-0.036
|
|
|
|
0.075
|
0.369
|
0.155
|
-0.353
|
0.235
|
-0.136
|
0.315
|
-0.035
|
|
|
|
0.076
|
0.378
|
0.156
|
-0.352
|
0.236
|
-0.134
|
0.316
|
-0.034
|
|
|
|
0.077
|
0.388
|
0.157
|
-0.35
|
0.237
|
-0.133
|
0.317
|
-0.034
|
|
|
По данным таблицы 6 строим ВЧХ замкнутой АСР при
возмущении f, который приведен на рисунке 6.
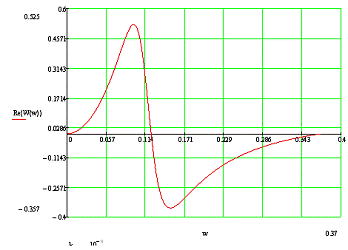
Рисунок 6 - ВЧХ замкнутой АСР при возмущении f
Переходный процесс в замкнутой АСР по каналу F-Y
можно рассчитать по методу трапеций, используя график ВЧХ замкнутой АСР при
возмущении f (рисунок 6).
Поэтому переходный процесс в замкнутой АСР по
каналу F-Y можно рассчитать по формуле:
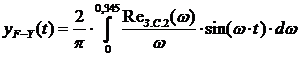 (23)
(23)
Как уже было сказано выше, для более точного
расчёта в качестве верхнего предела интеграла для yF-Y(t) принимают значение
частоты среза ωСР. По графику,
приведенному на рисунке 6, определяем, что ωСР
=0,345 с-1.
Задав диапазон изменения времени переходного
процесса 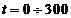 с
с шагом
с
с шагом 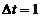 с,
рассчитываем переходный процесс в замкнутой АСР по каналу F-Y. Результаты
расчета сведём в таблицу 7, приведенную ниже.
с,
рассчитываем переходный процесс в замкнутой АСР по каналу F-Y. Результаты
расчета сведём в таблицу 7, приведенную ниже.
Таблица 7 - Расчёт переходного процесса в
замкнутой АСР по каналу F-Y
|
T
|
Y(t)
|
t
|
Y(t)
|
t
|
Y(t)
|
|
0
|
0
|
98
|
-7.782e-3
|
196
|
1.594e-3
|
|
1
|
-4.21e-3
|
99
|
-0.011
|
197
|
1.473e-3
|
|
2
|
-7.675e-3
|
100
|
-0.014
|
198
|
1.342e-3
|
|
3
|
-9.693e-3
|
101
|
-0.016
|
199
|
1.2e-3
|
|
4
|
-9.646e-3
|
102
|
-0.018
|
200
|
1.044e-3
|
|
5
|
-7.034e-3
|
103
|
-0.02
|
201
|
8.734e-4
|
|
6
|
-1.506e-3
|
104
|
-0.021
|
202
|
6.881e-4
|
|
7
|
7.127e-3
|
105
|
-0.022
|
203
|
4.902e-4
|
|
8
|
0.019
|
106
|
-0.023
|
204
|
2.833e-4
|
|
9
|
0.034
|
107
|
-0.023
|
205
|
7.237e-5
|
|
10
|
0.051
|
108
|
-0.023
|
206
|
-1.363e-4
|
|
11
|
0.07
|
109
|
-0.022
|
207
|
-3.36e-4
|
|
12
|
0.092
|
110
|
-0.021
|
208
|
-5.2e-4
|
|
13
|
0.114
|
111
|
-0.021
|
209
|
-6.822e-4
|
|
14
|
0.136
|
112
|
-0.019
|
210
|
-8.178e-4
|
|
15
|
0.158
|
113
|
-0.018
|
211
|
-9.234e-4
|
|
16
|
0.179
|
114
|
-0.017
|
212
|
-9.98e-4
|
|
17
|
0.199
|
115
|
-0.015
|
213
|
-1.042e-3
|
|
18
|
0.216
|
116
|
-0.013
|
214
|
-1.059e-3
|
|
19
|
0.23
|
117
|
-0.012
|
215
|
-1.052e-3
|
|
20
|
0.242
|
118
|
-9.711e-3
|
216
|
-1.026e-3
|
|
21
|
0.251
|
119
|
-7.818e-3
|
217
|
-9.878e-4
|
|
22
|
0.256
|
120
|
-5.903e-3
|
218
|
-9.422e-4
|
|
23
|
0.258
|
121
|
-3.991e-3
|
219
|
-8.942e-4
|
|
24
|
0.257
|
122
|
-2.105e-3
|
220
|
-8.473e-4
|
|
25
|
0.253
|
123
|
-2.736e-4
|
221
|
-8.035e-4
|
|
26
|
0.246
|
124
|
1.478e-3
|
222
|
-7.634e-4
|
|
27
|
0.237
|
125
|
3.124e-3
|
223
|
-7.26e-4
|
|
28
|
0.225
|
126
|
4.64e-3
|
224
|
-6.889e-4
|
|
29
|
0.211
|
127
|
6.004e-3
|
225
|
-6.491e-4
|
|
30
|
0.196
|
128
|
7.2e-3
|
226
|
-6.032e-4
|
|
31
|
0.179
|
129
|
8.215e-3
|
227
|
-5.481e-4
|
|
32
|
0.161
|
130
|
9.042e-3
|
228
|
-4.812e-4
|
|
33
|
0.143
|
131
|
9.679e-3
|
229
|
-4.014e-4
|
|
34
|
0.123
|
132
|
0.01
|
230
|
-3.09e-4
|
|
35
|
0.103
|
133
|
0.01
|
231
|
-2.057e-4
|
|
36
|
0.083
|
134
|
0.011
|
232
|
-9.466e-5
|
|
37
|
0.063
|
135
|
0.01
|
233
|
1.971e-5
|
|
38
|
0.044
|
136
|
0.01
|
234
|
1.323e-4
|
|
39
|
0.025
|
137
|
9.98e-3
|
235
|
2.378e-4
|
|
40
|
6.083e-3
|
138
|
9.576e-3
|
236
|
3.311e-4
|
|
41
|
-0.011
|
139
|
9.083e-3
|
237
|
4.082e-4
|
|
42
|
-0.028
|
140
|
8.514e-3
|
238
|
4.661e-4
|
|
43
|
-0.043
|
141
|
7.878e-3
|
239
|
5.033e-4
|
|
44
|
-0.057
|
142
|
7.185e-3
|
240
|
5.204e-4
|
|
45
|
-0.069
|
143
|
6.441e-3
|
241
|
5.191e-4
|
|
46
|
-0.079
|
144
|
5.653e-3
|
242
|
5.028e-4
|
|
47
|
-0.088
|
145
|
4.828e-3
|
243
|
4.756e-4
|
|
48
|
-0.095
|
146
|
3.973e-3
|
244
|
4.422e-4
|
|
49
|
-0.1
|
147
|
245
|
4.074e-4
|
|
50
|
-0.104
|
148
|
2.207e-3
|
246
|
3.75e-4
|
|
51
|
-0.105
|
149
|
1.318e-3
|
247
|
3.482e-4
|
|
52
|
-0.106
|
150
|
4.421e-4
|
248
|
3.286e-4
|
|
53
|
-0.104
|
151
|
-4.057e-4
|
249
|
3.166e-4
|
|
54
|
-0.102
|
152
|
-1.211e-3
|
250
|
3.111e-4
|
|
55
|
-0.098
|
153
|
-1.958e-3
|
251
|
3.095e-4
|
|
56
|
-0.093
|
154
|
-2.635e-3
|
252
|
3.089e-4
|
|
57
|
-0.087
|
155
|
-3.231e-3
|
253
|
3.056e-4
|
|
58
|
-0.08
|
156
|
-3.736e-3
|
254
|
2.96e-4
|
|
59
|
-0.073
|
157
|
-4.145e-3
|
255
|
2.773e-4
|
|
60
|
-0.065
|
158
|
-4.459e-3
|
256
|
2.475e-4
|
|
61
|
-0.056
|
159
|
-4.678e-3
|
257
|
2.059e-4
|
|
62
|
-0.048
|
160
|
-4.808e-3
|
258
|
1.532e-4
|
|
63
|
-0.039
|
161
|
-4.856e-3
|
259
|
9.145e-5
|
|
64
|
-0.03
|
162
|
-4.832e-3
|
260
|
2.393e-5
|
|
65
|
-0.021
|
163
|
-4.746e-3
|
261
|
-4.534e-5
|
|
66
|
-0.012
|
164
|
-4.608e-3
|
262
|
-1.119e-4
|
|
67
|
-3.817e-3
|
165
|
-4.427e-3
|
263
|
-1.715e-4
|
|
68
|
4.297e-3
|
166
|
-4.212e-3
|
264
|
-2.203e-4
|
|
69
|
0.012
|
167
|
-3.968e-3
|
265
|
-2.556e-4
|
|
70
|
0.019
|
168
|
-3.699e-3
|
266
|
-2.758e-4
|
|
71
|
0.025
|
169
|
-3.407e-3
|
267
|
-2.81e-4
|
|
72
|
0.031
|
170
|
-3.093e-3
|
268
|
-2.724e-4
|
|
73
|
0.036
|
171
|
-2.759e-3
|
269
|
-2.528e-4
|
|
74
|
0.04
|
172
|
-2.403e-3
|
270
|
-2.256e-4
|
|
75
|
0.044
|
173
|
-2.027e-3
|
271
|
-1.948e-4
|
|
76
|
0.046
|
174
|
-1.632e-3
|
272
|
-1.645e-4
|
|
77
|
0.048
|
175
|
-1.222e-3
|
273
|
-1.383e-4
|
|
78
|
0.049
|
176
|
-8.023e-4
|
274
|
-1.191e-4
|
|
79
|
0.049
|
177
|
-3.797e-4
|
275
|
-1.085e-4
|
|
80
|
0.049
|
178
|
3.752e-5
|
276
|
-1.069e-4
|
|
81
|
0.048
|
179
|
4.4e-4
|
277
|
-1.132e-4
|
|
82
|
0.046
|
180
|
8.182e-4
|
278
|
-1.255e-4
|
|
83
|
0.044
|
181
|
1.163e-3
|
279
|
-1.407e-4
|
|
84
|
0.041
|
182
|
1.467e-3
|
280
|
-1.554e-4
|
|
85
|
0.038
|
183
|
1.723e-3
|
281
|
-1.661e-4
|
|
86
|
0.035
|
184
|
1.928e-3
|
282
|
-1.696e-4
|
|
87
|
0.031
|
185
|
2.081e-3
|
283
|
-1.637e-4
|
|
88
|
0.028
|
186
|
2.183e-3
|
284
|
-1.471e-4
|
|
89
|
0.024
|
187
|
2.237e-3
|
285
|
-1.199e-4
|
|
90
|
0.02
|
188
|
2.25e-3
|
286
|
-8.339e-5
|
|
91
|
0.015
|
189
|
2.227e-3
|
287
|
-4.003e-5
|
|
92
|
0.011
|
190
|
2.176e-3
|
288
|
6.906e-6
|
|
93
|
7.134e-3
|
191
|
2.104e-3
|
289
|
5.361e-5
|
|
94
|
3.131e-3
|
192
|
2.017e-3
|
290
|
9.626e-5
|
|
95
|
-7.224e-4
|
193
|
1.921e-3
|
291
|
1.314e-4
|
|
96
|
-4.376e-3
|
194
|
1.817e-3
|
292
|
1.563e-4
|
|
97
|
0
|
195
|
1.708e-3
|
293
|
1.693e-4
|
По данным таблицы 7 строим переходный процесс в
замкнутой АСР по каналу F-Y, представленный на рисунке 7.
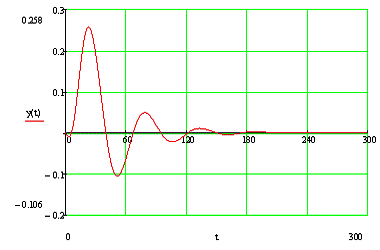
Рисунок 7 - Переходный процесс в замкнутой АСР
по каналу F-Y
Используя данные таблицы 7 и рисунка 7, произведём
оценку качества переходного процесса в замкнутой АСР по каналу F-Y.
Прямые критерии качества:
. Максимальная динамическая ошибка: А1=0,258;
. Перерегулирование:
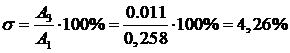 (24)
(24)
где 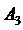 -
первое минимальное отклонение регулируемой величины;
-
первое минимальное отклонение регулируемой величины;
. Динамический коэффициент регулирования RД:
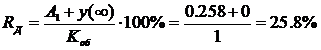 (25)
(25)
где 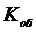 -
коэффициент передачи объекта;
-
коэффициент передачи объекта;
. Степень затухания переходного процесса:
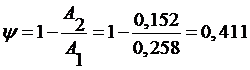 ; (26)
; (26)
. Статическая ошибка:
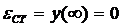 ;
;
. Время регулирования: 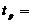 220
с. при величине
220
с. при величине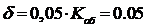
Так как в заданной АСР, представленной на
рисунке 2, имеется звено чистого транспортного запаздывания с передаточной
функцией 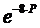 ,
то переходные процессы в этой системе имеет запаздывание на величину 8 с
относительно их начала. Для наглядности указанного факта изобразим начальные
части графиков переходных процессов по каналам S-Y и F-Y соответственно на
рисунке 8 и 9.
,
то переходные процессы в этой системе имеет запаздывание на величину 8 с
относительно их начала. Для наглядности указанного факта изобразим начальные
части графиков переходных процессов по каналам S-Y и F-Y соответственно на
рисунке 8 и 9.
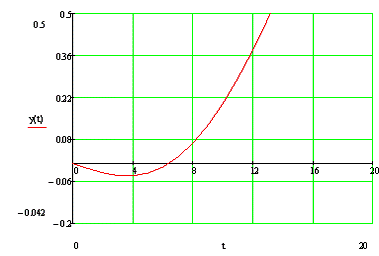
Рисунок 8 - Начальный участок переходного
процесса в замкнутой АСР по каналу S-Y
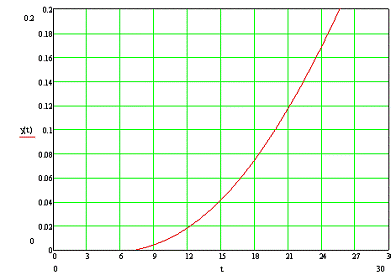
Рисунок 9 - Начальный участок переходного
процесса в замкнутой АСР по каналу F-Y
Заключение
В процессе написания курсовой работы был изучен
один из двух инженерных методов расчёта одноконтурных систем регулирования: корневой
метод (с использованием РАФЧХ). Поиск оптимальных параметров настройки
осуществляется вдоль границы заданного запаса устойчивости системы
регулирования до достижения экстремума принятого критерия качества. В данной
курсовой работе, согласно заданию, в качестве принятого критерия качества был
принят второй интегральный критерий.
В результате проделанной работы, были получены
переходные процессы по каналам S-Y и F-Y. Оценка качества этих процессов
показала, что они удовлетворяют требованиям к запасу устойчивости системы,
приведенных в исходных данных.
Критерии качества:
для S-Y - А1=0.741, для F-Y - А1= 0.258;
перерегулирование:
для S-Y - 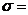 74,1%,
для F-Y -
74,1%,
для F-Y - 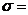 4,26%;
4,26%;
степень затухания переходного процесса:
для S-Y - 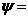 0,791,
для F-Y -
0,791,
для F-Y - 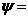 0,411;
0,411;
время регулирования:
для S-Y - 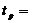 182c.,
для F-Y -
182c.,
для F-Y - 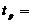 220;
220;
статическая ошибка для этих процессов равна: 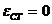 .
.
Список использованных источников
1. Андык
B.C. Библиотека программ по расчету систем автоматического регулирования на
программируемых микрокалькуляторах. Методические указания и программы к
выполнению курсовых работ, курсовых и дипломных проектов для студентов
специальности 210200. Томск: Изд. ТЛИ, 1991, - 35 с.
. Дудников
В.Г. Основы автоматического регулирования тепловых процессов. М.: ГЭИ, 1956. -
264 с.
. Стефани
Е.П. Основы расчета настройки регуляторов теплоэнергетических процессов. - М.:
ГЭИ, 1960. - 395 с.
. Стефани
Е.П. Основы расчета настройки регуляторов теплоэнергетических процессов. Изд.
2-е, перераб. М.: Энергия, 1972. - 376 с.
. Ротач
В.Я. Расчет настройки промышленных систем регулирования. - М.: ГЭИ, 1961.-344
с.
. Андык
B.C. Теория автоматического управления: Учебное пособие. - Томск: Изд- во ТПУ,
2000, 2004, 2005. - 108 с.