Аппроксимация функции методом наименьших квадратов
КУРСОВАЯ РАБОТА
по дисциплине: Информатика
Тема: Аппроксимация функции методом
наименьших квадратов
Оглавление
Введение
1. Постановка задачи
2. Расчётные формулы
. Расчёт с помощью таблиц, выполненных средствами
Microsoft Excel
. Схема алгоритма
. Расчет в программе MathCad
. Результаты, полученные с помощью функции Линейн
. Представление результатов в виде графиков
Выводы
Список используемой литературы
Введение
Целью курсовой работы является углубление знаний по информатике, развитие
и закрепление навыков работы с табличным процессором Microsoft Excel и
программным продуктом MathCAD и применение их для решения задач с помощью ЭВМ
из предметной области, связанной с исследованиями.
Аппроксимация (от латинского "approximare"
-"приближаться") - приближенное выражение каких-либо математических
объектов (например, чисел или функций) через другие более простые, более
удобные в пользовании или просто более известные. В научных исследованиях
аппроксимация применяется для описания, анализа, обобщения и дальнейшего
использования эмпирических результатов.
Как известно, между величинами может существовать точная (функциональная)
связь, когда одному значению аргумента соответствует одно определенное
значение, и менее точная (корреляционная) связь, когда одному конкретному
значению аргумента соответствует приближенное значение или некоторое множество
значений функции, в той или иной степени близких друг к другу. При ведении
научных исследований, обработке результатов наблюдения или эксперимента обычно
приходиться сталкиваться со вторым вариантом.
При изучении количественных зависимостей различных показателей, значения
которых определяются эмпирически, как правило, имеется некоторая их
вариабельность. Частично она задается неоднородностью самих изучаемых объектов
неживой и, особенно, живой природы, частично - обуславливается погрешностью
наблюдения и количественной обработке материалов. Последнюю составляющую не
всегда удается исключить полностью, можно лишь минимизировать ее тщательным
выбором адекватного метода исследования и аккуратностью работы. Поэтому при
выполнении любой научно-исследовательской работы возникает проблема выявления
подлинного характера зависимости изучаемых показателей, этой или иной степени
замаскированных неучтенностью вариабельности: значений. Для этого и применяется
аппроксимация - приближенное описание корреляционной зависимости переменных
подходящим уравнением функциональной зависимости, передающим основную тенденцию
зависимости (или ее "тренд").
При выборе аппроксимации следует исходить из конкретной задачи
исследования. Обычно, чем более простое уравнение используется для
аппроксимации, тем более приблизительно получаемое описание зависимости.
Поэтому важно считывать, насколько существенны и чем обусловлены отклонения
конкретных значений от получаемого тренда. При описании зависимости эмпирически
определенных значений можно добиться и гораздо большей точности, используя
какое-либо более сложное, много параметрическое уравнение. Однако нет никакого
смысла стремиться с максимальной точностью передать случайные отклонения
величин в конкретных рядах эмпирических данных. Гораздо важнее уловить общую
закономерность, которая в данном случае наиболее логично и с приемлемой
точностью выражается именно двухпараметрическим уравнением степенной функции.
Таким образом, выбирая метод аппроксимации, исследователь всегда идет на
компромисс: решает, в какой степени в данном случае целесообразно и уместно
«пожертвовать» деталями и, соответственно, насколько обобщенно следует выразить
зависимость сопоставляемых переменных. Наряду с выявлением закономерностей,
замаскированных случайными отклонениями эмпирических данных от общей
закономерности, аппроксимация позволяет также решать много других важных задач:
формализовать найденную зависимость; найти неизвестные значения зависимой
переменной путем интерполяции или, если это допустимо, экстраполяции.
В каждом задании формулируются условия задачи, исходные данные, форма
выдачи результатов, указываются основные математические зависимости для решения
задачи. В соответствии с методом решения задачи разрабатывается алгоритм
решения, который представляется в графической форме.
1. Постановка задачи
1.
Используя метод наименьших квадратов функцию 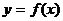 ,
заданную таблично, аппроксимировать:
,
заданную таблично, аппроксимировать:
а)
многочленом первой степени 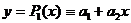 ;
;
б)
многочленом второй степени 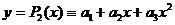 ;
;
в)
экспоненциальной зависимостью 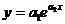 .
.
.
Для каждой зависимости вычислить коэффициент детерминированности.
.
Вычислить коэффициент корреляции (только в случае а).
.
Для каждой зависимости построить линию тренда.
.
Используя функцию ЛИНЕЙН вычислить числовые характеристики зависимости 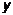 от
от 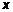 .
.
.
Сравнить свои вычисления с результатами, полученными при помощи функции ЛИНЕЙН.
.
Сделать вывод, какая из полученных формул наилучшим образом аппроксимирует
функцию 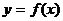 .
.
.
Написать программу на одном из языков программирования и сравнить результаты
счета с полученными выше.
Вариант
3. Функция 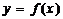 задана табл. 1.
задана табл. 1.
Таблица
1.
|
x
|
y
|
x
|
y
|
x
|
y
|
x
|
y
|
x
|
y
|
|
0.28
|
1.05
|
2.34
|
9.11
|
3.33
|
29.43
|
4.23
|
86.44
|
5.55
|
187.54
|
|
0.87
|
2.87
|
2.65
|
16.86
|
3.41
|
37.45
|
4.83
|
90.85
|
6.32
|
200.45
|
|
1.65
|
6.43
|
2.77
|
17.97
|
3.55
|
42.44
|
4.92
|
99.06
|
6.66
|
212.97
|
|
1.99
|
8.96
|
2.83
|
18.99
|
3.85
|
56.94
|
5.14
|
120.45
|
7.13
|
275.74
|
|
2.08
|
8.08
|
3.06
|
23.75
|
4.01
|
75.08
|
5.23
|
139.65
|
7.25
|
321.43
|
2. Расчётные формулы
Часто при анализе эмпирических данных возникает необходимость найти
функциональную зависимость между величинами x и y, которые получены в
результате опыта или измерений.
Хi (независимая величина) задается экспериментатором, а yi , называемая
эмпирическими или опытными значениями получается в результате опыта.
Аналитический вид функциональной зависимости, существующей между
величинами x и y обычно неизвестен, поэтому возникает практически важная задача
- найти эмпирическую формулу
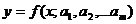 , (1)
, (1)
(где
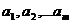 - параметры), значения которой при
- параметры), значения которой при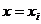 возможно мало отличались бы от опытных значений
возможно мало отличались бы от опытных значений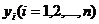 .
.
Согласно
методу наименьших квадратов наилучшими коэффициентами 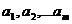 считаются те, для которых сумма квадратов отклонений
найденной эмпирической функции от заданных значений функции будет минимальной.
считаются те, для которых сумма квадратов отклонений
найденной эмпирической функции от заданных значений функции будет минимальной.
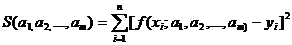 (2)
(2)
Используя
необходимое условие экстремума функции нескольких переменных - равенство нулю
частных производных, находят набор коэффициентов 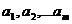 , которые
доставляют минимум функции
, которые
доставляют минимум функции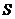 , определяемой формулой (2) и получают нормальную
систему для определения коэффициентов
, определяемой формулой (2) и получают нормальную
систему для определения коэффициентов 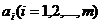 :
:
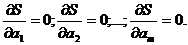 (3)
(3)
Таким
образом, нахождение коэффициентов 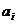 сводится
к решению системы (3).
сводится
к решению системы (3).
Вид
системы (3) зависит от того, из какого класса эмпирических формул мы ищем
зависимость (1). В случае линейной зависимости система (3) примет вид:
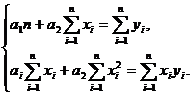
 (4)
(4)
В
случае квадратичной зависимости 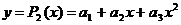 система
(3) примет вид:
система
(3) примет вид:
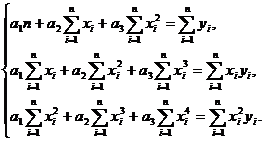 (5)
(5)
В
ряде случаев в качестве эмпирической формулы берут функцию в которую
неопределенные коэффициенты входят нелинейно. При этом иногда задачу удается
линеаризовать т.е. свести к линейной. К числу таких зависимостей относится
экспоненциальная зависимость
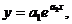 (6)
(6)
где
a1и a2 неопределенные коэффициенты.
Линеаризация
достигается путем логарифмирования равенства (6), после чего получаем
соотношение
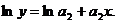 (7)
(7)
Обозначим
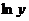 и
и 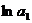 соответственно
через
соответственно
через 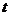 и
и 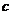 , тогда
зависимость (6) может быть записана в виде
, тогда
зависимость (6) может быть записана в виде 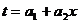 , что
позволяет применить формулы (4) с заменой a1 на
, что
позволяет применить формулы (4) с заменой a1 на 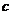 и
и 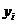 на
на 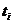 .
.
График
восстановленной функциональной зависимости y(x) по результатам измерений (xi,
yi), i=1,2,…,n называется кривой регрессии. Для проверки согласия построенной
кривой регрессии с результатами эксперимента обычно вводят следующие числовые
характеристики: коэффициент корреляции (линейная зависимость), корреляционное
отношение и коэффициент детерминированности.
Коэффициент
корреляции является мерой линейной связи между зависимыми случайными
величинами: он показывает, насколько хорошо в среднем может быть представлена
одна из величин в виде линейной функции от другой.
Коэффициент
корреляции вычисляется по формуле:
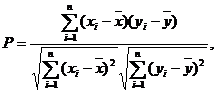 (8)
(8)
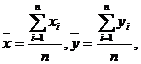 (9)
(9)
где
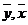 - среднее арифметическое значение соответственно по
x, y.
- среднее арифметическое значение соответственно по
x, y.
Коэффициент
корреляции между случайными величинами по абсолютной величине не превосходит 1.
Чем ближе 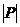 к 1, тем теснее линейная связь между x и y.
к 1, тем теснее линейная связь между x и y.
В случае нелинейной корреляционной связи условные средние значения
располагаются около кривой линии. В этом случае в качестве характеристики силы
связи рекомендуется использовать корреляционное отношение, интерпретация
которого не зависит от вида исследуемой зависимости.
Корреляционное отношение вычисляется по формуле:
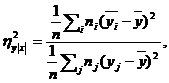 (10)
(10)
где
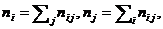 а числитель характеризует рассеяние условных средних
около
а числитель характеризует рассеяние условных средних
около 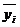 безусловного среднего
безусловного среднего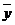 .
.
Всегда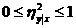 . Равенство
. Равенство 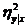 =
=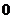 соответствует случайным некоррелированным величинам;
соответствует случайным некоррелированным величинам; 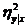 =
=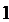 тогда и только тогда, когда имеется точная
функциональная связь между x и y. В случае линейной зависимости y от x
корреляционное отношение совпадает с квадратом коэффициента корреляции.
Величина
тогда и только тогда, когда имеется точная
функциональная связь между x и y. В случае линейной зависимости y от x
корреляционное отношение совпадает с квадратом коэффициента корреляции.
Величина 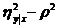 используется в качестве индикатора отклонения
регрессии от линейной.
используется в качестве индикатора отклонения
регрессии от линейной.
Корреляционное
отношение является мерой корреляционной связи y c x в какой угодно форме, но не
может дать представления о степени приближенности эмпирических данных к
специальной форме. Чтобы выяснить насколько точно построен5ная кривая отражает
эмпирические данные вводится еще одна характеристика - коэффициент
детерминированности.
Коэффициент
детерминированности определяется по формуле:
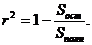 (11)
(11)
где
Sост =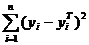 - остаточная сумма квадратов, характеризующая
отклонение экспериментальных данных от теоретических.полн
- остаточная сумма квадратов, характеризующая
отклонение экспериментальных данных от теоретических.полн 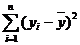 - полная сумма квадратов, где
- полная сумма квадратов, где 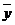 среднее значение yi.
среднее значение yi.
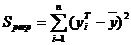 -
регрессионная сумма квадратов, характеризующая разброс данных.
-
регрессионная сумма квадратов, характеризующая разброс данных.
Чем
меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем
больше значение коэффициента детерминированности r2, который показывает,
насколько хорошо уравнение, полученное с помощью регрессионного анализа,
объясняет взаимосвязи между переменными. Если он равен 1, то имеет место полная
корреляция с моделью, т.е. нет различия между фактическим и оценочным
значениями y. В противоположном случае, если коэффициент детерминированности
равен 0, то уравнение регрессии неудачно для предсказания значений y.
Коэффициент
детерминированности всегда не превосходит корреляционное отношение. В случае
когда выполняется равенство 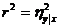 то можно
считать, что построенная эмпирическая формула наиболее точно отражает
эмпирические данные.
то можно
считать, что построенная эмпирическая формула наиболее точно отражает
эмпирические данные.
3. Расчёт с помощью таблиц, выполненных средствами Microsoft Excel
Для проведения расчётов данные целесообразно расположить в виде таблицы
2, используя средства табличного процессора Microsoft Excel.
Таблица 2
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
|
1
|
0,28
|
1,05
|
0,0784
|
0,294
|
0,021952
|
0,006147
|
0,08232
|
0,04879
|
0,013661
|
|
2
|
0,87
|
2,87
|
0,7569
|
2,4969
|
0,658503
|
0,572898
|
2,172303
|
1,054312
|
0,917251
|
|
3
|
1,65
|
6,43
|
2,7225
|
10,6095
|
4,492125
|
7,412006
|
17,50568
|
1,860975
|
3,070608
|
|
4
|
1,99
|
8,96
|
3,9601
|
17,8304
|
7,880599
|
15,68239
|
35,4825
|
2,19277
|
4,363613
|
|
5
|
2,08
|
8,08
|
4,3264
|
16,8064
|
8,998912
|
18,71774
|
34,95731
|
2,089392
|
4,345935
|
|
6
|
2,34
|
9,11
|
5,4756
|
21,3174
|
12,8129
|
29,9822
|
49,88272
|
2,209373
|
5,169932
|
|
7
|
2,65
|
16,86
|
7,0225
|
44,679
|
18,60963
|
49,31551
|
118,3994
|
2,824944
|
7,486101
|
|
8
|
2,77
|
17,97
|
7,6729
|
49,7769
|
21,25393
|
58,87339
|
137,882
|
2,888704
|
8,001709
|
|
9
|
2,83
|
18,99
|
8,0089
|
53,7417
|
22,66519
|
64,14248
|
152,089
|
2,943913
|
8,331272
|
|
10
|
3,06
|
23,75
|
9,3636
|
72,675
|
28,65262
|
87,677
|
222,3855
|
3,167583
|
9,692803
|
|
11
|
3,33
|
29,43
|
11,0889
|
98,0019
|
36,92604
|
122,9637
|
326,3463
|
3,382015
|
11,26211
|
|
12
|
3,41
|
37,45
|
11,6281
|
127,7045
|
39,65182
|
135,2127
|
435,4723
|
3,623007
|
12,35445
|
|
13
|
3,55
|
42,44
|
12,6025
|
150,662
|
44,73888
|
158,823
|
534,8501
|
3,748091
|
13,30572
|
|
14
|
3,85
|
56,94
|
14,8225
|
219,219
|
57,06663
|
219,7065
|
843,9932
|
4,041998
|
15,56169
|
|
15
|
4,01
|
75,08
|
16,0801
|
301,0708
|
64,4812
|
258,5696
|
1207,294
|
4,318554
|
17,3174
|
|
16
|
4,23
|
86,44
|
17,8929
|
365,6412
|
75,68697
|
320,1559
|
1546,662
|
4,459451
|
18,86348
|
|
17
|
4,83
|
90,85
|
23,3289
|
438,8055
|
112,6786
|
544,2376
|
2119,431
|
4,50921
|
21,77948
|
|
18
|
4,92
|
99,06
|
24,2064
|
487,3752
|
119,0955
|
585,9498
|
2397,886
|
4,595726
|
22,61097
|
|
19
|
5,14
|
120,45
|
26,4196
|
619,113
|
135,7967
|
697,9953
|
3182,241
|
4,791235
|
24,62695
|
|
20
|
5,23
|
139,65
|
27,3529
|
730,3695
|
143,0557
|
748,1811
|
3819,832
|
4,939139
|
25,8317
|
|
21
|
5,55
|
187,54
|
30,8025
|
170,9539
|
948,794
|
5776,701
|
5,233992
|
29,04866
|
|
22
|
6,32
|
200,45
|
39,9424
|
1266,844
|
252,436
|
1595,395
|
8006,454
|
5,300565
|
33,49957
|
|
23
|
6,66
|
212,97
|
44,3556
|
1418,38
|
295,4083
|
1967,419
|
9446,412
|
5,361151
|
35,70527
|
|
24
|
7,13
|
275,74
|
50,8369
|
1966,026
|
362,4671
|
2584,39
|
14017,77
|
5,619458
|
40,06674
|
|
25
|
7,25
|
321,43
|
52,5625
|
2330,368
|
381,0781
|
2762,816
|
16895,16
|
5,77278
|
41,85265
|
|
26
|
95,93
|
2089,99
|
453,3105
|
11850,65
|
2417,568
|
13982,99
|
71327,34
|
90,97713
|
415,0797
|
|
С У М М Ы
|
|
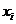 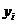 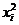 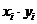 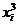 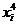 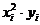 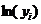 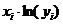
|
|
|
|
|
|
|
|
|
Поясним, как таблица 2 составляется.
Шаг 1.В ячейки А1:A25 заносим значения xi.
Шаг 2.В ячейки B1:B25 заносим значения уi.
Шаг 3.В ячейку С1 вводим формулу=А1^2.
Шаг 4.В ячейки С1:С25 эта формула копируется.
Шаг 5.В ячейку D1 вводим формулу=А1*B1.
Шаг 6.В ячейки D1:D25 эта формула копируется.
Шаг 7.В ячейку F1 вводим формулу=А1^4.
Шаг 8.В ячейки F1:F25 эта формула копируется.
Шаг 9.В ячейку G1 вводим формулу=А1^2*B1.
Шаг 10.В ячейки G1:G25 эта формула копируется.
Шаг 11.В ячейку H1 вводим формулу = LN(B1).
Шаг 12.В ячейки H1:H25 эта формула копируется.
Шаг 13.В ячейку I1 вводим формулу=А1*LN(B1).
Шаг 14.В ячейки I1:I25 эта формула копируется.
Последующие шаги делаем с помощью автосуммирования S.
Шаг 15. В ячейку А26 вводим формулу = СУММ(А1:А25).
Шаг 16. В ячейку В26 вводим формулу = СУММ(В1:В25).
Шаг 17. В ячейку С26 вводим формулу = СУММ(С1:С25).
Шаг 18. В ячейку D26 вводим формулу = СУММ(D1:D25).
Шаг 19. В ячейку E26 вводим формулу = СУММ(E1:E25).
Шаг 20. В ячейку F26 вводим формулу = СУММ(F1:F25).
Шаг 21. В ячейку G26 вводим формулу = СУММ(G1:G25).
Шаг 22. В ячейку H26 вводим формулу = СУММ(H1:H25).
Шаг 23. В ячейку I26 вводим формулу = СУММ(I1:I25).
Аппроксимируем
функцию 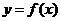 линейной функцией
линейной функцией 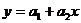 . Для
определения коэффициентов
. Для
определения коэффициентов 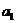 и
и 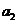 воспользуемся
системой (4). Используя итоговые суммы таблицы 2, расположенные в ячейках A26,
B26, C26 и D26, запишем систему (4) в виде
воспользуемся
системой (4). Используя итоговые суммы таблицы 2, расположенные в ячейках A26,
B26, C26 и D26, запишем систему (4) в виде
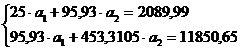 (11)
(11)
решив
которую, получим 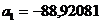 и
и 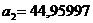 .
.
Систему решали методом Крамера. Суть которого состоит в следующем.
Рассмотрим систему n алгебраических линейных уравнений с n неизвестными:

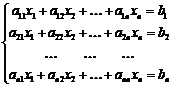 (12)
(12)
Определителем
системы называется определитель матрицы системы:
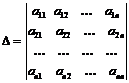 (13)
(13)
Обозначим
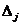 - определитель, который получится из определителя
системы Δ
заменой j-го столбца на столбец
- определитель, который получится из определителя
системы Δ
заменой j-го столбца на столбец
 (14)
(14)
Таким образом, линейная аппроксимация имеет вид
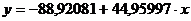 (15)
(15)
Решение
системы (11) проводим, пользуясь средствами Microsoft Excel. Результаты
представлены в таблице 3.
Таблица 3
|
A
|
B
|
C
|
D
|
E
|
|
28
|
25
|
95,93
|
2089,99
|
|
|
|
29
|
95,93
|
453,3105
|
11850,65
|
|
|
|
30
|
|
|
|
|
|
|
31
|
Обратная матрица
|
|
|
|
32
|
0,212802
|
-0,04503
|
|
a1=
|
-88,92081
|
|
33
|
-0,04503
|
0,011736
|
|
a2=
|
44,95997
|
В таблице 3 в ячейках A32:B33 записана формула {=МОБР(А28:В29)}.
В ячейках Е32:Е33 записана формула {=МУМНОЖ(А32:В33),(C28:С29)}.
Далее
аппроксимируем функцию 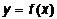 квадратичной функцией
квадратичной функцией 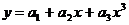 .
Для определения коэффициентов a1, a2 и a3 воспользуемся системой (5). Используя
итоговые суммы таблицы 2, расположенные в ячейках A26, B26, C26 , D26, E26,
F26, G26 запишем систему (5) в виде
.
Для определения коэффициентов a1, a2 и a3 воспользуемся системой (5). Используя
итоговые суммы таблицы 2, расположенные в ячейках A26, B26, C26 , D26, E26,
F26, G26 запишем систему (5) в виде
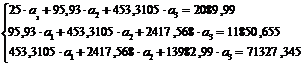 (16)
(16)
решив
которую, получим a1=10,663624, 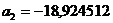 и
и 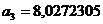
Таким
образом, квадратичная аппроксимация имеет вид
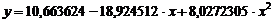 (17)
(17)
Решение
системы (16) проводим, пользуясь средствами Microsoft Excel. Результаты
представлены в таблице 4.
Таблица
4
|
A
|
B
|
C
|
D
|
E
|
F
|
|
36
|
25
|
95,93
|
453,3105
|
2089,99
|
|
|
|
37
|
95,93
|
453,3105
|
2417,568
|
11850,655
|
|
|
|
38
|
453,3105
|
2417,568
|
13982,99
|
71327,345
|
|
|
|
39
|
|
|
|
|
|
|
|
40
|
Обратная матрица
|
|
|
|
|
41
|
0,632687
|
-0,31439
|
0,033846
|
|
a1=
|
10,663624
|
|
42
|
-0,31439
|
0,184534
|
-0,021712
|
|
a2=
|
-18,924512
|
|
43
|
0,033846
|
-0,02171
|
0,002728
|
|
a3=
|
8,0272305
|
В таблице 4 в ячейках А41:С43 записана формула {=МОБР(А36:С38)}.
В ячейках F41:F43 записана формула {=МУМНОЖ(А41:C43),(D36:D38)}.
Теперь
аппроксимируем функцию 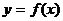 экспоненциальной функцией
экспоненциальной функцией 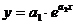 . Для определения коэффициентов
. Для определения коэффициентов 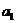 и
и 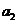 прологарифмируем
значения
прологарифмируем
значения 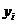 и, используя итоговые суммы таблицы 2, расположенные
в ячейках A26, C26, H26 и I26, получим систему
и, используя итоговые суммы таблицы 2, расположенные
в ячейках A26, C26, H26 и I26, получим систему
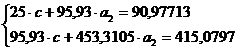 (18)
(18)
где
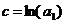 .
.
Решив
систему (18), получим 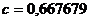 и
и 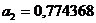 .
.
После
потенцирования получим 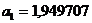 .
.
Таким
образом, экспоненциальная аппроксимация имеет вид
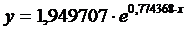 (19)
(19)
Решение
системы (18) проводим, пользуясь средствами Microsoft Excel. Результаты
представлены в таблице 5.
Таблица
5
|
B
|
C
|
D
|
E
|
F
|
|
46
|
25
|
95,93
|
90,97713
|
|
|
|
47
|
95,93
|
453,3105
|
415,0797
|
|
|
|
48
|
|
|
|
|
|
|
49
|
Обратная матрица
|
|
с=
|
0,667679
|
|
50
|
0,212802
|
-0,04503
|
|
а2=
|
0,774368
|
|
51
|
-0,04503
|
0,011736
|
|
а1=
|
1,949707
|
В ячейках А50:В51 записана формула {=МОБР(А46:В47)}.
В ячейках Е49:Е50 записана формула {=МУМНОЖ(А50:В51),(С46:С47)}.
В ячейке Е51 записана формула=EXP(E49).
Вычислим
среднее арифметическое 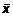 и
и 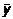 по
формулам:
по
формулам:
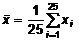 ;
; 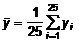 .
.
Результаты
расчета 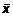 и
и 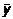 средствами
Microsoft Excel представлены в таблице 6.
средствами
Microsoft Excel представлены в таблице 6.
Таблица 6
|
B
|
C
|
|
54
|
Xср=
|
3,8372
|
|
55
|
Yср=
|
83,5996
|
В ячейке В54 записана формула=А26/25.
В ячейке В55 записана формула=В26/25
Для того, чтобы рассчитать коэффициент корреляции и коэффициент
детерминированности данные целесообразно расположить в виде таблицы 7, которая
является продолжением таблицы 2.
Таблица 7
|
A
|
B
|
J
|
K
|
L
|
M
|
N
|
O
|
|
1
|
0,28
|
1,05
|
293,6454
|
12,65367
|
6814,436
|
5987,976
|
24,44408
|
1,881775
|
|
2
|
0,87
|
2,87
|
239,5409
|
8,804276
|
6517,268
|
2774,722
|
6,733461
|
0,910717
|
|
3
|
1,65
|
6,43
|
168,7853
|
4,783844
|
5955,147
|
448,0357
|
26,39582
|
0,320737
|
|
4
|
1,99
|
8,96
|
137,8743
|
3,412148
|
5571,07
|
70,73588
|
17,36822
|
0,020626
|
|
5
|
2,08
|
8,08
|
132,703
|
3,087752
|
5703,21
|
12,13871
|
4,203942
|
2,824782
|
|
6
|
2,34
|
9,11
|
111,5258
|
2,241608
|
5548,701
|
51,48821
|
1,498588
|
7,995842
|
|
7
|
2,65
|
16,86
|
79,23325
|
1,409444
|
4454,174
|
178,573
|
0,00062
|
2,833825
|
|
8
|
2,77
|
17,97
|
70,03991
|
1,138916
|
4307,244
|
311,4631
|
3,477709
|
1,730596
|
|
9
|
2,83
|
18,99
|
65,07479
|
1,014452
|
4174,4
|
373,491
|
5,791436
|
2,382273
|
|
10
|
3,06
|
23,75
|
46,51511
|
0,60404
|
3581,975
|
620,3441
|
17,37549
|
8,423061
|
|
11
|
3,33
|
29,43
|
27,47482
|
0,257252
|
2934,346
|
983,8198
|
52,24621
|
13,94466
|
|
12
|
3,41
|
37,45
|
19,71511
|
0,1825
|
2129,786
|
725,9091
|
4,090409
|
102,2541
|
|
13
|
3,55
|
11,82104
|
0,082484
|
1694,113
|
797,8984
|
4,861044
|
143,3219
|
|
14
|
3,85
|
56,94
|
-0,34124
|
0,000164
|
710,7343
|
741,75
|
0,023142
|
342,3946
|
|
15
|
4,01
|
75,08
|
-1,47219
|
0,02986
|
72,58358
|
265,3212
|
126,0007
|
996,9257
|
|
16
|
4,23
|
86,44
|
1,115709
|
0,154292
|
8,067872
|
219,6288
|
148,7578
|
1214,778
|
|
17
|
4,83
|
90,85
|
7,198197
|
0,985652
|
52,5683
|
1397,703
|
245,6958
|
76,64891
|
|
18
|
4,92
|
99,06
|
16,74052
|
1,172456
|
239,024
|
1103,718
|
163,9776
|
121,868
|
|
19
|
5,14
|
120,45
|
48,0087
|
1,697288
|
1357,952
|
471,9084
|
25,17881
|
258,6007
|
|
20
|
5,23
|
139,65
|
78,067
|
1,939892
|
3141,647
|
43,16294
|
70,45155
|
769,9408
|
|
21
|
5,55
|
187,54
|
178,0291
|
2,933684
|
10803,61
|
725,3842
|
1200,529
|
1951,06
|
|
22
|
6,32
|
200,45
|
290,1162
|
6,164296
|
13654,02
|
27,28786
|
126,2827
|
3577,409
|
|
23
|
6,66
|
212,97
|
365,1868
|
7,9682
|
16736,7
|
6,038755
|
767,7885
|
15795,87
|
|
24
|
7,13
|
275,74
|
632,6799
|
10,84253
|
36917,93
|
1944,475
|
65,14693
|
44766,92
|
|
25
|
7,25
|
321,43
|
811,6676
|
11,6472
|
56563,3
|
7121,842
|
677,9664
|
45516,8
|
|
26
|
95,93
|
2089,9
|
3830,945
|
85,2079
|
199644
|
27404,82
|
3786,286
|
115678,1
|
|
С у м м ы
|
Остаточные суммы
|
|
X
|
Y
|
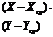 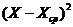 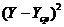 линейн.квадр.экспон. линейн.квадр.экспон.
|
|
|
|
|
|
Поясним как она составляется.
Ячейки А1:А26 и В1:В26 уже заполнены.
Далее делаем следующие шаги.
Шаг 1.В ячейку J1 вводим формулу = (А1-$B$54)*(B1-$B$55).
Шаг 2.В ячейки J2:J25 эта формула копируется.
Шаг 3.В ячейку K1 вводим формулу = (А1-$B$54)^2.
Шаг 4.В ячейки k2:K25 эта формула копируется.
Шаг 5.В ячейку L1 вводим формулу = (B1-$B$55)^2.
Шаг 6.В ячейки L2:L25 эта формула копируется.
Шаг 7.В ячейку M1 вводим формулу = ($E$32+$E$33*A1-B1)^2.
Шаг 8.В ячейки M2:M25 эта формула копируется.
Шаг 9.В ячейку N1 вводим формулу = ($F$41+$F$42*A1+$F$43*A1^2-B1)^2.
Шаг 10.В ячейки N2:N25 эта формула копируется.
Шаг 11.В ячейку O1 вводим формулу = ($E$51*EXP($E$50*A1)-B1)^2.
Шаг 12.В ячейки O2:O25 эта формула копируется.
Последующие шаги делаем с помощью авто суммирования S.
Шаг 13.В ячейку J26 вводим формулу = CУММ(J1:J25).
Шаг 14.В ячейку K26 вводим формулу = CУММ(K1:K25).
Шаг 15.В ячейку L26 вводим формулу = CУММ(L1:L25).
Шаг 16.В ячейку M26 вводим формулу = CУММ(M1:M25).
Шаг 17.В ячейку N26 вводим формулу = CУММ(N1:N25).
Шаг 18.В ячейку O26 вводим формулу = CУММ(O1:O25).
Теперь проведем расчеты коэффициента корреляции по формуле (8) (только
для линейной аппроксимации) и коэффициента детерминированности по формуле (10).
Результаты расчетов средствами Microsoft Excel представлены в таблице 8.
Таблица 8
|
A
|
B
|
|
57
|
Коэффициент корреляции
|
0,928833
|
|
58
|
Коэффициент
детерминированности (линейная аппроксимация)
|
0,862732
|
|
59
|
|
|
|
60
|
Коэффициент
детерминированности (квадратичная аппроксимация)
|
0,981035
|
|
61
|
|
|
|
62
|
Коэффициент
детерминированности (экспоненциальная аппроксимация)
|
0,420578
|
|
63
|
|
|
В ячейке E57 записана формула=J26/(K26*L26)^(1/2).
В ячейке E59 записана формула=1-M26/L26.
В ячейке E61 записана формула=1-N26/L26.
В ячейке E63 записана формула=1-O26/L26.
Анализ результатов расчетов показывает, что квадратичная аппроксимация
наилучшим образом описывает экспериментальные данные.
. Схема алгоритма
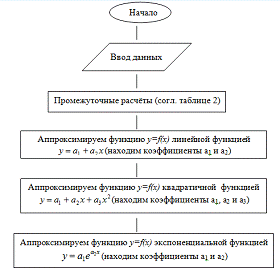
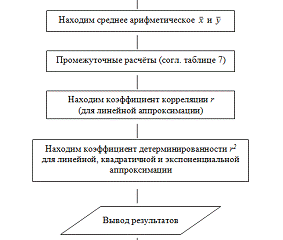

Рис. 1. Схема алгоритма для программы расчёта.
5. Расчет в программе MathCad
Линейная регрессия
· line (x, y) - вектор из двух элементов (b, a) коэффициентов
линейной регрессии b+ax;
· x - вектор действительных данных аргумента;
· y - вектор действительных данных значений того же размера.

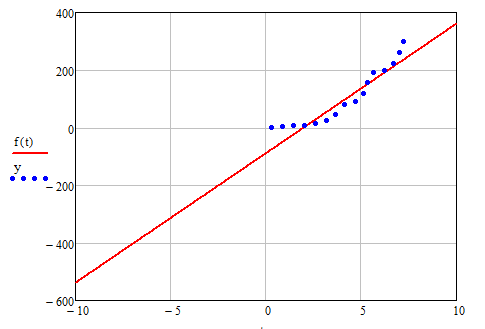
Рисунок 2.
Полиномиальная
регрессия означает приближение данных (х1, у1) полиномом k-й степени 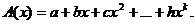 При k=i полином является прямой линией, при k=2 -
параболой, при k=3 - кубической параболой и т.д. Как правило, на практике
применяются k<5.
При k=i полином является прямой линией, при k=2 -
параболой, при k=3 - кубической параболой и т.д. Как правило, на практике
применяются k<5.
· regress (x,y,k) - вектор коэффициентов для построения
полиномиальной регрессии данных;
· interp (s,x,y,t) - результат полиномиальной регрессии;
· s=regress(x,y,k);
· x - вектор действительных данных аргумента, элементы которого
расположены в порядке возрастания;
· y - вектор действительных данных значений того же размера;
· k - степень полинома регрессии (целое положительное число);
· t - значение аргумента полинома регрессии.
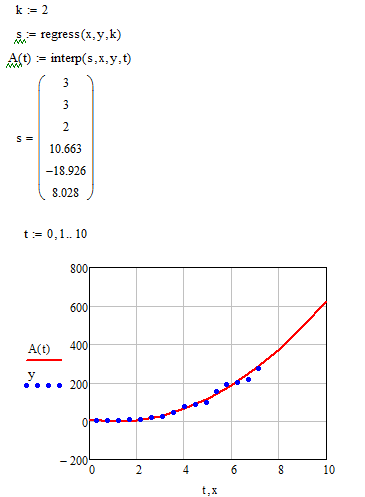
Рисунок 3
Кроме рассмотренных, в Mathcad встроено еще несколько видов
трехпараметрической регрессии, их реализация несколько отличается от
приведенных выше вариантов регрессии тем, что для них, помимо массива данных,
требуется задать некоторые начальные значения коэффициентов a, b, c.
Используйте соответствующий вид регрессии, если хорошо представляете себе,
какой зависимостью описывается ваш массив данных. Когда тип регрессии плохо
отражает последовательность данных, то ее результат часто бывает
неудовлетворительным и даже сильно различающимся в зависимости от выбора
начальных значений. Каждая из функций выдает вектор уточненных параметров a, b,
c.
. Результаты, полученные с помощью функции ЛИНЕЙН
Рассмотрим назначение функции ЛИНЕЙН.
Эта функция использует метод наименьших квадратов, чтобы вычислить прямую
линию, которая наилучшим образом аппроксимирует имеющиеся данные.
Функция возвращает массив, который описывает полученную прямую. Уравнение
для прямой линии имеет следующий вид:
= m1x1 + m2x2 + ... + b или y = mx + b,
алгоритм табличный microsoft программный
где зависимое значение y является функцией независимого значения x.
Значения m - это коэффициенты, соответствующие каждой независимой переменной x,
а b - это постоянная. Заметим, что y, x и m могут быть векторами.
Для получения результатов необходимо создать табличную формулу, которая
будет занимать 5 строк и 2 столбца. Этот интервал может располагаться в
произвольном месте на рабочем листе. В этот интервал требуется ввести функцию
ЛИНЕЙН.
В результате должны заполниться все ячейки интервала А65:В69 (как
показано в таблице 9).
Таблица 9.
|
А
|
В
|
|
65
|
44,95997
|
-88,9208
|
|
66
|
3,739466
|
15,92346
|
|
67
|
0,862732
|
34,51831
|
|
68
|
144,5549
|
23
|
|
69
|
172239,2
|
27404,82
|
Поясним назначение некоторых величин, расположенных в таблице 9.
Величины, расположенные в ячейках А65 и В65 характеризуют соответственно
наклон и сдвиг.- коэффициент детерминированности.- F-наблюдаемое значение.-
число степеней свободы.- регрессионная сумма квадратов.- остаточная сумма
квадратов.
. Представление результатов в виде графиков
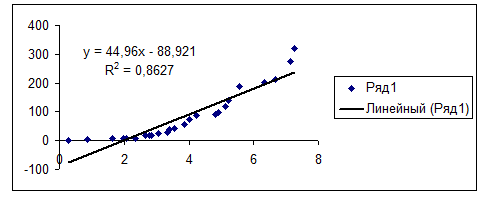
Рис. 4. График линейной аппроксимации
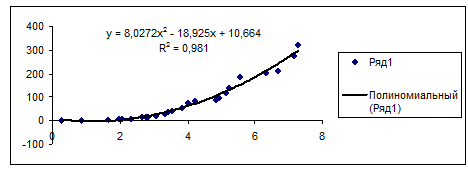
Рис. 5. График квадратичной аппроксимации
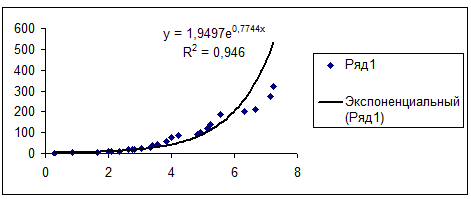
Рис. 6. График экспоненциальной аппроксимации
Выводы
Сделаем выводы по результатам полученных данных.
. Анализ результатов расчетов показывает, что квадратичная аппроксимация
наилучшим образом описывает экспериментальные данные, т.к. линия тренда для неё
наиболее точно отражает поведение функции на данном участке.
. Сравнивая результаты, полученные при помощи функции ЛИНЕЙН, видим, что
они полностью совпадают с вычислениями, проведенными выше. Это указывает на то,
что вычисления верны.
. Результаты, полученные с помощью программы MathCad, полностью совпадают
со значениями приведенными выше. Это говорит о верности вычислений.
Список используемой литературы
1
Б.П. Демидович,
И.А. Марон. Основы вычислительной математики. М: Государственное издательство
физико-математической литературы.
2
Информатика:
Учебник под ред. проф. Н.В. Макаровой. М: Финансы и статистика, 2007.
3
Информатика:
Практикум по технологии работы на компьютере под ред. проф. Н.В. Макаровой. М:
Финансы и статистика, 2010.
4
В.Б. Комягин.
Программирование в Excel на языке Visual Basic. М: Радио и связь, 2007.
5
Н. Николь, Р.
Альбрехт. Excel. Электронные таблицы. М: Изд. «ЭКОМ», 2008.
6
Методические
указания к выполнению курсовой работы по информатике (для студентов заочного
отделения всех специальностей), под ред. Журова Г. Н., СПбГГИ(ТУ), 2011.