|
Входные величины
|
MIN
|
MAX
|
|
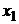 25 25
|
|
|
|
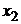 25.5 25.5
|
|
|
|
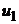 36 36
|
|
|
|
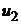 2.55 2.55
|
|
|
2.2 Исследование объекта на линейность/нелинейность
Для того чтобы определить, какой объект мы имеем, линейный или нелинейный,
проведем ряд экспериментов, где будем изменять одну из наших входные величин, а
именно X1, X2, U1, U2, и
смотреть, как будут изменяться выходные величины Y1, Y2,Y3.
На графиках ниже представлены зависимости выходных параметров от входных.
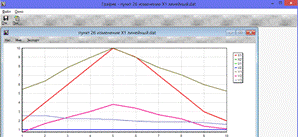
Рис.2.б.1. Зависимость выходных величин от Х1
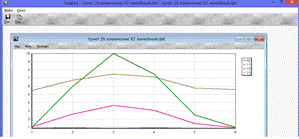
Рис.2.б.2. Зависимость выходных величин от Х2

Рис.2.б.3. Зависимость выходных величин от U1
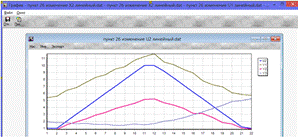
Рис.2.б.4. Зависимость выходных величин от U2
Выводы по пункту 2.2.
· Для входной переменной Х1( Рис.2.б.1.)
На графике видно, что выходные переменные Y1, Y2
зависят линейно от входной переменной Х1, а Y3 не зависит от Х1.
· Для входной переменной Х2(Рис.2.б.2.)
На графике видно, что выходные переменные Y1, Y2
зависят линейно от входной переменной Х2, а Y3 не зависит от Х2.
· Для входной переменной U1(Рис.2.б.3.)
На графике видно, что выходные переменные Y1, Y2
зависят линейно от входной переменной U1, а Y3 не зависит от U1.
· Для входной переменной U2(Рис.2.б.4.)
На графике видно, что выходные переменные Y1, Y2
зависят линейно от входной переменной U2, переменная Y3, в свою
очередь, нелинейно зависит от U2 .
Исходя из пунктов выше, можно сделать вывод, что имеется одна нелинейная
связь в ТОУ ”Химический реактор, что означает, что ТОУ является нелинейными.
2.3 Исследование объекта на стационарность/нестационарность
Для исследования объекта на стационарность сделаем два эксперимента при
одинаковых входных параметрах U1 и U2 через некоторый промежуток времени.
Вывод по пункту 2.3:
Из графиков приведенных экспериментов можно сделать вывод, что
технологический объект можно считать стационарным, т.к. значения выходных
переменных на них изменяются незначительно. Также из графиков видно, что
математическое ожидание (ТЭП 1) выходных переменных практически не изменилось,
что опять же свидетельствует о стационарности объекта управления.
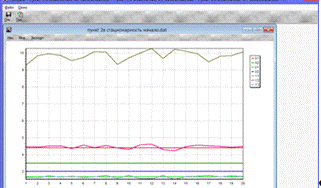
Рис. 2.в.1. 1-ый эксперимент, проведенный 3.09.14
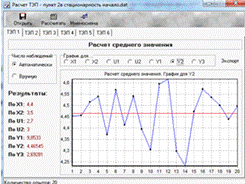
Рис. 2.в.2. Математическое ожидание(ТЭП 1) переменных для 1-ого
эксперимента
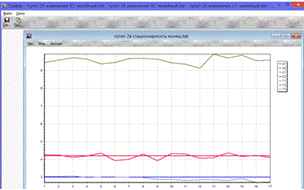
Рис. 2.в.3. 2-ой эксперимент, проведенный 17.09.14
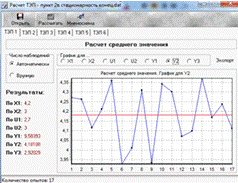
Рис. 2.в.4. Математическое ожидание(ТЭП 1) переменных для 2-ого
эксперимента(пункт 2в
стационарность конец.dat)
2.4 Определение детерминированности или случайности характера
контролируемых, но неуправляемых возмущений в режиме НЭ
Для того чтобы определить, какой характер носят контролируемые, но не
управляемые параметры объекта, надо осуществить следующий эксперимент: в режиме
НЭ при неизменных параметрах снимается график процесса и после оценивается
характер искомых возмущений.
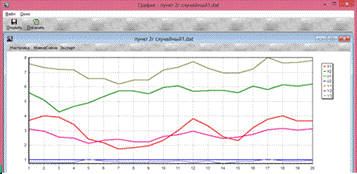
Рис.2.г. Оценка характера контролируемых, но неуправляемых возмущений
(детерминированный/случайный)
Управляемые контролируемые переменные U1 и U2
остаются постоянными, из чего можно сделать вывод, что изменение выходных
переменных Y1, Y2, Y3
происходит только за счет неконтролируемых переменных, влияющих на поведение
нашего объекта
Вывод по пункту 2.4:
Исходя из графика, можно отметить, что характер контролируемых, но
неуправляемых возмущений Х1, Х2 является случайным при режиме нормальной
эксплуатации.
.5 Выявление связей входных-выходных переменных. Составление блок-схемы
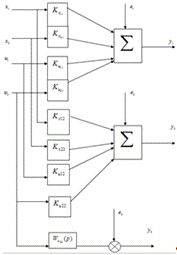
Рис.2.д. Блок-схема ТОУ.
Из блок-схемы ТОУ можно сделать выводы:
· Y1 зависит от всех входных переменных (X1,X2,U1,U2)
· Y2 так же зависит от всех входных переменных (X1,X2,U1,U2)
· Y3 зависит только от одной входной величины U2
Математическая модель ТОУ.
Y1 = Kx11*X1 + Kx21*X2 + Ku11*U1 + Ku21*U2 + e1
Y2 = Kx12*X1 + Kx22*X2 + Ku12*U1 + Ku22*U2 + e2
Y3 = Wu23*U2 + e3
2.6 Определение статических и динамических связей
По снятым графикам можно заметить, что при изменении X1, X2, U1, U2 практически мгновенно изменяются и
выходные переменные Y1, Y2, то связи между этими параметрами
статические, в свою очередь, связь между U2 и Y3
является динамической, что видно из графика(Рис.2.а.4).
Так как существует динамическая связь в нашем ТОУ, то и весь объект можно
считать динамическим.
2.7 Определение знаков влияния входных переменных на выходные
Для того чтобы оценить влияние входных переменных на выходные, необходимо
поочередно увеличивать и уменьшать одну из входных переменных и наблюдать за
изменением выходных переменных.
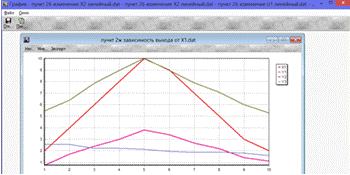
Рис.2.ж.1. Влияние Х1 на выходные переменные
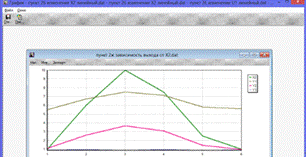
Рис.2.ж.2. Влияние Х2 на выходные переменные
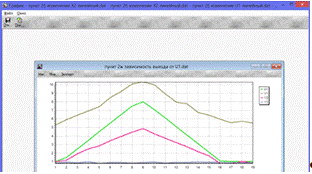
Рис.2.ж.3. Влияние U1 на выходные переменные
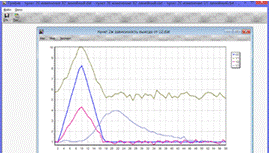
Рис.2.ж.4. Влияние U2 на выходные переменные
Выводы по пункту 2.7:
По графикам (Рис.2.ж.1 - Рис.2.ж.4) можно сделать вывод, что при увеличении
любого из входных параметров X1, X2, U1, U2
увеличиваются Y1, Y2, а при уменьшении - уменьшаются. При этом можно заметить,
что лишь увеличение и уменьшение U2
влияет на изменение выходного параметра Y3.
2.8 Определения наличия случайных неконтролируемых переменных
Из схемы Рис.2.д мы видим, что в нашей моделе присутствуют случайные
неконтролируемые возмущения, учесть которые мы не можем. Наличие случайных и
неконтролируемых переменных - признак реальной модели, т.к. в них, в отличие от
идеальных моделей, всегда присутствуют помехи, которые очень затруднительно
определить и внести в математическую модель.
Общий вывод.
Мы провели исследование нашей системы, в результате чего смогли
определить множество связей, присутствующих в ней, смогли определить характерные
ее особенности.
Очень важно, что была произведена декомпозиция системы, то есть мы смогли
“целую” систему разбить на совокупность ее подсистем(частей) и связей между
ними, в следствии чего понятно, что каждая подсистема играет важную роль для
функционирования системы.
Можно понять, что декомпозиция системы на части дала нам понять связи в
ТОУ, мы более детально раскрыли систему, рассматривая систему как “целое”, мы
смогли ясно определить ее смысл и значение.
3. Выбор критерия функционирования объекта и технико-экономических
показателей(ТЭП)
В качестве выбранного критерия функционирования объекта взята выходная
переменная Y2 - выход побочного продукта, в
качестве технико-экономических показателей выбраны показатели из ППО: ТЭП1 -
оценка математического ожидания исследуемой величины и ТЭП2 - оценка дисперсии
исследуемой величины.
4. Алгоритм ручного управления
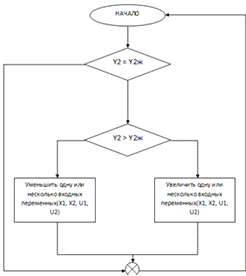
Рис. 4.1 Алгоритм ручного управления.
5. Исследование целесообразности ручного управления
Для того чтобы понять, какое управление объектом лучше проведем два
эксперимента: в первом - объект будет находиться в условиях нормальной
эксплуатации(НЭ), во втором - объект будет управляться вручную по алгоритму
представленному на рис. 4.1. Затем необходимо сравнить ТЭП1 и ТЭП2 и сделать
вывод о целесообразности использования ручного управления.
Для начала проведем эксперимент в режиме нормальной эксплуатации.
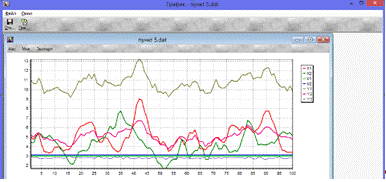
Рис.5.1Режим НЭ
Проведем эксперимент в режиме ручного управления.
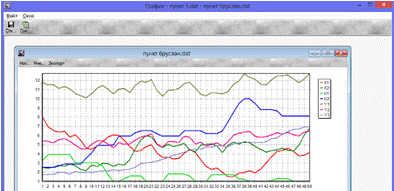
Рис. 5.2 Режим ручного управления
Рассчет мат.ожидания для двух режимов.
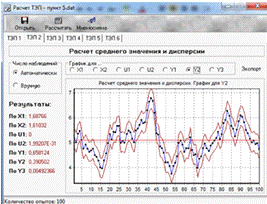
Рис. 5.3. Оценка дисперсии выбранного критерия функционирования(Y2) в
режим НЭ
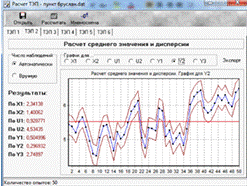
Рис. 5.4. Оценка дисперсии выбранного критерия функционирования(Y2) в
ручном режиме
Выводы по режимам эксплуатации:
· Исходя из рис. 5.1 и рис. 5.3, находим дисперсию Y2 в режиме
НЭ: Dнэ[Y2] = 0.39
· Исходя из рис. 5.2 и рис. 5.4, находим дисперсию Y2 в режиме
ручной эксплуатации:рэ[Y2] = 0.29
Общий вывод по режимам:
Так как оценка дисперсии в режиме ручной эксплуатации меньше оценки
дисперсии в режиме НЭ, можно сделать вывод, что алгоритм, предложенный для РУ,
выбран правильно.
В течение 180-250 секунд при фиксированных значениях U1 и U2 и НЭ режиме X1, X2 снимаем значения переменных (нас
интересуют X1 и X2).
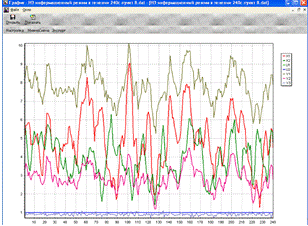
Рис. 5.5. График входных-выходных переменных, при зафиксированных U1, U2
Воспользуемся корреляционным анализом.
Корреляционный анализ - основа для исследования и понимания связей между переменными в
объекте. Процесс анализа происходит с помощью сравнения двух картин. Это
сравнение можно произвести с помощью корреляционной функции. Эта функция
показывает степень сходства между сигналом и его сдвинутой копией - чем больше
значение корреляционной функции, тем это сходство сильнее. Поскольку здесь
функция сравнивается сама с собой, ее называют автокорреляционной функцией. С
помощью автокорреляционной функции можно определить время корреляции (интервал
времени, на котором функция уменьшается в е раз. С помощью времени корреляции
исследователь может определить наиболее подходящий интервал съема данных с
объекта при его исследовании.
Интервал корреляции может быть грубо оценен через соотношение:
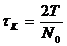 (*)
(*)
где
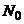 - число пересечений реализацией
- число пересечений реализацией 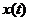 за время
за время  линии,
соответствующей среднему значению процесса.
линии,
соответствующей среднему значению процесса.
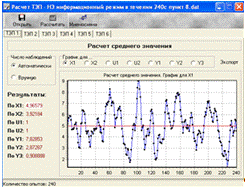
Рис.5.6.
Статистические характеристика ТЭП 1(мат. ожидание) для Х1
Для
нахождения интервала корреляции подсчитываем число пересечений оценки среднего
значения процесса (пересечения с красной линией в ТЭП1 для X1 и
потом для X2)
Для
X1 получил 35 пересечений. Интервал корреляции: t=2*240/35=13,71
[с].
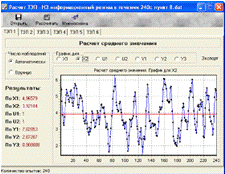
Рис.5.7.
Статистические характеристика ТЭП 1(мат. ожидание) для Х2
Для
X2 получил 35 пересечения. T=2*240/35=13,71
[c]
Тогда
получившийся интервал дискретизации ∆t=13.71/10=1.371
Для
нашего интервала дискритизации снимем информационный режим для 150 значений и
рассчитаем автокорреляцию для 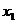 и
и 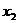 при данном интервале корреляции.
при данном интервале корреляции.
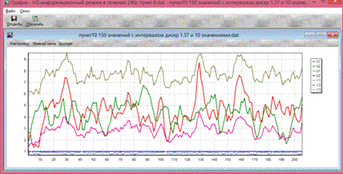
Рис.5.8.Эксперимент с интервалом дискретизации равным 1.371
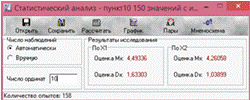
Рис.5.9. Расчет статистических характеристик
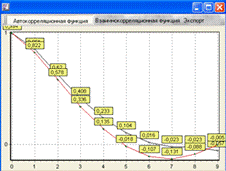
Рис.5.10. Автокорреляционная функция для ∆t =
1,37
Из графика видно, что автокорреляционая функция для Х2 практически входит
в допустимый диапазон(5%), автокорреляционная функция для Х1 входит в него, но
резко повышается, что говорит о том, что вскоре она может выйти из него.
Поэтому пересчитаем интервал дискретизации, изменив количество ординат n = 15.
Теперь снова снимаем информационный режим для 150 значений при выбранном
интервале дискретизации, равном 0.91. И приведем график автокорреляционной
функции (Рис. 5.10)

Рис.5.11. Автокорреляционная функция для ∆t =
0,91
По данному графика можно сделать вывод, что Х1 входит в допустимые 5%, в
свою очередь Х2 в нее не входит.
Пересчитаем интервал дискретизации для n = 5.
∆t = 2.74
Теперь снова снимаем информационный режим для 150 значений при выбранном
интервале дискретизации, равном 2.74. И приведем график автокорреляционной
функции (Рис. 5.11).
На графике четко видно, что автокорреляционные функции ни для Х1, ни для
Х2 не входят в допустимые 5%.
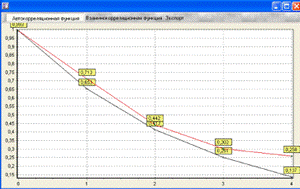
Рис.5.12. Автокорреляционная функция для ∆t = 2.74
Снимем 150 значений в информационном режиме с интервалом дискретизации ∆t = 1.7, а затем построим автокорреляционную функцию.
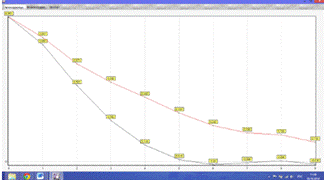
Рис.5.13. Автокорреляционная функция для ∆t =
1.7
Из графика видно, что переменная Х2 попала в допустимый интервал.
Вывод: при количестве ординат n = 15 и ∆t =
0,91 мы добились, что наша автокорреляционная функция входит в допустимый
интервал для Х1 (Рис. 5.9). На рис. 5.13 продемонстрирован график
автокорреляционной функции с ∆t = 1.7, из которого ясно видно, что мы добились, чтобы переменная Х2
также входила в аш допустимый пятипроцентный интервал.
6. Построение регрессионной модели
Построим уравнение регрессии для нашего объекта
Построение регрессионной модели нужно для анализа и синтеза нашей системы
оптимального управления ТП. Рассмотрим детерминированные уравнения нашей
системы. Как и было представлено ранее наше уравнение - полином первого порядка
с неизвестными пока коэффициентами перед входными переменными, стоящими в
уравнениях.
Для
решения задачи проведем пассивный эксперимент, т.е. снимем данные входа-выхода
в режиме НЭ без управляющего изменения входных переменных с интервалом
дискретизации, рассчитанным исходя из соотношения: 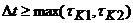 . В нашем случае мы взяли ∆t =
25, а количество точек съема данных 15. Получившийся график приведен ниже (Рис.
6.1):
. В нашем случае мы взяли ∆t =
25, а количество точек съема данных 15. Получившийся график приведен ниже (Рис.
6.1):
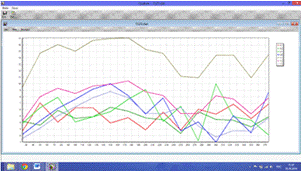
Рис.6.1.
Проведение пассивного режима
Используя
программу для нахождения коэффициентов регрессионного уравнения, найдем
коэффициенты в равнении для Y1. Заметим, что все коэффициенты получились
значимыми.
1. Уравнение регрессии для Y1.

Получившееся уравнение для Y1:
Y1 =
0.53451*X1 + 0.25341*X2 + 0.69663*U1 +
0.62886*U2 + 2.8867
Рассмотрев коэффициент множественной корреляции(0,999), можно сделать
вывод, что наше уравнение регрессионной модели точно описывает ТОУ.
Аналогично найдем коэффициенты для уравнения с Y2. Опять же заметим на значимость всех коэффициентов.
. Уравнение регрессии для Y2.

Получившееся уравнение для Y2:
Y2 =
0.37462*X1 + 0.27464*X2 + 0.55207*U1 +
0.46926*U2 - 1.0808
Рассмотрев коэффициент множественной корреляции(0,999), можно сделать
вывод, что наше уравнение регрессионной модели точно описывает ТОУ.
химический реактор управление регрессионный
7. Определение оптимального режима функционирования
технологического ОУ
Определение оптимального режима функционирования - важная и далеко не
всегда легко решаемая задача, которая позволяет АСУТП наилучшим образом
получать, обрабатывать входные данные и вырабатывать управляющие воздействия,
исходя из необходимости обеспечить оптимальное управление ТП, используя
принятые критерии. Вообще, качество работы АСУТП, ее эффективность принято
связывать с правильностью выбора оптимального режима функционирования.
Постараемся формализовать задачу выбора оптимального режима и сделать ее
поэтапной
1.
Определим вектор входных воздействий 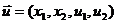 . Наша
задача найти оптимальные значения каждой составляющей вектора для выбранного
критерия эффективности(в моем случае Y2).
. Наша
задача найти оптимальные значения каждой составляющей вектора для выбранного
критерия эффективности(в моем случае Y2).
.
Определим критерий оптимальности Y2 - выход побочного продукта. Как уже говорилось, он
был задан ранее.
Y2(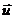 ) = 0.37462*X1 + 0.27464*X2 +
0.55207*U1 + 0.46926*U2 - 1.0808
) = 0.37462*X1 + 0.27464*X2 +
0.55207*U1 + 0.46926*U2 - 1.0808
.
Определим ограничения на допустимую область с помощью ограничений на входные
переменные, а после из них также определим ограничения на выходную величину Y1(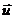 ).
).
Ограничения
выглядят следующим образом:
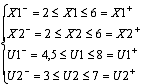
Теперь
определим ограничения на Y1max и Y1min . Для
этого решим 2 задачи оптимизации.
Y1 = 0.53451*X1 +
0.25341*X2+0.69663*U1+0.62886*U2+2.8867-> max
< X1 < 5
< X2 < 5.5
< U1 < 6
2
< U2 < 5
Решение:
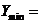 9.17 при
9.17 при 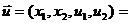 (2, 2, 3,
2)
(2, 2, 3,
2)
Y1 = 0.53451*X1+0.25341*X2+0.69663*U1+0.62886*U2 +
2.8867 -> min
<
X1 < 5
<
X2 < 5.5
<
U1 < 6
<
U2 < 5
Решение:
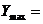 17.589 при
17.589 при 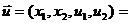 (5,5.5,6,5)
(5,5.5,6,5)
Таким
образом, имеем следующую задачу оптимизации:
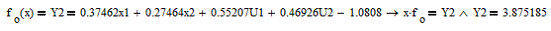
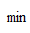
2
< X1 < 5
<
X2 < 5.5
<
U1 < 6
<
U2 < 5
Y1 > 5.73
Y1 < 10.89
Наша
задача детерминированная, Изначально мы исходим из предпосылок, что зависимости
выходных величин от входных 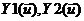 точно
известны, но на самом деле это не так. Коэффициенты при переменных
точно
известны, но на самом деле это не так. Коэффициенты при переменных 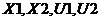 нам точно неизвестны, мы можем только оценить их
значения.
нам точно неизвестны, мы можем только оценить их
значения.
Оптимизация
по регрессионным моделям.
.
Сведение стохастической задачи оптимизации к детерминированной.
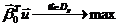
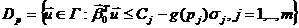
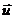 - вектор
управляемых переменных,
- вектор
управляемых переменных,
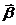 - вектор
коэффициентов модели,
- вектор
коэффициентов модели,
Г
- множество всех режимов u, удовлетворяющих ограничениям:
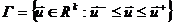
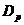 -
допустимое множество задачи,
-
допустимое множество задачи,
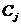 -
пороговые значения для функциональных ограничений,
-
пороговые значения для функциональных ограничений,
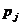 -
заданная вероятность, с которой функциональное ограничение не выйдет за
соответствующее пороговое значение,
-
заданная вероятность, с которой функциональное ограничение не выйдет за
соответствующее пороговое значение,
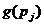 - квантиль
нормированного нормального распределения для заданной вероятности
- квантиль
нормированного нормального распределения для заданной вероятности 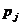 ,
,
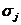 -
среднеквадратическое отклонение.
-
среднеквадратическое отклонение.
Построим
нашу задачу:
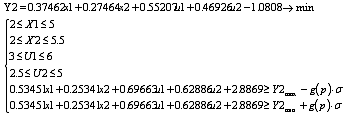
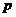 =0,975 -
доверительная вероятность
=0,975 -
доверительная вероятность
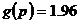
Т.о.
задача приобретает вид:
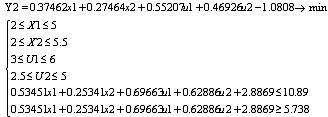
Оптимальный
план поставленной задачи: 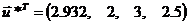
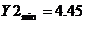
Таким
образом, мы нашли оптимальный, с точки зрения выбранного критерия эффективности
(минимум выхода побочного продукта реакции), работы химического реактора.
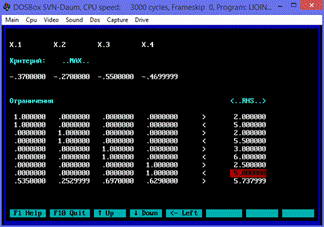
Рис.7.1.
Задача оптимизации
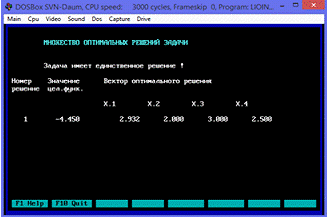
Рис.7.2. Оптимальное решение задачи
Определим наихудший случай, когда наш критерий максимален. То есть,
говоря другими словами, проверим наши ограничения на пассивность.
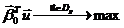
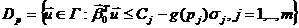
С
учетом этих формул наша задача приобретает вид:

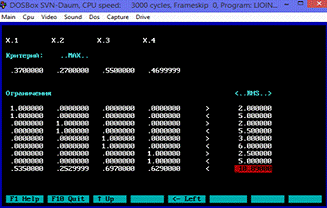
Рис.7.3.
Задача оптимизации
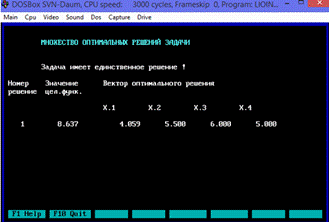
Рис.7.4. Оптимальное решение задачи.
Оптимальный
план поставленной задачи: 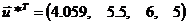
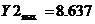
8.
Исследование чувствительности оптимального решения к ошибкам
Пусть
коэффициенты 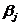 в регрессионных моделях меняются в некоторых
ограниченных пределах:
в регрессионных моделях меняются в некоторых
ограниченных пределах:
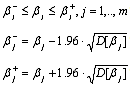
Здесь
можно сказать, что такие соотношения получились в предположении, что 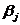 попадет в интервал
попадет в интервал 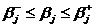 с
вероятностью
с
вероятностью 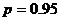 .
.
Чтобы
найти дисперсии коэффициентов регрессии, воспользуемся ковариационной матрицей
коэффициентов. В ней на главной диагонали и будут располагаться дисперсии.
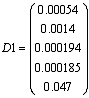 -
Дисперсии коэффициентов регрессионной модели для Y1.
-
Дисперсии коэффициентов регрессионной модели для Y1.
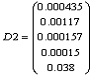 -
Дисперсии коэффициентов регрессионной модели для Y2.
-
Дисперсии коэффициентов регрессионной модели для Y2.
Используя
полученные дисперсии, можно по выше указанным формулам вычислить границы
областей наших коэффициетов 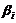 .
.
Для
модели Y1:
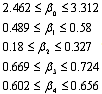
Для модели Y2:

Для
того чтобы определить границы изменения критерия оптимизации необходимо решить
две задачи: одну с «широкой» допустимой областью 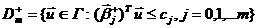 (с
коэффициентами
(с
коэффициентами 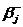 ), другую с «узкой» допустимой областью
), другую с «узкой» допустимой областью 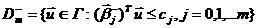 (с коэффициентами
(с коэффициентами 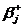 ) ,и для
каждого варианта задачи рассчитать оптимальное значение критерия.
) ,и для
каждого варианта задачи рассчитать оптимальное значение критерия.
Для
«широкой» допустимой области задача имеет вид:
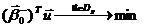
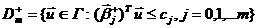
С
учетом формул сформируем задачу на минимум для «широкой» области.
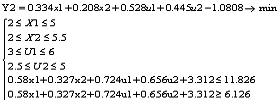
Оптимальный
план поставленной задачи: 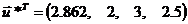
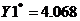 .
.
Для
«узкой» допустимой области задача имеет вид:
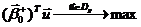
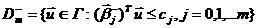
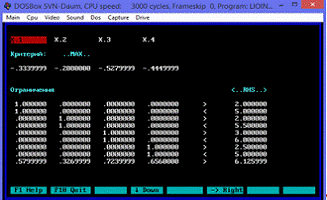
Рис.8.1.
Задача оптимизации
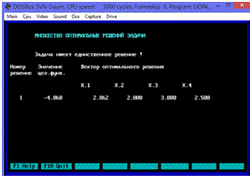
Рис.8.2.
Оптимальное решение задачи (23).
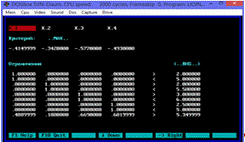
Рис.8.3.
Задача оптимизации
С учетом формул выше сформируем задачу на минимум для «узкой» области.

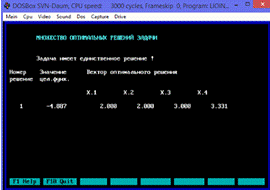
Рис.8.4. Оптимальное решение задачи.
Оптимальный
план поставленной задачи: 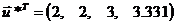
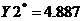 .
.
При
любых коэффициентах регрессионной модели 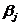 , лежащих
в пределах
, лежащих
в пределах 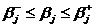 , наилучшее значение критерия оптимизации будет лежать
в пределах:
, наилучшее значение критерия оптимизации будет лежать
в пределах:
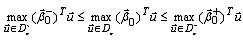

Ошибочное
определение коэффициентов может привести к серьезным изменениям в оптимальном
плане задачи.
Решим
ту же самую задачу для максимума выхода побочного продукта. Необходимо
отметить, что при решении задачи на минимум и на максимум «широкая» так же, как
и «узкая» области соответственно не совпадают.
Для
«узкой» допустимой области задача имеет вид:
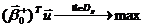
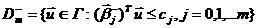
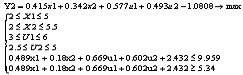
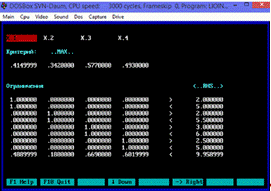
Рис.8.5.
Задача оптимизации
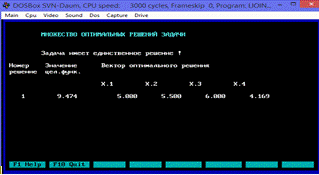
Рис.8.6.
Оптимальное решение задачи (29).
Оптимальный
план поставленной задачи: 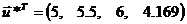
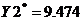 .
.
Для
«широкой» допустимой области задача имеет вид:

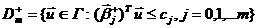
С
учетом формул выше сформируем задачу на максимум для «широкой» области.
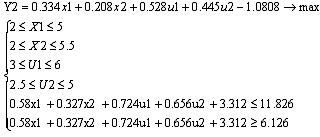
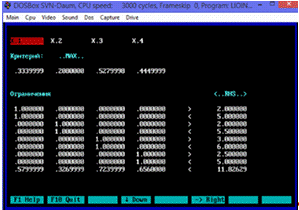
Рис.8.7.
Задача оптимизации
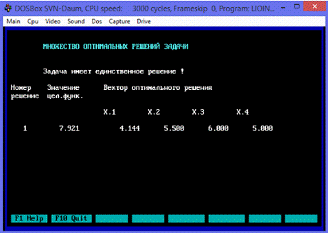
Рис.8.8.
Оптимальное решение задачи.
Оптимальный
план поставленной задачи: 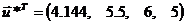
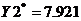 .
.
Границы
изменения наихудшего значения критерия оптимизации определяются так:
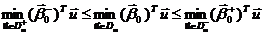
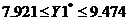
. Испытание статистических гипотез.
Возьмем критерий испытание статистических гипотез и найдем решение для задачи
оптимизации:
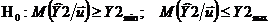
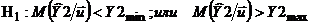
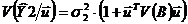
где
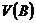 - ковариационная матрица коэффициентов регрессионной
модели. Допустимая область для вероятности
- ковариационная матрица коэффициентов регрессионной
модели. Допустимая область для вероятности 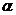 имеет
следующий вид:
имеет
следующий вид:
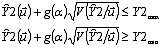
Если
имеются два допустимых решения 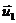 и
и 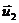 , то целесообразно считать вектор
, то целесообразно считать вектор 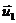 «лучше»
«лучше» 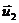 в смысле
критерия оптимизации, если вектору
в смысле
критерия оптимизации, если вектору 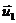 соответствует
меньшее значение порога критерия оптимизации:
соответствует
меньшее значение порога критерия оптимизации:
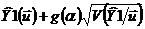
Запишем нашу задачу оптимизации в виде:
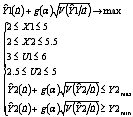
Или по-другому, немного преобразовав:
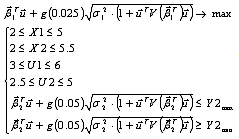
где
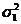 ,
,  -
дисперсия Y1 и Y2 соответственно.
-
дисперсия Y1 и Y2 соответственно.
Дисперсии
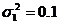 и
и 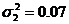
Тогда
наша задача примет вид:

Оптимальный
план поставленной задачи: 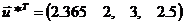
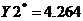 .
.
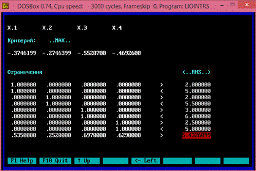
Рис.8.9. Задача оптимизации

Рис.8.10. Оптимальное решение задачи.
Сформулируем задачу на максимум.

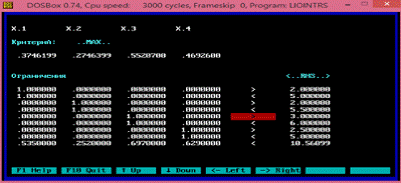
Рис.8.11. Задача оптимизации

Рис.8.12. Оптимальное решение задачи.
Оптимальный
план поставленной задачи: 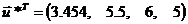
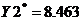
Табл.2. Таблица проведенных исследований методов оптимизации.
|
Y2->min
|
Y2->max
|
Y2->min(b-)
|
Y2->min(b0)
|
Y2->min(b+)
|
Y2->max(b-)
|
Y2->max(b0)
|
Y2->max(b+)
|
Y2->min
|
Y2->max
|
|
Ц.ф.
|
4.45
|
8.637
|
4.068
|
4.45
|
4.887
|
7.921
|
8.637
|
9.474
|
4.264
|
8.463
|
|
Х1
|
2.932
|
4.059
|
2.862
|
2.932
|
2
|
3.144
|
4.059
|
5
|
2.365
|
3.454
|
|
Х2
|
2
|
5.5
|
2
|
2
|
2
|
5.5
|
5.5
|
5.5
|
2
|
5.5
|
|
U1
|
3
|
6
|
3
|
3
|
3
|
6
|
6
|
6
|
3
|
6
|
|
U2
|
2.5
|
5
|
2.5
|
2.5
|
3.331
|
5
|
5
|
4.169
|
2.5
|
5
|
|
ОГРАНИЧЕНИЯ
|
|
Y1min
|
5.738
|
5.738
|
6.126
|
5.738
|
5.34
|
6.126
|
5.738
|
5.34
|
5.4326
|
5.4326
|
|
Y1max
|
10.89
|
10.89
|
11.826
|
10.89
|
9.959
|
11.826
|
10.89
|
9.959
|
10.56
|
10.56
|
|
Сведение к детерминированной задаче
|
чувствительность оптимального решения к ошибкам
|
Испытание стат. гипотез
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По результатам проведенных исследований методов оптимизации для
изучаемого ТОУ можно выбрать оптимизацию критерия эффективности на основе
проверки статистических гипотез, так как именно этот алгоритм дает наиболее
объективные результаты. Этот алгоритм будем использовать при разработке
гипотетической микропроцессорной системы оптимального управления.
9. Исследование динамических свойств выходной величины Y3
Для идентификации динамических характеристик обычно используют три вида
специальных входных сигналов:
· ступенчатые
· импульсные
· синусоидальные
Самый простой для применения сигнал - ступенчатый. Его мы и будем
использовать. Проведём два опыта: в одном подадим «большую» ступеньку, а в
другом «маленькую». По разгонным характеристикам, построенным в результате этих
двух экспериментов, можно будет определить вид динамического звена и его
характеристики.
. Эксперимент с «маленькой» ступенькой.
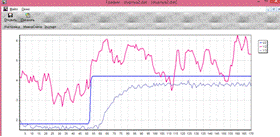
Рис.9.1. Вид
разгонной характеристики Y3 при ступенчатом воздействии U2 (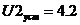 )
)
Вид
передаточной функции звена:
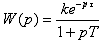
Параметры:
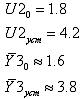
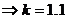 -
коэффициент усиления
-
коэффициент усиления
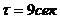 - время
запаздывания
- время
запаздывания 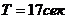 - постоянная времени
- постоянная времени
.
Эксперимент со «средней» ступенькой.
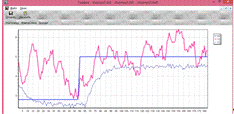
Рис.9.2. Вид
разгонной характеристики Y3 при ступенчатом воздействии U2 (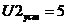 )
)
Вид
передаточной функции звена:
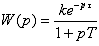
Параметры:
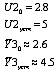
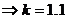 -
коэффициент усиления
-
коэффициент усиления
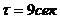 - время
запаздывания
- время
запаздывания
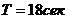 -
постоянная времени
-
постоянная времени
.
Эксперимент с «большой» ступенькой.
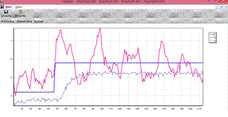
Рис.9.3. Вид
разгонной характеристики Y3 при ступенчатом воздействии U2 (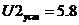 )
)
Вид
передаточной функции звена:

Параметры:
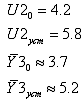
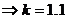 -
коэффициент усиления
-
коэффициент усиления
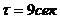 - время
запаздывания
- время
запаздывания
 -
постоянная времени
-
постоянная времени
Возьмем
средние значения параметров звена: 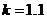 -
коэффициент усиления
-
коэффициент усиления
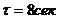 - время
запаздывания
- время
запаздывания
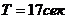 -
постоянная времени
-
постоянная времени
В
результате передаточная функция запаздывающего звена имеет вид:
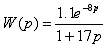
10. Регуляторы
П-регуляторы:
с 20%-ным перерегулированием: Кр = 1.27
с минимальным временем: Кр = 3.63
без перерегулирования: Кр = 0.33
ПИ-регуляторы:
с 20%-ным перерегулированием: Кр = 1.6; Tи = 12
с минимальным временем: Кр = 1.6; Tи = 16
без перерегулирования: Кр = 0.68; Tи = 14
с минимальной интегральной оценкой: Кр =2.73 ; Tи = 22
ПИД-регуляторы:
с 20%-ным перерегулированием: Кр = 2.5; Tи = 11.2;Tд =
3.12
с минимальным временем: Кр = 2.95; Tи = 14;Tд =
3.6
без перерегулирования: Кр = 1.36; Tи = 14;Tд =
2.8
с минимальной интегральной оценкой: Кр = 3.18; Tи = 9.6;Tд =
3.76
Нам даны 11 различных видов регуляторов. Постараемся определить, какой
регулятор лучше для нашего объекта, для этого будем подавать возмущения по
уставке и по нагрузке. Возмущением по уставке является возмущение, когда в
регуляторе изменяют уставку. Чтобы подать возмущение по нагрузке будем
переходить в ручное управление, затем изменять уставку, включать регулятор и
смотреть на отработку им изменения уставки.
П-регуляторы:
П-регулятор с 20%-ным перерегулированием: Кр = 1.27 Рис.10.1
П-регулятор с минимальным временем: Кр = 3.63 Рис.10.2
П-регулятор без перерегулирования: Кр = 0.33 Рис.10.3
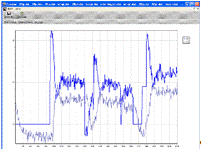
Рис.10.1. Работа П-регулятора с 20% перерегулированием
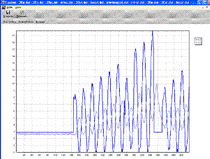
Рис.10.2. Работа П-регулятора с минимальным
временем
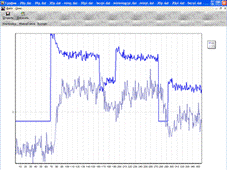
Рис.10.3. Работа П-регулятора без
перерегулирования
На регулятор подавалась уставка 4-3-4, по графикам (Рис.10.1-10.3). Очевидно, что регулятор не отрабатывал требуемые
уставки, так как значение Y3 не
достигает уставки. В результате проведенных исследований можно отметить, что в
целом П-регулятор в нашей системе работает достаточно плохо и вряд ли подходит
для нашего объекта.
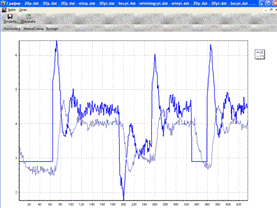
Рис.10.4. Работа ПИ-регулятора с 20%
перерегулированием
ПИ-регуляторы:
с 20%-ным перерегулированием: Кр = 1.6; Tи = 12
Рис.10.4
Пи-регулятор с минимальным временем: Кр = 1.6; Tи = 16
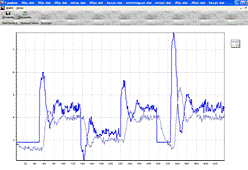
Рис.10.5. Работа ПИ-регулятора с
минимальным временем
Пи-регулятор без перерегулирования: Кр = 0.68; Tи = 14
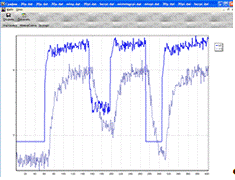
Рис.10.6. Работа ПИ-регулятора без
перерегулирования
Пи-регулятор с минимальной интегральной оценкой: Кр =2.73 ; Tи = 22
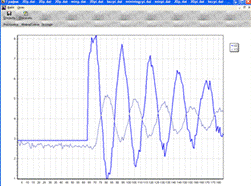
Рис.10.7. Работа ПИ-регулятора с
минимальной интегральной оценкой
На графиках (Рис.14.4-14.7) подавали уставку 4-3-4. Можно заметить, что
регулятор отработал все уставки достаточно хорошо, причем время регулирования
ПИ-регулятором с минимальным временем регулирования оказалось меньше, чем
ПИ-регулятора с 20% перерегулированием. При этом можно заметить, что
ПИ-регулятор с минимальной интегральной оценкой совсем не отрабатывает уставки.
Из этого можно сделать предположение, что скорее всего именно ПИ-регулятор с
минимальным временем подходит для регулирования процессов в нашем ТОУ.
ПИД-регуляторы:
с 20%-ным перерегулированием: Кр = 2.5; Tи = 11.2;Tд =
3.12
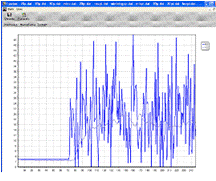
Рис.10.8. Работа ПИД-регулятора с 20%
перерегулированием
ПИД-регулятор с минимальным временем: Кр = 2.95; Tи = 14;Tд =
3.6
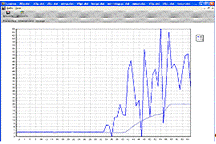
Рис.10.9. Работа ПИД-регулятора с
минимальным временем
ПИД-регулятор без перерегулирования: Кр = 1.36; Tи = 14;Tд =
2.8

Рис.10.10. Работа ПИД-регулятора без
перерегулирования
ПИД-регулятор с минимальной интегральной оценкой: Кр = 3.18; Tи = 9.6; Tд=3.76
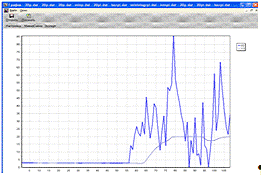
Рис.10.11. Работа ПИД-регулятора с
минимальной интегральной оценкой
Из графиков (Рис.10.8-10.11) видно, что регулятор не
отрабатывает заданные уставки при подаче возмущения по уставке и выводит
систему из рабочей области.
В результате проведенных исследований можно сделать вывод о том, что
ПИД-регулятор с найденными параметрами настроек не подходит для регулирования
нашего ТОУ.
Остановимся на ПИ-регуляторе:
· с 20%-ным перерегулированием: Кр = 1.6; Tи = 12
· с минимальным временем: Кр = 1.6; Tи = 16
· без перерегулирования: Кр = 0.68; Tи = 14
Исследуем более подробно его работу.
11. Принципы автоматизированного
управления сложной системой
Существуют три основных принципа автоматизированного управления сложной
системой:
Управление в режиме советчика оператора
Данный режим управления работает по следующему принципу: управляющие
воздействия осуществляются оператором, который использует советы от ЭВМ, а
далее сам, в соответствие со своим опытом, решает придерживаться их или нет.
(Рис.11.1).
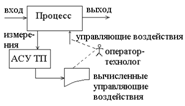
Рис.11.1. АСУТП в режиме советчика
оператора.
Все необходимые управляющие воздействия вычисляются ЭВМ в соответствии с
моделью ТП, результаты вычислений представляются оператору в печатном виде (или
в виде сообщений на дисплее). Оператор управляет процессом, изменяя уставки
регуляторов. Регуляторы являются средствами поддержания оптимального управления
ТП, причем оператор играет роль следящего и управляющего звена. АСУ ТП играет
роль устройства, безошибочно и непрерывно направляющего оператора в его усилиях
оптимизировать ТП.
Преимущества данного режима управления:
Оно удовлетворяет требованиям осторожного подхода к новым методам
управления. Режим советчика обеспечивает хорошие возможности для проверки новых
моделей ТП; в качестве оператора может выступать инженер-технолог, "тонко
чувствующий" процесс. Он наверняка обнаружит неправильную комбинацию
уставок, которую может выдать не окончательно отлаженная программа АСУТП. Кроме
того, АСУТП может следить за возникновением аварийных ситуаций, так что
оператор имеет возможность уделять больше внимания работе с уставками, при этом
АСУТП следит за большим числом аварийных ситуаций, чем оператор.
· Можно поставить инженера-технолога
o который хорошо понимает специфику ТП и знает все нюансы.
Такой специалист легко обнаружит неправильные уставки и быстро устранит
неисправности или неполадки
o который может предложить другие, возможно лучшие, модели ТП,
а также методики для проверки этих моделей
Недостатки данного режима управления:
· Обязательное наличие человека оператора в цепи управления
· Невозможность управления ТП, который имеет большое количество
входных/выходных переменных, в следствие психофизиологических особенностей
каждого человека
Распределенные системы управления
Распределённая система управления(РСУ) (англ. Distributed Control System, DCS) -
система управления технологическим процессом, отличающаяся построением
распределённой системы ввода-вывода и децентрализацией обработки данных.
РСУ применяются для управления непрерывными технологическими процессами
(хотя, строго говоря, сфера применения РСУ только этим не ограничена)
РСУ - система с иерархической структурой, что позволяет решать задачи
разных уровней управления. Такие системы имеют модульную структуру, что
гарантирует надежность и автономность всех уровней при осуществлении функций
системы.
РСУ - система с открытой архитектурой, что позволяет существующим
устройствам и системам интегрироваться в одну систему, а также самой системе
интегрироваться в более высокие уровни иерархии управления.
Сферы применения РСУ многочисленны:
· Химия и нефтехимия.
· Нефтепереработка и нефтедобыча.
· Стекольная промышленность.
· Пищевая промышленность: молочная, сахарная, пивная.
· Газодобыча и газопереработка.
· Металлургия.
· Энергоснабжение и т. д.
Требования к современной РСУ:
· Отказоустойчивость и безопасность.
· Простота разработки и конфигурирования.
· Поддержка территориально распределённой архитектуры.
· Единая конфигурационная база данных.
· Развитый
человеко-машинный интерфейс
<https://ru.wikipedia.org/wiki/%D0%A7%D0%B5%D0%BB%D0%BE%D0%B2%D0%B5%D0%BA%D0%BE-%D0%BC%D0%B0%D1%88%D0%B8%D0%BD%D0%BD%D1%8B%D0%B9_%D0%B8%D0%BD%D1%82%D0%B5%D1%80%D1%84%D0%B5%D0%B9%D1%81>.
Супервизорное управление
В этой схеме АСУТП используется в замкнутом контуре, т.е. установки
регуляторам задаются непосредственно системой (Рис.11.2.).
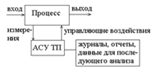
Рис.11.2. схема супервизорного управления
В супервизорном режиме АСУТП поддерживает ТП в зонах уставки воздействия
на управляемый сигнал неким или, в общем случае, некими управляющими
величинами. В данном режиме не нужно долгое присутствие человека-оператора. АСУ
ТП по определенному алгоритму из коэффициентов, введенных человеком оператором
высчитывает уставки , а затем работает без участия человека оператора
длительный срок.
Наиболее приемлемые варианты супервизорного управления:
· Автоматическая коррекция заданных значений регулируемых
величин
· Автоматическая коррекция динамических параметров настройки
автоматической системы регулирования нижнего уровня.
Используя первый режим супервизорного управления, то есть изменение
уставок, осуществим управление объектом. Будем изменять уставку по следующим
значениям 3-7-4-2. Опыт для ПИ-регулятора с 20%-ным перерегулированием: Кр =
1.6; Tи = 12 (Рис.11.3).

Рис.11.3. Супервизарное управление
(ПИ-регулятор с 20% перерегулированием)
Как видно из графика, регулятор хорошо отработал все уставки, мы можем
применять его для управления нашим объектом.
Опыт для ПИ-регулятора с минимальным временем: Кр = 1.6; Tи = 16
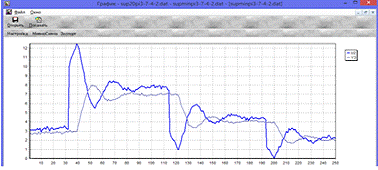
Рис.11.4. Супервизарное управление
(ПИ-регулятор с минимальным временем)
Как видно из графика, регулятор хорошо отработал все уставки, поэтому его
можно применить для управления нашим объектом.
Опыт для ПИ-регулятора без перерегулирования: Кр = 0.68; Tи = 14
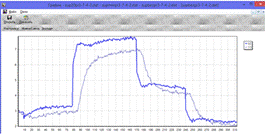
Рис.11.5. Супервизарное управление
(ПИ-регулятор без перерегулирования)
Как видно из графика, регулятор хорошо отработал все уставки, поэтому его
можно применить для управления нашим объектом.
При прочих равных оценим время регулирования для различных видов
ПИ-регуляторов.
Очевидно, что ПИ-регулятор с минимальным временем регулирования дает
минимальное время регулирование(40 сек), поэтому можно сказать, что он является
наилучшим для нашего вида технологического объекта управления.
Несильно хуже себя показал ПИ-регулятор с 20%-ным перерегулированием. Его
время регулирования составляет 45 секункд.
Самым худшим из этих трех регуляторов является ПИ-регулятор без
перерегулирования, т.к. время регулирования составляет порядка 60 секунд.
12. Синтез
гипотетической микропроцессорной системы управления ТОУ
Для исследования нашего объекта управления ”Химический реактор” мы
использовали декомпозицию САУ, в которой наша система была совокупностью
технологических процессов, протекающих в химреакторе, и частей системы
управления, которые управляют ТП, т.е декомпозиция состоит из двух подмножеств:
ТП и система управления.
Для описания системы управления применяем теоретико-множественную
концепцию, а так же предположение об иерархии ее внутренней структуры.
Наиболее существенными характеристиками иерархической структуры являются:
· Последовательное (вертикальное) расположение подсистем,
составляющих данную систему («вертикальная» декомпозиция функций управления)
· Приоритет действий и право вмешательства подсистем более
высокого уровня по отношению к нижним
· Зависимость действий подсистем верхнего уровня от
фактического исполнения нижними уровнями своих функций.
Существуют три основных подхода к описанию структуры иерархической
системы:
· Стратифицированный
Системы управления, выполненные с разных точек зрения, то есть с разных
уровней абстрагирования - страт, называют стратифицированными описаниями.
При изучении варианта системного анализа и синтеза сложных систем
целесообразно провести стратифицированное описание иерархических систем на
уровнях:
математических принципов(система мат. уравнений, описывающих ТОУ )
функциональных структур
технических структур.
· Организационный
С точки зрения организационной структуры удобно рассматривать
иерархическую систему, состоящую из четко выделенных взаимодействующих
подсистем, в каждой из которых содержится “активный” элемент, способный
принимать решения. В иерархической системе элементы, принимающие решения,
находятся иерархически(находятся на разных уровнях или эшелонах), поэтому
возможны конфликтные ситуации. Очевидно, что речь идет не о конфликте
достижения общей цели, а о малых углах несовпадения вектора “глобальной” цели.
Подход, основанный на “вертикальной” композиции процессов принятия
решений в системе. При этом будет получена структура, показывающая «путь
наверх» информации от объекта и встречный поток сигналов управления.
Декомпозиция системы выполняется по организационно-технологическому
принципу вплоть до выделения локальных подсистем управления конкретными
участками технологических процессов. Проведя декомпозицию химического реактора
можно выделить два подпроцесса:
· расход реагента U1
· расход теплоносителяU2
Подсистемы нижнего уровня, непосредственно примыкающие к технологическому
процессу, называют локальными. Этим подчеркивается, что дальнейшая декомпозиция
нецелесообразна на данной страте описания системы.
В нашей системе присутствуют 2 локальные подсистемы. Представим их в виде
двухуровневой системы управления.
Отобразим информационные связи между подсистемами в составе иерархической
управляющей системы в нашем случае химического реактора (Рис.12.1).
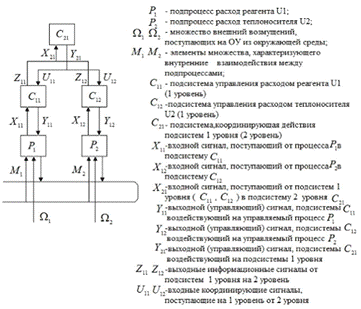
Рис.12.1. Отображение информационных связей
между подсистемами в составе иерархической управляющей системы.
Параллельная независимая работа блоков и подсистем осуществляется на
основе единой системы коммуникаций и обеспечивает необходимую автономность и
живучесть системы, делает систему открытой и позволяет повысить ее реактивность.
Однако при этом необходимо обеспечить надежную и достаточно быстродействующую
связь.
Кроме того, каждая подсистема должна иметь в любой момент времени все
данные, достаточные для реализации ее функций. То есть необходимо построение и
поддержание в реальном времени распределенной базы данных управления.
Основой любого управления является процесс принятия решения. Этот процесс
происходит в замкнутом контуре, в который входят объект управления, источники
информации о состоянии объекта, активный элемент, который и принимает решение в
соответствии с заданным алгоритмом и информацией поступающей от объекта и
вышестоящей подсистемы управления. Также в этот замкнутый контур входит
исполнительный автомат, получающий сигналы управления от элемента, принимающего
решение. Он подает полученные сигналы на исполнительный механизм, который в
нашем случае должен непосредственно действовать на управляемый объект.
Необходимо отдельно отметить, что в состав локального контура должна
входить подсистема Y3(U2), имеющая динамический характер,
которая должна управляться выбранным ПИ-регулятором изолированно от других
контуров.
Необходимо предусмотреть аварийную защиту, которая будет предохранять
систему в случае перегрева в камере реагирования, возгорание смеси, превышение
предельно допустимых концентраций выхода основного и побочного продуктов
реакции.
Информацию о состоянии управляемого объекта будем получать от датчика
выхода основного продукта Y1,
датчика выхода побочного продукта Y2, датчика температуры в камере Y3, датчика расхода реагента U1, датчика расхода теплоносителя U2.
На основе проделанной работы изобразим гипотетическую систему
оптимального управления технологическим процессом и оборудованием технического
объекта Химический реактор (Рис.11.2).
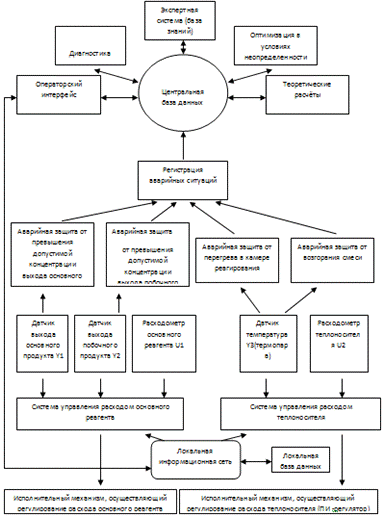
Рис.11.2. Структурно-функциональная схема
гипотетической системы управления ТП.
Заключение
С помощью аппарата системного анализа и синтеза сложных систем мы провели
исследование технологического объекта «Химический реактор». Мы пришли к выводу,
что химреактор - сложная система, которую можно разбить на составные
части(подсистемы) с помощью декомпозиции, что несомненно облегчает понимание
процессов в системе. В результате разбиения и изучения объекта на подсистемы, с
использованием математического аппарата корреляционного и регрессионного
анализа мы смогли получить необходимые нам сведения для разработки
гипотетической системы оптимального управления технологического процесса и
оборудования технического объекта химический реактор. Разработка гипотетической
системы управления являлась основной целью данного курса. Разработка
гипотетической системы управления - результат проведенной работ, а также наша
конечная цель.
Библиографический список
1. Рюкин А.Н. Системный анализ и синтез сложных систем:
Эргатические системы управления: методическое пособие. - М.: Издательство МЭИ,
2005.- 92 с.
. Рюкин А.Н. Системный анализ и синтез сложных систем:
Оптимизационное исследование в условиях неопределенности: методическое пособие.
- М.: Издательство МЭИ, 2006.- 64с.
. Рюкин А.Н. Авторский конспект лекций по курсу АИУС.
Приложение
Таблица 1. Изменение U1 многосвязный. Результаты опроса
|
N
|
Tтeк
|
X1
|
X2
|
U1
|
U2
|
Y1
|
Y2
|
Y3
|
|
0
|
0.0
|
2.0000
|
1.0000
|
1.0000
|
5.2599
|
1.0336
|
0.9990
|
|
1
|
1.0
|
2.0000
|
1.0000
|
1.0000
|
1.0000
|
5.2988
|
0.9950
|
0.8344
|
|
2
|
2.0
|
2.0000
|
1.0000
|
1.5000
|
1.0000
|
5.9212
|
1.1714
|
0.9517
|
|
3
|
3.0
|
2.0000
|
1.0000
|
2.5000
|
1.0000
|
6.4516
|
1.9086
|
0.8648
|
|
4
|
4.0
|
2.0000
|
1.0000
|
3.5000
|
1.0000
|
6.9492
|
2.4817
|
1.0031
|
|
5
|
5.0
|
2.0000
|
1.0000
|
4.5000
|
1.0000
|
7.4274
|
2.8568
|
0.7817
|
|
6
|
6.0
|
2.0000
|
1.0000
|
5.5000
|
1.0000
|
8.4978
|
3.4430
|
0.8884
|
|
7
|
7.0
|
2.0000
|
1.0000
|
6.5000
|
1.0000
|
9.2062
|
3.9486
|
0.8994
|
|
8
|
8.0
|
2.0000
|
1.0000
|
7.5000
|
1.0000
|
10.1186
|
4.4605
|
0.8316
|
|
9
|
9.0
|
2.0000
|
1.0000
|
8.0000
|
1.0000
|
10.3154
|
4.8730
|
0.8926
|
|
10
|
10.0
|
2.0000
|
1.0000
|
7.1000
|
1.0000
|
10.0455
|
4.2727
|
0.9686
|
|
11
|
11.0
|
2.0000
|
1.0000
|
6.1000
|
1.0000
|
8.9397
|
3.7401
|
0.8289
|
|
12
|
12.0
|
2.0000
|
1.0000
|
5.1000
|
1.0000
|
7.9724
|
3.2395
|
0.9093
|
|
13
|
13.0
|
2.0000
|
1.0000
|
4.1000
|
1.0000
|
7.7495
|
2.7364
|
0.8713
|
|
14
|
14.0
|
2.0000
|
1.0000
|
3.1000
|
1.0000
|
6.7627
|
2.1832
|
0.9805
|
|
15
|
15.0
|
2.0000
|
1.0000
|
2.1000
|
1.0000
|
6.4255
|
1.6748
|
0.9108
|
|
16
|
16.0
|
2.0000
|
1.0000
|
1.1000
|
1.0000
|
5.9589
|
0.8291
|
0.9480
|
|
17
|
17.0
|
2.0000
|
1.0000
|
1.0000
|
1.0000
|
5.5428
|
0.7927
|
0.8988
|
|
18
|
18.0
|
2.0000
|
1.0000
|
1.0000
|
1.0000
|
5.7246
|
1.0263
|
0.9093
|
|
19
|
19.0
|
2.0000
|
1.0000
|
1.0000
|
1.0000
|
5.4957
|
0.8939
|
0.8996
|
Таблица 2
Изменение U2 многосвязный.Результаты опроса
|
N
|
Tтeк
|
X1
|
X2
|
U1
|
U2
|
Y1
|
Y2
|
Y3
|
|
0
|
0.0
|
2.0000
|
1.0000
|
1.0000
|
1.0000
|
5.9266
|
0.8608
|
1.8697
|
|
1
|
1.0
|
2.0000
|
1.0000
|
1.0000
|
1.0000
|
5.3887
|
0.8232
|
1.9252
|
|
2
|
2.0
|
2.0000
|
1.0000
|
1.0000
|
1.0000
|
5.6054
|
0.8322
|
1.7794
|
|
3
|
3.0
|
2.0000
|
1.0000
|
1.0000
|
2.0000
|
6.4443
|
1.4976
|
1.8178
|
|
4
|
4.0
|
2.0000
|
1.0000
|
1.0000
|
3.0000
|
6.7969
|
1.9402
|
1.6202
|
|
5
|
5.0
|
2.0000
|
1.0000
|
1.0000
|
4.0000
|
7.5925
|
2.3601
|
1.7236
|
|
6
|
6.0
|
2.0000
|
1.0000
|
1.0000
|
5.0000
|
8.2914
|
2.8796
|
1.5520
|
|
7
|
7.0
|
2.0000
|
1.0000
|
1.0000
|
6.0000
|
8.6712
|
3.2737
|
1.5643
|
|
8
|
8.0
|
2.0000
|
1.0000
|
1.0000
|
7.0000
|
9.4622
|
3.8256
|
1.4291
|
|
9
|
9.0
|
2.0000
|
1.0000
|
1.0000
|
8.0000
|
9.8338
|
4.2070
|
1.4381
|
|
10
|
10.0
|
2.0000
|
1.0000
|
1.0000
|
9.0000
|
10.7301
|
4.5836
|
1.6091
|
|
11
|
11.0
|
2.0000
|
1.0000
|
1.0000
|
10.0000
|
11.2562
|
5.1457
|
1.5103
|
|
12
|
12.0
|
2.0000
|
1.0000
|
1.0000
|
10.0000
|
11.6710
|
5.2012
|
1.6525
|
|
13
|
13.0
|
2.0000
|
1.0000
|
1.0000
|
9.2000
|
10.4876
|
4.6732
|
1.9949
|
|
14
|
14.0
|
2.0000
|
1.0000
|
1.0000
|
8.2000
|
10.0944
|
4.3362
|
2.1850
|
|
15
|
15.0
|
2.0000
|
1.0000
|
1.0000
|
7.2000
|
9.4276
|
3.8757
|
2.5163
|
|
16
|
16.0
|
2.0000
|
1.0000
|
1.0000
|
6.2000
|
8.9351
|
3.1369
|
2.9431
|
|
17
|
17.0
|
2.0000
|
1.0000
|
1.0000
|
5.2000
|
7.7912
|
3.0970
|
3.3732
|
|
18
|
18.0
|
2.0000
|
1.0000
|
4.2000
|
7.2329
|
2.5713
|
3.8369
|
|
19
|
19.0
|
2.0000
|
1.0000
|
1.0000
|
3.2000
|
6.9451
|
1.8433
|
4.2720
|
|
20
|
20.0
|
2.0000
|
1.0000
|
1.0000
|
2.2000
|
6.0971
|
1.6202
|
4.8427
|
|
21
|
21.0
|
2.0000
|
1.0000
|
1.0000
|
1.2000
|
5.8285
|
1.0134
|
4.9410
|
|
22
|
22.0
|
2.0000
|
1.0000
|
1.0000
|
1.0000
|
5.6987
|
0.9143
|
5.2668
|
Таблица 3 Изменение X1 многосвязный. Результаты
опроса
|
N
|
Tтeк
|
X1
|
X2
|
U1
|
U2
|
Y1
|
Y2
|
Y3
|
|
0
|
0.0
|
2.0000
|
1.0000
|
1.0000
|
1.0000
|
5.3632
|
0.9051
|
2.7832
|
|
1
|
1.0
|
2.0000
|
1.0000
|
1.0000
|
1.0000
|
5.4492
|
0.7496
|
2.5542
|
|
2
|
2.0
|
4.0000
|
1.0000
|
1.0000
|
1.0000
|
6.3893
|
1.6992
|
2.5578
|
|
3
|
3.0
|
6.0000
|
1.0000
|
1.0000
|
1.0000
|
7.8597
|
2.3844
|
2.2317
|
|
4
|
4.0
|
8.0000
|
1.0000
|
1.0000
|
1.0000
|
8.9694
|
3.0117
|
2.2096
|
|
5
|
5.0
|
10.0000
|
1.0000
|
1.0000
|
1.0000
|
10.0181
|
3.8144
|
2.1355
|
|
6
|
6.0
|
9.0000
|
1.0000
|
1.0000
|
1.0000
|
8.9640
|
3.3764
|
1.9387
|
|
7
|
7.0
|
7.0000
|
1.0000
|
1.0000
|
1.0000
|
7.8740
|
2.6558
|
1.8643
|
|
8
|
8.0
|
5.0000
|
1.0000
|
1.0000
|
1.0000
|
7.0738
|
2.2014
|
1.8906
|
|
9
|
9.0
|
3.0000
|
1.0000
|
1.0000
|
1.0000
|
5.9842
|
1.4089
|
1.7940
|
|
10
|
10.0
|
2.0000
|
1.0000
|
1.0000
|
1.0000
|
5.2856
|
1.1052
|
1.5819
|
Таблица 4 Изменение X2 многосвязный. Результаты
опроса
|
N
|
Tтeк
|
X1
|
X2
|
U1
|
U2
|
Y1
|
Y2
|
Y3
|
|
0
|
0.0
|
2.0000
|
1.0000
|
1.0000
|
1.0000
|
5.3475
|
1.0827
|
0.9153
|
|
1
|
1.0
|
2.0000
|
1.0000
|
1.0000
|
1.0000
|
5.4898
|
1.0829
|
0.8871
|
|
2
|
2.0
|
2.0000
|
6.0000
|
1.0000
|
1.0000
|
6.7401
|
2.6131
|
0.9585
|
|
3
|
3.0
|
2.0000
|
10.0000
|
1.0000
|
1.0000
|
7.5002
|
3.6699
|
0.8696
|
|
4
|
4.0
|
2.0000
|
7.5000
|
1.0000
|
1.0000
|
7.1285
|
3.0751
|
0.9705
|
|
5
|
5.0
|
2.0000
|
2.5000
|
1.0000
|
1.0000
|
5.8013
|
1.4551
|
0.8601
|
|
6
|
6.0
|
2.0000
|
1.0000
|
1.0000
|
1.0000
|
5.6071
|
0.9661
|
0.9127
|
Таблица 5 Изменение U1 линейный. Результаты
опроса
|
N
|
Tтeк
|
X1
|
X2
|
U1
|
U2
|
Y1
|
Y2
|
Y3
|
|
0
|
0.0
|
2.0000
|
1.0000
|
1.0000
|
1.0000
|
5.2599
|
1.0336
|
0.9990
|
|
1
|
1.0
|
2.0000
|
1.0000
|
1.0000
|
1.0000
|
5.2988
|
0.9950
|
0.8344
|
|
2
|
2.0
|
2.0000
|
1.0000
|
1.5000
|
1.0000
|
5.9212
|
1.1714
|
0.9517
|
|
3
|
3.0
|
2.0000
|
1.0000
|
2.5000
|
1.0000
|
6.4516
|
1.9086
|
0.8648
|
|
4
|
4.0
|
2.0000
|
1.0000
|
3.5000
|
1.0000
|
6.9492
|
2.4817
|
1.0031
|
|
5
|
5.0
|
2.0000
|
1.0000
|
4.5000
|
1.0000
|
7.4274
|
2.8568
|
0.7817
|
|
6
|
6.0
|
2.0000
|
1.0000
|
5.5000
|
1.0000
|
8.4978
|
3.4430
|
0.8884
|
|
7
|
7.0
|
2.0000
|
1.0000
|
6.5000
|
1.0000
|
9.2062
|
3.9486
|
0.8994
|
|
8
|
8.0
|
2.0000
|
1.0000
|
7.5000
|
1.0000
|
10.1186
|
4.4605
|
0.8316
|
|
9
|
9.0
|
2.0000
|
1.0000
|
8.0000
|
1.0000
|
10.3154
|
4.8730
|
0.8926
|
|
10
|
10.0
|
2.0000
|
1.0000
|
7.1000
|
1.0000
|
10.0455
|
4.2727
|
0.9686
|
|
11
|
11.0
|
2.0000
|
1.0000
|
6.1000
|
1.0000
|
8.9397
|
3.7401
|
0.8289
|
|
12
|
12.0
|
2.0000
|
1.0000
|
5.1000
|
1.0000
|
7.9724
|
3.2395
|
0.9093
|
13.0
|
2.0000
|
1.0000
|
4.1000
|
1.0000
|
7.7495
|
2.7364
|
0.8713
|
|
14
|
14.0
|
2.0000
|
1.0000
|
3.1000
|
1.0000
|
6.7627
|
2.1832
|
0.9805
|
|
15
|
15.0
|
2.0000
|
1.0000
|
2.1000
|
1.0000
|
6.4255
|
1.6748
|
0.9108
|
|
16
|
16.0
|
2.0000
|
1.0000
|
1.1000
|
1.0000
|
5.9589
|
0.8291
|
0.9480
|
|
17
|
17.0
|
2.0000
|
1.0000
|
1.0000
|
1.0000
|
5.5428
|
0.7927
|
0.8988
|
|
18
|
18.0
|
2.0000
|
1.0000
|
1.0000
|
1.0000
|
5.7246
|
1.0263
|
0.9093
|
|
19
|
19.0
|
2.0000
|
1.0000
|
1.0000
|
1.0000
|
5.4957
|
0.8939
|
0.8996
|