Алгоритмы решения задач

Алгоритмы решения задач

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение

Высшего профессионального образования

«Пензенский государственный технологический университет»

(ПензГТУ)

Факультет «Информационных и образовательных технологий»

Кафедра «Информационные технологии и системы»

Дисциплина «Языки программирования»

КОНТРОЛЬНАЯ РАБОТА №2

на тему «Алгоритмы решения задач»

Выполнил: студент группы 13ИС2Б

Чинков М.Ю.

Проверил: ст. преподаватель каф. ИТС

Володин К.И.

Пенза 2014

СОДЕРЖАНИЕ

ВВЕДЕНИЕ

.        МЕТОДЫ ИНТЕГРИРОВАНИЯ

.        СРАВНЕНИЕ МЕТОДОВ ИНТЕГРИРОВАНИЯ

.        МЕТОДЫ РЕШЕНИЯ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

.        ЭНТРОПИЯ

.        МЕТОД МОНТЕ-КАРЛО

ЗАКЛЮЧЕНИЕ

СПИСОК ЛИТЕРАТУРЫ

ВВЕДЕНИЕ

Цель данной контрольной работы - актуализация знаний в области языков программирования. Основное задание - реализовать алгоритмы решения задач на языках программирования высокого уровня.

В рамках контрольной работы было выполнено 5 заданий:

.        Реализация интегрирования функции вида f(x) методами прямоугольников, трапеций, Симпсона.

.        Построение графика сравнения точности решения методов интегрирования в зависимости от количества разбиений.

.        Реализация методов решения системы линейных уравнений (GaussJordan, Cramer). Построение графика увеличения времени решения системы и объема занимаемой памяти с ростом размерности системы.

.        Реализация алгоритма расчета энтропии файлов с заданным расширением. Построение графика зависимости времени расчета от размера входного файла.

.        Реализация алгоритма определения значения числа Пи методом Монте-Карло (методом статистических испытаний). Построение графика зависимости точности расчета значения интеграла в зависимости от числа испытаний.

Задания №1, 2, 3 были реализованы на языке программирования C. Задание №4 было реализовано на языке программирования Java. Задание №5 было реализовано на языке программирования Pascal.

.       

1.      МЕТОДЫ ИНТЕГРИРОВАНИЯ

Численное интегрирование - вычисление значения определённого интеграла, как правило, приближённое. Под численным интегрированием понимают набор численных методов для нахождения значения определённого интеграла.

Численное интегрирование применяется, когда:

.        Сама подынтегральная функция не задана аналитически. Например, она представлена в виде таблицы (массива) значений в узлах некоторой расчётной сетки.

.        Аналитическое представление подынтегральной функции известно, но её первообразная не выражается через аналитические функции.

Задачи, которые стоят в данном разделе - реализации интегрирования функции вида f(x) методами прямоугольников, трапеций, Симпсона (метод парабол). Подынтегральная функция была взята из лабораторной работы №1 по дисциплине «Языки программирования».

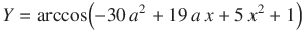
функция алгоритм энтропия интегрирование

Метод прямоугольников заключается в замене подынтегральной функции на многочлен нулевой степени на каждом элементарном отрезке. Если рассмотреть график подынтегральной функции, то метод будет заключаться в приближённом вычислении площади под графиком суммирования площадей конечного числа прямоугольников, ширина которых будет определяться расстоянием между соответствующими соседними узлами интегрирования, а высота - значением подынтегральной функции в этих узлах.

Метод трапеций заключается в замене на каждом элементарном отрезке подынтегральной функции на многочлен первой степени, то есть линейную функцию. Площадь под графиком функции аппроксимируется прямоугольными трапециями. Алгебраический порядок точности равен 1.

Метод Симпсона заключается в приближении подынтегральной функции на отрезке [a,b] интерполяционным многочленом второй степени, то есть приближение графика функции на отрезке параболой. Метод Симпсона имеет порядок погрешности 4 и алгебраический порядок точности 3.

Программа была реализована на языке C. Среда разработки - Visual Studio 2012.

В реализации были добавлены подынтегральная функция, все три метода интегрирования и функция main, которая принимает входные данные от пользователя и выводит результаты интегрирования.

Текст программы:

#include <stdio.h>

#include <math.h>InFunction(double x,double a)

{acos(-30*a*a+19*a*x+5*x*x+1);

}CalcIntegralRectangleMethod(double a, double b, int n,double number_a)

{result, h;i;= (b-a)/n; //Шаг сетки= 0;(i=1; i <= n; i++)

{+= InFunction(a + h * i - h/2,number_a); //Вычисляем в средней точке и добавляем в сумму

}*= h;result;

}CalcIntegralMethodTrapeze(double a, double b, int n,double number_a)

{result, h;i;= 0;=(b-a)/n;(i = 1; i < n; i++)

{+= InFunction(a + i*h,number_a);

}*= h;result;

}CalcIntegralSimpsonMethod(double a, double b, int n,double number_a)

{i;S1=0, result=0, h;=(b - a) / (2*n);(i = 1; i <= 2*n-1; i++)

{(i % 2 == 0)+= 2 * InFunction(a + i * h,number_a);S1+= 4 * InFunction(a + i * h,number_a);

}=((InFunction(a,number_a)+InFunction(b,number_a)+S1))*h/3;result;

}main(void)

{integral,number_a,a,b;n;("enter a, b, accuracy of calculations and number a\n");("%lf%lf%d%lf", &a,&b,&n,&number_a);= CalcIntegralRectangleMethod(a,b,n,number_a);("The value of the integral Rectangle method is: %lf \n", integral);= CalcIntegralMethodTrapeze(a,b,n,number_a);("The value of the integral Method Trapeze is: %lf \n", integral);= CalcIntegralSimpsonMethod(a,b,n,number_a);("The value of the integral Simpson's method is: %lf \n", integral);("%lf",&number_a);0;

}

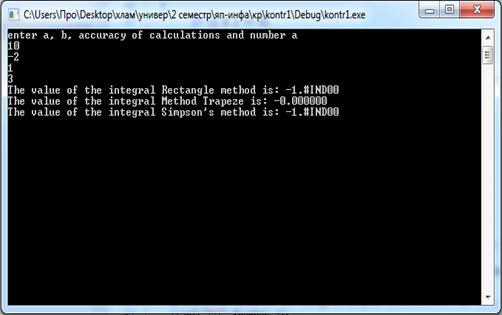
Результат работы программы:

2.      СРАВНЕНИЕ МЕТОДОВ ИНТЕГРИРОВАНИЯ

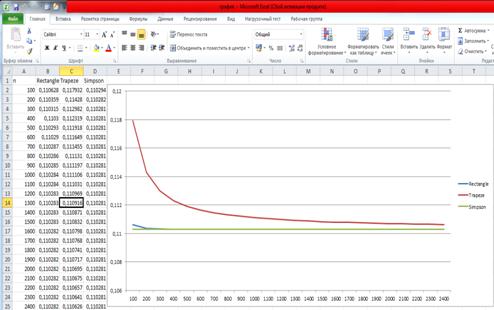
Задачи, решенные в данном разделе - построение графика сравнения точности решения методов интегрирования (метод прямоугольников, метод трапеций, метод Симпсона, реализованные в разделе №1) в зависимости от количества разбиений и построение графиков по каждому из методов.

Программа была реализована на языке C. Среда разработки - Visual Studio 2012.

Все графики представлены на одном графике для сравнения. По сравнению с заданием №1, в программу была добавлена реализация записи результатов интегрирования в текстовый файл.

Текст программы:

#include <math.h>InFunction(double x,double a)

{       //Подынтегральная функцияacos(-30*a*a+19*a*x+5*x*x+1);

}CalcIntegralRectangleMethod(double a, double b, int n,double number_a)

{result, h;i;= (b-a)/n; //Шаг сетки= 0;(i=1; i <= n; i++)

{+= InFunction(a + h * i - h/2,number_a); //Вычисляем в средней точке и добавляем в сумму

}*= h;result;

}CalcIntegralMethodTrapeze(double a, double b, int n,double number_a)

{result, h;i;= 0;=(b-a)/n;(i = 1; i < n; i++)

{+= InFunction(a + i*h,number_a);

}*= h;result;

}CalcIntegralSimpsonMethod(double a, double b, int n,double number_a)

{i;S1=0, result=0, h;=(b - a) / (2*n);(i = 1; i <= 2*n-1; i++)

{(i % 2 == 0)+= 2 * InFunction(a + i * h,number_a);S1+= 4 * InFunction(a + i * h,number_a);

}=((InFunction(a,number_a)+InFunction(b,number_a)+S1))*h/3;result;

}main(void)

{p;integral1,integral2,integral3,number_a,a,b;n;*file;("enter a, b, accuracy of calculations and namber a\n");("%lf%lf%lf", &a,&b,&number_a);= (FILE *)fopen("resultat.txt", "w+");(file, "n\tRectangle\tTrapeze\tSimpson\n");(n=500;n<2500;n=n+50)

{= CalcIntegralRectangleMethod(a,b,n,number_a);= CalcIntegralMethodTrapeze(a,b,n,number_a);= CalcIntegralSimpsonMethod(a,b,n,number_a);(file, "%d\t%lf\t%lf\t%lf\n",n,integral1,integral2,integral3);

}(file);("%d", &p);

return 0;

}

Результаты работы программы.

Текстовый файл:

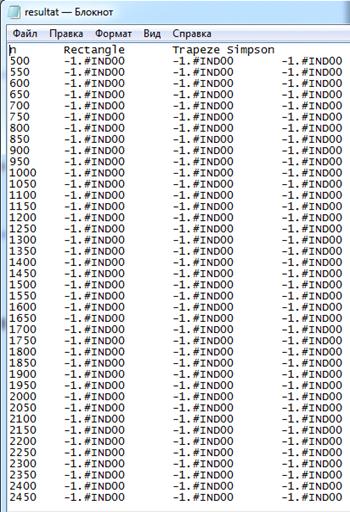
График:

3.      МЕТОДЫ решения системы линейных уравнений

Система линейных алгебраических уравнений <#"792043.files/image006.gif">                                 (1)

Здесь m - количество уравнений, а - количество неизвестных; x1, x2, …, xn - неизвестные, которые надо определить, a11, a12,…, amn - коэффициенты системы, b1, b2, … bm - свободные члены - предполагаются известными. Индексы коэффициентов системы обозначают номера уравнения и неизвестного, при котором стоит этот коэффициент.

Задачи, реализованные в данном разделе - реализация двух методов решения системы линейных уравнений (метод Гаусса-Жордана, метод Крамера), сравнение и построение графика увеличения времени решения системы и объема занимаемой памяти с ростом размерности системы.

Метод Гаусса-Жордана заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы.

Метод Крамера - способ решения с числом уравнений равным числу неизвестных с ненулевым главным определителем матрицы коэффициентов системы.

Программа была реализована на языке C. Среда разработки - Visual Studio 2012.

Текст программы:

#include <stdio.h>

#include <conio.h>

#include <malloc.h>

#include <omp.h>

#include <locale.h>time_on_gaus,time_off_gaus,time_on_cramer,time_off_cramer;print_matrix(int str,int stb,float **mass)//вывод матрицы в консоль

{(int i=0;i<str;i++)

{(int j=0;j<stb;j++)("a[%d][%d]=%.2f \t",i,j,mass[i][j]);("\n");

}("\n");

}

// Решениеgaus(int str,float **mass,float *x)

{i,j,k;

//прямой ход

for(i=0;i<str;i++)

{a=mass[i][i];(j=i+1;j<str;j++)

{b=mass[j][i];(k=i;k<str+1;k++)[j][k]=mass[i][k]*b-mass[j][k]*a;

}

}

//обратный ход(i=str-1;i>=0;i--)

{summ=0.;(j=i+1;j<str;j++)+=mass[i][j]*x[j];=mass[i][str]-summ;(mass[i][i]==0)0;[i]=summ/mass[i][i];

}1;

}gaus_det(int str,float **mass,float *det)

{i,j,k;

*det=1.0f;

//создаём копию матрицы, так как элементы матрицы мы будем использовать повторно

float **copy_mass=(float**)malloc(str*sizeof(float));(i=0;i<str;i++)

{_mass[i]=(float*)malloc(str*sizeof(float));(j=0;j<str;j++)_mass[i][j]=mass[i][j];

}

//прямой ход метод Гаусса(i=0;i<str;i++)

{(j=i+1;j<str;j++)

{(copy_mass[i][i]==0)

{( int i=0; i<str; i++)(copy_mass[i]);(copy_mass);0;

}b=copy_mass[j][i]/copy_mass[i][i];(k=i;k<str;k++)_mass[j][k]=copy_mass[j][k]-copy_mass[i][k]*b;

}

*det *= copy_mass[i][i];//вычисление определителя

}( int i=0; i<str; i++)(copy_mass[i]);(copy_mass);1;

}main()

{str,stb;=stb=0;**mass;*x;*in;* logfile;*file_name = "text.txt";*file_name1 = "text1.txt";*file_name2 = "text2.txt";(int chet=0;chet<3;chet++)

{(chet==0) printf( "Error 1: open file %s\n", file_name);(chet==1) printf( "Error 1: open file %s\n", file_name1);(chet==2) printf( "Error 1: open file %s\n", file_name2);();1;

}

// чтение размеров матрицы(in, "%d %d", &str, &stb);=(float**)malloc(str*sizeof(float)); // память под массив указателей на строки( int i=0; i<str; i++)[i] = (float*)malloc(stb*sizeof(float)); // память под каждую строку( int i=0; i<str; i++) // чтение матрицы(int j=0; j<stb;j++)(in,"%f",&mass[i][j]);(in);(LC_ALL,"Russian");("_______________Матрица_______________\n");_matrix(str,stb,mass); // печать матрицы

printf("\n_______________Решение методом Гауса_______________\n");

x = (float *)malloc( sizeof(float)*str );_on_gaus = omp_get_wtime();

if(gaus(str,mass,x)==1)//решение системы линейных уравнений методом Гаусса и

//печать результата при удачном выполнение

{

time_off_gaus = omp_get_wtime();(int i=0;i<str;i++)("x[%d]=%.2f \t",i+1,x[i]);

printf("\n");//вывод результата

}

{("Ошибка\n");

}("\n_______________Решение методом Крамера_______________\n");

float *det=(float *)malloc( sizeof(float)*(stb+1) );//массив определителей

float *t=(float *)malloc( sizeof(float)*str );//временная переменная для хранения столбца матрицы

time_on_cramer = omp_get_wtime();(int i=0;i<stb;i++)

{(gaus_det(str,mass,&det[i])!=1)//вычисление определителя используя метод Гаусса

{("Ошибка\n");

// освобождение памяти( int i=0; i<str; i++)(mass[i]);(mass);(det);(t);();

return 0;

}(int j=0;j<str;j++)//последовательная замена столбцов матрицы

{(i>0)[j][i-1]=t[j];//восстанавливаем значение столбца[j]=mass[j][i];//сохраняем значения i - столбца матрицы в переменной t[j][i]=mass[j][stb-1];//в i - столбец матрицы записываем столбец свободных членов

}

}_off_cramer = omp_get_wtime();(int i=1;i<stb;i++)("x[%d]=%.2f \t",i,det[i]/det[0]);//вывод результата("\n\n");= (FILE *)fopen("logfile.txt", "a");(logfile,"%lf\t%lf\n",time_off_gaus-time_on_gaus,time_off_cramer-time_on_cramer);(logfile);

// освобождение памяти( int i=0; i<str; i++)(mass[i]);(mass);(x);(det);(t);

}();0;

}

Результаты работы программы:

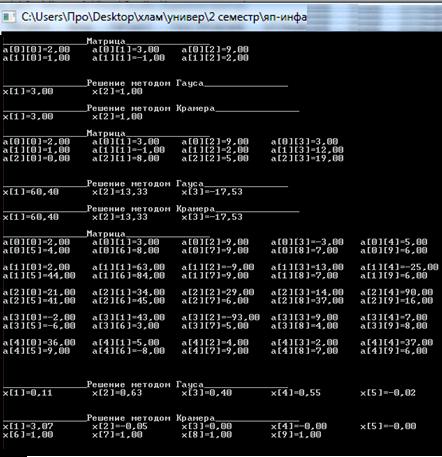
График:

4.      ЭНТРОПИЯ ФАЙЛОВ

Информационная энтропия - мера неопределённости или непредсказуемости информации, неопределённость появления какого-либо символа первичного алфавита. При отсутствии информационных потерь численно равна количеству информации на символ передаваемого сообщения. Например, в последовательности букв, составляющих какое-либо предложение на русском языке, разные буквы появляются с разной частотой, поэтому неопределённость появления для некоторых букв меньше, чем для других. Если же учесть, что некоторые сочетания букв встречаются очень редко, то неопределённость уменьшается еще сильнее.

Задачи, которые стоят в данном разделе - реализация алгоритма расчета энтропии файлов с заданным расширением и построение графика зависимости времени расчета от размера входного файла.

Программа была реализована на языке C++. Среда разработки - Visual Studio 2012.

В начале функции были введены переменные некого файлового потока, количества символов в тексте, массив частот символов и саму энтропию (entr). Затем был реализован ввод имени файла для его анализа. Открываем файл в режиме чтения и вводим логический оператор if для того случая, если файл не откроется. Затем читаем файл посимвольно, подсчитывая при этом частоту символов. Если символ не является последним в файле, то переходим к следующему символу, если является - закрываем файл. Затем был реализован сам расчет энтропии с замером времени. В конце функции процесс вывода на экран результатов энтропии, а также времени расчета.

Текст программы:

#include <iostream>

#include <fstream>

#include <string>

#include <math.h>

#include <omp.h>

#include <conio.h>namespace std;main()

{f;file_name;total=0;code[256] = {0};entr=0,;t1,t2;<< "Input file name: " ;>> file_name;.open( file_name.c_str(), ios::in | ios::binary);( !f )

{<< "Error 1: open input file " << file_name << endl;1;

}= omp_get_wtime();ch;.unsetf(ios::skipws);( !f.eof() )

{>> ch;( !f.eof() )

{[(int)ch]++;++;

}

}.close();( int i=0; i < 256; i++ )

{( code[i] == 0 );=code[i]/(float)total;=prob*log(prob)/log(2.0f);

}= omp_get_wtime();<< "Bytes: " << total << endl;.setf(ios::fixed);.precision(3);<< "Entropy: " << entr << endl;.precision(10);<< "Time: " << t2-t1 << endl;

_getch();0;

}

Результаты работы программы.

Окно вывода программы:

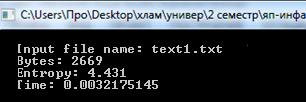
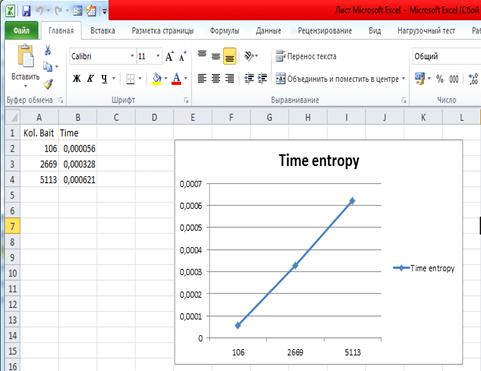
График зависимости времени расчета от размера входного файла:

5.      определениЕ числа Пи МЕТОДОМ МОНТЕ-КАРЛО

Задачи, реализованные в данном разделе - реализация алгоритма определения значения числа Пи методом Монте-Карло (методом статистических испытаний) и построение графика зависимости точности расчета значения интеграла в зависимости от числа испытаний.

При определении значения числа Пи метод Монте-Карло - самый простой и легкий в реализации метод.

Рассмотрим произвольный квадрат с центром в начале координат и вписанный в него круг. Будем рассматривать только первую координатную четверть. В ней будет находиться четверть круга и четверть квадрата. Обозначим радиус круга r, тогда четверть квадрата тоже будет квадратом(очевидно) со стороной r.

Будем случайным образом выбирать точки в этом квадрате и считать количество точек, попавших в четверть круга с помощью функции randomize. Благодаря теории вероятности мы знаем, что отношение попаданий в четверть круга к попаданиям 'в молоко' равно отношению площадей - Пи/4. Чем больше взятых наугад точек мы проверим, тем точнее будет отношение площадей.

Данный метод был реализован на языке Pascal. Среда разработки - PascalABC.NET.

Текст программы:

uses Crt;=10000000;=46340;=46340*46340;,pass : LongInt;,y : real;

{$F+};:=0;i:=1 to n do:=Random(r+1);:=Random(r+1);( x*x+y*y < r2 ) then INC(pass);;(GREEN);('Число ПИ равно: ',(pass/i*4):0:5);

ReadLn;.

Результат работы программы:

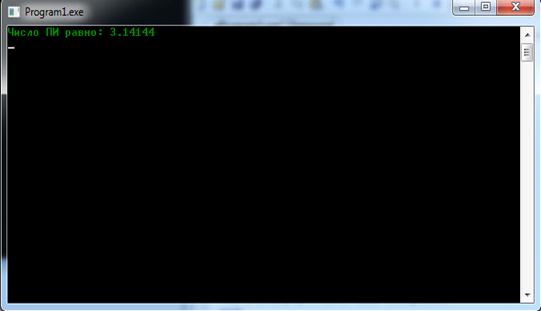
График:

заключение

В рамках контрольной работы были изучены различные алгоритмы решения задач на языках программирования высокого уровня, а также принцип построения графиков по итогам реализации алгоритмов.

Было выполнено 5 заданий:

.        Реализация интегрирования функции вида f(x) методами прямоугольников, трапеций, Симпсона.

.        Построение графика сравнения точности решения методов интегрирования в зависимости от количества разбиений.

.        Реализация методов решения системы линейных уравнений (GaussJordan, Cramer). Построение графика увеличения времени решения системы и объема занимаемой памяти с ростом размерности системы.

.        Реализация алгоритма расчета энтропии файлов с заданным расширением. Построение графика зависимости времени расчета от размера входного файла.

.        Реализация алгоритма определения значения числа Пи методом Монте-Карло (методом статистических испытаний). Построение графика зависимости точности расчета значения интеграла в зависимости от числа испытаний.

Задания №1, 2, 3 были реализованы на языке программирования C. Задание №4 было реализовано на языке программирования Java. Задание №5 было реализовано на языке программирования Pascal.

список литературы

1.      Нахождение интеграла с заданной точностью на C. Метод Симпсона. - SourcePrograms.Ru © 2011-2014 - . - Режим доступа : http://sourceprograms.ru/industries_programming/calculable_mathematics/15-nahozhdenie-integrala-s-zadannoy-tochnostyu-na-c-metod-simpsona.html. − Загл. с экрана.

.        МЕТОД ЖОРДАНА-ГАУССА - . - Режим доступа : http://ios.sseu.ru/public/eresmat/metod/met5/parmet5_3.htm. − Загл. с экрана.

.        Энтропия и WinRAR - TM © 2006-2014 - . - Режим доступа : http://habrahabr.ru/post/180803. − Загл. с экрана.

.        Вычисление с нужной точностью числа Пи - Kantor Ilia - . - Режим доступа : http://algolist.manual.ru/maths/count_fast/pi.php. − Загл. с экрана