Использование инструментов Excel для решения задач оптимизации

МИНИСТЕРСТВО СВЯЗИ И ИНФОРМАТИЗАЦИИ РЕСПУБЛИКИ БЕЛАРУСЬ

Учреждение образования

«ВЫСШИЙ ГОСУДАРСТВЕННЫЙ КОЛЛЕДЖ СВЯЗИ»

ФАКУЛЬТЕТ ЭКОНОМИКИ И ПОЧТЫ

КАФЕДРА ИНФОРМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ

Пояснительная записка к курсовому проекту

«Использование инструментов Excel для решения задач оптимизации»

по дисциплине

«Основы алгоритмизации и программирования»

Выполнила студентка гр. ПС-161

Д.Д.Одинцова

Руководитель преподаватель

Е.В. Новиков

Минск 2013

ВВЕДЕНИЕ

Оптимизация как процесс получения наилучших результатов при определенных начальных условиях находит в настоящее время самое широкое применение в науке, технике, экономике и других областях человеческой деятельности. Оптимизация - целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях.

Постановка задачи оптимизации предполагает существование конкурирующих свойств процесса. Выбор компромиссного варианта для указанных свойств и представляет собой процедуру решения оптимизационной задачи.

В зависимости от своей постановки, задачи оптимизации могут решаться различными методами, и наоборот - любой метод может применяться для решения многих задач. Методы оптимизации могут быть скалярными, векторными, поисковыми, аналитическими, а также вычислительными, теоретико-вероятностными и теоретико-игровыми.

Линейное программирование - один из первых и наиболее подробно изученных разделов математического программирования.

Линейное программирование применимо для построения математических моделей тех процессов, в основу которых может быть положена гипотеза линейного представления реального мира: экономических задач, задач управления и планирования, оптимального размещения оборудования и пр.

Задачами линейного программирования называются задачи, в которых линейны как целевая функция, так и ограничения в виде равенств и неравенств. Кратко задачу линейного программирования можно сформулировать следующим образом: найти вектор значений переменных, доставляющих экстремум линейной целевой функции при наборе ограничений в виде линейных равенств или неравенств.

В настоящее время линейное программирование является одним из наиболее употребительных аппаратов математической теории оптимального принятия решения. Для решения задач линейного программирования разработано сложное программное обеспечение, дающее возможность эффективно и надежно решать практические задачи больших объемов. В частности, и программный пакет Excel снабжен развитыми системами подготовки исходных данных, средствами их анализа и представления полученных результатов.

В данном курсовом проекте необходимо решить оптимизационную задачу линейного программирования по составлению оптимального плана перевозок, а также найти точки экстремума заданной функции.

1. ИССЛЕДОВАНИЕ ФУНКЦИИ

Дана следующая функция:

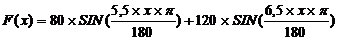
 изменяется в пределах от 100 до 500, А = 127

Производная функции:

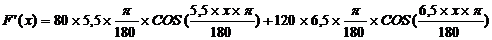
Решение задачи нужно реализовать с помощью табличного редактора Microsoft Excel.

Все необходимые данные занесем в таблицу. В столбце «B» внесем значения х с шагом равным 5. В столбце «C» находиться сама функция F(x). В столбце «D» будет находиться производная данной функции, т. е. в ячейку «D4» запишем формулу

«=(80*5,5*ПИ()/180*COS(5,5*B4*ПИ()/180)+120*6,5*ПИ()/180*

*COS(6,5*B4*ПИ()/180))*5»

В границах того интервала, где производная будет изменять свой знак с минуса на плюс, будет находиться минимум функции.

Найдем произведение двух соседних значений производной. Если полученное произведение будет меньше нуля, то на данном интервале будет находиться экстремум функции. В ячейку E5 запишем формулу «=D4*D5». Для нахождения минимумов функции в ячейку F5 запишем формулу =ЕСЛИ(E5>0;" ";ЕСЛИ(D5<0;" ";"МИНИМУМ")). Т. е. если произведение двух соседних значений производной больше нуля, то на данном интервале функция монотонно убывает или возрастает, иначе, если значение производной меньше или равно нулю, то на данном интервале находится минимум функции.

В столбце «B» (Х) внесем значения x, x изменяется от 100 до 500 с шагом равным 5. Следовательно, в первую строку столбца «B» введем значение 100, а в следующую сроку этого же столбца введем значение 105, выделим эти два значения и растянем до 500.

В столбце «С» запишем функцию F(x). Это значит, что в первую строку этого столбца запишем формулу:

,

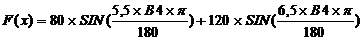где “В4” - это ссылка на ячейку, содержащую «х».

В столбце «D» вносим значение постоянной производной.

В столбце «E5» записываем формулу, представляющую собой произведение строк производной D4*D5.

Для нахождения экстремума функции - минимум в строку «F5» записываем соответствующую формулу с помощью логической функции «ЕСЛИ». =ЕСЛИ(E5>0;"-";ЕСЛИ(D5<0;"-";"МИНИМУМ"))

Результаты произведенных расчетов приведены в таблице 1.

Таблица 1 - Исследование функции F(x)

По данным столбцов «А», «F(x)», «F’(x)» построим график функции и ее производной.

координата компьютерный оптимизационный решение

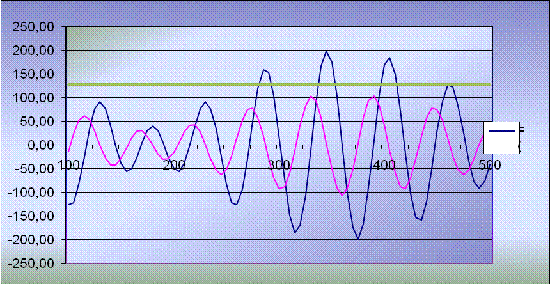
Рисунок 1 - График функции и ее производной

Имеется 8 пересечений в интервалах (100;105); (155;160); (200;205); (255;260); (315;320); (370;375); (430;435); (485;490). Для нахождения точек пересечения воспользуемся методом половинного деления. Для этого для каждого интервала создадим таблицу состоящую из столбцов: Xн, Хк, Хср, F'(Xн), F'(Xк),F’(Xср), F'(Xср),F(Xср).

Суть метода половинного деления заключается в следующем: берется интервал и делится пополам, затем определяется, на какой половине находится точка пересечения. Затем берется эта половина и снова делиться пополам. Эти действия повторяются до тех пор пока не получим необходимую нам точность.

Для первого интервала (100;105) в таблицу заносим данные. В первые строки столбца «Xн» заносим значение 100, столбца «Хк» - 105, столбца «Хср» - формулу среднего арифметического значений столбцов «Xн» и «Хк». В столбцы F'(Xн), F'(Xк),F’(Xср) заносим производную соответственно от Xн, Хк, Хср .

Значения второй и последующих строк столбцов «Xн» и «Хк» будут зависеть от того, в какой половине будет точка пересечения. Поэтому в эти строки заносим формулы, созданные с помощью логической функции «ЕСЛИ», суть которых заключается в следующем: если произведение F'(Xн) и F’(Xср) будет меньше или равно 0, то точка пересечения будет находиться на первой половине. Исходя из этого, начальной точкой будет начальная точка всего интервала, а конечной точкой уже станет среднее значение предыдущего интервала.

Результаты расчетов по первому интервалу представлены в таблице 2.

Таблица 2 - Метод половинного деления для интервала (100;105)

График изменения погрешности при нахождении первой точки пересечения будет иметь следующий вид:

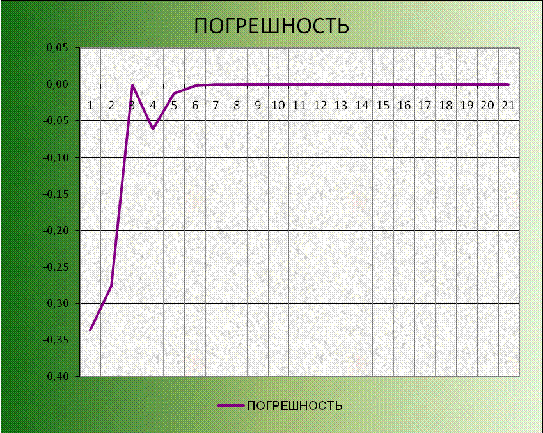
Рисунок 2 - Погрешность от количества шагов при нахождении первой точки пересечения

Результаты расчетов по второму интервалу представлены в таблице 3.

Таблица 3 - Метод половинного деления для интервала (155;160)

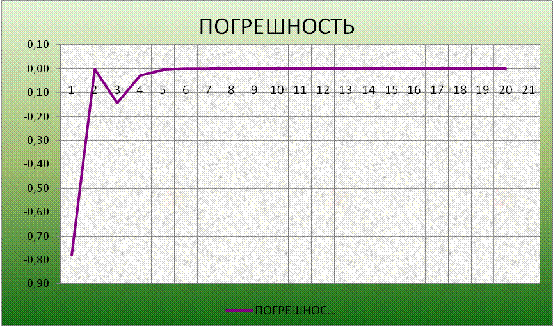
Рисунок 3 - Погрешность от количества шагов при нахождении первой точки пересечения

И так для каждого интервала.

Правильность нахождения координат точек можно проверить с помощью «Подбора параметра». Подбор параметра - это способ поиска определенного значения ячейки путем изменения значения в другой ячейке. Для этого из пункта меню «Сервис» выбираем «Подбор параметра». В открывшемся окне в поле «Установить в ячейке» ссылаемся на ячейку с данной нам функцией. В поле «Значение» указываем значение необходимого нам параметра. В поле «Изменяя значение ячейки» ссылаемся на ячейку со значением переменной, где указано ближайшее значение найденного интервала.

Проверка правильности нахождения точек пересечения по средствам «Подбора параметра» показала, что координаты точек, найденные методом половинного деления, оказались правильными.

При сопоставлении результатов, полученных методами половинного деления и с помощью подбора параметра, определили, что метод подбора параметра лучше, так как экономиться время и результаты представляются всего одной таблицей.

. РЕШЕНИЕ ТРАНСПАРТНОЙ ЗАДАЧИ С ПОМОЩЬЮ СРЕДСТВ EXCEL

Экономико-математические задачи, цель которых состоит в нахождении наилучшего, то есть оптимального с точки зрения одного или нескольких критериев варианта использования имеющихся ресурсов, называются оптимизационными.

Оптимизационные задачи решаются с помощью оптимизационных моделей методами математического программирования.

Математическое программирование - это раздел прикладной математики, который изучает задачи оптимизации и методы их решения с ориентацией на современные средства компьютерной техники.

Структура оптимизационной модели включает целевую функцию, области допустимых решений и системы ограничений, определяющих эту область.

Область допустимых решений - это область, в пределах которой осуществляется выбор решений. В экономических задачах она ограничена наличными ресурсами и условиями, которые записываются в виде системы ограничений, состоящей из уравнений и неравенств.

Главная задача математического программирования - это нахождение экстремума функций при выполнении указанных ограничений. Если система ограничений несовместима, то область допустимых решений является пустой.

Сущность задач оптимизации: определить значение переменных х1, х2,..., хn, которые обеспечивают экстремум целевой функции Е, с учетом ограничений, наложенных на аргументы этой функции.

"Поиск решения" позволяет задавать ограничения для изменяемых ячеек. Подобного рода условия называются ограничениями для решаемой задачи. "Поиск решения" доставляет не заранее известный конкретный результат для целевой функции, а отыскивает оптимальное (минимальное или максимальное), т.е. наилучшее из возможных решение.

Условие задачи:

На складах w1, w2, w3 хранятся соответственно 15, 25, 20 кроватей, которые должны быть распределены по четырем магазинам ml, m2, m3, m4, где требуется 20, 12, 5 и 9 кроватей. Пусть стоимость перевозки одной кровати со склада в магазин задается следующей таблицей в условных единицах:

Как следует планировать перевозку для минимизации стоимости?

Обозначим искомые объемы перевозок от поставщиков к потребителям следующим образом:

а11 - количество кроватей, перевезенных с первого склада первому магазину;

а12 - количество кроватей, перевезенных с первого склада второму магазину;

а13 - количество кроватей, перевезенных с первого склада третьему магазину;

а14 - количество кроватей, перевезенных с первого склада четвертому магазину;

а21 - количество кроватей, перевезенных со второго склада первому магазину;

а22 - количество кроватей, перевезенных со второго склада второму магазину;

а23 - количество кроватей, перевезенных со второго склада третьему магазину;

а24 - количество кроватей, перевезенных со второго склада четвертому магазину;

а31 - количество кроватей, перевезенных с третьего склада первому магазину;

а32 - количество кроватей, перевезенных с третьего склада второму магазину;

а33 - количество кроватей, перевезенных с третьего склада третьему магазину;

а34 - количество кроватей, перевезенных с третьего склада четвертому магазину.

Формулируем целевую функцию, которая представляет собой сумму произведений количества кроватей, перевозимых с конкретного склада конкретному магазину на стоимость перевозки одной кровати. Для составления оптимального плана перевозки целевая ячейка должна быть минимальной, так как затраты на перевозку должны быть минимальными.

Затраты на перевозку составят:

Z=2*а11 + 2*а12 + 2*a13 + 4*а14 + 3*а21 + 1*а22 + 1*a23+ 3*а24 + 3*а31 + 6*а32 + 3*a33+ 4*а34.

Изменяя значения параметров и удовлетворяя всем ограничениям, получим минимальные затраты на перевозку кроватей.

Вводим формулы в ячейки:

В ячейку I15: =C15+D15+E15+F15+G15. Это объемы поставок с первого склада.

В ячейку I16: =C16+D16+E16+F16+G16. Это объемы поставок со второго склада.

В ячейку I17: =C17+D17+E17+F17+G17. Это объемы поставок с третьего склада.

В ячейку С19: =C15+C16+C17. Это суммарная потребность первого магазина в кроватях.

В ячейку D19: =D15+D16+D17. Это суммарная потребность второго магазина в кроватях.

В ячейку E19: =E15+E16+E17. Это суммарная потребность третьего магазина в кроватях.

В ячейку F19: =F15+F16+F17. Это суммарная потребность четвертого магазина в кроватях.

В ячейку G19: =G15+G16+G17. Это сумма всех невостребованных кроватей.

Тогда в ячейку C20 запишем формулу для нахождения минимальных затрат на перевозку: =C6*C15+C7*C16+C8*C17+D7*D16+D6*D15+D8*D17+

+E6*E15+E7*E16+E8*E17+F6*F15+F7*F16+F8*F17+G15*G6+G7*G16+G8*G17

После создания целевой ячейки для решения задачи воспользуемся поиском решения. В поле «Установить целевую» дается ссылка на ячейку с функцией, для которой будет находиться минимум.

В поле «Изменяя ячейки» выделяем диапазон ячеек (C15;G17).

Далее составляем ограничения на потребность в кроватях:

для первого магазина: а11 + а21 + a31 =20

для второго магазина: a12 + а22 + а32 =12

для третьего магазина: а13 + а23 + a33 =5

для четвертого магазина: а14 + а24 + a34 =9

количество невостребованных кроватей: а15 + а25 + a35 =14.

Составляем ограничения на вместимость складов:

для первого склада: а11 + а12 + a13+ а14 + а15 =15

для второго склада: а21 + а22 + a23+ а24 + а25 =20

для третьего склада: а31 + а32 + a33+ а34 + a35 =25

Все значения, которые будут найдены, должны быть целыми числами и неотрицательными. Потребности магазинов должны быть удовлетворены полностью, однако количество кроватей не должно превышать количества кроватей, находящихся на складах.

После этого нажимаем кнопку «Выполнить» и на экране отображается оптимальное решение данной задачи.

Полученный результат представлен в таблице 4.

Таблица 4 - Результат решения задачи

Из таблицы видно, что потребности магазинов были полностью удовлетворены. А затраты на перевозку кроватей оказались минимальными и составили 95 условных единиц.

Проверим найденный план на оптимальность. Для этого найдем потенциалы строк и столбцов.

Найдем оценки пустых ячеек:

S12 =2-(0+1)=1

S13 =2-(0+1)=1

S14 =4-(0+3)=1

S15 =0-(0-1)=1

S21 =3-(0+2)=1

S25 =0-(0-1)=1

S32 =6-(1+1)=4

S33 =3-(1+1)=1

Так как оценки пустых ячеек больше нуля, то найденный план оптимален. Следовательно, решение, полученное с помощью возможностей Excel (с помощью поиска решения), является оптимальным.

ЗАКЛЮЧЕНИЕ

В данной курсовой работе были решены оптимизационные задачи с использованием программных средств Excel.

В ходе решения первой задачи был построен график функции F(x) в заданном диапазоне значений переменной Х. Были найдены интервалы значений переменной Х, в пределах которых функция принимает минимальные значения. С использованием метода половинного деления были найдены значения переменной, при которых функция принимает минимальные значения, в соответствии с заданной точностью вычислений, равной 0,0001. Проверка правильности вычислений была осуществлена с помощью «Подбора параметра».

Решение второй задачи осуществлялось с помощью «Поиска решений» средствами Excel. Была составлена целевая функция и ограничения (соответствующие условию задачи). В результате был найден оптимальный план решения задачи.

ЛИТЕРАТУРА

1.   Новиков Е.В., Лавшук О.А. Решение оптимизационных задач средствами Excel. Методическое пособие по дисциплине «Вычислительная техника и программное обеспечение» для студентов специальностей 1-45 01 04 - Почтовая связь.

2.      Левкович О.А., Шелкоплясов Е.С., Шелкоплясова Т.Н. Основы компьютерной грамотности. Учебное пособие. - М.: «Тетрасистемс»,2005 -514с.

.        3. Е.К. Овчаренко, О.П. Ильина, Е.В. Балыбердин. Финансово-экономические расчеты в Excel. Издание 2-е, дополненное - М.: Информационно-издательский дом «Филинъ», 1998.-184 с.