Движение математического маятника
Министерство образования и науки
Российской Федерации
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
"СЫКТЫВКАРСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ"
Кафедра математического моделирования
и кибернетики
КУРСОВАЯ РАБОТА
Тема: "Движение математического
маятника"
Направление подготовки: 010200.62 -
Математика и компьютерные науки
Научный руководитель: Беляева Н.А.,
Исполнитель: Ерофеевская Е.П.,
Сыктывкар, 2013
Оглавление
1§. Введение
2§. Составление уравнения движения математического маятника
3§. Решение уравнения
4§. Эллиптический интеграл
5§. Закон движения маятника (в эллиптических функциях)
6§. Графики траекторий движения маятника
7§. Заключение
8§. Список литературы
9§. Приложение
1§.
Введение
Движение математического маятника - одна из тем изучения по
дисциплине "Дифференциальные уравнения". Выявляя траекторию движения,
мы увидели, что при разных условиях, например, произвольные или малые
колебания, с трением движение маятника или без, различаются уравнения движения
математического маятника, способ решения уравнений и графики траекторий.
В своей работе я рассмотрю движение математического маятника
без трения в случае произвольных колебаний.
Объект исследования: математический маятник.
Цель исследования: построить численно
соответствующие кривые движения при различных начальных условиях.
Для достижения данной цели были поставлены следующие
задачи:
1. Изучить учебную литературу о колебаниях.
. Составить уравнение движения математического маятника без
трения.
. Найти закон движения (в эллиптических функциях).
. Изучить учебную литературу об эллиптическом интеграле.
. Научиться строить графики траекторий в математической
системе Maple.
. Сделать выводы.
Элементы новизны нашей работы заключаются
в том, что мы изучили движения математического маятника при произвольных
колебаниях без трения и построили график движения.
По структуре работа представлена в таком виде:
В 1-ом разделе рассказывается об устройстве
математического маятника, составлении уравнения движения его.
Во 2-ом разделе - находится поэтапное решение уравнения
движения математического маятника.
В 3-ем разделе изучается теория об эллиптическом интеграле.
В 4-ом разделе находится закон движения маятника, выраженный
через эллиптическую функцию.
В 5-ом разделе строятся численно соответствующие кривые
движения при различных условиях.
В приложении будет представлен код построения кривых движения
маятника в математической системе Maple. А в заключении будут подведены итоги всей
работы.
При написании этой работы я пользовалась следующей литературой:
Бухгольц Н.Н. Основной курс теоретической механики. М.:
Наука. 1969.
Боровой А., Херувимов А. Колебания и маятники. Ж. Квант. № 8,
1981. - помогли в выводе и составлении уравнения движения маятника;
Беляева Н.А. Обыкновенные дифференциальные уравнения
Сыктывкар, 2012 - в решении дифференциального уравнения движения маятника;
Фихтенгольц Г.М. Курс дифференциального и интегрального
исчисления 2 том М.: Наука. 1969. - в изучении теории об эллиптическом
интеграле и нахождении закона движения маятника, выраженного через
эллиптическую функцию.
движение математический маятник траектория
2§.
Составление уравнения движения математического маятника
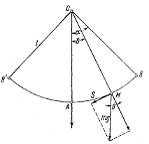
Пусть материальная точка массы m подвешена на
нерастяжимой нити или стержне длины l (весом которых пренебрегаем) так, что может
двигаться по дуге окружности (рис.). Эта система называется математическим
маятником. Выведя маятник из положения равновесия OA в положение OB (α<π/2), предоставим маятник
самому себе, не сообщая ему начальной скорости.
Маятник перейдёт в симметричное положение OB’, потом вернётся в
положение OB и т.д. Пусть θ - угол отклонения
маятника от вертикали. Задача состоит в установлении характера колебаний
маятника, т.е. в выяснении зависимости между углом θ = AOM и времени t. Для определённости рассмотрим движение точки M по дуге AB, отсчитывая пройденный
путь s=АВ=lθ от точки А, а время t-от момента прохождения маятника через положение
равновесия.
Составим естественное уравнение движения. Это уравнение
образуется из уравнения движения
mW=F+N, (1)
где F - действующая на точку активная сила, а N
- реакция связи.
Уравнение (1) мы получили по второму закону Ньютона, который
является основным законом динамики и гласит, что производная по времени от
количества движения материальной точки равна действующей на неё силе,
т.е. 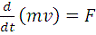
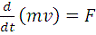 . (2)
. (2)
Считая массу постоянной, можно представить предыдущее уравнение в
виде
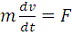
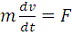 или mW=F, где W есть ускорение точки.
или mW=F, где W есть ускорение точки.
Итак, уравнение (1) в проекции на ось t даст нам одно из
естественных уравнений движения точки по заданной неподвижной гладкой кривой:
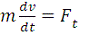
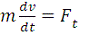 или
или 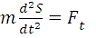
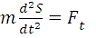 .
.
В нашем случае получим в проекции на ось t
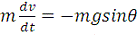
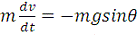 , где m есть масса маятника.
, где m есть масса маятника.
Также согласно законам механики, угловое ускорение 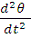
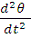 пропорционально моменту силы веса:
пропорционально моменту силы веса: 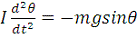
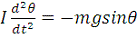 . Здесь
. Здесь 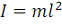
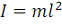 - момент инерции.
- момент инерции.
Так как 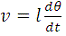
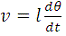 (тангенциальное
ускорение), отсюда находим
(тангенциальное
ускорение), отсюда находим
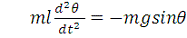
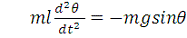 .
.
Сократим на m и положим 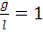
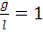 , тогда уравнение движения маятника без трения при произвольных
колебаниях будет иметь следующий вид:
, тогда уравнение движения маятника без трения при произвольных
колебаниях будет иметь следующий вид:
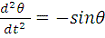
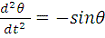 . (3)
. (3)
3§. Решение
уравнения
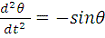
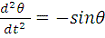
уравнение движения математического маятника без трения.
Для решения используем метод понижения порядка.
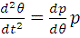
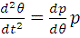 ;
;
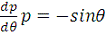
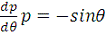 - применяем замену;
- применяем замену;
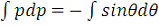
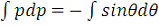 - разделили переменные;
- разделили переменные;
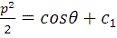
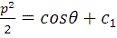 - проинтегрировали;
- проинтегрировали;
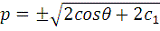
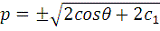 - нашли решение по переменной p;
- нашли решение по переменной p;
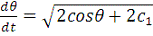
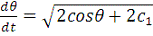 - вернулись к исходным данным;
- вернулись к исходным данным;

 - разделили переменные.
- разделили переменные.
Интегрируя слева от 0до t, а
справа от 0 до θ, приходим
к искомой зависимости:
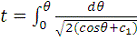
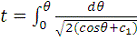 - проинтегрировали (4)
- проинтегрировали (4)
Возьмём 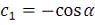
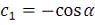 , то
, то
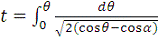
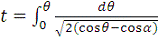 (5)
(5)
общее решения уравнения в явном виде.
4§.
Эллиптический интеграл
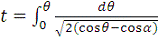
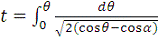 (5)
(5)
общее решения уравнения в явном виде.
Перед нами эллиптический интеграл.
В интегральном исчислении
<#"782360.files/image025.gif">, которая может быть представлена в
следующем виде:
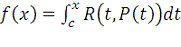
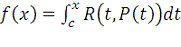 ,
,
где 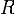 - рациональная функция
<#"782360.files/image028.gif"> - квадратный корень из многочлена
<#"782360.files/image029.gif"> - константа.
- рациональная функция
<#"782360.files/image028.gif"> - квадратный корень из многочлена
<#"782360.files/image029.gif"> - константа.
Это название, в точном смысле, относят обычно лишь к тем из них,
которые не берутся в конечном виде; другие же называют псевдоэллиптическими.
В общем случае, эллиптический интеграл не может быть выражен в
элементарных функциях; исключением являются случаи, когда P имеет повторяющиеся корни или когда R (x,y) не содержит нечётных степеней y. Однако для каждого эллиптического интеграла существует механизм
приведения его к сумме элементарных функций и трёх нормальных эллиптических
интегралов (то есть эллиптических интегралов первого, второго и третьего
рода).
Эллиптические интегралы часто представляют в виде функции ряда
различных аргументов. Эти различные аргументы полностью эквивалентны (они дают
одни и те же интегралы), но может возникнуть путаница, связанная с их различным
происхождением. В большинстве работ авторы придерживаются канонического
наименования. Прежде чем определить сами интегралы, необходимо ввести
наименования для аргументов:
· α - модулярный угол (иногда
модулярный угол обозначается лигатурой
<#"782360.files/image030.gif">);
· 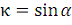
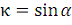 - модуль эллиптического интеграла;
- модуль эллиптического интеграла;
· 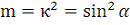
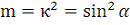 - параметр;
- параметр;
Заметим, что представленные выше величины
определяются одна через другую; определение одной из них задаёт и две
остальные.
Эллиптический интеграл зависит также и от
другого параметра, который, как и предыдущий, можно ввести несколькими
способами:
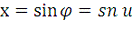
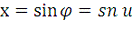 , где
, где 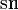 - эллиптическая функция Якоби
<#"782360.files/image035.gif">
- эллиптическая функция Якоби
<#"782360.files/image035.gif">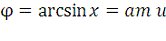 - амплитуда;
- амплитуда;
Определение одного из этих параметров определяет остальные. Таким
образом, они могут использоваться вперемешку. Заметим, что u зависит
также и от m. Несколько дополнительных уравнений связывают 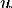 с другими параметрами:
с другими параметрами:
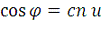
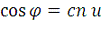 и
и 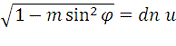
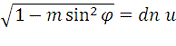
Последнее иногда называется дельта амплитуда и записывается
как
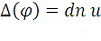
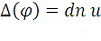 .
.
Иногда в литературе ссылаются на дополнительный параметр, дополнительный
модуль или дополнительный модулярный угол. Их вводят следующим
способом:
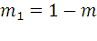
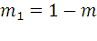 - дополнительный параметр
- дополнительный параметр
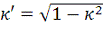
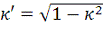 - дополнительный модуль
- дополнительный модуль
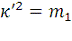
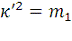 - дополнительный модулярный угол
- дополнительный модулярный угол
Все эллиптические интегралы с помощью элементарных подстановок - и
с точностью до слагаемых, выражающихся в конечном виде, - приводятся к
следующим трём стандартным интегралам:
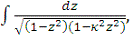
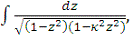
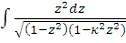
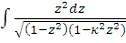 и
и

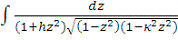
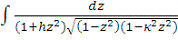 ,
,
где (0<κ<1).
Эти интегралы, как показал Луивилль, в конечном виде не берутся.
Их Лежандр назвал эллиптическими интегралами, соответственно, 1-го, 2-го и 3-го
рода. Первые два содержат лишь один параметр κ, а последний, кроме него, ещё
(комплексный) параметр h. Лежандр внес
в эти интегралы ещё дальнейшие упрощения, выполнив в них подстановку z=sinφ (φ изменяется от 0 до π/2). При этом из них непосредственно
переходит в интеграл 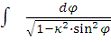
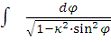 . (A)
. (A)
Второй преобразуется так:
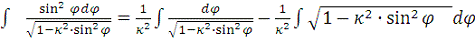
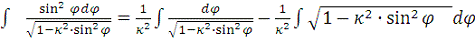 ,
,
т.е. приводится к предыдущему интегралу и к новому интегралу
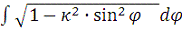
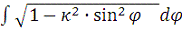 . (B)
. (B)
Наконец, третий интеграл при указанной подстановке переходит в
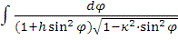
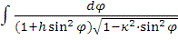 . (C)
. (C)
Интегралы (A), (B) и (C) также
называются эллиптическими интегралами 1-го,2-го и 3-го рода - в форме Лежандра.
5§. Закон
движения маятника (в эллиптических функциях)
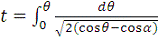
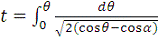 (5)
(5)
общее решения уравнения в явном виде.
Видно, что квадратура в конечном виде не берётся: интеграл справа
непосредственно приводится к эллиптическому интегралу 1го рода.
Так как 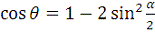
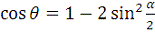 ,
, 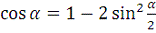
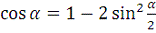 ,
,
то 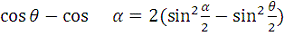
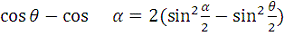
Подставляя этот результат в уравнение (5), получаем:
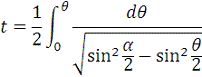
и положив 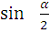
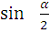 =κ (0< κ<1), введём новую переменную интегрирования φ
=κ (0< κ<1), введём новую переменную интегрирования φ
по формулам 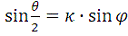
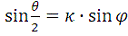 ,
, 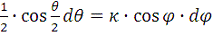
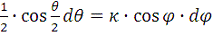 ; (6)
; (6)
откуда 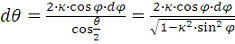
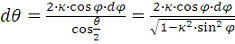
Кроме того,
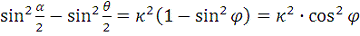
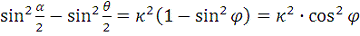
при этом изменению θ от 0 до α отвечает изменение φ от 0 до π/2. Тогда получим закон движения маятника в
виде
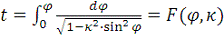
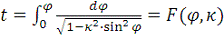 (7)
(7)
Интеграл, стоящий в правой части равенства (7), представляет
собой эллиптический интеграл первого рода. Величина κ называется модулем эллиптического интеграла.
Так как по первой из формул (6) легко выразить φ через θ, то зависимость t от θ можно считать установленной.
Этот интеграл есть функция верхнего предела и модуля. Желая
выразить, наоборот, θ через t, мы нуждаемся в
обращении эллиптического интеграла
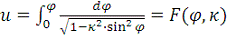
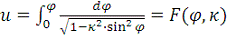 (8)
(8)
Если в равенстве (8) рассматривать верхний предел, а как функцию
от интеграла u, монотонно возрастающую непрерывную (и
даже дифференцируемую) функцию от φ в промежутке (-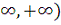
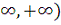 ; то такая функция носит название амплитуды u (am u) - как её обозначил Якоби - и обозначается так:
; то такая функция носит название амплитуды u (am u) - как её обозначил Якоби - и обозначается так: 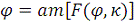
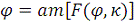 , или
, или 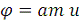
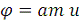 . (9)
. (9)
А мы обозначим так: 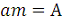
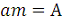 , то
, то 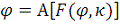
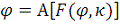 , или
, или 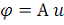
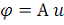 .
.
Из (8) теперь ясно, что 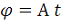
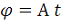 и, значит,
и, значит, 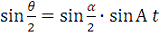
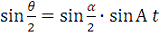 .
.
Беря от обеих частей равенства (9) синус, мы получим:
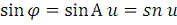
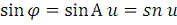 (10)
(10)
Функция sn u представляет собой так называемую эллиптическую функцию
Якоби. Поскольку, согласно уравнению (7), u=t, то, переходя в равенстве (10) с помощью
формулы (6), найдём закон движения маятника, выраженный через эллиптическую
функцию sn, в виде
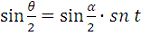
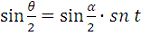 . (11)
. (11)
6§. Графики
траекторий движения маятника
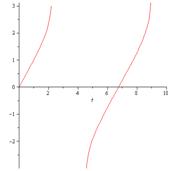
Построим численно кривые движения математического маятника при
различных начальных условиях используя закон движения маятника, выраженный
через эллиптическую функцию 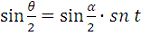
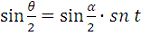 . Задавая угол
. Задавая угол 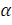
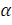 и промежуток времени, мы строим графики зависимости
и промежуток времени, мы строим графики зависимости 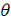
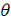 (
(
 ). Возьмём
). Возьмём 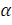
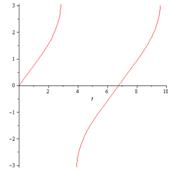
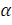 =Pi/4 и для точности определения зависимости
=Pi/4 и для точности определения зависимости 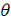
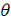 (
(
 ) возьмём t1=0.10, t2=0.20, t3=0.30. При
) возьмём t1=0.10, t2=0.20, t3=0.30. При 
 =5 - >
=5 - > 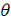
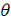 (
(
 ) = - 1,2;
) = - 1,2; 
 =15 - >
=15 - > 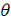
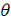 (
(
 ) =1,2 Замечаем, что через каждые 10с, повторяется угол
отклонения.
) =1,2 Замечаем, что через каждые 10с, повторяется угол
отклонения.
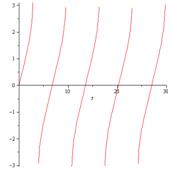
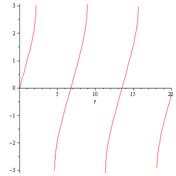
Возьмём 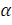
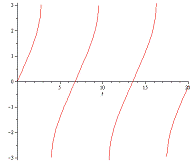
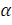 =Pi/3 и для точности определения зависимости
=Pi/3 и для точности определения зависимости 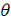
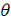 (
(
 ) возьмём t1=0.10, t2=0.20, t3=0.30.
) возьмём t1=0.10, t2=0.20, t3=0.30.
При 
 =5 - >
=5 - > 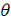
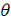 (
(
 ) = - 1,84;
) = - 1,84; 
 =8,44 - >
=8,44 - > 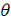
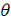 (
(
 ) =1,86 Замечаем, что через почти каждые 3,5с, повторяется угол
отклонения.
) =1,86 Замечаем, что через почти каждые 3,5с, повторяется угол
отклонения.
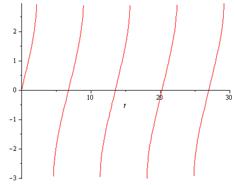
Таким образом, мы видим, что движение маятника периодическое. За 1
период при увеличении времени угол сначала увеличивается, а потом уменьшается.
7§.
Заключение
В данной работе мы выполнили поставленные задачи и достигли
заданной цели. Мы познакомились с такими понятиями, как "математический
маятник", "эллиптическая функция" и "эллиптический
интеграл"… Отметили, как численно строить соответствующие кривые движения
при различных начальных условиях.
8§. Список
литературы
1.
Беляева Н.А. Обыкновенные дифференциальные уравнения Сыктывкар, 2012
.
Боровой А., Херувимов А. Колебания и маятники. Ж. Квант. № 8, 1981.
.
Бухгольц Н.Н. Основной курс теоретической механики. М.: Наука. 1969.
.
Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления 2 том М.:
Наука. 1969.