Оптимизация производственной программы предприятия
Федеральное
государственное бюджетное образовательное учреждение
высшего
профессионального образования
Московский
государственный индустриальный университет
(ГОУ МГИУ)
Кафедра
"Экономика и управление производством"
Отчет
по
расчетно-графической работе
Оптимизация
производственной программы предприятия
Вариант №14
Группа 8113
Студент А.В. Прохорова
Преподаватель Т.В. Дедешко
Москва 2012
Содержание
Введение
1. Организационно-экономическая сущность
задачи
2. Оптимизация производственной программы
3. Математическая постановка задачи и
метод её решения
3.1 Формализация задачи
3.2 Метод решения
3.3 Решение задачи
Вывод
Библиографический
список
Введение
Цель работы - ознакомление студентов с одним из
методов оптимизации производственной программы предприятия, приобретение
практических навыков выбора наилучшего решения из множества вариантов.
1. Организационно-экономическая
сущность задачи
Производственная программа - это задание по
производству и реализации определенного количества продукции установленной
номенклатуры и качества.
Номенклатурой продукции называется классифицированный
перечень изделий, выпускаемых предприятием. Задания по количеству выпускаемой
продукции устанавливаются исходя из народнохозяйственных потребностей в
продукции определенного вида, а также имеющихся производственных ресурсов.
Производственная программа занимает ведущее место
среди показателей производственно-хозяйственной деятельности предприятия. На ее
основе определяется потребность в материально-технических и трудовых ресурсах,
величина дохода и прибыли, получаемых предприятием, уровень рентабельности.
В условиях перехода к рыночной экономике целью деятельности каждого
экономического субъекта становится максимизация его доходов и прибылей.
Величина получаемого предприятием дохода непосредственно зависит от
номенклатуры и объема выпускаемой продукции.
Показатели производственной программы устанавливаются
в натуральном и в стоимостном выражении. Натуральные показатели определяют
объем производства каждого вида продукции. На этой основе рассчитывается объем
производства в денежном выражении по показателям товарной, валовой и
реализованной продукции и возможная величина дохода предприятия.
Товарная продукция характеризует объем продукции,
предназначенной для реализации на сторону, своему капитальному строительству и
для непромышленных нужд и включает стоимость готовых изделий, стоимость
полуфабрикатов, выработанных основным и вспомогательным производствами и
предназначенных к продаже, стоимость работ, выполняемых по заказам со стороны.
Валовая продукция - это общий объем производства на
предприятии, определяется как товарная продукция с учетом изменения остатков
незавершенного производства.
Реализованная продукция определяется как стоимость
предназначенных к отгрузке и подлежащих оплате в рассматриваемом периоде
готовых изделий, полуфабрикатов и услуг; определяется как объем товарной
продукции с учетом изменения остатков готовой продукции на складах и
неоплаченных остатков готовой продукции.
2. Оптимизация производственной программы
Задача оптимизации производственной программы может быть сформулирована в
двух вариантах:
определение производственной программы, позволяющей получить наилучший
результат (максимальный доход, прибыль) при заданных объемах ресурсов;
определение производственной программы, обеспечивающей получение
заданного объема производства при наименьших затратах.
3. Математическая
постановка задачи и метод её решения
3.1 Формализация задачи
Пусть 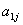 - нормативная трудоемкость изготовления одного изделия j-го
типа (чел.-час);
- нормативная трудоемкость изготовления одного изделия j-го
типа (чел.-час);
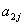 -
нормативная металлоемкость одного изделия j-го типа (кг);
-
нормативная металлоемкость одного изделия j-го типа (кг);
в1 - суммарная трудоемкость производственной программы
предприятия (чел.-час);
в2 - суммарная металлоемкость производственной программы
предприятия (кг);
Сj - отпускная цена одного изделия j- го типа (руб.);
Хj- объем производства (количество) изделий j-го типа
(шт.); j = 1, 2, 3.
Необходимо определить оптимальную производственную программу предприятия
Х0 = (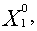
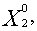
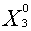 ), т.е. такое распределение объемов производства Х = (
), т.е. такое распределение объемов производства Х = (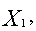
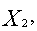
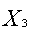 ), при котором достигается наибольший доход:
), при котором достигается наибольший доход:
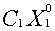 +
+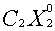 +
+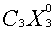 = max (
= max (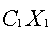 +
+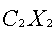 +
+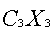 ),
),
(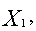
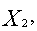
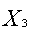 ).
).
При ограничениях на трудоемкость и металлоемкость:
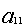
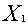 +
+ 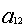
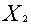 +
+ 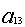
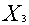 =
= 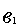 ;
;
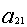
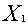 +
+ 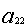
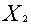 +
+ 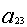
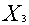 =
= 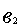 .
.
В настоящей работе мы будем предполагать следующее:
- нормы трудоемкости и металлоемкости строго положительны:
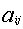 > 0; i = 1,2; j = 1,2,3;
> 0; i = 1,2; j = 1,2,3;
объемы производства неотрицательны 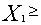 0,
0, 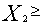 0,
0, 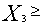 0, так что если
0, так что если 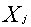 = 0, то изделие j-го типа не
включается в производственную программу, i = 1, 2, 3;
= 0, то изделие j-го типа не
включается в производственную программу, i = 1, 2, 3;
оптимальная производственная программа (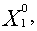
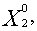
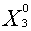 ), где
), где 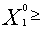 0,
0, 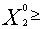 0,
0, 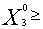 0 существует, т.е. ограничения трудоемкости и металлоемкости
сбалансированы;
0 существует, т.е. ограничения трудоемкости и металлоемкости
сбалансированы;
ограничения по трудоемкости и металлоемкости независимы в том смысле, что
линейно независима любая пара из векторов (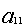 ,
,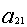 ), (
), (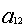 ,
,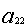 ), (
), (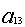 ,
,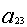 ).
).
В контрольном примере, рассмотренном ниже, а также во всех вариантах
заданий, указанные предположения выполняются в реальных производственных программах.
3.2 Метод решения
В пространстве переменных (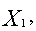
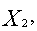
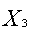 ) каждое из ограничений вида
) каждое из ограничений вида 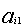
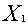 +
+ 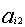
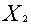 +
+ 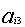
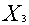 =
= 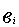 по трудоемкости или металлоемкости определяет плоскость
по трудоемкости или металлоемкости определяет плоскость 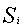 , проходящую через точки:
, проходящую через точки:
(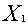 =
= 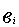 /
/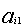 ,
, 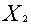 = 0,
= 0, 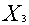 = 0)
= 0) 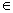
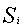 ,
,
(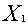 = 0,
= 0, 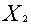 =
= 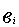 /
/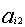 ,
, 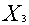 = 0)
= 0) 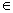
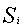 ,
,
(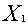 = 0,
= 0, 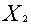 = 0,
= 0, 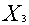 =
= 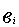 /
/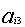 )
) 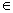
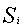 ,= 1, 2.
,= 1, 2.
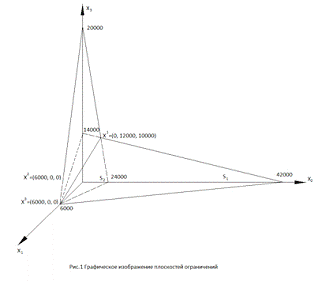
Пример изображения этих плоскостей приведен на рис. 1.
Точки, лежащие на линии пересечения плоскостей 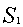 и
и 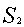 , удовлетворяют ограничениям по
трудоемкости и металлоемкости одновременно. При этом линия пересечения
существует в силу принятого предположения об отсутствии взаимной зависимости ограничений.
, удовлетворяют ограничениям по
трудоемкости и металлоемкости одновременно. При этом линия пересечения
существует в силу принятого предположения об отсутствии взаимной зависимости ограничений.
Наконец, условия 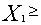 0,
0, 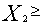 0,
0, 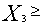 0 определяют отрезок линии пересечения плоскостей
0 определяют отрезок линии пересечения плоскостей 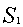 и
и 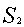 , лежащий между координатными
плоскостями. Такой отрезок тоже существует в силу сбалансированности
ограничений. Точки отрезка (и только они) удовлетворяют всем ограничениям и
предположениям, принятым в задаче.
, лежащий между координатными
плоскостями. Такой отрезок тоже существует в силу сбалансированности
ограничений. Точки отрезка (и только они) удовлетворяют всем ограничениям и
предположениям, принятым в задаче.
Целевая функция y = 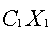 +
+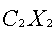 +
+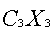 является линейной по переменным (
является линейной по переменным (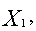
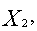
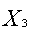 ) и, следовательно, достигает своего наибольшего и
наименьшего значения на концах построенного отрезка, один из которых и является
решением задачи.
) и, следовательно, достигает своего наибольшего и
наименьшего значения на концах построенного отрезка, один из которых и является
решением задачи.
3.3 Решение задачи
Приведем пример оптимизации производственной программы предприятия при
ограничениях на трудоемкость и металлоемкость.
Нормы трудоемкости изготовления трех изделий имеют значения:
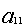 = 2,2 (чел.-час);
= 2,2 (чел.-час); 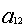 = 0,8 (чел.-час);
= 0,8 (чел.-час); 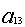 = 0,2 (чел.-час),
= 0,2 (чел.-час),
а нормы металлоемкости тех же изделий - значения:
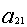 = 7 (кг);
= 7 (кг); 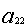 = 0,8 (кг);
= 0,8 (кг); 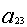 = 5 (кг).
= 5 (кг).
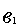 = 8800 (чел.-час),
= 8800 (чел.-час),
а суммарная металлоемкость -
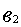 = 28000 (кг).
= 28000 (кг).
Изделия отпускаются с предприятия по ценам за штуку:
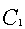 = 20000 (руб);
= 20000 (руб); 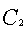 = 6000 (руб);
= 6000 (руб); 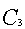 = 12000 (руб).
= 12000 (руб).
Задача оптимизации производственной программы предприятия
может быть сформулирована следующим образом: указать производственную программу
(распределение объемов производства изделий) (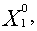
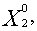
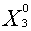 ), при выполнении которой достигается наибольшее
значение дохода предприятия:
), при выполнении которой достигается наибольшее
значение дохода предприятия:
= 20000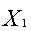 + 6000
+ 6000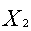 + 12000
+ 12000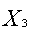 ;
;
,2 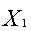 + 0,8
+ 0,8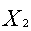 + 0,2
+ 0,2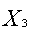 = 8800;
= 8800;
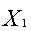 + 0,8
+ 0,8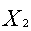 + 5
+ 5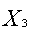 = 60000;
= 60000;
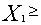 0,
0, 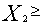 0,
0, 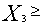 0.
0.
В пространстве переменных (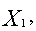
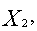
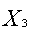 ) первое из ограничений (по трудоемкости) определяет
плоскость
) первое из ограничений (по трудоемкости) определяет
плоскость 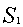 , проходящую через точки:
, проходящую через точки:
(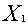 = 8800/2,2= 4000,
= 8800/2,2= 4000, 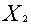 = 0,
= 0, 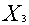 = 0)
= 0) 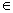
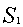 ;
;
(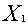 = 0,
= 0, 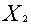 = 8800/0,8 = 11000,
= 8800/0,8 = 11000, 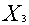 = 0)
= 0) 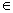
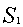 ;
;
(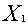 = 0,
= 0, 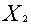 = 0,
= 0, 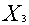 = 8800/0,2 = 44000)
= 8800/0,2 = 44000) 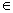
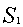 .
.
Графическое изображение этой плоскости приведено на рис. 1.
Второе ограничение (по металлоемкости) определяет плоскость 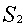 , проходящую через точки:
, проходящую через точки:
(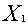 = 28000/7 = 4000,
= 28000/7 = 4000, 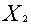 = 0,
= 0, 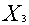 = 0)
= 0) 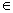
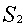 ;
;
(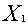 = 0,
= 0, 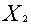 = 28000/0,8 = 35000,
= 28000/0,8 = 35000, 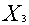 = 0)
= 0) 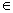
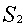 ;
;
(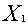 = 0,
= 0, 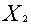 = 0,
= 0, 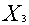 = 28000/5 = 5600)
= 28000/5 = 5600) 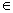
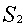 .
.
Плоскость 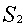 также изображена на рис. 1.
также изображена на рис. 1.
Из графического изображения плоскостей-ограничений вытекает следующее:
линия пересечения плоскостей-ограничений существует и пересекает
координатные плоскости 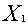 = 0,
= 0, 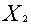 = 0,
= 0, 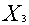 = 0 в точках
= 0 в точках 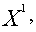
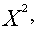
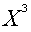 соответственно. Ограничения трудоемкости и металлоемкости
линейно независимы;
соответственно. Ограничения трудоемкости и металлоемкости
линейно независимы;
условия 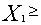 0,
0, 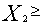 0,
0, 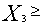 0 определяют отрезок линии пересечения, лежащей между
координатными плоскостями
0 определяют отрезок линии пересечения, лежащей между
координатными плоскостями 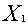 = 0,
= 0, 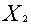 = 0, а конец этого отрезка суть точки
= 0, а конец этого отрезка суть точки 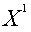 и
и 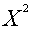 . Следовательно, оптимальная
производственная программа существует (ограничения по трудоемкости и
металлоемкости сбалансированы) и реализуется либо в точке
. Следовательно, оптимальная
производственная программа существует (ограничения по трудоемкости и
металлоемкости сбалансированы) и реализуется либо в точке 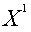 , либо в точке
, либо в точке 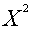 ;
;
точка 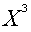 содержит отрицательную вторую компоненту и производственной
программой служить не может.
содержит отрицательную вторую компоненту и производственной
программой служить не может.
Находим координаты точки 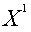 = (
= (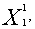
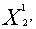
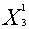 ) решая систему уравнений:
) решая систему уравнений:
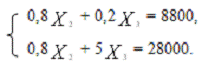
Получаем:
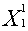 = 0;
= 0;
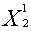 = (8800*5 - 0,2*28000)/(0,8*5 - 0,2*0,8) = 10000;
= (8800*5 - 0,2*28000)/(0,8*5 - 0,2*0,8) = 10000;
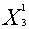 = (0,8*28000 - 8800*0,8)/(0,8*5 - 0,2*0,8) = 4000.
= (0,8*28000 - 8800*0,8)/(0,8*5 - 0,2*0,8) = 4000.
Поскольку оба найденных решения неотрицательны и могут определять объемы
производства, вычисляем значение целевой функции в точке 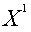 :
:
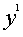 = 6000*10000 + 12000*4000 =108000000.
= 6000*10000 + 12000*4000 =108000000.
Находим координаты точки 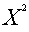 = (
= (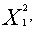
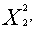
 ), решая систему уравнений:
), решая систему уравнений:

Получаем:
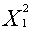 = (8800*5 - 0,2*28000)/(2,2*5 - 0,2*7) = 4000;
= (8800*5 - 0,2*28000)/(2,2*5 - 0,2*7) = 4000;
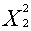 = 0;
= 0;
 = (2,2*28000 - 8800*7)/(2,2*5 - 0,2*7) = 0.
= (2,2*28000 - 8800*7)/(2,2*5 - 0,2*7) = 0.
Поскольку оба найденных решения неотрицательны и могут определять объемы
производства, вычисляем значение целевой функции в точке 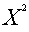 :
:
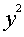 = 20000*4000 + 6000*0 = 80000000.
= 20000*4000 + 6000*0 = 80000000.
При вычислении координат точки 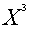 = (
= (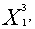
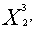
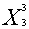 ) путем решения системы уравнений
) путем решения системы уравнений
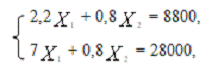
получаем:
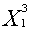 = (8800*0,8 - 0,8*28000)/(2,2*0,8 - 0,8*7) = 4000;
= (8800*0,8 - 0,8*28000)/(2,2*0,8 - 0,8*7) = 4000;
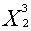 = (2,2*28000 - 8800*7)/(2,2*0,8 - 0,8*7) = 0;
= (2,2*28000 - 8800*7)/(2,2*0,8 - 0,8*7) = 0;
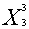 = 0.
= 0.
Значение второй компоненты отрицательное, что ранее было замечено (см.
рис. 1). В этом случае значение целевой функции можно вычислить:
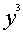 =20000*4000 - 12000*0 = 80000000,
=20000*4000 - 12000*0 = 80000000,
но согласно алгоритму решения задачи мы полагаем доход предприятия равным
нулю, 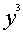 = 0.
= 0.
Расположим полученные значения целевой функции в порядке возрастания:
≤ 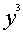 =
=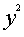 <
< 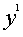 .
.
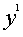 =108000000;
=108000000; 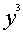 =
=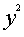 =80000000
=80000000
Можно видеть, что значение целевой функции второй и третей
производственных программ равны. Опуская дробные части в значениях объемов
производства, приходим к выводу:
объем производства первого типа изделий не следует включать в оптимальную
производственную программу предприятия -
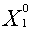 = 0;
= 0;
- изделия второго типа запланировать в количестве
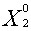 = 10000 (шт.);
= 10000 (шт.);
объем производства изделий третьего типа запланировать в количестве
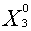 = 4000 (шт.).
= 4000 (шт.).
При этом предприятие получит наибольший возможный доход:
 = 6000*10000 + 12000*4000 = 108000000 (руб.), т.е. 108 млн.
руб.
= 6000*10000 + 12000*4000 = 108000000 (руб.), т.е. 108 млн.
руб.
Или:
объем производства изделий первого типа запланировать в количестве
 = 4000 (шт.);
= 4000 (шт.);
изделия второго типа не следует включать в оптимальную производственную
программу предприятия -
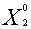 = 0;
= 0;
объем производства изделий третьего типа запланировать в количестве
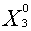 = 0 (шт.).
= 0 (шт.).
При этом предприятие получит наибольший возможный доход:
Незначительным резервом трудоемкости и остатком металла, получающимися в
результате опускания дробных частей в значениях объемов производства, по
существу задачи можно пренебречь.
Результаты расчетов представим в виде таблицы 1.
Таблица 1 Оптимальная производственная
программа предприятия
|
Тип изделия
|
1
|
2
|
3
|
|
Объем производства, шт.
|
0
|
10000
|
4000
|
|
Доход предприятия, руб.
|
108000000
|
Вывод
При определении оптимальной производственной программы в результате
расчётов был получен максимальный доход 144 млн. руб., которому соответствует
первая производственная программа.
По первой, объем производства продукции второго типа составляет 12000
шт., продукции третьего типа -10000 шт., а продукция первого типа не должна
быть включена в оптимальную производственную программу предприятия.
По второй, объем производства продукции первого типа составляет 12000
шт., продукции третьего типа -5000 шт., а продукция второго типа не должна быть
включена в оптимальную производственную программу предприятия.
Библиографический
список
производственный программа оптимизация
доход
1. Экономика машиностроительного производства / Под ред. И.Э. Берзиня и
В.П.Калинина. - М.: Высшая школа, 1988.
. Экономика автомобильной промышленности и тракторостроения / Под ред.
А.А. Невелева и В.И. Козырева. - М.: Высшая школа, 1989.
. В.Г. Карманов. Математическое программирование. - М.: Наука, 1975.
. Т. Ху. Целочисленное программирование и потоки в сетях. - М.: Мир,
1974.