Метод многомерной нелинейной оптимизации – метод наискорейшего спуска

Радиотехнический факультет

ОТЧЕТ

по лабораторной работе:

"Метод многомерной нелинейной оптимизации - метод наискорейшего спуска"

Самара 2013

Задание

1       Изучить особенности метода многомерной нелинейной оптимизации - метод наискорейшего спуска;

2       Разработка математической модели и алгоритма для выбранного метода;

         По составленному алгоритму написать демонстрационный вариант программы, отражающий основные этапы выбранного метода на языке программирования Borland Delphi 7.

Реферат

Пояснительная записка __ с, 6 рисунков, 3 источника, 1 приложение.

МЕТОД НАИСКОРЕЙШЕГО СПУСКА, МИНИМУМ ФУНКЦИИ, ГРАДИЕНТНЫЕ МЕТОДЫ, НЕЛИНЕЙНЫЕ ФУНКЦИИ.

Цель работы - изучение методов нахождения минимума функций градиентным методом наискорейшего спуска, моделирование метода и нахождение минимума функции двух переменных с помощью ЭВМ.

Часто, при исследовании функций сигналов РЭА возникает потребность нахождения экстремума этой функции. Такие задачи относятся к нелинейному программированию. Одними из наиболее реализуемых методов решения этих задач являются градиентные методы, в частности, метод наискорейшего спуска

Содержание

1. Теоретические основы метода

2. Алгоритм программы

4. Контрольный пример

Заключение

Список использованных источников

1. Теоретические основы метода

В этом методе из некоторой начальной точки движение осуществляется вдоль направления градиента до тех пор, пока производная по этому направлению не будет равна нулю. Далее из этой точки определяем новый градиент и т.д. Отличие здесь в том, что длина шага из точки X^k определяется из условия, чтобы обеспечить [2]:

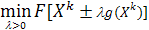
Эту вспомогательную задачу одномерной оптимизации можно решать на основе рассмотренных методов прямого поиска (дихотомии и т.д.)

Наискорейший и покоординатный методы называют методами с длинным шагом. Кроме этого существуют методы, использующие вторую производную для определения длины шага, например, метод Ньютона [2]:

X^k+1=X^k+ [F” (X^k)] - ¹g (X^k)

где [F” (X^k)] - ^{1 -} обратная матрица вторых производных в точке X^k.

Рассмотрим нахождение минимума функции двух переменных

.

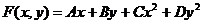Задаемся исходной точкой (x⁰; y⁰).

. Сначала найдём частные производные по x и y:

 .

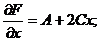
нелинейная оптимизация наискорейший спуск

2. Если обе производные в точке (x⁰; y⁰) равны нулю, то задача решена, и минимум функции находится в этой точке. В противном случае необходимо определить координаты новой точки (x¹; y¹):

,

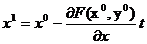. Теперь полученные значения принимаем за исходные (x¹=x⁰; y¹=y⁰) и возвращаемся к пункту 2.

Шаг t находится из условия минимума функции: 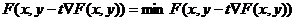. То есть необходимо найти такое значение t, при котором функция  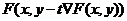имеет минимум. В нашем случае:

;

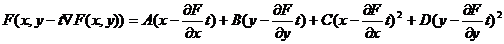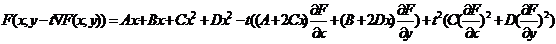
Минимум этой функции находится из равенства первой ее производной по t к нулю:

Отсюда находим t:

.

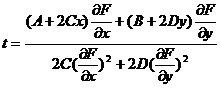Для некоторых нелинейных функций этот процесс не позволяет найти такие значения x и y, при которых производная равнялась бы нулю. Поэтому для обеспечения конечности числа итераций в этом случае вводим точность Е, тогда вычисления прекращаются либо когда производная в точке становится равной нулю (в этом случае значение Е задается равным нулю), либо когда |x^k-1 - x^k| будет меньше наперед заданной точности Е.

2. Алгоритм программы

3. Листинг программы

unit Unit1;, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,, StdCtrls, ExtCtrls;= class (TForm): TLabeledEdit;: TLabeledEdit;: TLabeledEdit;: TLabeledEdit;: TButton;: TLabel;: TLabel;: TLabeledEdit;: TLabeledEdit;: TLabel;: TLabel;: TLabel;: TLabel;: TLabeledEdit;: TLabel;Button1Click (Sender: TObject);

{ Private declarations }

{ Public declarations };: TForm1;, B, C, D, E: real;: array [0.100] of real;: array [0.100] of real;: array [0.100] of real;: array [0.100] of real;: array [0.100] of real;: integer;

{$R *. dfm}TForm1. Button1Click (Sender: TObject);l1;(LabeledEdit1. Text='') or (LabeledEdit2. Text='') or (LabeledEdit3. Text='') or (LabeledEdit4. Text='') or (LabeledEdit5. Text='') or (LabeledEdit6. Text='') or (LabeledEdit7. Text='') then. Caption: ='Заполните все поля! '. Caption: ='';: =strtofloat (LabeledEdit1. Text);: =strtofloat (LabeledEdit2. Text);: =strtofloat (LabeledEdit3. Text);: =strtofloat (LabeledEdit4. Text);: = strtofloat (LabeledEdit7. Text);[0]: =strtofloat (LabeledEdit5. Text);[0]: =strtofloat (LabeledEdit6. Text);: =0;[i]: =A+2*C*x [i];[i]: =B+2*D*y [i];( (dx [i] <>0) and (dy [i] <>0)) {or ( (dx [i] >E) or (dx [i] < (0-E))) and ( (dy [i] >E) or (dy [i] < (0-E))) }dot [i]: = ( ( (A+2*C*x [i]) *dx [i]) + ( (B+2*D*y [i]) *dy [i])) / ( (2*C*sqr (dx [i])) + (2*D*sqr (dy [i])));[i+1]: =x [i] - t [i] *dx [i];[i+1]: =y [i] - t [i] *dy [i];( ( (x [i+1] - x [i]) <=E) and ( (x [i+1] - x [i]) >= (0-E))) and ( ( (y [i+1] - y [i]) <=E) and ( (y [i+1] - y [i]) >= (0-E))) thenl1 else[i+1]: =A+2*C*x [i+1];[i+1]: =B+2*D*y [i+1];: =i+1;;: begin. Caption: ='xmin = '+floattostr (x [i]);. Caption: ='ymin = '+floattostr (y [i]);. Caption: ='Минимум функции F (x,y) ='+floattostr (A) +'x+'+floattostr (B) +'y+'+floattostr (C) +' (x) ^2+'+floattostr (D) +' (y) ^2 с заданной точностью равен: ';

end;;;.

4. Контрольный пример

Рисунок 1 - Начальное окно программы

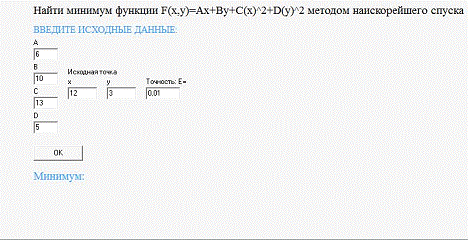
Рисунок 2 - Задание параметров в программу

Рисунок 3 - Результат расчетов по выбранному методу

Список использованных источников

1        СТО СГАУ 02068410-004 - 2007. Стандарт организации. Общие требования к учебным текстовым документам [Текст] - Самара: СГАУ, 2007. - 30с.

2       Матюнин, С.А. Методы Гаусса-Зейделя и наискорейшего спуска [Текст] /: методические указания для выполнения лабораторных работ/С.А. Матюнин, Б.В. Скворцов. - Самара: СГАУ, 1996. - 19с.

         Баженова, И.Ю. Delphi 7. Самоучитель программиста [Текст] /И.Ю. Баженова. - М.: КУДИЦ - Образ, 2003. - 448с.

         Фленов, М.В. Библия Delphi [Текст] / М.В. Фленов. - СПБ.: БХВ-Петербург, 2011. - 686с.