Точность оценки, доверительная вероятность (надежность)

Точность оценки, доверительная вероятность (надежность)

Доверительный интервал

При выборке малого объема следует пользоваться интервальными оценками т.к. это позволяет избежать грубых ошибок, в отличие от точечных оценок.

Интервальной называют оценку, которая определяется двумя числами - концами интервала, покрывающего оцениваемый параметр. Интервальные оценки позволяют установить точность и надежность оценок.

Пусть найденная по данным выборки статистическая характеристика Q* служит оценкой неизвестного параметра Q. Будем считать Q постоянным числом (Q может быть и случайной величиной). Ясно, что Q* тем точнее определяет параметр в, чем меньше абсолютная величина разности |Q - Q* |. Другими словами, если d>0 и |Q - Q* | < d, то чем меньше d, тем оценка точнее. Таким образом, положительное число d характеризует точность оценки.

Однако статистические методы не позволяют категорически утверждать, что оценка Q* удовлетворяет неравенству |Q - Q*|<d, можно лишь говорить о вероятности g, с которой это неравенство осуществляется.

Надежностью (доверительной вероятностью) оценки Q по Q* называют вероятность g, с которой осуществляется неравенство |Q - Q*|<d. Обычно надежность оценки задается наперед, причем в качестве g берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.

Пусть вероятность того, что |Q - Q*|<d, равна g т.е.

Р(|Q - Q*|<d)=g

Заменив неравенство |Q - Q*|<d равносильным ему двойным неравенством -d<|Q - Q*|<d, или Q*- d<Q<Q*+d, имеем

Р(Q*- d< Q <Q*+d)=g.

Доверительным называют интервал (Q*- d, Q*+d), который покрывает неизвестный параметр Q с заданной надежностью g.

Доверительные интервалы для оценки математического ожидания нормального распределения при известном s.

Интервальной оценкой с надежностьюg математического ожидания а нормально распределенного количественного признака Х по выборочной средней `х при известном среднем квадратическом отклонении s генеральной совокупности служит доверительный интервал

`х - t(s/n^½) < a < `х + t(s/n^½),

где t(s/n^½)=d - точность оценки, n - объем выборки, t - значение аргумента функции Лапласа Ф(t), при котором Ф(t)=g/2.

Из равенства t(s/n^½)=d, можно сделать следующие выводы:

1.      при возрастании объема выборки n число d убывает и, следовательно, точность оценки увеличивается;

2.      увеличение надежности оценки g = 2Ф(t) приводит к увеличению t (Ф(t) - возрастающая функция), следовательно, и к возрастанию d; другими словами, увеличение надежности классической оценки влечет за собой уменьшение ее точности.

Пример. Случайная величина X имеет нормальное распределение с известным средним квадратическим отклонением s=3. Найти доверительные интервалы для оценки неизвестного математического ожидания a по выборочным средним х, если объем выборки n = 36 и задана надежность оценки g = 0,95.

Решение. Найдем t. Из соотношения 2Ф(t) = 0,95 получим Ф (t) = 0,475. По таблице находим t=1,96.

точность доверительный интервал измерение

d=t(s/n^½)= ( 1 ,96 . 3)/ /36 = 0,98.

Доверительный интервал таков: (`х - 0,98; `х + 0,98). Например, если `х = 4,1, то доверительный интервал имеет следующие доверительные границы:

`х - 0,98 = 4,1 - 0,98 = 3,12; `х + 0,98 = 4,1+ 0,98 = 5,08.

Таким образом, значения неизвестного параметра а, согласующиеся с данными выборки, удовлетворяют неравенству 3,12 < а < 5,08. Подчеркнем, что было бы ошибочным написать Р (3,12 < а < 5,08) = 0,95. Действительно, так как а - постоянная величина, то либо она заключена в найденном интервале (тогда событие 3,12 < а < 5,08 достоверно и его вероятность равна единице), либо в нем не заключена (в этом случае событие 3,12 < а < 5,08 невозможно и его вероятность равна нулю). Другими словами, доверительную вероятность не следует связывать с оцениваемым параметром; она связана лишь с границами доверительного интервала, которые, как уже было указано, изменяются от выборки к выборке.

Поясним смысл, который имеет заданная надежность. Надежность g= 0,95 указывает, что если произведено достаточно большое число выборок, то 95% из них определяет такие доверительные интервалы, в которых параметр действительно заключен; лишь в 5% случаев он может выйти за границы доверительного интервала.

Если требуется оценить математическое ожидание с наперед заданной точностью d и надежностью g, то минимальный объем выборки, который обеспечит эту точность, находят по формуле

N=t^2s^2/d^2

Доверительные интервалы для оценки математического ожидания нормального распределения при неизвестном s

Интервальной оценкой с надежностьюg математического ожидания а нормально распределенного количественного признака Х по выборочной средней `х при неизвестном среднем квадратическом отклонении s генеральной совокупности служит доверительный интервал

`х - t(g)(s/n^½) < a < `х + t(g)(s/n^½),

где s -«исправленное» выборочное среднее квадратическое отклонение, t(g) находят по таблице по заданным g и n.

Пример. Количественный признак X генеральной совокупности распределен нормально. По выборке объема n=16 найдены выборочная средняя `x = 20,2 и «исправленное» среднее квадратическое отклонение s = 0,8. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью 0,95.

Решение. Найдем t(g). Пользуясь таблицей, по g = 0,95 и n=16 находим t(g)=2,13.

Найдем доверительные границы:

`х - t(g)(s/n^½) = 20,2 - 2,13 *. 0 ,8/16^½ = 19,774

`х + t(g)(s/n^½) = 20,2 + 2,13 * 0 ,8/16^½ = 20,626

Итак, с надежностью 0,95 неизвестный параметр а заключен в доверительном интервале 19,774 < а < 20,626

Оценка истинного значения измеряемой величины

Пусть производится n независимых равноточных измерений некоторой физической величины, истинное значение а которой неизвестно.

Будем рассматривать результаты отдельных измерений как случайные величины Хl, Х2,…Хn. Эти величины независимы (измерения независимы). Имеют одно и то же математическое ожидание а (истинное значение измеряемой величины), одинаковые дисперсии s^2 (измерения равноточные) и распределены нормально (такое допущение подтверждается опытом).

Пример. По данным девяти независимых равноточных измерений физической величины найдены среднее арифметической результатов отдельных измерений `х = 42,319 и «исправленное» среднее квадратическое отклонение s = 5,0. Требуется оценить истинное значение измеряемой величины с надежностью g = 0,95.

Решение. Истинное значение измеряемой величины равно ее математическому ожиданию. Поэтому задача сводится к. оценке математического ожидания (при неизвестном s) при помощи доверительного интервала покрывающего а с заданной надежностью g = 0,95.

х - t(g)(s/n^½) < a < `х + t(g)(s/n^½)

Пользуясь таблицей, по у = 0,95 и л = 9 находим

Найдем точность оценки:

t(g)(s/n^½) = 2 ,31 * 5/9^½=3.85

Найдем доверительные границы:

`х - t(g)(s/n^½) = 42,319 - 3,85 = 38,469;

`х + t(g)(s/n^½) = 42,319 +3,85 = 46,169.

Итак, с надежностью 0,95 истинное значение измеряемой величины заключено в доверительном интервале 38,469 < а < 46,169.

Доверительные интервалы для оценки среднего квадратического отклонения s нормального распределения.

Пусть количественный признак X генеральной совокупности распределен нормально. Требуется оценить неизвестное генеральное среднее квадратическое отклонение s по «исправленному» выборочному среднему квадратическому отклонению s. Для этого воспользуемся интервальной оценкой.

Интервальной оценкой (с надежностью g) среднего квадратического отклонения о нормально распределенного количественного признака X по «исправленному» выборочному среднему квадратическому отклонению s служит доверительный интервал

s (1 - q) < s < s (1 + q) (при q < 1),

< s< s (1 + q) (при q > 1),

где q находят по таблице по заданным n н g.

Пример 1. Количественный признак X генеральной совокупности распределен нормально. По выборке объема n = 25 найдено «исправленное» среднее квадратическое отклонение s = 0,8. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение s с надежностью 0,95.

Решение. По таблице по данным g = 0,95 и n = 25 найдем q = 0,32.

Искомый доверительный интервал s (1 - q) < s < s (1 + q) таков:

0,8(1- 0,32) < s < 0,8(1+0,32), или 0,544 < s < 1,056.

Решение. По таблице приложения по данным g = 0,999 и n=10 найдем 17= 1,80 (q > 1). Искомый доверительный интервал таков:

< s < 0,16(1 + 1,80), или 0 < s < 0,448.

Оценка точности измерений

В теории ошибок принято точность измерений (точность прибора) характеризовать с помощью среднего квадратического отклонения s случайных ошибок измерений. Для оценки s используют «исправленной» среднее квадратическое отклонение s. Поскольку обычно результаты измерений взаимно независимы, имеют одно и то же математическое ожидание (истинное значение измеряемой величины) и одинаковую дисперсию (в случае равноточных измерений), то теория, изложенная в предыдущем параграфе, применима для оценки точности измерений.

Пример. По 15 равноточным измерениям найдено «исправленное» среднее квадратическое отклонение s = 0,12. Найти точность измерений с надежностью 0,99.

Решение. Точность измерений характеризуется средним квадратическим отклонением s случайных ошибок, поэтому задача сводится к отысканию доверительного интервала s (1 - q) < s < s (1 + q) , покрывающего s с заданной надежностью 0,99

По таблице приложения по g = 0,99 и n=15 найдем q = 0,73.

Искомый доверительный интервал

,12(1- 0,73) < s < 0,12(1+0,73), или 0.03 < s < 0,21.

Оценка вероятности (биномиального распределения) по относительной частоте

Интервальной оценкой (с надежностью g) неизвестной вероятности p биномиального распределения по относительной частоте w служит доверительный интервал (с приближенными концами p1 и р2)

p1 < p < p2,

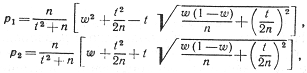
где n - общее число испытаний; m - число появлений события; w - относительная частота, равная отношению m/n; t - значение аргумента функции Лапласа, при котором Ф(t) = g/2.

Замечание. При больших значениях n (порядка сотен) можно принять в качестве приближенных границ доверительного интервала