Синтез и моделирование многомерной системы управления реактором
Содержание
Введение
1. Краткая
характеристика объекта автоматизации
Математическая
модель объекта
.
Структурный и алгоритмический синтез несвязанной системы управления многомерным
объектом
.
Параметрический синтез системы управления
.
Моделирование системы управления
.1
Программа моделирования системы управления в среде Mathcad
.2
Инвариантность к возмущениям
.3
Ковариантность с заданием
.
Моделирование системы управления с более сложной структурой
.1
Программа моделирования системы управления в среде Mathcad
.2
Инвариантность к возмущениям
Вывод
Список
используемых источников
Введение
Химический реактор является основным аппаратом
во многих технологических системах. Работа химического реактора определяет во
многом качество продукции, поэтому вопросам автоматического управления и
регулирования реакторами уделяется большое внимание.
Как объект управления в большинстве случаев
реактор является многомерным объектом и по многим каналам нелинейным объектом.
В настоящей работе проведено исследование
системы управления реактором с использованием методом математического
моделирования. Установлена возможность применения линейных регуляторов на
нелинейных объектах.
1. Краткая характеристика объекта
автоматизации

Рис. 1.1 Принципиальная схема процесса
Аппарат емкостного типа объёма 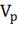 с
мешалкой и рубашкой объёма
с
мешалкой и рубашкой объёма 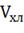 . Исходный
компонент реакции подается в аппарат с потоком -
. Исходный
компонент реакции подается в аппарат с потоком - 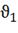 .
Второй входной поток с расходом
.
Второй входной поток с расходом 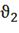 служит для
разбавления смеси до необходимой концентрации. В рубашку с расходом
служит для
разбавления смеси до необходимой концентрации. В рубашку с расходом 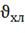 и
температурой
и
температурой  подается
хладоагент. В аппарате проводятся экзотермические реакции.
подается
хладоагент. В аппарате проводятся экзотермические реакции.
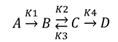
Смесь из реактора забирается насосом, величина
потока может регулироваться клапаном. Благодаря интенсивному перемешиванию
структура потоков в реакторе может быть описана моделью идеального смешения.
Аппарат работает в политропическом режиме.
Назначение:
осуществление сложной многостадийной реакции. Цель функционирования:
получение реакционной смеси с заданным значением концентрации целевого
вещества.
Классификация переменных
Параметры состояния объекта: объём (уровень)
реакционной смеси -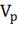 ; концентрации
компонентов в выходном потоке -
; концентрации
компонентов в выходном потоке - 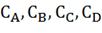 ;
;
· температура смеси в аппарате - 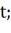
· температура хладоагента на выходе из
рубашки tхл.
Входные параметры объекта:
· расходы потоков на входе и выходе из аппарата - 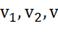 ;
;
· концентрация веществ А во входном
потоке -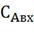 ;
;
· температуры входных потоков - 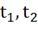 ;
;
· расход хладоагента  ;
;
· входная температура хладоагента tхл.
Критерий эффективности
Математическое выражение критерия эффективности
называют целевой функцией или критерием оптимальности. Целью функционирования
является получение концентрации компонента В в заданном количестве. Показателем
эффективности:
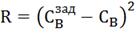 , где
, где
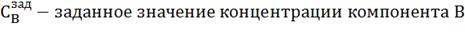
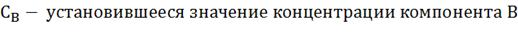
Критерием эффективности управления
является: 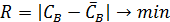
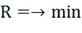
Таблица
1
Исходные данные
|
Схема
превращений
|
Тип
реакции
|
Тепловой
режим действия аппарата
|
Агрегатное
состояние теплоносителя
|
Организация
ввода реагентов в реактор
|
|
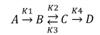
|
Экзотерми-ческая
|
Политропический
|
Жидкость
|
Во
входном потоке υ1 исходный
реагент А(CAвx)
|
Математическая модель объекта
Модель химического реактора представляет собой
систему нелинейных обыкновенных дифференциальных уравнений.
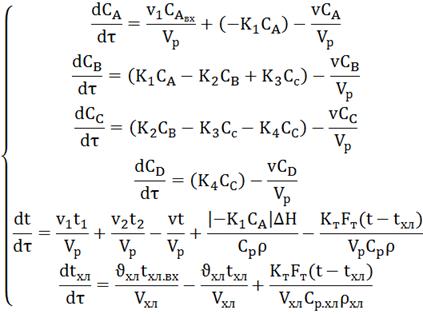
Начальные условия:
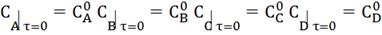
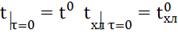
Таблица
2
Численные значения параметров модели
|
№
п/п
|
Наименование
|
Единица
измерения
|
Численное
значение
|
Обозначение
|
|
1.
|
Объем
аппарата
|
л
|
500
|
Vp
|
|
2.
|
Объем
рубашки
|
л
|
200
|
Vхл
|
|
3.
|
Теплоемкость
вещества в аппарате и входных потоках
|
кДж/(кг К) К)
|
4.19
|
Ср
|
|
4.
|
Теплоемкость
хладоагента
|
кДж/(кг К) К)
|
4.19
|
Ср.хл.
|
|
5.
|
Плотность
вещества в аппарате и входных потоках
|
кг/л
|
1.2
|

|
|
6.
|
Плотность
хладоагента
|
кг/л
|
0.978
|
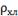
|
|
7.
|
Коэффициент
теплопередачи
|
кДж/(м2 мин мин К) К)
|
11
|
КТ
|
|
8.
|
Поверхность
теплообмена
|
м2
|
2.768
|
FТ
|
|
9.
|
Тепловой
коэффициент реакции
|
кДж/моль
|
750
|
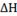
|
|
10.
|
Предэкспоненциальный
множитель константы скорости
|
л/(мин моль) моль)
|
1500
1 2 8
|
k10 k20 k30 k40
|
|
11.
|
Энергия
активации
|
Дж/моль
|
45000
20000 25000 40000
|
Е1
Е2 Е3 Е4
|
|
12.
|
Концентрация
компонента А на входе
|
моль/л
|
1
|
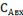
|
|
13.
|
Расход
первого потока в реактор
|
л/мин
|
0.75
|
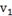
|
|
14.
|
Расход
второго потока в реактор
|
л/мин
|
0.25
|
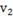
|
|
15.
|
Расход
хладоагента
|
л/мин
|
0.487
|
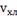
|
|
16.
|
Температура
первого потока в реактор
|
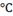
|
30
|
t1
|
|
17.
|
Температура
второго потока в реактор
|
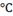
|
40
|
t2
|
|
18.
|
Оптимальная
температура
|
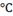
|
90
|
t
|
|
19.
|
Температура
хладоагента
|
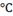
|
86.307
|
tхл
|
|
20.
|
Диаметр
аппарата
|
м
|
0.542
|
d
|
|
21.
|
Уровень
жидкости
|
м
|
0.542
|
h
|
|
22.
|
Концентрация
компонента: А на выходе В на выходе С на выходе D на выходе
|
моль/л
|
0.213
0.352
0.184 1.296 10-3 10-3
|
Ca Сb
Cc Cd
|
Таблица
3
Численные данные передаточных функций
|
Канал
|
Статика
|
Динамика
|
Средние
значения
|
 (мин) (мин)
|
|
К
|
К
безразм.
|
К
|
К
безразм.
|
T
(мин)
|
К
|
Коб.
безразм.
|
|
|
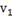 →CВ →CВ
|
0,256
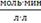
|
0,545
|
0,256
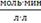
|
0,546
|
785
|
0,256
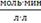
|
0,5455
|
411
|
|
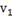 →t →t
|
55,336
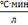
|
0,461
|
55,404
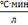
|
0,462
|
1051
|
55,37
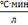
|
0,4615
|
502
|
|
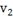 →CВ →CВ
|
-0,78
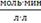
|
-0,554
|
-0,79
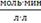
|
-0,561
|
885
|
-0,785
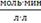
|
-0,5575
|
-
|
|
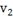 →t →t
|
-170,53
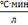
|
-0,474
|
-169,5
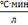
|
-0,471
|
1283
|
-170
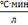
|
-0,4725
|
-
|
|
t1→CВ
|
0,005
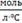
|
0,426
|
0,005
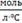
|
0,426
|
1125
|
0,005
|
0,426
|
-
|
|
t1→t
|
1,875

|
0,625
|
1,777

|
0,592
|
1007
|
1,826

|
0,6085
|
-
|
|
t2→CВ
|
0,0014
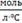
|
0,159
|
0,0014
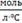
|
0,159
|
660
|
0,0014
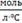
|
0,159
|
-
|
|
t2→t
|
0,584

|
0,26
|
0,566

|
0,252
|
857
|
0,575

|
0,256
|
-
|
|
 →CВ →CВ
|
0,8
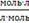
|
2,273
|
0,885
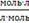
|
2,514
|
1002
|
0,843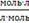
|
2,3935
|
-
|
|
 →t →t
|
166,68
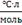
|
1,852
|
192,34
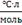
|
2,137
|
1343
|
179,51
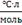
|
1,9945
|
-
|
|
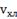 →CВ →CВ
|
-0,25
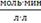
|
-0,346
|
-0,25
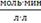
|
-0,346
|
694
|
-0,25
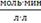
|
-0,346
|
-
|
|
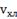 →t →t
|
-103,562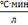
|
-0,56
|
-99,395
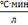
|
-0,538
|
1200
|
-101,479
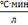
|
-0,549
|
-
|
|
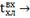 CB CB
|
0,0021
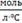
|
0,179
|
0,0021
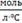
|
0,179
|
845
|
0,0021
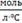
|
0,179
|
-
|
|
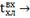 t t
|
0,854

|
0,285
|
0,854

|
0,284
|
965
|
0,854

|
0,2845
|
-
|
2. Структурный и алгоритмический
синтез несвязанной системы управления многомерным объектом
Структурный синтез
заключается в выборе структуры системы регулирования каждой выходной
переменной. Выбираем одноконтурную замкнутую систему автоматической
стабилизации по каждой входной переменной.
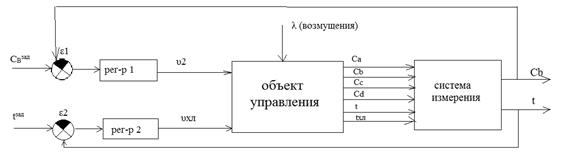
Рис. 2.1 Функциональная структурная схема
регулирования
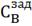 - концентрация
компонента В на входе с заданным значением
- концентрация
компонента В на входе с заданным значением
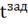 - оптимальная
температура объекта с заданным значением на входе
- оптимальная
температура объекта с заданным значением на входе
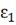 - ошибка
регулирования
- ошибка
регулирования
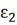 - ошибка
регулирования
- ошибка
регулирования
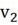 - расход второго
потока в реактор
- расход второго
потока в реактор
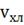 - расход
хладоагента
- расход
хладоагента
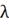 - подаваемые
возмущения
- подаваемые
возмущения
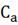 - концентрация
компонента А на выходе из аппарата
- концентрация
компонента А на выходе из аппарата
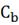 - концентрация компонента
B на выходе из
аппарата
- концентрация компонента
B на выходе из
аппарата
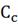 - концентрация
компонента C на выходе из
аппарата
- концентрация
компонента C на выходе из
аппарата
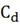 концентрация
компонента D на выходе из
аппарата
концентрация
компонента D на выходе из
аппарата
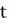 - оптимальная температура
объекта на выходе из аппарата
- оптимальная температура
объекта на выходе из аппарата
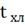 - температура
хладоагента на выходе из аппарата
- температура
хладоагента на выходе из аппарата
Алгоритмический синтез
заключается в разработке математической модели элементов, входящих в систему
управления. В нашем случае математическая модель объекта представляет собой в
форме нелинейных ОДУ.
Следовательно, необходимо выбрать какой-либо
типовой закон регулирования. Учитывая динамические свойства объекта (отсутствие
запаздывания) выбираем ПИ-закон регулирования.
ПИ-закон обладает следующими положительными
свойствами:
· Обеспечивает минимальную статическую ошибку
регулирования.
· Достаточно прост в настройке, т.к.
настраиваются только два параметра, а именно коэффициент усиления Кр и
постоянная времени интегрирования Ti. В таком регуляторе имеется возможность
оптимизации величины отношения Кр/Тi→min, что обеспечивает управление с
минимально возможной среднеквадратичной ошибкой регулирования.
· Малая чувствительность к шумам в
канале измерения (в отличие от ПИД-регулятора)
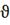 2
= KP1
2
= KP1  (
( 1
+
1
+ 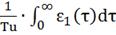
 1
=
1
= 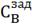 -
-
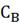
Преобразуем уравнение к удобному виду для
моделирования на ЭВМ. Для этого уравнения для работы регулятора необходимо
преобразовать в дифференциальную форму:
 = KP1
= KP1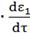 +
+ 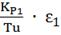
 = KP1
= KP1 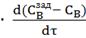 +
+
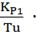 (
(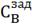 -
-

 = - KP1
= - KP1
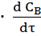 +
+
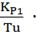 (
(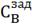 -
-

Следовательно, второе уравнение имеет вид:
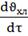 = - KP2
= - KP2
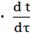 +
+
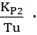 (
(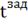 -
-
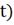
В программе необходимо к системе уравнений
объекта добавить два уравнения для регуляторов.
Выражения для 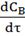 ,
,
 берем
из уравнения математической модели объекта управления.
берем
из уравнения математической модели объекта управления.
Параметрический синтез заключается в определении
численных значений коэффициентов (параметров), входящих в уравнения модели
объекта и регулятора.
Параметры настроек определяем методом
моделирования процессов управления на ЭВМ. Уточняются настройки до тех пор,
пока переходный процесс управления не будет отвечать заданным показателям
качества и эффективности управления.
Параметрический синтез может быть осуществлен
различными способами (Циглера-Никольса, методом расширенных частотных
характеристик) настроек регулятора. Используем упрощенный метод настроек ПИ
регулятора [1].
Передаточные функции по каналам регулирования
имеют вид апериодического звена первого порядка [2].
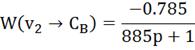
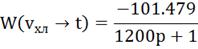
Определим настройки регулятора, используя
графики приведенные в литературе [1].
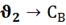
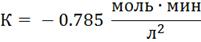

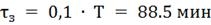
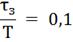
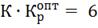
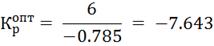

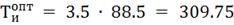

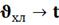
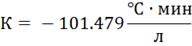
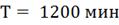
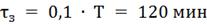
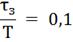
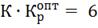
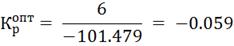
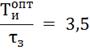
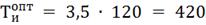
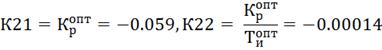
4. Моделирование системы управления
Моделирование системы управления осуществляется
с целью исследования следующих свойств системы:
· инвариантность к возмущениям
· ковариантность с заданием
· устойчивость
Для моделирования необходимо записать полную
модель системы в единообразной форме. Для этого преобразуем уравнение работы
регулятора в дифференциальную форму, включая уравнения модели объекта и уравнения
модели регуляторов.
 = KP1
= KP1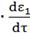 +
+ 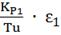 ;
;
 1
=
1
= 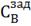 -
у1; у1= СВ
-
у1; у1= СВ
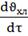 = KP2
= KP2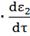 +
+ 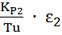 ;
;
 2
= tзад
- у4; у4= t
2
= tзад
- у4; у4= t
4.1
Программа моделирования системы управления в среде Mathcad
Таблица
4
Таблица соответствия переменных
Исходные данные:
объем аппарата, л - 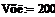
объем рубашки, л - 
теплоемкость вещества в аппарате и входных
потоках, кДж/(кг*К) - 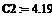
теплоемкость хладоагента т, кДж/(кг*К) - 
плотность вещества в аппарате и
входных потоках, кг/л - 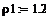
плотность хладоагента, кг/л - 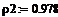
поверхность теплообмена, м2 - 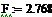
коэффициент теплопередачи,
кДж/(м2*мин*К) - 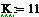
тепловой эффект реакции,
кДж/моль - 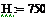
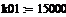
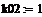
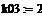
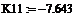
предэкспоненциальный множитель
константы скорости, 1/мин
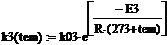
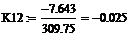
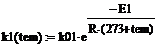
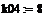
энергия активации, Дж/моль - 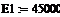
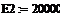
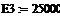
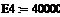
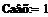
концентрация компонента А на входе, моль/л - 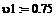
расход первого потока на входе в реактор, л/мин
- 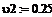
расход второго потока на входе в реактор, -
л/мин,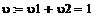
расход на выходе из реактора, л/мин - 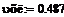
расход хладоагента, л/мин
температура второго потока на входе в реактор, С
температура первого потока на входе в реактор, -
С 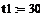
температура хладоагента на входе, С - 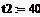
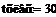
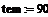
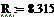
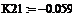
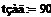
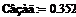
Константа скорости
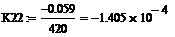
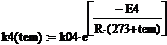
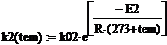
Вектор-функция правых частей диф.уравнений
модели
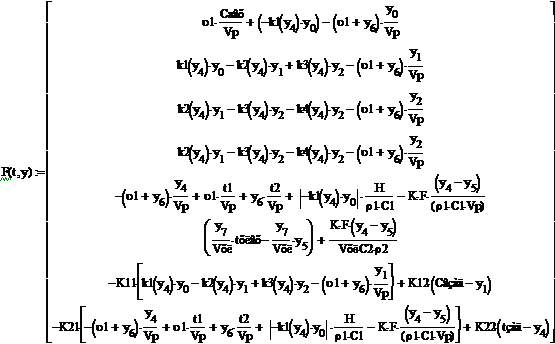
начальные условия
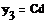
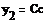


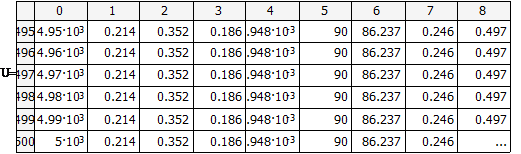
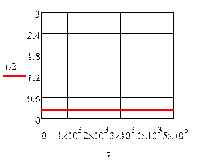
При отсутствии возмущения на объект и при
условии задания в качестве исходных данных значений переменных в статике
процесс регулирования представляет собой прямые линии параллельные оси времени.
На рис.4.1.1. представлены графики изменения выходных переменных и упрощающих
воздействий для изложенных условий.
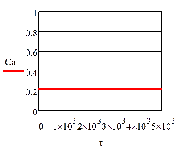
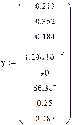
а)

б)
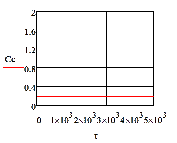
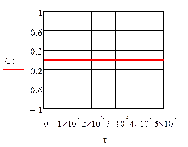
в) г)
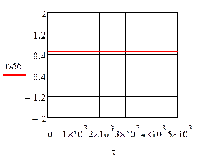
ж) з)
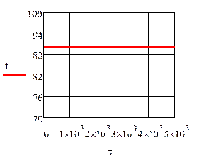
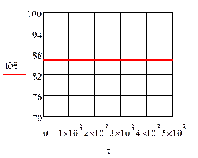
и) к)
Рис.4.1.1. Процесс регулирования при
отсутствии возмущений: а)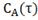 ; б)
; б)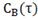 ; в)
; в)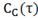 ; г)
; г)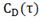 ; д)
; д)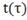 ; е)
; е)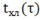 ; ж)
; ж)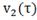 ; з)
; з)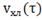 .
.
Для уточнения параметров подадим
возмущение по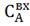 . Процент
отклонения 25%.
. Процент
отклонения 25%. 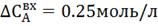 .
.
Исходя из требований к безопасности ведения
технологического процесса и требований к качеству продукции величины допустимых
значений статической ошибки, динамической ошибки и времени регулирования
принимаются следующими:
∆( =0.352
=0.352
 = ∆(
= ∆(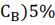 =0.0176
=0.0176
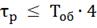
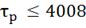 ∆(
∆(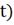 =90
=90
 = ∆(
= ∆(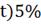 =4.5
=4.5
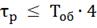
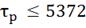
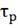 = 360 мин
= 360 мин
 = 0.01818
= 0.01818
∆=0
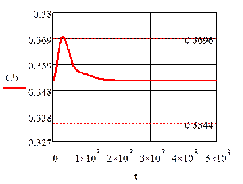
Рис. 4.1.2 Процесс регулирования концентрации
при возмущении 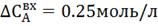
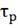 = 0мин
= 0мин
 = 1.844
= 1.844
∆=0
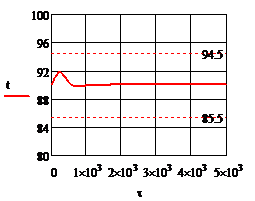
Рис. 4.1.3 Процесс регулирования температуры при
возмущении 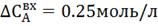
Можно сделать вывод, что настройки регулятора
удовлетворены. Следовательно, значения параметров алгоритмов регулирования
следующие:
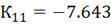
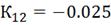
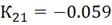
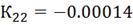
4.2 Инвариантность
к возмущениям
Инвариантность к возмущениям означает
способность системы компенсировать возмущения при заданной величине задания по
каждому контуру.
∆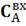 =
=
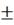 0,25
моль/л,
0,25
моль/л,
Процент отклонения 25%
∆( =0.352
=0.352
 = ∆(
= ∆(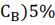 =0.0176
=0.0176
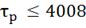
∆(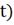 =90
=90
 = ∆(
= ∆(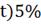 =4.5
=4.5
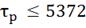
 а)
а)
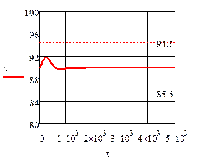 б)
б)
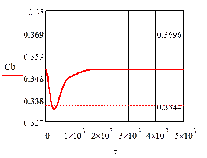 в)
в)
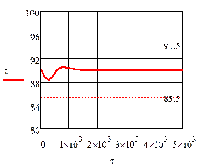 г)
г)
Рис. 4.2.1 Изменение регулируемых переменных
(Св, t) и регулирующих
воздействий при ∆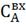 =
0,25 моль/л: а)
=
0,25 моль/л: а)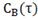 ; б)
; б)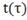 ;в)
;в)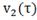 ;г)
;г)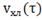 .
.
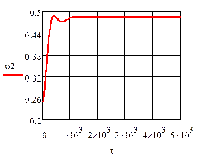
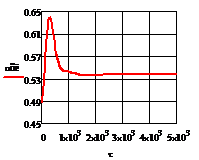
а) б)
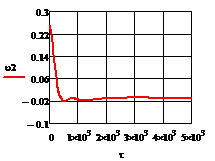
в) г)
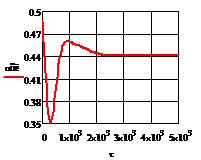
Рис. 4.2.2 Изменение регулируемых переменных
(Св, t) и регулирующих
воздействий при ∆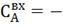 0,25 моль/л: а)
0,25 моль/л: а)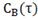 ; б)
; б)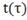 ;в)
;в)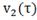 ;г)
;г)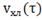 .
.
Анализ результатов моделирования представленных
на рис. 4.2.1 и рис. 4.2.2 показывает:
· Величина статической и динамической ошибки лежат
в переделах допустимых значений;
· Время регулирования также
удовлетворяет сформулированным требованиям;
· Значение расхода 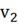 ,
при отрицательной подаче возмущения, оказалось отрицательным, что не имеет
физического смысла и не может быть реализовано.
,
при отрицательной подаче возмущения, оказалось отрицательным, что не имеет
физического смысла и не может быть реализовано.
Следовательно, необходимо проанализировать
работу системы при меньших возмущениях или наложить ограничения на регулирующие
воздействия: если 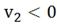 , то принять
, то принять 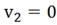 .
.
Подадим возмущение по 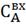 с
процентом отклонения 20%.
с
процентом отклонения 20%.
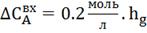 = 1
= 1
а)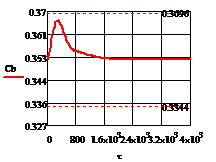 б)
б)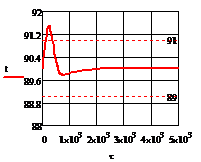
в) 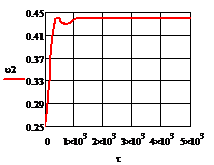 г)
г)
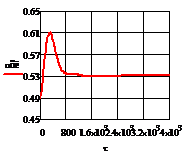
Рис. 4.2.3 Изменение регулируемых переменных
(Св, t) и регулирующих
воздействий
при ∆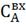 =
0,2 моль/л
=
0,2 моль/л
а)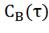 ;
б)
;
б)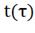 ;в)
;в)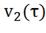 ;г)
;г)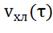 .
.
∆( =0
=0
 = 0.01402
= 0.01402
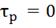
∆(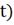 =0
=0
 = 1.42
= 1.42
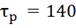
а)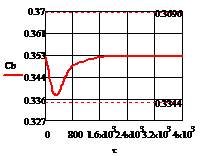 б)
б)
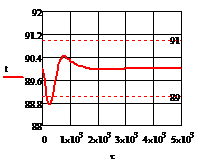
в)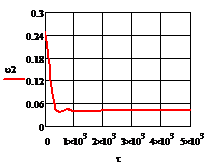 г)
г)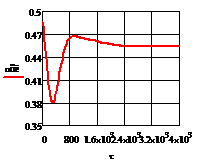
Рис. 4.2.4 Изменение регулируемых переменных
(Св, t) и регулирующих
воздействий при ∆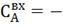 0,2 моль/л: а)
0,2 моль/л: а)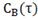 ; б)
; б)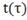 ;в)
;в)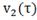 ;г)
;г)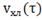 .
.
∆( =0
=0
 = 0.01507
= 0.01507
∆(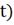 =0
=0
 = 1.282
= 1.282
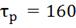
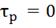
Анализ результатов моделирования представленных
на рис. 4.2.3 - рис. 4.2.4 показывают:
· Величина статической и динамической ошибки лежат
в переделах допустимых значений;
· Время регулирования также
удовлетворяет сформулированным требованиям;
· Значения расходов 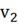 и
и
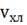 при
подаче возмущений имеют физический смысл.
при
подаче возмущений имеют физический смысл.
1) ∆t1=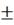 10
10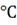 ,Процент
отклонения 33%
,Процент
отклонения 33%
∆( =0.352
=0.352
 = ∆(
= ∆(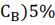 =0.0176
=0.0176
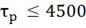
∆(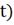 =90
=90
 = ∆(
= ∆(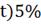 =4.5
=4.5
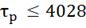
а) 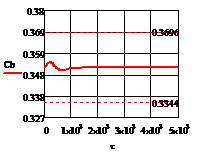 б)
б)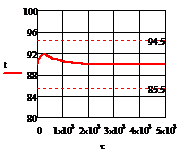
в)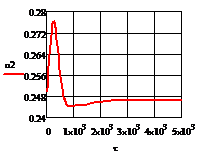 г)
г)
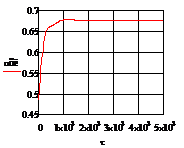
Рис. 4.2.5 Изменение регулируемых переменных
(Св, t) и регулирующих
воздействий при ∆t1=10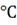 :
а)
:
а)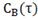 ; б)
; б)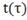 ;в)
;в)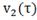 ;г)
;г)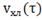 .
.
∆( =0
=0
 = 0.00237
= 0.00237
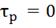
∆(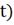 =0
=0
 = 1.838
= 1.838
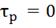
а) 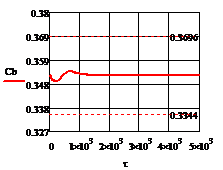 б)
б)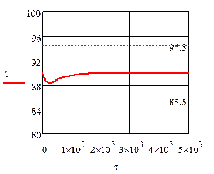
в)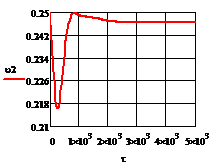 г)
г)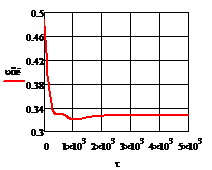
Рис. 4.2.6 Изменение регулируемых переменных
(Св, t) и регулирующих
воздействий при ∆t1=
- 10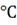 :
а)
:
а)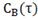 ; б)
; б)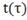 ;в)
;в)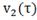 ;г)
;г)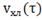 .
.
∆( =0
=0
 = 0.00296
= 0.00296
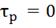
∆(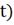 =0
=0
 = 1.695
= 1.695
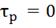
2) ∆t2=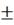 10
10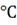 ,
Процент
отклонения 25%
,
Процент
отклонения 25%
∆( =0.352
=0.352
 = ∆(
= ∆(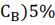 =0.0176
=0.0176
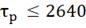
∆(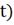 =90
=90
 = ∆(
= ∆(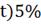 =4.5
=4.5
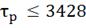
а)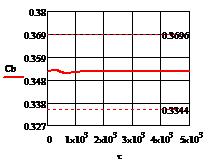 б)
б)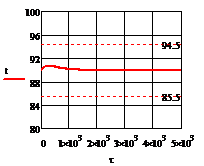
г)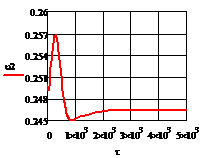 д)
д)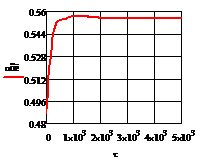
Рис. 4.2.7 Изменение регулируемых переменных
(Св, t) и регулирующих
воздействий при ∆t2=
10 :
а)
:
а)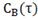 ; б)
; б)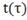 ;в)
;в)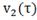 ;г)
;г)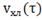 .
.
∆( =0
=0
 = 0.00062
= 0.00062
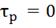
∆(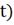 =0
=0
 = 0.69
= 0.69
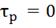
программа математический
автоматизированный реактор
а) б)
б)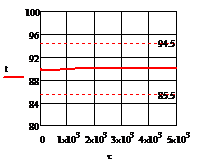
в)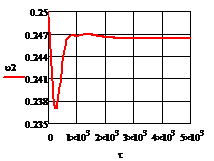 г)
г)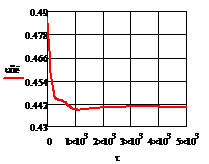
Рис. 4.2.8 Изменение регулируемых переменных
(Св, t) и регулирующих
воздействий при ∆t2=
- 10 :
а)
:
а)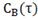 ; б)
; б)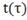 ;в)
;в)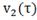 ;г)
;г)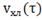 .
.
∆( =0
=0
 = 0.00115
= 0.00115
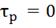
∆(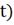 =0
=0
 = 0.482
= 0.482
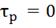
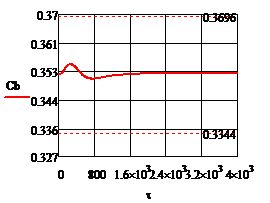
а) б)
в) г)
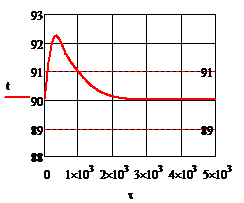
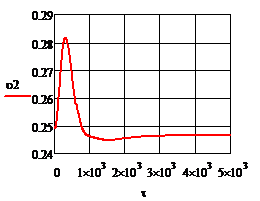
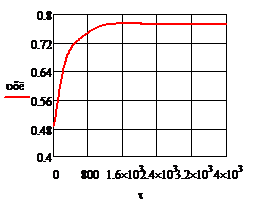
Рис. 4.2.9 Изменение регулируемых переменных
(Св, t) и регулирующих
воздействий при ∆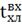 = 20
= 20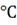 :
а)
:
а)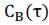 ;
б)
;
б)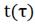 ;в)
;в)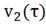 ;г)
;г)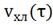 .
.
3) ∆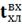 =
= 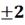 0
0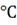 ,
Процент
отклонения 67%
,
Процент
отклонения 67%
∆( =0
=0
 = 0.0025
= 0.0025
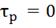
∆(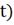 =0
=0
 = 2.24
= 2.24
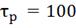
а)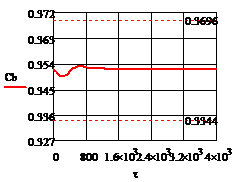 б)
б)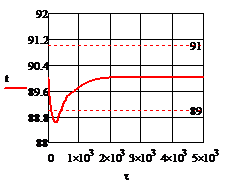
в)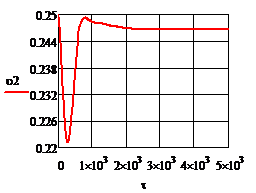 г)
г)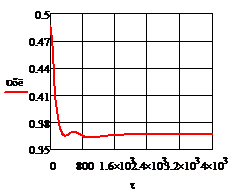
Рис. 4.2.10. Изменение регулируемых переменных
(Св, t) и регулирующих
воздействий при ∆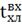 = - 20
= - 20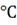 :
а)
:
а)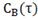 ; б)
; б)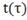 ;в)
;в)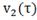 ;г)
;г)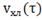 .
.
∆( =0
=0
 = 0.00245
= 0.00245
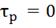
∆(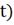 =0
=0
 = 1.391
= 1.391
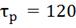
4) ∆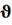 1
=
1
= 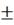 0,2
л/мин,
0,2
л/мин,
Процент отклонения 27%
∆( =0.352
=0.352
 = ∆(
= ∆(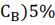 =0.0176
=0.0176
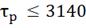
∆(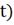 =90
=90
 = ∆(
= ∆(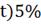 =4.5
=4.5
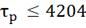
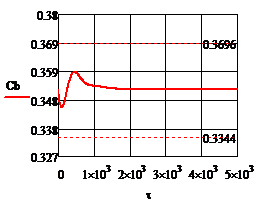
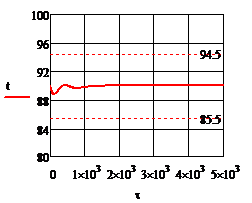
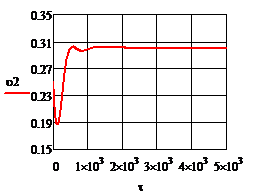
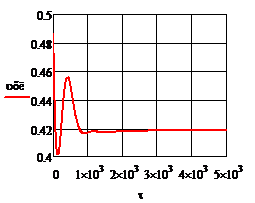
Рис. 4.2.11. Изменение регулируемых переменных
(Св, t) и регулирующих
воздействий при ∆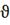 1
= 0,2 л/мин: а)
1
= 0,2 л/мин: а)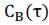 ; б)
; б)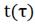 ;в)
;в)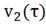 ;г)
;г)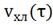 .
.
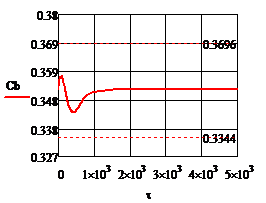
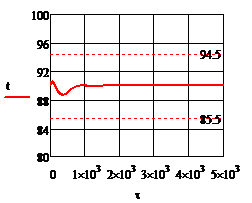
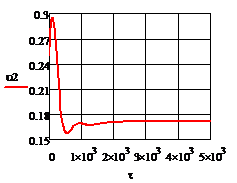
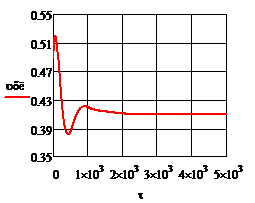
Рис. 4.2.12. Изменение регулируемых переменных
(Св, t) и регулирующих
воздействий при ∆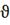 1
= - 0,2 л/мин: а)
1
= - 0,2 л/мин: а)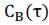 ; б)
; б)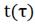 ;в)
;в)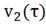 ;г)
;г)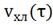 .
.
Анализ результатов моделирования представленных
на рис. 4.2.5. и рис.4.2.12. показывает:
· Величина статической и динамической ошибки лежат
в переделах допустимых значений;
· Время регулирования также
удовлетворяет сформулированным требованиям;
· Значения расходов 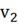 и
и
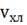 при
подаче возмущений имеют физический смысл.
при
подаче возмущений имеют физический смысл.
4.3 Ковариантность
с заданием
Ковариантность с заданным возмущением означает
способность системы отслеживать изменение задания в отсутствие других
возмущений.
1. ∆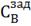 =
25% =
=
25% = 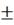 0,088 моль/л
0,088 моль/л
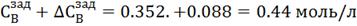
а)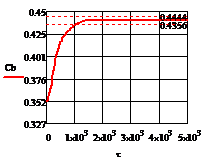 б)
б)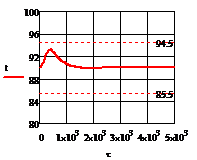
в)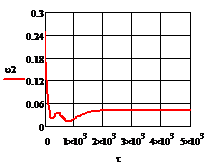 г)
г)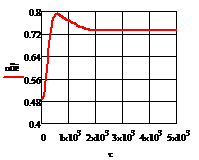
Рис. 4.3.1 Изменение регулируемых переменных
(Св, t) и регулирующих
воздействий при 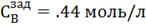 : а)
: а)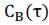 ;
б)
;
б)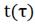 ;в)
;в)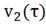 ;г)
;г)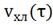 .
.
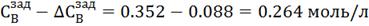
а)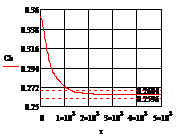 б)
б)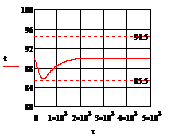
в)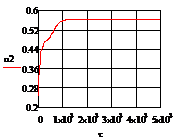 г)
г)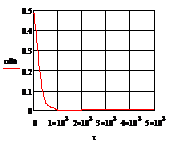
Рис. 4.3.2 Изменение регулируемых переменных
(Св, t) и регулирующих
воздействий при 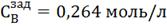 : а)
: а)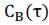 ;
б)
;
б)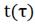 ;в)
;в)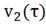 ;г)
;г)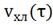
2. ∆tзад
= 20% = 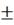 18
18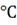
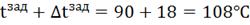
а)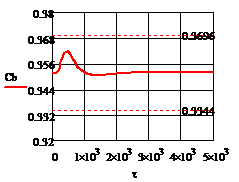 б)
б)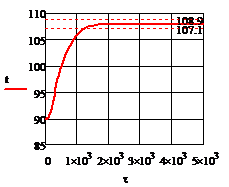
в)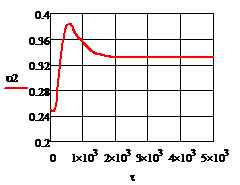 г)
г)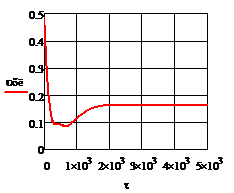
Рис. 4.3.3 Изменение регулируемых переменных
(Св, t) и регулирующих
воздействий при 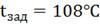 : а)
: а)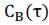 ;
б)
;
б)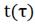 ;в)
;в)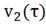 ;г)
;г) .
.
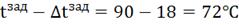
а)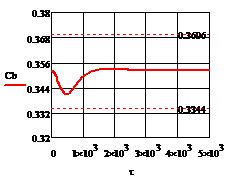 б)
б)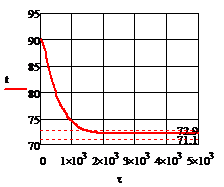
а)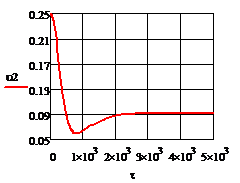 б)
б)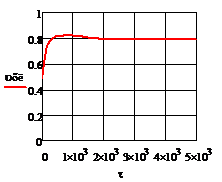
Рис. 4.3.4 Изменение регулируемых переменных
(Св, t) и регулирующих
воздействий при 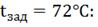 а)
а)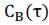 ;
б)
;
б)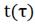 ;в)
;в)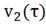 ;г)
;г)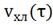 .
.
3. ∆tзад
= 20% = 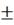 18
18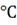 ,
∆
,
∆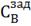 = 25% =
= 25% = 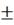 0,088
моль/л
0,088
моль/л
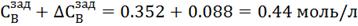
а)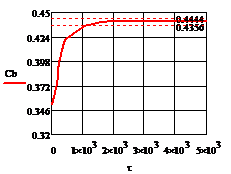 б)
б)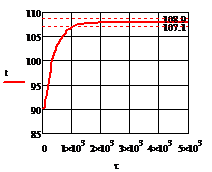
в)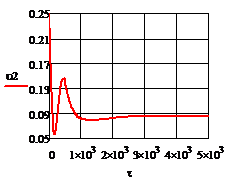 г)
г)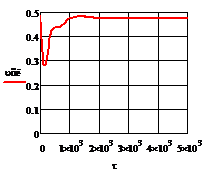
Рис.4.3.5. Изменение регулируемых переменных
(Св, t) и регулирующих
воздействий при 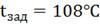 ,
, 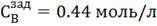
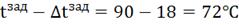
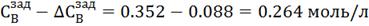
а)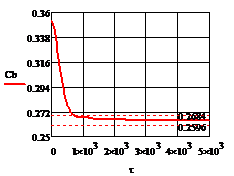 б)
б)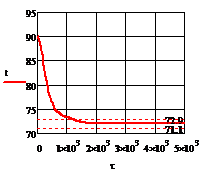
в)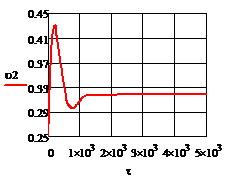 г)
г)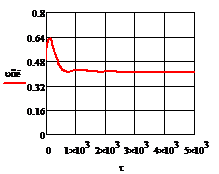
Рис. 4.3.5 Изменение регулируемых переменных
(Св, t) и регулирующих
воздействий при  ,
, 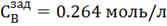
Таблица
5
|
канал
|
положительное
отклонение
|
отрицательное
отклонение
|
|
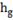
|
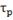
|
∆
|
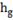
|
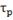
|
∆
|
|
инвариантность
|
|
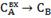
|
0.01402
|
0
|
0
|
0.01507
|
0
|
0
|
|
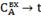
|
1.42
|
140
|
0
|
1.282
|
160
|
0
|
|
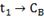
|
0.00237
|
0
|
0
|
0.00296
|
0
|
0
|
|
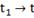
|
1.838
|
0
|
0
|
1.695
|
0
|
0
|
|
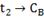
|
0
|
0
|
0.00115
|
0
|
0
|
|
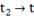
|
0.69
|
0
|
0
|
0.482
|
0
|
0
|
|
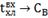
|
0.0025
|
0
|
0
|
0.00245
|
0
|
0
|
|
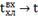
|
2.24
|
100
|
0
|
1.391
|
120
|
0
|
|
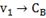
|
0.00655
|
0
|
0
|
0.00478
|
0
|
0
|
|
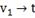
|
1.172
|
0
|
0
|
0.52
|
0
|
0
|
|
ковариантность
|
|
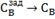
|
0.088
|
1000
|
0
|
0.088
|
1260
|
0
|
|
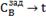
|
3.059
|
0
|
0
|
4.289
|
0
|
0
|
|
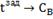
|
0.00944
|
0
|
0
|
0.01113
|
0
|
0
|
|
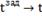
|
18
|
1190
|
0
|
18
|
1410
|
0
|
|
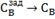 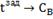
|
0.088
|
1140
|
0
|
0.088
|
640
|
0
|
|
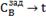 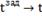
|
18
|
1080
|
0
|
18
|
1200
|
0
|
По результатам исследования инвариантности и
ковариантности можно сделать следующие выводы:
· система устойчива, так как переходные процессы
управления затухают при 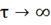 ;
;
· система инвариантна к возмущениям с
отклонением в 20-33% и ковариантна с заданием с отклонением 20-25%.
Многомерная система несвязанного управления
нелинейным объектом при использовании линейных ПИ алгоритмов работы регуляторов
работоспособна.
5. Моделирование системы управления
с более сложной структурой
Реализация каскадной системы регулирования
температурой имеет вид представленный на рис. 5.1.
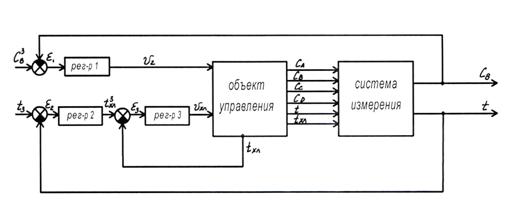
Рис. 5.1 Структурная каскадная схема
регулирования
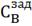 - концентрация
компонента В на входе с заданным значением
- концентрация
компонента В на входе с заданным значением
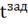 - оптимальная
температура объекта с заданным значением на входе
- оптимальная
температура объекта с заданным значением на входе
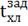 - оптимальная
температура хладоагента с заданным значением на входе
- оптимальная
температура хладоагента с заданным значением на входе
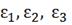 - ошибки
регулирования
- ошибки
регулирования
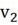 - расход второго
потока в реактор
- расход второго
потока в реактор
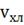 - расход
хладоагента
- расход
хладоагента
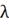 - подаваемые
возмущения
- подаваемые
возмущения
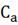 - концентрация
компонента А на выходе из аппарата
- концентрация
компонента А на выходе из аппарата
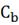 - концентрация
компонента B на выходе из
аппарата
- концентрация
компонента B на выходе из
аппарата
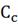 - концентрация
компонента C на выходе из
аппарата
- концентрация
компонента C на выходе из
аппарата
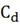 концентрация
компонента D на выходе из
аппарата
концентрация
компонента D на выходе из
аппарата
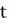 - оптимальная
температура объекта на выходе из аппарата
- оптимальная
температура объекта на выходе из аппарата
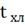 - температура
хладоагента на выходе из аппарата
- температура
хладоагента на выходе из аппарата
5.1 Программа моделирования
системы управления в среде Mathcad
Таблица
6
Таблица соответствия переменных
Вектор-функция правых частей диф.уравнений
модели
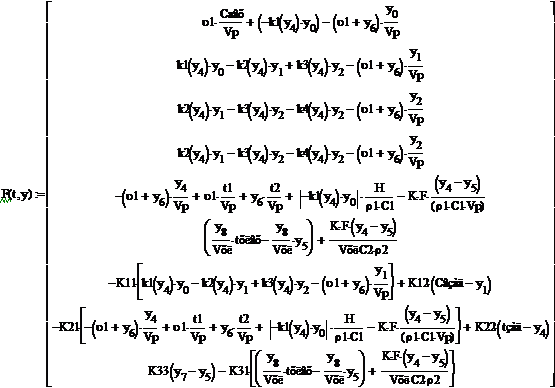
При отсутствии возмущения на объект и при
условии задания в качестве исходных данных значений переменных в статике
процесс регулирования представляет собой прямые линии параллельные оси времени.
На рис. 5.1.1 представлены графики изменения выходных переменных и упрощающих
воздействий для изложенных условий.
а)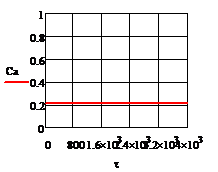 б)
б)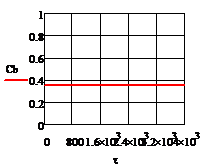
в)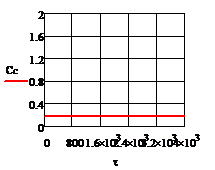 г)
г)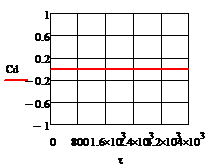
д)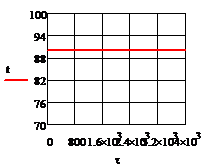 е)
е)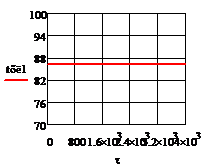
ж)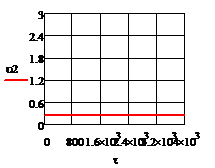 з)
з)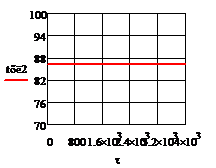
и)
Рис. 5.1.1 Процесс регулирования при
отсутствии возмущений а) ; б)
; б) ; в)
; в) ; г)
; г)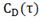 ; д)
; д)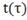 ; е)
; е)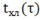 ; ж)
; ж)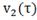 ; з)
; з)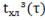 ;и)
;и) 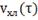 .
.
Для уточнения параметров подадим
возмущение по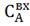 . Процент
отклонения 20%.
. Процент
отклонения 20%. 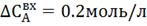 .
.
Исходя из требований к безопасности ведения
технологического процесса и требований к качеству продукции величины допустимых
значений статической ошибки, динамической ошибки и времени регулирования
принимаются следующими:
∆( =0.352
=0.352
 = ∆(
= ∆(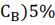 =0.0176
=0.0176
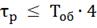
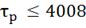
∆(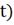 =90
=90
 = 1
= 1
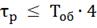
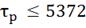
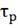 =0
=0
 = 0.00673
= 0.00673
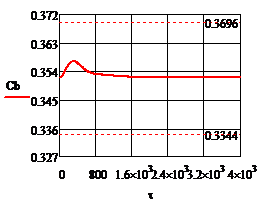
Рис. 5.1.2 Процесс регулирования концентрации
при возмущении 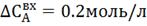
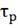 = 0
= 0
 = 0.571
= 0.571
∆=0
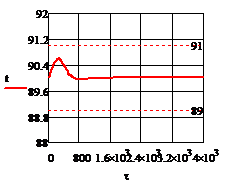
Рис. 5.1.3 Процесс регулирования температуры при
возмущении 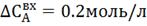
Можно сделать вывод, что настройки регулятора
удовлетворены. Следовательно, значения параметров алгоритмов регулирования,
вычисленные методом подстановки, следующие:
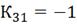
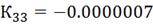
5.2 Инвариантность
к возмущениям
) ∆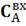 =
=
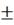 0,2
моль/л, Процент отклонения 20%
0,2
моль/л, Процент отклонения 20%
∆( =0.352
=0.352
 = ∆(
= ∆(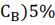 =0.0176
=0.0176
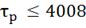
∆(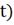 =90
=90
 = 1
= 1
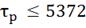
а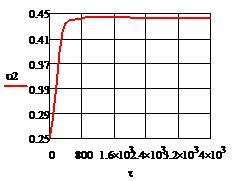 б)
б)
в) г)
г)
Рис. 5.2.1 Изменение регулируемых переменных
(Св, t) и регулирующих воздействий
при ∆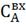 =
0,2 моль/л а)
=
0,2 моль/л а)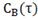 ; б)
; б)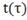 ;в)
;в)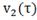 ;г)
;г)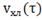 .
.
∆( =0
=0
 = 0.00673
= 0.00673
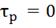
∆(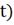 =0
=0
 = 0.571
= 0.571
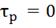
а)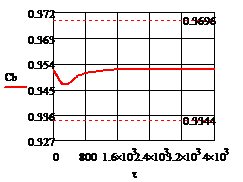 б)
б)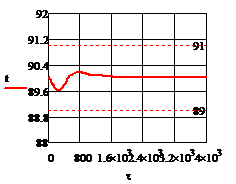
в)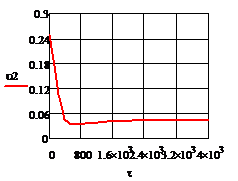 г)
г)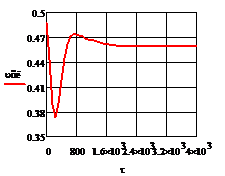
Рис. 5.2.2 Изменение регулируемых переменных
(Св, t) и регулирующих
воздействий при ∆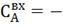 0,2 моль/л а)
0,2 моль/л а)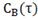 ; б)
; б)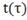 ;в)
;в)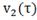 ;г)
;г)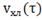 .
.
∆( =0
=0
 = 0.00538
= 0.00538
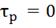
∆(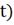 =0.0
=0.0
 = 0.394
= 0.394
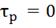
2) ∆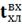 =
= 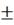 20
20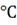 ,
Процент
отклонения 67%
,
Процент
отклонения 67%
∆( =0.352
=0.352
 = ∆(
= ∆(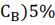 =0.0176
=0.0176
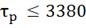 ∆(
∆(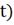 =90
=90
 = 1
= 1

а)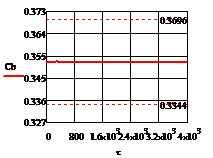 б)
б)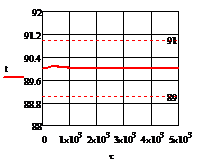
в)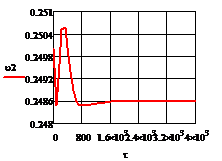 г)
г)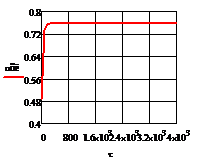
Рис. 5.2.3 Изменение регулируемых переменных
(Св, t) и регулирующих
воздействий при ∆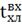 = 20
= 20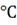 :
а)
:
а)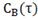 ; б)
; б)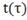 ;в)
;в)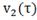 ;г)
;г)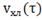 .
.
∆( =0
=0
 = 0.00209
= 0.00209
 0
0
∆(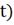 =0
=0
 = 0.052
= 0.052
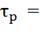 0
0
а)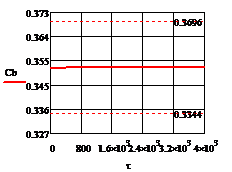 б)
б)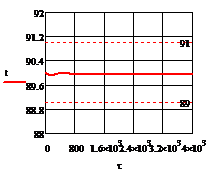
в)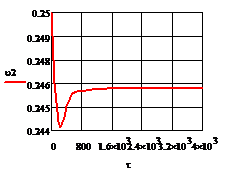 г)
г)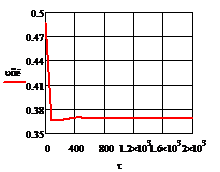
Рис. 5.2.4 Изменение регулируемых переменных
(Св, t) и регулирующих
воздействий при ∆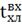 = - 10
= - 10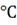 :
а)
:
а)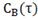 ; б)
; б)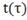 ;в)
;в)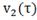 ;г)
;г)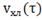 .
.
Таблица
7
|
канал
|
положительное
отклонение
|
отрицательное
отклонение
|
|
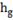
|
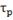
|
∆
|
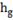
|
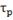
|
∆
|
|
инвариантность
|
|
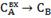
|
0.00673
|
0
|
0
|
0.00538
|
0
|
0
|
|
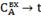
|
0.571
|
0
|
0
|
0.394
|
0
|
0
|
|
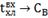
|
0.00209
|
0
|
0
|
0.00147
|
0
|
0
|
|
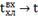
|
0.052
|
0
|
0
|
0.071
|
0
|
0
|
Анализ результатов моделирования представленных
на рис.5.2.1 - рис. 5.2.12 показывают:
· Величина статической и динамической ошибки лежат
в переделах допустимых значений;
· Время регулирования также
удовлетворяет сформулированным требованиям;
· Значения расходов 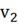 и
и
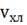 при
подаче возмущений имеют физический смысл.
при
подаче возмущений имеют физический смысл.
Вывод
При исследовании объекта на инвариантность к
возмущениям, сравнив таблицу 5 и таблицу 7, можно сделать вывод, что реализация
каскадной системы регулирования температурой будет более приемлемой. Так как
моделирование системы управления с более сложной структурой обладает меньшей
динамической ошибкой, и регулирующее воздействие не выходит за установленные
пределы регулирования.
Список используемых источников
1. Ротач
В.Я., Автоматизация настройки систем управления. - М.: Энергоатомиздат. 1984;
2. Кузьменко
А.Н., Курсовая работа по ТПП. - ИГХТУ. 2013.