|
Тип АД
|
РА
|
|
Номинальная
мощность
|
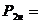 11 кВт 11 кВт
|
|
Номинальное
напряжение
|
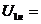 380/220 В 380/220 В
|
|
Номинальная
частота вращения
|
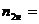 970 об/мин 970 об/мин
|
|
КПД
|
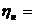 86 % 86 %
|
|
Коэффициент
мощности
|
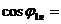 0,86 0,86
|
|
Кратность
пускового тока
|
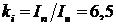
|
|
Кратность
пускового момента
|
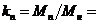 1,4 1,4
|
|
Перегрузочная
способность
|
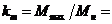 2,2 2,2
|
|
Отношение
минимального момента к номинальному
|
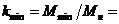 0,95 0,95
|
|
Число пазов
статора
|
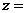 54 54
|
|
Число витков в
катушке обмотки статора
|
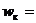 10 10
|
|
Число
параллельных ветвей фазы обмотки статора
|
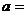 2 2
|
|
Длина активной
части проводника
|
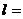 140 мм 140 мм
|
|
Диаметр якоря
|
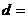 185 мм 185 мм
|
|
Воздушный зазор
между статором и ротором
|
 0,45 мм 0,45 мм
|
|
Сопротивление
фазы обмотки статора при 20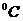
|
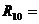 0,52 Ом 0,52 Ом
|
2. Расчет
основных параметров обмотки АД
2.1 Расчет и
построение двухслойной статорной обмотки с оптимально укороченным шагом
Для этого воспользуемся известными соотношениями из §§65-67,
[1] и найдем:
число пар полюсов 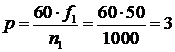 ;
;
число пазов на полюс и фазу 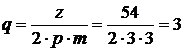 ;
;
диаметральный шаг 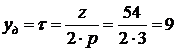 ;
;
оптимально укороченный шаг 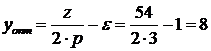 ;
;
Угол между соседними пазами 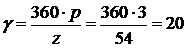 (градусов
электрических).
(градусов
электрических).
Тогда между началами фаз 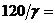 120/20 = 6 (пазовых
делений).
120/20 = 6 (пазовых
делений).
На чертеже обмотки покажем все 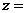 54 пронумерованных пазов,
а затем полностью, с учетом лобовых, межкатушечных и межгрупповых соединений,
изобразим обмотку фазы А, а также укажем пазы, с которых начинается укладка
обмотки фаз В и С.
54 пронумерованных пазов,
а затем полностью, с учетом лобовых, межкатушечных и межгрупповых соединений,
изобразим обмотку фазы А, а также укажем пазы, с которых начинается укладка
обмотки фаз В и С.
Т.к. 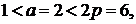 то катушечные группы соединены
последовательно-параллельно, и включены между собой сосредоточенным способом.
то катушечные группы соединены
последовательно-параллельно, и включены между собой сосредоточенным способом.
2.2 Расчет
обмоточных коэффициентов 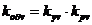 для 1-ой,
5-ой и 7-ой гармоник кругового вращающегося магнитного потока
для 1-ой,
5-ой и 7-ой гармоник кругового вращающегося магнитного потока
Для 1-ой гармоники:
относительный шаг
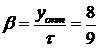 ;
;
коэффициент укорочения шага обмотки
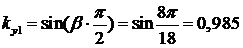 ;
;
угол фазной зоны
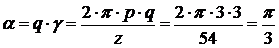 ;
;
коэффициент распределения обмотки
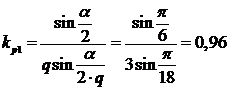 ;
;
обмоточный коэффициент
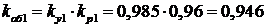 .
.
Для 5-ой гармоники:
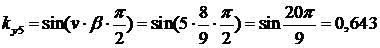 ;
;
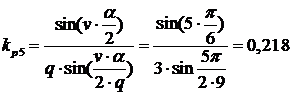 ;
;
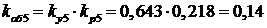 .
.
Для 7-ой гармоники:
 ;
;
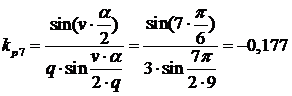 ;
;
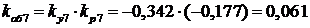 .
.
2.3 Определение
сильнейших гармоник зубцового порядка
Для определения порядка зубцовых гармоник воспользовались
формулой (20-34) из [2]:
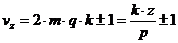 , где k=1,2,3,4, ….
, где k=1,2,3,4, ….
Или для трех фазной обмотки
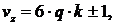 т.е.:
т.е.:
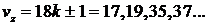
2.4 Расчет
величины потока вращающегося магнитного поля и амплитуд создающего его МДС
Расчет ведем для первой гармоники по приближенному
соотношению;
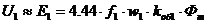 ;
;
где 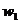 - число витков фазы обмотки статора, которое
может быть определено по формуле (22-17) из [2]:
- число витков фазы обмотки статора, которое
может быть определено по формуле (22-17) из [2]:
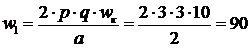 витков;
витков;
Затем находим 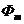 :
:
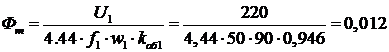 Вб.
Вб.
Затем определяем амплитудное значение индукции: 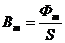 ; (Тл) где
; (Тл) где 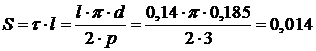
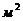 - площадь под полюсным делением. Тогда
- площадь под полюсным делением. Тогда
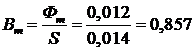 Тл.
Тл.
После этого рассчитываем амплитуду МДС, приходящуюся на один
воздушный зазор:
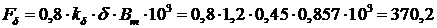 А
А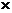 витков,
витков,
где 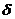 - воздушный зазор,
- воздушный зазор, 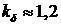 - коэффициент воздушного
зазора.
- коэффициент воздушного
зазора.
Амплитуду полной МДС трехфазной обмотки 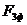 , создающей круговое
вращательное магнитное поле, можно ориентировочно посчитать по формуле:
, создающей круговое
вращательное магнитное поле, можно ориентировочно посчитать по формуле:
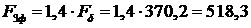 А
А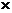 витков.
витков.
2.5
Определение величины тока статорной обмотки на холостом ходу АД
Амплитудное значение МДС фазы 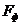 находим с помощью
известного соотношения:
находим с помощью
известного соотношения:
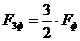 отсюда
отсюда 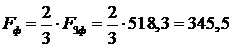 А
А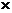 витков.
витков.
МДС и ток намагничивания связаны выражением (22-19) из [2]:
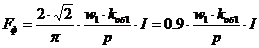 ;
;
откуда ток намагничивания
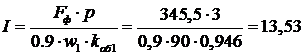 А.
А.
2.6 Сравнение
амплитуды МДС 5-ой, 7-ой гармоник и сильнейшей гармоники зубцового порядка с
амплитудой 1-ой гармоники
Для сравнения гармоник воспользуемся соотношением:
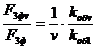 ;
;
где 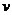 - порядок высшей гармоники.
- порядок высшей гармоники.
Сравниваем амплитуды 5-ой и 7-ой гармоник с амплитудой 1-ой гармоники:
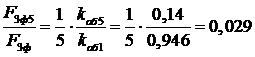 ;
;
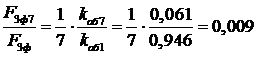 .
.
обмотка асинхронный двигатель электрический
3. Расчет
основных параметров АД
На основании исходных данных определяем:
3.1
Скольжение в номинальном режиме
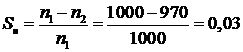 .
.
3.2
Номинальный момент на валу двигателя 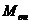
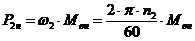 ;
;
откуда момент
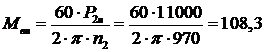
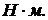
3.3 Пусковой
и критические моменты на валу:
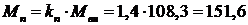
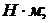
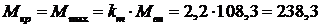
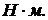
3.4 Мощность,
потребляемая двигателем из сети в номинальном режиме
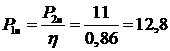 кВт.
кВт.
3.5 Линейный
ток АД в номинальном режиме
Фазный ток обмотки статора:
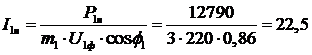 А.
А.
Тогда линейный ток при соединении обмоток статора:
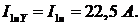
А линейный ток при соединении обмоток статора:
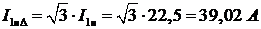 .
.
4. Расчет
параметров упрощенной Г-образной схемы замещения АД
Упрощенная Г-образная схема замещения получается при
следующих допущениях:
) пренебрегаем зависимостью сопротивлений активного 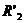 и реактивного рассеяния
и реактивного рассеяния 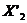 ротора и реактивного
рассеяния
ротора и реактивного
рассеяния 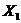 статора от скольжения, т.е. сопротивления
статора от скольжения, т.е. сопротивления 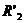 ,
, 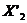 ,
, 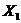 считаются постоянными;
считаются постоянными;
2) пренебрегаем активным 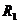 и реактивным
и реактивным 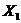 сопротивлениями статора
в контуре намагничивания как составляющими малую часть от последовательно
включенных с ними сопротивлений
сопротивлениями статора
в контуре намагничивания как составляющими малую часть от последовательно
включенных с ними сопротивлений 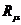 и
и 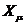 контура намагничивания.
В результате этого принимаем комплекс
контура намагничивания.
В результате этого принимаем комплекс 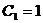 ;
;
) номинальный момент на валу и электромагнитный момент
равны между собой 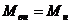 .
.
В результате получается схема замещения, представленная на
рис.1.
На рис.1 приняты обозначения:
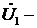 напряжение сети;
напряжение сети;
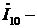 ток контура намагничивания;
ток контура намагничивания;
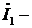 ток обмотки статора;
ток обмотки статора;
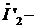 ток обмотки ротора, приведенный к обмотке
статора.
ток обмотки ротора, приведенный к обмотке
статора.
Расчет параметров упрощенной схемы замещения выполняем в
следующем порядке:
4.1 Расчет
величины реактивного сопротивления короткого замыкания 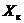
Выражение для определения величины 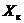 получаем из формулы
(25-19), [2] с учетом допущения о том, что
получаем из формулы
(25-19), [2] с учетом допущения о том, что 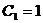 .
.
В этом случае можем записать:
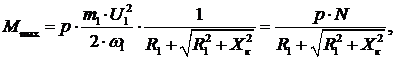
где 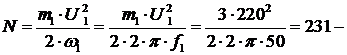 постоянная величина.
постоянная величина.
отсюда 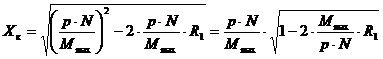 ;
;
где
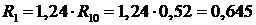 Ом - сопротивление фазы обмотки в нагретом
состоянии.
Ом - сопротивление фазы обмотки в нагретом
состоянии.
Тогда:
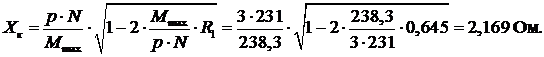
4.2 Расчет
величины активного сопротивления ротора 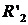
Для получения величины 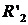 воспользуемся формулой
(25-6), [2] и подставим значения
воспользуемся формулой
(25-6), [2] и подставим значения 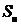 и
и 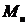 , в результате чего
получим равенство:
, в результате чего
получим равенство:
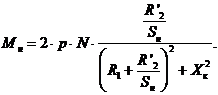
В этом равенстве только одно неизвестное - сопротивление 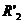 . После выполнения
соответствующих преобразований получаем квадратное уравнение:
. После выполнения
соответствующих преобразований получаем квадратное уравнение:
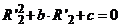
где 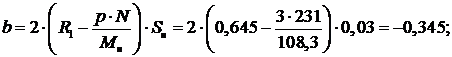
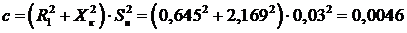 .
.
Учитывая, что коэффициент при 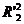 равен 1, находим
дискриминант:
равен 1, находим
дискриминант:
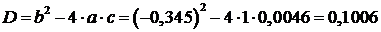 .
.
Уравнение имеет 2 корня:
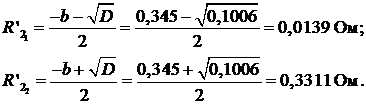
Таким образом, возможны 2 значения 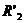 , при которых
характеристика
, при которых
характеристика 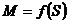 проходит через точку с координатами
проходит через точку с координатами 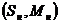 - рис.2.
- рис.2.
При большем значении корня получается характеристика 1, при
меньшем - 2. Точка a, соответствующая номинальному режиму, находится на устойчивой
части характеристики 1, поэтому из двух значений 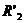 необходимо выбрать
большее.
необходимо выбрать
большее.
В нашем случае 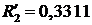 Ом.
Ом.
4.3 Расчет
активного 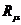 и реактивного
и реактивного 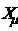 сопротивлений
контура намагничивания
сопротивлений
контура намагничивания
Предварительно находим вектор тока идеального холостого хода:
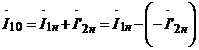 ;
;
Если вектор фазного напряжения 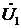 направить на комплексной
плоскости по оси вещественных чисел
направить на комплексной
плоскости по оси вещественных чисел 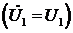 , то вектор
, то вектор 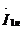 может быть найден в
виде:
может быть найден в
виде:
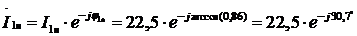 ;
;
Вектор 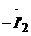 определяется через сопротивление Г-образной
схемы замещения:
определяется через сопротивление Г-образной
схемы замещения:
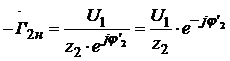
где 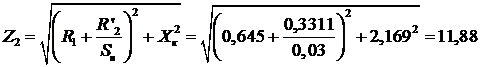 Ом;
Ом;
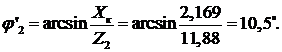
Тогда
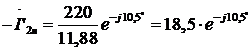
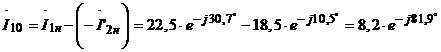
После определения вектора 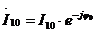 можно найти:
можно найти:
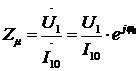 .
.
В нашем случае
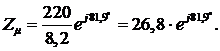
Тогда активное и реактивное сопротивление контура
намагничивания определяем по формулам:
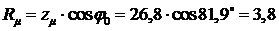 Ом;
Ом;
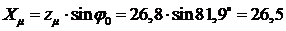 Ом.
Ом.
5. Расчет и
построение упрощенной круговой диаграммы
Определяем диаметр окружности:
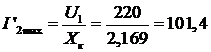 А.
А.
Построение КД начинаем с изображения векторов 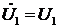 и
и 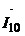 , а также диаметра
окружности. Если комплексное число
, а также диаметра
окружности. Если комплексное число 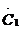 в соответствии с
принятыми допущениями считать вещественным числом, то диаметр окружности будет
перпендикулярен вектору
в соответствии с
принятыми допущениями считать вещественным числом, то диаметр окружности будет
перпендикулярен вектору 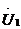 .
.
После построения окружности с помощью циркуля откладываем
отрезки, равные длинам векторов 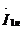 и
и 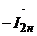 и выполняем проверку на
схождение их концов в одной точке КД.
и выполняем проверку на
схождение их концов в одной точке КД.
После этого на КД отмечаем точку 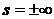 , соответствующую
, соответствующую
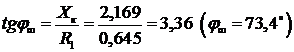
и точку 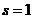 , соответствующую
, соответствующую
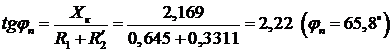 .
.
6. Построение
рабочих характеристик
Для построения рабочих характеристик АД воспользуемся
упрощенной КД, полученной в п.5. Рабочие характеристики, представляющие собой
зависимости тока статора 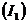 , электромагнитного момента
, электромагнитного момента 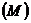 , потребляемой мощности
, потребляемой мощности 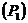 , КПД
, КПД 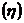 , коэффициента мощности
, коэффициента мощности 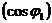 , частоты вращения
, частоты вращения 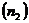 , скольжения
, скольжения 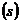 от полезной мощности
от полезной мощности 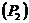 , строим в соответствии с
теоретическим материалом, изложенным в §130 [1]. При определении этих
зависимостей измеряем
, строим в соответствии с
теоретическим материалом, изложенным в §130 [1]. При определении этих
зависимостей измеряем 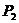 в диапазоне от холостого хода до максимальной
полезной мощности
в диапазоне от холостого хода до максимальной
полезной мощности 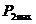 . Величину
. Величину 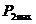 находим проведением
перпендикуляра из центра окружности к линии полезной мощности, проходящей через
точки окружности, соответствующие
находим проведением
перпендикуляра из центра окружности к линии полезной мощности, проходящей через
точки окружности, соответствующие 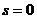 и
и 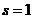 . Значение всех
параметров АД для заданных значений полезной мощности, найденные с помощью КД,
записываются в таблицу 1.
. Значение всех
параметров АД для заданных значений полезной мощности, найденные с помощью КД,
записываются в таблицу 1.
По данным таблицы все рабочие характеристики строим на одном
графике в относительных единицах, приняв за базисные номинальные значения
параметров АД (рис.3). Эти данные заносим в таблицу 2.
При построении рабочих характеристик и проверке правильности
построения КД выбираем следующую последовательность действий:
. Фазный ток статора 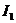 и потребляемая мощность
и потребляемая мощность 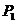 .
.
Для начала находим ток 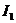 :
: 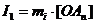 .
.
Затем находим:

где 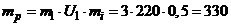 (Вт/мм) - масштаб мощности.
(Вт/мм) - масштаб мощности.
. Полезная мощность 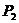 .
.
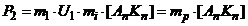
Максимальная полезная мощность:
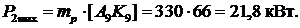
. Электромагнитный момент 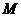 .
.
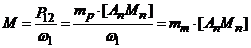 ,
,
где 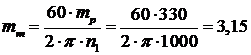 Н·м/мм - масштаб электромагнитного момента.
Максимальный электромагнитный момент:
Н·м/мм - масштаб электромагнитного момента.
Максимальный электромагнитный момент:
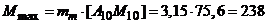 Н·м
Н·м
. Коэффициент полезного действия 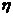 .
.
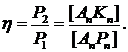
. Коэффициент мощности 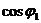 .
.
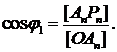
. Скольжение 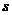 .
.
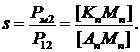
При пуске АД:
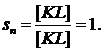
. Частота вращения ротора 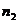 .
.
Определяется через скольжение по формуле:
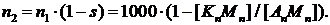
Таблица 1
|
P2,
кВт
|
I1, A
|
M, Н∙м
|
P1,
кВт
|
KПД η
|
cosφ1
|
n2,
об/мин
|
s
|
|
0
|
8,2
|
0
|
0,8
|
0
|
0,141
|
1000
|
0
|
|
2,4
|
9,6
|
23
|
3,2
|
0,75
|
0,507
|
994,5
|
0,005
|
|
4,8
|
12,3
|
46,4
|
5,7
|
0,84
|
0,707
|
996,6
|
0,003
|
|
7,3
|
16
|
71
|
8,5
|
0,86
|
0,804
|
981,8
|
0,018
|
|
9,7
|
20,1
|
95
|
11,2
|
0,87
|
0,847
|
974,5
|
0,026
|
|
12,1
|
24,7
|
119,5
|
14,1
|
0,86
|
0,866
|
966,5
|
0,033
|
|
14,5
|
29,9
|
144,6
|
17,2
|
0,84
|
0,872
|
956,9
|
0,043
|
|
16,9
|
35,9
|
170,7
|
20,6
|
0,82
|
0,867
|
945
|
0,055
|
|
19,4
|
44,1
|
233,1
|
24,7
|
0,79
|
0,848
|
927,1
|
0,073
|
|
21,8
|
60,8
|
235,1
|
31,3
|
0,7
|
0,780
|
878,8
|
0,121
|
Таблица 2
|
P2,
о. е. I1, о. е. M, о. е. P1, о. е. KПД η, о. е. cosφ1, о. е. n2,
о. е. s, о. е.
|
|
|
|
|
|
|
|
|
0
|
0,36
|
0
|
0,06
|
0
|
0,16
|
1,03
|
0
|
|
0,22
|
0,43
|
0,21
|
0,25
|
0,87
|
0,59
|
1,03
|
0,17
|
0,55
|
0,43
|
0,45
|
0,98
|
0,82
|
1,03
|
0,1
|
|
0,66
|
0,71
|
0,66
|
0,66
|
1
|
0,93
|
1,01
|
0,6
|
|
0,88
|
0,89
|
0,88
|
0,88
|
1,01
|
0,98
|
1
|
0,87
|
|
1,1
|
1,1
|
1,1
|
1,1
|
1
|
1,01
|
1
|
1,1
|
|
1,32
|
1,33
|
1,34
|
1,34
|
0,98
|
1,01
|
0,99
|
1,43
|
|
1,54
|
1,6
|
1,58
|
1,61
|
0,95
|
1,01
|
0,97
|
1,83
|
|
1,76
|
1,96
|
2,15
|
1,93
|
0,92
|
0,99
|
0,96
|
2,43
|
|
1,98
|
2,7
|
2,17
|
2,45
|
0,81
|
0,91
|
0,91
|
4,03
|
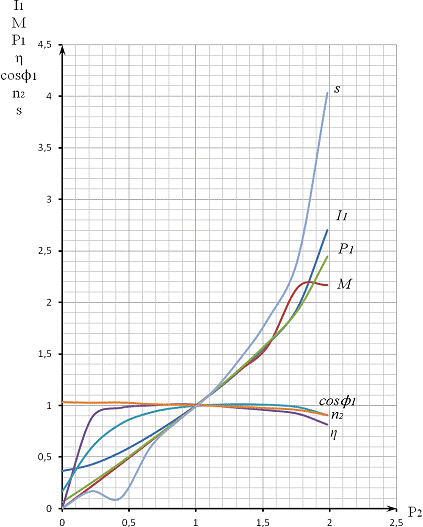
Рис.3 Рабочие характеристики АД в относительных единицах
7. Расчет и
построение зависимости момента АД от скольжения
Расчет и построение зависимостей 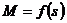 (рис.4) выполняется в
относительных единицах в следующем порядке:
(рис.4) выполняется в
относительных единицах в следующем порядке:
7.1
Построение кривой 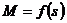 , проходящей через точку с
координатами
, проходящей через точку с
координатами 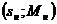 , выполняем по упрощенной формуле
Клосса
, выполняем по упрощенной формуле
Клосса
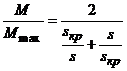 ;
;
Для этого подставим в упрощенную формулу Клосса, приведенную
в §126, [1], значения 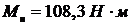 и
и 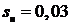 , в результате чего после
преобразований получаем уравнение:
, в результате чего после
преобразований получаем уравнение:
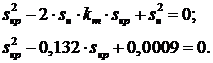
Решая это уравнения, получим 2 корня, выберем наибольшее
значение корня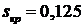 .
.
Так как 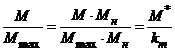 , то из упрощенной формулы Клосса получаем:
, то из упрощенной формулы Клосса получаем:
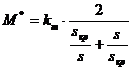 .
.
Подставляя в это выражение разные значения s, получим величины 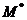 и запишем их в таблицу
3.
и запишем их в таблицу
3.
Таблица 3
|
S
|
0,1
|
0,3
|
0,5
|
0,7
|
1,0
|
Sн=0,03
|
Sкp=0,125
|
|
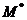
|
2,15
|
1,56
|
1,04
|
0,76
|
0,54
|
1
|
2,2
|
По табличным данным, а также с учетом того, что момент 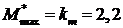 имеет место при
имеет место при 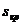 = 0,125, строим
зависимость
= 0,125, строим
зависимость 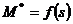 .
.
Полученная кривая показывает, в частности, что расчетное
значение пускового момента существенно отличается от величины, приведенной в
справочнике.
7.2
Построение кривой 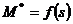 по полной формуле Клосса
по полной формуле Клосса
С этой целью из формулы (25-23), [2] получим выражение:
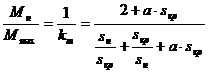 ,
,
где a - безразмерная величина, которая определяется по формуле
(25-24), [2]. С учетом, что 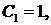 получаем:
получаем:
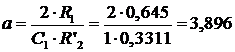 .
.
После соответствующих алгебраических преобразований получаем
квадратное уравнение:
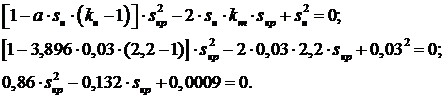
В результате решения уравнения находим уточненное значение 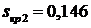 . Далее, вернувшись к
полной формуле Клосса в виде зависимости:
. Далее, вернувшись к
полной формуле Клосса в виде зависимости:
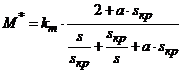 ,
,
и подставляя разные значения 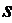 , заполним таблицу 4. С
учетом равенства
, заполним таблицу 4. С
учетом равенства 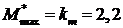 при новом значении
при новом значении 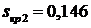 построим уточненную
зависимость
построим уточненную
зависимость 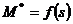 на том же графике, что и построенная по
упрощенной формуле Клосса.
на том же графике, что и построенная по
упрощенной формуле Клосса.
Таблица 4
|
S
|
0,1
|
0,3
|
0,5
|
0,7
|
1,0
|
Sн=0,03
|
Sкp2=0,146
|
|
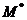
|
2,08
|
1,82
|
1,32
|
1,01
|
0,75
|
1
|
2,2
|
7.3
Построение кривой 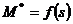 через точку, соответствующую
пусковому моменту, взятому из исходных паспортных данных
через точку, соответствующую
пусковому моменту, взятому из исходных паспортных данных
При пуске 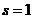 ,
, 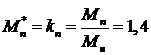 . После подстановки этих значений в упрощенную
формулу Клосса получается:
. После подстановки этих значений в упрощенную
формулу Клосса получается:
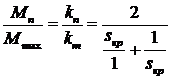 . Откуда
. Откуда 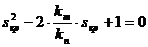 , то есть:
, то есть:
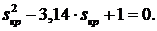
В этом случае надо взять меньший из корней, так как точка 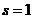 лежит на неустойчивой
части характеристики. Выбираем
лежит на неустойчивой
части характеристики. Выбираем 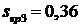 .
.
Далее, подставляя разные значения 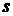 и занося их в таблицу 5,
рассчитаем и построим кривую
и занося их в таблицу 5,
рассчитаем и построим кривую 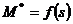 на том же графике, что и в п.7.2 и 7.1
Построенная кривая также дает большую погрешность, но уже в области нормальных
режимов работы (при
на том же графике, что и в п.7.2 и 7.1
Построенная кривая также дает большую погрешность, но уже в области нормальных
режимов работы (при 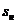 расчетное значение момента значительно меньше номинального
значения).
расчетное значение момента значительно меньше номинального
значения).
Таблица 5
|
S
|
0,1
|
0,3
|
0,5
|
0,7
|
1,0
|
Sн=0,03
|
Sкp3=0,36
|
|
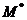
|
1,13
|
2,16
|
2,09
|
1,79
|
1,4
|
0,36
|
2,2
|
7.4
Построение рабочего участка зависимости 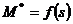
Для этого проводим прямую линию через начало координат и
точку 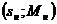 , в результате чего
получается линейная зависимость
, в результате чего
получается линейная зависимость 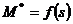 .
.
Из графика видно хорошее совпадение прямолинейной зависимости
и зависимости построенной в п.7.1, в области нормальных режимов работы и даже
при небольших перегрузках.
7.5
Построение зависимости 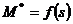 по паспортным данным АД
по паспортным данным АД
На основании проделанных выше расчетов и паспортных данных АД
на участке 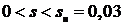 зависимость
зависимость 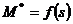 можно считать линейной.
Затем она отклоняется от прямой линии и достигает величины
можно считать линейной.
Затем она отклоняется от прямой линии и достигает величины 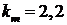 при скольжении
при скольжении 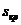 , большем
, большем 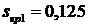 и
и 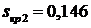 , полученных в п.7.1 и
7.2, но меньшем, чем
, полученных в п.7.1 и
7.2, но меньшем, чем 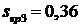 , полученном в п.7.3 При
, полученном в п.7.3 При 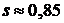 момент
момент 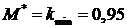 и при
и при 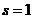 будет
будет 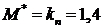 .
.
Провал характеристики в области 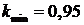 объясняется влиянием
высших гармонических составляющих вращающегося магнитного поля.
объясняется влиянием
высших гармонических составляющих вращающегося магнитного поля.
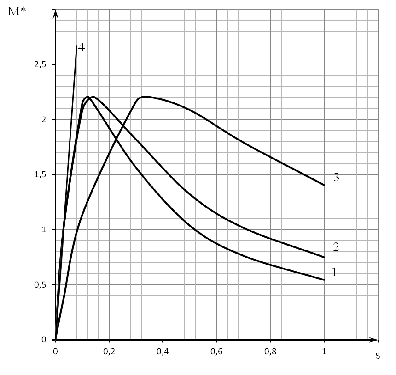
Рис.4 Зависимость момента АД от скольжения M*=f (s)
1 - по упрощенной формуле Клосса
- по полной формуле Клосса
- через точку, соответствующую пусковому моменту,
взятому из исходных паспортных данных
- рабочий участок зависимости
- по паспортным данным АД
8. Расчет
механических характеристик АД при неноминальных параметрах электрической сети
В соответствии с требованиями Регистра допускается
кратковременное снижение напряжения электрической сети на 20% и частоты на 10% от
номинального значения, что возможно при набросах нагрузки на электростанцию.
В связи с этим представляет интерес расчет и анализ
механических характеристик 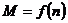 АД отдельно при напряжении
АД отдельно при напряжении 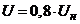 и частоте
и частоте 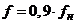 , а затем при
одновременном уменьшении напряжения и частоты до
, а затем при
одновременном уменьшении напряжения и частоты до 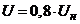 и
и 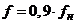 .
.
Эти характеристики рассчитаем, пользуясь упрощенной формулой
Клосса.
Новые значения критических момента и скольжения определим по
известным формулам:
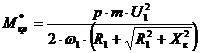 ;
; 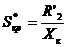 .
.
При этом будем иметь в виду, что индуктивное сопротивление 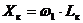 зависит от частоты сети,
т.к.
зависит от частоты сети,
т.к. 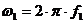 . Результаты расчета
сведем в таблицы 6, 7 и 8, а затем построим по ним все характеристики на одном
графике с механической характеристикой
. Результаты расчета
сведем в таблицы 6, 7 и 8, а затем построим по ним все характеристики на одном
графике с механической характеристикой 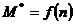 , построенной для
номинальных значений напряжения и частоты. Индуктивность
, построенной для
номинальных значений напряжения и частоты. Индуктивность 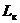 при изменении параметров
сети не изменяется. Находим ее по формуле:
при изменении параметров
сети не изменяется. Находим ее по формуле:
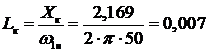 Гн.
Гн.
Затем рассчитываем механические характеристики по следующей
последовательности:
8.1 При
номинальных параметрах сети
Для этого случая 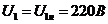 ,
, 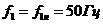 .
.
Механическая характеристика для этого случая рассчитывается в
п.7.1 Отметим, что здесь для критического скольжения 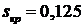 критический момент
критический момент 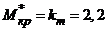 .
.
8.2 При
пониженном напряжении сети
Для этого случая 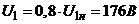 ,
, 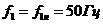 .
.
Находим значения критических момента и скольжения:
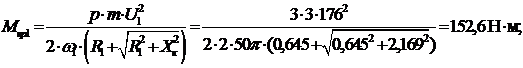
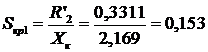 .
.
Рассчитываем значения моментов по упрощенной формуле Клосса
(см. п.7.1) и данные сводим в таблицу 6.
Таблица 6
|
Sн
|
0,1
|
0,3
|
0,5
|
0,7
|
1,0
|
Sн=0,03
|
Sкр1=0,153
|
|
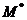
|
1,25
|
1,14
|
0,79
|
0,59
|
0,42
|
0,53
|
Km=1,41
|
8.3 При
пониженной частоте сети
Для этого случая 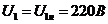 ,
, 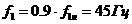 .
.
Находим индуктивное сопротивление:
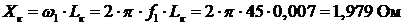 .
.
Находим значения критических момента и скольжения:
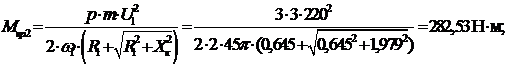
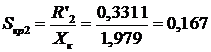 .
.
Рассчитываем значения моментов по упрощенной формуле Клосса
(см п.7.1) и данные сводим в таблицу 7.
Таблица 7
|
Sн0,10,30,50,71,0Sн=0,03Sкр2=0,167
|
|
|
|
|
|
|
|
|
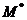
|
2,3
|
2,22
|
1,57
|
1,18
|
0,85
|
0,91
|
Km=2,61
|
8.4 При
пониженных напряжении и частоте сети
Для этого случая 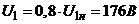 ,
, 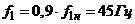 ,
, 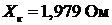 .
.
Находим значения критических момента и скольжения:
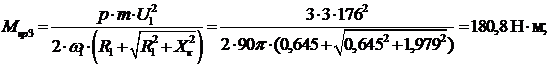
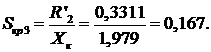
Рассчитываем значения моментов по упрощённой формуле Клосса
(см. п.7.1) и сводим данные в таблицу 8.
Таблица 8
|
Sн0,10,30,50,71,0Sн=0,03Sкр3=0,167
|
|
|
|
|
|
|
|
|
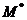
|
1,47
|
1,42
|
1
|
0,75
|
0,54
|
0,58
|
Km=1,67
|
По полученным данным построим все характеристики на одном
графике с механической характеристикой, построенной для номинальных значений
напряжения и частоты (рис.5).
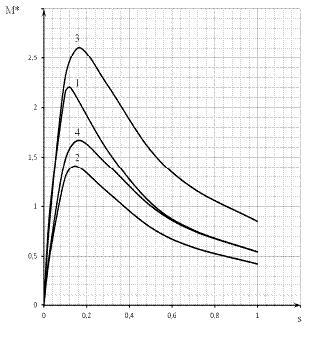
Рис.5 Зависимость момента АД от скольжения M*=f (s)
1- при номинальных параметрах сети
2- при пониженном напряжении сети
- при пониженной частоте сети
- при пониженных напряжении и частоте сети
Список
использованной литературы
1)
Мезин Е.К. Судовые электрические машины. - Л. Судостроение, 1985. - 320 с.
)
Вольдек А.И. Электрические машины - 3-е изд., перераб. - Л.: Энергия, 1978. -
832 с.
)
Проектирование электрических машин: Учеб. для вузов/под ред. И.П. Копылова. -
3-е изд., испр. и доп. - М.: Высш. шк., 2002. - 757 с.