Исследование кинематики движения материальной точки в системе MathCAD
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
УЧРЕЖДЕНИЕ
ОБРАЗОВАНИЯ
ГОМЕЛЬСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
ИМЕНИ П.О. СУХОГО
ЗАОЧНЫЙ
ФАКУЛЬТЕТ
КАФЕДРА
ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
РАСЧЕТНО-ПОЯСНИТЕЛЬНАЯ
ЗАПИСКА
к курсовой
работе
по
дисциплине «Информатика»
на тему
«Исследование
кинематики движения материальной точки в системе MathCAD»
вариант
Выполнил
студент гр.ЗТМ-11с
Красовский В.И.
Гомель 2013
Введение
Курсовое проектирование является необходимым этапом подготовки и обучения
студентов, становления их как высококвалифицированных специалистов и играет
важную роль в формировании самостоятельного творческого мышления студента.
Курсовая работа представляет собой комплексную учебно-исследовательскую работу
студента, которая выполняется на основе теоретических и практических знаний,
накопленных в процессе обучения дисциплине "Информатика". Она
является многоцелевым элементом учебного процесса и позволяет привить студентам
навыки и умения сбора, анализа, обобщения информации по данной предметной
области, решения конкретной прикладной задачи с применением обоснованно
выбранной компьютерной системы.
В данной курсовой работе необходимо с использованием системы Mathcad
исследовать зависимость движения материальной точки от времени.
Системы MathCAD традиционно занимают особое место среди множества таких
систем (Eureka, Mercury, MatLAB, Mathematica, Maple и др.) и по праву могут
называться самыми современными, универсальными, и массовыми математическими
системами. Они позволяют выполнять как численные, так и аналитические
(символьные) вычисления, имеют чрезвычайно удобный математико-ориентированный
интерфейс и прекрасные средства графики.
Создание математических моделей позволяет ускорить и упростить весь
процесс разработки, а также предположить закон движения материальной точки в
различных условиях.
Курсовая работа призвана реализовать несколько задач, основными из них
являются следующие:
углубление и расширение теоретических знаний по математическому
моделированию;
приобретение навыков самостоятельного решения прикладной инженерной
задачи с использованием компьютерных систем;
умение формулировать выводы по проделанным исследованиям.
Для выполнения курсовой работы была выбрана система MathCAD 2001 Professional, так как она по сравнению с другими
системами вычислений достаточно легко позволяет произвести построение
математической модели
1.
Математическое моделирование технического объекта
1.1 Понятие математической модели,
свойства и классификация
Математическое моделирование занимает центральное место в построении
эффективной технологии автоматизированного проектирования и исследования.
Математическая модель никогда не бывает полностью тождественна объекту,
процессу или системе. Она строится на основе упрощений и является приближением
объекта, процесса или системы. Для любого объекта, процесса или системы можно
построить множество математических моделей.
Математическая модель согласно [1,с.59] - это совокупность математических
объектов и отношений между ними, адекватно отображающая физические свойства
создаваемого технического объекта. В качестве математических объектов выступают
числа, переменные, множества, векторы, матрицы и т. п. Для осуществления
вычислительного эксперимента на ЭВМ необходимо разработать алгоритм реализации
математической модели.
К классификации математических моделей в
соответствии с [1 с.86 ] разные авторы подходят по-своему, положив в основу
классификации различные принципы. Можно классифицировать модели по отраслям
наук (математические модели в физике, биологии, социологии и т.д.) - это
естественно, если к этому подходит специалист в какой-то одной науке. Можно
классифицировать по применяемому математическому аппарату (модели, основанные
на применении обыкновенных дифференциальных уравнений, дифференциальных
уравнений в частных производных, стохастических методов, дискретных
алгебраических преобразований и т.д.) - это естественно для математика,
занимающегося аппаратом математического моделирования.
Структурные математические модели предназначены для отображения
структурных свойств объектов.
Функциональные математические модели предназначены для отображения
информационных, физических, временных процессов, протекающих в работающем
оборудовании, в ходе выполнения технологических процессов и т.д.
Аналитические математические модели представляют собой явные
математические выражения выходных параметров как функций от параметров входных
и внутренних.
Алгоритмические математические модели выражают связи между выходными
параметрами и параметрами входными и внутренними в виде алгоритма.
Имитационные математические модели - это алгоритмические модели,
отражающие развитие процесса (поведение исследуемого объекта) во времени при
задании внешних воздействий на процесс.
Теоретические математические модели создаются в результате исследования
объектов (процессов) на теоретическом уровне.
Эмпирические математические модели создаются в результате проведения
экспериментов (изучения внешних проявлений свойств объекта с помощью измерения
его параметров на входе и выходе) и обработки их результатов методами
математической статистики.
Детерминированные математические модели описывают поведение объекта с
позиций полной определенности в настоящем и будущем. Примеры таких моделей:
формулы физических законов, технологические процессы обработки деталей и т.д.
Вероятностные математические модели учитывают влияние случайных факторов
на поведение объекта, т.е. оценивают его будущее с позиций вероятности тех или
иных событий. Примеры таких моделей: описание ожидаемых длин очередей в
системах массового обслуживания, ожидаемых объемов выпуска сверхплановой
продукции производственным участком, точности размеров в партии деталей с
учетом явления рассеяния и т.д.
Под математическим моделированием, в узком смысле слова, понимают
описание в виде уравнений и неравенств реальных физических, химических,
технологических, биологических, экономических и других процессов. Для того
чтобы использовать математические методы для анализа и синтеза различных
процессов, необходимо уметь описать эти процессы на языке математики, то есть описать
в виде системы уравнений и неравенств.
Как методология научных исследований математическое моделирование
сочетает в себе опыт различных отраслей науки о природе и обществе, прикладной
математики, информатики и системного программирования для решения
фундаментальных проблем. Математическое моделирование объектов сложной природы
- сквозной единый цикл разработок от фундаментального исследования проблемы до
конкретных численных расчетов показателей эффективности объекта. Результатом
разработок бывает система математических моделей, которые описывают качественно
разнородные закономерности функционирования объекта и его эволюцию в целом как
сложной системы в различных условиях. Вычислительные эксперименты с
математическими моделями дают исходные данные для оценки показателей
эффективности объекта. Поэтому математическое моделирование как методология
организации научной экспертизы крупных проблем незаменимо при проработке
народнохозяйственных решений.
Схема построения математических моделей следующая:
·
Выделение
параметра или функции, подлежащей исследованию.
·
Выбор закона,
которому подчиняется эта величина.
·
Выбор области, в
которой требуется изучить данное явление.
1.2 Численные методы математического
моделирования
Основным инструментом для решения сложных
математических задач в настоящее время являются численные методы, позволяющие
свести решение задачи к выполнению конечного числа арифметических действий над
числами; при этом результаты получаются в виде числовых значений. Многие
численные методы разработаны давно, однако при вычислениях вручную они могли
использоваться лишь для решения не слишком трудоемких задач.
С появлением ЭВМ начался период бурного развития
численных методов и их внедрения в практику. Только вычислительной машине под
силу выполнить за сравнительно короткое время объем вычислений, в миллионы,
миллиарды и более операций, необходимых для решения многих современных задач.
Алгебраическими уравнениями согласно [2,с.199]
называются уравнения, содержащие только алгебраические функции (целые,
рациональные, иррациональные). В частности, многочлен является целой
алгебраической функцией. Уравнения, содержащие другие функции
(тригонометрические, показательные, логарифмические и др.), называются
трансцендентными.
Рассмотрим систему m линейных алгебраических
уравнений относительно n неизвестных x1 , x2 , ..., xn:
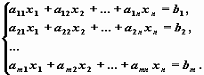 (1.1)
(1.1)
Решением
системы называется совокупность n
значений неизвестных
x1=x'1 , x2 =x'2 , ..., xn=x'n ,
при
подстановке которых все уравнения системы обращаются в тождества.
Система
линейных уравнений может быть записана в матричном виде: (1.2)
где
A - матрица системы, b - правая часть, x
- искомое решение, Ap - расширенная
матрица системы:
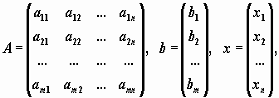
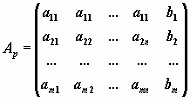 (1.3)
(1.3)
Система,
имеющая хотя бы одно решение, называется совместной; система, не имеющая ни
одного решения - несовместной.
Однородной
системой линейных уравнений называется система, правая часть которой равна
нулю:
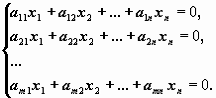 (1.4)
(1.4)
Если
однородная система имеет единственное решение, то это единственное решение -
нулевое, и система называется тривиально совместной. Если же однородная система
имеет более одного решения, то среди них есть и ненулевые и в этом случае
система называется нетривиально совместной. Применив к матрице системы алгоритм
гауссова исключения
<#"722233.files/image005.gif">.(1.5)
Число r ненулевых строк в ступенчатой форме матрицы
называется рангом матрицы, обозначаем r=rg(A)
Доказано, что среди бесконечного множества решений однородной системы
можно выделить ровно n-r линейно независимых решений.
Совокупность n-r линейно независимых решений однородной системы
называется фундаментальной системой решений. Любое решение системы линейно
выражается через фундаментальную систему. Таким образом, если ранг r матрицы A
однородной линейной системы Ax=0 меньше числа неизвестных n и векторы e1 , e2 ,
..., en-r образуют ее фундаментальную систему решений (Aei =0, i=1,2, ...,
n-r), то любое решение x системы Ax=0 можно записать в виде
x=c1 e1 + c2 e2 + ... + cn-r en-r , (1.6)
где c1 , c2 , ..., cn-r - произвольные постоянные.
Записанное выражение называется общим решением однородной системы.
В инженерной деятельности часто возникает необходимость описать в виде
функциональной зависимости связь между величинами, заданными таблично или в
виде набора точек с координатами (xi,yi), i=0,1,2,...n, где n - общее
количество точек. Как правило, эти табличные данные получены экспериментально и
имеют погрешности. При аппроксимации желательно получить относительно простую
функциональную зависимость (например, полином), которая позволила бы
"сгладить" экспериментальные погрешности, получить промежуточные и
экстраполяционные значения функций, изначально не содержащиеся в исходной
табличной информации.
модель кинематика алгоритм mathcad
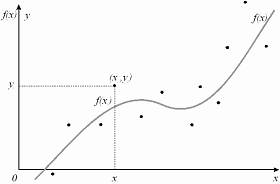
Рисунок 1.1- Графическая интерпретация аппроксимации.
Эта функциональная (аналитическая) зависимость должна с достаточной
точностью соответствовать исходной табличной зависимости. Используют критерий
наименьших квадратов, т.е. определяют такую функциональную зависимость, при
которой S = (fi-yi)2 , обращается в минимум.
Отыскание же значений параметров а0, а1, а2,…, аn, которые доставляют min
значение функции.
Согласно [2,с.219] Решение
выражения  сводится к решению системы уравнений
сводится к решению системы уравнений
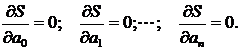 (1.8)
(1.8)
Наиболее
распространен способ выбора функции f(xk; а0, а1, а2,…, аn) в виде линейной
комбинации:
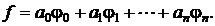 (1.9)
(1.9)
Здесь
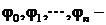 базисные функции (известные); n << k; а0, а1,
а2,…, аn - коэффициенты, определяемые методом наименьших квадратов.
базисные функции (известные); n << k; а0, а1,
а2,…, аn - коэффициенты, определяемые методом наименьших квадратов.
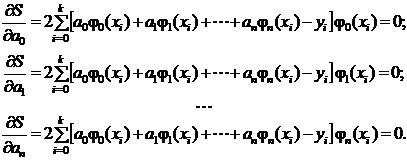 (1.10)
(1.10)
Из
системы линейных уравнений определяются все коэффициенты ak. Система называется
системой нормальных уравнений, матрица которой имеет вид
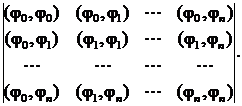 (1.11)
(1.11)
1.3 Характеристика элементов системы
Mathcad
Согласно [3,с.12] Система MathCAD является одной из
самых мощных и эффективных систем математического направления. Она
ориентирована на широкий круг пользователей и позволяет выполнять
математические расчеты, как в численном, так и в символьном аналитическом виде.
Система имеет очень удобный математико-ориентированный интерфейс и обладает
обширными графическими возможностями.
Система MathCAD разработана фирмой MathSoft(CШA) и
является на данный момент единственной математической системой, в которой
описание решения математических задач задается с помощью привычных
математических формул и знаков. В названии системы аббревиатура САД являющаяся
сокращением от Computer Aided Design, указывает на принадлежность системы ж
системам автоматизированного проектирования.
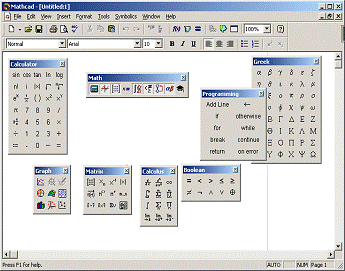

На рисунке 1.2 приведены основные палитры математических символов и
операторов, позволяющие вводить общепринятые математические знаки, операторы
программирования, шаблоны графиков и т.д. в месте расположения курсора.
Для вывода с помощью палитр необходимого объекта нужно поместить курсор
ввода (красный крестик) в желаемое место окна редактирования и затем
активизировать пиктограмму нужного объекта.
Окна с палитрами появляются в окне редактирования документа при активизации
соответствующих пиктограмм. Любую палитру можно переместить в удобное место
экрана, наведя указатель мыши на заголовок окна палитры и перетаскивая палитру
при нажатой левой клавиши мыши. Если палитра больше не нужна, ее можно закрыть
с помощью соответствующей системной кнопки в правом верхнем углу окна палитры.
Согласно [4,с.35] MathCAD дает возможность решать системы уравнений и
неравенств.
Наиболее распространенным методом решения уравнений в Mathcad является
блочный метод. Для решения системы этим методом необходимо выполнить
следующее:) задать начальное приближение для всех неизвестных, входящих в
систему уравнений;
б) задать ключевое слово Given, которое указывает, что далее следует
система уравнений;
в) ввести уравнения и неравенства в любом порядке (использовать кнопку
логического равенства на панели знаков логических операций  для набора знака «=» в уравнении);
для набора знака «=» в уравнении);
г) ввести любое выражение, которое включает функцию Find.
Решающим блоком называется часть документа, расположенная между ключевыми
словами Given и Find.
После набора решающего блока Mathcad возвращает точное решение уравнения
или системы уравнений.
Задача регрессии заключается в получении параметров этой функции такими,
чтобы функция приближала облако исходных точек (заданных векторами VX и VY) с
наименьшей среднеквадратичной погрешностью. Чаще всего используется линейная
регрессия, при которой функция у(х) имеет вид
у(х) =а+ Ь*х
и описывает отрезок прямой. Для проведения линейной регрессии в систему встроен
ряд приведенных ниже функций:(VX, VY) - возвращает скаляр - коэффициент
корреляции Пирсона;(VX, VY) - возвращает значение параметра а (смещение линии
регрессии по вертикали);(VX, VY) - возвращает значение параметра b (наклона
линии регрессии).
Прямая регрессии проходит в «облаке» исходных точек с максимальным
среднеквадратичным приближением к ним. Чем ближе коэффициент корреляции к 1,
тем точнее представленная исходными точками зависимость приближается к линейной
В MathCAD реализована возможность выполнения линейной регрессии общего
вида При ней заданная совокупность точек приближается функцией вида
(x, К1 ,К2, ., Kn)= K1, F1(x)+K2 F2(x)+ +КnFn(x)
Таким образом, функция регрессии является линейной комбинацией функций
F1(x), F2(x), ., Fn(x), причем сами эти функции могут быть нелинейными, что
резко расширяет возможности такой аппроксимации и распространяет ее на
нелинейные функции
Для реализации линейной регрессии общего вида используется функция
linfit(VX,VY,F)
Эта функция возвращает вектор коэффициентов линейной регрессии общего
вида К, при котором среднеквадратичная погрешность приближения облака исходных
точек, если их координаты хранятся в векторах VX и VY, оказывается минимальной
Вектор F должен содержать функции F1(x), F2(x), Fn(x), записанные в символьном
виде.
Введена в MathCAD и функция для обеспечения полиномиальной регрессии при
произвольной степени полинома регрессии regress(VX,VY, n)
2.
Алгоритмический анализ задачи
2.1 Полная постановка задачи
1. С использованием системы MathCAD создать таблично заданную функцию по ее графику.
2. Подобрать аппроксимирующую аналитическую функцию указанного в
задании вида к имеющейся табличной функции, получить функцию закона движения
материальной точки. Построить график исходной табличной и результирующей
аналитической функций.
3. Рассчитать значения проекций скоростей материальной точки на оси X и Y при заданном значении x=x1.
4. Рассчитать значения проекций ускорения материальной точки на оси X и Y при заданном значении x=x1.
5. Вычислить модуль ускорения и радиус кривизны траектории движения
материальной точки.
6. Провести расчеты п.п.3 -5 для значений x, указанных в задании.
. Построить графики проекций скорости, проекций ускорения, модуля
ускорения и радиус кривизны траектории движения материальной точки в
зависимости от значений x.
2.2 Описание математической модели
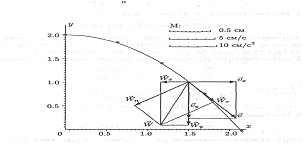
Рисунок 2.1 -График движения материальной точки
Точка движется по плоской кривой Y=Y(X) с постоянной скоростью v. Для нахождения проекций скорости движения
точки на оси X и Y (vx, vy) нужно при заданном значении х
решить систему уравнений вида:
 , (2.1)
, (2.1)
где
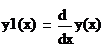 - первая производная по координате х, y(x) -
заданный закон движения точки.
- первая производная по координате х, y(x) -
заданный закон движения точки.
Для
нахождения проекций ускорения на оси X и Y (Wx, Wy)
нужно при заданном значении х решить систему уравнений вида:
 (2.2)
(2.2)
где
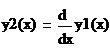 - первая производная от функции скорости y1(x) по
координате х.
- первая производная от функции скорости y1(x) по
координате х.
Модуль
ускорения вычисляется по формуле:
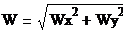 (2.3)
(2.3)
Радиус
кривизны траектории движения точки вычисляется по формуле:
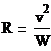 (2.4)
(2.4)
2.3 Анализ исходных и результирующих
данных
Исходными данными для работы являются:
v -
постоянная скорость движения точки;
вид функции закона движения точки, заданный графически;
x1..x7 - значения координаты х, при
которых нужно выполнить расчеты.
v=5,1
м/с - постоянная скорость движения точки;
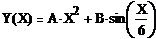 -вид
функции закона движения точки, заданный графически;
-вид
функции закона движения точки, заданный графически;
x1=0,25 х2=0,65
х3=0,98 х4=1,24 х5=1,53 х6=1,88 x7=2 - значения координаты х, при которых нужно
выполнить расчеты.
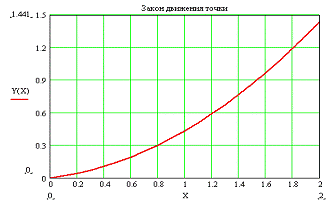
Рисунок 2.2- Закон движения материальной точки
В качестве численного метода выбираем
блочный метод для решения систем линейных уравнений при помощи стандартных
функций пакета Mathcad
В результате выполнения курсовой работы мы должны
получить:,vy - значения скоростей в 7 конкретных моментах времени, wy,W -
значения ускорений в 7 конкретных моментах времени- значения радиуса кривизны
Все эти данные должны быть представлены в виде векторов и построены
графические зависимости данных векторов от времени.
2.4 Графическая схема алгоритма и ее
описание
Графическая схема алгоритма, изображенного на рисунке 2.3 имеет вначале
линейный тип зависимости: ввод исходных данных, определение аналитической зависимости
заданного графика, аппроксимация функции и нахождение значения коэффициентов,
построение графиков исходной и результирующей функции, расчет 1 и 2 производной
от полученного закона распределения, а затем циклический тип зависимости -
решение системы линейных уравнений и вычисление модуля ускорения для 7 опытов.
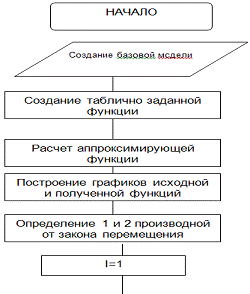
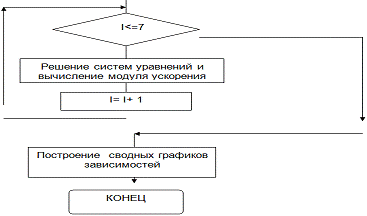
Рисунок 2.3 - Графическая схема алгоритма
3.
Описание реализации задачи в MathCAD
.1 Описание реализации базовой модели
и описание исследований MathCAD
Запускаем математический пакет Mathcad. Задаем исходные данные согласно поставленной задачи при
помощи оператора присваивания. Приводим все единицы измерения к системе СИ.
Введем значение скорости и присвоим системной
переменной ORIGIN:=1

Векторы и матрицы можно задавать различными способами: с помощью кнопки с
изображением матриц на наборной панели математических инструментов; как
переменную с индексами перечислением элементов массива с разделение запятой; с
помощью аналитического выражения.
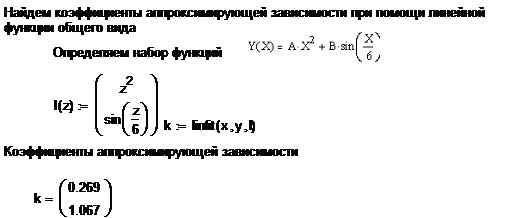
Построим графики исходной и результирующей аналитической функции
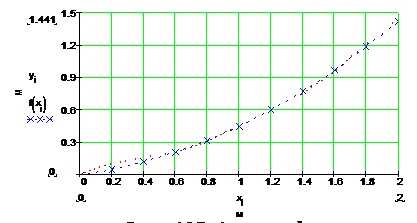
Рис. 3.1 - Графики функций в MathCAD
Проведем исследования для заданных значений х
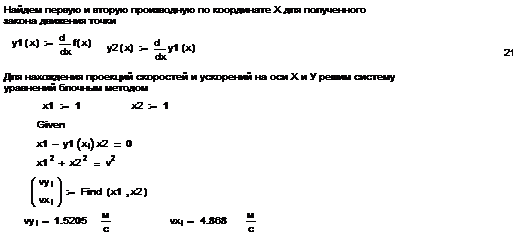
Произведем расчеты проекций скорости, проекций ускорения, модуля
ускорения и радиуса кривизны траектории движения материальной точки для 7
значений x, указанных в задании, используя ранжированную
переменную i:=1.. 7
3.2 Выводы по результатам
исследований в MathCAD
В результате исследований мы получили вектора значений проекций скорости,
проекций ускорения, модуля ускорения и радиуса кривизны траектории движения
материальной точки

Построили графики проекций скорости, проекций ускорения, модуля ускорения
и радиус кривизны траектории движения материальной точки в зависимости от
значений x (Приложение Б, рисунки Б.1 - Б.3)
После построения графиков можно сделать следующие выводы:
. При увеличении значения координат х от 0,13 до 1 проекции скорости по
оси Х - уменьшаются, а по оси У - увеличиваются, модуль скорости остается
постоянным =5,1 м/с.
. При увеличении значения координат х проекции ускорения по оси Х и по
оси У уменьшаются, модуль ускорения также уменьшается с 12,153 до 3,377 м/с2
. При увеличении значения координат х радиус кривизны траектории движения
материальной точки увеличивается по параболическому закону и является величиной
обратно пропорциональной модулю ускорения.
Заключение
В результате выполнения данной курсовой работы мы с использованием
системы MathCAD создали таблично заданную функцию по ее графику и подобрали
аппроксимирующую аналитическую функцию указанного в задании вида к имеющейся
табличной функции при помощи метода наименьших квадратов, вычислили
коэффициенты регрессии А=0,269, В=1,067 и получили функцию закона движения
материальной точки (Приложение А рисунок А.2)
Затем рассчитали значения проекций скоростей, ускорения, модуль ускорения
и радиус кривизны траектории движения материальной точки при заданном значении
x=0,25 и повторили расчеты для всех значений x, указанных в задании. Расчет
проекций произвели при помощи блочного метода решения систем уравнений используя специальный вычислительный блок, открываемый
служебным словом Given , завершаемый функцией find.
Построили графики проекций скорости, проекций ускорения, модуля ускорения
и радиус кривизны траектории движения материальной точки в зависимости от
значений x по результатам расчетов.
После построения графиков сделали соответствующие выводы.
В процессе выполнения и оформления работы были использованы такие пакеты
как MathCAD, Microsoft Word. При решении данной работы были получены
соответствующие навыки в использовании этих пакетов.
Построенная модель может бить использована для исследования процессов
кинематики движения материальной точки.
Список
использованных источников
1 Тарасик В.П. Математическое моделирование технических систем:
Учебник для вузов 2-е изд., испр. и доп./В.П. Тарасик - Мн.: Дизайн-ПРО,2004-604с.
2 Турчак
Л.И. Основы численных методов: Учебное пособие для студентов высших учебных
заведений / Л.И. Турчак, П.В. Плотников.- 2-е изд., перераб. и доп.- М.:
Физматлит, 2003.- 304 с.
3 Дьяконов
В.П. Справочник по MathCAD PLUS 7.0 PRO: Универсальная система математических
расчетов. - М.: СК Пресс, 1998.-320с
4 Трохова
Т.А. Практическое пособие к выполнению контрольных работ по теме «Решение задач
в среде MathCad» по курсу "Информатика"
для студентов технических специальностей заочного отделения / Т.А. Трохова,
Т.Л. Романькова, И.В. Стрижак. - Гомель: ГГТУ им.П.О.Сухого, 2005-48с
5 Трохова Т.А. Практическое руководство к курсовому
проектированию по одноименному курсу для студентов технических специальностей
дневной и заочной форм обучения/ Т.А. Трохова, Н.В. Самовендюк, Т.Л. Романькова
- Гомель: ГГТУ им. П.О. Сухого, 2005-34с.
6 Токочаков В.И. Решение систем алгебраических
уравнений в среде MathCAD Windows. - Гомель, ГГТУ, 2000.-28с