Задача упаковки в контейнеры

Задача упаковки в контейнеры

МИНОБРНАУКИ РОССИИ

Федеральное государственное автономное образовательное учреждение

высшего профессионального образования

«ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

ИНЖЕНЕРНАЯ ТЕХНОЛОГИЧЕСКАЯ АКАДЕМИЯ В Г. ТАГАНРОГЕ

(ТРТИ Южного федерального университета)

Факультет АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ

РЕФЕРАТ

по учебной дисциплине

«Теория принятия решений»

на тему

«Задача упаковки в контейнеры»

Выполнила: студентка гр. А-31,

Панченко Е.Л.

Проверил:   Грищенко А. С.

Таганрог, 2014 г.

Введение

В теории сложности вычислений <#"721935.files/image001.gif">

Множества Bj называют контейнерами.

Требуется упаковать предметы в минимальное число контейнеров.

Задача NP-трудна и часто возникает в приложениях.

.1.     Алгоритм «Следующий подходящий» (NF)

В произвольном порядке упаковываем предметы по следующему правилу.

Первый предмет помещаем в первый контейнер.

На k-м шаге пытаемся поместить k-й предмет в текущий контейнер.

Если предмет входит, то помещаем его и переходим к следующему шагу, иначе помещаем предмет в новый контейнер.

Т = О(n), П = О(1), если не считать место для исходных данных.

Теорема(L) ≤ 2OPT(L).

Доказательство. Пусть

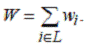
Так как любые два последовательных контейнера содержат предметы суммарным весом не меньше единицы, то NF(L) < 2⎡W⎤.

Кроме того, OPT(L) ≥ ⎡W⎤, откуда и следует требуемое.

Пример.

Замечание. NF(L) ≤ 2OPT(L) - 1 для всех L.

Пусть алгоритм A для множества L порождает A(L) контейнеров и

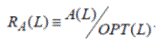
Для задачи на минимум гарантированная относительная точность RA для алгоритма A определяется как RA ≡ inf {r ≥ 1 | RA (L) ≤ r для всех L}.

Определение. Асимптотическая гарантированная относительная точность для алгоритма A определяется как

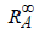≡ inf {r ≥ 1 | ∃ N > 0 такое, что RA (L) ≤ r для всех L с OPT(L) ≥ N}.

1.2.   Алгоритм «Первый подходящий» (FF)

В произвольном порядке упаковываем предметы по следующему правилу.

Первый предмет помещаем в первый контейнер.

На k-м шаге находим контейнер с наименьшим номером, куда помещается k-й предмет, и помещаем его туда. Если такого контейнера нет, то берем новый

 пустой контейнер и помещаем предмет в него. Т = О(n2), П = О(n).

Теорема. для всех L и существуют примеры со сколь угодно большими значениями OPT, для которых

 (Без доказательства).

Пример.

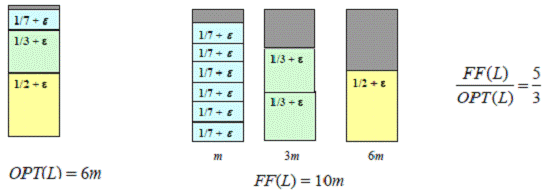
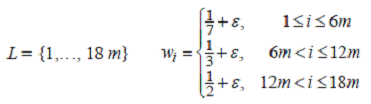
1.3.   Алгоритм «Наилучший подходящий» (BF)

В произвольном порядке упаковываем предметы по следующему правилу.

Первый предмет помещаем в первый контейнер.

На k-м шаге размещаем k-й предмет. Находим частично заполненные контейнеры, где достаточно для него свободного места и выбираем среди них наиболее заполненный. Если таких нет, то берем новый пустой контейнер и помещаем k-й предмет в него. Т = О(n2), П = О(n).

Теорема.

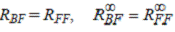
и существуют примеры со сколь угодно большими значениями OPT(L), для которых BF(L) = 4/3 FF(L) и FF(L) = 3/2 BF(L).

.4.     Алгоритмы типа On-line

Предметы поступают в непредсказуемом порядке. Требуется упаковать их в минимальное число контейнеров. Упакованный предмет нельзя перемещать в другой контейнер. Место для предварительного хранения предметов отсутствует.

Алгоритмы NF, FF, BF являются On-line алгоритмами.

Теорема. Для любого On-line алгоритма A справедливо неравенство

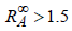 (Без доказательства).

1.5.   Алгоритмы с ограниченным доступом к контейнерам

line алгоритм называют алгоритмом с ограниченным доступом к контейнерам, если на каждом шаге алгоритм имеет возможность помещать предметы только в один из K контейнеров (K - const). Эти контейнеры называются открытыми. Если контейнер закрыли, то он уже не открывается (например, отправляется потребителю). Прежде чем добавить пустой открытый контейнер, нужно закрыть один из K открытых контейнеров.

Алгоритм NF - пример для K = 1.

Правила для выбора контейнера:

. Закрыть контейнер с наименьшим номером

. Закрыть самый заполненный контейнер.

Примеры алгоритмов с ограниченным доступом- алгоритм FF с правилом 1.- алгоритм FF с правилом 2.- алгоритм BF с правилом 1.- алгоритм BF с правилом 2.

.6.     Алгоритм «Первый подходящий с упорядочиванием» (FFD)

• Сортируем предметы по невозрастанию весов w1 ≥ w2 ≥ … ≥ wn

• Применяем алгоритм FF (BF).

Теорема.

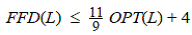
для всех L и существуют примеры со сколь угодно большими значениями OPT(L), для которых

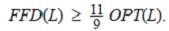
Кроме того

 (Без доказательства).

Пример

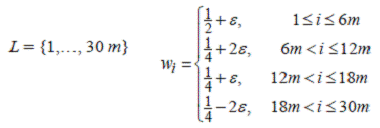
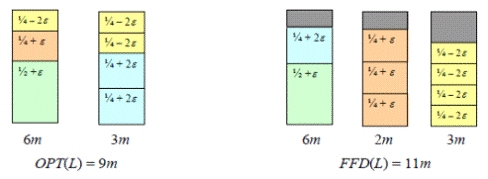
Асимптотические гарантированные оценки точности

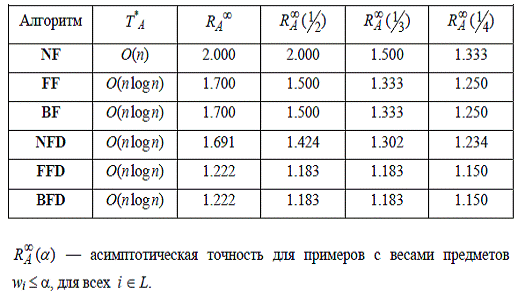
Теорема. Для любого ε ∈ (0,1] существует алгоритм Aε , который находит упаковку с числом контейнеров не более (1 + 2ε) OPT + 1.

Трудоемкость Aε полиномиально зависит от n .

(Без доказательства).

.7.     Алгоритм Aε

. Удалить предметы с весом менее ε.

. Упорядочить оставшиеся предметы и разбить их на K = ⎡1/ε2⎤ групп.

3. В каждой группе увеличить веса предметов до максимального веса в группе.

. Найти оптимальную упаковку предметов, имеющих только K различных весов каждый из которых не менее ε.

. Вернуть исходные веса предметов и применить алгоритм FF для предметов с весом менее ε.

Негативный результат

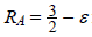
Теорема. Для любого ε > 0 существование приближенного полиномиального алгоритма A с гарантированной точностью влечет P = NP.

Доказательство. Пусть такой алгоритм А существует. Покажем, как с его помощью можно решить точно одну из NP-полных задач, а именно задачу о разбиении. Дано n неотрицательных чисел a1,…, an.

Можно ли разбить их на два подмножества так, чтобы сумма чисел в каждом подмножестве равнялась.

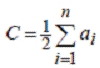
Рассмотрим задачу упаковки в контейнеры с весами предметов wi =ai/C, i = 1,…, n. Если их можно упаковать в два контейнера, ответ в задаче

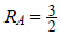
 о разбиении - «ДА». Применим алгоритм А к задаче о контейнерах.

Если OPT = 2, то алгоритм А тоже дает 2, иначе , то есть алгоритм А точный.

.8.     Релаксация линейного программирования

Заменим условие булевости переменных на условия:

≤ yj ≤ 1, j = 1,…, n

≤ xij ≤ 1, i, j = 1,…, n.

Тогда одно из оптимальных решений имеет вид

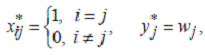
что дает нижнюю оценку

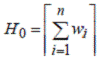
(предметы можно резать произвольным образом).

.9.     Оценки Martello & Toth

Для примера L = {1,…, n}, 0 ≤ wi < 1 и произвольного 0 ≤ α ≤ 1/2 положим

= { i∈L | wi > 1 - α } - крупные предметы= { i∈L | 1- α ≥ wi > 1/2 } - средние предметы= { i∈L | 1/2 ≥ wi ≥ α } - мелкие предметы

Теорема. Для любого 0 ≤ α ≤ 1/2 величина является нижней оценкой для OPT(L).

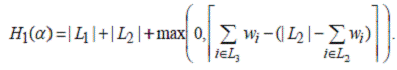
Доказательство. Каждый предмет из множества L1 ∪ L2 требует отдельный контейнер. Поэтому в любом допустимом решении не менее | L1 | + | L2 | контейнеров. Предметы из множества L3 не лежат вместе с предметами из L1.

Значит, они лежат либо вместе с предметами из L2 , либо в отдельных  контейнерах. В контейнерах для L2 осталось свободного места.

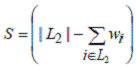
Следовательно, для предметов из множества L3 требуется как минимум отдельных контейнеров.

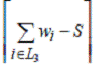
Теорема. Для любого 0 ≤ α ≤ 1/2 величина

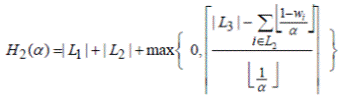
является нижней оценкой для OPT(L).

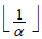
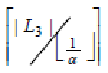
Доказательство. Заменим вес каждого предмета из множества L3 на α.

Тогда в один контейнер войдет предметов, и для множества L3 потребовалось бы дополнительных контейнеров.

Но часть предметов из L3 можно уложить в контейнеры для L2. Каждый из них

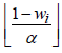
имеет 1- wi, i∈L2 свободного места, где поместится предметов из L3.

Следствие 1. Величина H = max{H1(α ), H2(α ), 0 ≤α ≤ 0,5} является нижней оценкой для OPT(L).

Следствие 2.

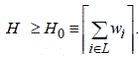
Доказательство. При α = 0 получаем H ≥ H1(0) = max{|L2|, H0}≥ H0.

Как найти H, не перебирая все значения α ?

Следствие 3. Пусть V - множество всех различных значений wi ≤ 0,5.

Тогда

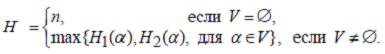
2.      Общий алгоритм решения задачи об упаковке

1.      Предварительное упорядочивание объектов в соответствии с отношением доминирования.

Исследование соотношений по качеству объектов. Путём попарного сравнения объектов определяется асимметричное транзитивное отношение доминирования:

P0={(yi,yj)ÎY´Y | "k=1,…,N; yik£ yjk и $p: yip< yjp }

.        Выделение паретовых слоёв.

В соответствии с отношением P0 на множестве объектов можно выделить подмножество недоминируемых объектов. После их удаления можно выделить второе подмножество и т.д. до исчерпания множества. Выделенные слоя являются паретовыми слоями.

.        Предварительная упаковка объектов.

Она заключается в применении алгоритма АОЧ по слоям.

Пусть упаковка объектов (i-1) первых слоёв возможна, но объекты i-го слоя уже не входят. Рассмотрим частный случай, когда каждый объект (i-1)-го слоя превосходит каждый объект i-го слоя и каждый объект i-го слоя в свою очередь превосходит каждый объект (i+1)-го слоя, причём объекты, принадлежащие одному слою, эквиваленты по качеству. В этом случае можно сразу переходить к шагу 6, т.к. имеется вся необходимая информация для упаковки объектов в месте их предполагаемого "разреза" на группы упакованных и неупакованных объектов.

В общем случае такая информация отсутствует. Для уменьшения неопределённости требуются шаги 4,5.

.        Определение информации, требующейся для предварительного упорядочивания объектов.

Производится сравнение объектов (i-1), i и (i+1) слоёв, т.е. тех слоёв, где вероятно произойдёт разделение объектов при упаковке. Определяется объём информации, необходимый для упорядочения этих объектов по качеству.

Если объекты этих слоёв находятся в отношении доминирования или "почти" доминирования (т.е. доминирования по всем критериям, кроме одного), то информация для упорядочения этих объектов может быть получена от ЛПР путём прямого опроса. ЛПР предъявляют объекты (попарно) и выясняют, какой из них для ЛПР является более ценным. При возникновении противоречий (A>B>C>A) необходимо указывать на эти противоречия ЛПР для их разрешения.

В общем случае объекты отличаются оценками по нескольким критериям и при этом являются достаточно представительными элементами множества Y. Для их упорядочения требуется дополнительная информация о предпочтениях ЛПР.

Например, если все объекты можно расположить в соответствии с оценками так, как это приведено на рис. 3.1,а ,то объекты 2 и 5, 4 и 6, 4 и 7 оказываются несравнимыми. Для их упорядочения нужна дополнительная информация от ЛПР (рис. 3.1,б).

Методы прямого опроса в данной ситуации используются редко, т.к. это достаточно сложная для ЛПР операция выбора. Выявление предпочтений ЛПР осуществляется с помощью построения решающего правила ЛПР (мы рассмотрим это позже).

Рис. 3.1. Пример построения квазипорядка для объектов

5.      Построение квазипорядка на множестве объектов.

На основе сформированного на шаге 4 бинарного отношения можно построить квазипорядок (рис. 3.1,в) и выделить паретовые слои. При этом считается, что объект, принадлежащий высшему слою, "потенциально" лучше объекта из низшего слоя.

.        Нахождение различных вариантов упаковки.

К построенному квазипорядку итеративно применяется алгоритм АОЧ. Среди объектов, упакованных на первом этапе, выделяется подмножество объектов, превосходящих каждый из остальных упакованных, если таковые имеются. Это подмножество подлежит обязательной упаковке. Далее к списку применяется алгоритм АОЧ, но объекты из вышеуказанного подмножества не отбрасываются. Т.о., алгоритм применяется, начиная с i-го слоя объектов.

Будем применять алгоритм АОЧ до исчерпания списка. Получим варианты с различными значениями критериев, например, для случая двух критериев (рис. 3.2)

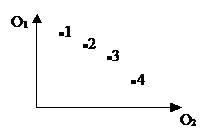
Рис. 3.2. Примеры оценок вариантов решений по двум критериям

7.      Определение компромисса между критериями (3) и (4).

ЛПР может выбрать один из полученных вариантов или указать соотношение значений критериев, по которому будет произведён этот выбор, например:

K = max (0.9O1 + 0.3O2)

Метод решения задачи об упаковке может быть распространён на случаи, когда:

1)      часть объектов может быть упакована только в определённые контейнеры;

2)      несколько объектов имеют общие части и должны быть упакованы вместе.

Вывод

Существует множество разновидностей этой задачи (двумерная упаковка <http://ru.wikipedia.org/w/index.php?title=%D0%94%D0%B2%D1%83%D0%BC%D0%B5%D1%80%D0%BD%D0%B0%D1%8F_%D1%83%D0%BF%D0%B0%D0%BA%D0%BE%D0%B2%D0%BA%D0%B0&action=edit&redlink=1>, линейная упаковка <http://ru.wikipedia.org/w/index.php?title=%D0%9B%D0%B8%D0%BD%D0%B5%D0%B9%D0%BD%D0%B0%D1%8F_%D1%83%D0%BF%D0%B0%D0%BA%D0%BE%D0%B2%D0%BA%D0%B0&action=edit&redlink=1>, упаковка по весу <http://ru.wikipedia.org/w/index.php?title=%D0%A3%D0%BF%D0%B0%D0%BA%D0%BE%D0%B2%D0%BA%D0%B0_%D0%BF%D0%BE_%D0%B2%D0%B5%D1%81%D1%83&action=edit&redlink=1>, упаковка по стоимости <http://ru.wikipedia.org/w/index.php?title=%D0%A3%D0%BF%D0%B0%D0%BA%D0%BE%D0%B2%D0%BA%D0%B0_%D0%BF%D0%BE_%D1%81%D1%82%D0%BE%D0%B8%D0%BC%D0%BE%D1%81%D1%82%D0%B8&action=edit&redlink=1> и т. п.), которые могут применяться в разных областях, как собственно в вопросе оптимального заполнения контейнеров, загрузки грузовиков с ограничением по весу, созданием резервных копий на съёмных носителях и т. д. Так как задача является NP-трудной <http://ru.wikipedia.org/wiki/NP-%D1%82%D1%80%D1%83%D0%B4%D0%BD%D0%BE%D1%81%D1%82%D1%8C>, то использование точного переборного алгоритма возможно только при небольших размерностях. Обычно для решения задачи используют эвристические <http://ru.wikipedia.org/wiki/%D0%AD%D0%B2%D1%80%D0%B8%D1%81%D1%82%D0%B8%D0%BA%D0%B0> приближённые полиномиальные алгоритмы.

алгоритм линейный упаковка контейнер

Список литературы

1. Э.Х. Гимади. О некоторых математических моделях и методах планирования крупномасштабных проектов //Модели и методы оптимизации.

. Труды Института математики. Новосибирск. Наука. Сиб. Отделение. 2011. с. 89-115.

. М. Гэри, Д. Джонсон. Вычислительные машины и труднорешаемые задачи. М.: Мир, 2009. с. 154-191.