Использование симплексного метода для решения задач линейного программирования. Способы решения транспортной задачи
Министерство
образования и науки Российской Федерации
Федеральное
государственное бюджетное образовательное учреждение
высшего
профессионального образования
Псковский
государственный университет
Кафедра
экономики и управления на предприятии
Контрольная
работа
Дисциплина:
Методы принятия управленческих решений
Псков
Содержание
Задание 1
Задание 2
Задание 3
Задание 4
Задание 5
Список литературы
Задание 1
Для производства трех видов продукции (А, В и С)
предприятие использует два вида сырья, удельный расход которого представлен в
таблице 1.
Таблица 1
Расход сырья и прибыль от реализации 1 т
продукции
|
Сырье
|
Расход
сырья на 1 т продукции, т
|
Запас
сырья, т/сут.
|
|
А
|
В
|
С
|
|
|
1
|
18
|
38
|
32
|
12800
|
|
2
|
32
|
18
|
28
|
15200
|
|
Прибыль
от реализации 1 т, тыс. д. е.
|
28
|
32
|
18
|
|
Составить математическую модель задачи. С
использованием симплексного метода решения задач линейного программирования
рассчитать такой суточный объем производства каждого вида продукции, при
котором прибыль от его реализации будет максимальной.
Решение
. Экономико-математическая модель задачи
имеет следующий вид:
Переменные:
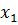 - объем
производства товаров группы А, т
- объем
производства товаров группы А, т
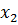 - объем
производства товаров группы В, т
- объем
производства товаров группы В, т
 - объем
производства товаров группы С, т
- объем
производства товаров группы С, т
Целевая функция:
Максимум прибыли от реализации товаров, тыс. д.
е.
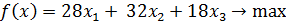
Ограничения:
1) По использованию сырья 1 на 1 т
продукции, т
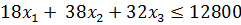
) По использованию сырья 2 на 1 т продукции, т
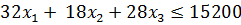
) Условие неотрицательности переменных 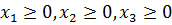
2. Составим первый опорный план (см.
таблицу 2)
Перейдем от системы неравенств к системе
уравнений путем введения базисных переменных 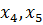 .
.
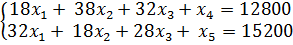
Решим систему уравнений относительно базисных
переменных:
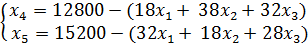
Функцию цели запишем в виде уравнения
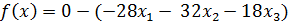
Полагая, что основные переменные 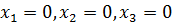 ,
получим первый опорный план, который заносим в симплексную таблицу 2.
,
получим первый опорный план, который заносим в симплексную таблицу 2.
Таблица 2
Первый план симплексной таблицы
|
План
|
Базисные
переменные
|
Свободные
члены
|
Основные
переменные
|
Дополнительные
переменные
|
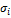
|
|
|
|
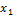
|
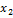
|
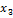
|
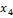
|
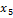
|
|
|
I
|
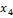
|
12800
|
18
|
38
|
32
|
1
|
0
|
336,84
|
|
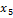
|
15200
|
32
|
18
|
28
|
0
|
1
|
844,44
|
|
Индексная
строка
|
f(x)
|
0
|
-28
|
-32
|
-18
|
0
|
0
|
|
Первый опорный план, представленный в первой
симплексной таблице неоптимальный, т.к. в индексной строке находятся
отрицательные коэффициенты: -28; -32; -18.
Определим ведущие столбец и строку
Из отрицательных коэффициентов индексной строки
выбираем наибольший по абсолютной величине, что и определяет ведущий столбец,
который показывает, какая переменная на следующей итерации перейдет из свободных
в базисные.
За ведущий столбец выберем столбец,
соответствующий переменной 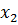 , т.к. сравнивания
по модулю
, т.к. сравнивания
по модулю 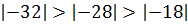 .
.
Строка симплексной таблицы, соответствующая
минимальному значению 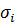 , является ведущей.
Она определяет переменную
, является ведущей.
Она определяет переменную 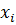 , которая на
следующей итерации выйдет из базиса и станет свободной.
, которая на
следующей итерации выйдет из базиса и станет свободной.
Вычислим значения 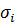
 по строкам, для
этого элементы столбца свободных членов симплексной таблицы делим на
положительные элементы ведущего столбца.
по строкам, для
этого элементы столбца свободных членов симплексной таблицы делим на
положительные элементы ведущего столбца.
/38 = 336,84 (min); 15200/18 = 844,44 ⇒
строка 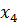 является
ведущей.
является
ведущей.
Разрешающий элемент находится на пересечении
ведущего столбца и ведущей строки и равен 38.
. Построим второй план (см. таблицу 3)
Переход к новому плану осуществляется в
результате пересчета симплексной таблицы методом Жордана-Гаусса. Сначала
заменим переменные в базисе, т.е. вместо 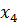 в
базис войдет переменная
в
базис войдет переменная 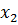 , соответствующая
ведущему столбцу.
, соответствующая
ведущему столбцу.
Разделим все элементы ведущей строки предыдущей
симплексной таблицы на разрешающий элемент и результаты деления занесем в
начальную строку следующей симплексной таблицы, т.е. для строки 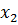 :
:
/38 = 336,84; 18/38 = 0,47; 38/38 = 1; 32/38 =
0,84; 1/38 = 0,03; 0/38 = 0.
Все остальные коэффициенты других строк
определяются по формуле: новый элемент = соответствует коэффициент предыдущего
плана - (коэффициент ведущего столбца предыдущей таблицы ×
коэффициент начальной строки нового плана).
Для строки 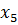 :
:
- 18·336,84 = 9136,88
- 18·0,47 = 23,54
- 18·1 = 0
- 18·0,84 = 12,88
- 18·0,03 = -0,54
- 18·0 = 1
Для строки 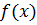 :
:
- (-32)·336,84 = 10778,88
- (-32)·0,47 = -12,96
- (-32)·1 = 0
- (-32)·0,84 = 8,88
- (-32)·0,03 = 0,96
- (-32)·0 = 0
За ведущий столбец выберем столбец,
соответствующий переменной 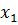 (отрицательное
значение в индексной строке только одно и равно - 12,96).
(отрицательное
значение в индексной строке только одно и равно - 12,96).
Вычислим значения 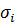 по
строкам
по
строкам
,84/0,47 = 716,68; 9136,88/23,54 = 388,14 (min) ⇒
строка 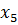 является
ведущей.
является
ведущей.
Разрешающий элемент находится на пересечении
ведущего столбца и ведущей строки и равен 23,54.
Таблица 3
Второй план симплексной таблицы
|
План
|
Базисные
переменные
|
Свободные
члены
|
Основные
переменные
|
Дополнительные
переменные
|
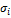
|
|
|
|
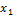
|
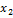
|
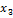
|
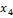
|
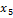
|
|
|
II
|
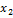
|
336,84
|
0,47
|
1
|
0,84
|
0,03
|
0
|
716,68
|
|
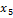
|
9136,88
|
23,54
|
0
|
12,88
|
-0,54
|
1
|
388,14
|
|
Индексная
строка
|
f(x)
|
10778,88
|
-12,96
|
0
|
8,88
|
0,96
|
0
|
|
Анализ второго плана:
План не оптимальный, т.к. в индексной строке
имеется отрицательный коэффициент (-12,96). Максимальную прибыль в размере 10
778,88 тыс. д.е. предприятие получит от продажи товаров второй группы В в
объеме 336,84 т (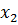 ). Среди базисных
переменных находится дополнительная переменная
). Среди базисных
переменных находится дополнительная переменная 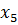 .
Это указывает на то, что ресурсы второго вида недоиспользованы на 9136,88т.
.
Это указывает на то, что ресурсы второго вида недоиспользованы на 9136,88т.
4. Построим третий план (см.
таблицу 4)
Заменим переменные в базисе, вместо 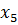 в
базис войдет переменная
в
базис войдет переменная 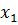 , соответствующая
ведущему столбцу.
, соответствующая
ведущему столбцу.
Разделим все элементы ведущей строки предыдущей
симплексной таблицы на разрешающий элемент и результаты деления занесем в
начальную строку следующей симплексной таблицы, т.е. для строки 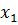 :
:
,88/23,54 = 388,14; 23,54/23,54 = 1; 0/23,54 =
0; 12,88/23,54 = 0,55;
-0,54/23,54 = -0,02; 1/23,54 = 0,04.
Определим коэффициенты других строк.
Для строки 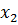 :
:
,84 - 0,47·388,14 = 154,41
,47- 0,47·1 = 0
- 0,47·0 = 1
,84 - 0,47·0,55 = 0,58
,03 - 0,47·(-0,02) = 0,04
- 0,47·(0,04) = -0,02
Для строки 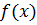 :
:
,88 - (-12,96)·388,14 = 15809,17
,96- (-12,96)·1 = 0
- (-12,96)·0 = 0
,88- (-12,96)·0,55 = 16,01
,96- (-12,96)·( -0,02) = 0,7
- (-12,96)·0,04 = 0,52
Таблица 4
Третий план симплексной таблицы
|
План
|
Базисные
переменные
|
Свободные
члены
|
Основные
переменные
|
Дополнительные
переменные
|
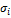
|
|
|
|
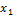
|
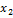
|
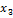
|
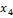
|
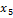
|
|
|
III
|
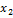
|
154,41
|
0
|
1
|
0,58
|
0,04
|
-0,02
|
|
|
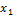
|
388,14
|
1
|
0
|
0,55
|
-0,02
|
0,04
|
|
|
Индексная
строка
|
f(x)
|
15809,17
|
0
|
0
|
16,01
|
0,7
|
0,52
|
|
Анализ третьего плана:
Необходимо производить товары первой группы А в объеме
388,14 т и второй группы В - 154,41 т. При этом предприятие получает
максимальную прибыль в размере 15 809,17 тыс. д.е. Товары группы С не
производятся.
В оптимальном плане среди базисных переменных
дополнительные переменные отсутствуют. Это указывает на то, что ресурсы
используются полностью.
Ответ:
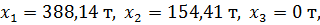
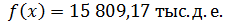
Задание 2
Груз должен быть полностью перевезен из трех
складов четырем фирмам-потребителям. В транспортной матрице (таблица 5) указаны
запасы груза на складах (в тоннах), потребности фирм (в тоннах) и стоимость
перевозки 1 тонны груза от каждого склада соответствующей фирме (руб.).
Таблица 5
Исходные параметры транспортной задачи
|
Склады
|
Фирмы-потребители
|
Запасы,
т
|
|
1
|
2
|
3
|
4
|
|
|
1
|
43
|
62
|
42
|
33
|
42
|
|
2
|
18
|
82
|
48
|
52
|
28
|
|
3
|
72
|
47
|
38
|
28
|
30
|
|
Потребности,
т
|
32
|
18
|
27
|
23
|
|
Определить опорный план перевозок с помощью
метода северо-западного угла или минимального элемента. Рассчитать оптимальный
план перевозок, имеющий минимальную стоимость с использованием метода
потенциалов.
Решение
1. Экономико-математическая модель
задачи имеет следующий вид:
Переменные:
х11 - объем груза, перевозимого c
I склада в фирму №
1, т;
х12 - объем груза, перевозимого c
I склада в фирму №
2, т;
х13 - объем груза, перевозимого c
I склада в фирму №
3, т;
х14 - объем груза, перевозимого c
I склада в фирму №
4, т;
х21 - объем груза, перевозимого cо
II склада в фирму №
1, т;
х22 - объем груза, перевозимого cо
II склада в фирму №
2, т;
х23 - объем груза, перевозимого cо
II склада в фирму №
3, т;
х24 - объем груза, перевозимого cо
II склада в фирму №
4, т;
х31 - объем груза, перевозимого c
III склада в фирму №
1, т;
х32 - объем груза, перевозимого c
III склада в фирму №
2, т;
х33 - объем груза, перевозимого c
III склада в фирму №
3, т;
х34 - объем груза, перевозимого c
III склада в фирму №
4, т.
Ограничения:
) по возможности I
склада, т х11 + х12 + х13 + х14 = 42
) по возможности II
склада, т х21 + х22 + х23 + х24 = 28
) по возможности III
склада, т х31 + х32 + х33 + х34 = 30
) по потребности фирмы № 1, т х11 + х21
+ х31 = 32
) по потребности фирмы № 2, т х12 + х22
+ х32 = 18
) по потребности фирмы № 3, т х13 + х23
+ х33 = 27
) по потребности фирмы № 4, т х14 + х24
+ х34 = 23
Целевая функция:
F(x)
= 43х11 + 62х12 + 42х13 + 33х14 + 18х21 + 82х22 + 48х23 +52х24 +72х31+ + 47х32
+ 38х33 + 28х34 → min
. Проверка задачи на
сбалансированность
Рассматриваемая задача является
сбалансированной, то есть сумма запасов продукции во всех пунктах отправления
равняется суммарной потребности во всех пунктах потребления (100 т = 100 т).
Поэтому не требуется вводить фиктивного поставщика или фиктивного потребителя.
3. Построение первоначального
опорного плана транспортной задачи
Для получения первоначального исходного плана
перевозок в нашей задаче используем метод минимального элемента (см. таблицу
6). При этом количество занятых клеток должно составить:
m + n
- 1 = 3 + 4 - 1 = 6,
где m
- количество поставщиков;
n - количество
потребителей.
х11 = 4 т
х21 = 28 т
х12 = 18 т
х33 = 7 т
х13 = 20 т
х34 = 23 т
F (x)
= 43·4 + 62·18 + 42·20 + 18·28+ 38·7+ 28·23 = 3542 руб.
Таблица 6
План задачи после первой итерации
|
Склады
|
Фирмы-потребители
|
Запасы,
т
|
|
1
|
2
|
3
|
4
|
|
|
1
|
43
4
|
62
18 -
|
42
+ 20
|
33
|
42
|
|
2
|
18
28
|
82
|
48
|
52
|
28
|
|
3
|
72
|
47
+
|
38
- 7
|
28
23
|
30
|
|
Потребности,
т
|
32
|
18
|
27
|
23
|
|
. Определение оптимального решения
методом потенциалов
1) Исследуем план на оптимальность
Для проверки плана на оптимальность необходимо
определить потенциалы по каждой строке и столбцу по формуле:
Для занятых клеток
Vj + Ui
= Cij,
(1)
где Vj
- потенциал столбца;
Ui - потенциал
строки;
Cij - тариф
(показатель) занятой клетки.
Для занятых клеток (1.1), (1.2), (1.3), (2.1),
(3.3), (3.4):
.1) U1
+ V1 =
43 U1 = 0 V1
= 43
1.2) U1
+ V2 = 62
V2
= 62
.1) U2
+ V1 =
18 U2
= - 25
.3) U3
+ V3 =
38 U3
= - 4
3.4) U3
+ V4 =
28 V4 = 32
Для свободных клеток характеристика определяется
по формуле:
dij= Cij
- (Vj + Ui)
(2)
где dij
- характеристика свободной клетки;
Vj - потенциал
столбца;
Ui - потенциал
строки;
Cij - тариф
свободной клетки.
При решении задачи на min
целевой функции dij
³ 0
Характеристика свободных клеток (1.4), (2.2),
(2.3), (2.4), (3.1), (3.2):
.4) d1.4
= 33 - (U1 +V4)
= 33 - (0 + 32) = 1
2.2) d2.2 = 82 - (U2 +V2) = 82 - (-
25 + 62) = 45
.3) d2.3 = 48 - (U2 +V3) = 48 - (-
25 + 42) = 31
.4) d2.4 = 52 - (U2 +V4) = 52 - (-
25 + 32) = 45
.1) d3.1 = 72 - (U3 +V1) = 72 - (- 4
+ 43) = 33
3.2) d3.2
= 47 - (U3 +V2)
= 47 - (- 4 + 62) = - 11
т.к. d3.2
= - 11, следовательно, план, представленный в таблице 6, не оптимальный.
2) Улучшим план путем сдвига по
циклу за счет клетки с наименьшей отрицательной характеристикой
Объемы в отрицательных вершинах цикла клетки
(3.2) - 7 и 18, наименьший из них - 7. Произведем сдвиг по циклу. Этот
наименьший объем прибавим к объемам в положительных вершинах, и вычтем от
объемов в отрицательных вершинах, т.е. получим новый план (см. таблицу 7).
Таблица 7
План задачи после второй итерации
|
Склады
|
Фирмы-потребители
|
Запасы,
т
|
|
1
|
2
|
3
|
4
|
|
|
1
|
43
4
|
62
11 -
|
42
27
|
33
+
|
42
|
|
2
|
18
28
|
82
|
48
|
52
|
28
|
|
3
|
72
|
47
7 +
|
38
|
28
- 23
|
30
|
|
Потребности,
т
|
32
|
18
|
27
|
23
|
|
3) Исследуем новый план на
оптимальность
Для занятых клеток (1.1), (1.2), (1.3), (2.1),
(3.2), (3.4):
.1) U1
+ V1 =
43 U1 = 0 V1
= 43
.2) U1
+ V2 =
62 V2 = 62
.3) U1
+ V3 =
42 V3 = 42
.1) U2
+ V1 =
18 U2 = - 25
.2) U3
+ V2 =
47 U3 = - 15
.4) U3
+ V4 =
28 V4 = 43
Характеристика свободных клеток (1.4), (2.2),
(2.3), (2.4), (3.1), (3.3):
.4) d1.4
= 33 - (U1 +V4)
= 33 - (0 + 43) = - 10
.2) d2.2
= 82 - (U2 +V2)
= 82 - (- 25 + 62) = 45
.3) d2.3
= 48 - (U2 +V3)
= 48 - (- 25 + 42) = 31
.4) d2.4
= 52 - (U2 +V4)
= 52 - (- 25 + 43) = 34
.1) d3.1
= 72 - (U3 +V1)
= 72 - (- 15 + 43) = 44
.3) d3.3
= 38 - (U3 +V3)
= 38 - (- 15 + 42) = 11
т.к. d1.4
= - 10, следовательно, план, представленный в таблице 6, не оптимальный.
4) Улучшим план путем сдвига по
циклу за счет клетки с наименьшей отрицательной характеристикой
Объемы в отрицательных вершинах цикла клетки
(3.2) - 11 и 23, наименьший из них - 11. Произведем сдвиг по циклу. Получим
новый план (см. таблицу 8).
Таблица 8
План задачи после третьей итерации
|
Склады
|
Фирмы-потребители
|
Запасы,
т
|
|
1
|
2
|
3
|
4
|
|
|
1
|
43
4
|
62
|
42
27
|
33
11
|
42
|
|
2
|
18
28
|
82
|
48
|
52
|
28
|
|
3
|
72
|
47
18
|
38
|
28
12
|
30
|
|
Потребности,
т
|
32
|
18
|
27
|
23
|
|
) Исследуем новый план на
оптимальность
Для занятых клеток (1.1), (1.3), (1.4), (2.1),
(3.4), (3.2):
.1) U1
+ V1 =
43 U1 = 0 V1
= 43
.3) U1
+ V3 =
62 V3 = 42
.4) U1
+ V4 =
42 V4 = 43
.1) U2
+ V1 =
18 U2 = - 25
.4) U3
+ V4 =
47 U3 = - 15
.2) U3
+ V2 =
28 V2 = 62
Характеристика свободных клеток (1.2), (2.2),
(2.3), (2.4), (3.1), (3.3):
.2) d1.2
= 62 - (U1 +V2)
= 62 - (0 + 62) = 0
.2) d2.2
= 82 - (U2 +V2)
= 82 - (- 25 + 62) = 45
.3) d2.3
= 48 - (U2 +V3)
= 48 - (- 25 + 42) = 31
.4) d2.4
= 52 - (U2 +V4)
= 52 - (- 25 + 43) = 34
.1) d3.1
= 72 - (U3 +V1)
= 72 - (- 15 + 43) = 44
.3) d3.3
= 38 - (U3 +V3)
= 38 - (- 15 + 42) = 11
т.к. dij
³ 0, то план, представленный в
таблице 8, оптимальный.
Затраты на перевозку составят:
F (x)
= 43·4 + 42·27 + 43·11 + 18·28+ 47·18+ 28·12 = 3465 руб.
Ответ:
груз будет доставлен с I
склада (42 т) в фирму 1 - 4 т, фирму 3 - 27 т, фирму 4 - 11 т; cо
II склада (28 т) в
фирму 1 - 28 т; с III
склада (30 т) в фирму 2 - 18 т, фирму 4 - 12 т. Затраты на перевозку составят
3465 руб.
Задание 3
Необходимо выбрать оптимальный вариант
специального передвижного оборудования для технического обеспечения процесса
управления производством. На основе информации соответствующих
заводов-изготовителей определены локальные критерии функционирования
оборудования и веса этих критериев (таблица 9).
Таблица 9
Локальные критерии функционирования оборудования
|
Вариант
оборудования
|
Времени
подготовки к работе, час.
|
Стоимость
оборудования, тыс. руб.
|
Объем
памяти, Гбайт
|
Масса,
кг
|
Число
выполняемых функций, ед.
|
|
1
|
0,38
|
520
|
192
|
122
|
27
|
|
2
|
0,72
|
380
|
128
|
142
|
16
|
|
3
|
0,28
|
620
|
232
|
98
|
32
|
|
4
|
0,62
|
580
|
168
|
128
|
13
|
|
Коэффициенты
веса
|
0,1
|
0,2
|
0,1
|
0,2
|
0,4
|
Решение
Для решения данной задачи используем аддитивный
критерий оптимальности (обобщенная функция цели), который определяется по
формуле:
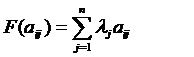 (3)
(3)
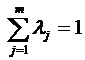 ,
(4)
,
(4)
где aij
-
значение частного (локального) критерия;
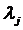 - вес (важность) j-го частного
критерия.
- вес (важность) j-го частного
критерия.
1. Выполним нормализацию критериев
1) Определим max
каждого локального критерия
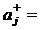 max aij
(5)
max aij
(5)
Выберем максимальные значения по каждому столбцу
а+1 = 0,72; а+2 = 620; а+3 = 232;
а+4 = 142; а+5 = 32
2) В соответствии с критерием max
эффективности пересчитаем значения частных критериев по формулам (4) и (5)
âij =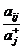 (6)
(6)
âij = 1- 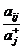 (7)
(7)
Формула (6) используется для
критериев, которые необходимо максимизировать, а формула (7) - для критериев,
которые минимизируют.
Нам необходимо максимизировать
критерии объема памяти и числа выполняемых функций, а минимизировать критерии
времени подготовки к работе, стоимости и массы.
Для критериев «Время подготовки к
работе», «Стоимость оборудования» и «Масса» будем использовать формулу (7):
â 1.1= 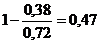 â 1.2 =
â 1.2 = 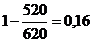 â 1.4 =
â 1.4 = 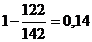
â2.1 =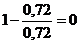 â 2.2 =
â 2.2 = 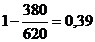 â 2.4 =
â 2.4 = 
â3.1 =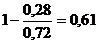 â 3.2 =
â 3.2 = 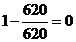 â 3.4 =
â 3.4 = 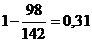
â4.1 =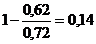 â 4.2 =
â 4.2 = 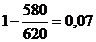 â 4.4 =
â 4.4 = 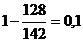
Расчет критериев «Объем памяти» и
«Число выполняемых функций» произведем в соответствии с формулой (6):
â13 =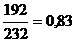 â15 =
â15 =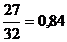
â23 =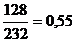 â25 =
â25 =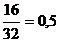
â33 =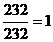 â35
=
â35
=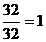
â43 =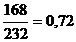 â45
=
â45
=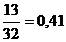
2. Рассчитаем значения аддитивного
критерия оптимальности по формуле (3):
F1
=0,1∙0,47 + 0,2∙0,16 + 0,1∙0,83 + 0,2∙0,14 + 0,4∙0,84
= 0,526
F2
=0,1∙0 + 0,2∙0,39 + 0,1∙0,55 + 0,2∙0+ 0,4∙0,5 =
0,333
F3
=0,1∙0,61 + 0,2∙0 + 0,1∙1 + 0,2∙0,31 + 0,4∙1 =
0,623
F4
=0,1∙0,14 + 0,2∙0,07 + 0,1∙0,72 + 0,2∙0,1 + 0,4∙0,41
= 0,284
Ответ:
необходимо выбрать вариант оборудования №3, так как он соответствует
наибольшему значению аддитивного критерия оптимальности.
Задание 4
Планируется производство легковых автомобилей.
Имеются четыре варианта проекта автомобиля Rj
(j = 1,..,4).
Ожидаемые значения прибыли для различных проектов и состояний спроса на рынке
приведены в таблице 10 (млрд. руб.).
модель оптимальный перевозка
Таблица 10
Ожидаемые значения прибыли для различных
проектов и состояний спроса на рынке
|
Проекты
автомобиля
|
Состояние
спроса на автомобили
|
|
S1
|
S2
|
S3
|
|
R1
|
32
|
37
|
33
|
|
R2
|
31
|
26
|
28
|
|
R3
|
37
|
30
|
30
|
|
R4
|
27
|
32
|
42
|
Определите оптимальную стратегию Rj,
используя критерии Лапласа, Вальда, Сэвиджа и Гурвица (α
= 0,5; α = 0,8). Сделайте выводы.
Решение
1.
Критерий
Лапласа
Критерий Лапласа предполагает все
состояния природы равновероятными, т.е. каждому состоянию Si
ставится
в соответствии вероятность qi,
определяемая по формуле:
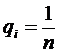 , (8)
, (8)
где n -
количество состояний природы Si .
Критерий Лапласса имеет вид:
 , (9)
, (9)
где W - значение
критерия Лапласа;
Vij - результат
решения (выигрыш или потеря).
При этом для матрицы выигрышей
выбирается действие, дающее наибольший ожидаемый выигрыш.
Для нашей задачи:
W1 = 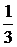 ·
(32+37+33)=34
·
(32+37+33)=34
W2 = 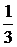 ·
(31+26+28)=28,33
·
(31+26+28)=28,33
W3 = 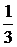 ·
(37+30+30)=32,33
·
(37+30+30)=32,33
W4 = 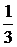 ·
(27+32+42)=33,67
·
(27+32+42)=33,67
Так как дана матрица выигрышей, то выбираем
проект с наибольшим значением прибыли - 34 млрд. руб. Следовательно, наилучшим
проектом автомобиля, согласно критерию Лапласа, является 1-ый.
2.
Критерий
Вальда
Если в исходной матрице каждый элемент Vij
представляет
собой выигрыши, то при выборе оптимальной стратегии используют максиминный
критерий Вальда:
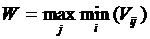 (10)
(10)
Выберем оптимальную стратегию с
помощью критерия Вальда. В нашем случае будет использоваться максиминный
критерий:
min (32; 37;
33) = 32(31; 26; 28) = 26(37; 30; 30) = 30(27; 32; 42) = 27= max (32; 26; 30;
27) =32
В соответствии с критерием Вальда
наилучшим проектом будет 1-ый.
3.
Критерий
Севиджа
Критерий Севиджа используется только для матрицы
рисков, поэтому нашу матрицу выигрышей необходимо пересчитать в матрицу рисков
по формуле (11).
rij
= max
{Vij}
- Vij
,
(11)
где rij
-
элемент матрицы рисков;
Vij
-
элемент матрицы выигрышей.
max (32; 31;
37; 27) = 37
max (37; 26;
30; 32) = 37
max (33; 28;
30; 42) = 42
Рассчитаем матрицу рисков:
|
S1 S2
S3
|
|
R1 R2 R3 R4
|
5
|
0
|
9
|
|
|
6
|
11
|
14
|
|
|
0
|
7
|
12
|
|
|
10
|
5
|
0
|
|
В соответствии с критерием Севиджа к матрице
рисков всегда применяют минимальный критерий.
max (5; 0; 9) = 9(6; 11; 14) =
14(0; 7; 12) = 12(10; 5; 0) = 10
min max (rij) = min (9;
14; 12; 10)=9
Критерий Севиджа указывает, что оптимальным
проектом будет 1-ый, он позволит избежать большого риска.
4.
Критерий
Гурвица
Если исходной является матрица выигрышей, то
значение данного критерия вычисляется по формуле:
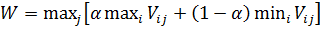 , (12)
, (12)
где α
-
коэффициент доверия.
Применим к условию задачи критерий Гурвица при α
=0,5 и α
=0,8 (см. таблицу 11).
Таблица 11
Выбор оптимальной стратегии по критерию Гурвица
|
Wj
|
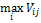
|
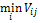
|
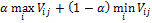
|
maxWj
|
|
|
|
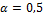
|
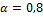
|
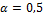
|
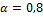
|
|
W1 W2 W3 W4
|
37
31 37 42
|
32
26 30 27
|
34,5
28,5 33,5 34,5
|
36
30
35,6
39
|
34,5
- - 34,5
|
-
- - 39
|
В соответствии с критерием Гурвица при
коэффициенте доверия α=0,5
оптимальными
проектами являются 1-ый и 4-ый, при α=0,8
оптимальным
проектом является 4-ый.
Ответ:
если ситуация полностью не определена (α=0,5),
в соответствии со всеми критериями оптимальным проектом будет 1-ый. Если ЛПР
(лицо, принимающее решение) ожидает в будущем наступление очень благоприятной
ситуации (α=0,8),
то возможен выбор 4-го проекта.
Задание 5
Фирма 1 планирует освоить
производство одного из четырех однородных товаров (А, В, С, D),
которые будет реализовывать на рынке, где возможна продажа конкурентом (фирмой
2) аналогичных товаров. На основе проведенного маркетингового исследования
фирме 1 стали известны доли продаж своих товаров при наличии на рынке
товаров-конкурентов (табл. 12).
Таблица 12
Платежная матрица игры
|
Товар
фирмы 2 Товар
фирмы 1
|
А
|
В
|
С
|
D
|
|
A
|
0,82
|
0,92
|
0,62
|
0,72
|
|
B
|
0,62
|
0,72
|
0,52
|
0,62
|
|
C
|
0,92
|
0,82
|
0,62
|
0,52
|
|
D
|
0,72
|
0,82
|
0,42
|
0,82
|
Определите чистую цену игры,
оптимальные чистые стратегии продвижения товара на рынок фирмами. Укажите долю
рынка каждой фирмы в ситуации равновесия.
Решение
При определении наилучших
стратегий игроков следует учитывать, что противники, участвующие в игре,
одинаково разумны, и каждый из них делает все для того, чтобы добиться своей
цели. Выбирая i-ю
стратегию игрока 1, мы должны рассчитывать, что игрок 2 ответит на нее той из
своих j-х
стратегий, для которой выигрыш игрока 1 будет минимальным. Найдем минимальное
число в каждой строке матрицы и, обозначив его αi,
запишем рядом с платежной матрицей (см. таблицу 13) в добавочный столбец.
Игрок 1, зная свои минимальные выигрыши при
любой стратегии игрока 2, будет предпочитать такую стратегию, при которой
значение αi
является
максимальным, то есть
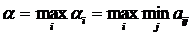 (13)
(13)
Величина α
- это гарантированный выигрыш, который может обеспечить себе игрок 1. Она
называется нижней ценой игры (максимином). Стратегия, обеспечивающая
получение нижней цены игры, называется максиминной стратегией. Если игрок 1
будет придерживаться своей максиминной (перестраховочной) стратегии, то ему
гарантирован выигрыш не меньший величины α
при любом поведении игрока 2.
Игрок 2 заинтересован уменьшить
свой проигрыш или, что то же самое, выигрыш игрока 1 обратить в минимум.
Поэтому для выбора своей наилучшей стратегии он должен найти максимальное
значение выигрыша игрока 1 в каждом из столбцов и среди этих значений выбрать
наименьшее. Максимальный элемент в каждом столбце обозначим через βj.
Эти элементы будем записывать в дополнительной строке таблицы 13.
Наименьшее значение среди βj
обозначим β - это верхняя
цена игры (минимакс), которая определяется по формуле
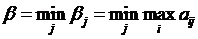 (14)
(14)
Использование игроком 2 своей
минимаксной стратегии позволит ему при любом поведении игрока 1 проиграть не
больше величины β.
Таблица 13
Платежная матрица игры c
добавочным столбцом и добавочной строкой
|
Товар
фирмы 2 Товар
фирмы 1
|
А
|
В
|
С
|
D
|
αi
|
|
A
|
0,82
|
0,92
|
0,72
|
0,62
|
|
B
|
0,62
|
0,72
|
0,52
|
0,62
|
0,52
|
|
C
|
0,92
|
0,82
|
0,62
|
0,52
|
0,52
|
|
D
|
0,72
|
0,82
|
0,42
|
0,82
|
0,42
|
|
βj
|
0,92
|
0,92
|
0,62
|
0,82
|
|
Найдем нижнюю цену игры:
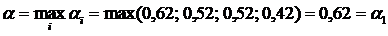 .
.
Определим верхнюю цену игры:
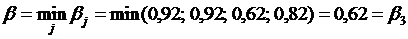 .
.
Игра имеет седловую точку, так как α=β=0,62. Чистая
цена игры γ=0,62.
Оптимальными чистыми стратегиями
являются:
- 1-ая стратегия для рассматриваемой
фирмы 1 (производство и реализация товара А);
3-я стратегия для фирмы 2
(производство и реализация товара С).
При выборе каждым игроком своей оптимальной
чистой стратегии (ситуация равновесия), гарантированная доля продаж будет 0,62.
Ответ:
оптимальными чистыми стратегиями будут являться - реализация товара А для фирмы
1 и продажа товара С для фирмы 2 при гарантированной доли продаж 0,62.
Список литературы
1. Бережная, Елена Викторовна.
Математические методы моделирования экономических систем : учеб. пособие для
вузов / Е.В. Бережная, В.И. Бережной.- М. : Финансы и статистика, 2006 .- 432
с.
. Дятлов Ю.Н. Исследование
операций в экономике. Методические рекомендации для студентов заочной формы
обучения по экономическим специальностям. - Псков, Изд-во ППИ, 2010. - 32 с.
. Феоктистова В.А., Васильева
Н.А. Требования к оформлению студенческих работ. Методические рекомендации. -
Псков: Издательство ППИ, 2007.