Случайные события в элементарной теории вероятностей
МИНИСТЕРСТВО ВЫСШЕГО И СРЕДНЕГО СПЕЦИАЛЬНОГО
ОБРАЗОВАНИЯ РЕСПУБЛИКИ УЗБЕКИСТАН
Ташкентский Архитектурно-Строительный Институт
Факультет: Инженерный Сервис
Кафедра «Математика и естественные науки»
Самостоятельная работа
по предмету «Высшая математика»
на тему: «Случайные события в
элементарной теории вероятностей»
Ташкент
2010г.
Содержание
Случайные события, их классификация
Действия над событиями
Случайные события. Алгебра событий.
(Теоретико-множественная трактовка)
Свойство статистической устойчивости
относительной частоты события
Статистическое определение
вероятности
Классическое определение вероятности
Элементы комбинаторики
Примеры вычисления вероятностей
Геометрическое определение
вероятности
Аксиоматическое определение вероятности
Свойства вероятностей
Конечное вероятностное пространство
Условные вероятности
Вероятность произведения событий.
Независимость событий
Вероятность суммы событий
Формула полной вероятности
Формула Байеса (теорема гипотез)
Независимые испытания. Схема Бернулли
Формула Бернулли
Предельные теоремы в схеме Бернулли
Случайные
события, их классификация
Сначала определим понятие «случайное событие» исходя
из его интуитивного, наглядного понимания. Пусть проводится некоторый опыт
(эксперимент, наблюдение, испытание), исход которого предсказать заранее
нельзя. Такие эксперименты в теории вероятностей называют случайными. При этом
рассматриваются только такие эксперименты, которые можно повторять, хотя бы
теоретически, при неизменном комплексе условий произвольное число раз.
Случайным событием (или просто: событием) называется
любой исход опыта, который может произойти или не произойти.
События обозначаются, как правило, заглавными буквами
латинского алфавита: А, В, С, ... .
Пример 1.1. Опыт: бросание игральной кости; событие А
- выпадение 5 очков, событие В - выпадение четного числа очков, событие С -
выпадение 7 очков, событие D -
выпадение целого числа очков, событие Е - выпадение не менее 3-х очков, ….
Непосредственные исходы опыта называются элементарными
событиями и обозначаются через ω. Элементарные события (их называют
также «элементами», «точками», «случаями») рассматриваются как неразложимые и
взаимоисключающие исходы ω1, ω2, ω3 … этого опыта.
Множество всех элементарных событий называется
пространством элементарных событий или пространством исходов, обозначается
через Ω.
Рассмотрим пример 1.1. Здесь 6 элементарных событий ω1, ω2, ω3 ω4, ω5, ω6. Событие ωi означает, что в результате бросания
кости выпало i очков, i = 1,2,3,4,5,6. Пространство элементарных событий таково: Ω - {ω1, ω2, ω3 ω4, ω5, ω6} или Ω = {1,2,3,4,5,6}.
Событие называется достоверным, если оно обязательно
наступит в результате данного опыта, обозначается через Ω.
Событие называется невозможным если оно заведомо не
произойдет в результате проведения опыта, обозначается через ∅.
В примере 1.1 события A и В - случайные, событие С - невозможное, событие D -- достоверное.
Два события называются несовместными, если появление
одного из них исключает появление другого события в одном и том же опыте, т. е.
не смогут произойти вместе в одном опыте. В противном случае события называются
совместными.
Так, в примере 1.1 события А и В - несовместные, А и Е
- совместные.
События А1, А2, …, Аn называются попарно-несовместными, если любые два из них
несовместны.
Несколько событий образуют полную группу, если они
попарно несовместны и в результате каждого опыта происходит одно и только одно
из них.
В примере 1.1 события ω1 - ω6 образуют полную группу, ω1 - ω5 - нет.
Несколько событий в данном опыте называются
равновозможными, если ни одно из них не является объективно более возможным,
чем другие, т. е. все события имеют равные «шансы».
В примере 1.1 элементарные события ω1, ω2, ω3 ω4, ω5, ω6 равновозможны. Выпадение герба (А)
или решки (В) при бросании монеты равновозможные события, если, конечно, монета
имеет симметричную форму, не погнута, ....
Действия над
событиями
Введем основные операции над событиями; они полностью
соответствуют основным операциям над множествами.
Суммой событий An В называется событие С = А + В, состоящее в наступлении хотя
бы одного из них (т.е. или А, или В, или А и В вместе).
Произведением событий А и В называется событие С = А ∙
В, состоящее в совместном наступлении этих событий (т. е. и А и В
одновременно).
Разностью событий А и В называется событие С = А - В,
происходящее тогда и только тогда, когда происходит событие А, но не происходит
событие В.
Противоположным событию А называется событие Ā, которое происходит тогда и только
тогда, когда не происходит событие А (т. е. Ā означает, что событие А не
наступило).
Событие А влечет событие В (или А является частным
случаем В), если из того, что происходит событие А, следует, что происходит
событие В; записывают А 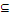 В.
В.
Если А 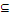 В и В
В и В 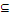 Л, то события А и В называются равными; записывают А = В.
Л, то события А и В называются равными; записывают А = В.
Так, в примере 1.1 (п. 1.2) В = {2,4,6}, Е =
{3,4,5,6}, А = {5}, D = {1,2,3,4,5,6}.
Тогда: В + Е = {2,3,4,5,6}, В ∙ Е = {4,6}, В - Е = {2}, Ā = {1,2,3,4,6}, B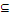 D, D = Ω = {1,2,3,4,5,6}.
D, D = Ω = {1,2,3,4,5,6}.
События и действия над ними можно наглядно
иллюстрировать с помощью диаграмм Эйлера-Венна: достоверное событие Ω изображается прямоугольником;
элементарные случайные события - точками прямоугольника; случайное событие -
областью внутри него. Действия над событиями можно изобразить так, как показано
на рис. 1-5.
Операции над событиями обладают следующими свойствами:
§ A + B = B + A, A ∙ B = B ∙ A (переместительное);
§ (A + B) ∙ C = A ∙
C + B ∙ C, A ∙ B + C = (A + C) ∙ (B + C) (распределительное);
§ ( A + B) + С = A + (B + C), (A ∙ B) ∙
C = A ∙ (B ∙ C) (сочетательное);
§ А + А = А, А ∙ А = А;
§ А + Ω = Ω, А ∙ Ω = А;
§ А + Ā = Ω, А ∙ Ā = ∅;
§ 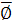 = Ω,
= Ω, 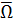 = ∅,
= ∅, 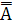 = A;
= A;
§ A - B = A ∙ 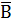 ;
;
§ 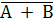 =
= 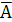 ∙
∙ 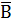 и
и 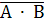 =
= 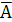 +
+ 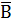 - законы де Моргана
- законы де Моргана
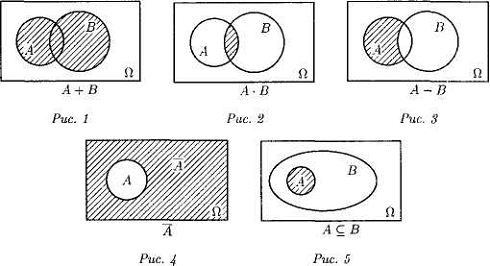
В их справедливости можно убедиться с помощью диаграмм
Эйлера-Венна.
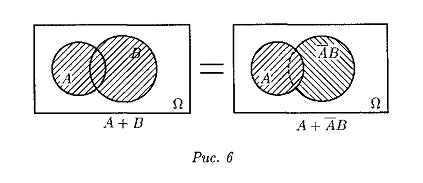
Пример 1.2. Доказать формулу
A + B = A + ĀВ
Используя некоторые из выше приведенных правил,
получаем:
А + В = (А + B)∙Ω = A∙Ω + B∙Ω = A∙Ω + B∙(A+Ā) = A∙Ω + (A+Ā)∙B = A∙Ω + A∙B + Ā∙B = (Ω+B)∙A + Ā∙B = A + Ā∙B.
Таким образом, сумму любых двух событий можно
представить в виде суммы двух несовместных событий.
Геометрическое доказательство представлено на рис. 6.
Случайные
события. Алгебра событий. (Теоретико-множественная трактовка)
Определим теперь основные понятия теории вероятностей,
следуя теоретико-множественному подходу, разработанному академиком Колмогоровым
А. Н. в 1933 году.
Пусть производится некоторый опыт со случайным
исходом.
Множество Ω - {ω} всех возможных взаимоисключающих
исходов данного опыта называется пространством элементарных событий (коротко:
ПЭС), а сами исходы ω - элементарными событиями (или
«элементами», «точками»).
Случайным событием А (или просто событием А)
называется любое подмножество множества Ω, если Ω конечно или счетно (т. е. элементы
этого множества можно пронумеровать с помощью множества натуральных чисел): А 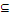 Ω.
Ω.
Элементарные события, входящие в подмножество А
пространства Ω, называются благоприятствующими событию А.
Множество Ω называется достоверным событием. Ему
благоприятствует любое элементарное событие; в результате опыта оно обязательно
произойдет.
Пустое множество ∅ называется невозможным событием; в
результате опыта оно произойти не может.
Пример 1.3. Опыт: один раз бросают игральную кость. В
этом случае ПЭС таково: Ω = {1,2,3, 4,5,6} или Ω = {ω1, ω2, ω3 ω4, ω5, ω6}, где ωi - элементарное событие, состоящее в
выпадении грани с i очками (i = 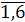 ). В данном случае Ω конечно. Примером события А
является, например, выпадение нечетного числа очков; очевидно, что А = {ω1,ω3,ω5}; событию А благоприятствуют
элементарные события ω1,ω3,ω5. Однако если нас интересует только
факт выпадения четного числа очков, то ПЭС можно построить иначе: Ω = {ω1, ω2}, где ω1 - выпадение четного числа очков, ω2 нечетного.
). В данном случае Ω конечно. Примером события А
является, например, выпадение нечетного числа очков; очевидно, что А = {ω1,ω3,ω5}; событию А благоприятствуют
элементарные события ω1,ω3,ω5. Однако если нас интересует только
факт выпадения четного числа очков, то ПЭС можно построить иначе: Ω = {ω1, ω2}, где ω1 - выпадение четного числа очков, ω2 нечетного.
Пример 1.4. Опыт: стрельба по цели до первого
попадания. Тогда
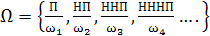
где П означает попадание в цель, Н - непопадание.
Исходов у этого опыта бесконечно (теоретически); Ω счетно.
Пример 1.5. Опыт: наблюдение за временем безотказной
работы некоторого агрегата. В этом случае в качестве результата может появиться
любое число t ≥ 0; время t меняется непрерывно; ПЭС таково: Q = {t, 0 ≤ t ≤ ∞}. Исходов у этого опыта бесконечно, Ω несчетно (континуально).
Над событиями можно проводить все операции, выполнимые
для множеств.
Сумма (или объединение) двух событий А 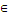 Ω и В
Ω и В 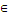 Ω (обозначается А + В или A
Ω (обозначается А + В или A  В) - это множество, которое содержит элементы, принадлежащие
хотя бы одному из событий А и В.
В) - это множество, которое содержит элементы, принадлежащие
хотя бы одному из событий А и В.
Произведение двух событий А 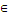 Ω и В
Ω и В 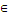 Ω (обозначается АВ или А
Ω (обозначается АВ или А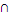 В) это множество, которое содержит
элементы, общие для событий А и В.
В) это множество, которое содержит
элементы, общие для событий А и В.
Разность событий A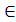 Ω и B
Ω и B 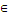 Ω (обозначается А - В или А\В) - это множество, которое
содержит элементы события А, не принадлежащие событию В.
Ω (обозначается А - В или А\В) - это множество, которое
содержит элементы события А, не принадлежащие событию В.
Противоположное событию А 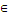 Ω событие Ā = Ω\А. (Ā называют также дополнением множества
A.)
Ω событие Ā = Ω\А. (Ā называют также дополнением множества
A.)
По определению: ∅ 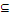 А для любого А.
А для любого А.
События A и В
называются несовместными, если их произведение есть невозможное событие, т. е.
А ∙ В = ∅.
Несколько событий А1, A2,..., Аn образуют полную группу несовместных событий, если
их сумма представляет все ПЭС, а сами события несовместны, т. е.
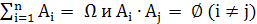
Полную группу образуют, например, события А и Ā (А + Ā = Ω, А∙А=∅).
В случае несчетного пространства Ω в качестве событий рассматриваются
не все подмножества Ω, а лишь некоторые классы этих
подмножеств, называемые алгебрами и 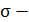 алгебрами множеств.
алгебрами множеств.
Класс S
подмножеств пространства Ω называется алгеброй множеств
(событий), если:
1.∅ 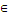 S, Ω
S, Ω 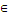 S;
S;
2.из A 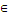 S вытекает, что Ā
S вытекает, что Ā 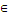 S;
S;
3.из А 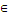 S, В
S, В 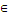 S вытекает, что А + В
S вытекает, что А + В 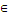 S, А ∙ В
S, А ∙ В 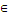 S.
S.
Заметим, что в условии 3 достаточно требовать либо А +
В 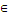 S, либо АВ
S, либо АВ 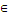 S, так как А + В =
S, так как А + В =
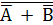 , А ∙ В =
, А ∙ В = 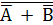 .
.
Алгебру событий образует, например, система
подмножеств S = {∅, Ω}. Действительно, в результате
применения любой из вышеприведенных операций к любым двум элементам класса S снова получается элемент данного
класса: ∅ + Ω = Ω, ∅ ∙ Ω = ∅, 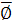 = Ω, Ω = ∅.
= Ω, Ω = ∅.
При расширении операций сложения и умножения на случай
счетного множества алгебра множеств S называется 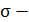 алгеброй,
алгеброй,
если из Аn 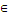 S, n = 1,2,3,..., следует
S, n = 1,2,3,..., следует
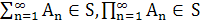
(достаточно требовать либо 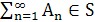 , либо
, либо 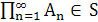 ).
).
Множество всех подмножеств множества Ω, если оно конечно или счетно,
образует алгебру.
Свойство
статистической устойчивости относительной частоты события
Пусть в n повторяющихся опытах некоторое событие А
наступило nA раз. Число nA называется частотой события A, а отношение
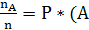
называется относительной частотой (или частостью)
события А в рассматриваемой серии опытов.
Относительная частота события обладает следующими
свойствами:
1. Частость любого события заключена
между нулем и единицей, т. е.
0 ≤ P * (A) ≤ 1
2. Частость невозможного события равна
нулю, т. е.
Р * (∅) = 0.
3. Частость достоверного события равна
1, т.е.
Р * (Ω) = 1.
4. Частость суммы двух несовместных
событий равна сумме частоты этих событий, т. е. если АВ = ∅, то
P * (A + B) = P * (A) + P * (B)
Свойства очевидны, так как 0 ≤ nA ≤ n для
любого события А; для невозможного события nA = 0; для достоверного события nA = n;
если события А и В несовместны (АВ = ∅), то nA+B= nA + nB, следовательно
Р*(А + В) = 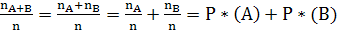
Частость обладает еще одним фундаментальным свойством,
называемым свойством статистической устойчивости: с увеличением числа опытов
(т. е. n) она принимает значения, близкие к
некоторому постоянному числу (говорят: частость стабилизируется, приближаясь к
некоторому числу, частость колеблется около некоторого числа, или ее значения
группируются около некоторого числа).
Так, например, в опыте - бросание монеты (однородной,
симметричной, ...) - относительная частота появления герба при 4040 бросаниях
(Ж. Бюффон) оказалась равной 0,5069 = 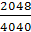 а в опыте с 12000 и 24000 бросаниями
(К. Пирсон) она оказалась равной соответственно 0,5015 =
а в опыте с 12000 и 24000 бросаниями
(К. Пирсон) она оказалась равной соответственно 0,5015 =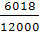 и 0,5005 =
и 0,5005 =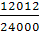 , т.е. частность приближается к числу
, т.е. частность приближается к числу
 = 0,500.... А частость рождения
мальчика, как показывают наблюдения, колеблется около числа 0,515.
= 0,500.... А частость рождения
мальчика, как показывают наблюдения, колеблется около числа 0,515.
Отметим, что теория вероятностей изучает только те
массовые случайные явления с неопределенным исходом, для которых предполагается
наличие устойчивости относительной частоты.
аксиоматический вероятность бернулли событие
Статистическое
определение вероятности
Для математического изучения случайного события
необходимо ввести какую-либо количественную оценку события. Понятно, что одни
события имеют больше шансов («более вероятны») наступить, чем другие. Такой
оценкой является вероятность события, т. е. число, выражающее степень
возможности его появления в рассматриваемом опыте. Математических определений
вероятности существует несколько, все они дополняют и обобщают друг друга.
Рассмотрим опыт, который можно повторять любое число
раз (говорят: «проводятся повторные испытания»), в котором наблюдается
некоторое событие А.
Статистической вероятностью события А называется
число, около которого колеблется относительная частота события А при достаточно
большом числе испытаний (опытов).
Вероятность события А обозначается символом Р(А).
Согласно данному определению
P (A) ≈ P * (A) = 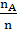
Математическим обоснованием близости относительной
частоты Р*(А) и вероятности Р{А) некоторого события А служит теорема Я.
Бернулли.
Вероятности Р(А) приписываются свойства 1-4
относительной частоты:
1. Статистическая вероятность любого события
заключена между нулем и единицей, т. е.
0 ≤ P (A) ≤ 1
2. Статистическая вероятность невозможного
события равна нулю, т. е.
P (∅) = 0
3. Статистическая вероятность достоверного
события равна единице, т.е.
Р(Ω) = 1.
4. Статистическая вероятность суммы несовместных
событий равна сумме вероятностей этих событий, т. е. если А ∙ В = ∅, то
Р (А + В) = Р(А) + Р(В).
Статистический способ определения вероятности,
опирающийся на реальный опыт, достаточно полно выявляет содержание этого
понятия. Некоторые ученые (Р. Мизес и другие) считают, что эмпирическое
определение вероятности (т. е.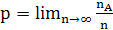 ) следует считать основным определением вероятности.
) следует считать основным определением вероятности.
Недостатком статистического определения является
неоднозначность статистической вероятности; так в примере с бросанием монеты
(п. 1.5) в качестве вероятности можно принять не только число 0,5, но и 0,49
или 0,51 и т. д. Для надежного определения вероятности нужно проделать большое
число испытаний (опытов), что не всегда просто (или дешево).
Классическое
определение вероятности
Существует простой способ определения вероятности
события, основанный на равновозможности любого из конечного числа исходов
опыта. Пусть проводится опыт с n
исходами, которые можно представить в виде полной группы несовместных
равновозможных событий. Такие исходы называются случаями, шансами,
элементарными событиями, опыт - классическим. Про такой опыт говорят, что он
сводится к схеме случаев или схеме урн (ибо вероятностную задачу для такого
опыта можно заменить эквивалентной ей задачей с урнами, содержащими шары разных
цветов).
Случай ω, который приводит к наступлению
события А, называется благоприятным (или - благоприятствующим) ему, т. е.
случай ω влечет событие A: ω 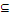 А.
А.
Вероятностью события А называется отношение числа m случаев, благоприятствующих этому
событию, к общему числу n
случаев, т. е.
P (A) = 
Наряду с обозначением Р(А) для вероятности события А
используется обозначение р, т.е. р = Р(А).
Из классического определения вероятности (1.3)
вытекают следующие свойства:
1. Вероятность любого события заключена между нулем
и единицей, т.е.
≤ P (A) ≤ 1.
. Вероятность невозможного события равна нулю,
т. е.
Р(∅) = 0.
3. Вероятность достоверного события равна единице,
т. е.
Р(Ω) = 1.
. Вероятность суммы несовместных событий равна
сумме вероятностей этих событий, т. е. если А ∙ В = ∅, то
Р(А + В) = Р(А) + Р(В).
Они проверяются так же, как и для относительной
частоты (п. 1.5). В настоящее время свойства вероятности определяются в виде
аксиом (см. п. 1.11).
Пример 1.6. В урне (емкости) находятся 12 белых и 8
черных шаров. Какова вероятность того, что наудачу вынутый шар будет белым?
Пусть А - событие, состоящее в том, что вынут белый
шар. Ясно, что n = 12 + 8 = 20 - число всех равновозможных случаев (исходов
опыта). Число случаев, благоприятствующих событию А, равно 12, т.е. m = 12. Следовательно, по формуле
(1.3) имеем: Р(А) = 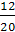 , т.е. P(A) = 0,6.
, т.е. P(A) = 0,6.
Элементы
комбинаторики
Согласно классическому определению подсчет вероятности
события А сводится к подсчету числа благоприятствующих ему исходов. Делают это
обычно комбинаторными методами.
Многие комбинаторные задачи могут быть решены с
помощью следующих двух важных правил, называемых соответственно правилами
умножения и сложения.
Правило умножения (основной принцип): если из
некоторого конечного множества первый объект (элемент х) можно выбрать n1 способами и после каждого такого
выбора второй объект (элемент у) можно выбрать n2 способами, то оба объекта (x и у) в указанном порядке можно выбрать n1 ∙ n2 способами.
Этот принцип, очевидно, распространяется на случай
трех и более объектов.
Пример 1.7. Сколько трехзначных чисел можно составить
из цифр 1, 2, 3, 4, 5, если: а) цифры не повторяются? б) цифры могут
повторяться?
Имеется 5 различных способов выбора цифры для первого
места (слева в трехзначном числе). После того как первое место занято, на
пример, цифрой 2, осталось четыре цифры для заполнения второго места. Для
заполнения третьего места остается выбор из трех цифр. Следовательно, согласно
правилу умножения имеется 5 ∙ 4 ∙ 3 = 60 способов расстановки цифр,
т.е. искомое число трехзначных чисел есть 60. (Вот некоторые из этих чисел:
243, 541, 514, 132, ...) Понятно, что если цифры могут повторяться, то
трехзначных чисел 5 ∙ 5 ∙ 5 = 125. (Вот некоторые из них: 255, 333,
414, 111, ...).
Правило суммы. Если некоторый объект x можно выбрать n1 способами, а объект у можно выбрать
n2 способами, причем первые и вторые
способы не пересекаются, то любой из указанных объектов (х или у), можно
выбрать n1 + n2 способами.
Это правило распространяется на любое конечное число
объектов.
Пример 1.8. В студенческой группе 14 девушек и 6
юношей. Сколькими способами можно выбрать, для выполнения различных заданий,
двух студентов одного пола?
По правилу умножения двух девушек можно выбрать 14 ∙
13 = 182 способами, а двух юношей - 6 ∙ 5 = 30 способами. Следует выбрать
двух студентов одного пола: двух студенток или двух юношей. Согласно правилу
сложения таких способов выбора будет 182 + 30 = 212.
Решение вероятностных (и не только их) задач часто
облегчается, если использовать комбинаторные формулы. Каждая из них определяет
число всевозможных исходов в некотором опыте (эксперименте), состоящем в выборе
наудачу m элементов из n различных элементов рассматриваемого
множества.
Существуют две схемы выбора т элементов (0 < т ≤
n) из исходного множества: без
возвращения (без повторений) и с возвращением (с повторением). В первом случае
выбранные элементы не возвращаются обратно; можно отобрать сразу все т
элементов или последовательно отбирать их по одному. Во второй схеме выбор
осуществляется поэлементно с обязательным возвращением отобранного элемента на
каждом шаге.
Схема выбора без возвращений
Пусть дано множество, состоящее из n различных элементов.