|
U, В
|
S, Кв. см
|
n
|
m
|
U1, В
|
I1, А
|
U2, В
|
I2, А
|
U3, В
|
I3, А
|
|
110
|
4
|
0,82
|
2
|
9
|
5,0
|
6
|
5,0
|
-
|
-
|
Для расчетов используются следующие приближенные зависимости:
Габаритная мощность (P) трансформатора
вычисляется по формуле
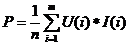 (ватт),
(ватт),
где m - количество вторичных обмоток, n -
коэффициент полезного действия; U (i) - напряжение на i-ой
вторичной обмотке (вольт); I (i) - величина тока в i-ой вторичной обмотке (ампер).
Количество витков первичной обмотки трансформатора определяется
зависимостью:
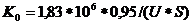
где U - напряжение сети (вольт); S - площадь сечения сердечника (кв. см).
Диаметр провода первичной обмотки определяется по формуле:
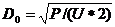 (мм).
(мм).
Количество витков i-ой вторичной
обмотки - по выражению:
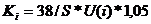 .
.
Диаметр провода i - ой вторичной
обмотки - по формуле:
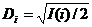 (мм).
(мм).
Структура программы:
1. Подключение библиотек
2. Ввод исходные данные
. Написание функции calc для вычисления K (i), D
(i), Ko и Do в зависимости от введенного пользователем U, Ui, Ii, i
. Описание в окне буквенных обозначений
. Создание виджетов
5.2. Создание в окне ячеек для выведения конечного
результата
.3. Создание в окне кнопок
.4. Отображение главного окна
Код программы:
# - * - coding: utf-8 - *-
# импорт библиотекmath import*Tkinter import*
# ввод исходных данных (из табл.1)=4=0.82= []= []
# написание функции для вычисления K (i), D (i), Ko и Do в
зависимости от введенного пользователем U, Ui, Ii, i
def calc ():=0=int (x_entry. get ())=x-1=int
(U_entry. get ()). append (int (U1_entry. get ())). append (int (U2_entry. get
())). append (int (I1_entry. get ())). append (int (I2_entry. get ()))i in
range (2):+=Ui [i] *Ii [i]
P=P/n= (1.83) * (10**6) * (0.95) / (U*S)='%.3f' %
Ko
Ko_label. configure (text= ('Ko=',Ko))=sqrt (P/
(U*2))='%.3f' % Do_label. configure (text= ('Do=',Do))
Pk=38*Ui [x] *1.05/S='%.3f' % Pk
Ki_label. configure (text= ('Ki=',Pk))=sqrt (Ii
[x] /2.0)='%.3f' % Pd_label. configure (text= ('Di=',Pd))
программирование трансформатор питание алгоритмический
# осуществление вывода на экран окна программы и последующим
выводом результатов вычисления
root = Tk (). title ("Задание № 1")
frame = Frame (root). pack ()_label = Label
(frame, bg='green', text="Вычисление количества витков и диаметра провода i-ой вторичной обмотки трансформатора",
font='arial 10')_label. grid (row=0, column=1, columnspan=4, padx=25,pady=15)
# написание в окне буквенных обозначений_label = Label
(frame, text="P - габаритная мощность трансформатора;
")_label. grid (row=1, column=0, columnspan=4, sticky=W, padx=5)
t4_label = Label (frame, text="m - количество вторичных
обмоток; ")
t4_label. grid (row=2, column=0, columnspan=4,
sticky=W, padx=5)_label = Label (frame, text="n - коэффициент полезного действия;
")_label. grid (row=3, column=0, columnspan=4, sticky=W, padx=5)_label =
Label (frame, text="U (i) - напряжение на i-ой вторичной обмотке;
")_label. grid (row=4, column=0, columnspan=4, sticky=W, padx=5)_label =
Label (frame, text="I (i) - величина тока в i-ой вторичной обмотке;
")_label. grid (row=5, column=0, columnspan=4, sticky=W, padx=5)
t8_label = Label (frame, text="Ko - количество витков
первичной обмотки трансформатора. ")
t8_label. grid (row=6, column=0, columnspan=4, sticky=W, padx=5)
t9_label = Label (frame, text="U - напряжение сети; ")
t9_label. grid (row=1, column=3, columnspan=4,
sticky=W, padx=5)_label = Label (frame, text="S - площадь сечения сердечника;
")_label. grid (row=2, column=3, columnspan=4, sticky=W, padx=5)
t11_label = Label (frame, text="Do - диаметр провода
первичной обмотки трансформатора; ")
t11_label. grid (row=3, column=3, columnspan=4,
sticky=W, padx=5)
t12_label = Label (frame, text="K (i) - количество
витков i-ой вторичной обмотки трансформатора; ")
t12_label. grid (row=4, column=3, columnspan=4,
sticky=W, padx=5)_label = Label (frame, text="D (i) - диаметр провода i-ой вторичной обмотки трансформатора;
")_label. grid (row=5, column=3, columnspan=4, sticky=W, padx=5)
# поле для введения пользователем U, Ui, Ii, i
x_label = Label (frame, text="Введите i (от 1 до
2)")_label. grid (row=7, column=0, padx=5)_entry = Entry (frame,
)_entry. grid (row=7, column=1,sticky=W, pady=5, padx=5)
#_label = Label (frame, text="Введите U")_label.
grid (row=7, column=2)
U_entry = Entry (frame,)_entry. grid
(row=7, column=3,sticky=W, pady=5, padx=5)
#_label = Label (frame, text="Введите U1")_label.
grid (row=8, column=0, padx=5)
U1_entry = Entry (frame,)_entry. grid
(row=8, column=1,sticky=W, pady=5, padx=5)
#_label = Label (frame, text="Введите U2")_label.
grid (row=9, column=0, padx=5)
U2_entry = Entry (frame,)_entry. grid
(row=9, column=1,sticky=W, pady=5, padx=5)
#_label = Label (frame, text="Введите
I1")_label. grid (row=8, column=2, padx=5)_entry = Entry (frame,
)_entry. grid (row=8, column=3,sticky=W, pady=5, padx=5)
#_label = Label (frame, text="Введите
I2")_label. grid (row=9, column=2, padx=5)_entry = Entry (frame,
)_entry. grid (row=9, column=3,sticky=W, pady=5, padx=5)
# размещение в окне ячеек для выведения конечного результата
Ko_label = Label (frame, bg='white', text=
("Ko=?"))_label. grid (row=7, column=4, sticky=W, padx=2)_label =
Label (frame,, bg='white', text="Ki=?")_label. grid (row=7,
column=5,pady=5)_label = Label (frame, bg='white', text=
("Do=?"))_label. grid (row=8, column=4, sticky=W, padx=2)_label =
Label (frame, bg='white', text="Di=?")_label. grid (row=8,
column=5,pady=5)
# выведение в окне кнопок "Вычислить" и "Выйти"_button
= Button (frame, bg='green', text="Вычислить",
command=calc)_button. grid (row=9, column=4, sticky=W, pady=10)_button = Button
(frame, bg='grey', text="Выйти", command=root. destroy)_button. grid
(row=9, column=5, padx=10,pady=10)
#. mainloop ()
Результат решения:
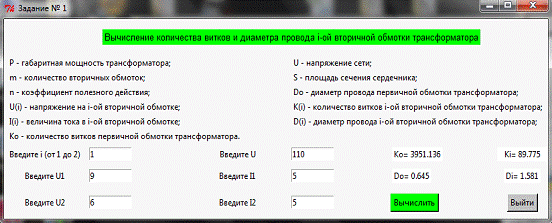

Вывод:
По заданным значениям напряжения сети, площади сечения
выбранного сердечника, требуемому количеству вторичных обмоток, величинам их
напряжения и тока было рассчитано количество витков и диаметр провода в каждой
обмотке.
2. Расчет и
построение амплитудно-частотной характеристики колебательного контура
Постановка задачи:
По заданному выражению для амплитудно-частотной
характеристики резонансного контура
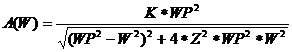 ,
,
Где K - коэффициент усиления, WP - резонансная частота, W - текущая частота,
Z - относительный коэффициент затухания, рассчитать таблицу
значений A (W) при изменении частоты W от 0 до
Wкон с шагом DW=0,1*Wкон при различных значениях относительного коэффициента
затухания Z, изменяющегося от Zнач до Zкон с шагом Zшаг.
По данным таблицы построить на осях координат A (W), W графики изменения амплитуды A (W) от частоты W для различных значений Z.
Исходные данные:
|
K
|
WP
|
Wкон
|
Zнач
|
Zкон
|
Zшаг
|
|
7,5
|
8,5
|
17
|
0,2
|
0,8
|
Структура программы:
1. Подключение библиотек
2. Введение исходных данных
. Расчет значений Z
. Создание виджетов
4.1. Создание главного окна
4.2. Создание графика относительно исходных данных
.3. Описание в окне буквенных обозначений
.4. Создание таблицы значений
.5. Отображение главного окна
Код программы:\
# * - coding: utf-8 - *-Tkinter import *math
import*=7.5=8.5=17=0=1.7=0.2=0.8=0.3=zn= []=0= []zn <= 0.8:= []i in range
(0, 17.01):= (k* (wp**2)) / (sqrt ( ( ( (wp**2) - (w0**2)) **2) + 4* (zn**2) *
(wp**2) * (w0**2))). append (a1)=w0+dw
zn=zn+dz. append (s)
root = Tk () # создание окна. title ("2 задание ")
#=Canvas (root,bg='white', width =200,
height=220). grid (row=5, column=1,padx=10,pady=10)=m [0]= []=1.7i in range
(0,17):=point1 [i]= (12*i*dx, 200-11*y). append (pp)line1 ():. create_line
(points1,fill="blue",smooth=1). create_text (40,75,text="при
z=0.2")=m [1]= []=1.7i in range (0,17):=point2 [i]= (12*i*dx, 200-100*y).
append (pp)line2 ():. create_line (points2,fill="red",smooth=1).
create_text (40,175,text="при z=0.5")=m [2]= []=1.7i in range
(0,17):=point3 [i]= (12*i*dx, 200-200*y). append (pp)line3 ():. create_line (points3,fill="black",smooth=1).
create_text (105, 209,text="при z=0.8")
#_axe= []= (10,0)_axe. append (yy)
yy= (10,220)_axe. append (yy). create_line
(y_axe,fill="black",width=1). create_line
(8,8,10,3,fill="black",width=1). create_line
(10,3,12,8,fill="black",width=1). create_text (25,15,text="A
(W)")
#_axe= []= (0, 200)_axe. append (xx)= (299,
200)_axe. append (xx). create_line (x_axe,fill="black",width=1).
create_line (192, 198, 197, 200,fill="black",width=1). create_line
(192, 202, 197, 200,fill="black",width=1). create_text
(190,213,text="W")
#_label = Label (root, bg='green', fg='black',
text="Расчет и построение амплитудно-частотной характеристики \nс колебательного контура",
font='arial 12')_label. grid (row=0, column=0, columnspan=2, padx=25,pady=15)_label
= Label (root, text="A (W) - амплитуда колебаний; ")_label. grid (row=1, column=1,
columnspan=4, sticky=W, padx=5)
t3_label = Label (root, text="W - частота; ")
t3_label. grid (row=2, column=1, columnspan=4,
sticky=W, padx=5)_label = Label (root, text="Z - относительный коэффициент затухания;
")_label. grid (row=3, column=1, columnspan=4, sticky=W, padx=5)
#_button = Button (root, bg='green',
fg='black',text="График при Z =0.2",
,command=line1)_button. grid (row=1, column=0, padx=10,pady=10)_button
= Button (root, bg='green', fg='black',text="График при Z =0.5",
,command=line2)_button. grid (row=2, column=0, padx=10,pady=10)_button
= Button (root, bg='green', fg='black',text="График при Z =0.8",
,command=line3)_button. grid (row=3, column=0, padx=10,pady=10)
#_button = Button (root, bg='grey',
fg='black',text="Exit",,command=root. destroy)_button. grid
(row=4, column=0, padx=10,pady=10)
#=Text (root,width=30, height=15, font =
"areal 10"). grid (row=5, column=0,padx=10,pady=10)
text1. insert (END, "W\t A (Z1) \t A (Z2) \t
A (Z3) \n")
for i in range (11):. insert (END, "%.2f \t
%.2f \t %.2f \t %.2f\n" % (i*dw,point1 [i],point2 [i], point3 [i]))
#. mainloop ()
Результат решения:
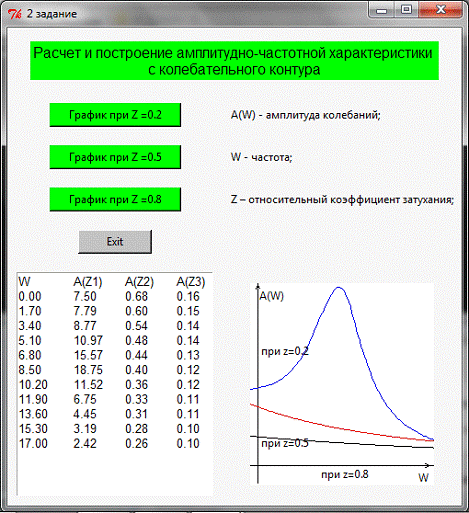
Вывод:
Была рассчитана таблицу значений A (W) при изменении частоты W от 0 до Wкон, при различных значениях
относительного коэффициента затухания Z, изменяющегося от Zнач до Zкон. По данным таблицы были
построены на осях координат A (W), W графики изменения амплитуды A (W) от частоты W для различных значений Z.
Из графика видно, что при увеличении относительного
коэффициента затухания амплитуда резонансного контура возрастает при средних
значениях текущей частоты.
3. Численное
интегрирование аналитически заданной функции
Постановка задачи:
По заданному выражению аналитической функции f (x) вычислить приближенно
определенный интеграл от этой функции на заданном интервале [a,b]:
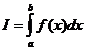 ,
,
используя одну из трех квадратурных формул:
1. прямоугольников;
2. трапеций;
. парабол.
Сравнить результаты вычислений для различных чисел разбиений
интервала n
Исходные данные:
|
f
(x)
|
a
|
b
|
№ формулы
|
n1
|
n2
|
|
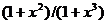 342816 342816
|
|
|
|
|
|
Метод трапеций:
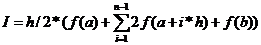
Структура программы:
1. Подключение библиотек
2. Описывание данной функции
. Описание функции I для вычисления интеграла
. Создание виджетов
1.1. Создание окна
1.2. Описание в окне буквенных обозначений
.3. Создание полей для введения пользователем a, b, n
.4. Создание полей для введения пользователем a, b, n
.5. Создание кнопок
.6. Отображение главного окна
Код программы:
# * - coding: utf-8 - *-math import*Tkinter
import*f (x):
= (1+x**2) / (1+x**3)
FI ():=0.0= float (a_entry. get ())= float
(b_entry. get ())= int (n_entry. get ())= (b-a) /ni in range (0,n-1):=2*f (a+
(i+1) *h)=k+p=h/2* (f (a) +k+f (b))= '%.6f' % I_label. configure (text=I)
# создание виджетов_label = Label (frame, bg='green',
text="Вычисление определенного интеграла \nс использованием численного
метода трапеций", font='arial 10')_label. grid (row=0, column=0,
columnspan=3,pady=15,padx=15) # размещение виждета в окне
t2_label = Label (frame, text="a - нижний предел интегрирования")
t2_label. grid (row=2, column=0, columnspan=3,
sticky=W,padx=10)_label = Label (frame, text="b - верхний предел интегрирования")_label.
grid (row=3, column=0, columnspan=3, sticky=W,padx=10)
t4_label = Label (frame, text="n - число разбиений
отрезка интегрирования")
t4_label. grid (row=4, column=0, columnspan=3,
sticky=W,padx=10)_label = Label (frame, text="z - результат интегрирования")_label.
grid (row=5, column=0, columnspan=3, sticky=W,padx=10)_label = Label (frame,
text="Введите данные для расчёта:",
font='arial 8')_label. grid (row=6, column=0, columnspan=3, sticky=W,
pady=5,padx=10)
#_label = Label (frame,
text="a=")_label. grid (row=7, column=0,pady=5)_entry = Entry (frame,
)_entry. grid (row=7, column=1,pady=5)
#_label = Label (frame,
text="b=")_label. grid (row=8, column=0,pady=5)_entry = Entry (frame,
)_entry. grid (row=8, column=1,pady=5)
#_lebel = Label (frame, text="n=")
n_lebel. grid (row=9, column=0,pady=5)_entry =
Entry (frame,)_entry. grid (row=9, column=1,pady=5)
#_label = Label (frame,
text="z=")_label. grid (row=10, column=0,pady=5)_label = Label
(frame, bg='white', text="?",width=10)_label. grid (row=10,
column=1,pady=5)
#_button = Button (frame,bg='green', text="Вычислить",
, command=I)_button. grid (row=11, column=0,sticky=W,
pady=10,padx=15)_button = Button (frame, bg='grey', text="Выйти",
, command=root. destroy)_button. grid (row=11, column=1,
padx=10,pady=10)
#= Canvas (frame, width =160, height=60)=
PhotoImage (file='. /3. gif'). create_image (90, 35, image=img, anchor=CENTER).
grid (row=1, column=0,columnspan=3, sticky=N+S, pady=5,padx=2). mainloop ()
Результат решения:
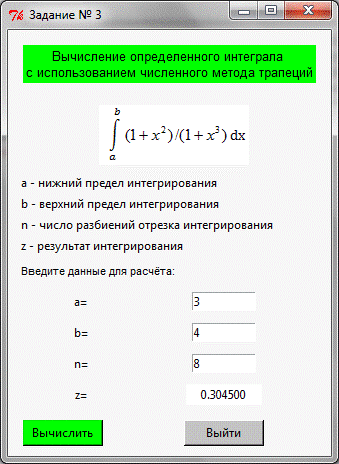
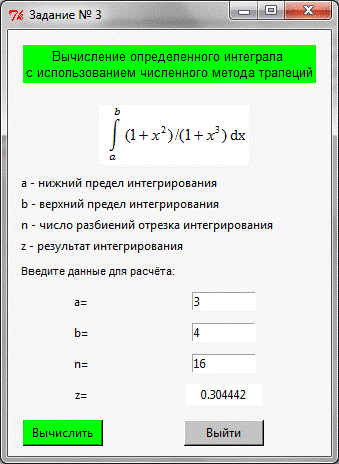
Вывод:
По заданному выражению аналитической функции f (x) =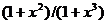 был вычислен приближенно определенный
интеграл от этой функции на заданном интервале [a,b]. Было выяснено, что от количества
разбиений "n" зависит точность решения. Чем число
разбиений больше, тем выше точность измерений.
был вычислен приближенно определенный
интеграл от этой функции на заданном интервале [a,b]. Было выяснено, что от количества
разбиений "n" зависит точность решения. Чем число
разбиений больше, тем выше точность измерений.
4. Численное
решение нелинейных уравнений с заданной точностью
Постановка задачи:
По заданному нелинейному уравнению F (x) =0,где F (x) - некоторое нелинейное
аналитическое выражение, определенное на интервале [a, b], вычислить корни этого
уравнения с требуемой точностью E одним из трех методов:
. итераций;
2. половинного деления;
. Ньютона.
Проверяется, имеет ли место перемена ее знака (переход через
нуль) на интервале [a, b].
Исходные данные:
|
F
(x)
|
a
|
b
|
Метод
|
Точность
|
|
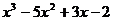 1.2630.000001 1.2630.000001
|
|
|
|
|
Метод Ньютона (касательных) основан также на
последовательном задании значений x и вычислении функции F (x), причем очередное
значение x определяется формулой:
x (n+1) =x (n) - F (x (n)) /F’ (x (n)),
где F’ (x (n)) - производная от функции F (x) в точке x (n).
Геометрически производная от F (x), как известно, по
величине равна тангенсу угла наклона касательной к кривой F (x) в точке x. Тогда точка x (n+1) есть точка пересечения с
осью абсцисс касательной к кривой F (x), проведенной в точке x=x (n). См. рис.5.
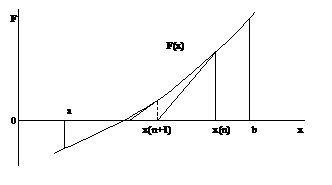
Рис. 5. Геометрическое представление метода Ньютона
Как и в методе итераций, начальное значение x задается как ближайшее табличное к месту
перехода функции F (x) через
нуль.
Выражение для производной F’ (x) получают аналитически в результате
дифференцирования функции F (x). Значение производной может быть получено приближенно и численным
методом:
F’ (x) = (F (x+E) - F (x)) /E.
Итерационный процесс приближения к корню (последовательное
вычисление x (n+1))
продолжается до тех пор, пока будет выполняться условие
|x (n+1) - x (n) |>=E.
Структура программы:
1. Подключение библиотек
2. Описание данной функции
3. Описание функции R и calculate для вычисления корня
уравнения
. Создание виджетов
4.1. Создание окна
4.2. Создание кнопок и полей для введения пользователем
значений
.3. Вставка рисунка
.4. Создание графика исходной функции
.5. Отображение главного окна
Код программы:
# * - coding: utf-8 - *-
# импорт математической библиотекиmath import *
# подключение библиотеки Tkinter
from Tkinter import *
# описание функцийF (x):
return x**3-5*x**2+3*x-2
def F1 (x):
return 3*x**2-10*x+3
def R (a,b,e,n):
P= []
for i in range (n+1):. append (F (a+h*i))= []i in
range (1,len (P)):(P [i-1] >0 and P [i] <0) or (P [i-1] <0 and P [i]
>0):(abs (P [i-1]) - 0) <= (abs (P [i]) - 0):. append (P [i-1]):. append
(P [i])len (T) ==0:
t1_lebel = Label (frame, text="Решений нет")
t1_lebel. grid (row=7, column=1):i in range (len
(T)):=T [i]_next=x-F (x) /F1 (x)abs (x_next-x) >=e:=x_next_next=x-F (x) /F1
(x)x_nextcalculate ():= float (a1_entry. get ())
#= float (b1_entry. get ())
#= float (e1_entry. get ())
#= float (n1_entry. get ())
# использование обработки исключений. Сначала выполняется
ветвь try
try:_x = "%11.10f" %R (a1,b1,e1,n1)
# если во время выполнения try возникает исключение,
# то дальнейшее выполнение try прекращается и выполняется
ветвь except
except:_x = "?"_label. configure
(text=f_x)
# создание экземпляра класса Tk, отвечающего за создание
окон= Tk ()
# определение заголовка окна. title ("Задание 4")
frame = Frame (root). pack ()
t1_label = Label (frame, bg='green', text="Численное
решение нелинейного уравнения \n с заданной точностью", font='arial 12')
t1_label. grid (row=0, column=0, columnspan=4, padx=5,pady=5)
# создание кнопки нижнего значения интервала
a1_entry = Entry (frame,)_entry. grid
(row=3, column=1, padx=5,pady=5)_lebel = Label (frame, text="Начало интервала")1_lebel. grid (row=3, column=0,padx=5,pady=5)
# создание кнопки верхнего значения интервала
b1_entry = Entry (frame,)_entry. grid
(row=4, column=1)_lebel = Label (frame, text="Конец интервала")_lebel.
grid (row=4, column=0)
# точность_entry = Entry (frame,)_entry.
grid (row=5, column=1)
e1_lebel = Label (frame, text="Точность:
")_lebel. grid (row=5, column=0)
# Количество разбиений
n1_entry = Entry (frame,)_entry. grid
(row=6, column=1)_lebel = Label (frame, text="Количество разбиений:
")_lebel. grid (row=6, column=0)_lebel = Label (frame, text="Корень:
")_lebel. grid (row=7, column=0)_label = Label (frame, text="?")_label. grid (row=7, column=1)
# создание кнопки вычисления значения интеграла
eval_button = Button (frame, bg='green',text="Вычислить",
,command=calculate)_button. grid (row=9, column=0)
# создание кнопки закрытия приложения_button =
Button (frame, bg='grey',text="Выход",,command=root.
destroy)_button. grid (row=9, column=1, padx=25,pady=15)
#= Canvas (frame, width =160, height=50)=
PhotoImage (file='. /4. gif'). create_image (90, 35, image=img, anchor=CENTER).
grid (row=1, column=0, sticky=N+S, pady=5,padx=2)
# непосредственное создание окна
root. mainloop ()
Результат решения:
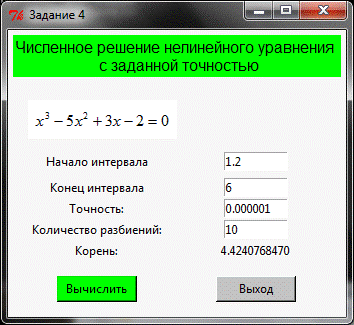
Вывод:
По заданному нелинейному уравнению 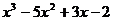 =0, определенном на интервале [a, b], были вычислены корни этого уравнения с
требуемой точностью E методом Ньютона.
=0, определенном на интервале [a, b], были вычислены корни этого уравнения с
требуемой точностью E методом Ньютона.
Были взяты две произвольные точки на функции и получен отрезок,
ограниченный слева и справа этими точками, задан класс точности вычислений и
выяснено, что точность вычислений зависит от того, какой класс точности задать,
так же было определено, что если корень не попадает в заданный нами интервал,
то программа не выдает должного ответа.
5. Численное
решение дифференциальных уравнений первого порядка
Постановка задачи:
С помощью численных методов решить дифференциальное уравнение
первого порядка у'=f (x,y).
. Метод Эйлера.
. Модифицированный метод Эйлера (вариант 1).
. Модифицированный метод Эйлера (вариант 2).
. Метод Рунге-Кутта третьего порядка.
. Метод Рунге-Кутта четвертого порядка
Исходные данные:
|
Уравнение
|
Метод
|
a
|
b
|
x0
|
y0
|
|
у'=exp (-x) -
2x
|
1,4
|
1
|
2
|
1
|
1
|
1. Метод Эйлера
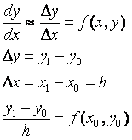
|
y1=y0+h*f
(x0,y0) x1=x0+h
|
Расчетные
формулы для 1-го шага
|
|
yi+1=yi+h*f
(xi,yi) xi+1=xi*h
|
Расчетные
формулы для i-го шага
|
2. Метод Рунге-Кутта третьего порядка
уi+1=уi+ (k1+4k2+k3) /6,k1=hf (xi, yi),
k2=hf (xi+h/2, yi+k1/2),
Структура программы:
1. Подключение библиотек
2. Описание данной функции
3. Описание функции fx метода Эйлера
. Описание функции rk метода Рунге-Кутта
. Описание функции calculate для нахождения значения
. Создание виджетов
6.1. Создание окна
6.2. Создание кнопок и полей для введения пользователем
значений
.3. Вставка рисунка
.4. Отображение главного окна
Код программы:
# * - coding: utf-8 - *-
# подключение библиотеки Tkinter
from Tkinter import *
# импорт математической библиотекиmath import *
# описание функцииdu (x,y):
return exp (-x) - 2*x
def fx (x_0,y_0,x_k,n_1):
# шаг интегрирования= (x_k-x_0) /n_1
#Метод Эйлера
for i in range (0,n_1):
y1=y_0+h*du (x_0,y_0)=x_0+h_0=x1_0=y1y1rk
(x_0,y_0,x_k,n_1):
h= (x_k-x_0) /n_1
# метод рунге-кутта
for i in range (0,n_1):
k1=h*du (x_0,y_0)=h*du (x_0+h/2,y_0+k1/2)
k3=h*du (x_0+h,y_0+2*k2-k1)=y_0+ (k1+4*k2+k3)
/6_0=x_0+h_0=y1y1
def calculate_y1 ():
# начальные условия= float (x0_entry. get ())= float (y0_entry. get
())
# конечная точка= float (xk_entry. get ())
# число разбиений= int (n_entry. get ())
# использование обработки исключений. Сначала выполняется
ветвь try
try:= "%11.3f" % fx (x0,y0,xk,n)
y2 = "%11.3f" % rk (x0,y0,xk,n)
# если во время выполнения try возникает исключение,
# то дальнейшее выполнение try прекращается и выполняется
ветвь except
except:= "?"= "?"_label.
configure (text=y1)_label. configure (text=y2)
# создание экземпляра класса Tk, отвечающего за создание
окон=Tk ()
# определение заголовка окна. title ("Задание 5")
frame = Frame (root). pack ()
t1_label = Label (frame, bg='green', text="Численное
решение дифференциального уравнения первого порядка", font='arial 12')
t1_label. grid (row=0, column=0, columnspan=5, padx=25,pady=5)
# создание окна ввода величины начального значения числа X
x0_entry = Entry (frame,)_entry. grid
(row=1, column=2,pady=5)0_lebel = Label (frame, text="Начальное значение X: ")
x0_lebel. grid (row=1, column=1,pady=5)
# создание окна ввода величины начального значения числа Y
y0_entry = Entry (frame,)
y0_entry. grid (row=2, column=2,pady=5)_lebel =
Label (frame, text="Начальное значение Y:
")_lebel. grid (row=2, column=1,pady=5)
# оздание окна ввода величины конечной точки
xk_entry = Entry (frame,)_entry. grid
(row=1, column=4,pady=5)
xk_lebel = Label (frame, text="Конечное значение Х:
")
xk_lebel. grid (row=1, column=3,pady=5)
# создание окна ввода величины точности интегрирования)
n_entry = Entry (frame,)_entry. grid
(row=2, column=4,pady=5)_lebel = Label (frame, text="Число разбиений:
")_lebel. grid (row=2, column=3,pady=5)
# создание поля вывода ответа (метод эйлера)
y1_label = Label (frame,
text="?")_label. grid (row=3, column=1,padx=5,pady=5)_lebel = Label
(frame, text="Метод Эйлера: ")_lebel.
grid (row=3, column=0,padx=5,pady=5)
# создание поля вывода ответа (метод рунге-кутта)
y2_label = Label (frame,
text="?")_label. grid (row=4, column=1,padx=5,pady=5)_lebel = Label
(frame, text="Метод Рунге-Кутта 3го порядка: ")_lebel.
grid (row=4, column=0,padx=5,pady=5)
# создание кнопки вычисления значения интеграла_button = Button
(frame,bg='green', text="Вычислить",,command=calculate_y1)
eval_button. grid (row=4, column=3,padx=5,pady=5)
# создание кнопки закрытия приложения_button =
Button (frame, bg='grey', text="Выход",,command=root.
destroy)_button. grid (row=4, column=4,padx=5,pady=5)= Canvas (frame, width
=140, height=60)= PhotoImage (file='. /5. gif'). create_image (60, 40,
image=img, anchor=CENTER). grid (row=1, column=0, sticky=N+S)
# непосредственное создание окна
root. mainloop ()
Результат решения:
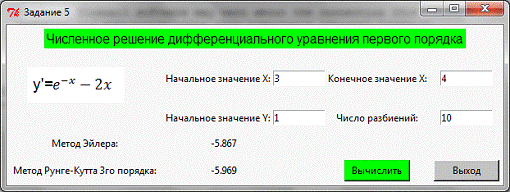
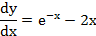
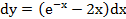
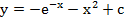

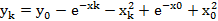
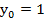
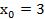
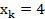
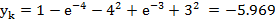
Вывод
Для решения дифференциального уравнения первого порядка были
использованы выше описанные методы Рунге-Кутта и метод Эйлера. Было
установлено, что метод Рунге-Кутта точнее, чем метод Эйлера в сравнении с
аналитическим методом вычисления, и требует меньшего числа разбиений участка
функции, для выявления результата.
Заключение
В процессе решения данных задач с помощью языка
программирования Python были запрограммированы и реализованы алгоритмы численных методов
решения нелинейных уравнений, дифференциальных уравнений первого порядка,
интегрирования аналитически заданных функций, автоматизированы процессы
расчетов и вычислений некоторых инженерно-технических задач.
Были применены полученные знания в области визуального
объектно-ориентированного программирования: создание виджетов, составление
вычислительных функций, применение различных электронных библиотек, добавление
графических объектов, использование циклов и т.д. Данные программы включали в
себя численные методы решения, построение графиков, вывод таблиц. Для решения
задач были использованы функции для вычисления требуемых данных и поставленных
задач.
Для упрощения работы с программами созданы диалоговые окна с
необходимыми командами. Во всех программах использовались компоненты типов:
label, button, text, entry, frame. В некоторых из них так же использовались
canvas для создания графических объектов. Для сокращения программы
использовались циклы, типа for, while. Для расположения виджетов в окне использовался
менеджер grid. Для математических вычислений был задействован математический
модуль math, а для визуального программирования модуль tkinter.
Список
используемой литературы
1. Бизли
Д. Python. Подробный справочник: Символ плюс, 2010
2. Валишев
М.Г., Повзнер А.А. Курс общей физики: Лань, 2010
. Лутц
М. Изучаем Python: Символ плюс, 2011
. Россум
Г., Дрейк Ф.Л. Дж., Откидач Д.С. Язык программирования Python
. Саммерфилд
М. Программирование на Python: Санкт-Петербург, 2009
. Соболев
А.Б., Рыбалко А.Ф. Математика: Академия, 2009
. Сузи
Р.А. Язык программирования Python: ИНТУИТ, 2005
. Чаплыгин
А.Н. Учимся программировать вместе с Питоном; 2004