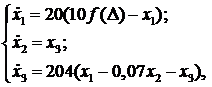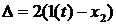Моделирование моделей
1. Задание 1
Тип нелинейности
Передаточная функция:
,
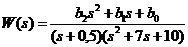где:
,
,
.
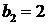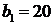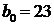Тогда передаточная
функция примет окончательный вид:
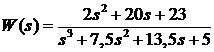
Получим дифференциальное
уравнение системы 3-его порядка:
;
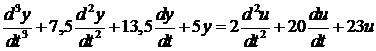Метод последовательного
интегрирования
Первое уравнение системы
будет иметь вид:
.
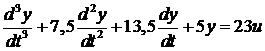Ему соответствует
передаточная функция
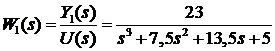
Суть метода
последовательного интегрирования состоит в том, что дифференциальное уравнение
разрешают относительно старшей производной:
,
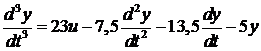а младшие производные и
сам выходной сигнал получают последовательным интегрированием сигнала старшей
производной. При этом выходная переменная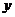 
и ее производные
заменяется машинными переменными:
, 
,
,
.
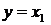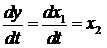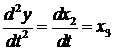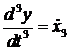Тогда уравнение
принимает вид:
.
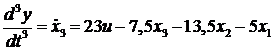Для составления схем для
второго уравнения системы обратимся к передаточной функции
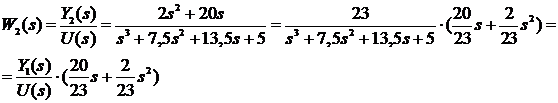
Из последнего выражения
следует:
,
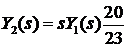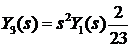
отсюда из теоремы
Лапласа об изображении производной получаем:
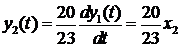
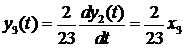
Тогда выходной сигнал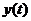 
представляется
в виде суммы сигналов:
.
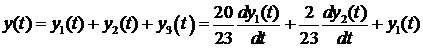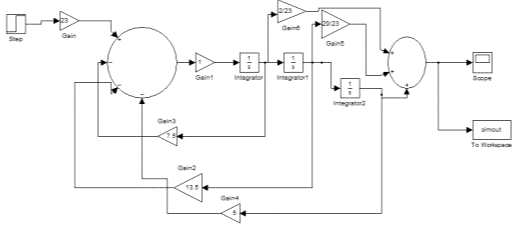
Схема моделирования
методом последовательного интегрирования
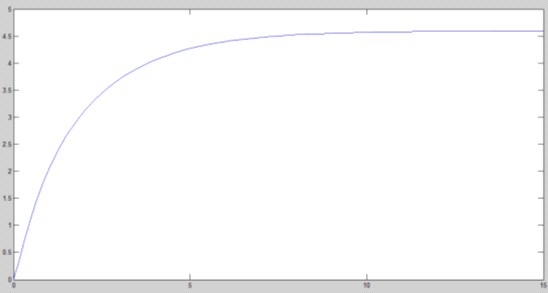
Результат моделирования
методом последовательного интегрирования
Система дифференциальных
уравнений, схеме моделирования рисунка 1, имеет вид:
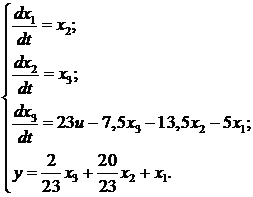
Метод канонической формы
Суть метода состоит в
том, что исходное уравнение разрешают относительно искомой переменной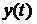 
.
Для этого его записывают в операторной форме:
,
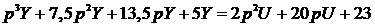и делят на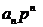
(
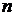- порядок уравнения):
.
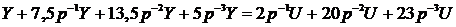Далее уравнение
разрешают относительно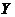 
и
группируют по степеням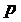 
:
.
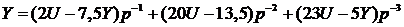Отсюда получают
выражение для выходного сигнала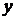 
:
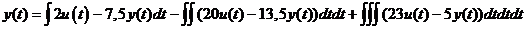
Схема моделирования
методом канонической формы имеет вид, представленный на рисунке 3.
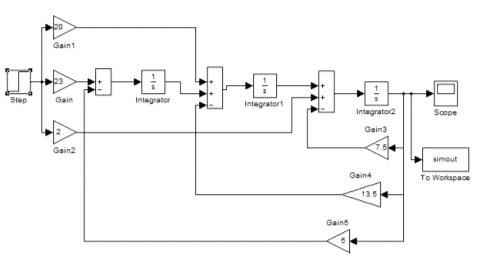
Схема моделирования
методом канонической формы
Вводим в командную
строку: plot (simout.time(:), simout.signals.values(:, 1)).
Результат моделирования
методом канонической формы
Система дифференциальных
уравнений, соответствующая схеме моделирования на рисунке 3, имеет вид:
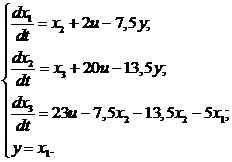
Метод вспомогательной
переменной
Вводим вспомогательную
переменную:
.
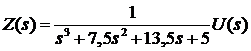Этой передаточной функции
соответствует уравнение:
,
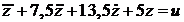отсюда
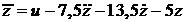. (13)
Из передаточной функции
следует, что в операторной форме
,
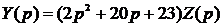отсюда, на основании
обратного преобразования Лапласа:
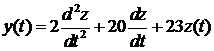. (14)
Введем переменные:
Уравнения (13), (14), с
учетом переменных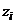 
,
образуют систему уравнений, решающую дифференциальное уравнение (10):
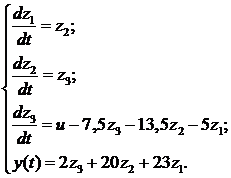
Схема моделирования,
соответствующая системе уравнений, представлена на рисунке 5.
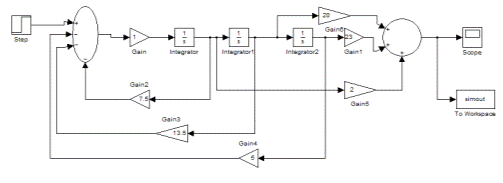
Схема моделирования
методом вспомогательной переменной
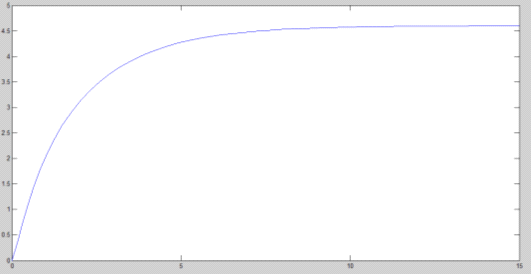
Результат моделирования
методом вспомогательной переменной
Модель в пространстве
состояний в нормальной форме
Составляем
дифференциальное уравнение:
,
.
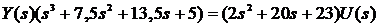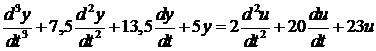Производим переход к
машинным переменным
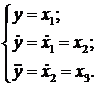
Вектор состояний состоит
из 3-х элементов:
.
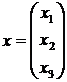Дифференциальное уравнение
приобретает вид:
.
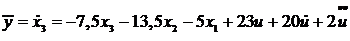Получаем следующую
систему уравнений:
.
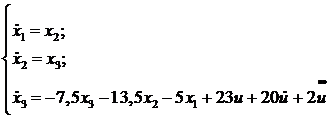
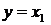Отсюда находим матрицы
пространства состояний:
.
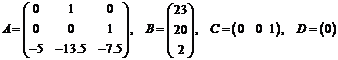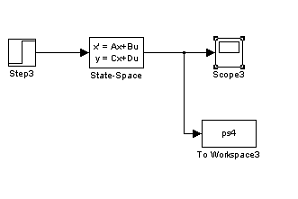
Схема моделирования
методом модели в пространстве состояний в нормальной форме
Результат моделирования
методом модели в пространстве состояний в нормальной форме
Модель в пространстве
состояний в канонической форме
Перейдем к канонической
форме передаточной функции. Корни знаменателя равны:
,
,
.
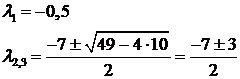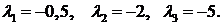моделирование
дифференциальный уравнение интегрирование
Следовательно,
,
,
,
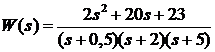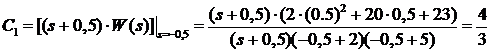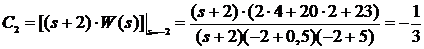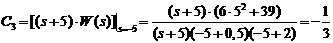
и передаточная функция
окончательно принимает вид:
.
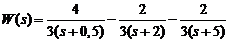Отсюда находим матрицы
пространства состояний:
, 
,
,
,
.
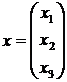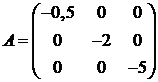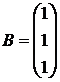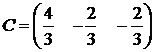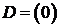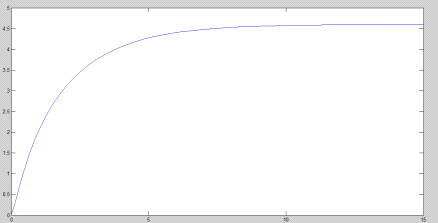
Результат моделирования
методом модели в пространстве состояний в канонической форме
Модель в пространстве
состояний в форме простых сомножителей
Пусть передаточная
функция задана в нормальной форме
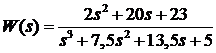
Представим передаточную
функцию в виде сомножителей. Корни знаменателя равны: ,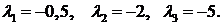
следовательно,
передаточная функция принимает вид:
.
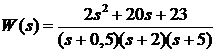Отсюда находим матрицы
пространства состояний:
, 
,
,
,
.
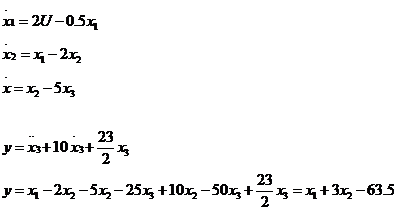
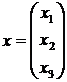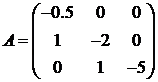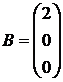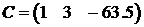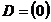Во всех рассмотренных
нами методах моделирования мы получили одинаковые результаты, потому что в
основе моделирования лежит теория подобия, которая утверждает, что
абсолютное подобие может иметь место лишь при замене одного объекта другим
точно таким же.
2. Задание 2
Дано:
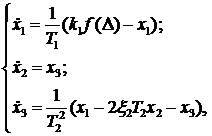
где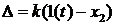 
.
Параметры системы
уравнений:
, 
,
,
,
,
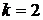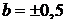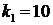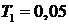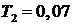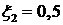
Нелинейность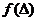 
:
Подставляя значения получим:
