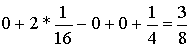|
Сырье
|
Элементы
|
Стоимость
|
|
медь
|
железо
|
цинк
|
|
|
I
|
5
|
2.5
|
1
|
5000
|
|
II
|
3
|
3
|
1.3
|
2000
|
|
План
|
³250
|
³150
|
³100
|
|
Математическая модель задачи
- Выражение для целевой функции
Обозначим через x1, x2 количество породы соответственно I и II типа.
Целевая функция:
z=5000x1+2000x2 ®min
Система ограничений задачи
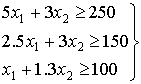
x1³0, x2³0
Приведем к виду основной задачи линейного программирования:
z1=-z=-5000x1-2000x2®max
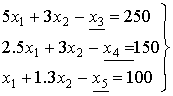
z1=-z=-5000x1-2000x2+0x3+0x4+0x5®max
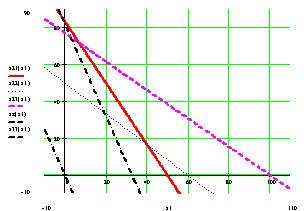
Геометрическая трактовка модели задачи и ее решения
Определение области допустимых значений
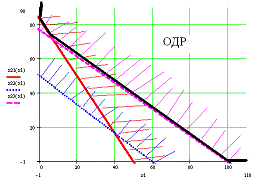
Определим
на графике точку, доставляющую экстремальное значение целевой функции.
Точка
пересечения прямой 1 оси x2.
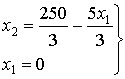 Þ (0; 83.333)
Þ (0; 83.333)
Откуда
экстремальное значение целевой функции: F=166666.67.
Ответ
Для
минимизации затрат на сырье можно ограничиться сырьем второго типа в количестве
83.33 ед./день, при этом затраты на сырье составят 166666.67 р.
Задание 2
- Исходные данные
С = [ 25 -1 3 -1 0 0 ]= [ 7 7 12 ]
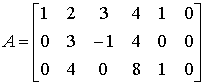
- Условия в развернутой форме
=25x1-x2+3x3-x4 → min
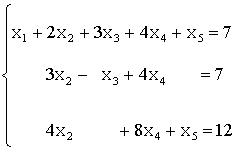
-
Определим, существуют ли допустимые решения, для этого необходимо проверить
совместность системы, т.е. найти ранги матрицы и расширенной матрицы
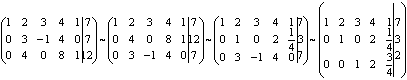
r(A)=r(R)=3,
следовательно,
система совместна.
Приведем
условия задачи к каноническому виду. Выберем в качестве базисных переменных x1, x3 и x5.
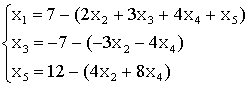
Подставив
выражения для x3 и x5 в первое уравнение системы, получим x1=16-(7x2+8x4).
Т.о., имеем:
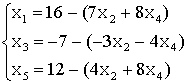
Целевая
функция:
=25x1-x2+3x3-x4 → min=-Q=-25x1+x2-3x3+x4
→ max
Подставив уравнения из системы в выражение для целевой функции, получим
=-379-(-167x2-211x4)
Для решения построим симплексную таблицу
|
b
|
X2
|
X4
|
|
Q1
|
-379
|
-167
|
-211
|
|
|
 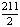 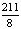
|
|
|
|
|
X1
|
16
|
7
|
8
|
|
|
-12
|
-4
|
|
-1
|
|
X3
|
-7
|
-3
|
-4
|
|
|
6
|
2
|
|
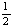
|
|
X5
|
12
|
|
4
|
|
8
|
|
|
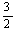 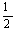 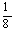
|
|
|
|
|
|
|
|
|
|
|
Т.к. в столбце свободных членов есть отрицательный элемент, то план не
является опорным. Возьмем в качестве разрешающего столбца столбец x4 как содержащий наибольшее по модулю
отрицательное число. Для выбора разрешающей строки сравним отношения элементов
столбца свободных членов к элементам столбца x4. выберем строку с наименьшим отношением. Т.о., разрешающий
элемент находится на пересечении строки x5 и столбца x4.
Все прочие элементы разрешающей строки умножим на величину, обратную
разрешающему элементу. Элементы разрешающего столбца умножим на величину,
обратную разрешающему элементу, взятую со знаком «-». Результаты запишем в
правой нижней части каждой ячейки. Для прочих элементов запишем в правой нижней
части ячейки произведение нового элемента столбца на старый элемент строки.
Перепишем таблицу, заменив переменные. Элементы разрешающего столбца и
строки заменим числами, стоящими в нижних частях этих ячеек. Каждый из
оставшихся элементов - суммой чисел, стоящих в верхней и нижней части этой
ячейки. Т.к. величина элементов столбца свободных членов уменьшилась по
абсолютной величине, есть основания надеяться, что замена элементов правомерна.
Повторим вышеизложенные операции (выбор разрешающего элемента, вычисление новых
значений) для новой таблицы.
|
b
|
X2
|
X5
|
|
Q1
|
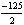 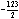 
|
|
|
|
82
|
|
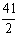 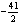
|
|
|
X1
|
4
|
|
3
|
-1
|
|
|
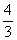 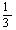 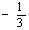
|
|
|
|
|
X3
|
-1
|
-1
|
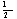
|
|
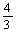 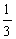 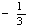
|
|
|
|
|
X4
|
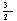 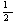 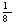
|
|
|
|
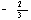 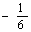 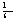
|
|
|
|
|
|
|
|
|
|
|
Еще раз пересчитаем таблицу.
Т.к. ни столбец свободных, ни строка целевой функции не имеют ни одного
отрицательного элемента, то оптимальное решение найдено.
X=(0; 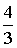 ;
; 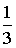 ;
; 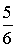 ; 0)
; 0)
Значение
целевой функции Q=-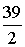
Проверим
найденные значения, подставив их в первоначальную систему:
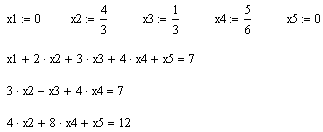
Задание
3
Условия задачи в матричной форме
Поставки A=[600080003000]
Потребности B=[5000 2000 10000
6000 3000]
Тарифы
C=
∑Ai=17000,
∑Bi=26000, следовательно, необходимо ввести фиктивного поставщика
Aф с запасом 26000-17000=9000 ед.
Определим
опорный план задачи методом минимального элемента
|
B1
|
B2
|
B3
|
B4
|
B5
|
Запасы
|
|
A1
|
0.1
|
0.15
|
0.05
|
0.07
|
0.1
|
6000
|
|
|
|
6000
|
|
|
|
|
A2
|
0.15
|
0.015
|
0.08
|
0.06
|
0.09
|
8000
|
|
|
2000
|
|
6000
|
|
|
|
A3
|
0.12
|
0.14
|
0.1
|
0.09
|
0.08
|
3000
|
|
|
|
|
|
3000
|
|
|
Aф
|
0
|
0
|
0
|
0
|
0
|
9000ф
|
|
5000
|
|
4000
|
|
|
|
|
Потребности
|
5000
|
2000
|
10000
|
6000
|
3000
|
|
Т.к. число заполненных клеток должно быть 4+5-1=8, то введем две нулевые
перевозки
|
B1
|
B2
|
B3
|
B4
|
B5
|
Запасы
|
|
A1
|
0.1
|
0.15
|
0.05
|
0.07
|
0.1
|
6000
|
|
|
|
6000
|
|
|
|
|
A2
|
0.15
|
0.015
|
0.08
|
0.06
|
0.09
|
8000
|
|
|
2000
|
|
6000
|
|
|
|
A3
|
0.12
|
0.14
|
0.1
|
0.09
|
0.08
|
3000
|
|
|
|
|
|
3000
|
|
|
Aф
|
0
|
0
|
0
|
0
|
0
|
9000ф
|
|
5000
|
0
|
4000
|
|
0
|
|
|
Потребности
|
5000
|
2000
|
10000
|
6000
|
3000
|
|
Найдем значение функции при данном опорном плане:
F=
Определим
оптимальный план задачи
Проверим
оптимальность плана. Воспользуемся методом потенциалов. Для каждой заполненной
клетки выполняется соотношение ui+vj=cij. Примем u1=0, остальные потенциалы
вычисляются через базисные клетки.
|
B1
|
B2
|
B3
|
B4
|
B5
|
ui
|
|
A1
|
0.1
|
0.15
|
0.05
|
0.07
|
0.1
|
0
|
|
|
|
6000
|
|
|
|
|
A2
|
0.15
|
0.015
|
0.08
|
0.06
|
0.09
|
-0.035
|
|
|
2000
|
|
6000
|
|
|
|
A3
|
0.12
|
0.14
|
0.1
|
0.09
|
0.08
|
0.03
|
|
|
|
|
|
3000
|
|
|
Aф
|
0
|
0
|
0
|
0
|
0
|
-0.05
|
|
5000
|
0
|
4000
|
|
0
|
|
|
vj
|
0.05
|
0.05
|
0.05
|
0.095
|
0.05
|
|
Далее
для свободных клеток найдем т.н. псевдотарифы 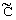 ij следующим образом:
ij следующим образом: 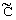 ij= ui+vj.
ij= ui+vj.
Таблица
|
|
B1
|
B2
|
B3
|
B4
|
B5
|
ui
|
|
A1
|
0.1
|
0.15
|
0.05
|
0.07
|
0.1
|
0
|
|
0.05
|
0.05
|
6000
|
0.095
|
0.05
|
|
|
A2
|
0.15
|
0.015
|
0.08
|
0.06
|
0.09
|
-0.035
|
|
0.015
|
2000
|
0.015
|
6000
|
0.015
|
|
|
A3
|
0.12
|
0.14
|
0.1
|
0.09
|
0.08
|
0.03
|
|
0.08
|
0.08
|
0.08
|
0.125
|
3000
|
|
|
Aф
|
0
|
0
|
0
|
0
|
0
|
-0.05
|
|
5000
|
0
|
4000
|
0.09
|
0
|
|
|
vj
|
0.05
|
0.05
|
0.05
|
0.095
|
0.05
|
|
Найдем
клетки, для которых разность cij-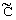 ij отрицательна.
ij отрицательна.
Пересечение
строки A3 и столбца B4 cij-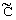 ij=0.09-0.125=-0.035
ij=0.09-0.125=-0.035
Пересечение
строки Aф и столбца B4 cij-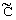 ij=0 - 0.09 =
-0.09
ij=0 - 0.09 =
-0.09
Построим
цикл пересчета для клетки, находящейся на пересечении строки Aф и
столбца B4.
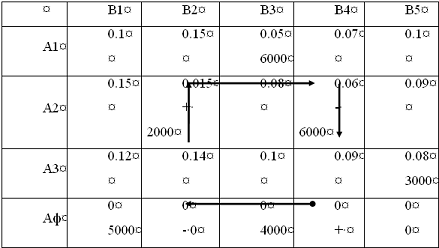
Т.к.
в нашем случае имеет место вырожденный опорный план, то поставка, перевозимая
по циклу, равна нулю.
Новая
симплекс-таблица:
|
B1
|
B2
|
B3
|
B4
|
B5
|
|
A1
|
0.1
|
0.15
|
0.05
|
0.07
|
0.1
|
|
|
|
6000
|
|
|
|
A2
|
0.15
|
0.015
|
0.08
|
0.06
|
0.09
|
|
|
2000
|
|
6000
|
|
|
A3
|
0.12
|
0.14
|
0.1
|
0.09
|
0.08
|
|
|
|
|
|
3000
|
|
Aф
|
0
|
0
|
0
|
0
|
0
|
|
5000
|
|
4000
|
0
|
0
|
Найдем значение функции: F=930,
общая стоимость перевозок не изменилась, т.к. поставка, перевозимая по циклу,
равна нулю.
Проверим оптимальность плана
|
B1
|
B2
|
B3
|
B4
|
B5
|
ui
|
|
A1
|
0.1
|
0.15
|
0.05
|
0.07
|
0.1
|
0
|
|
0.05
|
0.005
|
6000
|
0.05
|
0.05
|
|
|
A2
|
0.15
|
0.015
|
0.08
|
0.06
|
0.09
|
0.01
|
|
0.06
|
2000
|
0.06
|
6000
|
0.06
|
|
|
A3
|
0.12
|
0.14
|
0.1
|
0.09
|
0.08
|
0.03
|
|
0.08
|
0.035
|
0.08
|
0.08
|
3000
|
|
|
Aф
|
0
|
0
|
0
|
0
|
0
|
-0.05
|
|
5000
|
0
|
4000
|
0
|
0
|
|
|
vj
|
0.05
|
0.005
|
0.05
|
0.05
|
0.05
|
|
В
таблице нет свободных клеток с отрицательной разностью cij- ij, значит,
оптимальный план найден. Для клетки, находящейся на пересечении строки Aф и
столбца B2 cij-
ij, значит,
оптимальный план найден. Для клетки, находящейся на пересечении строки Aф и
столбца B2 cij- ij=0, это
означает, что существует еще один или несколько оптимальных планов с такой же
общей стоимостью перевозок F=930.
ij=0, это
означает, что существует еще один или несколько оптимальных планов с такой же
общей стоимостью перевозок F=930.
Задание 4
Исходные данные:
A=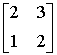
B=[5 1]
c11=1, c12=-2,
c22=2
P=[15 10]
Т.о.,
целевая функция
F = c11x12+c22x22+c12x1x2+b1x1+b2x2 =x12 + 2x22 -
2x1x2 + 5x1 + x2 (min)=-F= -x12 - 2x22 + 2x1x2 - 5x1 - x2 (max)
Условия
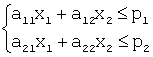
т.е.,
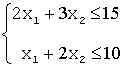 , или
, или 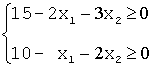
Определим
стационарную точку целевой функции
Найдем
частные производные целевой функции и приравняем их к нулю
По
x1: -2x1+2x2-5=0
По
x2: 2x1 -4x2-1=0
Откуда
получаем стационарную точку (-5.5; -3).
Исследуем
функцию на вогнутость в окрестностях стационарной точки
Найдем
вторые частные производные
Проверим на вогнутость:
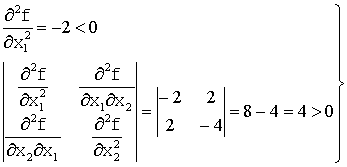 =>
функция вогнута.
=>
функция вогнута.
Составим
функцию Лагранжа
L (x1,x2,u1,u2)= -x12 - 2x22 + 2x1x2 - 5x1 - x2+
u1(15-2x1-3x2)+ u2(10-x1-2x2)
Найдем
частные производные для функции Лагранжа
Приведем полученные неравенства к следующему виду:
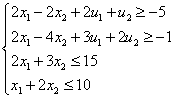
Преобразуем
неравенства в равенства:
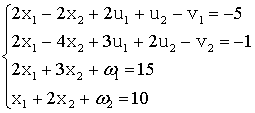
Используя
метод искусственных переменных, составим симплекс-таблицу
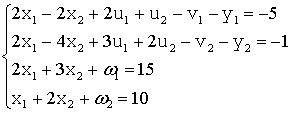
Составим
псевдоцелевую функцию: ц=My1+My2 ® min
Выберем
в качестве базисных переменные y1,y2,щ1, щ2.
Тогда
система примет вид:
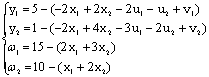
Псевдоцелевая
функция: ц’=-My1-My2 ® max
Подставив
выражения для y1 и y2 из системы, получим ц’=-6M-(4Mx1-6Mx2+5Mu1+3Mu2-Mv1-Mv2).
Занесем
полученные значения в симплекс-таблицу.
|
b
|
X1
|
X2
|
U1
|
U2
|
V1
|
V2
|
|
ц’
|
-6M
|
4M
|
-6M
|
5M
|
3M
|
-M
|
-M
|
|
15M
|
-6M
|
|
3M
|
-6M
|
-3M
|
3M
|
0
|
|
y1
|
5
|
|
-2
|
|
2
|
-2
|
|
-1
|
|
1
|
|
0
|
|
|
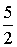 -1 -1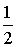 -1 -1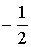 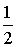 0 0
|
|
|
|
|
|
|
|
|
y2
|
1
|
-2
|
4
|
-3
|
-2
|
0
|
1
|
|
-10
|
4
|
|
-2
|
4
|
2
|
-2
|
0
|
|
щ1
|
15
|
2
|
3
|
0
|
0
|
0
|
0
|
|
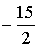 3 3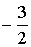 3 3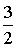 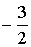 0 0
|
|
|
|
|
|
|
|
|
щ2
|
10
|
1
|
2
|
0
|
0
|
0
|
0
|
|
-5
|
2
|
|
-1
|
2
|
1
|
-1
|
0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следующий шаг
|
b
|
X1
|
y1
|
U1
|
U2
|
V1
|
V2
|
|
ц’
|
9M
|
-2M
|
3M
|
-M
|
0
|
2M
|
-M
|
|
-9M
|
2M
|
-2M
|
M
|
0
|
|
M
|
M
|
|
x2
|
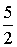 -1 -1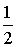 -1 -1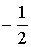 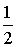 0 0
|
|
|
|
|
|
|
|
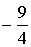 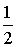 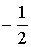 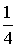 0 0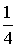 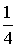
|
|
|
|
|
|
|
|
|
y2
|
-9
|
2
|
-2
|
1
|
0
|
-2
|
1
|
|
|
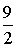 -11 -11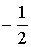 0 0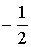 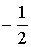
|
|
|
|
|
|
|
|
|
|
|
|
|
|
щ1
|
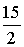 5 5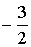 3 3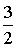 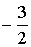 0 0
|
|
|
|
|
|
|
|
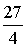 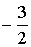 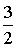 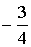 0 0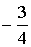 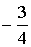
|
|
|
|
|
|
|
|
|
щ2
|
5
|
3
|
-1
|
2
|
1
|
-1
|
0
|
|
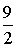 -11 -11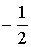 0 0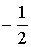 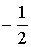
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т.к. на следующем шаге на пересечении строки ц’ и столбца свободных
членов образуется нуль, поэтому пересчитаем лишь столбец b и строку ц’.
|
b
|
X1
|
y1
|
U1
|
U2
|
V1
|
V2
|
|
ц’
|
0
|
0
|
M
|
0
|
0
|
M
|
0
|
|
|
|
|
|
|
|
|
|
x2
|
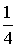
|
|
|
|
|
|
y2
|
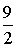
|
|
|
|
|
|
щ1
|
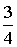
|
|
|
|
|
|
щ2
|
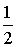
|
|
|
|
|
Т.о.,
x1=0, x2=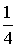
Проверим,
выполняются ли условия дополняющей нежесткости:
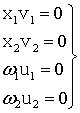
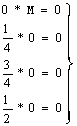
Подставим
для проверки найденные значения в исходную систему ограничений:
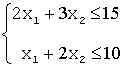
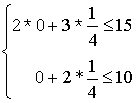
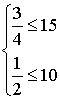
Т.к.
условия дополняющей нежесткости выполняются, то решение найдено.
Итак,
x1=0, x2=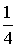 ;
;
F = x12 +
2x22 - 2x1x2 + 5x1 + x2 =