Разработка цифрового преобразователя Гильберта
ВВЕДЕНИЕ
В наше время в системах связи, передачи и приема
информации наиболее перспективными являются цифровая форма представления
сигнала и их преобразования.
Развитие цифровых систем передачи объясняется
достоинствами этих систем по сравнению с аналоговыми системами передачи:
высокой помехоустойчивостью, лучшему использованию пропускной способности при
передаче дискретных сообщений и др.
В данной расчетной работе изложены материалы по
функциональному преобразованию сигналов с использованием КИХ - структур и
метода «быстрой» свертки. Приведены характерные примеры преобразования
Гильберта.
Работа была выполнена с использованием
компьютера и отладочного модуля.
1. ОБЗОРНАЯ ЧАСТЬ
.1 Определение преобразования
Гильберта
Преобразование Гильберта (ПГ)- это математическая
процедура, выполняемая над действительным сигналом x(t) и дающая новый
действительный сигнал xht(t). И наша цель состоит в том, чтобы xht(t)
представлял собой сдвинутую на π/2 версию
сигнала x(t).
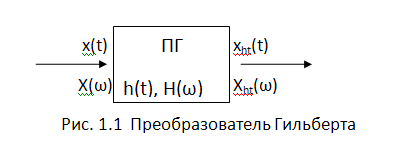
Рисунок 1.1
где x(t) - исходный сигнал(t)- преобразованный
по Гильберту сигнал
H(ω) и h(t)- частотная и
импульсные характеристики ПГ(t) и Xht(t)- преобразование Фурье исходного и ПГ
сигнала(t)=h(t)*x(t), спектр xht(t) определяется как Xht(ω)=H(ω)∙X(ω),
где H(ω)= -j
для ω>0(ω)=
j
для ω<0.
Это можно показать тем, что все компоненты
xht(t) с положительными частотами равны компонентам x(t) c положительными
частотами, сдвинутым по фазе на -900, а все компоненты xht(t) с отрицательными
частотами равны компонентам x(t) c отрицательными частотами, сдвинутым по фазе
на +900.
Преобразователь Гильберта имеет следующую
идеальную импульсную g(t) характеристику и коэффициент передачи К(f)
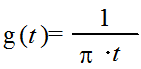 (1.1)
(1.1)
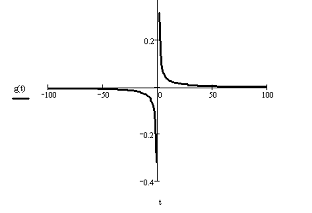
Рисунок 1.2 - Идеальная импульсная
характеристика преобразователя Гильберта
Коэффициент передачи(КП) идеального ПГ по
определению равен:
К0(f)=-jsign(f)=exp{-j sign(f)}(1.2)
sign(f)}(1.2)
, x<0
гдеsign(x)=0,
x=0
, x>0
Амплитудно-частотная характеристика (АЧХ):
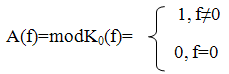 (1.3)
(1.3)
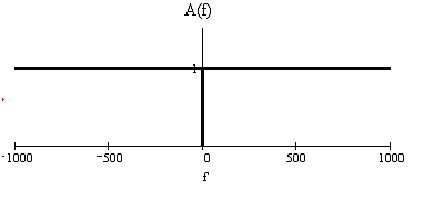
Рисунок 1.3 - АЧХ для идеального ПГ
Фаза Частотная Характеристика (ФЧХ):
φ(f)=argK0(f)= -π/2∙sign(f)(1.4)
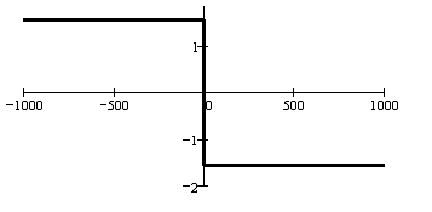
Рисунок 1.4 - ФЧХ для идеального ПГ
1.2 Проблемы разработки аналоговых
ПГ
В теории сигналов важное значение имеют две
теоремы - о свертке и произведении сигналов:
S12(t) = S1(t)*S2(t)↔U1(f)∙U2(f) (1.5)
S1∙S2= U1(f)*U2(f) = U12(f) (1.6)
где *- обозначена операция интегральной свертки
↔ - отображение по Фурье
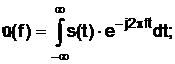 (1.7)
(1.7)
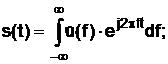 (1.8)
(1.8)
Пусть у нас есть линейная система с
постоянными параметрами g(t) и K(f). (напр. - ПГ), тогда выходной сигнал будет
равен:
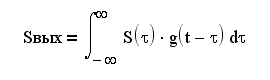 (1.9)
(1.9)
Этот интеграл можно представить в
виде суммы двух интегралов:
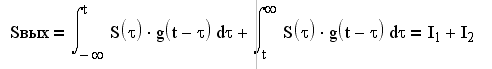 (1.10)
(1.10)
Здесь I1 - реакция системы на
“прошлое” воздействие (до момента t), g(t) для t ≥0; I2 - реакция система
на “будущее” воздействие, g(t), для t<0, из чего можно сделать вывод, что
для реальных аналоговых систем I2=0. Здесьработает принцип причинности:
реальные системы не могут реагировать на “будущее” воздействие- g(t)=0, для
t<0. Из всего этого можно сделать вывод, что в реальных системах из-за
отсутствия I2 в Sвых точный результат свертки не достижим.
Еще одной особенностью идеальных
характеристик цифровых систем (ПГ в частности) является их протяженность во
времени. Эти характеристики бесконечны по времени и по частоте. Ясно, что
реализовать их невозможно. В практических случаях используют усечение и сдвиг
по времени:
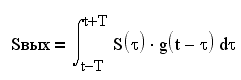 (1.11)
(1.11)
Видно, что свертка (1.11) учитывает
интеграл I2,а значит будет точнее результат свертки. Однако реализация этой
свертки в аналоговом варианте опять же невозможна, поэтому для реализации ПГ
переходят к дискретизации, где сдвиг и усечение возможно благодаря регистрам
памяти.
.3 Особенности и варианты
проектирования цифровых ПГ
Существует два класса фильтров -
КИХ- и БИХ-фильтры (с конечной и бесконечной импульсными характеристиками
соответственно). Оба класса фильтров относятся к классу линейных систем с
постоянными параметрами (ЛПП-системы), в которых входная Хn и выходная Уn
последовательности связаны отношениями типа свертки. Если обозначить через
gкотклик системы на единичный импульс (импульсную характеристику ЛПП-системы),
то получим свертку вида:
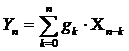 , n=0,1,2… (1.13)
, n=0,1,2… (1.13)
где Хn, Уn- отсчеты входного и выходного сигналов;
Хn-k - выходной отсчет, задержанный на k интервалов дискретизации.
В КИХ-фильтре отсчет выходного сигнала
определяется только значением входного сигнала, а в БИХ-фильтре - значениями
входного и выходного сигналов. Это хорошо видно из линейных разностных
уравнений с постоянными коэффициентами, которые описывают данный класс
дискретных систем. В общем виде разностное уравнение, описывающее БИХ-фильтр,
имеет вид:
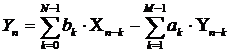 . (1.14)
. (1.14)
где М, N - постоянные целые числа;
bk, ak - постоянные коэффициенты, описывающие конкретную систему; Хn, Уn -
отсчеты входного и выходного сигналов.
КИХ- фильтр задается уравнением:
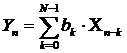 ,
(1.15)=b0·Xn+b1·Xn-1+b2·Xn-2+…+bn·Xn-N+1. (1.16)
,
(1.15)=b0·Xn+b1·Xn-1+b2·Xn-2+…+bn·Xn-N+1. (1.16)
Таким образом, для построения систем
цифровой фильтрации требуется эффективная реализация соотношения типа
дискретной свертки, которая раскладывается на операции умножения и
суммирования, а также операции задержки.
.3.1 Метод временной выборки
Структуры фильтров могут быть
разнообразными и определяются формой представления обобщенной передаточной
функции Dg(z):
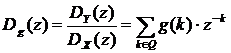 , (1.17)
, (1.17)
где Q - множество натуральных чисел.
Если импульсная характеристика g(k)≠0 для всех k€(-∞,∞), то
схема не реализуема. Схема может быть реализуема в случае, если g(k)≠0,
k€Q=[0,∞). Она будет относиться к БИХ-фильтрам (возможно неустойчивым).
Наконец, если g(k)≠0, k€Q=[0,N-1], то схема реализуема и устойчива
(КИХ-фильтр).
Структура эквивалентной ЛПП-системы
непосредственно следует из (1.17) и представлена на рисунке 1.5. Она
иллюстрирует метод временной выборки (имеются в виду выборки импульсной
характеристики).

Рисунок 1.5 - Структурная схема эквивалентной
ЛПП-системы
Схема имеет вид нерекурсивного фильтра. Ее еще
называют трансверсальным (поперечным) фильтром или ”схемой с многоотводной
линией задержки” (при z=ej·ω·∆t).
Характерным является то, что передаточная функция (1.17) не имеет полюсов,
поэтому схему рисунка 1.5 называют фильтром без полюсов. Ясно, что такой фильтр
является КИХ-фильтром.
Достоинства КИХ-фильтров следующие: они всегда
устойчивы; “шум”, обусловленный эффектами квантования, можно минимизировать;
позволяют получать заданные АЧХ с линейными фазовыми характеристиками; в форме
весовой обработки на основе алгоритмов БПФ они вполне конкурируют с
БИХ-фильтрами. Недостатком является то, что наклон фазовой характеристики может
быть равен только целому числу интервалов дискретизации (или включать еще
половину интервала).
Ясно, что КИХ-фильтр дает наилучшие результаты
аппроксимации, когда аналоговый прототип имеет импульсную характеристику
конечной протяженности.
.3.2 Метод частотной выборки
Большое разнообразие форм представления
ЛПП-систем дает использование интерполяционных формул для передаточной функции,
значения которой Dg(zk) заданы или рассчитаны в фиксированных точках Zk.
Наиболее распространенной является формула Лагранжа. Точки Zkудобно задать
равномерно расположенными на единичной окружности
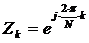 , k=0,1,…,N-1. (1.18)
, k=0,1,…,N-1. (1.18)
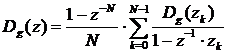 . (1.19)
. (1.19)
Соответствующая структура
ЛПП-системы приведена на рисунке 1.6.
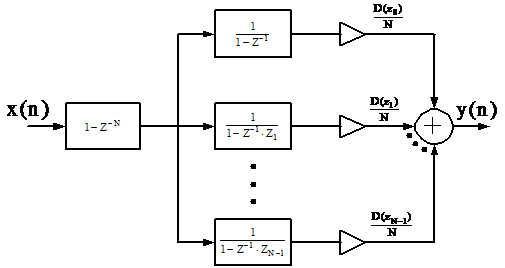
Рисунок 1.6 - Структурная схема
ЛПП-системы
Эту схему называют схемой на основе
частотной выборки, так как исходными данными являются значения передаточной
функции Dg(ejω)=K∆(ω) в точках
Zk=ej∆ωk,
где
∆ω=2π/N,
k=0,1,…,N-1.
Отметим особенность схемы,
приведенной на рисунке 1.6. В силу указанной эквивалентности в целом она не
должна иметь полюсов. Следовательно, полюса параллельных звеньев должны
компенсироваться нулями цепи с передаточной функцией 1-Z-N. Однако реально в
результате арифметических операций с конечной точностью этой компенсации
полностью не происходит. Практически схема будет иметь нули и полюса, то есть
импульсная характеристика будет неограниченной (БИХ-фильтр).
Преимущества данной схемы начинают
проявляться в тех случаях, когда синтезируются узкополосные фильтры. При этом
большинство весовых коэффициентов D(zi)/N в силу малости можно отбросить и схема
существенно упрощается.
.3.3 Метод быстрой свертки
До сих пор, по существу,
рассматривались методы весовой обработки входной последовательности Х(k) путем
моделирования ЛПП-системы. Однако эта обработка может быть реализована
непосредственно на основе вариантов теоремы о свертках с использованием быстрых
алгоритмов преобразования Фурье.
Положим, входная последовательность
Х(k) и импульсная реакция g(k) ЛПП-системы являются периодическими функциями с
периодом N отсчетов. Тогда имеем:
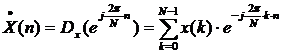 , (1.20)
, (1.20)
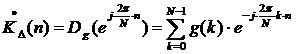 . (1.21)
. (1.21)
В силу теоремы о свертках, для
выходной последовательности:
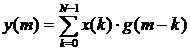 , (1.22)
, (1.22)
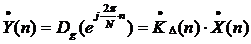 . (1.23)
. (1.23)
где y(m) и 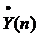 связаны
также дискретным преобразованием Фурье (ДПФ) и являются периодическими
функциями с периодом N.
связаны
также дискретным преобразованием Фурье (ДПФ) и являются периодическими
функциями с периодом N.
Весовая обработка выполняется
следующим образом: находятся БПФ входной последовательности и импульсной
реакции, результаты перемножаются, и вычисляется ОБПФ. В итоге получается
выходная последовательность y(n). Такая процедура называется методом быстрой
свертки, так как в основе используются алгоритмы БПФ.
Особенность процедуры заключается в
том, что для вычисления БПФ необходимо “запомнить” все выборочные значения
x(k), k=0,1,…,N-1 входной последовательности.
Метод быстрой свертки можно
использовать и в случае апериодических последовательностей x(k) и g(k), длины
которых равны N1 и N2 соответственно. Тогда линейная свертка данных
последовательностей
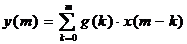 . (1.24)
. (1.24)
является также последовательностью
конечной длины N1+N2-1. Как видно, длина входной и выходной последовательностей
неодинакова. Однако, дополнив последовательности x(k) и g(k) нулевыми отсчетами
так, чтобы все три последовательности оказались равными по длине N1+N2-1, можно
теперь использовать метод быстрой свертки (1.20) - (1.23) с (N1+N2-1)-точечным
БПФ.
В отдельных случаях обработки
сигналов возникает ситуация, когда последовательности x(k) намного больше g(k).
Здесь формальное дополнение нулями последовательности g(k) уже может приводить
к нежелательным последствиям. Выше отмечалось, что результат в методе быстрой
свертки появляется после введения всех входных отсчетов. Следовательно, в
рассматриваемом случае обработка будет выполнятся с большой задержкой.
.4 Эффекты квантования параметров
Для представления коэффициентов
системы (коэффициентов разностного уравнения или передаточной функции) и
отсчетов обрабатываемого сигнала в цифровой системе используют элементы памяти
(регистры, элементы памяти), разрядность которых конечна. Ограничение
разрядности элементов памяти и операционных устройств системы приводит к
операции квантования.
Квантование - это нелинейная
операция. Ее введение в алгоритм обработки сигналов, описываемых линейным
дискретным уравнением, вызывает появление ошибок в реализации алгоритма. Эти
ошибки называет ошибками квантования.
Источниками ошибок квантования в
цифровых системах являются:
аналого-цифровое
преобразование(АЦП), при котором квантуются дискретные сигналы;
умножение цифровых сигналов;
квантование коэффициентов цифровой
системы (коэффициентов разностного уравнения или передаточной функции).
Для упрощения эффектов квантования в
цифровых системах вводится следующее допущение. Ошибки в выходном сигнале,
вызванные квантованием входного сигнала, и ошибки, обусловленные квантованием
результатов арифметических операций в цифровой системе не зависят друг от
друга.
Собственный шум цифровой системы:
Собственный шум системы - это
выходной шум квантования, обусловленный округлением (усечением) результатов
операций умножения.
Собственный шум и его оценки
определяют в три этапа:
)Составляется линейная модель
цифровой системы, учитывающая шумы квантования в тех точках системы, в которых
выполняется операция квантования.
)Вычисляются реакции системы на
каждый шумовой сигнал (составляющие собственного шума).
)На основе полученных составляющих
формируется собственный шум цифровой системы, находятся его вероятностные и
детерминированная оценки.
Составляющие собственного шума -
реакция цифровой системы на шумовые сигналы от каждого источника шума
eY, вых - собственный шум- кол-во источников
шума(m) - ИХ источника
Полный выходной шум
Полный выходной шум системы, обусловленный
квантованием входного сигнала и квантованием результатов арифметических
операций умножения, определяется суммой соответствующих ошибок, т.е.
вых (n)= eA, вых (n) + ey, вых (n)(1.26)
, вых (n) - шум АЦП, мощность которого равна Δ/12
.5 Назначение и области применение
ПГ
ПГ часто оказывается полезным во множестве
приложений обработки комплексных (квадратурных) сигналов в следующих областях:
квадратурная модуляция и демодуляция,
автоматическая регулировка усиления,
анализ 2-х и 3-х мерных сигналов,
построение изображений в медицине, анализ
сейсмических данных и океанических волн,
оценка мгновенной частоты,
обработка сигналов в радарах /сонарах,
измерение задержки приема сигналов,
приемники телевиденья высокой четкости (HDTV),
и т.д.
Рассмотрим в качестве примера ПГ в QAM
модуляции:
Преобразование Гильберта для любого
произвольного сигнала представляет собой идеальный широкополосный
фазовращатель, который осуществляет поворот начальных фаз всех частотных
составляющих сигнала на угол, равный 90о (сдвиг на /2). Применение
преобразования Гильберта позволяет выполнять квадратурную модуляцию сигналов, в
каждой текущей координате модулированных сигналов производить определение
огибающей и мгновенной фазы и частоты сигналов, выполнять анализ каузальных
систем обработки сигналов.
На рисунке 1.7 приведен пример использования
преобразователя Гильберта при QAM модуляции. Квадратурная амплитудная модуляция
(quadratureamplitudemodulation - QAM) является популярным методом аналоговой
передачи сигналов, используемым в некоторых беспроводных стандартах. Данная
схема модуляции совмещает в себе амплитудную и фазовую модуляции. В методе QAM
использованы преимущества одновременной передачи двух различных сигналов на
одной несущей частоте, но при этом задействованы две копии несущей частоты,
сдвинутые относительно друг друга на 90°. При квадратурной амплитудной
модуляции обе несущие являются амплитудно-модулированными. Итак, два независимых
сигнала одновременно передаются через одну среду. В приемнике эти сигналы
демодулируются, а результаты объединяются с целью восстановления исходного
двоичного сигнала. Для получения двух несущих сдвинутых относительно друг друга
на 90° и используют преобразователь Гильберта.
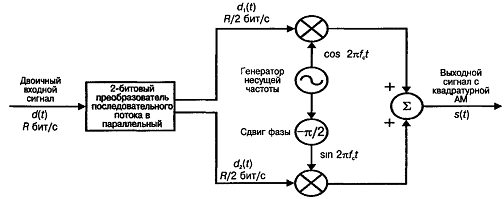 исунок 1.7 -
Модулятор QAM
исунок 1.7 -
Модулятор QAM
2. РАСЧЕТНАЯ ЧАСТЬ
.1 Преобразователь Гильберта как
КИХ-фильтр
.1.1 Задание эталонных (КП и ИХ)
характеристик
Переходя к дискретному времени и частоте, мы еще
не решили вопросы реализации ПГ. Полученные нами характеристики (КП и ИХ) (1.3
И 1.4) аналогового прототипа необходимо модифицировать определенным образом.
Модифицированные характеристики назовем эталонными[1].
ИХ и КП идеализированного ПГ в аналоговом варианте
имеют бесконечную протяженность, и для реализации ПГ необходимо их усечь:
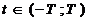 ,
, 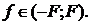 (2.1)
(2.1)
При этом мы должны сохранить строгую
симметрию и асимметрию компонент в частотной и временной областях.
Для формирования эталонных
характеристик воспользуемся прямоугольной стробирующей функцией[1]:
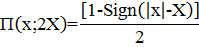 (y;2X)=2X∙Sinc(2πyX) (2.2)
(y;2X)=2X∙Sinc(2πyX) (2.2)
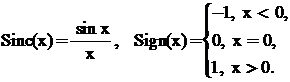 (2.3)
(2.3)
Здесь W(y,2X) - преобразование Фурье
от функции П(x,2X). Переменные x и y могут играть роль времени или частоты.
Усечение КП по частоте дает[1]:
KF(f)=K0(f)∙П(f;2F),KF(0)=0(2.4)
По условию F=4∙27∙100=10800 Гц.
Приведем графики усеченных АЧХ и ФЧХ ПГ (рис. 2.2).
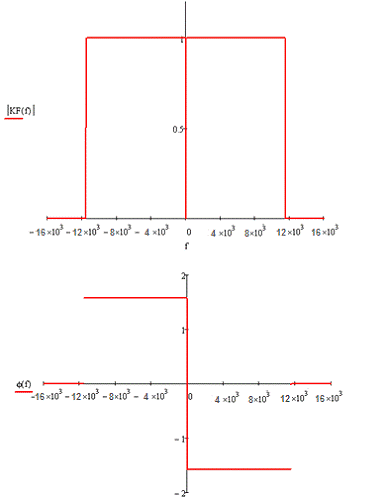
Рисунок 2.1 - Усеченные АЧХ и ФЧХ ПГ
Из рис. 2.1 видно, что АЧХ и ФЧХ ПГ сохранили
свои прежние значения в полосе частот (-F; F), а вне этой полосы их значения
равны нулю.
ИХ определим следующим образом[1]:
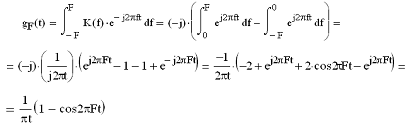
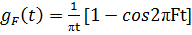 (2.5)
(2.5)
Возникает неопределенность вида (0/0) в момент
t=0 - пользуемся правилом Лопиталя:
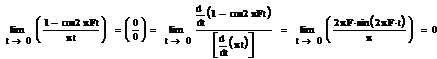
Таким образом, имеем:
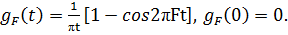 (2.6)
(2.6)
Приведем график усеченной ИХ ПГ (рис. 2.2).
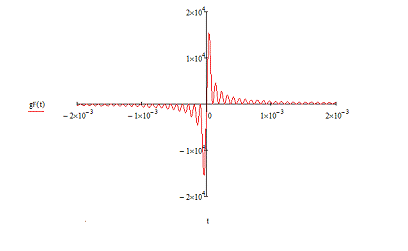
Рисунок 2.2 - Усеченная импульсная
характеристика ПГ
Как видно на рис. 2.3 ИХ имеет продолжение в
отрицательной области. Тем самым нарушатся принцип причинности. Поэтому в целях
обеспечения реализуемости рассматривают усечённую импульсную характеристику,
сохраняя её основное свойство - нечетность[1].
Примем значение базы B=8, следовательно, имеем:
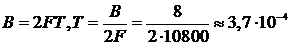 [c](2.7)
[c](2.7)
Далее смещаем ИХ gF(t) на отрезок T
и усекаем ее отрезком 2T. В результате получим:
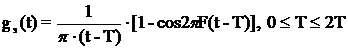 (2.8)
(2.8)
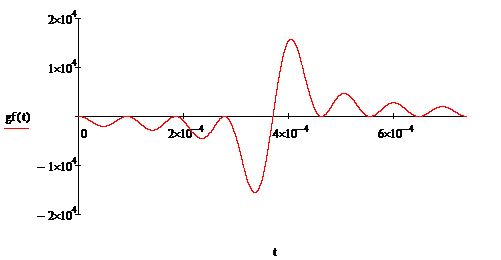
Рисунок 2.3 - Эталонная ИХпри B=8
Для нахождения эталонного КП возьмем
прямое преобразование Фурье отИХ (2.8):
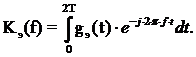
В итоге получим,
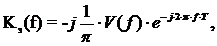 (2.9)
(2.9)
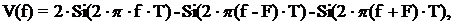
(x) - интегральный синус.
Преобразуем к более компактному
виду: для этого введем параметрB=2FT[1].
На безразмерной оси частот(f=xF)
эталонный КП равен:
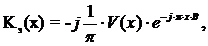 (2.10)
(2.10)
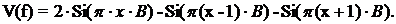
Параметр B задает базу усеченной ИХ
(2B=4FT).
Для анализа изменения КП (АЧХ и ФЧХ)
и ИХ в зависимости от базы построим эти характеристики для В=4, В=8 и В=20
(рис. 2.5-2.7).
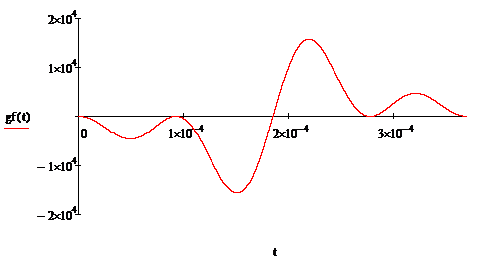
Рисунок 2.4
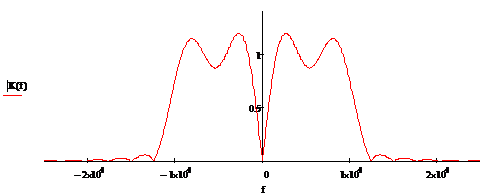
Рисунок 2.5
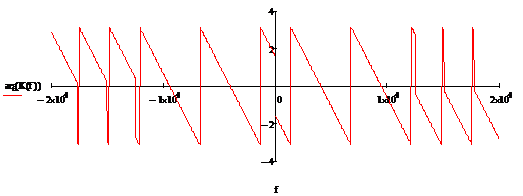
Рисунок 2.6 - Эталонные ИХ, АЧХ,
ФЧХПГсоответственно приВ = 4

Рисунок 2.7
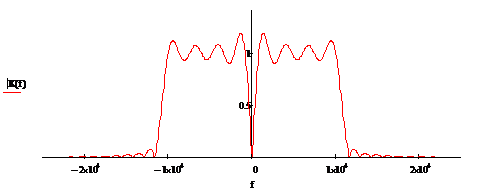
Рисунок 2.8
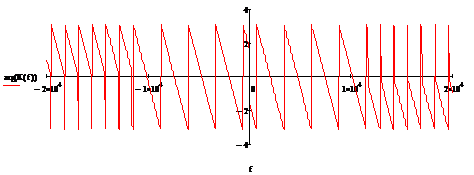
Рисунок 2.9 - Эталонные ИХ, АЧХ,
ФЧХПГсоответственно приВ = 8
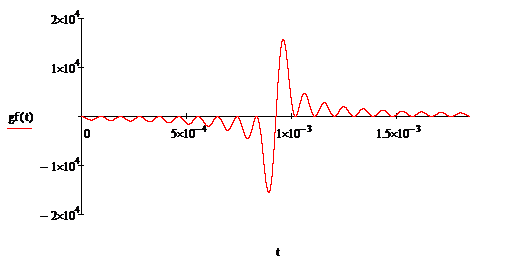
Рисунок 2.10
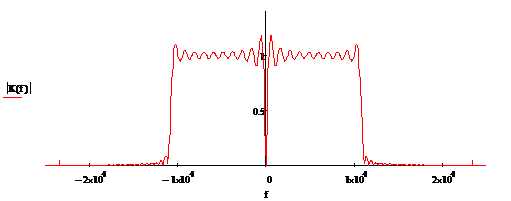
Рисунок 2.11
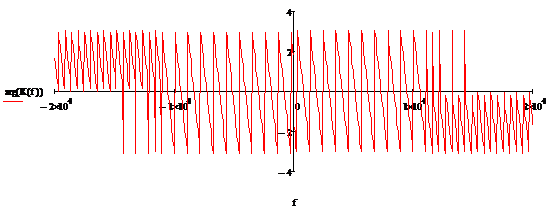
Рисунок 2.12 - Эталонные ИХ, АЧХ,
ФЧХПГсоответственно приВ = 20
Проанализировав рисунки 2.5-2.7, можно сделать
вывод, что cувеличением базы В (следовательно, и периода Т) коэффициент
передачи ПГ всё больше стремиться к идеальному.
2.1.2 Энергетические потери при
усечении ИХ
При усечении бесконечной импульсной
характеристики идеального ПГ, возникают энергетические потери [1]:
Q(T) = 1 - η(T) = 1 - ET/E
(2.11)
сохраняемая при усечении энергия ИХ,
Е - полная энергия ИХ.
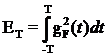
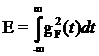 (2.12)
(2.12)
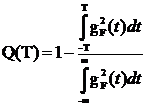 (2.13)
(2.13)
Энергетические потери при усечении
бесконечной импульсной характеристики идеального ПГ при увеличении базы
уменьшаются (B=2FT). Можно подобрать такое значение базы, при котором потери
практически будут равны нулю.
.1.3 Выбор частоты дискретизации
В аналоговом варианте усечение и
сдвиг импульсной характеристики может быть реализовано с использованием линий
задержки, инвертора, сумматора и интегратора, причём характеристики этих блоков
должны стремиться к идеальным, что крайне сложно реализовать. Совсем иначе дело
обстоит в дискретном варианте, когда сдвиг и усечение выполняются естественным образом
благодаря регистрам памяти.
Для перехода к дискретному времени,
прежде всего, необходимо задать частоту дискретизации[1]:
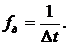 (2.14)
(2.14)
Практически частоту дискретизации
выбирают с запасом в диапазоне для минимизации перехлеста в частотной области:
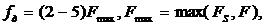 (2.16)
(2.16)
иF - граничные частоты сигнала и
преобразователя.
Как правило, преобразователь должен
«работать» в полосе частот сигнала, поэтому Fmax=FS=F.
Исходя из вышесказанного, выберем
частоту дискретизации, равной:
2.1.4 Импульсная характеристика
дискретного ПГ
В ИХ введем дискретное время [1]:
(2.17)
Полагаем, что на отрезке 2T взято
целое число (N) отсчетов:
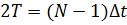 . (2.18)
. (2.18)
Это дает:
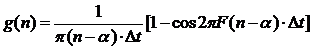
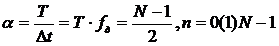 (2.19)
(2.19)
Частота дискретизации fд=2F=21600
Гц, следовательно α=B.
Точку n = α включим в
общий массив n = 0(1)N-1, т.е. α - целое число. Это позволит нам в
дальнейшем использовать схему со средней точкой[1].
Итак, определены все параметры:
N-нечетное, α
и
B - четные и нечетные.
Реализуемая ИХ с нечетной симметрией
относительно точки, n= αравна:
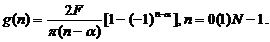 (2.18)
(2.18)
В частности, имеем:
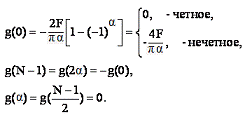 (2.19)
(2.19)
При дискретизации стробирующая
функция П(t;2T) становится не совсем “прямоугольной”. Ее концевые отсчеты
вместо 1 принимают значения по 0,5. Поэтому ИХ ПГ необходимо уточнить [1]:
Пусть α и
N-нечетные:
выберем значение базыB =9,
следовательно
α=B =9=>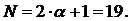
Расчеты произведем в среде mathcad:
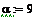 9:=10800
9:=10800
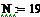
9
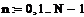
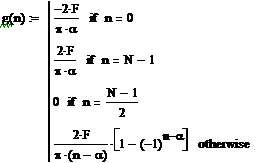
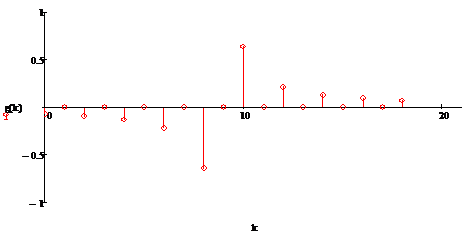
Рисунок 2.13 - Дискретная ИХ (для α=9)
Пусть α - четное,
N-нечетное: выберем значение базыB =10, следовательно
α=B =10=>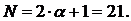
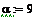 10:=10800
10:=10800
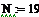
21
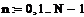
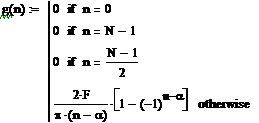
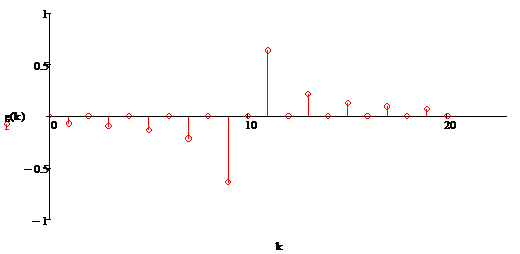
Рисунок 2.14 - Дискретная ИХ (для α=6)
Различия ИХ для α - четного или
нечетного - заключаются в отсутствии или наличии концевых отсчетов. Дискретная
ИХ с четным N практического применения не нашла, т.к. невозможно применять
схему со средней точкой. В данной работе мы ее рассматривать не будем. Схема
дискретного преобразователя Гильберта (2.18) для α нечетного
показана на рис. 2.10. Парные множители, отличающиеся знаком, объединены [1].
Параметры схемы задаются следующим
образом:
Системная функция такой схемы будет равна:
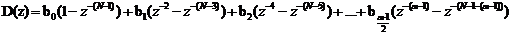
Вычислим в среде MathCadпараметры
данной схемы bm:
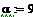 9
9
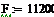 10800
10800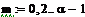
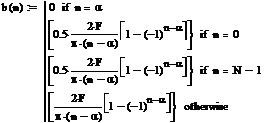
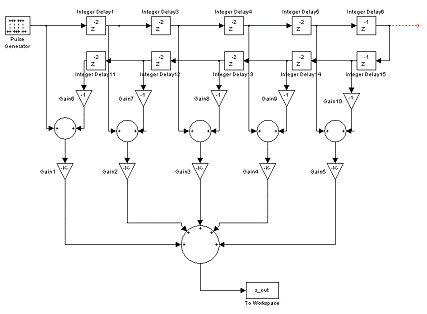
Рисунок 2.15 - Схема дискретного
преобразователя Гильберта сИХ для α=9
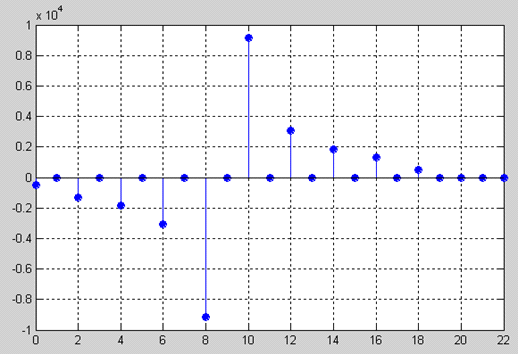
Рисунок 2.16 - Дискретная ИХ (для α=9)
Как видим, дискретные ИХ для α=9,
построенные
в средах MathCad и Matlabсовпали, что свидетельствует о правильности всех схем
и алгоритмов.
Схема дискретного преобразователя Гильберта сИХ
(2.18) для α четного показана
на рис. 2.12[1].
Параметры схемы задаются следующим образом:
Звено с параметром b0будет отсутствовать.
Системная функция:
гильберт преобразование свертка
фильтр
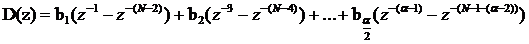
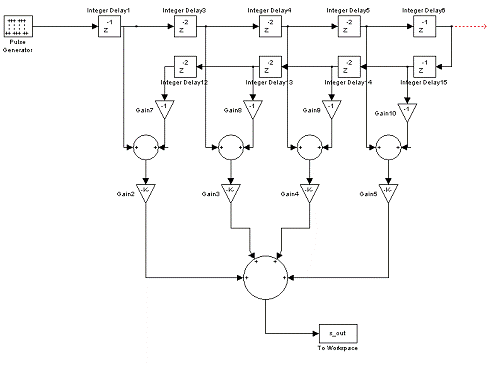
Рисунок 2.17 - Схема дискретного преобразователя
Гильберта для α=8
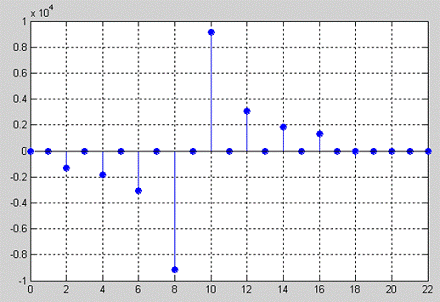
Рисунок 2.18 - Дискретная ИХ (для α=8)
Как видим, и в этом случае дискретные ИХ для α=8,
построенные
в средах MathCadи Matlabсовпали - все схемы и алгоритмы составлены верно.
2.1.5 Коэффициент передачи
дискретного ПГ
Частотную характеристику дискретного ПГ найдем
заменой переменной z=ej2πfΔt в
системной функции[1]:
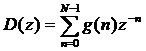 (2.25)
(2.25)
Из формулы суммирования Пуассона:
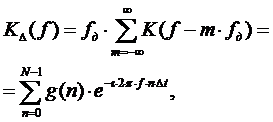 (2.26)
(2.26)
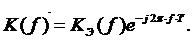
Подставим для 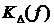 ИХ (2.18) (с
той же частотой дискретизации на безразмерной оси xд=2). Учтем нечетную симметрию
ИХ g(α+m)
= -g(α-m), m=1,2,…,α. С условием g(α)=0, концевые
отсчетыg(0) и g(2α)для
ИХ (2.18) (с
той же частотой дискретизации на безразмерной оси xд=2). Учтем нечетную симметрию
ИХ g(α+m)
= -g(α-m), m=1,2,…,α. С условием g(α)=0, концевые
отсчетыg(0) и g(2α)для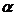 введем с
весом 0,5(см. (2.21)). Устраним различия в размерностях эталонного и
реализуемого КП делением на частоту дискретизации [1]:
введем с
весом 0,5(см. (2.21)). Устраним различия в размерностях эталонного и
реализуемого КП делением на частоту дискретизации [1]:
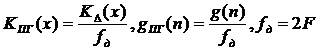 (2.27)
(2.27)
В итоге частотная характеристика
дискретного ПГ принимает вид:
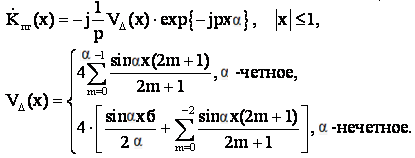 (2.28)
(2.28)
Приведем графики АЧХ и ФЧХ дискретного ПГ для
четного и нечетного α (рис. 2.14 и
рис. 2.15).
Рисунок 2.19 - Графики АЧХ, ФЧХ дискретного ПГ
для α=9
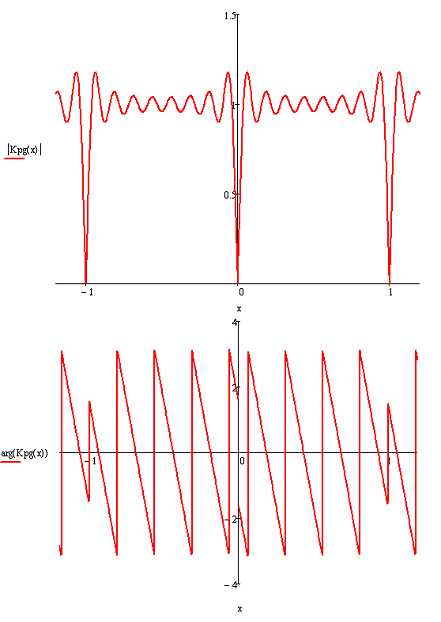
Рисунок 2.20 - Графики АЧХ, ФЧХ дискретного ПГ
для α=8
Из рисунков 2.14 и 2.15 видно, что
КП KΔ
дискретного
фильтра является непрерывной и периодической функцией (с периодом fд).
Тиражирование эталонного КП может приводить к наложению копий и искажению
частотной характеристики фильтра. Эти искажения можно уменьшить только путем
повышения частоты дискретизации 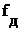 .
.
2.1.6 Анализ прохождения сигнала
через цифровой ПГ
По условию задания входные сигналы - два
гармонических сигнала:
Si(t)=A cos(2
cos(2
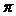
 fi
fi t), i=1,2; A=1 В,
(2.29)
t), i=1,2; A=1 В,
(2.29)
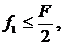
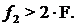
Примем f1=0,25F=27000 Гц и
f2=5F=54000 Гц.
Представим эти сигналы в дискретной
форме [3]:
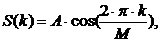 (2.30)
(2.30)
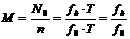 (2.31)
(2.31)
- число отсчетов на период
гармонической функции.
Перепишем (2.30) в иной форме:
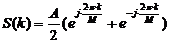 (2.32)
(2.32)
Воспользуемся свойством
геометрической прогрессии и найдем D(z):
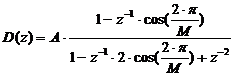 (2.33)
(2.33)
Найдем параметры идеального
косинусного резонатора для двух исходных сигналов[3]:
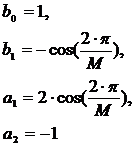 (2.34)
(2.34)
ДляS1(k):
A=1,
f0=f1=0,25F, fд=2F
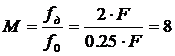
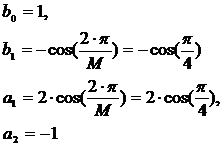
ДляS2(k):
A=1,
f0=f2=5F, fд=2F
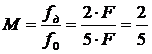
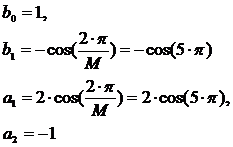
Схема генерации дискретного сигнала представлена
на рис. 2.16.
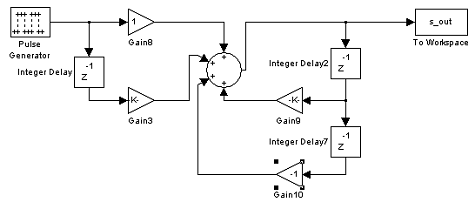
Рисунок 2.21 - Схема генерации дискретного
сигнала S(k)
Пропустим дискретные сигналы S1(k) и S2(k) через
дискретный ПГ с ИХ для α=9.
Схема прохождения дискретных сигналов S1(k) и
S2(k) через дискретный ПГ имеет следующий вид (рис. 2.22):
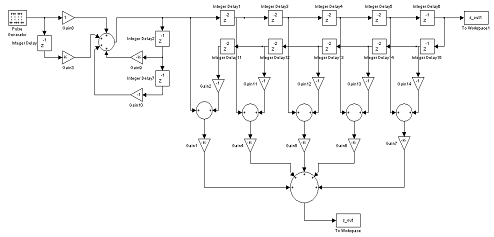
Рисунок 2.22 - Схема прохождения дискретных
сигналов S1(k) и S2(k) через дискретный ПГ с ИХ для α=9
Результаты прохождения дискретных сигналов S1(k)
и S2(k) через дискретный ПГ представлены на рис. 2.18 и рис. 2.19.
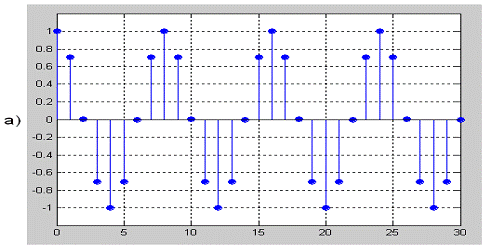
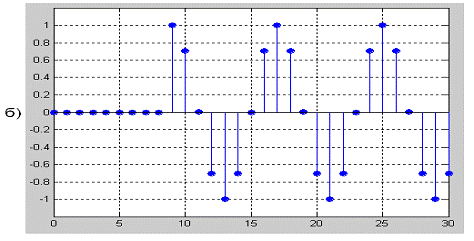
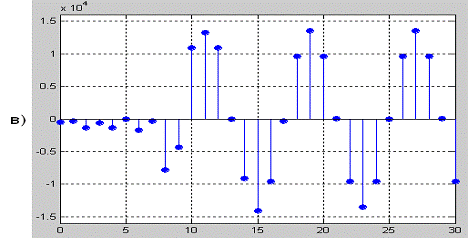
Рисунок 2.23 - Прохождения дискретного сигнала
S1(k) через дискретный ПГ с ИХ для α=9: а)
исходный дискретный сигнала S1(k);б) задержанная на (α=9)
копия
S1(k); в) преобразованный по Гильберту сигнал S1(k)
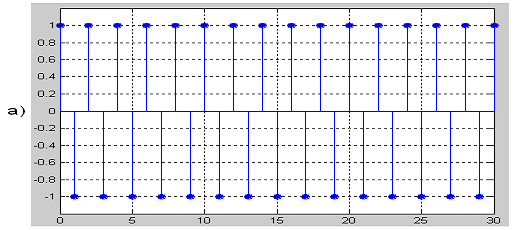
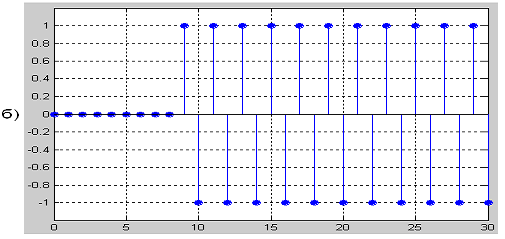
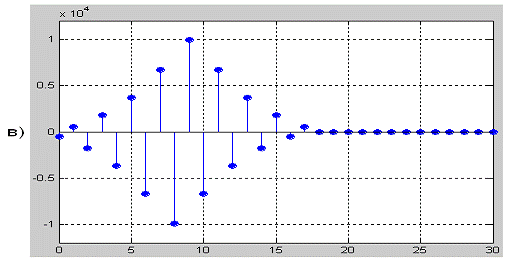
Рисунок 2.24 - Прохождения дискретного сигнала
S2(k) через дискретный ПГ с ИХ для α=9: а)
исходный дискретный сигнала S2(k); б) задержанная на (α=9)
копия
S2(k); в) преобразованный по Гильберту сигнал S2(k)
Схема ПГ со средней точкой“выдает” два сигнала:
задержанную копию входного сигнала (на выходе средней точки)и его
преобразования по Гильберту (на общем выходе). Используя оба выхода, мы, к
примеру, можем получить аналитический сигнал.
Заметим, что при подаче гармонического сигнала
S1(t)= cos(2
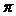
 f1
f1 t),
t),
у которого
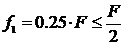 ,
,
(т.е. данный сигнал входит в полосу
преобразования ПГ) на вход ПГ, на выходе получим преобразованный по Гильберту
сигнал (см. рис. 2.18). А при подаче S2(t)= cos(2
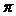
 f2
f2 t), у которого
t), у которого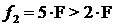 (т.е. данный
сигнал не входит в полосу преобразования ПГ), - получим ноль (см. рис. 2.19).
Значение первых нескольких отсчетов получились вследствие переходных процессов
(когда использовались не все отсчеты ИХ ПГ).
(т.е. данный
сигнал не входит в полосу преобразования ПГ), - получим ноль (см. рис. 2.19).
Значение первых нескольких отсчетов получились вследствие переходных процессов
(когда использовались не все отсчеты ИХ ПГ).
Также заметим, что для
гармонического сигнала S1(t)= cos(2
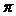
 f1
f1 t),
t), 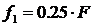 схема будет выдавать повернутую на π/2 копию
входного сигнала (на общем выходе), начиная с отсчета, равного (α-1=8), что
подтверждает определение ПГ как идеального фазовращателя, т.е. фазовый сдвиг
между выходом средней точки и общим выходом составляет
схема будет выдавать повернутую на π/2 копию
входного сигнала (на общем выходе), начиная с отсчета, равного (α-1=8), что
подтверждает определение ПГ как идеального фазовращателя, т.е. фазовый сдвиг
между выходом средней точки и общим выходом составляет  (см. рис.
2.18-в).
(см. рис.
2.18-в).
2.2 Моделирование преобразования
Гильберта методом быстрой свертки
Для моделирования ПГ методом быстрой свертки
необходимо найди коэффициенты ДПФ импульсной характеристики дискретного ПГ и
гармонического сигнала. Далее перемножим полученные коэффициенты БПФ по
принципу «каждый с каждым», и от полученного результата найти коэффициенты ОБПФ
(см. рисунок 2.25) [1].
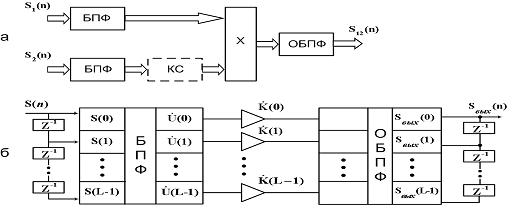
Рисунок 2.25 - Схема реализации метода БПФ
Определим соответствующие множители K(l), l =
0(1)L-1 в схеме на рис. 2.20-б.
В формулу для частотной характеристики
дискретного ПГ (2.20) внесем следующие изменения. Ось частоты переведем в
машинную x Є [0,xД], xД=2, и дискретную с шагом Δx:x→l∙Δx,l=0(1)L-1,L∙Δx=2,
что
дает:
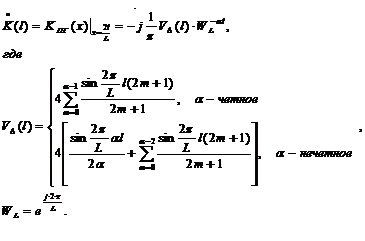
Параметр L задает “частотное”
разрешение преобразователя Гильберта. Массив данных L задается с запасом:
=2r ≥ N+Ns-1,
- число отсчетов гармонического
сигнала,число отсчетов импульсной характеристики дискретногоПГ.
Необходимо обеспечить выполнение
условия:Ns>N.
Пусть α=9 и,
соответственно, N=19.Гармонический сигнал количеством отсчетов не ограничен. А
Lпримем равным: L=64.
Итак, для α=9 и,
соответственно, N=19 коэффициенты ДПФ дляИХ ПГ имеют следующий вид [1]:
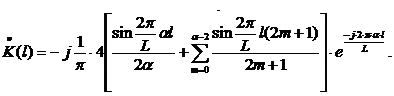
Коэффициенты ДПФ гармонического
сигнала (для гармонического сигналаS1(t)=cos(2πft), f=0.25F=2700 Гц,
входящего в полосу преобразования ПГ):
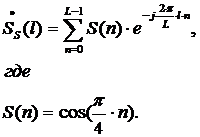
Дополним ИХ ПГ и сигнал отсчетами,
доведя их общее количество до L=64 (см. рис. 2.21и рис. 2.22)
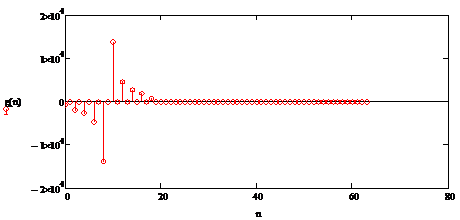
Рисунок 2.26 - ИХ ПГ, дополненная
нулевыми отсчетами до значения L=64
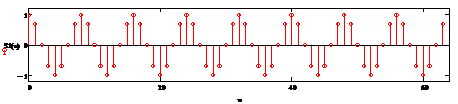
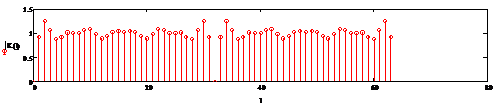
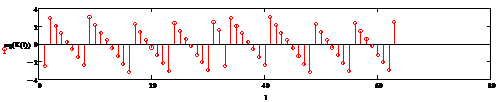
Рисунок 2.28 - График модулей и аргументов
коэффициентов ДПФ ИХ ПГ соответственно
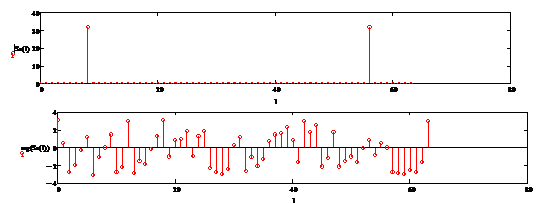
Рисунок 2.29 - График модулей и
аргументов коэффициентов ДПФ гармонического сигнала соответственно
Для нахождения сигнала на выходе
схемы быстрой свертки перемножим полученные коэффициенты ДПФ ПГ и
гармонического сигнала, а затем найдем ОДПФ от результата перемножения [1].
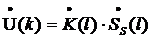 (2.39)
(2.39)

Рисунок 2.30
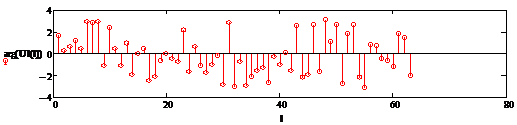
Рисунок 2.31 - График амплитудной и
фазовой характеристик функции 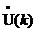 соответственно
соответственно
Найдем преобразованный по Гильберту
входной гармонический сигнал, который входит в полосу преобразования Гильберта,
по методу быстрой свертки (рис. 2.26) [1]:
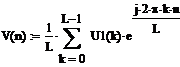
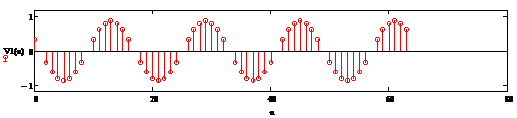
Рисунок 2.32 - Преобразованный по
Гильберту входной гармонический сигнал, который входит в полосу преобразования
Гильберта
Исследуем также прохождение через ПГ
гармонического сигналаS2(t)=cos(2πft), f=5F=54000Гц,
невходящего в полосу преобразования.
Применим туже методику, что и для
сигнала, входящего в полосу преобразования ПГ.
Коэффициенты ДПФ для
соответствующего гармонического сигнала:
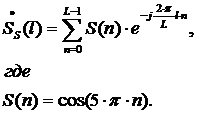
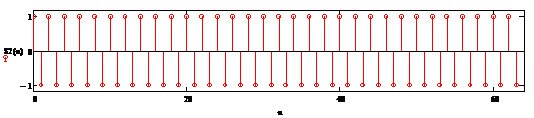
Рисунок 2.33 - Гармонический сигнал
в дискретном виде, не входящий в полосу преобразования ПГ
На выходе ПГ получим следующее (рис.
2.34):

Рисунок 2.34 - Гармонический сигнал,
который не входит в полосу преобразования, на выходе ПГ
Как видим, и в методе быстрой
сверткидля гармонического сигнала, входящего в полосу преобразования, на выходе
ПГ получили повернутую на π/2 копию входного сигнала, что
подтверждает определение ПГ как идеального фазовращателя.
А на выходе ПГ длягармонического
сигнала, не входящего в полосу преобразования, мы также получили ноль.
Итак, результаты прохождения двух
входных гармонических сигналов через ПГ, проектированный по методам КИХ-фильтра
и быстрой свертки полностью совпали, что свидетельствует о правильности
выполнения всех процедур и расчетов.
ЗАКЛЮЧЕНИЕ
В данной расчетной работе была выполнена разработка
цифрового преобразователя Гильберта. В результате чего были решены следующие
задачи:
произведено задание эталонных (КП и ИХ)
характеристик, определены энергетические потери при усечении ИХ;
построена импульсная характеристика дискретного
ПГ, также произведен анализ коэффициента передачи;
произведен анализ прохождения сигнала через
цифровой ПГ;
выполнено проектирование ПГ методом быстрой
свертки
Также была доказана невозможность реализации
характеристик идеального ПГ. Решением проблемы анализа и синтеза оказался
переход на дискретное время и частоту. Реализация цифровых ПГ может быть
выполнена методами временной или частотной выборок.
При анализе прохождения нашего сигнала через
схему, ПГ подтверждает свое определение как идеального фазовращателя. На основе
чего можно сделать вывод о правильности проведенных расчетов.
ЛИТЕРАТУРА
1. Овсянников
В.А. Методы формирования и цифровой обработки сигналов: учеб. - метод. пособие.
В 2 ч. Ч. 2: Дискретное преобразование Фурье, фильтрация и модуляция.- Мн.:
БГУИР, 2010. - 136 с.
2. Овсянников
В.А. Методическое руководство ”Функциональное преобразование сигналов методом
быстрой свертки”.
. Овсянников
В.А. Основы цифровой обработки сигналов. Методическая разработка для
самостоятельной работы студентов по курсу “Теория электрической связи”. В 2-х
частях. - Мн.: МРТИ, 1989.
. Лайонс
Ричард. Цифровая обработка сигналов. М.: Издательство “Бином”. 2006.
. Кореневский
С.А.“Методы и устройства формирования и обработки телекоммуникационных
сигналов. Часть 3”: Метод. пособие по курсовому проектированию для студ. спец.
“Системы радиосвязи, радиовещания и телевидения”, “Многоканальные системы
телекоммуникаций” /всех форм обуч. ЭУМК, Мн.: БГУИР, 2006. - 52 с.