Спектральный анализ аналоговых сигналов и расчет откликов на выходе линейной цепи
Пояснительная
записка к курсовой работе по дисциплине
Методы
математического описания сигналов» (ММОС)
СПЕКТРАЛЬНЫЙ
АНАЛИЗ АНАЛОГОВЫХ СИГНАЛОВ И РАСЧЕТ ОТКЛИКОВ НА ВЫХОДЕ ЛИНЕЙНОЙ ЦЕПИ
РЕФЕРАТ
Целью данной курсовой работы является практическое освоение методов
анализа аналоговых периодических и непериодических сигналов во временной и
частотной областях, а также расчет прохождения этих сигналов через линейную
цепь на примере решения конкретной задачи.
В ходе курсовой работы было произведено разложение сигнал на его типовые
составляющие. Найдена спектральная плотность аналогового непериодического
сигнала, на основе которого рассчитаны коэффициенты комплексного ряда Фурье,
описывающего аналоговый периодический сигнал. Построены спектральные характеристики
аналогового периодического сигнала, а также найдена ширина спектра сигнала.
Восстановлен периодический сигнал усечённым рядом Фурье. Рассчитана и построена
погрешность представления аналогового периодического сигнала усечённым рядом
Фурье. Для заданной цепи найден комплексный коэффициент передачи. Рассчитаны и
построены амплитудно-частотная и фазочастотная характеристики. Также были
рассчитаны и построены переходная и импульсная характеристики операторным
методом расчёта. Найдены и построены отклики прохождения периодического и
непериодического сигнала через аналоговую линейную электрическую цепь.
Расчеты и построение графиков проводились в среде MathCad 15. Пояснительная записка
выполнена в текстовом редакторе Microsoft Office Word 2007 и представлена в текстовом
формате.
Введение
Методы математического описания сигналов является базовым курсом в
системе подготовки современного инженера в области радиотехники и
радиоэлектроники. Его целью является изучение фундаментальных закономерностей
связанных с получением сигналов, их передачей по каналам связи, обработкой и
преобразованием в радиотехнических цепях.
Радиоэлектроника является отраслью знаний, чрезвычайно быстро
развивающейся как в научном, так и в техническом плане. Появляются новые
направления, использующие как новые научные методы, так и новые схематические
решения, новую техническую базу. Однако и некоторые «старые», традиционные
методы и идеи не отмирают, остаются необходимыми в арсенале инженера.
Целью данной курсовой работы является практическое освоение методов
анализа аналоговых периодических и непериодических сигналов во временной и
частотной областях, а также расчет прохождения этих сигналов через линейную
цепь на примере решения конкретной задачи. Также будет рассмотрен математический
аппарат, применяемый при анализе прохождения сигналов. Будут представлены
формулы для расчетов и приведены графики работы линейной цепи.
1.
СПЕКТРАЛЬНЫЙ АНАЛИЗ АНАЛОГОВЫХ ПЕРИОДИЧЕСКИХ И НЕПЕРЕОДИЧЕКИХ СИГНАЛОВ
1.1. ИСХОДНЫЕ
ДАННЫЕ
Код сигнала: 33;
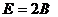 -
амплитуда импульса;
-
амплитуда импульса;
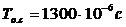 - период
описания сигнала;
- период
описания сигнала;
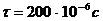 -
длительность импульса.
-
длительность импульса.
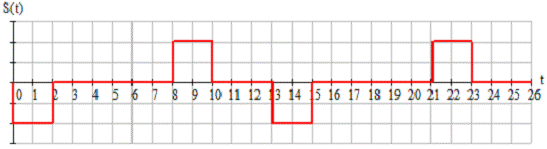
Рисунок
1.1 - Временное представление исходного аналогового сигнала
1.2. РАЗЛОЖЕНИЕ
СИГНАЛА НА ТИПОВЫЕ СОСТАВЛЯЮЩИЕ
Разложим
аналоговый сигнал на его типовые составляющие, которые включаются в
определенный момент времени. Для этого будем исходить из временного
представления сигнала (рисунок 1.1) и использовать единичную функцию включения 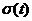 .
.
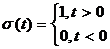
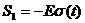
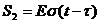
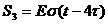
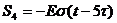

Рисунок
1.2 - Временное представление типовых составляющих сигнала
1.3. РАСЧЕТ
СПЕКТРАЛЬНОЙ ПЛОТНОСТИ АНАЛОГОВОГО СИГНАЛА
Спектральная
плотность - это плотность спектральных линий приходящихся на единицу частоты.
Спектральная характеристика является комплексной функцией частоты 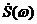 :
:
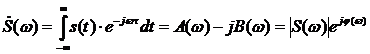
Исходный
сигнал описывается нечетной функцией времени, значит, спектральная плотность
будет описываться вещественной функцией частоты 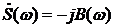 .
.
Для
того чтобы упростить нахождение спектральной характеристики рассмотрим
одиночный импульс из нашего сигнала.
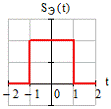
Рисунок
1.3 - Временное представление одиночного импульса
Представим
сигнал  с помощью типовых составляющих:
с помощью типовых составляющих:
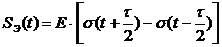
Применяя
прямое преобразование Лапласа, найдем изображение 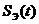 :
:
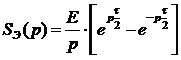
Из
полученного выражения путем замены  найдем
спектральную плотность элементарного составляющего сигнала
найдем
спектральную плотность элементарного составляющего сигнала
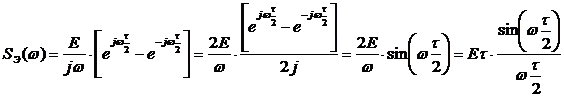
Возьмем
два знакочередующихся импульса прямоугольной формы из исходного сигнала,
сместив ось ординат в центр между этими импульсами.
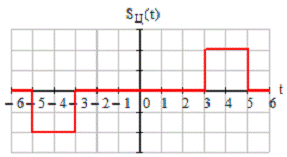
Рисунок
1.4 - Временное представление «центрированного» сигнала
Моделируем
сигнал 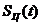 из
из 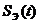 :
:
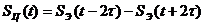
Применяя
теорему сдвига, определим спектральную плотность 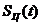 :
:
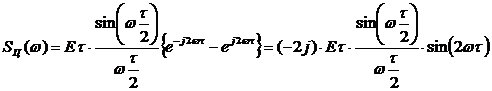 .
.
Возвращаем
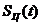 в исходное место, для нахождения спектральной
плотности нашего аналогового сигнала (рисунок 1.1):
в исходное место, для нахождения спектральной
плотности нашего аналогового сигнала (рисунок 1.1):
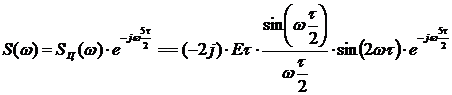 .
.
Фазовый
множитель 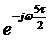 свидетельствует о сдвиге сигнала во временной области
на
свидетельствует о сдвиге сигнала во временной области
на 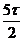 .
.
1.4.
РАСЧЕТ И ПОСТРОЕНИЕ СПЕКТРА КОЭФФИЦИЕНТОВ КОМПЛЕКСНОГО РЯДА ФУРЬЕ
Рядом Фурье называется разложение аналогового сигнала на сумму
гармонических функций с разными амплитудами и начальными фазами. Амплитуды
составляющих гармонических функций называются коэффициентами комплексного ряда
Фурье.
Сигнал, изображенный на рисунке 1.1, представляет собой знакочередующуюся
последовательность импульсов прямоугольной формы, поэтому постоянная
составляющая равна нулю:
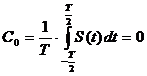 .
.
Путем дискретизации спектральной плотности нашего сигнала определим
комплексные коэффициенты Фурье:
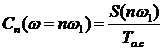 ;
;
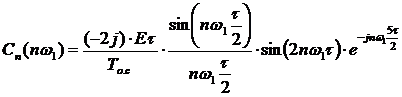 ,
,
где
 - циклическая частота сигнала.
- циклическая частота сигнала.
Запишем
расчетную формулу для комплексных коэффициентов Фурье
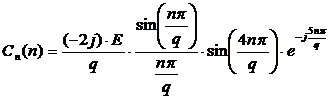 , где
, где  - скважность.
- скважность.
Таблица
1 - Коэффициенты комплексного ряда Фурье
|
n
|
Алгебраическое
представление 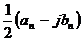 Модуль Модуль 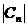 Аргумент Аргумент
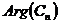
|
|
|
|
0
|
0
|
0
|
0
|
|
1
|
- 0.367 + j0.414
|
0.553
|
2.296
|
|
2
|
- 0.345 +j0.042
|
0.347
|
|
3
|
0.161 + j0.111
|
0.196
|
0.604
|
|
4
|
0.071 + j0.287
|
0.295
|
1.329
|
|
5
|
- 0.019 + j0.036
|
0.04
|
2.054
|
|
6
|
0.039 - j0.015
|
0.042
|
-0.362
|
|
7
|
- 0.033 - j0.013
|
0.036
|
-2.779
|
|
8
|
0.012 + j0.022
|
0.025
|
1.087
|
|
9
|
- 0.031 + j0.127
|
0.131
|
1.812
|
|
10
|
- 0.048 + j0.033
|
0.059
|
2.537
|
|
11
|
0.063 + j0.00761
|
0.063
|
0.121
|
|
12
|
0.031 + j0.035
|
0.046
|
0.846
|
|
13
|
0
|
0
|
-1.571
|
|
14
|
- 0.026 + j0.03
|
0.04
|
2.296
|
|
15
|
- 0.046 + j0.00558
|
0.046
|
3.021
|
|
16
|
0.03 + j0.021
|
0.037
|
0.604
|
|
17
|
0.017 + j0.067
|
0.07
|
1.329
|
|
18
|
- 0.00522 + j0.00994
|
0.011
|
2.054
|
|
19
|
0.012 - j0.00468
|
0.013
|
-0.362
|
|
20
|
- 0.012 - j0.00445
|
-2.779
|
|
21
|
0.00447 +
j0.00852
|
0.00962
|
1.087
|
|
22
|
- 0.013 + j0.052
|
0.054
|
1.812
|
|
23
|
- 0.021 + j0.015
|
0.026
|
2.537
|
|
24
|
0.029 + j0.00349
|
0.029
|
0.121
|
|
25
|
0.015 + j0.017
|
0.022
|
0.846
|
|
26
|
0
|
0
|
-1.571
|
Построим спектральные характеристики периодического сигнала. Под
спектральными характеристиками понимают распределение амплитуд и начальных фаз
по частотам и называют спектрами амплитуд и фаз соответственно.
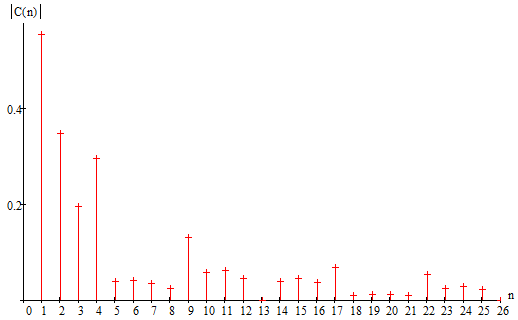
Рисунок 1.5 - Спектр коэффициентов комплексного ряда Фурье
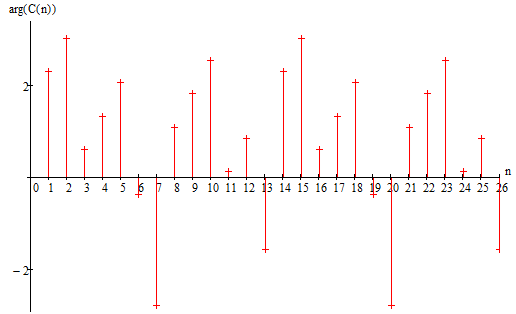
Рисунок 1.6 - Спектр фаз коэффициентов комплексного ряда Фурье
Спектр фаз коэффициентов комплексного ряда Фурье имеет большую линейную
составляющую, которая мешает увидеть значимую часть фазочастотной
характеристики (ФЧХ).
Для
компенсации линейной составляющей ФЧХ умножим комплексные коэффициенты Фурье на
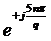 , тогда спектр фаз примет, следующий вид
, тогда спектр фаз примет, следующий вид
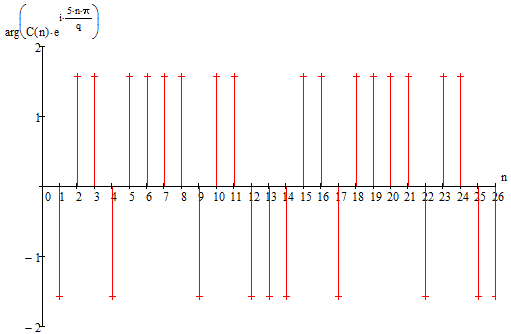
Рисунок
1.7 - Спектр фаз коэффициентов комплексного ряда Фурье с компенсированной
линейной составляющей
1.5. РАСЧЕТ
ШИРИНЫ СПЕКТРА СИГНАЛА
Под шириной спектра понимают эффективную область частот, в пределах
которой сосредоточена основная энергия сигнала.
Для ограничения спектра сигнала необходимо задаться пороговым критерием.
Из рисунка 1.5 видно, что наибольшей энергией обладает первая гармоника,
поэтому пороговый критерий для нахождения ширины спектра сигнала определим как
десятую часть амплитуды первой гармоники.
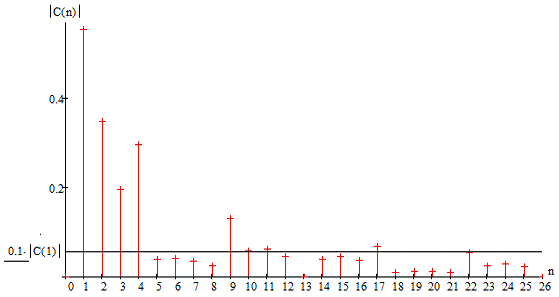
Рисунок 1.8 - Спектр амплитуд коэффициентов комплексного ряда Фурье с
пороговым критерием
Прямая линия (рисунка 1.8), параллельная частотной оси, определяется
пороговым критерием. Нетрудно заметить, что семнадцатый коэффициент - это
последний коэффициент с амплитудой, превышающей порог. Следовала бы ширину
спектра брать по восемнадцати гармоническим колебаниям, но, посмотрев на график
и проверив по таблице 1, мы обнаружим, что двадцать второй коэффициент меньше
пороговой критерии всего на 0,0013. С целью не потерять значимую часть энергии
сигнала, восстановление сигнала произведем по двадцати шести гармоническим
колебаниям, т. е. взяв лепесток, содержащий двадцать второй коэффициент.
1.6. ВОССТАНОВЛЕНИЕ
СИГНАЛА УСЕЧЕННЫМ РЯДОМ ФУРЬЕ
Сигнал,
представленный усеченным рядом Фурье, называется оценкой  . Учитывая нормировку
. Учитывая нормировку
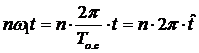
оценка
опишется следующим рядом
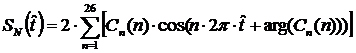
Рисунок
1.9 - Восстановление сигнала усеченным рядом Фурье по 26 гармоническим
колебаниям
Восстановленный
сигнал имеет периодический, пульсирующий характер. Периодизация сигнала
произошла из-за дискретизации спектральной плотности в частотной области, а
пульсирует восстановленный сигнал из-за ограниченной двадцатью шестью
гармониками ширины спектра сигнала.
Рисунок 1.10 - Восстановление сигнала усеченным рядом Фурье по 100
гармоническим колебаниям
Из рисунков 1.9 и 1.10 видно, что при увеличении числа гармоник
восстановленный сигнал становится все более похожим на исходный, т. е
уменьшается «завал» переднего и заднего фронта.
1.7. РАСЧЕТ
И ПОСТРОЕНИЕ ПОГРЕШНОСТИ ПРЕДСТАВЛЕНИЯ АНАЛОГОВОГО ПЕРИОДИЧЕСКОГО СИГНАЛА
УСЕЧЕННЫМ РЯДОМ ФУРЬЕ
Относительное значение погрешности аппроксимации аналогового
периодического сигнала усечённым рядом Фурье определяется как:
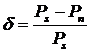
где
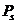 - средняя мощность сигнала,
- средняя мощность сигнала, 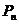 - мощность оценки
- мощность оценки 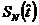 .
.
Средняя мощность сигнала равна отношению энергии периодического сигнала к
периоду:
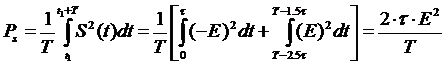 .
.
Мощность
оценки можно определить по спектру как сумму мощностей отдельных гармонических
составляющих:
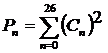
Среднеквадратическая
погрешность представления аналогового периодического сигнала усечённым рядом
Фурье равна
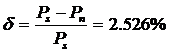 .
.
Найдем
среднюю мощность погрешности аппроксимации  :
:
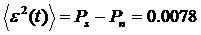 ВТ.
ВТ.
Построим
погрешность
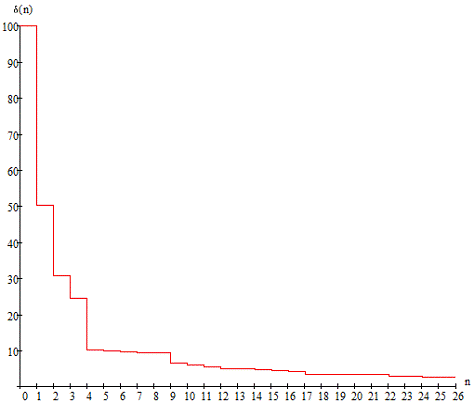
Рисунок
1.11 - Погрешность представления аналогового периодического сигнала усечённым
рядом Фурье
Как
мы можем видеть, с увеличением числа гармонических колебаний погрешность
уменьшается. Если устремить число гармонических колебаний к бесконечности, то
погрешность будет стремиться к нулю.
2.
АНАЛИЗ АНАЛОГОВОЙ ЛИНЕЙНОЙ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
2.1 ИСХОДНЫЕ
ДАННЫЕ
Табличное представление исходных данных:
|
№ варианта
|
№ бригады
|
Z1
|
Z2
|
Z4
|
Z5
|
Z6
|
Z7
|
Z8
|
№схемы
|
|
09
|
3
|
R
|
2pL
|
R
|
R
|
2pL
|
R
|
R
|
R
|
3
|
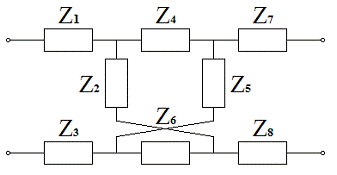
Рисунок 2.1 - Схема исходного аналогового фильтра-прототипа
Известно соотношение постоянной времени цепи
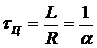
2.2 РАСЧЕТ
И ПОСТРОЕНИЕ ЧАСТОТНЫХ ХАРАКТЕРИСТИК АНАЛОГОВОГО ФИЛЬТРА
Передаточной функцией называется отношение комплексной амплитуды
гармонического сигнала на выходе цепи к комплексной амплитуде гармонического
сигнала на входе цепи. В общем виде комплексная передаточная функция
представляет собой дробно-рациональную функцию, в которой числитель и
знаменатель представляют собой комплексные полиномы. Частотные характеристики
цепи полностью определяются зависимостями модуля и аргумента комплексного
коэффициента передачи от частоты.
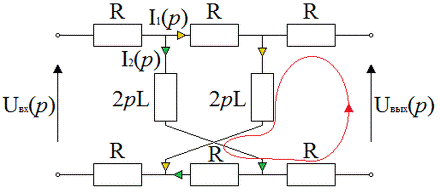
Рисунок 2.2 - Схема аналогового фильтра
Найдём передаточную функцию цепи, применив операторный метод расчёта, т.
е. получим операторное изображение коэффициента передачи, от которого легко
получить зависимость передаточной функции от частоты.
Передаточная функция цепи рассчитывается по следующей формуле:
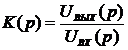 .
.
Так
как через 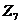 и
и 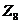 не может
протекать ток, то мы можем ими пренебречь. Найдем напряжение на выходе цепи,
для этого найдем токи
не может
протекать ток, то мы можем ими пренебречь. Найдем напряжение на выходе цепи,
для этого найдем токи 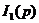 и
и 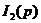 .
.
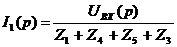 ;
; 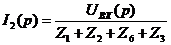 .
.
Подставляя
значения параметров, получим:
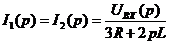 .
.
Составим
уравнение выходного напряжения цепи, пользуясь вторым законом Кирхгофа. Обходя
контур против часовой стрелки (рисунок 2.2), записываем падения напряжения на  и
и 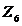 с
положительным знаком, если их направление совпадает с направлением обхода, в
противном случае с отрицательным знаком.
с
положительным знаком, если их направление совпадает с направлением обхода, в
противном случае с отрицательным знаком.
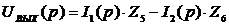 ;
;
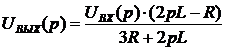 .
.
Расчет
передаточной функции цепи фильтра 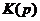 :
:
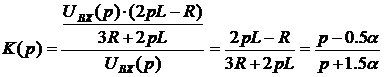 .
.
От
операторного изображения коэффициента передачи исследуемой цепи перейдём к
комплексному коэффициенту передачи 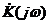 , заменив
в полученном выражении операторную переменную
, заменив
в полученном выражении операторную переменную 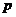 на
множитель
на
множитель 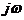 :
:
 .
.
Найдём
выражения модуля и фазы коэффициента передачи, предварительно осуществив
нормировку 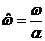
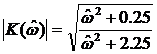 ;
;
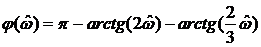 .
.
По
полученным формулам построим зависимости модуля коэффициента передачи и его
фазы от частоты для аналогового фильтра-прототипа.
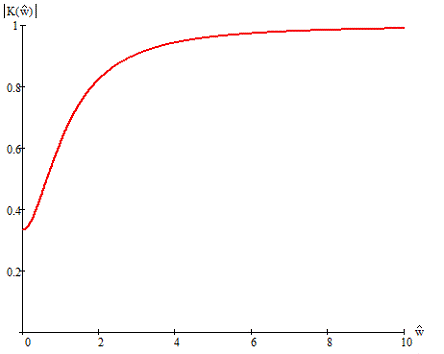
Рисунок
2.3 - АЧХ аналогового фильтра

Рисунок
2.4 - ФЧХ аналогового фильтра
Из
частотных характеристик видно, что наш фильтр является фильтром верхних частот
(ФВЧ).
2.3 РАСЧЕТ
И ПОСТРОЕНИЕ ВРЕМЕННЫХ ХАРАКТЕРИСТИК АНАЛОГОВОГО ФИЛЬТРА
Временными характеристиками цепи называются откликами на типовые
составляющие исходного сигнала.
Переходная
характеристика цепи - это отклик цепи с нулевыми начальными условиями на
воздействие единичной функции (функции Хевисайда). Переходная характеристика
определяется из операторной передаточной функции путем её деления на оператор 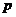 , и нахождения оригинала от получившегося изображения
с помощью обратного преобразования Лапласа через вычеты.
, и нахождения оригинала от получившегося изображения
с помощью обратного преобразования Лапласа через вычеты.
Импульсная
характеристика цепи - это отклик цепи на воздействие дельта-функции 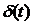 .
. 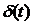 -
бесконечно короткий по длительности и бесконечно большой по амплитуде импульс
единичной площади. Импульсная характеристика определяется путем нахождения
вычетов от передаточной функции цепи.
-
бесконечно короткий по длительности и бесконечно большой по амплитуде импульс
единичной площади. Импульсная характеристика определяется путем нахождения
вычетов от передаточной функции цепи.
Временные
характеристики цепи будем искать также операторным методом. Для этого нужно
найти операторное изображение входного сигнала, умножить его на коэффициент
передачи в операторной форме и от полученного выражения найти оригинал, т. е
зная коэффициент передачи цепи, мы можем найти отклик на любое воздействие.
Нахождение импульсной характеристики сводится к нахождению реакции цепи
на дельта-функцию. Известно, что для дельта-функции изображением является 1.
Применяя обратное преобразование Лапласа, найдем импульсную характеристику.
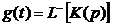 .
.
Выделим
целую часть для передаточной функции цепи, так как степени старших
коэффициентов в числителе и в знаменателе равны:
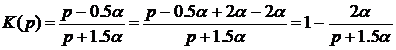 .
.
Найдем
особые точки передаточной функции, приравняв знаменатель к нулю.
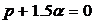 ;
; .
.
Имеем
всего одну особую точку, теперь берем вычет в этой особой точке.
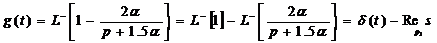 .
.
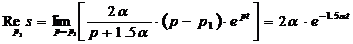 .
.
Выражение
для импульсной характеристики запишется следующим образом:
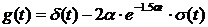 .
.
Аналогично
найдем переходную характеристику цепи, зная, что для функции Хевисайда
изображением является функция 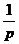 .
.
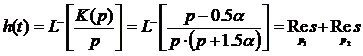 ;
;
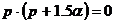 ;
; 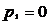 ,
, 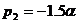 ;
;
 ;
;
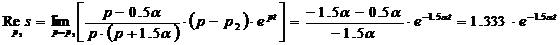 ;
;
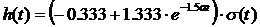 .
.
Переходная
и импульсная характеристики связаны между собой, так же как и входные
воздействия 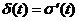 :
:
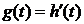 ;
;
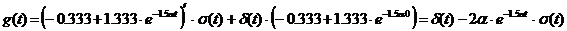
Проверим
выполнение предельных соотношений между частотными и временными
характеристиками цепи, т.е. выполнение следующих условий:
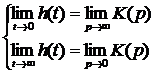
Подставляем
в систему конкретные выражения для характеристик цепей.
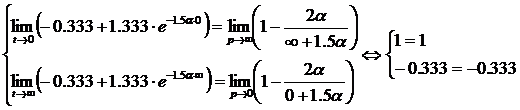 .
.
Как
видим, условия выполняются, что говорит о правильности найденных формул.
Запишем
конечные формулы для временных характеристик, учитывая нормировку
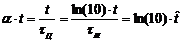
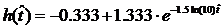
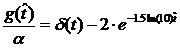
По вышеуказанным формулам построим графики этих функций.
фурье
сигнал аналоговый линейный
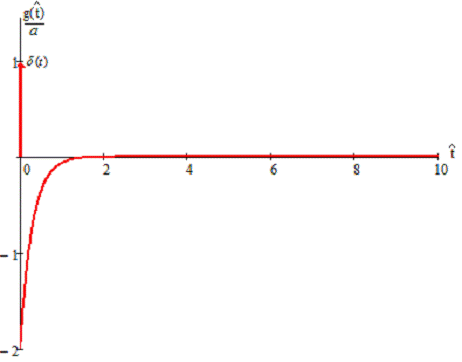
Рисунок 2.5 - Импульсная характеристика аналогового фильтра-прототипа
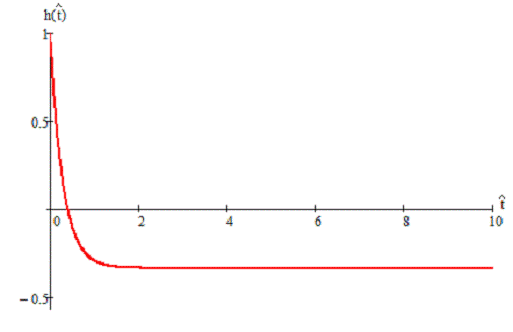
Рисунок 2.6 - Переходная характеристика аналогового фильтра-прототипа
Временные
характеристики существуют только при 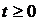 , так как
отклики не могут опережать воздействия.
, так как
отклики не могут опережать воздействия.
Наша цепь является дифференцирующей, поэтому переходная характеристика
ведет себя так. Дифференцирующая цепь заостряет переходный процесс и пропускает
передний фронт. За «бросок» отвечают прошедшие высокие частоты, а за завал - не
прошедшие низкие частоты.
Переходная
характеристика при 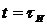 равна:
равна:

2.4 РАСЧЕТ
И ПОСТРОЕНИЕ ПЕРИОДИЧЕСКОГО СИГНАЛА ЧЕРЕЗ АНАЛОГОВУЮ ЛИНЕЙНУЮ ЭЛЕКТРИЧЕСКУЮ
ЦЕПЬ
Периодический
сигнал, проходя через ЛЭЦ, не теряет своей периодической природы, поэтому
сигналы на входе и выходе цепи можно представить бесконечной суммой
непериодических сигналов, сдвинутых друг от другу на период. Для расчета
прохождение периодического сигнала через ЛЭЦ используем метод комплексных
амплитуд, зная передаточную функцию цепи 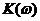 .
.
Постоянная
составляющая на выходе прямо пропорциональна значению коэффициента передачи при
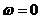 . Амплитуды гармонических колебаний умножаются на
значения модуля передаточной функции на частотах
. Амплитуды гармонических колебаний умножаются на
значения модуля передаточной функции на частотах 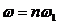 .
Начальные фазы гармонических колебаний суммируются со значениями фазочастотной
характеристики ЛЭЦ на частотах
.
Начальные фазы гармонических колебаний суммируются со значениями фазочастотной
характеристики ЛЭЦ на частотах 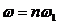 .
.
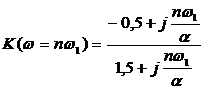
где
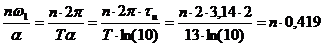 .
.
Периодический
сигнал на выходе ЛЭЦ описывается рядом:
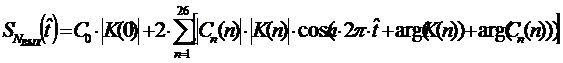
Изобразим графически отклик для периодического сигнала
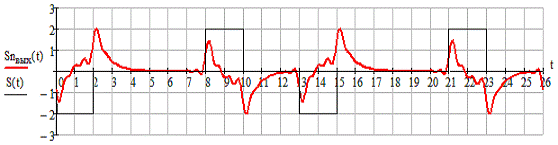
Рисунок 2.7 - Периодический сигнал на выходе ЛЭЦ по 26 гармоническим
колебаниям
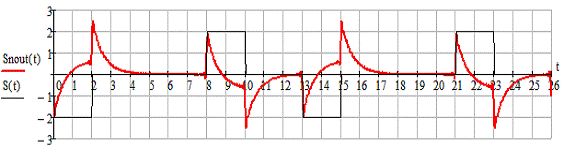
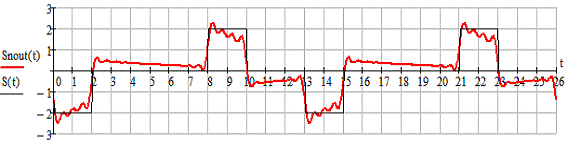
Рисунок 2.8 - Периодический сигнал на выходе ЛЭЦ по 100 гармоническим
колебаниям
На рисунке 2.7 и 2.8 наблюдаем, что при увеличении числа рассматриваемых
гармоник «бросок» становится более четким, т. е. исчезает пульсирующий
характер.
Рисунок
2.9 - Периодический сигнал на выходе ЛЭЦ при 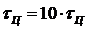
Рисунок
2.10 - Периодический сигнал на выходе ЛЭЦ при 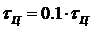
Анализируя
полученные графики (рисунки 2.7, 2.9 и 2.10) можно сказать, что с увеличением 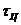 в десять раз отклик становится все более похожим на
входной сигнал, а с уменьшением
в десять раз отклик становится все более похожим на
входной сигнал, а с уменьшением 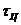 в десять
раз входной сигнал переворачивается, и наша цепь работает как инвертор.
в десять
раз входной сигнал переворачивается, и наша цепь работает как инвертор.
2.5 РАСЧЕТ
И ПОСТРОЕНИЕ НЕПЕРИОДИЧЕСКОГО СИГНАЛА ЧЕРЕЗ АНАЛОГОВУЮ ЛИНЕЙНУЮ ЭЛЕКТРИЧЕСКУЮ
ЦЕПЬ
Исследуем прохождение непериодического сигнала через ЛЭЦ, т. е. найдём
форму сигнала на выходе этой цепи при однократном воздействии непериодического
сигнала. Отклик можно легко найти, если представить входной сигнал как сумму
единичных воздействий. Тогда на выходе мы получим сумму реакций на эти
единичные воздействия, т.е. сумму переходных характеристик исследуемой цепи с
учетом весов и сдвигов по времени.
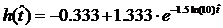 .
.
Исходя
из выше сказанного, опишем выходной сигнал следующей формулой:
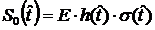 ;
;
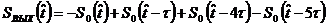 .
.
Построим
отклик на прямоугольный сигнал ЛЭЦ, используя полученную формулу.
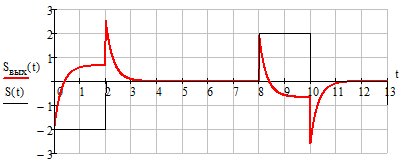
Рисунок
2.11 - Непериодический сигнал на выходе ЛЭЦ
Отклик непериодического сигнала на выходе ЛЭЦ подобен периодическому
сигналу, построенный по 100 гармоникам (рисунок 2.8). Отсюда можно сделать
вывод, что если непериодический сигнал имеет во временном представлении такую
же форму и такие же параметры как и периодический сигнал, то можно предсказать
его поведение во временной области, зная поведение периодического сигнала.
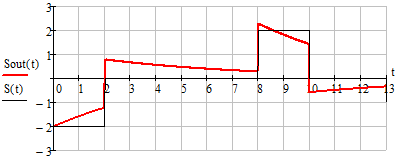
Рисунок
2.12 - Непериодический сигнал на выходе ЛЭЦ при 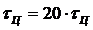
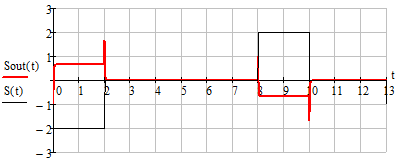
Рисунок
2.13 - Непериодический сигнал на выходе ЛЭЦ при 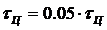
Так
же как и у периодического сигнала, с увеличением 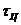 отклик
непериодического сигнала на выходе ЛЭЦ становится похожим на входной сигнал, а
с уменьшением
отклик
непериодического сигнала на выходе ЛЭЦ становится похожим на входной сигнал, а
с уменьшением 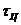 цепь работает как инвертор.
цепь работает как инвертор.
Заключение
В ходе курсовой работы был произведен спектральный анализ аналоговых
непериодического и периодического сигналов. С помощью единичной функции
включения разложили сигнал на его типовые составляющие, которые включаются в
определенный момент времени. Нашли спектральную плотность аналогового
непериодического сигнала, на основе которого рассчитали коэффициенты
комплексного ряда Фурье, описывающего аналоговый периодический сигнал.
Так
как исходный сигнал описывался нечетной функцией времени, то спектральная
плотность описывалась вещественной функцией частоты. Кроме этого сигнал
представлял собой знакочередующуюся последовательность импульсов прямоугольной
формы, из-за чего постоянная составляющая комплексного ряда Фурье оказалась
равной нулю. Построили спектральные характеристики аналогового периодического
сигнала. Обнаружили, что с ростом номера гармоник амплитуды убывают, форма
огибающей спектральных составляющих имеет лепестковый характер. Задав пороговый
критерий равной десятой части амплитуды первой гармоники, нашли ширину спектра
сигнала. Восстановили периодический сигнал усечённым рядом Фурье по двадцати
шести гармоникам. Построенный график давал возможность судить о форме и
свойствах сигнала. Восстановленный сигнал имел периодический, пульсирующий
характер. Периодизация сигнала произошла из-за дискретизации спектральной
плотности в частотной области, а пульсировал восстановленный сигнал из-за
ограниченной двадцатью шестью гармониками ширины спектра сигнала. При
увеличении числа гармоник восстановленный сигнал становился все более похожим
на исходный аналоговый сигнал. Рассчитали и построили погрешность представления
аналогового периодического сигнала усечённым рядом Фурье, которая составила 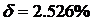 . Увидели, что с увеличением числа рассматриваемых
гармоник уменьшается погрешность построения сигнала.
. Увидели, что с увеличением числа рассматриваемых
гармоник уменьшается погрешность построения сигнала.
Произвели
анализ аналоговой линейной электрической цепи во временной и частотной области.
Для заданной цепи нашли операторное выражение передаточной функции, от которого
перешли к комплексному коэффициенту передачи, заменив в полученном выражении
операторную переменную 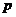 на множитель
на множитель 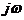 .
Рассчитали и построили амплитудно-частотную, фазочастотную характеристики, взяв
модуль и аргумент соответственно от комплексного коэффициента передачи. Также
были рассчитаны и построены переходная и импульсная характеристики операторным
методом расчёта.
.
Рассчитали и построили амплитудно-частотную, фазочастотную характеристики, взяв
модуль и аргумент соответственно от комплексного коэффициента передачи. Также
были рассчитаны и построены переходная и импульсная характеристики операторным
методом расчёта.
Удостоверились
в правильности найденных формул, проверив с помощью предельных соотношений
между частотными и временными характеристиками цепи. Используя метод
комплексных амплитуд, нашли прохождение периодического сигнала через аналоговую
линейную электрическую цепь. Также рассчитали прохождение непериодического
сигнала через заданную цепь, представив входной сигнал как сумму единичных
воздействий. Вследствие чего на выходе мы получили сумму переходных
характеристик исследуемой цепи с учетом весов и сдвигов по времени. Для
прохождений периодического и непериодического сигнала через цепь были построены
отклики. Увидели, что отклик непериодического сигнала на выходе линейной
электрической цепи подобен периодическому сигналу, построенный по большому
количеству гармоник. Отсюда мы сделали вывод, что если непериодический сигнал
имеет во временном представлении такую же форму и такие же параметры как и
периодический сигнал, то можно предсказать его поведение во временной области, зная
поведение периодического сигнала. Обнаружили, что с увеличением 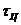 отклик становится похожим на входной сигнал, а с
уменьшением
отклик становится похожим на входной сигнал, а с
уменьшением 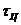 цепь работает как инвертор.
цепь работает как инвертор.
Список использованной литературы
1. Баскаков
С. И. Радиотехнические цепи и сигналы. М.: Высш. школа, 2009. - 462 с. (304
экз.) ISBN: 5-06-003843-2.
2. Каратаева Н. А.
Радиотехнические цепи и сигналы. Теория сигналов и линейные цепи. Учебное
пособие. Томск: ТУСУР, 2012. - 261 с. Режим доступа:
<http://edu.tusur.ru/training/publicatos/2798>.
. Каратаева Н. А.
Радиотехнические цепи и сигналы. Теория сигналов и линейные цепи. Учебное
пособие. Томск: ТУСУР, 2010. - 255 с. (108 экз.) ISBN 5-86889-175-9.
. Учебное методическое
пособие. Радиотехнические цепи и сигналы. Часть 1. Теория сигналов и линейные
цепи. Каратаева Н. А, Киселев П. Томск: ТУСУР, 2012. - 33 с. Режим доступа:
<http://edu.tusur.ru/training/publicatos/2790>.