Определение длины волны. Относительная неопределенность скорости электрона. Функции частицы

Определение длины волны. Относительная неопределенность скорости электрона. Функции частицы

1. Найти дебройлевскую длину волны молекул водорода, соответствующую их наиболее вероятной скорости при .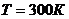

Дано:

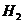
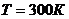
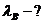
Решение:

Длина волны де Бройля определяется по формуле:

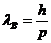
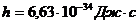 - постоянная Планка.

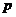 - импульс частицы, .

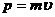Средняя квадратичная скорость молекул газа определяется выражением (Проверьте формулу)

,

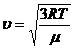где

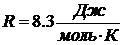 - универсальная газовая постоянная,  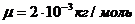- молярная масса водорода.

Массу одной молекулы найдем делением ее молярной массы на постоянную Авогадро (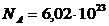моль^-1):

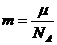
Тогда импульс частицы можно выразить формулой:

,

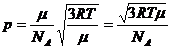а длину волны де Бройля - соотношением

.

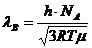Произведя вычисления по этой формуле, получим:

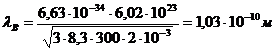. Ответ: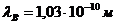

. Электрон с кинетической энергией 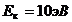локализован в области размером . Оценить с помощью соотношения неопределенностей 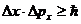относительную неопределенность 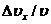его скорости.

Дано:

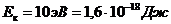
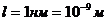
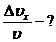
Решение

Соотношение неопределенностей Гейзенберга для координаты и импульса имеет вид:

,

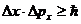где 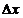 - неопределенность координаты,

 - неопределенность импульса,

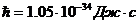 - постоянная Планка,

Поскольку неопределенность координаты 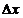 не больше линейного размера структуры 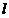, а неопределенность импульса можно выразить через неопределенность скорости 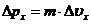, получаем:

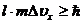, Откуда .

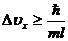Для определения относительной неопределенности скорости необходимо значение скорости; выразим ее из кинетической энергии для классического случая, поскольку выполняется условие Е_к << Е₀ (энергия покоя электрона Е₀ составляет 0,511 МэВ):

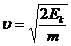
Находим относительную неопределенность скорости

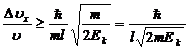
Подставляя значения величин, находим:

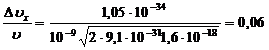 Ответ: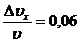

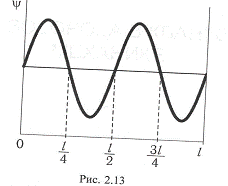
. Частица находится в одномерном потенциальном ящике с бесконечно высокими стенками. 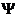 - функция имеет вид, показанный на рисунке. Найти вероятность пребывания частицы в области .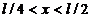

Дано

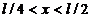
Вероятность пребывания микрочастицы в окрестностях точки х (в одномерном случае):

.

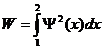Волновая функция частицы, находящейся в бесконечно глубоком одномерном прямоугольном потенциальном ящике:

.

Определим состояние 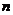 частицы из графических соображений. Как видно из рисунка,

,

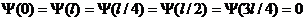поэтому можем записать равенства

.

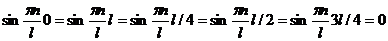Очевидно, что 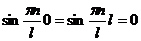 выполняются при любых значениях .

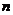Для того чтобы волновая функция обращалась в нуль во всех требуемых точках, аргументы функции синуса должны удовлетворять также условиям

,

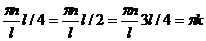где 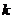 - целое число. Таким образом,  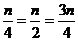должны быть целочисленными, откуда следует, что .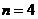

Находим вероятность пребывания электрона во второй четверти ящика:

.

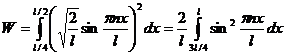Воспользовавшись тригонометрическим тождеством

,

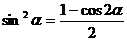приходим к выражению:

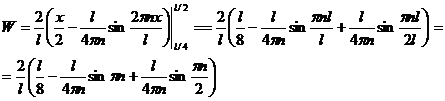
Подставляя значения величин, находим

.

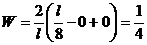Заметим, что графический метод определения вероятности дает такой же результат (площадь фигуры, ограниченной графиком функции в указанных пределах, составляет четверть от площади фигуры, ограниченной графиком на всей длине ящика). Ответ: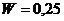

. Электрон в атоме находится в 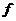 - состоянии. Найти орбитальный момент импульс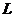а  электрона и максимальное значение проекции момента импульса 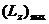 на направление внешнего магнитного поля.

Дано:

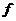 - состояние

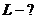
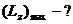
Решение

,

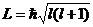где

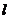 - орбитальное квантовое число.  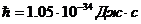- постоянная Планка.

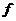 - состоянию электрона соответствует значение орбитального квантового числа .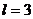

Проекция вектора орбитального момента импульса на направление внешнего магнитного поля так же квантуется, то есть может принимать лишь целочисленные значения, кратные :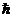

,

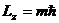где

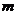 - магнитное квантовое число, может принимать значения .

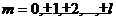Нетрудно видеть, что максимальное значение магнитного квантового числа равно орбитальному квантовому числу 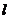, поэтому максимальное значение проекции момента импульса  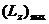на направление внешнего магнитного поля определяется выражением:

.

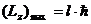Подставляем численные значения и вычисляем:

,

.

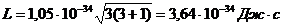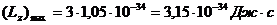Ответ: ;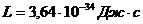

. Пси-функция основного состояния водородного атома имеет вид

,

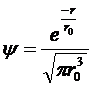где

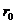 - радиус первой боровской орбиты.

Вычислить вероятность того, что электрон в основном состоянии атома водорода находится от ядра на расстоянии, превышающем значение .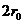

Дано:

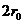
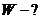
Решение

Квадрат модуля волновой функции определяет вероятность 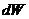 нахождения микрочастицы в некоторой области пространства, то есть вероятность найти электрон в элементарном объеме 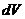, находящемся на расстоянии  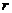от ядра, равна

.

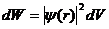В силу сферической симметрии функции 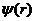элементарным объемом 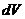, все точки которого удалены на одинаковое расстояние 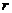от ядра, будет шаровой слой радиуса 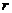и толщиной 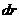, то есть

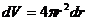, тогда .

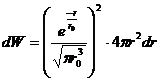Вероятность пребывания частицы на расстоянии, превышающем значение 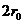, находим интегрированием в пределах от  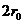до :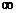

.

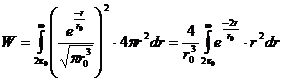Удобнее вычислить интеграл в пределах от 0 до 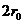, найдя вероятность  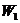пребывания электрона внутри этой области, а искомую вероятность найти как

,

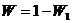поскольку полная вероятность нахождения электрона в области от 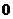 до 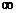равна 1.

.

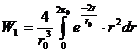Введем переменную 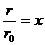, тогда интеграл в иной форме будет выглядеть:

,

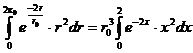а выражение для вероятности 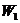 примет вид:

.

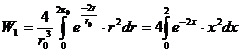После интегрирования по частям получаем:

электрон скорость частица волна

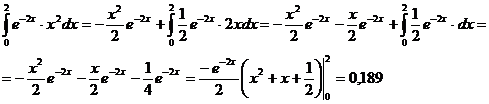
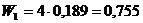 - вероятность пребывания электрона внутри сферы радиусом 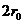, тогда искомая вероятность того, что электрон окажется за ее пределами

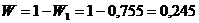. Ответ: