Расчет параметров цифрового фильтра
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ
АГЕНСТВО ПО ОБРАЗОВАНИЮ
«КУРГАНСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Кафедра
«Безопасность информационных и автоматизированных систем»
ПОЯСНИТЕЛЬНАЯ
ЗАПИСКА
ТЕМА:
РАСЧЕТ ПАРАМЕТРОВ ЦИФРОВОГО ФИЛЬТРА
АННОТАЦИЯ
Документ содержит общие сведения для решения
поставленных задач и сами решения. В аналитическом обзоре указаны основные
теоретические выкладки для расчёта параметров цифрового фильтра с заданными
требованиями. На основе решений составлено заключение.
1. АНАЛИТИЧЕСКИЙ ОБЗОР
Обратное z-преобразование
Обратное z-преобразование (z-1) позволяет
восстанавливать последовательность дискретного времени х(п) по ее z-образу. z-1
особенно полезно в операциях ЦОС, например, при поиске импульсной
характеристики цифровых фильтров. В символической форме обратное
z-преобразование можно определить как:
(n) = Z-1[X(z)],
где X(z) - это z-образ последовательности x(n),
а Z-1 - символ, обозначающий обратное z-преобразование.
Предположив, что последовательность причинна,
z-образ X(z) можно разложить в степенной ряд как:
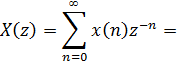
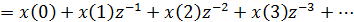
Видно, что значения последовательности х(n) -
это коэффициенты z-n (n = 0,1,...), и поэтому их можно найти непосредственно.
На практике X(z) часто выражается через отношение двух многочленов от z-1 или,
что эквивалентно, от z:
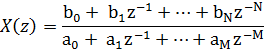
В этом виде обратное z-преобразование x(n) можно
найти с помощью одного из многих методов, например:
а) метода разложения в степенной ряд;
б) метода разложения на элементарные дроби;
У каждого метода есть свои преимущества и
недостатки. С точки зрения математической строгости метод вычетов, возможно,
самый элегантный. Однако метод степенных рядов лучше всего подходит для
компьютерных расчетов.
Метод степенных рядов
Если дано z-преобразование X(z) причинной
последовательности, то его можно разложить в бесконечный ряд относительно z-1
или z путем деления в столбик (иногда его называют синтетическим делением):
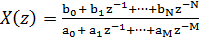 =
=
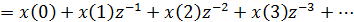
В этом методе числитель и знаменатель функции
X(z) сперва выражаются либо через уменьшающийся показатель степени z, либо
через увеличивающейся показатель степени z-1, а затем путем деления в столбик
находится частное.
Метод разложения на элементарные дроби
В этом методе z-преобразование вначале
раскладывается на сумму простых дробей. Затем по таблицам, подобным (смотреть в
приложении) находится обратное z-преобразование каждой элементарной дроби. Эти
образы суммируются, и получается общее обратное z-преобразование. На практике
во многих случаях z-преобразование задается как отношение многочленов по z или
z-1 и имеет уже знакомый вид
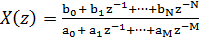 =
=
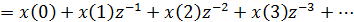 (1)
(1)
Если полюсы функции X(z) - первого порядка и N -
М, то X(z) можно разложить как:
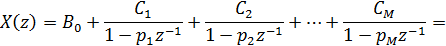
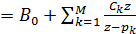 (2)
(2)
где pk - полюсы функции X(z), Ck - коэффициенты элементарных
дробей, a
= bN/aN.
Сk также называют вычетами функции X(z).
Если в уравнении (1) порядок числителя меньше,
чем порядок знаменателя, т.е. N < М, то В0 будет равно нулю. Если N > М,
то X(z) вначале нужно сократить, чтобы получить N < М, путем деления в
столбик многочленов числителя и знаменателя, записанных через уменьшающийся
показатель степени z-1. Остаток можно выразить так, как это сделано в уравнении
(2).
Коэффициент Ск, связанный с полюсом pк, можно
найти, умножив правую и левую части уравнения (2) на (z - pk)/z, а затем сделав
замену z = рк:
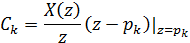
Если функция X(z) имеет один или несколько
полюсов больше первого порядка (т.е. совпадающих полюсов), то, чтобы учесть
это, в уравнение (2) нужно добавить дополнительные члены. Например, если
функция X(z) имеет полюс m-го порядка в точке z=рк, то в разложение на
элементарные дроби должны входить члены вида:
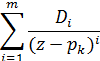
Коэффициенты Di можно найти из зависимости:
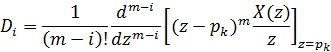
Так как наше z-преобразование представляет собой
обычный фильтр дискретного времени N-го порядка (где N=M):
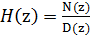 ,
,
где
(z)=b0zN+ b1zN-1+ b2zN-2+…+ bN,
D(z)=a0zN+ a1zN-1+ a2zN-2+…+ aN,
ak и bk - коэффициенты фильтра.
Если функция H(z) имеет полюсы в точках z=p1,
p2,… pN и нули в точках z=z1, z2,… zN, то H(z) можно разложить на множители и
представить в виде:
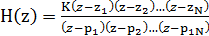 ,
,
где zi- i-й нуль, pi- i-й полюс, а K-
коэффициент усиления.
Полюсы такого z-преобразования, как H(z), - это
значения z, в которых функция H(z) равна бесконечности. Значения г, в которых
H(z) равна нулю, называют нулями. Полюсы и нули функции H(Z) могут быть
действительными или комплексными. Если они комплексные, они идут комплексно-сопряженными
парами, чтобы коэффициенты ak и bk были действительными. Если известны
положения полюсов и нулей функции H(z), то и саму функцию H(z) можно легко
восстановить с точностью до константы.
Оценка частотной характеристики
Существует множество случаев, когда нужно
оценить частотную характеристику системы дискретного времени. Например, при
проектировании дискретных фильтров часто приходится проверять спектр фильтра,
чтобы убедиться в том, что он удовлетворяет искомым спецификациям. Отметим, что
частотную характеристику системы можно запросто найти из ее z-преобразования.
Например, если взять z = еiɷT, т.е. найти
z-преобразование по единичной окружности, получим Фурье-образ системы:
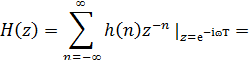
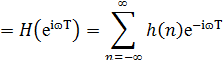
Н(eiɷT) называют частотной характеристикой
системы. Мы воспользовались символом Т, чтобы подчеркнуть зависимость частотной
характеристики системы дискретного времени от частоты дискретизации. В общем
случае Н(еiɷT) - комплексная величина. Ее модуль дает амплитудную, а фаза
- фазовую характеристику системы.
Частотную характеристику по z-преобразованию
можно найти несколькими методами.
Если необходимо знать полную частотную
характеристику, как правило, в передаточную функцию непосредственно подставляют
значение z=eiɷT и вычисляют получающееся в результате этого выражение:
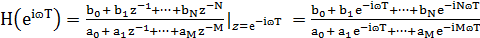 =
=
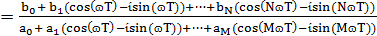 .
.
Разностное уравнение
Разностное уравнение описывает реальные
действия, которые система дискретного времени должна произвести над входными
данными во временной области, чтобы получить необходимый выход. Разностное
уравнение для большинства важных практических случаев можно записать в таком
виде:
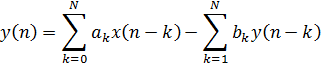
где x(n) - элемент входной последовательности,
y(n) - элемент выходной последовательности, y(n-k) - предыдущий выход, а ak, bk
- коэффициенты системы. Текущий выход y(n) получается из настоящего и прошлого
элементов входной последовательности и предыдущего выхода y(n-k).
Влияние структуры фильтра на эффекты конечной
разрядности
Как уже говорилось, БИХ-фильтры можно
представить с помощью разнообразных структур, которые теоретически
эквивалентны. В то же время, при реализации на процессорах ЦОС с фиксированной
или плавающей запятой поведение фильтров может существенно различаться.
 -разностное
уравнение
-разностное
уравнение
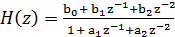 -передаточная
функция
-передаточная
функция
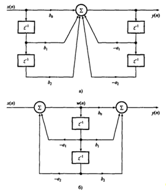
Рис. 1
Стандартные блоки БИХ-фильтров: а) звено второго
порядка, реализованное в прямой форме I; б) каноническое звено второго порядка.
Ошибки квантования коэффициентов
БИХ-фильтр характеризуется следующим уравнением:
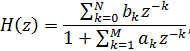
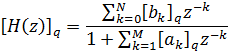
Где
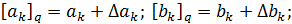
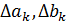 -изменение
коэффициентов aк и bк соответственно,-обозначает квантованную величину.
-изменение
коэффициентов aк и bк соответственно,-обозначает квантованную величину.
Основное влияние квантования коэффициентов
фильтра с использованием конечного числа битов проявляется в изменении
положения полюсов и нулей H(z) на комплексной плоскости. В узкополосных
фильтрах, например, полюса расположены близко к единичной окружности, так что
любое значительное изменение их положения может сделать фильтр неустойчивым.
Чем меньше число битов, используемых для представления коэффициентов, тем
большим будет изменение положения полюсов и нулей.
Помимо потенциальной неустойчивости смещение
положений полюсов и нулей также приводит к изменению частотной характеристики.
Квантованный фильтр всегда следует проанализировать, чтобы убедиться, что
используемой длины слова достаточно для обеспечения устойчивости и
удовлетворительной частотной характеристики. Следовательно, на этом этапе
разработчик должен определить число битов, требуемых для представления
коэффициентов фильтра. Требования к длинам коэффициентов с точки зрения
устойчивости и желаемой частотной характеристики. Далее обсуждение устойчивости
будет касаться только звеньев второго порядка, являющихся основой любого
фильтра. Рассмотрим звено второго порядка, которое характеризуется следующими
уравнениями:
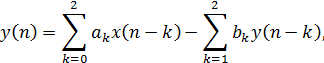
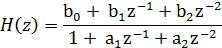
Полюса (или корни знаменателя) расположены в
точках
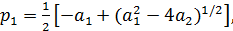 (3)
(3)
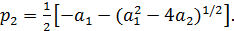 (4)
(4)
Каждое звено второго порядка может иметь полюса
трех типов: комплексно-сопряженные, неравные действительные и равные
действительные. Наиболее распространенный случай - это комплексно-сопряженные
полюса, которые появляются при 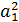 < 4а2. В данном
случае полюса расположены на окружности радиуса r с центром в начале координат
с угловыми координатами.
< 4а2. В данном
случае полюса расположены на окружности радиуса r с центром в начале координат
с угловыми координатами.
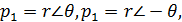 (5)
(5)
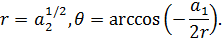
Небольшие изменения коэффициентов и а2 после
квантования коэффициентов приведут к изменениям r и θ.
Чтобы обеспечить устойчивость, коэффициенты
фильтра должны лежать внутри треугольника устойчивости, который ограничен
следующими линиями:
≤|а2|<1, (6.1)
|а1|≤1+а2. (6.2)
Выполнение первого условия гарантирует, что
полюса будут лежать внутри единичной окружности, поскольку радиус полюса
определяется уравнением (5).
Из уравнений (5) и (6) находим, что для оценки
числа битов, требуемых для поддержания устойчивости, можно получить несколько
простых формул, которые, впрочем, применимы к ограниченному набору классов.
Ошибки переполнения при сложении
В арифметике с дополнением до двух при сложении
двух больших чисел одного знака может произойти переполнение (т.е. получиться
результат, который превышает приемлемую длину слова), а это приведет к
изменению знака выходной выборки. Таким образом, очень большое положительное
число становится очень большим отрицательным числом, и наоборот. Вследствие
рекурсивной природы БИХ-фильтра переполнение в узле ɷ(n) переходит по
обратной связи и используется для вычисления следующего выхода, где оно может
вызвать дальнейшее переполнение и привести к нежелательным самоподдерживающимся
осцилляциям. Подобные масштабные граничные циклы переполнения трудно остановить
после их возникновения, чтобы их прекратить, следует повторно инициализировать
фильтр.
Масштабное переполнение происходит на выходах
сумматоров, и его можно предотвратить путем масштабирования входов сумматоров
так, чтобы выходы были малыми, хотя такое решение возможно за счет снижения
отношения сигнал-шум.
Таким образом, важно выбрать масштабные
множители так, чтобы предотвратить переполнение и при этом сохранить наибольшее
возможное отношение сигнал-шум.
Масштабный множитель s1 на входе фильтра
выбирается так, чтобы предотвратить переполнение или снизить его вероятность на
выходе левого сумматора. Чтобы поддержать общее усиление фильтра на предыдущем
уровне, коэффициенты числителя умножаются на s1.
Существует три распространенных метода
определения подходящих масштабных множителей фильтра.
В первом методе, который часто называют нормой
L1 масштабный множитель выбирается следующим образом:
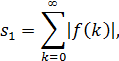
где f(k) - импульсная характеристика,
связывающая вход системы с выходом первого сумматора, т.е. узлом w(n).
Выбранный таким способом масштабный множитель s1 гарантирует, что общее
усиление фильтра от входа до узла w(n) равно единице, поэтому переполнение в
w(n) невозможно. Для получения импульсной характеристики f(k) можно вначале
определить соответствующую передаточную функцию F(z), а затем применить к ней
обратное z-преобразование.
Во втором методе, часто называемом нормой L2,
масштабный множитель s1 определяется следующим образом:
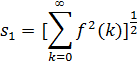
Нормировочный множитель L2 можно получить иначе,
использовав контурный интеграл
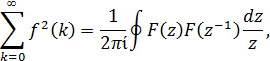
где F(z) - z-образ (результат применения
2-преобразования) 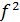 ,а
,а 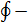 обозначает
контурный интеграл по единичной окружности |z| =1.
обозначает
контурный интеграл по единичной окружности |z| =1.
Вычисляя норму L2, получаем:
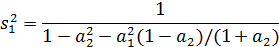
Шум квантования АЦП и качество сигнала
АЦП квантует аналоговый входной сигнал в
конечное число битов, обычно 8, 12 или 16, что приводит к появлению шума
квантования.
Как обсуждалось в главе 2, мощность шума
квантования (или дисперсия, 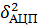 ) записывается
следующим образом:
) записывается
следующим образом:
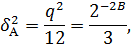
где q - размер шага квантования, а B - число
битов АЦП. Очевидно, что уровень шума можно легко уменьшить, увеличив число
битов АЦП. Кроме того, можно также снизить этот шум, используя методы обработки
при нескольких скоростях. Вообще, для значений B, превышающих 12 бит, шум из-за
ошибки квантования незначителен, исключая такие приложения, как
профессиональное аудио, где для получения приемлемого качества требуется не
менее 16 бит.
Шум, вызванный квантованием АЦП, существует в
системе ЦОС как неизбежная ошибка. Мощность шума, введенного АЦП, на выходе
системы ЦОС записывается следующим образом:
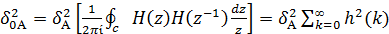 (7)
(7)
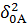 - шум квантования
АЦП на выходе системы;
- шум квантования
АЦП на выходе системы;
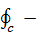 контурный
интеграл;(k) - импульсная характеристика системы.
контурный
интеграл;(k) - импульсная характеристика системы.
Выражение в квадратных скобках можно
рассматривать как "коэффициент усиления системы по мощности", который
определяет усиление (или изменение) шума АЦП в зависимости от характеристик
системы ЦОС.
Влияние шума квантования на производительность
фильтра.
Влияние шума квантования на производительность
фильтра зависит от типа используемой фильтрующей структуры и точки, в которой
квантуются результаты. Предполагается, что входные данные х(п), выход у(п) и
коэффициенты фильтра представляются как В-битовые числа (включая бит знака).
После умножения произведения квантуются до В бит путем округления (или
усечения).
Ошибка округления:
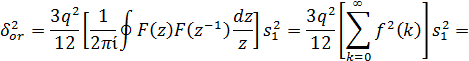
=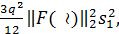
где

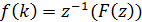
результат применения обратного z-преобразования
к F(z). Кроме того, f(k) - это импульсная характеристика каждого источника
шума, дающего вклад в выход фильтра,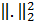 -
квадрат нормы L2, а q2/12 -мощность шума округления внутреннего произведения.
Общая мощность шума на выходе фильтра - это сумма мощности шума округления
произведений и мощности шума квантования АЦП:
-
квадрат нормы L2, а q2/12 -мощность шума округления внутреннего произведения.
Общая мощность шума на выходе фильтра - это сумма мощности шума округления
произведений и мощности шума квантования АЦП:
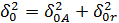
Предполагая, что источники шума не коррелируют,
общий вклад шума в полезный сигнал - это просто сумма отдельных шумовых
составляющих:
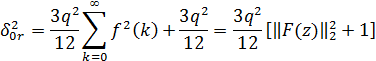
где f(k) - импульсная характеристика,
связывающая выход источника шума eх с выходом фильтра, а F(z) - соответствующая
передаточная функция:
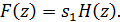
Общий шум (шум АЦП + шум округления) на выходе
фильтра записывается следующим образом:
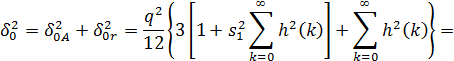
Использование масштабного множителя увеличивает
выходной шум.
2. ЗАДАНИЯ
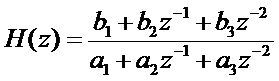
|
Вариант
|
b0
|
b1
|
b2
|
a0
|
a1
|
a2
|
|
11
|
1
|
-1,82387
|
-2,64512
|
1
|
1,15085
|
0,96912
|
Найдите импульсную характеристику системы
дискретного времени (обратное z-преобрзование z-образа) методами разложения в
степенной ряд и разложения на элементарные дроби.
Постройте ее диаграмму нулей и полюсов.
Постройте амплитудно-частотную и
фазово-частотную характеристики заданной системы дискретного времени.
Запишите разностное уравнение системы.
Постройте диаграммы реализации разностного
уравнения в виде блок схемы и в виде функциональной схемы.
Оцените величину смещения полюса при квантовании
коэффициентов фильтра до 8 бит (частота дискретизации 32 кГц).
Определите минимальное количество бит
необходимых для представления коэффициентов для обеспечения устойчивости
фильтра.
Рассчитайте масштабный множитель (норму L2) для
предотвращения переполнения фильтра при его реализации с помощью канонического
звена.
Изобразите диаграммы реализации в прямой и
канонической форме с указанными источниками ошибок округления.
Оцените общую входную мощность шума и ухудшение
выходного отношения сигнал-шум (в децибелах), вызванное ошибками округления
(предполагается, что фильтр реализуется в 8-ми битовой системе с коэффициентами
фильтра представленными 8-битовыми дробными величинами с фиксированной запятой,
каждое произведение квантуется до 8 бит непосредственно после умножения).
3. ВЫПОЛНЕНИЕ ЗАДАНИЙ
А) Нахождение импульсной характеристики методом
разложения в степенной ряд.
Используется метод деления в столбик.
_1-1,82387z-1-2,64512z-2
|1+1,15085z-1+0,96912z-2
+1,15085z-1+0,96912z-2
|1-2,97472z-1-0,19079z-2-3,10243z-3
_-2,97472z-1-3,61424z-2
,97472z-1-3,42345z-2-2,88286z-3
_-0,19079z-2+2,88286z-3
,19079z-2-0,21957z-3-0,18489z-4
,10243z-3+0,18498z-4
Степенной ряд:
(z)=1 - 2,97472z-1 - 0,19079z-2 - 3,10243z-3 + …
Обратное z-преобразование:
(0)= 1; x(1)= -2,97472; x(2)= -0,19079; x(3)=
-3,10243;…
Б) Нахождение импульсной характеристики методом
разложения на элементарные дроби.
Функция X(z) имеет комплексно-сопряжённые полюсы
первого порядка. Вначале X(z) выражается через положительные дроби:
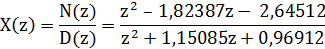
Так как полюсы функции X(z)-первого порядка, и
N=M,то X(z) можно разложить как:
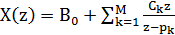 ,
,
где pk-полюс функции X(z),Ck-коэффициенты
элементарных дробей, а
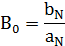
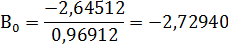
Полюса функции X(z) находим из решения
квадратного уравнения

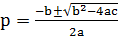 ,
,
где a и b-коэффициенты при z2 и z
соответственно, а c-постоянный член.
При a=1, b=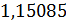 и c=
и c=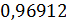 полюсы будут равны:
полюсы будут равны:
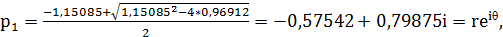
Где
=0,98443, а θ=125,76°
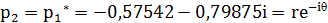
Теперь можно выразить функцию X(z) через её
полюсы:
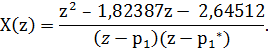
Так как числитель и знаменатель функции X(z)
одного порядка, разложение на элементарные дроби будет выглядеть так:
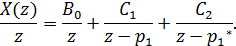
Чтобы найти C1, умножим обе стороны уравнения на
(z-p1), а затем сделаем замену z=p1:
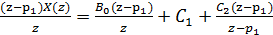 |z=p1.
|z=p1.
Таким образом,
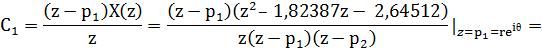
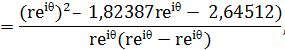
где r=0,98443, а θ=125,77°.
Выполнив некоторые преобразования и упростив выражение, получаем:
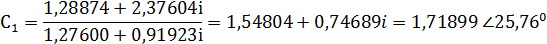
Поскольку p1 и p2- комплексно-сопряжённая пара,
то
Таким образом, z-преобразование можно выразить
так:
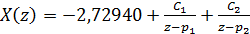 ,
,
Где
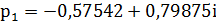 ,
,
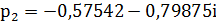 ,
,
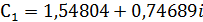 ,
,
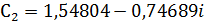 .
.
Так как наше z-преобразование представляет собой
обычный фильтр дискретного времени N-го порядка(где N=M):
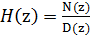 ,(z)=b0zN+ b1zN-1+
b2zN-2+…+ bN, D(z)=a0zN+ a1zN-1+ a2zN-2+…+ aN,
,(z)=b0zN+ b1zN-1+
b2zN-2+…+ bN, D(z)=a0zN+ a1zN-1+ a2zN-2+…+ aN,
ak и bk - коэффициенты фильтра.
Если функция H(z) имеет полюсы в точках z=p1,
p2,… pN и нули в точках z=z1, z2,… zN, то H(z) можно разложить на множители и
представить в виде:
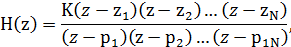
где zi- i-й нуль, pi- i-й полюс, а K-
коэффициент усиления.
Полюсы такого z-преобразования, как H(z), - это
значения z, в которых функция H(z) равна бесконечности. Значения г, в которых
H(z) равна нулю, называют нулями. Полюсы и нули функции H(Z) могут быть
действительными или комплексными. Если они комплексные, они идут
комплексно-сопряженными парами, чтобы коэффициенты ak и bk были
действительными. Если известны положения полюсов и нулей функции H(z), то и
саму функцию H(z) можно легко восстановить с точностью до константы.
Во-первых, выразим H(z) через положительные
показатели степени z, а затем разложим ее таким образом, чтобы можно было найти
полюсы и нули. Если умножить числитель и знаменатель на z3 - самую высокую
степень z, получится
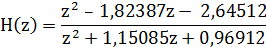
В результате разложения получаем
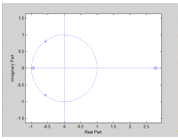
Рис. 2
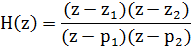
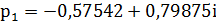 ,
,
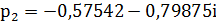 ,=2,77653,=
-0,95266.
,=2,77653,=
-0,95266.
Если необходимо знать полную частотную
характеристику, как правило, в передаточную функцию непосредственно подставляют
значение z=eiɷT и вычисляют получающееся в результате этого выражение:
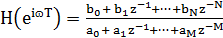 |z=eiɷT
|z=eiɷT 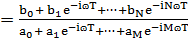 =
=
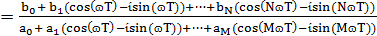 .
.
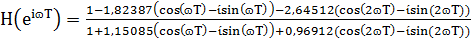 .
.
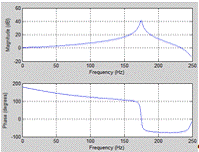
Рис. 3
=[1 -1.82387 -2.64512];=[1 1.15085
0.96912];(b,a,256,500)
Разностное уравнение описывает реальные
действия, которые система дискретного времени должна произвести над входными
данными во временной области, чтобы получить необходимый выход. Разностное
уравнение для большинства важных практических случаев можно записать в таком
виде:
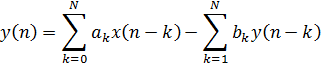
где x(n) - элемент входной последовательности,
y(n) - элемент выходной последовательности, y(n-k) - предыдущий выход, а ak, bk
- коэффициенты системы. Текущий выход y(n) получается из настоящего и прошлого
элементов входной последовательности и предыдущего выхода y(n-k).
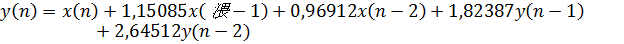
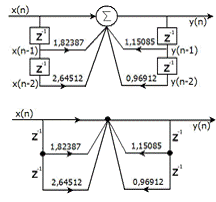
Рис. 4
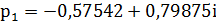 ,
,
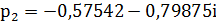 ,=0,98443, а θ=125,77°
,=0,98443, а θ=125,77°
Найденные величины соответствуют центральной
частоте:
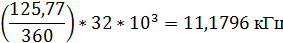
Далее квантуем коэффициенты до 8 бит. Поскольку
один коэффициент больше единицы, выделим 1 бит для хранения бита знака, 2 бита
- для целой части и 5 бит - для дробной части коэффициента. Таким образом,
после квантования коэффициенты приобретают такие значения:
=1,15085*25=36=100100=0,96912*25=31=11111
В дробной записи значения квантованных
коэффициентов имеют такой вид:
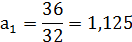
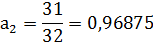
.5625 + 0.8077i
.5625 - 0.8077i
Новое положение полюса: r=0.98427, а θ=124.85°;
центральная
частота смещается в положение:
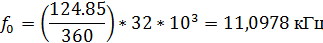
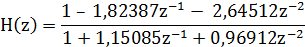
Коэффициенты знаменателя были проквантованы до B
бит (В=5,6,…,15),включая 1 бит знача и 2 бита для целой части. Затем для
каждого значения B были вычислены квантованные коэффициенты и положения полюсов
в полярных координатах.
Если при некоторой длине слова радиальное
расстояние от полюса до начала координат равно или превышает 1, возникает
потенциальная неустойчивость. При анализе было найдено, что для поддержания
устойчивости требуется не меньше В = 8 бит. Вообще, если полюс неквантованного
звена второго порядка лежит на окружности с радиусом r < 0,9, неустойчивость
маловероятна, если использовать длину слова 8 бит или больше. Пример расчета
для B=7 бит:
=1,15085*24+0,5=18,9136=18=0,96912*24+0,5=16,00592=16
В дробной записи:
a1=18/16=1.125. a2=16/16=1=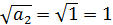
θ=arcos(-a1/2r)=
124.23∘
|
B
|
a1
|
a2
|
r
|
θ
|
Один
из полюсов
|
|
7
|
1.125
|
1
|
1
|
124.23∘
|
-0.5625+0.8268i
|
|
8
|
1.15625
|
0.96875
|
125.97∘
|
-0.5781+0.7966i
|
Масштабный множитель s1 на входе фильтра
выбирается так, чтобы предотвратить переполнение или снизить его вероятность на
выходе левого сумматора. Чтобы поддержать общее усиление фильтра на предыдущем
уровне, коэффициенты числителя умножаются на s1.
Существует три распространенных метода
определения подходящих масштабных множителей фильтра. В первом методе, который
часто называют нормой L1 масштабный множитель выбирается следующим образом:
коэффициент квантование множитель
фильтр
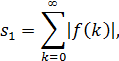
где f(k)- импульсная характеристика, связывающая
вход системы с выходом первого сумматора, т.е. узлом w(n). Выбранный таким
способом масштабный множитель s1 гарантирует, что общее усиление фильтра от
входа до узла w(n) равно единице, поэтому переполнение в w(n) невозможно. Для
получения импульсной характеристики f(k) можно вначале определить
соответствующую передаточную функцию F(z), а затем применить к ней обратное
z-преобразование.
Во втором методе, часто называемом нормой L2,
масштабный множитель s1 определяется следующим образом:
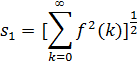
Нормировочный множитель L2 можно получить иначе,
использовав контурный интеграл
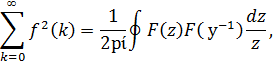
где F(z) - z-образ (результат применения
2-преобразования) 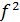 ,а
,а 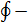 обозначает
контурный интеграл по единичной окружности
обозначает
контурный интеграл по единичной окружности
|z| =1. Вычисляя норму L2, получаем:
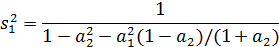
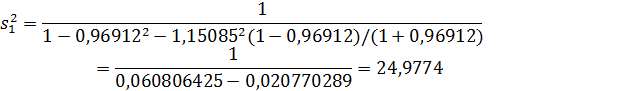
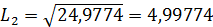
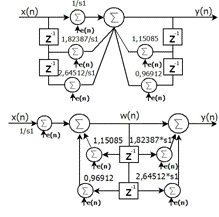
Рис. 5
Влияние шума квантования на производительность
фильтра зависит от типа используемой фильтрующей структуры и точки, в которой
квантуются результаты. Предполагается, что входные данные x(n), выход у(n) и
коэффициенты фильтра представляются как B-битовые числа (включая бит знака).
После умножения произведения квантуются до B бит путем округления (или
усечения).
Ошибка округления:
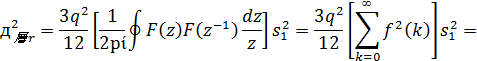
=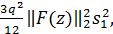
где

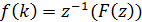
результат применения обратного z-преобразования
к F(z). Кроме того, f(k) - это импульсная характеристика каждого источника
шума, дающего вклад в выход фильтра,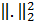 -
квадрат нормы L2, а q2/12 -мощность шума округления внутреннего произведения.
Общая мощность шума на выходе фильтра - это сумма мощности шума округления
произведений и мощности шума квантования АЦП:
-
квадрат нормы L2, а q2/12 -мощность шума округления внутреннего произведения.
Общая мощность шума на выходе фильтра - это сумма мощности шума округления
произведений и мощности шума квантования АЦП:
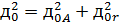
Предполагая, что источники шума не коррелируют,
общий вклад шума в полезный сигнал - это просто сумма отдельных шумовых
составляющих:
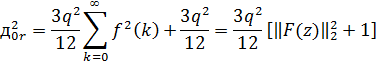
где f(k) - импульсная характеристика,
связывающая выход источника шума eх с выходом фильтра, а F(z) - соответствующая
передаточная функция:
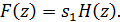
Общий шум (шум АЦП + шум округления) на выходе
фильтра записывается следующим образом:
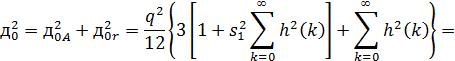
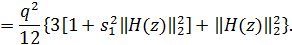
Использование масштабного множителя увеличивает
выходной шум.
Для определения выходной мощности шума,
порожденной ошибками округления, использовалась программа анализа эффектов конечной
разрядности:
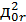 = 1448.55q2, где
предполагается использование нормы L2.
= 1448.55q2, где
предполагается использование нормы L2.
Из уравнения (7) выходной шум, порожденный АЦП,
равен 19.5318q2. Следовательно, общая мощность выходного шума равна:
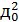 = (1448.55+
19.5318)q2= 1468,0818q2.
= (1448.55+
19.5318)q2= 1468,0818q2.
Выходная мощность сигнала (на входе
предполагается случайный сигнал) равна:
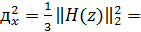 78,1270.
78,1270.
Отношение сигнал-шум (без ошибок округления)
равно:
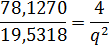
Отношение сигнал-шум (с ошибкой округления)
равно:
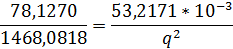
Ухудшение отношения сигнал-шум вследствие ошибки
округления равно:

ЗАКЛЮЧЕНИЕ
Создание цифрового фильтра является сложной
задачей, так как требует учёта многочисленных параметров и характеристик, а
также взаимосвязей между ними. Данную проблему необходимо решать, исходя из
принципа оптимального соотношения цены и качества.
ПРИЛОЖЕНИЕ
